Open Access Article
Open Access ArticleModulation of Fe–Fe distance and spin in diiron complexes using tetradentate ligands with different flanking donors†
Kyle D.
Spielvogel
a,
Emily J.
Campbell
 a,
Sabyasachi Roy
Chowdhury
a,
Sabyasachi Roy
Chowdhury
 b,
Florian
Benner
b,
Florian
Benner
 c,
Selvan
Demir
c,
Selvan
Demir
 c,
Gillian P.
Hatzis
d,
Hayley R.
Petras
c,
Gillian P.
Hatzis
d,
Hayley R.
Petras
 a,
Dunya
Sembukuttiarachchige
a,
James J.
Shepherd
a,
Dunya
Sembukuttiarachchige
a,
James J.
Shepherd
 a,
Christine M.
Thomas
a,
Christine M.
Thomas
 d,
Bess
Vlaisavljevich
d,
Bess
Vlaisavljevich
 ab and
Scott R.
Daly
ab and
Scott R.
Daly
 *a
*a
aThe University of Iowa, Department of Chemistry, E331 Chemistry Building, Iowa City, IA 52242, USA. E-mail: scott-daly@uiowa.edu
bThe University of South Dakota, Department of Chemistry, 414 E Clark St., Vermillion SD, 57069, USA
cMichigan State University, Department of Chemistry, 578 South Shaw Lane, East Lansing, Michigan 48824, USA
dThe Ohio State University, Department of Chemistry and Biochemistry, 100 West 18th Ave, Columbus, OH 43210, USA
First published on 19th July 2024
Abstract
Here we report the synthesis and characterization of diiron complexes containing triaryl N4 and N2S2 ligands derived from o-phenylenediamine. The complexes display significant differences in Fe–Fe distances and magnetic properties that depend on the identity of the flanking NMe2 and SMe donor groups.
Dinuclear iron complexes are renowned for their functional roles in metalloenzymes and biomimetic complexes.1 They are also highly relevant to efforts aimed at understanding chemical factors that govern the strength of metal–metal interactions with first-row transition metals, especially when combined with weak field ligands.2,3 These 3d complexes are often paramagnetic and adopt different spin configurations that depend sensitively on the degree of coupling between the metals. This has led to interest in understanding how ligand and structural modifications can be used to control spin states and associated magnetic properties for spin-based applications.3,4
Amido ligands have been featured prominently in efforts aimed at preparing dinuclear complexes with iron. Examples include Fe2[N(SiMe3)2]4 and related complexes that form a diamond Fe2N2 core in the solid state.5–7 Other examples include amido ligands containing appended metal-donor groups.8 These have been used most extensively to prepare diiron complexes that are C3 symmetric with respect to the Fe–Fe axis,9 but amido ligands derived from o-phenylenediamine have also been used to assemble iron complexes of various nuclearity. Betley and coworkers reported tripodal ligands containing three o-phenylenediamine units that can yield metal clusters containing up to six Fe atoms.10,11 Similarly, a dinuclear Fe2N2 complex containing N,N′-bis(pentafluorophenyl)-o-phenylenediamide was recently described.12
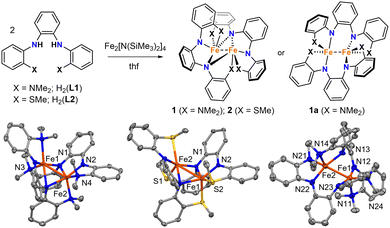
We previously reported the triaryl N4 and N2S2 ligands H2(L1) and H2(L2) (Fig. 1).13,14 Like the examples described above, these tetradentate ligands are derived from o-phenylenediamine, but they contain flanking aryl groups with NMe2 and SMe donor substituents. Here we report the synthesis and properties of homoleptic Fe(II) complexes with L1 and L2. Unlike previous examples with Ni and Ru,13,14 and prior studies of square-planar Fe(II) complexes with stronger field PNNP ligands,15 the aryl groups and donor atoms in L1 and L2 do not remain conjugated and coordinated in the same plane. Instead, they give rise to dinuclear Fe complexes with structures and spin configurations that are highly dependent on the identity of the flanking NMe2 and SMe donor groups.
Mixing H2(L1) or H2(L2) with in situ generated Fe2[N(SiMe3)2]4 in thf resulted in dark red solutions, and subsequent workup and crystallization by vapor diffusion of pentane into concentrated benzene solutions yielded large dark red crystals of 1 and 2. Both complexes were isolated as single crystals in good yields (67% and 85%, respectively).
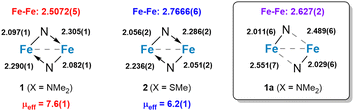
The dinuclear structures of 1 and 2 were revealed by single-crystal X-ray diffraction studies. Each complex has a butterfly Fe2N2 core supported by bridging amido groups on separate ligands (Fig. 1). The most apparent difference between the two structures is the Fe–Fe distances of 2.5072(5) and 2.7666(6) Å for 1 and 2, respectively (Fig. 2). The Fe–Fe distance in 1 is significantly shorter than those reported for amido-bridged complexes Fe2[N(SiMe3)2]4, Fe2[N(SiMe3)2]2[OC(CF3)2Ph]2, and Fe2(NPh2)4 at 2.663(2), 2.674(6), and 2.715(2) Å, respectively,6 and is effectively identical to the 2.5128(4) Å distance very recently reported for Fe2(TMP)2(C6F5)2 (TMP = tetramethylpiperidide).7 The distance corresponds to a formal shortness ratio (FSR) of 1.08, which is just beyond the range expected for a formal Fe–Fe single bond.3
The close Fe–Fe distances are supported by bridging, but inequivalent, Fe–N bonds in the Fe2N2 core. Each bridging amido group forms a covalent N–Fe bond (X-type donor) with one Fe and a dative N → Fe bond (L-type donor) with the other, as indicated by the differing Fe–N distances (Fig. 2). The Fe–N bonds in 2 are 0.04 Å shorter on average compared to those in 1.
Prior to assessing the magnetism of the complexes, unit cell checks were performed in addition to elemental analysis to confirm the purity of crystals obtained for different batches. It was during these checks that we discovered a second structural isomer of 1 in one of the batches prepared in the latter part of our investigation. To distinguish between the two structures, we will refer to the second isomer as 1a (Fig. 1). Crystals of both isomers were grown by vapor diffusion of pentane into benzene solutions of 1. Crystals of 1 with the intact Fe2N2 diamond core crystallize as relatively large blocks in the monoclinic space group P21/c with 1.5 equivalents of co-crystallized benzene, whereas 1a crystallizes as small irregular prisms in the triclinic space group P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) and has an equivalent of co-crystallized benzene and disordered solvent presumed to be pentane. The biggest change in the structure of 1a with respect to 1 is the opening of the Fe2N2 core. The L-type bonds associated with the amido bridges in 1 are no longer present in 1a. As a result, the Fe–Fe distance in 1 at 2.5072(5) Å elongates to 2.627(2) Å in 1a, and the X-type Fe–N bonds shorten by 0.05–0.08 Å. A second polymorph of 2 containing co-crystallized benzene was also discovered (2a), but unlike 1 and 1a, there were only subtle differences in their structures (Fig. S1, ESI†).
and has an equivalent of co-crystallized benzene and disordered solvent presumed to be pentane. The biggest change in the structure of 1a with respect to 1 is the opening of the Fe2N2 core. The L-type bonds associated with the amido bridges in 1 are no longer present in 1a. As a result, the Fe–Fe distance in 1 at 2.5072(5) Å elongates to 2.627(2) Å in 1a, and the X-type Fe–N bonds shorten by 0.05–0.08 Å. A second polymorph of 2 containing co-crystallized benzene was also discovered (2a), but unlike 1 and 1a, there were only subtle differences in their structures (Fig. S1, ESI†).
Magnetometry studies were performed to investigate the magnetic properties of 1 and 2. Given the possibility of two isomers for 1, we investigated the room temperature magnetic moments first in solution and then in the solid state on crystallographically authenticated samples of both complexes. Evans method magnetic measurements performed on benzene solutions of 1 and 2 revealed effective magnetic moments of 7.6 and 6.3 μB, respectively. Solid-state measurements made using a magnetic susceptibility balance at room temperature (294 K) yielded effectively identical magnetic moments of 7.6(1) μB for 1 and 6.2(1) μB for 2. This suggests that the differences in μeff for 1 and 2 cannot be attributed to phase-dependent differences in structure or crystal packing. It may also suggest that the structure of 1 persists in solution or that the structure of 1a has little influence on the magnetic moment.
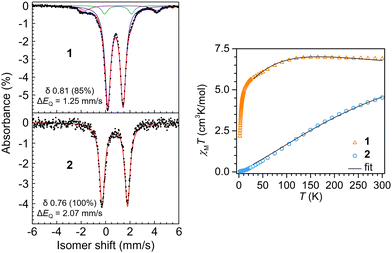
Dc magnetic susceptibility data were collected on polycrystalline samples of 1 and 2 using a SQUID magnetometer field of 1.0 T to measure the temperature dependence of the molar magnetic susceptibility times temperature (χMT vs. T) for each sample (Fig. 3). The room temperature effective magnetic moments of 7.43 μB (1) and 6.02 μB (2) are in excellent agreement with the moments determined via Evans method and susceptibility balance (Fig. S2–S5, ESI†). For 1, the room temperature χMT value of 6.900 cm3 K mol−1 remains largely unchanged when lowering the temperature to ∼110 K, below which a gradual decrease in χMT value of 5.002 cm3 K mol−1 is monitored (Fig. 3). Below ∼10 K a steep drop in χMT is observed, which is largely attributed to zero-field splitting and/or antiferromagnetic coupling. The magnetic data was modeled under consideration of a weak antiferromagnetic coupling interaction between the two Fe(II) centers with a J of −0.22(3) cm−1 (Table S2, ESI†). For 2, exhibiting the longer Fe–Fe distance, the trend in progression of the dc magnetic susceptibility data from 2 to 300 K varies significantly relative to 1. The room temperature χMT value is 4.528 cm3 K mol−1, which declines almost linearly with decreasing temperatures, resulting in a χMT value of 0.030 cm3 K mol−1 at 2 K, which is close to zero. Such static magnetic susceptibility behavior is indicative of strong antiferromagnetic coupling and hence, was modeled accordingly, yielding a J value of −37(1) cm−1. This magnitude of J represents a 168-fold increase in magnetic coupling for 2 compared to 1 despite the longer Fe–Fe distance in 2 (Table S3, ESI†).
57Fe Mössbauer spectra were collected on 1 and 2 to evaluate Fe oxidation states and electronic environment. The spectrum of 1 at 20 K revealed two quadrupole doublets (Fig. S6, ESI†). The major component (83%) had an isomer shift of δ 0.80 (ΔEQ = 1.25 mm s−1), consistent with high-spin Fe(II). A minor component was observed at a nearly identical isomer shift of δ 0.84, but it displayed a larger quadrupole splitting (2.43 mm s−1). Cooling the sample further to 4 K yielded no effective change in the major component (δ 0.81; 1.25 mm s−1; 85%), but the minor component appears to undergo additional hyperfine splitting (Fig. 3). As with our magnetic measurements, random unit cell checks of the crystal batch used for Mössbauer analysis were uniformly consistent with 1, but it is possible that the minor component could be attributed to small amounts of co-crystallized 1a. We think it is more likely that the minor component is attributed to a non-integer spin impurity, which would be consistent with the additional hyperfine splitting observed upon sample cooling.
The Mössbauer spectrum of 2 at 4 K revealed a quadrupole doublet that was modeled as a single high-spin Fe(II) species. The isomer shift of δ 0.76 is similar to the δ 0.81 shift for 1, but the spectrum for 2 displays a larger quadrupole splitting of 2.07 mm s−1. This increase is consistent with the reduction in spin due to the increased antiferromagnetic coupling. For example, Betley and coworkers showed that a reduction in S = 4 to S = 2 in o-phenylenediamido-supported triiron clusters capped with ancillary pyridine ligands at 105 K led to an increase in quadrupolar splitting from ΔEQ = 1.48 mm s−1 to ΔEQ = 2.22 mm s−1,11 but with nearly identical isomer shifts of δ 0.85 and 0.82, respectively, as observed for 1 and 2.
DFT calculations (B3LYP-D3/def2-TZVP)16 were performed to evaluate the energies and structural preferences of 1 with respect to 1a. All attempts to optimize 1 resulted in geometries with bond distances consistent with 1a, indicating that this species lies lower in energy (Tables S4–S6, ESI†). The DFT calculated Fe–Fe distance for 1a was 2.687 Å, only a 0.060 Å (2.3%) deviation from experiment. To calculate the structure of 1, the Fe atoms were fixed at their experimental positions while the remaining ligand atoms were allowed to relax. This fixed species, which is denoted herein as 1′, is nearly 3 kcal mol−1 higher in energy than 1a according to DFT (Tables S5 and S6, ESI†). Likewise, CASPT217 calculations yielded a consistent energy difference of 5.6 kcal mol−1 (Table S5, ESI†). These relatively small energy differences agree with our ability to isolate both structures.
Geometry optimizations of 2 also yielded a structure in excellent agreement with experiment (Fe–Fe distance of 2.807 Å; 0.040 Å (1.5%) deviation from XRD), as shown with overlays of the computed and experimental structures (Fig. S10, ESI†). Although DFT optimizations were performed only for the S = 4 DFT ground state (Tables S7 and S8, ESI†), CASPT2 calculations revealed that the lowest energy spin configuration for 1′, 1a, and 2 was S = 0 (Table S9, ESI†). However, the other spin states (S = 1, 2, 3, and 4) were all within 1.2 kcal mol−1, which falls within the error of the CASPT2 method. This indicates that the assignment of the ground spin state would require careful treatment of both spin–orbit coupling and electron correlation. The observation of closely spaced spin multiplets is consistent with no interaction between the Fe centers, as can be seen in the CASSCF natural orbitals (Fig. S8, ESI†). On the other hand, some orbital overlap is present in DFT (Fig. S9, ESI†), resulting in a Mayer bond-order between the metal ions of 0.1 for 1′ and 1a and 0.05 for 2 (Table S10, ESI†). These differing observations are consistent with the more localized bonding in the CASSCF natural orbitals, which suggest no Fe–Fe bonding, compared to the DFT Kohn–Sham orbitals, which suggest the existence of very weak Fe–Fe bonding.
In summary, we have described how triaryl tetradentate ligands derived from o-phenylenediamine form diiron complexes that have Fe–Fe distances and magnetic properties that are highly sensitive to the identity of the flanking donor substituents. These results compliment studies showing how ancillary ligand field strength can significantly alter Fe–Fe distances and spin states in triiron complexes supported by hexadentate ligands derived from o-phenylenediamine.11 Rather than using ancillary ligands, we have shown here that exchanging flanking donors can be used to achieve similar outcomes. In addition to our ongoing studies with iron, we are currently investigating these dinucleating ligand effects with other first-row transition metals. These efforts will be described in several upcoming reports.
KDS, DS, and SRD thank the NSF for support (CHE-1650894), and Dale Swenson for collecting the XRD data. The structure of 1a was collected using the instrument supported by NSF CHE-1828117. JJS, HRP, and EJC thank the University of Iowa for support. GPH and CMT acknowledge the NSF for support (CHE-2101002). SD and FB also thank the NSF for support through the CAREER award to SD (CHE-2339595). SRC and BV thank the U.S. DOE, Office of Science, BES, Computational Chemical Sciences program for support under award number DE-SC0019463. Computations supporting this project performed on high-performance computing systems were made possible by resources funded by NSF award OAC-1626516.
Data availability
Input and output files associated with all calculations are available both in a FigShare repository (https://doi.org/10.6084/m9.figshare.26121724) and in an ioChem-BD repository (https://doi.org/10.19061/iochem-bd-6-379). Crystallographic data has been deposited at the CCDC under 2357235–2357238. The remaining data have been included as part of the ESI.†Conflicts of interest
There are no conflicts to declare.Notes and references
- (a) A. J. Jasniewski and L. Que, Jr., Chem. Rev., 2018, 118, 2554–2592 CrossRef CAS PubMed; (b) Y. Li and T. B. Rauchfuss, Chem. Rev., 2016, 116, 7043–7077 CrossRef CAS PubMed; (c) T. B. Rauchfuss, Acc. Chem. Res., 2015, 48, 2107–2116 CrossRef CAS PubMed; (d) P. A. Lindahl, J. Inorg. Biochem., 2012, 106, 172–178 CrossRef CAS PubMed; (e) L. H. Do and S. J. Lippard, J. Inorg. Biochem., 2011, 105, 1774–1785 CrossRef CAS PubMed; (f) S. Friedle, E. Reisner and S. J. Lippard, Chem. Soc. Rev., 2010, 39, 2768–2779 RSC.
- (a) R. J. Eisenhart, L. J. Clouston and C. C. Lu, Acc. Chem. Res., 2015, 48, 2885–2894 CrossRef CAS PubMed; (b) R. H. Duncan Lyngdoh, H. F. Schaefer, III and R. B. King, Chem. Rev., 2018, 118, 11626–11706 CrossRef CAS PubMed.
- J. A. Chipman and J. F. Berry, Chem. Rev., 2020, 120, 2409–2447 CrossRef CAS PubMed.
- H. Oshio and M. Nihei, Bull. Chem. Soc. Jpn., 2007, 80, 608–620 CrossRef CAS.
- (a) R. A. Andersen, K. Faegri, Jr., J. C. Green, A. Haaland, M. F. Lappert, W. P. Leung and K. Rypdal, Inorg. Chem., 1988, 27, 1782–1786 CrossRef CAS; (b) S. Takemoto, S.-I. Ogura, H. Yo, Y. Hosokoshi, K. Kamikawa and H. Matsuzaka, Inorg. Chem., 2006, 45, 4871–4873 CrossRef CAS PubMed; (c) R. A. Lewis, S. Morochnik, A. Chapovetsky, G. Wu and T. W. Hayton, Angew. Chem., Int. Ed., 2012, 51, 12772–12775 CrossRef CAS PubMed; (d) T. Deschner, K. W. Törnroos and R. Anwander, Inorg. Chem., 2011, 50, 7217–7228 CrossRef CAS PubMed; (e) L. M. Aguirre Quintana, Y. Yang, A. Ramanathan, N. Jiang, J. Bacsa, L. Maron and H. S. La Pierre, Chem. Commun., 2021, 57, 6664–6667 RSC; (f) R. Köster, G. Seidel, R. Boese and B. Wrackmeyer, Chem. Ber., 1987, 120, 669–683 CrossRef; (g) T. Hatakeyama, R. Imayoshi, Y. Yoshimoto, S. K. Ghorai, M. Jin, H. Takaya, K. Norisuye, Y. Sohrin and M. Nakamura, J. Am. Chem. Soc., 2012, 134, 20262–20265 CrossRef CAS PubMed; (h) C. Ni, G. J. Long, F. Grandjean and P. P. Power, Inorg. Chem., 2009, 48, 11594–11600 CrossRef CAS PubMed; (i) S. Ohta, Y. Ohki, Y. Ikagawa, R. Suizu and K. Tatsumi, J. Organomet. Chem., 2007, 692, 4792–4799 CrossRef CAS.
- (a) M. M. Olmstead, P. P. Power and S. C. Shoner, Inorg. Chem., 1991, 30, 2547–2551 CrossRef CAS; (b) M. A. Chacon-Teran, S. E. Creutz, R. E. Rodriguez-Lugo, S. Demeshko, F. Meyer, A. Kajetanowicz and K. Grela, Organometallics, 2024, 43, 564–572 CrossRef CAS.
- A. Logallo, L. C. H. Maddock, M. Mu, L. Gravogl, N. Jin, M. N. Peñas-Defrutos, K. Meyer, M. García-Melchor and E. Hevia, Angew. Chem., Int. Ed., 2024, e202402907 CAS.
- (a) A. J. Elias, H. W. Roesky, W. T. Robinson and G. M. Sheldrick, J. Chem. Soc., Dalton Trans., 1993, 495–500 RSC; (b) J. Chai, H. Zhu, Q. Ma, Roesky, W. Herbert, H.-G. Schmidt and M. Noltemeyer, Eur. J. Inorg. Chem., 2004, 4807–4811 CrossRef CAS; (c) C. Koch, A. Malassa, C. Agthe, H. Görls, R. Biedermann, H. Krautscheid and M. Westerhausen, Z. Anorg. Allg. Chem., 2007, 633, 375–382 CrossRef CAS; (d) A. K. Das, Z. Moatazedi, G. Mund, A. J. Bennet, R. J. Batchelor and D. B. Leznoff, Inorg. Chem., 2007, 46, 366–368 CrossRef CAS PubMed; (e) A. Malassa, N. Herzer, H. Görls and M. Westerhausen, Dalton Trans., 2010, 39, 5356–5366 RSC.
- (a) J. P. Krogman and C. M. Thomas, Chem. Commun., 2014, 50, 5115–5127 RSC; (b) F. A. Cotton, L. M. Daniels, L. R. Falvello and C. A. Murillo, Inorg. Chim. Acta, 1994, 219, 7–10 CrossRef CAS; (c) F. A. Cotton, L. M. Daniels, L. R. Falvello, J. H. Matonic and C. A. Murillo, Inorg. Chim. Acta, 1997, 256, 269–275 CrossRef CAS; (d) C. M. Zall, D. Zherebetskyy, A. L. Dzubak, E. Bill, L. Gagliardi and C. C. Lu, Inorg. Chem., 2012, 51, 728–736 CrossRef CAS PubMed; (e) S. Kuppuswamy, T. M. Powers, B. M. Johnson, M. W. Bezpalko, C. K. Brozek, B. M. Foxman, L. A. Berben and C. M. Thomas, Inorg. Chem., 2013, 52, 4802–4811 CrossRef CAS PubMed; (f) S. Kuppuswamy, T. M. Powers, J. P. Krogman, M. W. Bezpalko, B. M. Foxman and C. M. Thomas, Chem. Sci., 2013, 4, 3557–3565 RSC; (g) S. Kuppuswamy, M. W. Bezpalko, T. M. Powers, M. J. T. Wilding, C. K. Brozek, B. M. Foxman and C. M. Thomas, Chem. Sci., 2014, 5, 1617–1626 RSC; (h) B. Wu, M. J. T. Wilding, S. Kuppuswamy, M. W. Bezpalko, B. M. Foxman and C. M. Thomas, Inorg. Chem., 2016, 55, 12137–12148 CrossRef CAS PubMed; (i) S. M. Greer, J. McKay, K. M. Gramigna, C. M. Thomas, S. A. Stoian and S. Hill, Inorg. Chem., 2018, 57, 5870–5878 CrossRef CAS PubMed; (j) B. A. Barden, G. Culcu, J. P. Krogman, M. W. Bezpalko, G. P. Hatzis, D. A. Dickie, B. M. Foxman and C. M. Thomas, Inorg. Chem., 2019, 58, 821–833 CrossRef CAS PubMed; (k) S. M. Greer, K. M. Gramigna, C. M. Thomas, S. A. Stoian and S. Hill, Inorg. Chem., 2020, 59, 18141–18155 CrossRef CAS PubMed; (l) L. J. Clouston, R. B. Siedschlag, P. A. Rudd, N. Planas, S. Hu, A. D. Miller, L. Gagliardi and C. C. Lu, J. Am. Chem. Soc., 2013, 135, 13142–13148 CrossRef CAS PubMed; (m) C. M. Zall, L. J. Clouston, V. G. Young, Jr., K. Ding, H. J. Kim, D. Zherebetskyy, Y.-S. Chen, E. Bill, L. Gagliardi and C. C. Lu, Inorg. Chem., 2013, 52, 9216–9228 CrossRef CAS PubMed; (n) S. J. Tereniak, R. K. Carlson, L. J. Clouston, V. G. Young, E. Bill, R. Maurice, Y.-S. Chen, H. J. Kim, L. Gagliardi and C. C. Lu, J. Am. Chem. Soc., 2014, 136, 1842–1855 CrossRef CAS PubMed; (o) R. C. Cammarota and C. C. Lu, J. Am. Chem. Soc., 2015, 137, 12486–12489 CrossRef CAS PubMed; (p) L. J. Clouston, V. Bernales, R. C. Cammarota, R. K. Carlson, E. Bill, L. Gagliardi and C. C. Lu, Inorg. Chem., 2015, 54, 11669–11679 CrossRef CAS PubMed; (q) R. J. Eisenhart, P. A. Rudd, N. Planas, D. W. Boyce, R. K. Carlson, W. B. Tolman, E. Bill, L. Gagliardi and C. C. Lu, Inorg. Chem., 2015, 54, 7579–7592 CrossRef CAS PubMed; (r) D. L. Miller, R. B. Siedschlag, L. J. Clouston, V. G. Young, Y.-S. Chen, E. Bill, L. Gagliardi and C. C. Lu, Inorg. Chem., 2016, 55, 9725–9735 CrossRef CAS PubMed; (s) J. T. Moore, S. Chatterjee, M. Tarrago, L. J. Clouston, S. Sproules, E. Bill, V. Bernales, L. Gagliardi, S. Ye, K. M. Lancaster and C. C. Lu, Inorg. Chem., 2019, 58, 6199–6214 CrossRef CAS PubMed; (t) J. R. Prat, C. A. Gaggioli, R. C. Cammarota, E. Bill, L. Gagliardi and C. C. Lu, Inorg. Chem., 2020, 59, 14251–14262 CrossRef CAS PubMed; (u) R. C. Cammarota, L. J. Clouston and C. C. Lu, Coord. Chem. Rev., 2017, 334, 100–111 CrossRef CAS; (v) A. Z. Spentzos, S. R. May, A. M. Confer, M. R. Gau, P. J. Carroll, D. P. Goldberg and N. C. Tomson, Inorg. Chem., 2023, 62, 11487–11499 CrossRef CAS PubMed.
- (a) T. D. Harris and T. A. Betley, J. Am. Chem. Soc., 2011, 133, 13852–13855 CrossRef CAS PubMed; (b) T. D. Harris, Q. Zhao, R. Hernandez Sanchez and T. A. Betley, Chem. Commun., 2011, 47, 6344–6346 RSC; (c) T. M. Powers, A. R. Fout, S.-L. Zheng and T. A. Betley, J. Am. Chem. Soc., 2011, 133, 3336–3338 CrossRef CAS PubMed; (d) Q. Zhao and T. A. Betley, Angew. Chem., Int. Ed., 2011, 50, 709–712 CrossRef CAS PubMed; (e) Q. Zhao, T. D. Harris and T. A. Betley, J. Am. Chem. Soc., 2011, 133, 8293–8306 CrossRef CAS PubMed; (f) E. V. Eames and T. A. Betley, Inorg. Chem., 2012, 51, 10274–10278 CrossRef CAS PubMed; (g) E. V. Eames, R. Hernandez Sanchez and T. A. Betley, Inorg. Chem., 2013, 52, 5006–5012 CrossRef CAS PubMed; (h) T. M. Powers and T. A. Betley, J. Am. Chem. Soc., 2013, 135, 12289–12296 CrossRef CAS PubMed; (i) T. M. Powers, N. X. Gu, A. R. Fout, A. M. Baldwin, R. Hernandez Sanchez, D. M. Alfonso, Y.-S. Chen, S.-L. Zheng and T. A. Betley, J. Am. Chem. Soc., 2013, 135, 14448–14458 CrossRef CAS PubMed; (j) R. Hernandez Sanchez and T. A. Betley, J. Am. Chem. Soc., 2015, 137, 13949–13956 CrossRef CAS PubMed; (k) R. Hernandez Sanchez, A. M. Willis, S.-L. Zheng and T. A. Betley, Angew. Chem., Int. Ed., 2015, 54, 12009–12013 CrossRef PubMed; (l) R. Hernandez Sanchez, A. K. Bartholomew, T. M. Powers, G. Menard and T. A. Betley, J. Am. Chem. Soc., 2016, 138, 2235–2243 CrossRef CAS PubMed; (m) R. Hernandez Sanchez and T. A. Betley, J. Am. Chem. Soc., 2018, 140, 16792–16806 CrossRef PubMed.
- E. V. Eames, T. D. Harris and T. A. Betley, Chem. Sci., 2012, 3, 407–415 RSC.
- A. Hernán-Gómez, M. Rodríguez, T. Parella and M. Costas, Angew. Chem., Int. Ed., 2019, 58, 13904–13911 CrossRef PubMed.
- (a) K. D. Spielvogel, N. C. Stumme, T. V. Fetrow, L. Wang, J. A. Luna, J. M. Keith, S. K. Shaw and S. R. Daly, Inorg. Chem., 2022, 61, 2391–2401 CrossRef CAS PubMed; (b) K. D. Spielvogel, J. A. Luna, S. M. Loria, L. P. Weisburn, N. C. Stumme, M. R. Ringenberg, G. Durgaprasad, J. M. Keith, S. K. Shaw and S. R. Daly, Inorg. Chem., 2020, 59, 10845–10853 CrossRef CAS PubMed; (c) G. Durgaprasad, J. A. Luna, K. D. Spielvogel, C. Haas, S. K. Shaw and S. R. Daly, Organometallics, 2017, 36, 4020–4031 CrossRef CAS.
- K. D. Spielvogel, E. J. Coughlin, H. Petras, J. A. Luna, A. Benson, C. M. Donahue, A. Kibasa, K. Lee, R. Salacinski, S. C. Bart, S. K. Shaw, J. J. Shepherd and S. R. Daly, Inorg. Chem., 2019, 58, 12756–12774 CrossRef CAS PubMed.
- (a) G. P. Hatzis and C. M. Thomas, Chem. Commun., 2020, 56, 8611–8614 RSC; (b) K. Lee and C. M. Thomas, Inorg. Chem., 2021, 60, 17348–17356 CrossRef CAS PubMed; (c) J. E. Stevens, C. E. Moore and C. M. Thomas, J. Am. Chem. Soc., 2023, 145, 794–799 CrossRef CAS PubMed.
- (a) A. D. Becke, J. Chem. Phys., 1996, 104, 1040–1046 CrossRef CAS; (b) A. D. Becke, J. Chem. Phys., 1997, 107, 8554–8560 CrossRef CAS; (c) C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789 CrossRef CAS PubMed; (d) F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC; (e) E. Caldeweyher, C. Bannwarth and S. Grimme, J. Chem. Phys., 2017, 147, 034112 CrossRef PubMed.
- (a) K. Andersson, P. Å. Malmqvist and B. O. Roos, J. Chem. Phys., 1992, 96, 1218–1226 CrossRef CAS; (b) K. Andersson, P. A. Malmqvist, B. O. Roos, A. J. Sadlej and K. Wolinski, J. Phys. Chem., 1990, 94, 5483–5488 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Experimental and computational details. CCDC 2357235–2357238. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d4cc02522a |
| This journal is © The Royal Society of Chemistry 2024 |