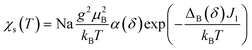Open Access Article
Open Access ArticleA tetrathiafulvalene salt of the nitrite (NO2−) anion: investigations of the spin-Peierls phase†
Loïc
Soriano
a,
Maylis
Orio
 b,
Olivier
Pilone
a,
Olivier
Jeannin
b,
Olivier
Pilone
a,
Olivier
Jeannin
 c,
Eric
Reinheimer‡
c,
Nicolas
Quéméré
c,
Pascale
Auban-Senzier
d,
Marc
Fourmigué
c,
Eric
Reinheimer‡
c,
Nicolas
Quéméré
c,
Pascale
Auban-Senzier
d,
Marc
Fourmigué
 *c and
Sylvain
Bertaina
*c and
Sylvain
Bertaina
 *a
*a
aCNRS, Aix-Marseille Université, IM2NP (UMR 7334), Institut Matériaux Microélectronique et Nanosciences de Provence, F-13397, Marseille, France. E-mail: sylvain.bertaina@cnrs.fr
bCNRS, Aix-Marseille Université, Centrale Marseille, ISM2, Institut des sciences moléculaires de Marseille, F-13397, Marseille, France
cUniversité de Rennes, CNRS, ISCR (Institut des Sciences Chimiques de Rennes), F-35042, Rennes, France. E-mail: marc.fourmigue@univ-rennes1.fr
dLaboratoire de Physique des Solides, Université Paris-Saclay, CNRS, UMR 8502, Orsay, 91405, France
First published on 24th January 2023
Abstract
Electrocrystallization of ortho-dimethyltetrathiafulvalene (o-DMTTF) in the presence of a nitrite (NO2−) anion affords a 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 phase, namely (o-DMTTF)2NO2, the first example of an isolated cation radical salt with NO2−. The o-DMTTF molecule organizes into strongly dimerized stacks that adopt a rare chessboard organization, associated with a strongly 1D structure. As a consequence of dimerization, the salt exhibits a semiconducting behavior (σRT = 5 S cm−1, Eact = 0.1 eV). The bent NO2− anion is disordered on the inversion center but does not exhibit any anion-ordering transition. Combined SQUID magnetometry and electron paramagnetic resonance (EPR) experiments demonstrate the appearance of a spin-Peierls transition with TSP = 70 K. The temperature dependence of the spin gap and associated dimerization parameter δ across the spin-Peierls transition have been determined. The low-temperature narrow EPR line observed below TSP is attributable to intrinsic magnetic defects localized on the o-DMTTF molecules themselves. The broadening of the EPR line at higher magnetic fields is associated with the disordered NO2− anions surrounding these magnetic defects, contributing to the inhomogeneity of their g factor.
1 phase, namely (o-DMTTF)2NO2, the first example of an isolated cation radical salt with NO2−. The o-DMTTF molecule organizes into strongly dimerized stacks that adopt a rare chessboard organization, associated with a strongly 1D structure. As a consequence of dimerization, the salt exhibits a semiconducting behavior (σRT = 5 S cm−1, Eact = 0.1 eV). The bent NO2− anion is disordered on the inversion center but does not exhibit any anion-ordering transition. Combined SQUID magnetometry and electron paramagnetic resonance (EPR) experiments demonstrate the appearance of a spin-Peierls transition with TSP = 70 K. The temperature dependence of the spin gap and associated dimerization parameter δ across the spin-Peierls transition have been determined. The low-temperature narrow EPR line observed below TSP is attributable to intrinsic magnetic defects localized on the o-DMTTF molecules themselves. The broadening of the EPR line at higher magnetic fields is associated with the disordered NO2− anions surrounding these magnetic defects, contributing to the inhomogeneity of their g factor.
10th Anniversary StatementJ. Mater. Chem. C provides a unique forum to present our progress on molecular conducting materials, establishing a bridge between organic/coordination chemistry and solid-state physics, building on the competences of both fields to unravel the solid-state properties of radical species, with emphasis on not only electronic but also structural characteristics and their associated phase transitions. The legitimate search for converting a material into a device (optical, magnetic or electronic) does not hinder the journal to welcome more fundamental results, a very important point as the original chemical systems presented in J. Mater Chem. C are often sources of inspiration to address other topics relevant to the sister journals J. Mater. Chem. A (energy and sustainability) and J. Mater. Chem. B (biology and medicine). We wish all the best to the journal on the occasion of this 10th anniversary and thanks all members of the editorial office for their efforts and commitment. |
1. Introduction
The spin-Peierls transition is a second-order phase transition associated with crystal lattice distortion in quasi-one-dimensional antiferromagnetic materials. Below the spin-Peierls temperature (TSP), deformation appears and the antiferromagnetic exchange coupling within the magnetic chain is no longer uniform (J) but alternated (J1 and J2). A temperature-dependent energy gap Δ(T) then forms between the fundamental energy level and a quasi-continuum of energy levels. By lowering the temperature, the magnetic susceptibility tends towards zero. First predicted in 1970,1–3 this type of transition can take place upon cooling in uniform, antiferromagnetically coupled spin chains to stabilize the fundamental level of energy and lift its degeneracy. In 1975, the first observation of a spin-Peierls transition was made by Bray et al. on the [TTF][CuS4C4(CF3)4] material below TSP = 12 K.4,5 Since then, spin-Peierls transitions have been mainly observed in organic conductors such as tetracyanoquinodimethane (TCNQ) salts6 or Fabre (TMTTF = tetramethyltetrathiafulvalene) salts,7 as well as certain inorganic compounds such as CuGeO38 or TiOX (X = Cl or Br).9,10 In (TMTTF)2PF6, it has been observed by the elastic scattering of neutrons11 at TSP = 18 K and in (TMTTF)2AsF6 at TSP = 13 K. Based on continuous-wave EPR measurements, we recently revealed that the spin dynamics in the low-temperature regime in Fabre salts was dominated by defects within spin-dimerized chains.12 Such defects polarize the antiferromagnetically coupled spins in their vicinity, thereby leading to a finite, local alternating magnetization around the defect site, which can be described as a soliton, i.e., a spin-½ quasi-particle comprising many correlated spins, pinned to the defect. Moreover, details of spin dynamics deep in this spin-Peierls phase were investigated by pulse ESR experiments, which revealed Rabi oscillations as signatures of coherent spin dynamics. However, there are limits in the possibilities of pulsed EPR measurements as no spin echo could be observed. Also, (TMTTF)2X salts have low spin-Peierls transition temperatures (10–20 K), which limits the temperature study of relaxation and coherence times.In this respect, a novel family of TTF derivatives, originally reported in 1983,13 is based on a non-centrosymmetric TTF, namely, ortho-dimethyltetrathiafulvalene, abbreviated as o-DMTTF here. The halide salts of o-DMTTF adopt a 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 stoichiometry,14 namely, (o-DMTTF)2X (X = Cl, Br, I), with a striking quadratic structure (space group I
1 stoichiometry,14 namely, (o-DMTTF)2X (X = Cl, Br, I), with a striking quadratic structure (space group I![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) 2d; Fig. 1), characterized with uniform o-DMTTF stacks organized in a chessboard-like pattern, with a 90° rotation of the long molecular axis in the nearest-neighbor stacks. This original structure gives the salts a highly 1D character and a metallic behavior at room temperature (RT).
2d; Fig. 1), characterized with uniform o-DMTTF stacks organized in a chessboard-like pattern, with a 90° rotation of the long molecular axis in the nearest-neighbor stacks. This original structure gives the salts a highly 1D character and a metallic behavior at room temperature (RT).
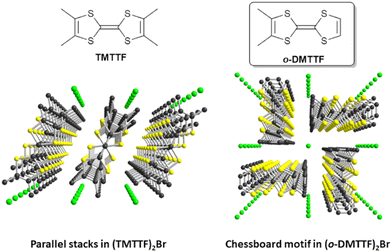 | ||
| Fig. 1 Comparative solid-state organizations of the mixed-valence stacks in the Fabre salt (TMTTF)2Br (left) and (o-DMTTF)2Br (right). | ||
Their temperature–pressure phase diagrams have been established by Foury et al. up to 1.8 GPa,15 demonstrating the appearance of a spin-Peierls transition at a much higher temperature (TSP = 50 K) than in (TMTTF)2PF6 (TSP = 19 K), which itself has the highest TSP value of the (TMTTF)2X series. In these o-DMTTF halides, the spin dynamics in the low-temperature regime is also dominated by solitons,16 and pulse ESR experiments in the spin-Peierls phase revealed Rabi oscillations as signatures of coherent spin dynamics. Further studies17 gave access to the temperature dependence of intrachain coupling Jeff(T), the temperature dependence of the dimerization parameter and the gap across the spin-Peierls transition, and the content of spin-chain defects. We also showed that one-half of the total number of solitons are isolated (as singlets), whereas the other half forms pairs (soliton dimers) with a strong magnetic coupling.
Looking for other salts with a similar structure and potentially even higher SP transition temperatures, we investigated the nitrate (NO3−) salt, i.e., (o-DMTTF)2NO3.18 It crystallized in a lower-symmetry monoclinic space group (P21/c), preserving the chessboard-like pattern (Fig. 1) found in (o-DMTTF)X (X = Cl, Br, I). The stacks are, however, now strongly dimerized, and the NO3− anion is disordered on the inversion center, with the nitrogen atom at the center, and the anion rotating around the fixed N atom. This semiconducting salt exhibits two decoupled phase transitions, an anion ordering one at 124 K and a spin-Peierls one at 90 K, which is an original feature compared with TMTTF salts with non-centrosymmetric anions such as BF4−, ClO4−, and ReO4−, where both transitions are coupled and observed at the same temperature.
To potentially avoid the disorder problems and anion-ordering processes encountered with the NO3− anion, we considered the use of the smaller nitrite (NO2−) anion. Surprisingly, this anion has never been isolated in cation radical salts, perhaps owing to its known reducing character. For example, the electrogenerated perylene cation radical is known to instantaneously react with a nitrite ion in a 100% electron transfer process, yielding perylene and dinitrogen tetroxide.19 The reaction between the two latter species leads to the formation of mononitroperylenes in excellent yields. Further, while working on similar naphthalene nitration, the electrochemical investigations of NO2− alone in CH3CN showed that the anion oxidizes around +0.50 V vs. SCE,20,21 while perylene oxidizes at +0.85 V and naphthalene at +1.62 V. It follows that the cation radicals of organic donor molecules oxidizing below +0.5 V vs. SCE should be stable in the presence of NO2−. Indeed, we have found that acetonitrile solutions of tetrabutylammonium nitrite could be used as an electrolyte to successfully perform electrocrystallization experiments with TTF derivatives oxidizing below +0.5 V. Here, we report the structure of the 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mixed-valence salt (o-DMTTF)2NO2, together with its transport and magnetic properties. Inspired by the observation of solitons and soliton dimers in the spin-Peierls phase of quadratic halide salts with the same donor molecule (o-DMTTF)2X (X = Cl, Br, I),16,17 by using EPR here, we comprehensively analyze the characteristics of the SP phase of (o-DMTTF)2NO2, taking advantage of the very high transition temperature found in this salt at TSP = 70 K.
1 mixed-valence salt (o-DMTTF)2NO2, together with its transport and magnetic properties. Inspired by the observation of solitons and soliton dimers in the spin-Peierls phase of quadratic halide salts with the same donor molecule (o-DMTTF)2X (X = Cl, Br, I),16,17 by using EPR here, we comprehensively analyze the characteristics of the SP phase of (o-DMTTF)2NO2, taking advantage of the very high transition temperature found in this salt at TSP = 70 K.
2. Experimental section
2.1 Synthesis
Here, o-DMTTF was prepared as previously described22 and TBA nitrite was obtained from Aldrich and used as received. The electrocrystallization of o-DMTTF (10 mg) was performed in two-compartment cells with Pt electrodes (length: 15 mm; diameter: 1 mm) in dry CH3CN (10 mL) containing TBA nitrite (100 mg) as the electrolyte, at a constant current (1 μA) and low temperature (5 °C). The crystals were harvested after ten days and washed with cold dry CH3CN.2.2 Structural characterization
A crystal of (o-DMTTF)2NO2 suitable for X-ray diffraction single-crystal experiment was selected and mounted with a cryoloop on the goniometer head of a D8 Venture diffractometer equipped with a (CMOS) PHOTON 100 detector, using Mo-Kα radiation (λ = 0.71073 Å; multilayer monochromator). The structure was solved by a dual-space algorithm using the SHELXT program,23 and then refined with full-matrix least-squares methods based on F2 (SHELXL program).24 All the non-hydrogen atoms were refined with anisotropic atomic displacement parameters. The H atoms were finally included in their calculated positions using the AFIX 137 procedure and treated as riding on their parent atom with constrained thermal parameters. Crystallographic data. C16H16NO2S8, M = 510.78, monoclinic, a = 6.9491(6), b = 12.3251(10), c = 12.0663(9) Å, β = 103.318(3)°, U = 1005.67(14) Å3, T = 150(2) K, space group P21/c (no. 14), Z = 2, 15795 reflections measured, 2295 unique (Rint = 0.0434), which were used in all the calculations. The final wR(F2) was 0.0386 (all data).2.3 Magnetic susceptibility measurements
The magnetic measurements were performed with a SQUID magnetometer MPMS-XL from Quantum Design, in the temperature range from 2 to 300 K. A large number of single crystals were harvested from several electrochemical cells to reach 37.35 mg of (o-DMTTF)2NO2 and enclosed in a Teflon pocket. The contribution from the Teflon bag as well as the diamagnetism of (o-DMTTF)2NO2 have been subtracted. The temperature dependence of susceptibility has been performed under a magnetic field of 5 T.2.4 Electron paramagnetic resonance
Electron paramagnetic resonance measurements have been performed using a conventional Bruker EMX spectrometer operating in the X band (about 9.39 GHz). A single crystal of (o-DMTTF)2NO2 was glued on a Suprasil rod using Apiezon grease. The sample holder was attached to an automatic goniometer and the sample was centered in the cavity. The temperature was controlled using an Oxford ITC and ESR900 cryostat. The low-temperature measurements were performed using a cryogen-free Stinger system from ColdEdge, allowing to reach 7 K of base temperature.2.5 Theoretical calculations
The tight-binding βHOMO–HOMO interaction energy calculations were based on the effective one-electron Hamiltonian of the extended Hückel method,25 as implemented in the Caesar 1.0 chain of programs.26 The off-diagonal matrix elements of the Hamiltonian were calculated according to the modified Wolfsberg–Helmholtz formula.27 All the valence electrons were explicitly taken into account in the calculations and the basis set consisted of double-ζ Slater-type orbitals for all the atoms except for H (simple-ζ Slater-type orbital) using the Roothaan–Hartree–Fock wave functions of Clementi & Roetti.28All the other theoretical calculations were based on density functional theory (DFT) calculations and were performed with the ORCA program package.29 Geometry optimization and electronic structure calculations were undertaken using the hybrid functional B3LYP30,31 in combination with the TZV/P basis set for all the atoms,32 and by taking advantage of the resolution of identity (RI) approximation in the Split-RI-J variant33 with the appropriate Coulomb fitting sets.34 Increased integration grids (Grid4 and GridX4 in ORCA convention) and tight SCF convergence criteria were used in the calculations.
3. Results and discussion
The electrocrystallization of o-DMTTF was performed in CH3CN at low temperatures (5 °C) as the salt proved to be too soluble at higher temperatures. The isolated crystals analyze as the 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
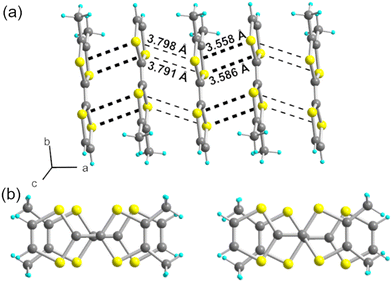
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 salt, i.e., (o-DMTTF)2NO2. The preparation of this salt demonstrates that the nitrite anion can be effectively used as an electrolyte, at least with electron donors with a low oxidation potential, opening the way to a variety of other radical cation salts. Here, (o-DMTTF)2NO2 crystallizes (at 150 K) in the monoclinic system, space group P21/c, with the o-DMTTF molecule in the general position, a structure very close to that of NO3− salt.18 A projection view along the stacking axis (Fig. 2a) shows the general solid-state organization, with a 90° rotation of the long molecular axis in the nearest-neighbor stacks, affording this rare chessboard-like motif in TTF salts, already observed in the halide and nitrate salts of o-DMTTF.14,18 The NO2− anion adopts the expected bent structure due to the presence of an active lone pair on the nitrogen atom, with an O–N–O angle of 144.6(4)°—a large value compared with those reported earlier.35 This NO2− anion is disordered on the inversion center, with both oxygen atoms common to both orientations. A set of six C–H⋯O hydrogen bonds can be identified involving the CH3 groups of o-DMTTF, with H⋯O distances of 2.669(3), 2.744(3), and 2.797(5) Å (× 2), with the associated CMe–H⋯O angles at 172.6(1)°, 165.6(1)°, and 151.3(1)° (Fig. 2b). Despite a closely related structure, this NO2− salt differs from the reported NO3− salt where anion ordering was associated with the strengthening of such C–H⋯O hydrogen bonds. The disorder model adopted here by the nitrite anion (at 150 K) lets us infer that a possible anion ordering would not change the atomic positions of the partially negatively charged oxygen atoms and hence would not significantly modify this C–H⋯O hydrogen bonding pattern at the organic/inorganic interface. An examination of the crystals at lower temperatures to tentatively observe the signature of an anion-ordering process was conducted on the CRYSTAL line at SOLEIL, above (85 K) and well below (35 K) the spin-Peierls transition (TSP = 70 K). A comparison with the structure at 150 K showed no changes, with the same P21/c space group, as well as the absence of any diffusion or substructure features.
1 salt, i.e., (o-DMTTF)2NO2. The preparation of this salt demonstrates that the nitrite anion can be effectively used as an electrolyte, at least with electron donors with a low oxidation potential, opening the way to a variety of other radical cation salts. Here, (o-DMTTF)2NO2 crystallizes (at 150 K) in the monoclinic system, space group P21/c, with the o-DMTTF molecule in the general position, a structure very close to that of NO3− salt.18 A projection view along the stacking axis (Fig. 2a) shows the general solid-state organization, with a 90° rotation of the long molecular axis in the nearest-neighbor stacks, affording this rare chessboard-like motif in TTF salts, already observed in the halide and nitrate salts of o-DMTTF.14,18 The NO2− anion adopts the expected bent structure due to the presence of an active lone pair on the nitrogen atom, with an O–N–O angle of 144.6(4)°—a large value compared with those reported earlier.35 This NO2− anion is disordered on the inversion center, with both oxygen atoms common to both orientations. A set of six C–H⋯O hydrogen bonds can be identified involving the CH3 groups of o-DMTTF, with H⋯O distances of 2.669(3), 2.744(3), and 2.797(5) Å (× 2), with the associated CMe–H⋯O angles at 172.6(1)°, 165.6(1)°, and 151.3(1)° (Fig. 2b). Despite a closely related structure, this NO2− salt differs from the reported NO3− salt where anion ordering was associated with the strengthening of such C–H⋯O hydrogen bonds. The disorder model adopted here by the nitrite anion (at 150 K) lets us infer that a possible anion ordering would not change the atomic positions of the partially negatively charged oxygen atoms and hence would not significantly modify this C–H⋯O hydrogen bonding pattern at the organic/inorganic interface. An examination of the crystals at lower temperatures to tentatively observe the signature of an anion-ordering process was conducted on the CRYSTAL line at SOLEIL, above (85 K) and well below (35 K) the spin-Peierls transition (TSP = 70 K). A comparison with the structure at 150 K showed no changes, with the same P21/c space group, as well as the absence of any diffusion or substructure features.
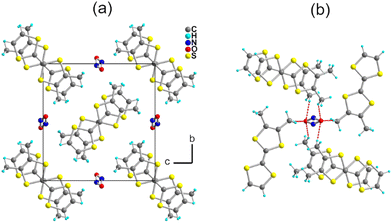 | ||
| Fig. 2 (a) Projection view along a of the unit cell of (o-DMTTF)2NO2. (b) Details of the C–H⋯O hydrogen bonds (red dotted lines). | ||
The donor molecules stack along the a axis, with an alternation of intermolecular overlaps within the chain (Fig. 3a): a strong overlap of nearly eclipsed molecules and a weaker one with the so-called bond-over-ring overlap (Fig. 3b). This analysis is corroborated by the calculation of the βHOMO–HOMO overlap interaction energies, with βintra = 0.71 and βinter = 0.39 eV. The degree of alternation of the stack, defined as 2(βintra − βinter)/(βintra + βinter), is found at 0.58, a value comparable with that found in NO3− salt (0.60), but much stronger than those reported in TMTTF salts with PF6− (0.38) or Br− (0.11).36
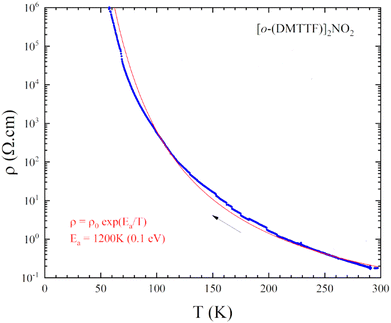
Resistivity measurements (Fig. 4) performed on single crystals show an RT conductivity of 5 S.cm−1 and, upon cooling, an activated behavior with ρ = ρ0exp(Eact/kT) with Eact = 0.1 eV. This indicates that electron localization takes place with a gap of charge Δρ ≈ 2Eact ≈ 0.2 eV, a combined effect of the strong 1D character and electron–electron correlations associated with the strong stack alternation.
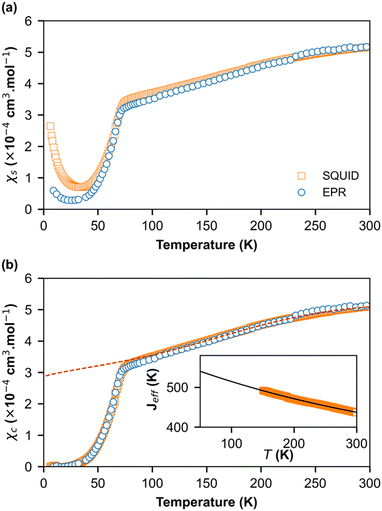
The temperature dependence of magnetic susceptibility χ(T) (Fig. 5a) has been evaluated using ESR and SQUID measurements. Here, χ(T) from ESR have been extracted from the spectra using eqn (1)
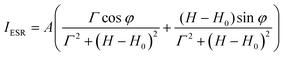 | (1) |
In order to obtain quantitative ESR susceptibility, we renormalized it using SQUID measurement of the same compound at T = 300 K. In Fig. 5a, the squares denote SQUID data whereas circles denote the ESR data. A good agreement was found between the SQUID and ESR data down to 50 K. However, below 50 K, the susceptibilities differ significantly, and a paramagnetic signal following Curie behavior is visible. At lower temperatures, a concentration of impurities of 0.079% and 0.37% was extracted from the Curie behavior assuming S = ½ and g = 2 from the ESR and SQUID data, respectively. Evidently, the quantity of impurities is clearly larger in SQUID measurements than in ESR. This difference can be attributed to the high selectivity of ESR measurements, which only provide information at a specific resonance frequency on a single crystal whereas SQUID magnetometry measures the total magnetic moment of a polycrystalline sample. Fig. 5b shows the spin-chain susceptibilities χc upon the removal of Curie contributions. Here, the SQUID and ESR data are identical for the full temperature range and within the limit of experimental error. Two behaviors are evident. From RT down to about 70 K, the susceptibility is weakly temperature dependent and can be described by a uniform-exchange Heisenberg spin chain. To quantitatively describe this part of susceptibility, it is common to use the well-known Bonner–Fisher curve.37 This method assumes that the exchange coupling integral J is temperature independent, which is not the case here like in most organic spin chains. Indeed, the thermal variation in the crystallographic unit-cell parameters (Table S1, ESI†) shows that the cell contraction essentially affects the stacking axis a and thus the distance between the spins in chains, which decreases when T decreases. In order to extract the temperature dependence of J, we used a method developed by Johnston et al.38 and successfully applied it to (o-DMTTF)2X (X = Cl, Br, I).17 The temperature dependence of J is presented in the inset of Fig. 5b. We have limited the temperature range of extraction of J from 150 K to 300 K to avoid any effect of fluctuations near the phase transition. We then extrapolate to lower temperatures. Finally, we have simulated the susceptibility in the full temperature range using the extrapolated J (red dashed line in Fig. 5b).
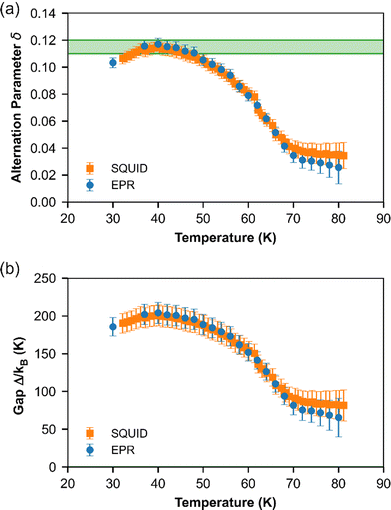
Below TSP = 70 K, the gapless Heisenberg uniform spin chain progressively enters into a non-magnetic gapped state through the spin-Peierls transition. The determination of spin gap Δ is imperative since it is related to the dimerization parameter δ. Since each spin is delocalized on an o-DMTTF dyad, this dimerization parameter is associated with the tetramerization of o-DMTTF stacks. However, the determination of an accurate value of Δ is tricky in spin-Peierls transitions, which are second-order transitions. Δ is temperature dependent close to TSP and this dependence has to be considered. We have first estimated Δ in the temperature-independent regime (for T < 0.5 TSP)39 using the Bulaevski model40 for the susceptibility of an alternated spin chain:
Note that this method can be used only if the susceptibility is not too close to zero. Therefore, for T < 30 K, no value is provided. The results given by EPR and SQUID measurements are comparable. For T < 40 K, the gap and dimerization factor are temperature independent; consequently, as the temperature increases, δ and Δ decrease but do not vanish at T = TSP and above. This behavior is attributed to the existence of a pseudo-gap close but above TSP, as already observed by X-ray diffraction studies in (o-DMTTF)2Br.15
Fig. 7 shows the temperature dependence of EPR linewidth Γ(T) of (o-DMTTF)2NO2. From 300 K down to TSP = 70 K, the linewidth decreases linearly as it is often observed in organic 1D conductors like Fabre salts (TMTTF)2X.41 On the contrary, in (o-DMTTF)2X salts, the temperature dependence of the linewidth is completely different. Γ(T) increases when T decreases for X = Cl, Br, I,15 while it decreases here for X = NO2. Moreover, Γ(T=TSP) is much bigger for centrosymmetric halide anions (up to 100 G for X = I) than for the non-centrosymmetric one with Γ(T=TSP) = 0.5G. In halide salts,15 the temperature dependence of Γ was possibly attributed to the existence of chains rotated by 90° in the crystal cell. However, this assumption cannot stand since with X = NO2, the crystal structure is similar but the linewidth increases with T while it decreases for X = Cl, Br, and I. We think that the temperature dependence of linewidth in this high-temperature range is more related the centro-/non-centrosymmetric nature of the counterion. However, in the absence of a microscopic model, we cannot go further in this analysis. Now, we analyze the temperature dependence of linewidth below TSP. For T decreasing from Tsp, the linewidth increases to reach a local maximum at about T = 40 K and then decreases. To explain these regimes, we calculated the temperature dependence of linewidth in the spin-Peierls phase using the method of moments for an odd and even number of spins in the chain (Fig. S3 in ESI†). The model is simple and suffers from size effects but qualitatively describes our measurements. For an even number of spins (which describes the full chain), the opening of the gap increases the linewidth but the intensity decreases exponentially (Fig. 2b), whereas for an odd number of spins (which corresponds to defects or end chains), the linewidth decreases but the intensity increases with a Curie-like behavior. We conclude that for 40 K < T < TSP, the linewidth is ruled by the full spin chain, whereas for T < 40 K, it describes the defects in the spin chain.
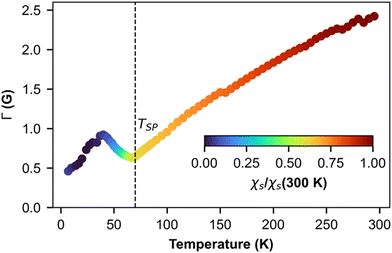 | ||
| Fig. 7 Temperature dependence of ESR linewidth. The color map represents the intensity of the line presented in Fig. 4a. | ||
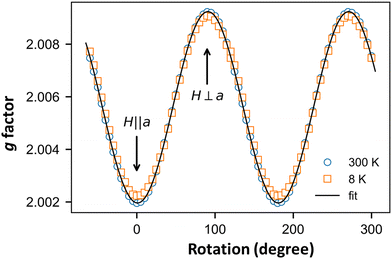
Finally, we focus on the low-temperature range (T < 30 K) where the susceptibility shows a Curie-like behavior (Fig. 5a). In this temperature range, the χ values obtained from the ESR and SQUID data are different. While SQUID measurements are not selective and contain the information from both extrinsic and intrinsic impurities, ESR—a spectroscopic technique—is very selective. The angular variation in the g-factor at RT and 8 K (Fig. 8) are identical, indicating that the signal at lower temperatures is not associated with extrinsic defects but with the o-DMTTF molecule in the stack.12,17,42
We used this intrinsic defect's EPR line to probe the crystal structure around it by performing low- and high-frequency EPR measurements (Fig. 9). Indeed, in the presence of a homogeneous g factor, the linewidth should not vary with the external field, as experimentally observed, for example, in (o-DMTTF)2X salts (X = Cl, Br, I).43 On the other hand, in (o-DMTTF)2NO2, the linewidth increases with frequency, indicating a pure Zeeman broadening effect. This behavior is usually observed in disordered or inhomogeneous systems. In the present case, (o-DMTTF)2NO2 is a single crystal and no Zeeman broadening has been observed in analogous centrosymmetric salts (o-DMTTF)2X (X = Br, Cl, I). Thus, the origin of this broadening can be explained by the non-centrosymmetric nature of NO2− counterion and its disorder in the crystal structure (Fig. 2). We have performed DFT calculations to estimate the g factors for many different orientations of NO2− (Fig. S4 in ESI†). Indeed, around the o-DMTTF-centered magnetic defects, each NO2− has two equivalent orientations and each defect is surrounded by many NO2− ions, potentially contributing to the inhomogeneity of the g factor. This method has been used, for example, to probe the structure of dimethylammonium magnesium formate, where the DMA cation is disordered on three equivalent positions.44,45 The number of configurations quickly becomes large and time-consuming for DFT. We have, therefore, chosen two extreme configurations: all NO2− ions pointing to the (o-DMTTF)2+ dyads and all NO2− ions pointing out of the (o-DMTTF)2+ dyads. The details of the results are presented in the ESI† (Table S2); we found that the distribution of g factor, based on these extreme configurations, is contained within ΔgDFT = 2.5 × 10−3. Experimentally, we can extract the distribution of g factor from the linewidth and we found Δgexp = 1.2 × 10−3, which is in good agreement with the DFT calculations.
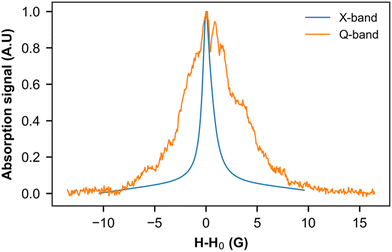 | ||
| Fig. 9 EPR signal of intrinsic defects measured at 8 K in the X band (9.39 GHz) and Q band (33.75 GHz). To facilitate comparison, the resonance field H0 has been subtracted from the magnetic field. | ||
4. Conclusions
We have demonstrated here that radical cation salts of the nitrite anion can be stable in normal conditions and isolated as single crystals from the electrocrystallization of a TTF derivative with tetrabutylammonium nitrite as the electrolyte. Potentially, all the donor molecules whose oxidation potential falls below +0.5 V (vs. SCE) can now be considered for such experiments. In (o-DMTTF)2NO2, the mixed-valence o-DMTTF molecules organize into strongly dimerized stacks, with the stacks adopting a rare chessboard organization, associated with a strongly 1D structure. The bent, non-centrosymmetric NO2− anion is disordered on the inversion center, with the N atom on two symmetry-related positions (with 0.5 occupancy), whereas the two O atoms are not disordered. This peculiar disorder model and the prevalence of short C–H⋯O hydrogen bonds at the organic/inorganic interface explain the absence of an anion-ordering transition in this salt, contrary to those observed in other TTF salts with NO3− or ClO4− anions where the oxygens atoms, which are the ones acting as hydrogen bond acceptors, are disordered in the high-temperature phase whereas the N or Cl central atom is not.18,46 In accordance with the strongly dimerized stacks and 1D nature of the electronic structure, the (o-DMTTF)2NO2 salt is a semiconductor with σRT = 5 S.cm−1 and Eact = 0.1 eV. Combined SQUID and EPR experiments demonstrate the appearance of a spin-Peierls transition with TSP = 70 K. We have quantified the temperature dependence of the spin gap and associated dimerization parameter δ across the spin-Peierls transition and shown the existence of a pseudo-gap above TSP. We also demonstrate that the low-temperature signal observed below TSP is attributable to intrinsic magnetic defects, as observed earlier in o-DMTTF halide salts, and that the broadening of the EPR line with the magnetic field can be associated with the disordered NO2− anions surrounding a magnetic defect, contributing to the inhomogeneity of the g factor.The next step in the investigations of the magnetic properties of this salt will involve pulsed EPR experiments to explore the dynamics of these low-temperature magnetic defects in the spin-Peierls phase, as reported in Fabre salts (TMTTF)2X (X = PF6−, AsF6−)12 and more recently in o-DMTTF halide salts.17 In the latter, it was indeed shown that in the vicinity of such strongly correlated defects, the spins are antiferromagnetically polarized, forming a magnetic soliton: a spin-½ quasiparticle comprising many correlated spins, pinned to the defect. Such studies are simplified here because of the high spin-Peierls transition temperature (70 K) of (o-DMTTF)2NO2 compared with Fabre salts (10–20 K). The outcome of these pulsed EPR experiments will be reported in future studies.
Data availability
The complete data that support the findings of this study are openly available in Zenodo at http://doi.org/10.5281/zenodo.7433815.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank E. Trzop (IPR Rennes) for the X-ray investigation at the CRYSTAL line at SOLEIL (Saclay, France). This work was supported by ANR (France) under contract numbers ANR-20-CE29-0011-01 and ANR-20-CE29-0011-02. Financial support from the IR INFRANALYTICS FR2054 for conducting the research is gratefully acknowledged.References
- D. B. Chesnut, J. Chem. Phys., 1966, 45, 4677–4681 CrossRef CAS.
- P. Pincus, Solid State Commun., 1971, 9, 1971–1973 CrossRef.
- E. Pytte, Phys. Rev. B: Solid State, 1974, 10, 4637–4642 CrossRef CAS.
- J. W. Bray, H. R. Hart, L. V. Interrante, I. S. Jacobs, J. S. Kasper, G. D. Watkins, S. H. Wee and J. C. Bonner, Phys. Rev. Lett., 1975, 35, 744–747 CrossRef CAS.
- I. S. Jacobs, J. W. Bray, H. R. Hart, L. V. Interrante, J. S. Kasper, G. D. Watkins, D. E. Prober and J. C. Bonner, Phys. Rev. B: Solid State, 1976, 14, 3036–3051 CrossRef CAS.
- S. Huizinga, J. Kommandeur, G. A. Sawatzky, B. T. Thole, K. Kopinga, W. J. M. de Jonge and J. Roos, Phys. Rev. B: Condens. Matter Mater. Phys., 1979, 19, 4723–4732 CrossRef CAS.
- A. Maarou, S. Flandrois, G. Fillion and J. P. Morand, Mol. Cryst. Liq. Cryst., 1985, 119, 311–315 CrossRef.
- M. Hase, I. Terasaki and K. Uchinokura, Phys. Rev. Lett., 1983, 70, 3651–3654 CrossRef PubMed.
- V. Kataev, J. Baier, A. Möller, L. Jongen, G. Meyer and A. Freimuth, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 68, 140405 CrossRef.
- D. V. Zakharov, J. Deisenhofer, H.-A. Krug von Nidda, P. Lunkenheimer, J. Hemberger, M. Hoinkis, M. Klemm, M. Sing, R. Claessen, M. V. Eremin, S. Horn and A. Loidl, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 094452 CrossRef.
- P. Foury-Leylekian, D. Le Bolloc'h, B. Hennion, S. Ravy, A. Moradpour and J.-P. Pouget, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 70, 180405 CrossRef.
- S. Bertaina, C.-E. Dutoit, J. Van Tol, M. Dressel, B. Barbara and A. Stepanov, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 060404 CrossRef CAS.
- A. Abderraba, R. Laversanne, E. Dupart, C. Coulon, P. Delhaes and C. Hauw, J. Phys. Colloques, 1983, 44–C3, 1243–1246 Search PubMed.
- M. Fourmigué, E. W. Reinheimer, K. R. Dunbar, P. Auban-Senzier, C. Pasquier and C. Coulon, Dalton Trans., 2008, 4652–4658 RSC.
- P. Foury-Leylekian, P. Auban-Senzier, C. Coulon, O. Jeannin, M. Fourmigué, C. Pasquier and J.-P. Pouget, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 195134 CrossRef.
- J. Zeisner, O. Pilone, L. Soriano, G. Gerbaud, H. Vezin, O. Jeannin, M. Fourmigué, B. Büchner, V. Kataev and S. Bertaina, Phys. Rev. B, 2019, 100, 224414 CrossRef CAS.
- L. Soriano, O. Pilone, M. D. Kuz’min, H. Vezin, O. Jeannin, M. Fourmigué, M. Orio and S. Bertaina, Phys. Rev. B, 2022, 105, 064434 CrossRef CAS.
- O. Jeannin, E. W. Reinheimer, P. Foury-Leylekian, J.-P. Pouget, P. Auban-Senzier, E. Trzop, E. Collet and M. Fourmigué, IUCrJ, 2018, 5, 361–372 CrossRef CAS PubMed.
- L. Eberson and F. Radner, Acta Chem. Scand., Ser. B, 1985, 39, 357–374 CrossRef.
- M. N. Cortona, N. Veltorazzi, J. J. Silber and L. Sereno, J. Electroanal. Chem., 1995, 394, 245–251 CrossRef.
- T. L. Broder, D. S. Silvester, L. Aldous, C. Hardacre and R. G. Compton, J. Phys. Chem. B, 2007, 111, 7778–7785 CrossRef CAS PubMed.
- F. Gerson, A. Lamprecht and M. Fourmigué, J. Chem. Soc., Perkin Trans. 2, 1996, 1409–1414 RSC.
- G. M. Sheldrick, Acta Crystallogr., 2015, A71, 3–8 CrossRef PubMed.
- G. M. Sheldrick, Acta Crystallogr., 2015, C71, 3–8 CrossRef PubMed.
- M.-H. Whangbo and R. Hoffmann, J. Am. Chem. Soc., 1978, 100, 6093–6098 CrossRef CAS.
- J. Ren, W. Liang and M.-H. Whangbo, Crystal and Electronic Structure Analysis Using CAESAR, PrimeColor Software Inc., 1998 Search PubMed.
- J. Ammeter, H.-B. Bürgi, J. Thibeault and R. Hoffmann, J. Am. Chem. Soc., 1978, 100, 3686–3692 CrossRef CAS.
- E. Clementi and C. Roetti, At. Data Nucl. Data Tables, 1974, 14, 177–478 CrossRef CAS.
- F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 73–78 CAS.
- A. D. Becke, J. Chem. Phys., 1993, 98, 1372–1377 CrossRef CAS.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789 CrossRef CAS PubMed.
- A. Schäfer, C. Huber and R. Ahlrichs, J. Chem. Phys., 1994, 100, 5829–5835 CrossRef.
- F. Weigend, Phys. Chem. Chem. Phys., 2006, 8, 1057–1065 RSC.
- A. Klamt and G. Schüürmann, J. Chem. Soc., Perkin Trans. 2, 1993, 799–805 RSC.
- A search in the CSD on other simple organic salts of the NO2− anion shows a wide range of O–N–O angles between 103 and 141°, as found in BEWGUH (109.26°), IZUGUF (103.73°), KUCPIH (117.20°), KUHNIK (116.84°), MAKRAR (115.10°), TEZVOJ (114.77°), VAJRIH (123.91°), YAWHIP (116.47°) and ZEMBUO (141.09°).
- J.-P. Pouget and S. Ravy, J. Phys. I, 1996, 6, 1501–1525 CrossRef CAS.
- J. C. Bonner and M. E. Fisher, Phys. Rev., 1964, 135, 640–658 CrossRef.
- D. C. Johnston, R. K. Kremer, M. Troyer, X. Wang, A. Klümper, S. L. Bud'ko, A. F. Panchula and P. C. Canfield, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 61, 9558–9606 CrossRef CAS.
- E. Orignac and R. Chitra, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 70, 1–12 CrossRef.
- L. Bulaevskii, Sov. Phys.-Solid State, 1969, 11, 1132 Search PubMed.
- C. Coulon and R. Clérac, Chem. Rev., 2004, 104, 5655–5687 CrossRef CAS PubMed.
- L. Soriano, J. Zeisner, V. Kataev, O. Pilone, M. Fourmigue, O. Jeannin, H. Vezin, M. Orio and S. Bertaina, Appl. Magn. Reson., 2020, 51, 1307–1320 CrossRef CAS.
- L. Soriano, unpublished results.
- M. Orio, J. K. Bindra, J. van Tol, M. Giorgi, N. S. Dalal and S. Bertaina, J. Chem. Phys., 2021, 154, 154201 CrossRef CAS PubMed.
- S. Bertaina, N. Abhyankar, M. Orio and N. S. Dalal, J. Phys. Chem. C, 2018, 122, 16431–16436 CrossRef CAS.
- J.-P. Pouget, Crystals, 2012, 2, 466–520 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available: Tables S1, S2 and Fig. S1–S4 in PDF. CCDC 2223882. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d2tc05431k |
| ‡ Current address: Rigaku Americas Corporation, 9009 New Trails Drive, The Woodlands, TX, 77381, USA. |
| This journal is © The Royal Society of Chemistry 2023 |