Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Raman spectra of 2D titanium carbide MXene from machine-learning force field molecular dynamics†
Ethan
Berger
 *a,
Zhong-Peng
Lv
*a,
Zhong-Peng
Lv
 b and
Hannu-Pekka
Komsa
b and
Hannu-Pekka
Komsa
 a
a
aMicroelectronics Research Unit, Faculty of Information Technology and Electrical Engineering, University of Oulu, P. O. Box 4500, Oulu, FIN-90014, Finland. E-mail: hannu-pekka.komsa@oulu.fi
bDepartment of Applied Physics, Aalto University, Aalto, FIN-00076, Finland
First published on 13th December 2022
Abstract
MXenes represent one of the largest classes of 2D materials with promising applications in many fields and their properties are tunable by altering the surface group composition. Raman spectroscopy is expected to yield rich information about the surface composition, but the interpretation of the recorded spectra has proven challenging. The interpretation is usually done via comparison to the simulated spectra, but there are large discrepancies between the experimental spectra and the earlier simulated spectra. In this work, we develop a computational approach to simulate the Raman spectra of complex materials which combines machine-learning force-field molecular dynamics and reconstruction of Raman tensors via projection to pristine system modes. This approach can account for the effects of finite temperature, mixed surfaces, and disorder. We apply our approach to simulate the Raman spectra of titanium carbide MXene and show that all these effects must be included in order to appropriately reproduce the experimental spectra, in particular the broad features. We discuss the origin of the peaks and how they evolve with the surface composition, which can then be used to interpret the experimental results.
1 Introduction
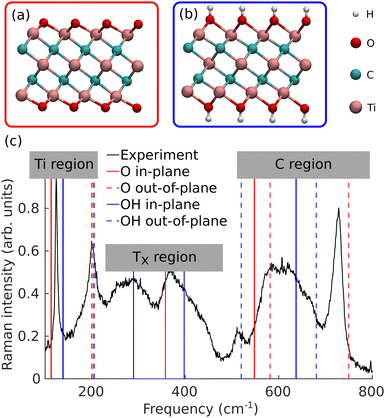
Two-dimensional (2D) materials have attracted a lot of attention from the scientific community in the last two decades. Among them, MXenes represent one of the largest classes of 2D materials with more than 40 synthesized compositions and many more still left to discover.1 Due to their high electrical conductivity, MXenes show potential for applications in various fields, including energy storage, gas sensors, and electromagnetic interference shielding.2–4 MXenes take the form Mn+1XnTx, where M is an early transition metal (e.g. titanium), X can be carbon or nitrogen, T is the surface terminations which depend on the synthesis methods, and n = 1–4 defines the thickness of the layer. The first synthesized and the most studied MXene Ti3C2Tx is obtained by selective etching of the Al layer from its precursor bulk phase Ti3AlC2.5 Due to this process, the surfaces are passivated by functional groups from the etching solution, with the most common ones being –O, –OH and –F. The ball-and-stick representations of pure –O and –OH surfaces of Ti3C2 are shown in Fig. 1(a and b), respectively. Under the common wet-etching synthesis conditions, the surface is never purely O or OH but contains a randomly arranged mixture of these functional groups.6–10 Unfortunately, it has become challenging to not only control the ratio of these terminations, but also to quantify them.One commonly used method to study the composition of 2D materials is Raman spectroscopy, which is a non-destructive method for characterizing the vibrational properties of molecules or solids. The Raman spectra of Ti3C2Tx have been recorded and carefully studied experimentally.11–13 To explain the experimental observations, Raman spectra have been calculated using density functional theory (DFT) for pure surfaces,14,15 but the comparison is not straightforward. To illustrate these problems, in Fig. 1(c), we reproduce the typical experimental Raman spectrum and the frequencies of the Raman active modes of pure surfaces (–O and –OH) from DFT (the description of the synthesis and the Raman measurement for the experimental results are available in the ESI†). For modes around 120 cm−1, 200 cm−1, and 700 cm−1, the experimental frequencies appear to be close to, or in between, those of the calculations for pure surfaces, and thus these peaks can be quite safely assigned to the calculated modes. More importantly, other peaks at around 300–400 cm−1 and 600 cm−1 show extremely broad features which cannot be explained by static calculations of pure surfaces. There are few possible origins for this discrepancy. First, static calculations do not provide any information about the width of the Raman peaks. The calculations of anharmonic interatomic force constants16 or molecular dynamics (MD) simulations are usually necessary to account for temperature effects and obtain realistic line widths. In the latter, Raman intensities can be obtained from the Fourier transform of the polarizability χ(t) autocorrelation function,17 but this requires tens of thousands of polarizability calculations. It has been successfully used to compute the Raman spectra of solid ice,18 liquid water,19 and molecules,20 but such calculations are very expensive and usually restricted to a small number of atoms. Secondly, wide peaks of the MXene Raman spectra might come from the structural disorder, i.e., the mixed surfaces. In order to simulate different surface terminations, it is necessary to use a large supercell, making the calculation of polarizabilities at every time step of an MD run computationally intractable.
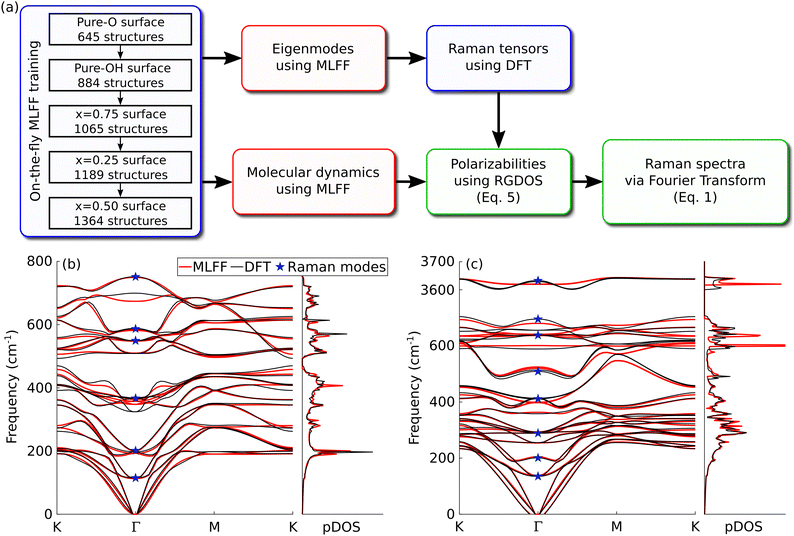
With the recent developments in machine-learning force fields (MLFFs), it has now become possible to carry out MD simulations for long times and large numbers of atoms efficiently, yet still nearly matching the accuracy of first-principles calculations.21–26 Moreover, by using MLFFs, it becomes possible to run MD over a large configurational space, such as different compositions and distributions of surface terminations in MXenes. Unfortunately, MLFFs usually cannot be used to evaluate polarizabilities as they only model energies and forces. To compute the polarizabilities of these large supercells, Hashemi et al. recently developed a computational scheme (denoted as RGDOS), which allows the Raman tensors of a supercell to be obtained from a projection onto those of the unit cell.27 The scheme has already been successfully applied to, e.g., transition metal dichalcogenide alloys (MoxW1−xS2 and ZrSxSe1−x),27,28 defects in MoS2,29 and SnS multilayer films.30 Adapting RGDOS for evaluating the time-dependent polarizability χ(t) and combining it with MLFF MD trajectories would lead to a highly efficient scheme to obtain the Raman spectra at a finite temperature and in large supercells. In this work, we present a scheme for combining MLFF trajectories with RGDOS (or DFT calculated Raman tensors) to evaluate the finite-temperature Raman spectra of complex systems. This method leads to highly efficient MD runs and calculations of the polarizabilities, allowing us to easily probe the large configurational space. We apply the method to 2D titanium carbide MXene to study the effect of heterogeneous surfaces on the Raman spectra and attempt to give a better description of the experimental results. We first investigate the effects of temperature and mixed surface terminations on the Raman spectrum, and finally study the effect of additional disorder by considering the vibrational modes outside a Γ-point. We discuss the origin of the peaks and broad features and how they evolve with the surface composition.
2 Methods
When using MD, the Raman spectrum is obtained as the Fourier transform of the autocorrelation function of polarizability χ:17,31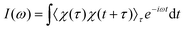 | (1) |
In this work, we adopt an approach conceptually similar to the RGDOS. We start by writing the polarizability as a Taylor expansion around a relaxed position r0, which leads to the following equation where χ0 is the polarizability at r0 and u represents the atomic displacement
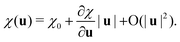 | (2) |
One can notice the resemblance between the partial derivative 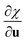 and the definition of Raman tensors
and the definition of Raman tensors 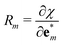 (in the Placzek approximation32,33), where
(in the Placzek approximation32,33), where 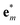 are the mass-scaled eigenvectors of the unit cell. This suggests that we could use the set of eigenvectors {
are the mass-scaled eigenvectors of the unit cell. This suggests that we could use the set of eigenvectors {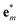 } as a basis for the expansion, with Raman tensors giving the expansion coefficients and the “distance” given by the projection of u to
} as a basis for the expansion, with Raman tensors giving the expansion coefficients and the “distance” given by the projection of u to 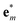 , written as
, written as
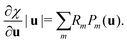 | (3) |
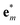 . We first note that, since eigenvectors {
. We first note that, since eigenvectors {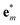 } do not form an orthogonal basis, the projection coefficients Pm(u) have to be found by solving the following system of linear equations
} do not form an orthogonal basis, the projection coefficients Pm(u) have to be found by solving the following system of linear equations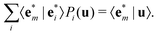 | (4) |
Moreover, since only Γ-point modes contribute to first-order Raman scattering, the projections are here performed from the supercell displacement u to the unit cell eigenmodes at Γ-point 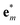 .
.
The final equation for the time-dependent polarizability is then
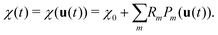 | (5) |
When the eigenmodes and the Raman tensors of the unit cell and the MD trajectories are known, χ(t) can easily be obtained from eqn (4) and (5). This method is therefore highly efficient and compatible with MLFF MD. We also note that in eqn (5), the second order term could be added, essentially corresponding to the second-order Raman scattering. In this case, the sum should also be carried over different points of the first Brillouin zone (BZ) to account for the modes outside of the gamma-point. In the case of MXenes, there is no indication of the dominant second order contribution and thus we have decided not to include the second order term.
3 Computational details
All calculations are performed using the Vienna ab initio simulation package (VASP).34,35 We adopt the Perdew–Burke–Ernzerhof exchange-correlation functional for solids (PBEsol)36 and set the plane-wave cutoff to 550 eV. Phonon eigenmodes are obtained using the Phonopy software.37 For determining the force constants, we used 4 × 4 supercells with the Brillouin zone sampled using a 4 × 4 k-point mesh. Once the eigenvectors are known, the Raman tensors were obtained from a centered finite difference scheme. Since MXenes are metallic, the polarizabilities have to be evaluated at a finite excitation energy ω, i.e., using χ(ω) instead of the ω → 0 limit normally used in nonresonant Raman. Although the Placzek approximation is derived under non-resonant conditions, it has been found to work well also under resonant conditions.38 Here, for the projections, we used the eigenvectors and Raman tensors of the –OH unit cell, and the latter evaluated at ω = 516 nm. More information regarding resonant Raman and the choice of Raman tensors is available in the ESI† (see in particular Fig. S1). The frequency-dependent polarizability (or the dielectric function) is computed using a summation over empty bands.39 To guarantee the accurate evaluation of small changes in χ(ω), a denser k-point mesh of 48 × 48 (in the unit cell) was adopted and the number of orbitals was increased to 120 (roughly 4 times the recommended amount). For phonon mode and Raman tensor calculations, the electronic structure was relaxed with a precision of 10−7 eV.The machine learning force field (MLFF) was trained using on-the-fly machine learning, as recently implemented in VASP.25,26 This method is based on the Gaussian approximation potential (GAP)23 and has already been successfully applied to different materials including different phases of zirconium40 and hybrid perovskites MAPbX3.41,42 A detailed presentation of the method as well as definitions of descriptors and the kernel can be found in ref. 26. Fig. 2(a) shows a schematic of the workflow and how the MLFF, MD, DFT and RGDOS are all combined to obtain the Raman spectrum. In the training, we again used 4 × 4 supercells with a 4 × 4 k-points mesh, but the electronic structure convergence criterion was decreased to 10−4 eV. The model was first trained for pure surfaces before being trained for mixed –O and –OH surfaces as well. F- and OH-terminated surfaces are expected to behave fairly similar chemically,10,43,44 and also for vibrational frequencies due to similar masses.45 On a practical level, the MLFF applicable to any mixed surfaces containing O, OH or F would have to be trained with a much larger number of surface compositions, which would be computationally costly in both the training stage and the MD runs. We carried out benchmarks using a model trained with few F compositions (see the ESI† and Fig. S2 in particular), which confirm our initial assumption that replacing –OH terminations by –F is found to have fairly little impact on the Raman spectra. Hence –F terminations are not included in the MLFF model used in the main text. Each step consisted of MD simulation in the NVT ensemble at 300 K for 20 hours (40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000–70
000–70![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 steps), and the MLFF configurations after each step carried on to the next step. In total, the training set contains 1364 configurations. During on-the-fly training, weights are calculated using Bayesian linear regression, which is necessary for error estimates. Once training is performed, the final model is retrained using singular value decomposition (SVD), which usually improves the quality of the MLFF. During training and retraining, we use 8 basis functions, a cutoff radius of 5 Å and a Gaussian broadening of 0.5 Å to build both radial and angular descriptors (these values correspond to the default parameters of VASP, see ref. 26 for a detailed definition of the descriptors).
000 steps), and the MLFF configurations after each step carried on to the next step. In total, the training set contains 1364 configurations. During on-the-fly training, weights are calculated using Bayesian linear regression, which is necessary for error estimates. Once training is performed, the final model is retrained using singular value decomposition (SVD), which usually improves the quality of the MLFF. During training and retraining, we use 8 basis functions, a cutoff radius of 5 Å and a Gaussian broadening of 0.5 Å to build both radial and angular descriptors (these values correspond to the default parameters of VASP, see ref. 26 for a detailed definition of the descriptors).
To benchmark the model, we compared the phonon dispersion curves from DFT and the MLFF model. Fig. 2(b and c) show the phonon bands and density of states (pDOS) of pure Ti3C2O2 and Ti3C2(OH)2, respectively. Overall, the results are in good agreement with the dispersion curves and the pDOS. The bands of Ti3C2O2 are in great agreement. Fortunately, few modes where errors at Γ-point are somewhat larger, such as the 350 and 700 cm−1 modes in Ti3C2O2, happen to be Raman-inactive modes. The comparison for Ti3C2(OH)2 is slightly worse. In particular, modes in the 400–700 cm−1 range show deviations that are larger than those in Ti3C2O2, but generally still within about 20 cm−1 and with largely correct band dispersions. We also note that part of the discrepancy may be ascribed to the fact that phonon dispersion curves are calculated around the equilibrium positions, essentially corresponding to spectra at 0 K, whereas our MLFF is fitted into finite-temperature trajectories, i.e., aimed at yielding accurate forces at room temperature. This becomes particularly true for light elements such as hydrogen and might explain the larger errors in Ti3C2(OH)2 phonon dispersion curves. The effect of temperature is further discussed below. The root mean square error (RMSE) between DFT and MLFF forces is 45.8 meV Å−1. These benchmarks indicate that the model is sufficiently trained and that we can use it for reliable MD production runs.
Molecular dynamics were performed using the MLFF model in the NVT ensemble using a Nosé–Hoover thermostat46,47 for 8 × 8 supercells (see Fig. S3(a) in the ESI† for a discussion on the choice of supercell size). The time step was set to 1 fs and 105 steps were performed, resulting in runs of 100 ps. To reduce noise in the final spectra, five runs with different random distributions of the surface terminations are performed for each concentration. Using different distributions of the surface termination does not impact the main features of the resulting Raman spectra, see Fig. S3(b) in the ESI† for more details.
4 Results and discussion
4.1 Effect of temperature
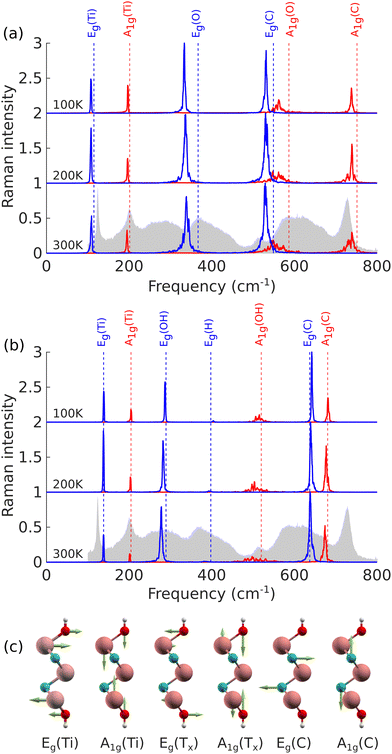
We first investigate the effect of temperature on the width of the peaks. Fig. 3(a and b) show the Raman spectra of Ti3C2O2 and Ti3C2(OH)2 at different temperatures, respectively. With the MLFF being trained at 300 K, MD runs were only performed at lower temperatures of 100 K and 200 K as trajectories for temperatures above 300 K might not be reliable. For a better understanding of the different vibrations, Fig. 3(c) shows a representation of the Raman-active modes. The peak frequencies compare well to the DFT results presented in Fig. 1(c) for both systems, showing that our approach leads to reasonable spectra. Overall, the frequencies do not shift markedly with temperature, but there is now a realistic description of the peak widths. Some peaks, such as the two modes at 100 and 200 cm−1 localized to titanium atoms, show weak dependence on temperature. While our results agree with experimental observations for the first, the width seems underestimated for the latter. For other peaks, the width increases with temperature. The A1g carbon mode at around 700 cm−1 shows a fairly narrow peak at a low temperature but it gets significantly wider with temperature, resulting in a better agreement with experiment at 300 K. Similar broadening with increasing temperature is observed for the in-plane modes of surface terminations and carbon at 300–400 and 500–600 cm−1, respectively. Since surface terminations (–OH groups in particular) should be strongly anharmonic, significant broadening could be expected for modes involving these atoms. In these cases however, the widths at 300 K are still underestimated and do not compare well to experiments. Overall, using finite temperature leads to a better comparison with experiments, but it is clear that something is still missing in order to correctly reproduce experimental observations.4.2 Effect of mixed surfaces
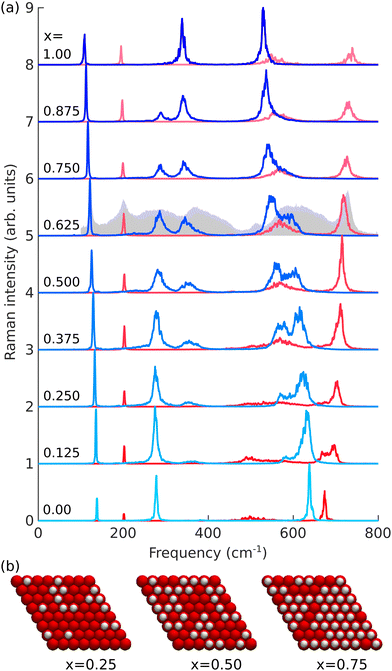
We next look at the effect of mixed surfaces. Fig. 4(a) shows the Raman spectra for different concentrations of surface terminations and Fig. 4(b) shows the distribution of surface terminations for different concentrations. The top and bottom lines show the results of pure Ti3C2O2 and Ti3C2(OH)2, respectively. The titanium A1g mode at 200 cm−1 is largely unaffected by the composition changes. The other two sharp peaks from both the titanium Eg mode at around 120 cm−1 and the carbon A1g mode at around 700 cm−1 show a straightforward linear shift with the O/OH ratio (a so-called one-mode behavior). This suggests that these peaks could be used to find the surface termination composition from the experimentally recorded spectrum. To this end, we extracted the frequencies by isolating the peaks and fitted them using a Lorentzian function (see Fig. S4 in the ESI† for details), and collected the results in Table 1 together with experimental values. In particular, we include the results from our experimental spectrum shown in Fig. 1(c) (and again in Fig. 4(a) below the x = 0.625 spectrum) and those from ref. 11, where these peaks were found to shift depending on the sample preparation conditions. First, if we use the Ti A1g mode as a probe for the accuracy of our calculations, we find that the calculated frequencies are 0–10 cm−1 lower than the experimental values. Second, by comparing the frequencies of the other two modes, best agreement with experiments is found for x around 0.5–0.625. Even accounting for the inaccuracies in the calculated frequencies, our results strongly point to all these samples having surfaces with a mixture of surface terminations. Interestingly, the composition range found from this comparison also agrees well with that predicted by first-principles calculations in ref. 9: O0.75OH0.25 (x = 0.75) at a higher pH and O0.5OH0.25F0.25 at a lower pH (corresponding to a total concentration of 0.5 for –OH and –F terminations). For these two peaks, calculations also reproduce well the widths of the experimental peaks.| Simulated | Experiments | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1.000 | 0.875 | 0.750 | 0.625 | 0.500 | 0.375 | 0.250 | 0.125 | 0.000 | Fig. 1 | Ref. 11 | |
| E g (Ti) | 108.4 | 112.5 | 116.8 | 121.6 | 125.7 | 129.3 | 132.9 | 135.7 | 138.1 | 123.7 | 119.8–124.5 |
| A 1g (Ti) | 194.9 | 197.7 | 199.2 | 200.3 | 202.3 | 202.6 | 202.5 | 202.3 | 201.5 | 199.6 | 201.0–206.7 |
| A 1g (C) | 737.4 | 729.4 | 725.2 | 718.9 | 714.5 | 709.9 | 702.0 | 690.2 | 673.9 | 728.3 | 737.7–719.6 |
In addition, there are two in-plane modes at 300–400 cm−1 and 500–650 cm−1, which show distinct two-mode behavior with changing composition. For the former, it seems that the two broad features in the experimental spectrum arise from these two modes. For the latter, it is difficult to distinguish the two peaks from the experimental spectrum, but as this feature is very broad it is consistent with being composed of two peaks as found in our calculations. Also note that at concentrations close to x = 0.5, the out-of-plane mode of carbon also seems to contribute at a similar frequency. Even though Raman spectra simulated using mixed surfaces agree much better with experiments and would appear to contain all the main features, the agreement is clearly still far from perfect. In particular, the widths of some peaks, mainly those arising from the surface terminations and the carbon Eg modes, are still greatly underestimated even when accounting for the F terminations (Fig. S2, ESI†) and by more than one might expect from instrumental broadening.
4.3 Effect of modes outside the Γ-point
The peak broadening could arise from the interaction of surface terminations with water or other surface adsorbates, from the interaction with neighboring MXene layers, or from disorder arising, e.g., from point defects, grain boundaries, etc. We simulated the Raman spectra of multilayer MXene flakes, but this did not lead to marked broadening of these features as shown in Fig. S5(a) in the ESI.† Moreover, the experimentally recorded spectra of monolayer flakes, multilayer flakes, and colloidal dispersions all show largely similar broadening.11–13 We also investigated the presence of (a small amount of) water on the surface, but it also did not yield the desired effect (see Fig. S5(b) in the ESI†).One might expect that the wet chemistry and strong acids used in the synthesis would lead to a large number of defects, in addition to the defects inherited from the precursor MAX phases.48–50 Consequently, there is also a large variety of possible defects: in addition to flake edges and grain boundaries,2,48,51 the reported point defects include Ti vacancies and Ti adatoms,52,53 C vacancies,54 and substitutional O in the C site.55 Recent secondary-ion mass-spectroscopy measurements have revealed that this last kind of defect can occupy up to 30% of the carbon sites, confirming the high defect concentration in the interior of MXenes.56 Unfortunately, the dominant types of defects and their density are largely unknown, which makes simulating the role of defects on the Raman spectra challenging.
To circumvent this problem, we simulate the effect of disorder by considering the modes outside the Γ-point. In ideal crystals, first order Raman spectra only come from modes at Γ-point because of the condition k = 0.57 However, in the presence of defects, the symmetry is lowered and the modes from the rest of the first Brillouin zone can contribute.58,59 In fact, this effect is already present in our calculations for randomly distributed surface terminations, but clearly the degree of disorder from surface terminations is insufficient. To explicitly include the contributions from modes outside the Γ-point, we study here the phonon density of state using the phonon-projected velocity-autocorrelation function (VACF).42,60–62 By projecting only onto the Raman active modes, we can isolate the corresponding part of the vibrational spectrum and in this way approximate the Raman spectrum. Note however that the peak intensities do not correspond to those obtained from Raman and only the frequencies and lineshapes are relevant. The comparison to the total pDOS (i.e. containing both infrared and Raman active modes) is presented in the ESI† (see Fig. S6).
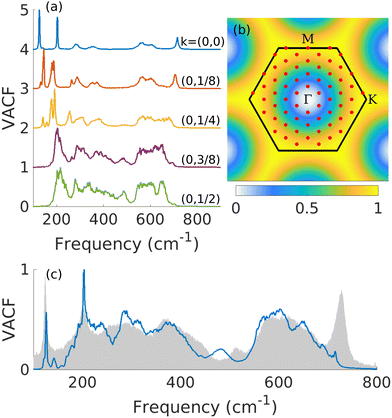
We focus here on x = 0.5 surfaces since we already determined this concentration as a good candidate to reproduce the experimental results. Every point of the reciprocal space is not expected to contribute to the Raman spectra with the same weight. To find the weights, we study the pDOS for each wave vector along the Γ–M path, which are shown in Fig. 5(a). pDOS at and close to Γ mostly show low frequency modes, coinciding with the Raman spectrum in Fig. 4. In experiment, these modes show narrow peaks which tends to indicate a small contribution from modes outside the Γ point. On the other hand, modes close to the edge of the first Brillouin zone show wide peaks at around 300–400 and 600 cm−1. Based on the experimental observations, we therefore choose larger weights for the modes close to the BZ edges. The selected weights are shown in Fig. 5(b) and built from a sum of two Gaussians such that the weight approaches 0 at Γ-point and 1 at the BZ edge, except that the pDOS at Γ-point is also added with a weight of 1.
The resulting pDOS using these weights is shown in Fig. 5(c). When summing the weighted pDOS with pDOS at Γ, we found great agreement with experiment. The very wide peaks in the 300–400 and 600 cm−1 regions are well reproduced. The peak at 200 cm−1 also gets wider with the additional contributions from outside Γ, further improving the agreement with experiment. As previously discussed, the pDOS does not reproduce well the intensities of peaks, which is especially true for the peak at 700 cm−1. Also note that the spectrum now shows an additional peak at around 500 cm−1 which also appears in the experimental results, even though the agreement in the frequency is not perfect. In Fig. 4(a), this peak shows up weakly in the OH-surfaces, but disappears in the mixed surfaces. However, since this mode is relatively flat [cf. the phonon dispersion in 2(c)], the inclusion of modes outside the Γ-point could lead to increased intensity. Thus, this peak seems to arise from the A1g (OH) mode with its intensity enhanced by disorder, which we could confirm by inspecting the eigenmode-projected VACF in Fig. S6(b) in the ESI.†
Similar pDOS for other concentrations is available in the ESI† (Fig. S7). The results in Fig. S7 (ESI†) and those in Fig. 4 suggest that the relative intensity of the two broad peaks at 300 cm−1 [Eg (OH)] and 400 cm−1 [Eg (O)] and of the two peaks that form the broad peak at 600 cm−1 [Eg (C)] could be used to probe the O/OH concentration, in addition to the shift of the sharp peaks. In fact, our results are in agreement with all the changes with increasing O content (as verified using XPS) observed in the experiments by Lioi et al.:12 for the sharp peaks, there is a downshift of 120 cm−1 [Eg (Ti)] peak, a downshift of 200 cm−1 [A1g (Ti)] peak, and an upshift of 700 cm−1 [A1g (C)] peak; for the broad features, there is enhancement of the 400 cm−1 [Eg (O)] peak and enhancement of the lower frequency side of the 600 cm−1 peak. Only 500 cm−1 [A1g (OH)] does not show a marked change. The results in Fig. S7 (ESI†) also illustrate that the surface concentration has a relatively minor impact on these peaks. This finding, together with previous computational predictions of a limited range of accessible surface compositions under typical synthesis conditions,9 explains why the Raman spectra of Ti3C2Tx appear to depend weakly on the adopted synthesis procedure and on the sample morphology.
5 Conclusion
In conclusion, we have developed a computational approach to efficiently compute the Raman spectra of complex materials at a finite temperature, which is based on a combination of machine-learning force fields and a method to efficiently evaluate the time-dependent susceptibility. Our approach can be applied to many other materials with high anharmonicity and pronounced temperature effects. Alternatively, it can be used for systems requiring large supercells when modeling, e.g., alloys and/or defects.Here, we applied the approach to 2D titanium carbide MXene to study the effects of temperature and surface terminations on the Raman spectra. We found that the temperature plays a relatively small role and does not explain the wide peaks observed experimentally. On the other hand, mixed surfaces play an important role in reproducing the experimental Raman spectra. We identified three peaks that underwent straightforward evolution with the surface composition and thus could also be used to extract the composition from the experimental spectra. Mixed surfaces lead to better agreement in the peak position for some peaks and, importantly, they also reproduce the two broad peaks observed at 300 and 400 cm−1. Additionally, the modes outside the Γ-point are found to play an important role, which is activated by the disorder such as defects. In particular, modes close to the Brillouin zone edge are found to contribute significantly to the widening of peaks at around 300–400 and 600 cm−1, as well as the appearance of an additional peak at around 500 cm−1. Only by including the effect of heterogeneous surfaces and contribution from modes outside the Γ-point, good agreement with the experimentally recorded spectra can be achieved.
Data availability statement
Data for this paper, including input files, atomic structures, energies and forces of the training set, and MD trajectories are available at Materials Cloud Archive at https://doi.org/10.24435/materialscloud:w2-g5.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We are grateful to the Academy of Finland for support under the Academy Research Fellow funding No. 311058 and Academy Postdoc funding No. 330214. We also thank the CSC-IT Center for Science Ltd for generous grants of computer time.References
- M. Naguib, M. W. Barsoum and Y. Gogotsi, Adv. Mater., 2021, 33, 2103393 CrossRef.
- A. Babak, M. K. Lukatskaya and Y. Gogotsi, Nat. Rev. Mater., 2017, 16098 Search PubMed.
- E. Lee and D.-J. Kim, J. Electrochem. Soc., 2019, 167, 037515 CrossRef.
- A. Iqbal, P. Sambyal and C. M. Koo, Adv. Funct. Mater., 2020, 30, 2000883 CrossRef.
- M. Naguib, M. Kurtoglu, V. Presser, J. Lu, J. Niu, M. Heon, L. Hultman, Y. Gogotsi and M. W. Barsoum, Adv. Mater., 2011, 23, 4248–4253 CrossRef PubMed.
- O. Mashtalir, M. Naguib, B. Dyatkin, Y. Gogotsi and M. W. Barsoum, Mater. Chem. Phys., 2013, 139, 147–152 CrossRef CAS.
- C. Shi, M. Beidaghi, M. Naguib, O. Mashtalir, Y. Gogotsi and S. J. L. Billinge, Phys. Rev. Lett., 2014, 112, 125501 CrossRef.
- H.-W. Wang, M. Naguib, K. Page, D. J. Wesolowski and Y. Gogotsi, Chem. Mater., 2016, 28, 349–359 CrossRef CAS.
- R. Ibragimova, M. J. Puska and H.-P. Komsa, ACS Nano, 2019, 13, 9171–9181 CrossRef CAS.
- R. Ibragimova, P. Erhart, P. Rinke and H.-P. Komsa, J. Phys. Chem. Lett., 2021, 12, 2377–2384 CrossRef CAS PubMed.
- A. Sarycheva and Y. Gogotsi, Chem. Mater., 2020, 32, 3480–3488 CrossRef CAS.
- D. B. Lioi, G. Neher, J. E. Heckler, T. Back, F. Mehmood, D. Nepal, R. Pachter, R. Vaia and W. J. Kennedy, ACS Appl. Nano Mater., 2019, 2, 6087–6091 CrossRef CAS.
- A. Sarycheva, M. Shanmugasundaram, A. Krayev and Y. Gogotsi, ACS Nano, 2022, 16, 6858–6865 CrossRef CAS PubMed.
- T. Hu, J. Wang, H. Zhang, Z. Li, M. Hu and X. Wang, Phys. Chem. Chem. Phys., 2015, 17, 9997–10003 RSC.
- T. Hu, M. Hu, B. Gao, W. Li and X. Wang, J. Phys. Chem. C, 2018, 122, 18501–18509 CrossRef CAS.
- L. Lindsay, D. A. Broido and T. L. Reinecke, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 165201 CrossRef.
- M. Thomas, M. Brehm, R. Fligg, P. Vöhringer and B. Kirchner, Phys. Chem. Chem. Phys., 2013, 15, 6608–6622 RSC.
- A. Putrino and M. Parrinello, Phys. Rev. Lett., 2002, 88, 176401 CrossRef.
- Q. Wan, L. Spanu, G. A. Galli and F. Gygi, J. Chem. Theory Comput., 2013, 9, 4124–4130 CrossRef CAS PubMed.
- S. Luber, M. Iannuzzi and J. Hutter, J. Chem. Phys., 2014, 141, 094503 CrossRef.
- E. Kocer, T. W. Ko and J. Behler, Annu. Rev. Phys. Chem., 2022, 73, 163–186 CrossRef PubMed.
- J. Behler and M. Parrinello, Phys. Rev. Lett., 2007, 98, 146401 CrossRef.
- A. P. Bartók, M. C. Payne, R. Kondor and G. Csányi, Phys. Rev. Lett., 2010, 104, 136403 CrossRef.
- Z. Fan, Z. Zeng, C. Zhang, Y. Wang, K. Song, H. Dong, Y. Chen and T. Ala-Nissila, Phys. Rev. B, 2021, 104, 104309 CrossRef CAS.
- R. Jinnouchi, J. Lahnsteiner, F. Karsai, G. Kresse and M. Bokdam, Phys. Rev. Lett., 2019, 122, 225701 CrossRef CAS PubMed.
- R. Jinnouchi, F. Karsai and G. Kresse, Phys. Rev. B, 2019, 100, 014105 CrossRef CAS.
- A. Hashemi, A. V. Krasheninnikov, M. Puska and H.-P. Komsa, Phys. Rev. Mater., 2019, 3, 023806 CrossRef CAS.
- S. M. Oliver, J. J. Fox, A. Hashemi, A. Singh, R. L. Cavalero, S. Yee, D. W. Snyder, R. Jaramillo, H.-P. Komsa and P. M. Vora, J. Mater. Chem. C, 2020, 8, 5732–5743 RSC.
- Z. Kou, A. Hashemi, M. Puska, A. V. Krasheninnikov and H.-P. Komsa, npj Comput. Mater., 2020, 6, 59 CrossRef CAS.
- P. Sutter, H. Komsa, H. Lu, A. Gruverman and E. Sutter, Nano Today, 2021, 37, 101082 CrossRef CAS.
- G. R. Medders and F. Paesani, J. Chem. Theory Comput., 2015, 11, 1145–1154 CrossRef CAS PubMed.
- G. Placzek, Rayleigh-streuung und Raman-effekt, Akademische Verlagsgesellschaft, 1934, vol. 2 Search PubMed.
- D. A. Long, The Raman effect, John Wiley & Sons: Chichester, England, 2002 Search PubMed.
- G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS.
- J. P. Perdew, A. Ruzsinszky, G. I. Csonka, O. A. Vydrov, G. E. Scuseria, L. A. Constantin, X. Zhou and K. Burke, Phys. Rev. Lett., 2008, 100, 136406 CrossRef PubMed.
- A. Togo and I. Tanaka, Scr. Mater., 2015, 108, 1–5 CrossRef CAS.
- M. Walter and M. Moseler, J. Chem. Theory Comput., 2020, 16, 576–586 CrossRef PubMed.
- M. Gajdoš, K. Hummer, G. Kresse, J. Furthmüller and F. Bechstedt, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 045112 CrossRef.
- P. Liu, C. Verdi, F. Karsai and G. Kresse, Phys. Rev. Mater., 2021, 5, 053804 CrossRef CAS.
- M. Bokdam, J. Lahnsteiner and D. D. Sarma, J. Phys. Chem. C, 2021, 125, 21077–21086 CrossRef CAS.
- J. Lahnsteiner and M. Bokdam, Phys. Rev. B, 2022, 105, 024302 CrossRef CAS.
- Y. Xie and P. R. C. Kent, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 235441 CrossRef.
- M. Khazaei, A. Ranjbar, M. Arai, T. Sasaki and S. Yunoki, J. Mater. Chem. C, 2017, 5, 2488–2503 RSC.
- T. Hu, M. Hu, Z. Li, H. Zhang, C. Zhang, J. Wang and X. Wang, Phys. Chem. Chem. Phys., 2016, 18, 20256–20260 RSC.
- S. Nosé, J. Chem. Phys., 1984, 81, 511–519 CrossRef.
- N. Shuichi, Prog. Theor. Phys. Suppl., 1991, 103, 1–46 CrossRef.
- H. Zhang, T. Hu, X. Wang and Y. Zhou, J. Mater. Sci. Technol., 2020, 38, 205–220 CrossRef CAS.
- R. He, Y. Wan, P. Zhao, P. Guo, Z. Jiang and J. Zheng, Comput. Theor. Chem., 2019, 1150, 26–39 CrossRef CAS.
- R. Ibragimova, P. Rinke and H.-P. Komsa, Chem. Mater., 2022, 34, 2896–2906 CrossRef CAS.
- R. Benitez, W. H. Kan, H. Gao, M. O’Neal, G. Proust and M. Radovic, Acta Mater., 2016, 105, 294–305 CrossRef CAS.
- L. H. Karlsson, J. Birch, J. Halim, M. W. Barsoum and P. O. Å. Persson, Nano Lett., 2015, 15, 4955–4960 CrossRef CAS PubMed.
- X. Sang, Y. Xie, M.-W. Lin, M. Alhabeb, K. L. Van Aken, Y. Gogotsi, P. R. C. Kent, K. Xiao and R. R. Unocic, ACS Nano, 2016, 10, 9193–9200 CrossRef CAS.
- T. S. Mathis, K. Maleski, A. Goad, A. Sarycheva, M. Anayee, A. C. Foucher, K. Hantanasirisakul, C. E. Shuck, E. A. Stach and Y. Gogotsi, ACS Nano, 2021, 15, 6420–6429 CrossRef CAS.
- Y. Tian, M. Ju, Y. Luo, X. Bin, X. Lou and W. Que, Chem. Eng. J., 2022, 446, 137451 CrossRef CAS.
- P. P. Michałowski, M. Anayee, T. S. Mathis, S. Kozdra, A. Wójcik, K. Hantanasirisakul, I. Jóźwik, A. Piatkowska, M. Możdżonek, A. Malinowska, R. Diduszko, E. Wierzbicka and Y. Gogotsi, Nat. Nanotechnol., 2022, 17, 1192–1197 CrossRef.
- M. Cardona and M. Brodsky, Light Scattering in Solids, Springer-Verlag; 1982 Search PubMed.
- S. Ushioda, Solid State Commun., 1974, 15, 149–153 CrossRef CAS.
- A. Eckmann, A. Felten, I. Verzhbitskiy, R. Davey and C. Casiraghi, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88, 035426 CrossRef.
- C. Z. Wang, C. T. Chan and K. M. Ho, Phys. Rev. B: Condens. Matter Mater. Phys., 1990, 42, 11276–11283 CrossRef CAS.
- D.-B. Zhang, T. Sun and R. M. Wentzcovitch, Phys. Rev. Lett., 2014, 112, 058501 CrossRef.
- T. Sun, D.-B. Zhang and R. M. Wentzcovitch, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 094109 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2tc04374b |
| This journal is © The Royal Society of Chemistry 2023 |