DOI:
10.1039/D2SM01549H
(Paper)
Soft Matter, 2023,
19, 892-904
Two-dimensional diffusiophoretic colloidal banding: optimizing the spatial and temporal design of solute sinks and sources
Received
26th November 2022
, Accepted 3rd January 2023
First published on 4th January 2023
Abstract
Diffusiophoresis refers to the phenomenon where colloidal particles move in response to solute concentration gradients. Existing studies on diffusiophoresis, both experimental and theoretical, primarily focus on the movement of colloidal particles in response to one-dimensional solute gradients. In this work, we numerically investigate the impact of two-dimensional solute gradients on the distribution of colloidal particles, i.e., colloidal banding, induced via diffusiophoresis. The solute gradients are generated by spatially arranged sources and sinks that emit/absorb a time-dependent solute molar rate. First we study a dipole system, i.e., one source and one sink, and discover that interdipole diffusion and molar rate decay timescales dictate colloidal banding. At timescales shorter than the interdipole diffusion timescale, we observe a rapid enhancement in particle enrichment around the source due to repulsion from the sink. However, at timescales longer than the interdipole diffusion timescale, the source and sink screen each other, leading to a slower enhancement. If the solute molar rate decays at the timescale of interdipole diffusion, an optimal separation distance is obtained such that particle enrichment is maximized. We find that the partition coefficient of solute at the interface between the source and bulk strongly impacts the optimal separation distance. Surprisingly, the diffusivity ratio of solute in the source and bulk has a much weaker impact on the optimal dipole separation distance. We also examine an octupole configuration, i.e., four sinks and four sources, arranged in a circle, and demonstrate that the geometric arrangement that maximizes enrichment depends on the radius of the circle. If the radius of the circle is small, it is preferred to have sources and sinks arranged in an alternating fashion. However, if the radius of the circle is large, a consecutive arrangement of sources and sinks is optimal. Our numerical framework introduces a novel method for spatially and temporally designing the banded structure of colloidal particles in two dimensions using diffusiophoresis and opens up new avenues in a field that has primarily focused on one-dimensional solute gradients.
1 Introduction
Diffusiophoresis is the phenomenon where colloidal particles move in response to solute concentration gradients. The understanding of this key physical principle and its applications is enabling innovation in paint film deposition,1 laundry,2 membrane separation,3,4 and hidden target searching.5 Solute concentration gradients in diffusiophoresis can be generated by a number of mechanisms:6 chemical reactions,7 mineral dissolution,8 and chemokine secretion,9 amongst others. The movement of colloidal particles due to concentration gradients can be divided into two broad categories: active and passive diffusiophoresis. In active diffusiophoresis,10–13 colloidal particles generate their own concentration gradients, while in passive diffusiophoresis,14–18 particles respond to an externally generated gradient.
Recently, there have been numerous experimental and theoretical reports exploring the motion of active diffusiophoretic particles. These include the effects of finite Peclet numbers,19,20 asymmetry in the form of Janus particles and bent rods,21–23 changes in the local fluid environment,10,13,24,25 and the use of active droplets instead of particles.26–28 Such systems have been proposed for uses in applications29 such as environmental remediation,30 drug delivery,31 and cellular transport.32
In contrast to active diffusiophoresis, there are several decades of literature on passive diffusiophoresis. One of the first series of studies to quantify the distribution of colloidal particles under diffusiophoresis was conducted by Staffeld et al.33,34 They showed, in electrolytic and non-electrolytic solutes, that the particle distribution exhibits a local maximum, resembling a band that moves with the diffusing solute front.33,34 This laid the groundwork for studies of diffusiophoretic banding in other systems, including the well-studied dead-end pore geometry.35–38 Experimental studies have been conducted on these dead-end pore systems to optimize nanoparticle transport in collagen hydrogels,39 show the size dependence of particle transport into pores,40 determine design criteria for particle capture by a pore,41 and develop a low cost zeta-potentiometer.42 In addition to dead-end pore geometries, similar studies have been conducted in other microfluidic systems. Cross-channel pores have been used to study surface-solute interactions17 and the aggregration of colloidal particles near flow junctions.43 CO2-induced concentration gradients across microfluidic channels have been used to predict exclusion zone formation in channel flows,44 remove bacteria from surfaces,45 provide crossflow migration of colloids,46 and enable membraneless water filtration.47 In a similar way, salt gradients have been used to induce colloidal banding in microfluidic channels.16,48
In addition to the breadth of experimental studies, analytical and numerical techniques have been used to study the phenomena observed in the aforementioned experimental systems. Anderson et al. showed that the diffusiophoretic velocity of a particle is dictated by surface interactions between the solute and particle.49–51 For ionic solutes, the diffusiophoretic velocity is given as uDP = Me∇ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) c, where Me is the mobility of the particle and c is the electrolyte concentration.50 For a particle moving in non-ionic solutes, the diffusiophoretic velocity is given as uDP = M∇c, where M is also a mobility parameter and c is the solute concentration.51 These mobility relationships can also be extended to include the effect of multiple ionic species,52–54 arbitrary double layer thicknesses,55 and ion sizes,56,57 amongst others. Numerical studies have been conducted on the spreading of diffusiophoretic particles in response to applied solute gradients with hydrodynamic background flows,58 in one-dimensional transient gradients,59,60 in concentrated electrolyte solutions,61 in solutes that exhibit Taylor dispersion due to a background/diffusioosmotic flow,14,62 and in the presence of multiple electrolytes.52
c, where Me is the mobility of the particle and c is the electrolyte concentration.50 For a particle moving in non-ionic solutes, the diffusiophoretic velocity is given as uDP = M∇c, where M is also a mobility parameter and c is the solute concentration.51 These mobility relationships can also be extended to include the effect of multiple ionic species,52–54 arbitrary double layer thicknesses,55 and ion sizes,56,57 amongst others. Numerical studies have been conducted on the spreading of diffusiophoretic particles in response to applied solute gradients with hydrodynamic background flows,58 in one-dimensional transient gradients,59,60 in concentrated electrolyte solutions,61 in solutes that exhibit Taylor dispersion due to a background/diffusioosmotic flow,14,62 and in the presence of multiple electrolytes.52
Despite the expansive literature on passive diffusiophoresis, most studies focus on the effects of one-dimensional transient or steady solute concentration profiles on particle motion. The number of studies that expand particle motion to two or three dimensions are limited,14,17,41,44,52,62–64 with most focusing on diffusiophoretic motion in two- and three-dimensional channel flows with one-dimensional driving solute gradients.
Recently, Bannerjee et al.65 developed “soluto-inertial” beacons that enable them to enact spatio-temporal control over solute gradients surrounding their beacons. This allows them to control and study diffusiophoretic particles moving in response to two- and three-dimensional gradients. They initially designed cylindrical hydrogel posts loaded with sodium dodecyl sulfate that attracted decane droplets and repelled polystyrene particles by releasing solute over a timescale of tens of minutes.65 By determining the appropriate diffusiophoretic velocity scale analytically in 3D and numerically in 2D, they were able to collapse the radial dependence of particle velocity.65 This proof-of-concept study showed that diffusiophoresis can be used as a mechanism to move colloidal particles deterministically over a length scale of hundreds of microns.65 The authors expanded this study to design temperature-triggered beacons, source and sink dipoles, dipoles with distinct solutes, and dipoles with reacting solutes.66 In follow-up studies, they developed design principles,67 which enabled them to manipulate colloidal distributions in suspension by a sedimenting beacon68 and deliver particles to hidden targets.5
Inspired by the work from Banerjee et al.66 on source and sink dipoles, we envisioned that multiple solute sources and sinks can be spatially and temporally designed to optimize diffusiophoretic banding in two dimensions. To this end, we outline a numerical procedure for simulating diffusiophoretic colloidal transport in response to a non-electrolytic solute gradient generated by an arbitrary number of point sources and sinks. We determine an appropriate time-dependent molar rate by semi-analytically solving for the flux from a finite-sized solute source. Using our numerical scheme, we determine the timescales governing particle separation in a dipole and octupole source/sink system. For the dipole system, we show that there exists an optimum separation distance between the source and sink that maximizes particle enrichment in a specific region. This optimal distance is set by a balance between interdipole diffusion and molar rate decay timescales. We find that the optimal separation distance depends primarily on the partition coefficient, K, of the source/sink and is weakly dependent on the diffusivity ratio, ![[D with combining circumflex]](https://www.rsc.org/images/entities/i_char_0044_0302.gif) . Lastly, we show how these principles change the optimal geometric arrangement of sources and sinks in an octupole configuration. Interestingly, we find that the optimal design of an octupole configuration depends on both the spatial arrangement of sources and sinks and the temporal decay of the solute molar rate. These results underscore the rich dynamics observed by expanding diffusiophoretic driving forces to two dimensions. Our results also broaden the potential design space of colloidal banding using diffusiophoresis and provide a numerical framework to study the banding of diffusiophoretic particles in response to an arbitrary arrangement of solute sources and sinks.
. Lastly, we show how these principles change the optimal geometric arrangement of sources and sinks in an octupole configuration. Interestingly, we find that the optimal design of an octupole configuration depends on both the spatial arrangement of sources and sinks and the temporal decay of the solute molar rate. These results underscore the rich dynamics observed by expanding diffusiophoretic driving forces to two dimensions. Our results also broaden the potential design space of colloidal banding using diffusiophoresis and provide a numerical framework to study the banding of diffusiophoretic particles in response to an arbitrary arrangement of solute sources and sinks.
2 Problem setup
To investigate the response of colloidal particles in two-dimensional solute gradients, described here as ∇c, we focus on the gradients generated by an arbitrary number of solute sources and sinks. As shown in Fig. 1, we denote the locations of the sources and sinks by ri, where the subscript i refers to the ith source or sink. The distance between the ith and jth source or sink is denoted as Δij. For simplicity, we consider that the sources emit solute at a molar rate J(t) and that the sinks absorb solute at a molar rate of −J(t). At time t = 0, we have a uniform concentration of particles and solute in our system. At t = 0+, the sinks and sources begin emitting and absorbing the solute, creating a time-dependent and spatially varying concentration gradient. The solute gradient generated by sources and sinks induces a diffusiophoretic velocity on particles, uDP = M∇c. If M > 0, particles are attracted to the sources and repelled from the sinks. In contrast, if M < 0, the particles are repelled from the sources and attracted to the sinks. At early times, the sources and sinks interact minimally, resulting in attraction/repulsion which transports particles towards the source and away from the sink (for M > 0). This creates local extrema of particle concentration, resulting in a banded distribution. As time progresses, the sources and sinks screen each other, much like electrostatic charges. At this timescale, the diffusiophoretic movement is diminished. In the following analysis, we seek to optimize particle enrichment by tuning the arrangement of sources and sinks, given a time-dependent molar rate, J(t).
 |
| | Fig. 1
Schematic illustration of problem setup. Solute sources and sinks are denoted by red and blue circles, respectively. The ith source/sink is located at a position ri ≡ (xi,yi). The separation between the ith and jth source/sink is denoted as Δij. The sources emit solute at a molar rate J(t), whereas sinks absorb solute at a molar rate −J(t). The emission and absorption of solute creates a concentration field, c(r,t), which induces a diffusiophoretic velocity uDP = M∇c on the particles, denoted by orange circles, where M is the diffusiophoretic mobility. | |
We acknowledge that in practical experimental setups, the emission and absorption rates are unlikely to be equal and opposite over time. However, while our numerical framework can handle arbitrary molar rates, we make this assumption to reduce the number of parameters in our system. In addition, we note that uDP as described above uses the non-electrolyte mobility relationship. The rationale to use this relationship is two-fold. First, the non-electrolytic mobility expression does not possess the singularity found in the electrolytic mobility expression. We acknowledge that the singularity can be addressed by considering a concentration dependent electrolytic mobility.61,69 For computational convenience, we refrain from incorporating a concentration dependent mobility relation. Second, if the concentration difference is relatively small, the two mobility relationships are equivalent; see Appendix A. Therefore, we choose the non-electrolytic mobility relationship. We acknowledge that there might be quantitative differences if a different mobility relationship is employed, and comment on this difference in Appendix A. Additionally, we acknowledge the limitation in using point sources and sinks, as spatial effects due to the presence of a finite-sized source/sink will yield differences. However, we observe that the qualitative features remain the same as reported in prior experiments;66 see Appendix B.
2.1 Solute and particle transport equations
The species conservation equation for solute concentration, c(r,t), is| |  | (1) |
where t is time, Ds is the solute diffusivity, ∇ is the gradient operator, Ji represents the strength of the ith source/sink, r is the position vector pointing from the origin, ri is the position of the ith source/sink and δ is the Dirac delta function. As is evident from eqn (1), we treat solute sources and sinks as point sources. If the ith solute patch is a source, Ji = J(t), and if the ith solute patch is a sink, Ji = −J(t). As we show later, we account for the finite-size effect of the patch by deriving the emitted flux from an isolated source. We note that eqn (1) neglects any advection terms in solute transport, which is typical for studies on diffusiophoresis without background flows.61,70
We calculate particle motion using two different approaches. First, we use Lagrangian particle tracking to determine the position of particles in time. The center of mass of the ith particle, xi, can be determined by solving the following differential equation
| | 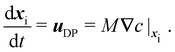 | (2) |
We note that
eqn (2) neglects Brownian fluctuations. This is a typical assumption for diffusiophoretic particles as particle radii are typically

.
62,63
Second, we calculate the concentration of colloidal particles, n(r,t). The conservation equation for particle concentration is
| |  | (3) |
where
Dn is the diffusivity of the colloidal particles. The response of the particles to the generated solute field is included as an advective term. We retain
Dn for numerical stability and assume

. The retention of
Dn helps smooth the sharp gradients near the moving particle band.
Eqn (1) and (2) or
eqn (1) and (3) are solved simultaneously to determine
c(
r,
t),
xi(
r,
t) and
n(
r,
t).
Before numerically solving, we non-dimensionalize eqn (1)–(3) as
| |  | (4) |
| |  | (5) |
| |  | (6) |
where

![[small delta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e125.gif)
= δ
L2,
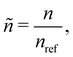





,
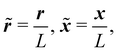
and
L is a reference length scale. We do not employ
a (
i.e., the source/sink radius) or
Δ as the reference length scale since
a only enters through our molar rate calculations and
Δ is the variable that we seek to vary. We emphasize that
L is a reference length scale and does not influence our calculations. We solve these equations in a two-dimensional Cartesian domain with
![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif)
,
ỹ ∈ [−10,10]. We impose no-flux boundary conditions for both
![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif)
and
ñ on the domain boundaries. We set initial conditions
ñ(
![[r with combining tilde]](https://www.rsc.org/images/entities/b_i_char_0072_0303.gif)
,0) =
ñ0 = 1 and
![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif)
(
![[r with combining tilde]](https://www.rsc.org/images/entities/b_i_char_0072_0303.gif)
,0) =
![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) 0
0 = 0. For simplicity, we take
![[D with combining tilde]](https://www.rsc.org/images/entities/i_char_0044_0303.gif)
= 10
−4.
52,61 Additionally, we note that
![[M with combining tilde]](https://www.rsc.org/images/entities/i_char_004d_0303.gif)
≤ 1 for most colloids
61 and use
![[M with combining tilde]](https://www.rsc.org/images/entities/i_char_004d_0303.gif)
= 0.5 for all simulations. To solve
eqn (4)–(6), we need an input of

which we discuss next.
To elucidate the effects of molar rate decay, we use three different scenarios for  . First, constant molar rates,
. First, constant molar rates,  where
where  is the strength of the step molar rate and
is the strength of the step molar rate and  is the heaviside function. In this scenario, there is no timescale associated with molar rate decay and the timescale for colloidal banding is dictated by the interaction between sources and sinks. The second choice of
is the heaviside function. In this scenario, there is no timescale associated with molar rate decay and the timescale for colloidal banding is dictated by the interaction between sources and sinks. The second choice of  is a boxcar function profile given by
is a boxcar function profile given by  where τ0 introduces an additional timescale.
where τ0 introduces an additional timescale.
Lastly, we derive  by calculating the flux emitting from an isolated, finite-sized source of radius a. This allows us to incorporate experimentally relevant parameters, i.e., the partition coefficient of the solute into the source K, and the diffusivity ratio of solute between the source and the bulk
by calculating the flux emitting from an isolated, finite-sized source of radius a. This allows us to incorporate experimentally relevant parameters, i.e., the partition coefficient of the solute into the source K, and the diffusivity ratio of solute between the source and the bulk ![[D with combining circumflex]](https://www.rsc.org/images/entities/i_char_0044_0302.gif) . To evaluate
. To evaluate  we briefly restore dimensions. We assume the origin to be the center of the source. The inner region refers to the concentration field inside of the source, i.e., r ≤ a and the outer region corresponds to the concentration field outside of the source, i.e., r > a. We assume that the concentration in the outer region is initially uniform such that cout = cref, and the source is saturated with solute such that the concentration in the inner region is cin = Kcref. At t = 0+, the concentration outside is switched to cout = 0, which leads the source to start emitting solute. The conservation equations for solute inside and outside the source are
we briefly restore dimensions. We assume the origin to be the center of the source. The inner region refers to the concentration field inside of the source, i.e., r ≤ a and the outer region corresponds to the concentration field outside of the source, i.e., r > a. We assume that the concentration in the outer region is initially uniform such that cout = cref, and the source is saturated with solute such that the concentration in the inner region is cin = Kcref. At t = 0+, the concentration outside is switched to cout = 0, which leads the source to start emitting solute. The conservation equations for solute inside and outside the source are
| |  | (7) |
| |  | (8) |
The initial and boundary conditions are
| |  | (9) |
We set the diffusivity of solute in the outer region to be the same as that of
eqn (1) and the diffusivity of the inner region to be
Din. In order to determine the appropriate time dependence of flux from the source, we first non-dimensionalize the equations as follows:
| |  | (10) |
| |  | (11) |
where


and

. We note that
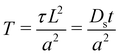
and is not influenced by
L. By Laplace transforming the set of equations from
T-space to
s-space, we find a solution for the interfacial flux
![[F with combining circumflex]](https://www.rsc.org/images/entities/i_char_0046_0302.gif)
(
s); see Appendix C
| |  | (12) |
where
In,b and
Kn,b are modified Bessel functions of the first and second kind, n
th order. We numerically invert the flux from
s-space to
T-space,
i.e.
, calculate the molar release rate, and appropriately scale the flux to get

is dependent on the partition coefficient
K and diffusivity ratio
![[D with combining circumflex]](https://www.rsc.org/images/entities/i_char_0044_0302.gif)
, which we discuss later.
2.2 Numerical schemes
Finite-volume method.
To solve the coupled partial differential eqn (4) and (6), we discretize both equations in space onto a square Cartesian grid with a grid size of 0.05 and write the resulting equations as coupled ordinary differential equations in time. We use a first-order upwinding scheme to resolve the convective term. We implement the point source/sink as a source term in the finite-volume cell, which contains the coordinates for the source/sink. For eqn (4) and (5), we discretize eqn (4) in space and solve the resulting equations with eqn (5) as coupled ordinary differential equations in time. We interpolate the solute gradient at the position of the ith particle during each time step in order to determine the particle velocity. The coupled differential equations are then integrated using an eighth-order Runge–Kutta integration scheme (DOP853) as implemented in Scipy. To gain confidence in our simulations, we compare our results qualitatively to the experimental results of Banerjee et al.66 and obtain a good agreement; see Appendix B.
Optimization.
We define an objective function, which inputs the locations of sources and sinks for a given arrangement, solves eqn (4) and (6) with a grid size of 0.1 and outputs a calculated fraction Φ(τ). The fraction is defined as| |  | (13) |
Φ(τ) represents the fractions of particles within a sub-region Ω1 of our domain Ω. We employ the objective function into an optimization scheme to determine a source/sink arrangement that maximizes Φ(τ). The optimization scheme uses a Nelder–Mead simplex algorithm implemented through the Scipy Optimization package.
3 Results and discussion
We begin our analysis with a dipole system, i.e., one source and one sink separated by a distance  see Fig. 2(a). The evolution of 3000 particle trajectories, as determined by eqn (4) and (5), for sources and sinks with constant strength
see Fig. 2(a). The evolution of 3000 particle trajectories, as determined by eqn (4) and (5), for sources and sinks with constant strength  and
and ![[M with combining tilde]](https://www.rsc.org/images/entities/i_char_004d_0303.gif) = 0.5 is provided in Fig. 2(b–d) (some representative contours for
= 0.5 is provided in Fig. 2(b–d) (some representative contours for ![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) (r,t) are provided in Appendix E). The evolution of particle concentration ñ(
(r,t) are provided in Appendix E). The evolution of particle concentration ñ(![[r with combining tilde]](https://www.rsc.org/images/entities/b_i_char_0072_0303.gif) ,τ) for identical parameters as determined by eqn (4) and (6) is displayed in Fig. 2(e–g). In both the particle and continuum simulations, since
,τ) for identical parameters as determined by eqn (4) and (6) is displayed in Fig. 2(e–g). In both the particle and continuum simulations, since ![[M with combining tilde]](https://www.rsc.org/images/entities/i_char_004d_0303.gif) > 0, particles are repelled from the sink and are attracted to the source, forming a depletion zone around the sink and enrichment zone around the source. As time increases, particles enrich around the source and the depletion zone increases in size. To quantify enrichment, Φ(τ) is calculated using eqn (13). We used a volume-averaged approach for quantifying enrichment as it is related to the enrichment phenomena observed experimentally.66Fig. 2(h) shows that the fraction increases monotonically in time as particles enrich near the source. Φ(τ) calculated with discrete and continuum simulations are in quantitative agreement. Since the results of continuum simulations and particle tracking simulations are equivalent, for the remaining analysis, results from continuum simulations will be used. While the particle tracking simulations provide a descriptive picture of particle trajectories, they are computationally more expensive than continuum simulations since they require a large number of particles (∼3000 in our analysis) to compute statistically significant volume averages.
> 0, particles are repelled from the sink and are attracted to the source, forming a depletion zone around the sink and enrichment zone around the source. As time increases, particles enrich around the source and the depletion zone increases in size. To quantify enrichment, Φ(τ) is calculated using eqn (13). We used a volume-averaged approach for quantifying enrichment as it is related to the enrichment phenomena observed experimentally.66Fig. 2(h) shows that the fraction increases monotonically in time as particles enrich near the source. Φ(τ) calculated with discrete and continuum simulations are in quantitative agreement. Since the results of continuum simulations and particle tracking simulations are equivalent, for the remaining analysis, results from continuum simulations will be used. While the particle tracking simulations provide a descriptive picture of particle trajectories, they are computationally more expensive than continuum simulations since they require a large number of particles (∼3000 in our analysis) to compute statistically significant volume averages.
 |
| | Fig. 2
Dipole simulations for a constant molar rate. (a) Schematic illustration of dipole setup where a source and a sink are separated by a distance d. The shaded region shows the Ω1 used in calculating Φ(τ) viaeqn (13) (b–d) ![[x with combining tilde]](https://www.rsc.org/images/entities/b_i_char_0078_0303.gif) i(τ = 0, 50, 100) for 3000 particles as calculated by solving eqn (4) and (5) for d = 3 and i(τ = 0, 50, 100) for 3000 particles as calculated by solving eqn (4) and (5) for d = 3 and ![[M with combining tilde]](https://www.rsc.org/images/entities/i_char_004d_0303.gif) = 0.5. (e–g) ñ( = 0.5. (e–g) ñ(![[r with combining tilde]](https://www.rsc.org/images/entities/b_i_char_0072_0303.gif) ,τ = 0, 50, 100), as determined by solving eqn (4) and (6) for d = 3 and ,τ = 0, 50, 100), as determined by solving eqn (4) and (6) for d = 3 and ![[M with combining tilde]](https://www.rsc.org/images/entities/i_char_004d_0303.gif) = 0.5. The color bar ranges from 0 to 1. All concentration values larger than 1 are truncated to 1. (h) Φ(τ) for a monopole and dipoles with d = 1–6. Continuum results are represented with a solid line while particle tracking results are shown by open circles. Results for a source monopole are plotted in black. (h inset) Φ(τ = 1) for a monopole and dipoles with d = 1–6 in the form of a bar chart. (i) τc, i.e., the crossover time at which Φ(τ) for the monopole overtakes a dipole with separation distance d, plotted versus d2. The dotted line represents the line of best fit with zero intercept. = 0.5. The color bar ranges from 0 to 1. All concentration values larger than 1 are truncated to 1. (h) Φ(τ) for a monopole and dipoles with d = 1–6. Continuum results are represented with a solid line while particle tracking results are shown by open circles. Results for a source monopole are plotted in black. (h inset) Φ(τ = 1) for a monopole and dipoles with d = 1–6 in the form of a bar chart. (i) τc, i.e., the crossover time at which Φ(τ) for the monopole overtakes a dipole with separation distance d, plotted versus d2. The dotted line represents the line of best fit with zero intercept.  for all panels. for all panels. | |
Fig. 2(h) (inset) reveals that smaller d values possess a higher Φ(τ) for early times. In contrast, larger d values display a higher Φ(τ) at later times. We also compare these values with the enrichment from a single source, referred here as a monopole. At early times, the monopole provides the least enrichment, Fig. 2(h) (inset). However, at long times, the monopole enrichment surpasses all dipoles. The time at which Φ(τ) of the monopole overtakes Φ(τ) of the dipoles is denoted as the crossover time, τc. Fig. 2(i) shows a linear trend between d2 and τc. To explain the trends outlined above, we examine eqn (6) more carefully. First, we ignore diffusion as ![[D with combining tilde]](https://www.rsc.org/images/entities/i_char_0044_0303.gif) = 10−4. Next, we integrate eqn (6) over Ω1 (defined by the shaded region shown in Fig. 2a), and write
= 10−4. Next, we integrate eqn (6) over Ω1 (defined by the shaded region shown in Fig. 2a), and write
| |  | (14) |
By employing
eqn (13) and divergence theorem, we obtain
| |  | (15) |
where
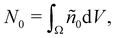 S1
S1 defines the outer perimeter of region
Ω1, and
ên is the unit normal vector pointing outwards from
S1. Essentially,
eqn (15) states that
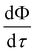
is affected by the convective flux entering through
S1. The convective flux has two parameters,
i.e.,

and
ñ.
At early times, dipoles have not had sufficient time to interact with each other. Therefore, we argue that to a first approximation,  are similar for both a monopole and the source in dipoles. If so, to explain the trend in Fig. 2(h) (inset), eqn (14) implies that at early times, ñ is higher for smaller d values. This appears surprising at first since the
are similar for both a monopole and the source in dipoles. If so, to explain the trend in Fig. 2(h) (inset), eqn (14) implies that at early times, ñ is higher for smaller d values. This appears surprising at first since the  from sources and sinks do not interact at this timescale. However, the depletion of particles around the sink increases the concentration of particles at S1, which consequently increases
from sources and sinks do not interact at this timescale. However, the depletion of particles around the sink increases the concentration of particles at S1, which consequently increases  (see Appendix D), leading to a larger Φ.
(see Appendix D), leading to a larger Φ.
We argue that dipoles start to interact with each other at τ ∼ d2, or the interdipole diffusion time. For τ ≳ d2, the dipoles screen each other, causing a rapid decline in  . After the interdipole diffusion time,
. After the interdipole diffusion time,  becomes localized between the source and sink and diminishes elsewhere. This results in a smaller
becomes localized between the source and sink and diminishes elsewhere. This results in a smaller  ; see eqn (15). Since screening occurs later for larger d, the decay in
; see eqn (15). Since screening occurs later for larger d, the decay in  starts later and Φ(τ) is higher; see Appendix D. Finally, for the monopole, screening never occurs, and concentration gradients do not diminish due to interactions with a sink. This is why the monopole overtakes dipoles around the interdipole diffusion time, which results in τc ∼ d2; see Fig. 2(i).
starts later and Φ(τ) is higher; see Appendix D. Finally, for the monopole, screening never occurs, and concentration gradients do not diminish due to interactions with a sink. This is why the monopole overtakes dipoles around the interdipole diffusion time, which results in τc ∼ d2; see Fig. 2(i).
The aforementioned discussion highlights the time-dependent nature of enrichment. Therefore, we seek to study the effects of a time-dependent molar rate. To this end, we employ a molar rate profile given by  where
where  is the Heaviside function; see Fig. 3(a). This molar rate provides us with two parameters: the strength of the molar rate
is the Heaviside function; see Fig. 3(a). This molar rate provides us with two parameters: the strength of the molar rate  and the time for the molar rate to decay to zero τ0. Fig. 3(b) shows Φ(τ) for
and the time for the molar rate to decay to zero τ0. Fig. 3(b) shows Φ(τ) for 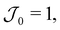 τ0 = 18.2 and d = 1–6. The choice for τ0 corresponds to the crossover time observed in Fig. 2 for d = 3. For τ > τ0 (represented by the dashed line in Fig. 3(b)), Φ(τ) increases slightly before leveling. At τ = τ0, we also observe that Φ(τ) increases with separation distance until d = 3 and then slightly decreases. Thus, there is an optimal separation distance. Using the described optimization scheme, we determined the optimal separation distance, dopt as a function of τ0 and
τ0 = 18.2 and d = 1–6. The choice for τ0 corresponds to the crossover time observed in Fig. 2 for d = 3. For τ > τ0 (represented by the dashed line in Fig. 3(b)), Φ(τ) increases slightly before leveling. At τ = τ0, we also observe that Φ(τ) increases with separation distance until d = 3 and then slightly decreases. Thus, there is an optimal separation distance. Using the described optimization scheme, we determined the optimal separation distance, dopt as a function of τ0 and  . In Fig. 3(c), we observe that a plot of d2optversus τ0 results in a linear trend. Additionally, from Fig. 3(d), we see that dopt is weakly dependent on
. In Fig. 3(c), we observe that a plot of d2optversus τ0 results in a linear trend. Additionally, from Fig. 3(d), we see that dopt is weakly dependent on  .
.
 |
| | Fig. 3
Effect of time-dependent molar rate on colloidal banding. (a) Time-dependent source/sink molar rate profile described by the equation  where where  is the heaviside function. is the heaviside function.  is the strength of the molar rate and τ0 represents the time at which the source/sink molar rate vanishes. (b) Φ(τ) for d = 1–6, J0 = 1 and τ0 = 18.2. The vertical dotted line is placed at τ = τ0. (c) d2optversus τ0 for is the strength of the molar rate and τ0 represents the time at which the source/sink molar rate vanishes. (b) Φ(τ) for d = 1–6, J0 = 1 and τ0 = 18.2. The vertical dotted line is placed at τ = τ0. (c) d2optversus τ0 for  where dopt is the optimal separation distances, as estimated by our optimization scheme. (d) doptversus where dopt is the optimal separation distances, as estimated by our optimization scheme. (d) doptversus for τ0 = 18.2. for τ0 = 18.2. | |
The dopt is set by a balance between the interdipole diffusion and molar rate decay timescales. This is seen by the linear trend between d2opt and τ0 observed in Fig. 3(c). When  the source and sink screen each other before the molar rate is turned off, leading to small Φ(τ). When
the source and sink screen each other before the molar rate is turned off, leading to small Φ(τ). When  the enrichment around the source is boosted due to depletion around the sink, however, the source and sink do not screen each other as the molar rate vanishes at the interdipole diffusion time. Finally, when
the enrichment around the source is boosted due to depletion around the sink, however, the source and sink do not screen each other as the molar rate vanishes at the interdipole diffusion time. Finally, when  the enrichment around the source is less impacted by the depletion around the sink. In effect,
the enrichment around the source is less impacted by the depletion around the sink. In effect,  becomes the optimal distance. In summary, the timescale of molar rate decay can be used as a parameter to optimize particle enrichment.
becomes the optimal distance. In summary, the timescale of molar rate decay can be used as a parameter to optimize particle enrichment.
 and
and  are not easy to realize experimentally. Instead, as shown by Banerjee et al.,65–67 solute fluxes arise due to solute partitioning between source and the bulk, described by a partition coefficient, denoted here as K. We also define the diffusivity ratio,
are not easy to realize experimentally. Instead, as shown by Banerjee et al.,65–67 solute fluxes arise due to solute partitioning between source and the bulk, described by a partition coefficient, denoted here as K. We also define the diffusivity ratio, ![[D with combining circumflex]](https://www.rsc.org/images/entities/i_char_0044_0302.gif) , as the ratio of solute diffusivity in the source and in the bulk. As such, we incorporate the effects of these parameters by determining
, as the ratio of solute diffusivity in the source and in the bulk. As such, we incorporate the effects of these parameters by determining  using eqn (12). Fig. 4(a) shows
using eqn (12). Fig. 4(a) shows  for different values of K and
for different values of K and ![[D with combining circumflex]](https://www.rsc.org/images/entities/i_char_0044_0302.gif) . As expected, the molar rate has a higher strength for a larger K value, and the decay is slower for a smaller value of
. As expected, the molar rate has a higher strength for a larger K value, and the decay is slower for a smaller value of ![[D with combining circumflex]](https://www.rsc.org/images/entities/i_char_0044_0302.gif) .
.
 |
| | Fig. 4
Optimal separation distance for experimentally realizable
 . (a) . (a)  as calculated by inverting eqn (12), for a finite-sized source of radius as calculated by inverting eqn (12), for a finite-sized source of radius 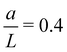 . K = 10, 1000 and . K = 10, 1000 and ![[D with combining circumflex]](https://www.rsc.org/images/entities/i_char_0044_0302.gif) = 10−1, 10−3. (b) Φ(τ) for K = 100 and = 10−1, 10−3. (b) Φ(τ) for K = 100 and ![[D with combining circumflex]](https://www.rsc.org/images/entities/i_char_0044_0302.gif) = 10−2, d = 1–8. (c) doptvs. = 10−2, d = 1–8. (c) doptvs. ![[D with combining circumflex]](https://www.rsc.org/images/entities/i_char_0044_0302.gif) for K = 500. (d) doptvs. K for for K = 500. (d) doptvs. K for ![[D with combining circumflex]](https://www.rsc.org/images/entities/i_char_0044_0302.gif) = 10−2. = 10−2. | |
We conduct dipole simulations by solving eqn (6) with  determined by inverting eqn (12). We evaluate Φ(τ) for different values for K and
determined by inverting eqn (12). We evaluate Φ(τ) for different values for K and ![[D with combining circumflex]](https://www.rsc.org/images/entities/i_char_0044_0302.gif) . Fig. 4(b) shows Φ(τ) with
. Fig. 4(b) shows Φ(τ) with  and for different d values. Much like Fig. 3, we observe an optimal separation distance, dopt ≈ 5. This demonstrates that dopt is a generic feature of a time-dependent molar rate. We investigate the dependence of dopt on K and
and for different d values. Much like Fig. 3, we observe an optimal separation distance, dopt ≈ 5. This demonstrates that dopt is a generic feature of a time-dependent molar rate. We investigate the dependence of dopt on K and ![[D with combining circumflex]](https://www.rsc.org/images/entities/i_char_0044_0302.gif) using the optimization scheme described earlier. Fig. 4(c) shows the variation of dopt with
using the optimization scheme described earlier. Fig. 4(c) shows the variation of dopt with ![[D with combining circumflex]](https://www.rsc.org/images/entities/i_char_0044_0302.gif) for K = 500, where we observe that dopt is weakly dependent on
for K = 500, where we observe that dopt is weakly dependent on ![[D with combining circumflex]](https://www.rsc.org/images/entities/i_char_0044_0302.gif) . However, Fig. 4(d) shows that dopt is strongly dependent on K.
. However, Fig. 4(d) shows that dopt is strongly dependent on K.
The result of dopt showing a weak dependence on ![[D with combining circumflex]](https://www.rsc.org/images/entities/i_char_0044_0302.gif) is surprising, as one would expect
is surprising, as one would expect ![[D with combining circumflex]](https://www.rsc.org/images/entities/i_char_0044_0302.gif) to impact the timescale of solute molar rate decay, which would ultimately impact the optimal separation distance. Therefore, we investigate this effect further. We note that there are two timescales for
to impact the timescale of solute molar rate decay, which would ultimately impact the optimal separation distance. Therefore, we investigate this effect further. We note that there are two timescales for  a short timescale, during which solute transport occurs over a small boundary layer within the source, and a longer timescale where concentration gradients inside of the source are fully developed. An expansion of eqn (12) around large s (small τ) shows that
a short timescale, during which solute transport occurs over a small boundary layer within the source, and a longer timescale where concentration gradients inside of the source are fully developed. An expansion of eqn (12) around large s (small τ) shows that
| |  | (16) |
Clearly, if the short timescale of molar rate decay balanced the interdipole diffusion timescale, then a dependence of
dopt on
![[D with combining circumflex]](https://www.rsc.org/images/entities/i_char_0044_0302.gif)
would be observed. Interestingly, an expansion of
eqn (12) around small
s yields
| |  | (17) |
Eqn (17) is not analytically inverted, but we emphasize that it is only dependent on
K. While an expansion for small
s cannot be directly related to large
τ,
Fig. 4(d) shows that
dopt only depends on
K. To this end, we argue that
dopt is determined by a balance between interdipole diffusion and long time scaling for
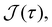
which primarily depends on
K.
Given our understanding of timescales and their impact on optimal banding in dipole systems, we seek to expand our work to probe how the geometric arrangement of four sources and four sinks around a circle of radius  , termed here as an octupole system, affects banding. Fig. 5(a) shows the four octupole arrangements we study. Case 1 refers to the arrangement where each source is nearest to two sinks and vice versa, i.e., a relatively symmetric arrangement. Case 4 refers to the most asymmetric scenario where four sources are arranged consecutively, followed by four sinks. Case 2 and Case 3 are in between, with Case 2 being more symmetric than Case 3. The shaded areas outlined by dashed lines represent the integration region that Φ(τ) is calculated over. Fig. 5(b and c) show simulation snapshots at τ = 100 for
, termed here as an octupole system, affects banding. Fig. 5(a) shows the four octupole arrangements we study. Case 1 refers to the arrangement where each source is nearest to two sinks and vice versa, i.e., a relatively symmetric arrangement. Case 4 refers to the most asymmetric scenario where four sources are arranged consecutively, followed by four sinks. Case 2 and Case 3 are in between, with Case 2 being more symmetric than Case 3. The shaded areas outlined by dashed lines represent the integration region that Φ(τ) is calculated over. Fig. 5(b and c) show simulation snapshots at τ = 100 for  with
with  (panel b) and
(panel b) and  (panel c). τ0 = 18.2 is used for all simulations.
(panel c). τ0 = 18.2 is used for all simulations.
 |
| | Fig. 5
Geometric and spatial effects on banding for an octupole. (a) Four arrangements studied in an octupole system with the shaded regions showing the Ω1 used in calculating Φ(τ) viaeqn (13). The sources and sinks are placed around a circle of radius  . (b and c) Simulation snapshots at τ = 100 with . (b and c) Simulation snapshots at τ = 100 with  for for  and and  . (d) . (d) 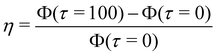 for Cases 1–4 with for Cases 1–4 with  varying from 1–5. varying from 1–5. | |
We quantify  i.e., the relative increase in Φ. Fig. 5(d) shows η for all four octupole arrangements, with
i.e., the relative increase in Φ. Fig. 5(d) shows η for all four octupole arrangements, with  varying from 1 to 5. For
varying from 1 to 5. For  Case 1 experiences the smallest increase in Φ(τ), while Case 4 experiences the largest increase. As
Case 1 experiences the smallest increase in Φ(τ), while Case 4 experiences the largest increase. As  increases from 1 to 5, this trend reverses and Case 1 experiences the largest increase in Φ(τ) while Case 4 experiences the smallest increase. To understand this trend, we invoke our understanding from the dipole arrangement. The octupole has multiple interpole diffusion timescales. The smallest timescale is associated with
increases from 1 to 5, this trend reverses and Case 1 experiences the largest increase in Φ(τ) while Case 4 experiences the smallest increase. To understand this trend, we invoke our understanding from the dipole arrangement. The octupole has multiple interpole diffusion timescales. The smallest timescale is associated with  and the longest timescale is associated with
and the longest timescale is associated with  . When
. When  the maximum
the maximum  . Therefore, all sources and sinks interact before the molar rate decays. In this scenario, the arrangement with the most geometric asymmetry, i.e., Case 4, has the largest η. Intuitively, in this case the source/sink screening is minimized, as the sources and sinks are collectively the furthest apart. When
. Therefore, all sources and sinks interact before the molar rate decays. In this scenario, the arrangement with the most geometric asymmetry, i.e., Case 4, has the largest η. Intuitively, in this case the source/sink screening is minimized, as the sources and sinks are collectively the furthest apart. When  the smallest
the smallest  implying that none of the sources and sinks interact. Case 1 performs best in this regime, as sources are able to benefit from a local increase in ñ(
implying that none of the sources and sinks interact. Case 1 performs best in this regime, as sources are able to benefit from a local increase in ñ(![[r with combining tilde]](https://www.rsc.org/images/entities/b_i_char_0072_0303.gif) ,τ) due to depletion from multiple nearby sinks. This effect is similar to the increase in performance for dipoles compared to a monopole observed earlier, see Fig. 2(h). Lastly, we note that η, for all four cases, increases with
,τ) due to depletion from multiple nearby sinks. This effect is similar to the increase in performance for dipoles compared to a monopole observed earlier, see Fig. 2(h). Lastly, we note that η, for all four cases, increases with  because dij also increases with
because dij also increases with 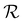 . As
. As 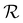 increases, the sinks and sources enrich particles for longer before interacting. We underscore that such complex banding patterns are unlikely to occur in one-dimensional diffusiophoretic systems as the motion of colloidal particles is restricted to one direction.
increases, the sinks and sources enrich particles for longer before interacting. We underscore that such complex banding patterns are unlikely to occur in one-dimensional diffusiophoretic systems as the motion of colloidal particles is restricted to one direction.
4 Conclusion
In summary, we present a numerical framework for studying the banding of colloidal particles in response to two-dimensional concentration gradients. By studying the enrichment of particles in a dipole system, we find that both the interdipole diffusion and molar rate decay timescales impact the optimal banding of colloidal particles. Interestingly, a balance between these two characteristic timescales yields an optimal dipole separation distance, one which balances enrichment before the source and sink screen each other. By determining the flux from a finite-sized partitioning source, we include the effects of a partition coefficient K and diffusivity ratio ![[D with combining circumflex]](https://www.rsc.org/images/entities/i_char_0044_0302.gif) into our molar rate profiles. We find that the optimal separation distance in this scenario depends primarily on K, with
into our molar rate profiles. We find that the optimal separation distance in this scenario depends primarily on K, with ![[D with combining circumflex]](https://www.rsc.org/images/entities/i_char_0044_0302.gif) only showing a weak effect. More importantly, we used the optimization of separation distance to elucidate that there are two timescales that impact the banding process. This discovery can be used to engineer complex systems with multiple sources and sinks. For instance, for an octupole arrangement of sources and sinks, we find that banding is also affected by geometric asymmetry. In fact, the optimal arrangement of sources and sinks is due to the interplay between multiple interpole diffusion timescales and the molar rate decay timescale.
only showing a weak effect. More importantly, we used the optimization of separation distance to elucidate that there are two timescales that impact the banding process. This discovery can be used to engineer complex systems with multiple sources and sinks. For instance, for an octupole arrangement of sources and sinks, we find that banding is also affected by geometric asymmetry. In fact, the optimal arrangement of sources and sinks is due to the interplay between multiple interpole diffusion timescales and the molar rate decay timescale.
Looking forward, our results provide design principles for engineering microfluidic devices5,65–67 that utilize diffusiophoresis to move colloidal particles and create banded patterns. By utilizing partition coefficients and spatial arrangement, one can impart temporal and spatial control over the banded structure of colloidal particles. From a fundamental perspective, our results can also be expanded to include flow effects such as dispersion due to diffusiophoresis or diffusioosmosis.14,37,52,58,62,71,72 Additionally, there is the potential to use such a system for applications that require precise control over colloid localization, such as biosensing,73 colloids separation,74 and two-dimensional micropatterning.75 Dipole and octupole systems, as envisioned, could be created using lithography similar to ref. 66. Our work also invites future studies that move away from point sinks and sources, include higher-order effects and investigate asymmetric fluxes between sources and sinks. The results, as outlined in this article, motivate future experimental and theoretical studies to investigate two- and three-dimensional diffusiophoretic banding.
Conflicts of interest
There are no conflicts to declare.
Appendices
A Electrolytic and non-electrolytic mobilities for small concentration differences
The diffusiophoretic velocity for a particle moving in an electrolyte gradient can be written as| |  | (18) |
If we consider a small concentration difference of the form c(r,t) = c0 + c1(r,t), where c0 is a constant concentration field and c1(r,t) is a small perturbation to that field such that  we can write eqn (18) as
we can write eqn (18) as| |  | (19) |
For small concentration differences, the electrolytic and non-electrolytic diffusiophoretic velocities have the same form. We note that M and Me′ will have different values.
If the concentration difference is significant compared to the background concentration, the electrolytic and non-electrolytic expressions will yield a different response. Specifically, for an electrolytic mobility expression, the additional  dependence will yield a higher uDP around the sink. In contrast, uDP will decrease around a source. We anticipate the qualitative features will remain the same. We invite interested readers to explore this effect quantiatively in future studies.
dependence will yield a higher uDP around the sink. In contrast, uDP will decrease around a source. We anticipate the qualitative features will remain the same. We invite interested readers to explore this effect quantiatively in future studies.
B Qualitative comparison with experimental results
We observe qualitative agreement with the work by Banerjee et al.66 If ![[M with combining tilde]](https://www.rsc.org/images/entities/i_char_004d_0303.gif) = −0.5, we see that particles move from the source towards the sink, Fig. 6(b), similar to that observed in Fig. 6(a). Additionally, as shown by the streaklines, we observe particles moving towards the side of the sink farthest from the source, similar to that observed in Fig. 6(a). The observed qualitative agreement with experimental observations highlights the potential for our system to be used as a design tool in two-dimensional banding systems.
= −0.5, we see that particles move from the source towards the sink, Fig. 6(b), similar to that observed in Fig. 6(a). Additionally, as shown by the streaklines, we observe particles moving towards the side of the sink farthest from the source, similar to that observed in Fig. 6(a). The observed qualitative agreement with experimental observations highlights the potential for our system to be used as a design tool in two-dimensional banding systems.
 |
| | Fig. 6
Comparison with experimental work by Banerjee
et al.
66 (a) Example of particles moving in response to gradients generated from a source and sink, reproduced and adapted from ref. 66 with permission under a Creative Commons Attribution NonCommercial License 4.0 (CC BY-NC). (b) Particle streaklines showing time-coded trajectories for particles with ![[M with combining tilde]](https://www.rsc.org/images/entities/i_char_004d_0303.gif) = −0.5. d = 3 and = −0.5. d = 3 and  . Simulation results are for . Simulation results are for ![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) ,ỹ ∈ [−10,10], but are zoomed in to ,ỹ ∈ [−10,10], but are zoomed in to ![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) ,ỹ ∈ [−3,3]. ,ỹ ∈ [−3,3]. | |
C Derivation of flux in the auxiliary problem
We Laplace transform eqn (10) and (11) from T to s-space as| |  | (20) |
| |  | (21) |
We drop the tildes for convenience. We now have a set of two ordinary differential equations. We substitute 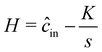 in eqn (20) and obtain
in eqn (20) and obtain
| |  | (22) |
Applying the product rule, we obtain the modified Bessel's equation
| |  | (23) |
which has a solution of the form
| |  | (24) |
where
I0,b and
K0,b are the zeroth-order modified Bessel functions of the first and second kind, respectively. Writing in terms of
ĉin, we get
| |  | (25) |
Applying the symmetry boundary condition at
r = 0, we obtain that
B(
s) = 0 as
K0,b → ∞ when
r → 0. Thus, our solution for the inner problem in Laplace space reads
| |  | (26) |
A(s) will be determined when applying the partition and flux-matching boundary conditions. Returning to the outer problem, we write eqn (21) in terms of a modified Bessel's equation
| |  | (27) |
which has a solution of the form
| | 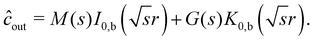 | (28) |
Applying the far field decay condition,
M(
s) must be zero because
I0,b → ∞ as
r → ∞. Our solution to the outer problem is
| |  | (29) |
To determine our unknown coefficients, we apply the partition and flux matching boundary conditions. Starting with the partition boundary condition,
| |  | (30) |
We solve for
G(
s) and obtain
| |  | (31) |
By applying the flux-matching condition, we write
| |  | (32) |
we solve for
A(
s) by substituting
eqn (31) into (32) to obtain
| |  | (33) |
G(
s) is thus given by
| |  | (34) |
We write our expression for ĉin and ĉout as
| |  | (35) |
| |  | (36) |
Lastly, we find an analytical expression for the flux  at the interface between the inner and outer region as
at the interface between the inner and outer region as
| |  | (37) |
D
 for dipole simulations with a constant molar rate
for dipole simulations with a constant molar rate
We also calculate  for the dipole simulations with a constant molar rate; see Fig. 7. Initially the dipoles have larger
for the dipole simulations with a constant molar rate; see Fig. 7. Initially the dipoles have larger  however, eventually
however, eventually  starts to decay. We argue that the initial increase in
starts to decay. We argue that the initial increase in  is caused by enrichment at S1 due to depletion from the sink. We observe that
is caused by enrichment at S1 due to depletion from the sink. We observe that  decays later for larger d. As the decay at longer times is caused by interactions between the sources and sinks, dipoles separated farther apart screen each other later.
decays later for larger d. As the decay at longer times is caused by interactions between the sources and sinks, dipoles separated farther apart screen each other later.
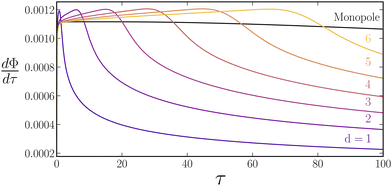 |
| | Fig. 7
 for
for
![[M with combining tilde]](https://www.rsc.org/images/entities/b_i_char_004d_0303.gif) = 0.5,
= 0.5,  . .  for a monopole (black line) and dipoles with d = 1 − 6 for a constant molar rate for a monopole (black line) and dipoles with d = 1 − 6 for a constant molar rate  . . | |
E Solute concentration field for a dipole with d = 3
Fig. 8 shows the concentration field generated by a point source and sink dipole. The mobility approximation is less applicable near the source and the sink since the magnitude of ![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) approaches unity. However, the magnitudes of
approaches unity. However, the magnitudes of ![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) are significantly smaller away from the source and sink, and our mobility approximation remains valid in most of the region. We note the negative concentration values as the initial concentration was taken to be zero. The values can be offset simply by choosing a different initial condition. The results will remain unaffected since the particle velocities only rely on the difference of concentrations and are not influenced by the absolute value.
are significantly smaller away from the source and sink, and our mobility approximation remains valid in most of the region. We note the negative concentration values as the initial concentration was taken to be zero. The values can be offset simply by choosing a different initial condition. The results will remain unaffected since the particle velocities only rely on the difference of concentrations and are not influenced by the absolute value.
 |
| | Fig. 8
Concentration field generated by a point source and sink dipole. (a–c) ![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) ( (![[r with combining tilde]](https://www.rsc.org/images/entities/b_i_char_0072_0303.gif) ,τ = 0, 10, 100) for a dipole with d = 3 and a molar rate ,τ = 0, 10, 100) for a dipole with d = 3 and a molar rate  . The color bar ranges between −1 and 1 and represents the value of . The color bar ranges between −1 and 1 and represents the value of ![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) ( (![[r with combining tilde]](https://www.rsc.org/images/entities/b_i_char_0072_0303.gif) ,τ). The point source and sink are visualized as a red and blue circle and are not representative of solute concentration at the location of the source and sink. ,τ). The point source and sink are visualized as a red and blue circle and are not representative of solute concentration at the location of the source and sink. | |
Acknowledgements
The authors would like to thank Filipe Henrique, Nathan Jarvey, Arkava Ganguly, Dr. Jin Gyun Lee, Cooper Thome, Nicole Day, Taylor Ausec, Kendra Kreienbrink, Gesse Roure, and Dr. Suin Shim for their feedback and insightful discussions leading to the completion of this work. The authors would also like to thank the anonymous referees for their insightful feedback. Ankur Gupta acknowledges support from the American Chemical Society (ACS) Petroleum Research Fund. C. Wyatt Shields IV acknowledges support from the National Science Foundation (NSF) CAREER grant (CBET 2143419).
References
- J. P. Ebel, J. L. Anderson and D. C. Prieve, Langmuir, 1988, 4, 396–406 CrossRef CAS.
- S. Shin, P. B. Warren and H. A. Stone, Phys. Rev. Appl., 2018, 9, 034012 CrossRef CAS.
- R. Guha, X. Shang, A. L. Zydney, D. Velegol and M. Kumar, J. Membr. Sci., 2015, 479, 67–76 CrossRef CAS.
- D. Florea, S. Musa, J. M. R. Huyghe and H. M. Wyss, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 6554–6559 CrossRef CAS PubMed.
- H. Tan, A. Banerjee, N. Shi, X. Tang, A. Abdel-Fattah and T. M. Squires, Sci. Adv., 2021, 7, eabh0638 CrossRef CAS PubMed.
- D. Velegol, A. Garg, R. Guha, A. Kar and M. Kumar, Soft Matter, 2016, 12, 4686–4703 RSC.
- N. Sharifi-Mood, J. Koplik and C. Maldarelli, Phys. Fluids, 2013, 25, 012001 CrossRef.
- J. J. McDermott, A. Kar, M. Daher, S. Klara, G. Wang, A. Sen and D. Velegol, Langmuir, 2012, 28, 15491–15497 CrossRef CAS PubMed.
- Y. V. Kalinin, L. Jiang, Y. Tu and M. Wu, Biophys. J., 2009, 96, 2439–2448 CrossRef CAS PubMed.
- J. F. Brady, J. Fluid Mech., 2021, 922, A10 CrossRef CAS.
- R. Golestanian, T. B. Liverpool and A. Ajdari, Phys. Rev. Lett., 2005, 94, 220801 CrossRef PubMed.
- R. Singh and R. Adhikari, J. Open Source Soft., 2020, 5, 2318 CrossRef.
- V. A. Shaik and G. J. Elfring, Phys. Rev. Fluids, 2021, 6, 103103 CrossRef.
- R. E. Migacz and J. T. Ault, Phys. Rev. Fluids, 2022, 7, 034202 CrossRef.
- N. Singh, G. T. Vladisavljević, F. Nadal, C. Cottin-Bizonne, C. Pirat and G. Bolognesi, Phys. Rev. Lett., 2020, 125, 248002 CrossRef CAS PubMed.
- B. Abécassis, C. Cottin-Bizonne, C. Ybert, A. Ajdari and L. Bocquet, Nat. Mater., 2008, 7, 785–789 CrossRef PubMed.
- J. T. Ault, S. Shin and H. A. Stone, Soft Matter, 2019, 15, 1582–1596 RSC.
- J.-P. Hsu, S.-H. Hsieh and S. Tseng, Sens. Actuators, B, 2017, 252, 1132–1139 CrossRef CAS.
- S. Michelin and E. Lauga, J. Fluid Mech., 2014, 747, 572–604 CrossRef.
- Y. C. Chang and H. J. Keh, Colloids Interfaces, 2019, 3, 44 CrossRef CAS.
- S. Michelin and E. Lauga, Eur. Phys. J. E: Soft Matter Biol. Phys., 2015, 38, 7 CrossRef PubMed.
- D. Venkateshwar Rao, N. Reddy, J. Fransaer and C. Clasen, J. Phys. D: Appl. Phys., 2019, 52, 014002 CrossRef.
-
A. Ganguly and A. Gupta, Going in circles: Slender body analysis of a self-propelling bent rod, arXiv, 2022, preprint, arXiv:2210.10894 DOI:10.48550/arXiv.2210.10894.
- L. F. Valadares, Y.-G. Tao, N. S. Zacharia, V. Kitaev, F. Galembeck, R. Kapral and G. A. Ozin, Small, 2010, 6, 565–572 CrossRef CAS PubMed.
- S. Wang and N. Wu, Langmuir, 2014, 30, 3477–3486 CrossRef CAS PubMed.
- M. Morozov and S. Michelin, J. Fluid Mech., 2019, 860, 711–738 CrossRef CAS.
- C. H. Meredith, P. G. Moerman, J. Groenewold, Y.-J. Chiu, W. K. Kegel, A. van Blaaderen and L. D. Zarzar, Nat. Chem., 2020, 12, 1136–1142 CrossRef CAS PubMed.
- Z. Izri, M. N. van der Linden, S. Michelin and O. Dauchot, Phys. Rev. Lett., 2014, 113, 248302 CrossRef PubMed.
- M. Safdar, S. U. Khan and J. Jänis, Adv. Mater., 2018, 30, 1703660 CrossRef PubMed.
- W. Gao, X. Feng, A. Pei, Y. Gu, J. Li and J. Wang, Nanoscale, 2013, 5, 4696 RSC.
- M. Xuan, J. Shao, X. Lin, L. Dai and Q. He, ChemPhysChem, 2014, 15, 2255–2260 CrossRef CAS PubMed.
- S. Sanchez, A. A. Solovev, S. Schulze and O. G. Schmidt, Chem. Commun., 2011, 47, 698–700 RSC.
- P. O. Staffeld and J. A. Quinn, J. Colloid Interface Sci., 1989, 130, 69–87 CrossRef CAS.
- P. O. Staffeld and J. A. Quinn, J. Colloid Interface Sci., 1989, 130, 88–100 CrossRef CAS.
- N. Shi and A. Abdel-Fattah, Phys. Rev. Fluids, 2021, 6, 053103 CrossRef.
- A. Kar, T.-Y. Chiang, I. Ortiz Rivera, A. Sen and D. Velegol, ACS Nano, 2015, 9, 746–753 CrossRef CAS PubMed.
- N. Singh, G. T. Vladisavljević, F. Nadal, C. Cottin-Bizonne, C. Pirat and G. Bolognesi, Langmuir, 2022, 38, 14053–14062 CrossRef CAS PubMed.
- S. Shim, J. K. Nunes, G. Chen and H. A. Stone, Phys. Rev. Fluids, 2022, 7, 110513 CrossRef.
- V. S. Doan, S. Chun, J. Feng and S. Shin, Nano Lett., 2021, 21, 7625–7630 CrossRef CAS PubMed.
- S. Shin, E. Um, B. Sabass, J. T. Ault, M. Rahimi, P. B. Warren and H. A. Stone, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, 257–261 CrossRef CAS PubMed.
- S. Battat, J. T. Ault, S. Shin, S. Khodaparast and H. A. Stone, Soft Matter, 2019, 15, 3879–3885 RSC.
- S. Shin, J. T. Ault, J. Feng, P. B. Warren and H. A. Stone, Adv. Mater., 2017, 29, 1701516 CrossRef PubMed.
- S. Shim and H. A. Stone, Proc. Natl. Acad. Sci. U. S. A., 2020, 117, 25985–25990 CrossRef CAS PubMed.
- S. Shim, M. Baskaran, E. H. Thai and H. A. Stone, Lab Chip, 2021, 21, 3387–3400 RSC.
- S. Shim, S. Khodaparast, C.-Y. Lai, J. Yan, J. T. Ault, B. Rallabandi, O. Shardt and H. A. Stone, Soft Matter, 2021, 17, 2568–2576 RSC.
- T. J. Shimokusu, V. G. Maybruck, J. T. Ault and S. Shin, Langmuir, 2020, 36, 7032–7038 CrossRef CAS PubMed.
- S. Shin, O. Shardt, P. B. Warren and H. A. Stone, Nat. Commun., 2017, 8, 15181 CrossRef PubMed.
- J. Palacci, B. Abécassis, C. Cottin-Bizonne, C. Ybert and L. Bocquet, Phys. Rev. Lett., 2010, 104, 138302 CrossRef PubMed.
- J. L. Anderson, Annu. Rev. Fluid Mech., 1989, 21, 61–99 CrossRef.
- D. C. Prieve, J. L. Anderson, J. P. Ebel and M. E. Lowell, J. Fluid Mech., 1984, 148, 247–269 CrossRef CAS.
- J. L. Anderson, M. E. Lowell and D. C. Prieve, J. Fluid Mech., 1982, 117, 107–121 CrossRef CAS.
- B. M. Alessio, S. Shim, E. Mintah, A. Gupta and H. A. Stone, Phys. Rev. Fluids, 2021, 6, 054201 CrossRef.
- N. Shi, R. Nery-Azevedo, A. I. Abdel-Fattah and T. M. Squires, Phys. Rev. Lett., 2016, 117, 258001 CrossRef PubMed.
- T.-Y. Chiang and D. Velegol, J. Colloid Interface Sci., 2014, 424, 120–123 CrossRef CAS PubMed.
- H. J. Keh and Y. K. Wei, Langmuir, 2000, 16, 5289–5294 CrossRef CAS.
- H. Ohshima, Colloid Polym. Sci., 2022, 300, 1229–1234 CrossRef CAS.
- R. F. Stout and A. S. Khair, Phys. Rev. Fluids, 2017, 2, 014201 CrossRef.
- H. C. W. Chu, S. Garoff, R. D. Tilton and A. S. Khair, Soft Matter, 2022, 18, 1896–1910 RSC.
- J. T. Ault, P. B. Warren, S. Shin and H. A. Stone, Soft Matter, 2017, 13, 9015–9023 RSC.
- H. C. W. Chu, S. Garoff, R. D. Tilton and A. S. Khair, Soft Matter, 2020, 16, 238–246 RSC.
- A. Gupta, S. Shim and H. A. Stone, Soft Matter, 2020, 16, 6975–6984 RSC.
- B. M. Alessio, S. Shim, A. Gupta and H. A. Stone, J. Fluid Mech., 2022, 942, A23 CrossRef CAS.
- J. T. Ault, S. Shin and H. A. Stone, J. Fluid Mech., 2018, 854, 420–448 CrossRef CAS.
- P. B. Warren, Phys. Rev. Lett., 2020, 124, 248004 CrossRef CAS PubMed.
- A. Banerjee, I. Williams, R. N. Azevedo, M. E. Helgeson and T. M. Squires, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, 8612–8617 CrossRef CAS PubMed.
- A. Banerjee and T. M. Squires, Sci. Adv., 2019, 5, eaax1893 CrossRef CAS PubMed.
- A. Banerjee, D. R. Vogus and T. M. Squires, Phys. Rev. E, 2019, 100, 052603 CrossRef CAS PubMed.
- A. Banerjee, H. Tan and T. M. Squires, Phys. Rev. Fluids, 2020, 5, 073701 CrossRef.
- S. Lee, J. Lee and J. T. Ault, Colloids Surf., A, 2023, 659, 130775 CrossRef CAS.
- J. L. Wilson, S. Shim, Y. E. Yu, A. Gupta and H. A. Stone, Langmuir, 2020, 36, 7014–7020 CrossRef CAS PubMed.
- S. Shin, J. T. Ault, P. B. Warren and H. A. Stone, Phys. Rev. X, 2017, 7, 041038 Search PubMed.
- S. Shim, Chem. Rev., 2022, 122, 6986–7009 CrossRef CAS PubMed.
- T. M. Squires, R. J. Messinger and S. R. Manalis, Nat. Biotechnol., 2008, 26, 417–426 CrossRef CAS PubMed.
- S. Shin, Phys. Fluids, 2020, 32, 101302 CrossRef CAS.
- W. M. Choi and O. O. Park, Nanotechnology, 2006, 17, 325–329 CrossRef CAS.
|
| This journal is © The Royal Society of Chemistry 2023 |
Click here to see how this site uses Cookies. View our privacy policy here.  a,
C. Wyatt
Shields
IV
a,
C. Wyatt
Shields
IV
 ab and
Ankur
Gupta
ab and
Ankur
Gupta
 *a
*a
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) c, where Me is the mobility of the particle and c is the electrolyte concentration.50 For a particle moving in non-ionic solutes, the diffusiophoretic velocity is given as uDP = M∇c, where M is also a mobility parameter and c is the solute concentration.51 These mobility relationships can also be extended to include the effect of multiple ionic species,52–54 arbitrary double layer thicknesses,55 and ion sizes,56,57 amongst others. Numerical studies have been conducted on the spreading of diffusiophoretic particles in response to applied solute gradients with hydrodynamic background flows,58 in one-dimensional transient gradients,59,60 in concentrated electrolyte solutions,61 in solutes that exhibit Taylor dispersion due to a background/diffusioosmotic flow,14,62 and in the presence of multiple electrolytes.52
c, where Me is the mobility of the particle and c is the electrolyte concentration.50 For a particle moving in non-ionic solutes, the diffusiophoretic velocity is given as uDP = M∇c, where M is also a mobility parameter and c is the solute concentration.51 These mobility relationships can also be extended to include the effect of multiple ionic species,52–54 arbitrary double layer thicknesses,55 and ion sizes,56,57 amongst others. Numerical studies have been conducted on the spreading of diffusiophoretic particles in response to applied solute gradients with hydrodynamic background flows,58 in one-dimensional transient gradients,59,60 in concentrated electrolyte solutions,61 in solutes that exhibit Taylor dispersion due to a background/diffusioosmotic flow,14,62 and in the presence of multiple electrolytes.52![[D with combining circumflex]](https://www.rsc.org/images/entities/i_char_0044_0302.gif) . Lastly, we show how these principles change the optimal geometric arrangement of sources and sinks in an octupole configuration. Interestingly, we find that the optimal design of an octupole configuration depends on both the spatial arrangement of sources and sinks and the temporal decay of the solute molar rate. These results underscore the rich dynamics observed by expanding diffusiophoretic driving forces to two dimensions. Our results also broaden the potential design space of colloidal banding using diffusiophoresis and provide a numerical framework to study the banding of diffusiophoretic particles in response to an arbitrary arrangement of solute sources and sinks.
. Lastly, we show how these principles change the optimal geometric arrangement of sources and sinks in an octupole configuration. Interestingly, we find that the optimal design of an octupole configuration depends on both the spatial arrangement of sources and sinks and the temporal decay of the solute molar rate. These results underscore the rich dynamics observed by expanding diffusiophoretic driving forces to two dimensions. Our results also broaden the potential design space of colloidal banding using diffusiophoresis and provide a numerical framework to study the banding of diffusiophoretic particles in response to an arbitrary arrangement of solute sources and sinks.
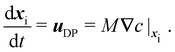
 .62,63
.62,63

 . The retention of Dn helps smooth the sharp gradients near the moving particle band. Eqn (1) and (2) or eqn (1) and (3) are solved simultaneously to determine c(r,t), xi(r,t) and n(r,t).
. The retention of Dn helps smooth the sharp gradients near the moving particle band. Eqn (1) and (2) or eqn (1) and (3) are solved simultaneously to determine c(r,t), xi(r,t) and n(r,t).




![[small delta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e125.gif) = δL2,
= δL2, 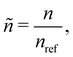




 ,
, 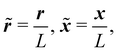 and L is a reference length scale. We do not employ a (i.e., the source/sink radius) or Δ as the reference length scale since a only enters through our molar rate calculations and Δ is the variable that we seek to vary. We emphasize that L is a reference length scale and does not influence our calculations. We solve these equations in a two-dimensional Cartesian domain with
and L is a reference length scale. We do not employ a (i.e., the source/sink radius) or Δ as the reference length scale since a only enters through our molar rate calculations and Δ is the variable that we seek to vary. We emphasize that L is a reference length scale and does not influence our calculations. We solve these equations in a two-dimensional Cartesian domain with ![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) ,ỹ ∈ [−10,10]. We impose no-flux boundary conditions for both
,ỹ ∈ [−10,10]. We impose no-flux boundary conditions for both ![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) and ñ on the domain boundaries. We set initial conditions ñ(
and ñ on the domain boundaries. We set initial conditions ñ(![[r with combining tilde]](https://www.rsc.org/images/entities/b_i_char_0072_0303.gif) ,0) = ñ0 = 1 and
,0) = ñ0 = 1 and ![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) (
(![[r with combining tilde]](https://www.rsc.org/images/entities/b_i_char_0072_0303.gif) ,0) =
,0) = ![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) 0 = 0. For simplicity, we take
0 = 0. For simplicity, we take ![[D with combining tilde]](https://www.rsc.org/images/entities/i_char_0044_0303.gif) = 10−4.52,61 Additionally, we note that
= 10−4.52,61 Additionally, we note that ![[M with combining tilde]](https://www.rsc.org/images/entities/i_char_004d_0303.gif) ≤ 1 for most colloids61 and use
≤ 1 for most colloids61 and use ![[M with combining tilde]](https://www.rsc.org/images/entities/i_char_004d_0303.gif) = 0.5 for all simulations. To solve eqn (4)–(6), we need an input of
= 0.5 for all simulations. To solve eqn (4)–(6), we need an input of  which we discuss next.
which we discuss next.
 . First, constant molar rates,
. First, constant molar rates,  where
where  is the strength of the step molar rate and
is the strength of the step molar rate and  is the heaviside function. In this scenario, there is no timescale associated with molar rate decay and the timescale for colloidal banding is dictated by the interaction between sources and sinks. The second choice of
is the heaviside function. In this scenario, there is no timescale associated with molar rate decay and the timescale for colloidal banding is dictated by the interaction between sources and sinks. The second choice of  is a boxcar function profile given by
is a boxcar function profile given by  where τ0 introduces an additional timescale.
where τ0 introduces an additional timescale. by calculating the flux emitting from an isolated, finite-sized source of radius a. This allows us to incorporate experimentally relevant parameters, i.e., the partition coefficient of the solute into the source K, and the diffusivity ratio of solute between the source and the bulk
by calculating the flux emitting from an isolated, finite-sized source of radius a. This allows us to incorporate experimentally relevant parameters, i.e., the partition coefficient of the solute into the source K, and the diffusivity ratio of solute between the source and the bulk ![[D with combining circumflex]](https://www.rsc.org/images/entities/i_char_0044_0302.gif) . To evaluate
. To evaluate  we briefly restore dimensions. We assume the origin to be the center of the source. The inner region refers to the concentration field inside of the source, i.e., r ≤ a and the outer region corresponds to the concentration field outside of the source, i.e., r > a. We assume that the concentration in the outer region is initially uniform such that cout = cref, and the source is saturated with solute such that the concentration in the inner region is cin = Kcref. At t = 0+, the concentration outside is switched to cout = 0, which leads the source to start emitting solute. The conservation equations for solute inside and outside the source are
we briefly restore dimensions. We assume the origin to be the center of the source. The inner region refers to the concentration field inside of the source, i.e., r ≤ a and the outer region corresponds to the concentration field outside of the source, i.e., r > a. We assume that the concentration in the outer region is initially uniform such that cout = cref, and the source is saturated with solute such that the concentration in the inner region is cin = Kcref. At t = 0+, the concentration outside is switched to cout = 0, which leads the source to start emitting solute. The conservation equations for solute inside and outside the source are





 and
and  . We note that
. We note that 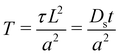 and is not influenced by L. By Laplace transforming the set of equations from T-space to s-space, we find a solution for the interfacial flux
and is not influenced by L. By Laplace transforming the set of equations from T-space to s-space, we find a solution for the interfacial flux ![[F with combining circumflex]](https://www.rsc.org/images/entities/i_char_0046_0302.gif) (s); see Appendix C
(s); see Appendix C
 , calculate the molar release rate, and appropriately scale the flux to get
, calculate the molar release rate, and appropriately scale the flux to get is dependent on the partition coefficient K and diffusivity ratio
is dependent on the partition coefficient K and diffusivity ratio ![[D with combining circumflex]](https://www.rsc.org/images/entities/i_char_0044_0302.gif) , which we discuss later.
, which we discuss later.

 see Fig. 2(a). The evolution of 3000 particle trajectories, as determined by eqn (4) and (5), for sources and sinks with constant strength
see Fig. 2(a). The evolution of 3000 particle trajectories, as determined by eqn (4) and (5), for sources and sinks with constant strength  and
and ![[M with combining tilde]](https://www.rsc.org/images/entities/i_char_004d_0303.gif) = 0.5 is provided in Fig. 2(b–d) (some representative contours for
= 0.5 is provided in Fig. 2(b–d) (some representative contours for ![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) (r,t) are provided in Appendix E). The evolution of particle concentration ñ(
(r,t) are provided in Appendix E). The evolution of particle concentration ñ(![[r with combining tilde]](https://www.rsc.org/images/entities/b_i_char_0072_0303.gif) ,τ) for identical parameters as determined by eqn (4) and (6) is displayed in Fig. 2(e–g). In both the particle and continuum simulations, since
,τ) for identical parameters as determined by eqn (4) and (6) is displayed in Fig. 2(e–g). In both the particle and continuum simulations, since ![[M with combining tilde]](https://www.rsc.org/images/entities/i_char_004d_0303.gif) > 0, particles are repelled from the sink and are attracted to the source, forming a depletion zone around the sink and enrichment zone around the source. As time increases, particles enrich around the source and the depletion zone increases in size. To quantify enrichment, Φ(τ) is calculated using eqn (13). We used a volume-averaged approach for quantifying enrichment as it is related to the enrichment phenomena observed experimentally.66Fig. 2(h) shows that the fraction increases monotonically in time as particles enrich near the source. Φ(τ) calculated with discrete and continuum simulations are in quantitative agreement. Since the results of continuum simulations and particle tracking simulations are equivalent, for the remaining analysis, results from continuum simulations will be used. While the particle tracking simulations provide a descriptive picture of particle trajectories, they are computationally more expensive than continuum simulations since they require a large number of particles (∼3000 in our analysis) to compute statistically significant volume averages.
> 0, particles are repelled from the sink and are attracted to the source, forming a depletion zone around the sink and enrichment zone around the source. As time increases, particles enrich around the source and the depletion zone increases in size. To quantify enrichment, Φ(τ) is calculated using eqn (13). We used a volume-averaged approach for quantifying enrichment as it is related to the enrichment phenomena observed experimentally.66Fig. 2(h) shows that the fraction increases monotonically in time as particles enrich near the source. Φ(τ) calculated with discrete and continuum simulations are in quantitative agreement. Since the results of continuum simulations and particle tracking simulations are equivalent, for the remaining analysis, results from continuum simulations will be used. While the particle tracking simulations provide a descriptive picture of particle trajectories, they are computationally more expensive than continuum simulations since they require a large number of particles (∼3000 in our analysis) to compute statistically significant volume averages.

![[x with combining tilde]](https://www.rsc.org/images/entities/b_i_char_0078_0303.gif) i(τ = 0, 50, 100) for 3000 particles as calculated by solving eqn (4) and (5) for d = 3 and
i(τ = 0, 50, 100) for 3000 particles as calculated by solving eqn (4) and (5) for d = 3 and ![[M with combining tilde]](https://www.rsc.org/images/entities/i_char_004d_0303.gif) = 0.5. (e–g) ñ(
= 0.5. (e–g) ñ(![[r with combining tilde]](https://www.rsc.org/images/entities/b_i_char_0072_0303.gif) ,τ = 0, 50, 100), as determined by solving eqn (4) and (6) for d = 3 and
,τ = 0, 50, 100), as determined by solving eqn (4) and (6) for d = 3 and ![[M with combining tilde]](https://www.rsc.org/images/entities/i_char_004d_0303.gif) = 0.5. The color bar ranges from 0 to 1. All concentration values larger than 1 are truncated to 1. (h) Φ(τ) for a monopole and dipoles with d = 1–6. Continuum results are represented with a solid line while particle tracking results are shown by open circles. Results for a source monopole are plotted in black. (h inset) Φ(τ = 1) for a monopole and dipoles with d = 1–6 in the form of a bar chart. (i) τc, i.e., the crossover time at which Φ(τ) for the monopole overtakes a dipole with separation distance d, plotted versus d2. The dotted line represents the line of best fit with zero intercept.
= 0.5. The color bar ranges from 0 to 1. All concentration values larger than 1 are truncated to 1. (h) Φ(τ) for a monopole and dipoles with d = 1–6. Continuum results are represented with a solid line while particle tracking results are shown by open circles. Results for a source monopole are plotted in black. (h inset) Φ(τ = 1) for a monopole and dipoles with d = 1–6 in the form of a bar chart. (i) τc, i.e., the crossover time at which Φ(τ) for the monopole overtakes a dipole with separation distance d, plotted versus d2. The dotted line represents the line of best fit with zero intercept.  for all panels.
for all panels.![[D with combining tilde]](https://www.rsc.org/images/entities/i_char_0044_0303.gif) = 10−4. Next, we integrate eqn (6) over Ω1 (defined by the shaded region shown in Fig. 2a), and write
= 10−4. Next, we integrate eqn (6) over Ω1 (defined by the shaded region shown in Fig. 2a), and write

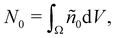 S1 defines the outer perimeter of region Ω1, and ên is the unit normal vector pointing outwards from S1. Essentially, eqn (15) states that
S1 defines the outer perimeter of region Ω1, and ên is the unit normal vector pointing outwards from S1. Essentially, eqn (15) states that 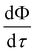 is affected by the convective flux entering through S1. The convective flux has two parameters, i.e.,
is affected by the convective flux entering through S1. The convective flux has two parameters, i.e.,  and ñ.
and ñ.
 are similar for both a monopole and the source in dipoles. If so, to explain the trend in Fig. 2(h) (inset), eqn (14) implies that at early times, ñ is higher for smaller d values. This appears surprising at first since the
are similar for both a monopole and the source in dipoles. If so, to explain the trend in Fig. 2(h) (inset), eqn (14) implies that at early times, ñ is higher for smaller d values. This appears surprising at first since the  from sources and sinks do not interact at this timescale. However, the depletion of particles around the sink increases the concentration of particles at S1, which consequently increases
from sources and sinks do not interact at this timescale. However, the depletion of particles around the sink increases the concentration of particles at S1, which consequently increases  (see Appendix D), leading to a larger Φ.
(see Appendix D), leading to a larger Φ. . After the interdipole diffusion time,
. After the interdipole diffusion time,  becomes localized between the source and sink and diminishes elsewhere. This results in a smaller
becomes localized between the source and sink and diminishes elsewhere. This results in a smaller  ; see eqn (15). Since screening occurs later for larger d, the decay in
; see eqn (15). Since screening occurs later for larger d, the decay in  starts later and Φ(τ) is higher; see Appendix D. Finally, for the monopole, screening never occurs, and concentration gradients do not diminish due to interactions with a sink. This is why the monopole overtakes dipoles around the interdipole diffusion time, which results in τc ∼ d2; see Fig. 2(i).
starts later and Φ(τ) is higher; see Appendix D. Finally, for the monopole, screening never occurs, and concentration gradients do not diminish due to interactions with a sink. This is why the monopole overtakes dipoles around the interdipole diffusion time, which results in τc ∼ d2; see Fig. 2(i). where
where  is the Heaviside function; see Fig. 3(a). This molar rate provides us with two parameters: the strength of the molar rate
is the Heaviside function; see Fig. 3(a). This molar rate provides us with two parameters: the strength of the molar rate  and the time for the molar rate to decay to zero τ0. Fig. 3(b) shows Φ(τ) for
and the time for the molar rate to decay to zero τ0. Fig. 3(b) shows Φ(τ) for 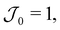 τ0 = 18.2 and d = 1–6. The choice for τ0 corresponds to the crossover time observed in Fig. 2 for d = 3. For τ > τ0 (represented by the dashed line in Fig. 3(b)), Φ(τ) increases slightly before leveling. At τ = τ0, we also observe that Φ(τ) increases with separation distance until d = 3 and then slightly decreases. Thus, there is an optimal separation distance. Using the described optimization scheme, we determined the optimal separation distance, dopt as a function of τ0 and
τ0 = 18.2 and d = 1–6. The choice for τ0 corresponds to the crossover time observed in Fig. 2 for d = 3. For τ > τ0 (represented by the dashed line in Fig. 3(b)), Φ(τ) increases slightly before leveling. At τ = τ0, we also observe that Φ(τ) increases with separation distance until d = 3 and then slightly decreases. Thus, there is an optimal separation distance. Using the described optimization scheme, we determined the optimal separation distance, dopt as a function of τ0 and  . In Fig. 3(c), we observe that a plot of d2optversus τ0 results in a linear trend. Additionally, from Fig. 3(d), we see that dopt is weakly dependent on
. In Fig. 3(c), we observe that a plot of d2optversus τ0 results in a linear trend. Additionally, from Fig. 3(d), we see that dopt is weakly dependent on  .
. the source and sink screen each other before the molar rate is turned off, leading to small Φ(τ). When
the source and sink screen each other before the molar rate is turned off, leading to small Φ(τ). When  the enrichment around the source is boosted due to depletion around the sink, however, the source and sink do not screen each other as the molar rate vanishes at the interdipole diffusion time. Finally, when
the enrichment around the source is boosted due to depletion around the sink, however, the source and sink do not screen each other as the molar rate vanishes at the interdipole diffusion time. Finally, when  the enrichment around the source is less impacted by the depletion around the sink. In effect,
the enrichment around the source is less impacted by the depletion around the sink. In effect,  becomes the optimal distance. In summary, the timescale of molar rate decay can be used as a parameter to optimize particle enrichment.
becomes the optimal distance. In summary, the timescale of molar rate decay can be used as a parameter to optimize particle enrichment. and
and  are not easy to realize experimentally. Instead, as shown by Banerjee et al.,65–67 solute fluxes arise due to solute partitioning between source and the bulk, described by a partition coefficient, denoted here as K. We also define the diffusivity ratio,
are not easy to realize experimentally. Instead, as shown by Banerjee et al.,65–67 solute fluxes arise due to solute partitioning between source and the bulk, described by a partition coefficient, denoted here as K. We also define the diffusivity ratio, ![[D with combining circumflex]](https://www.rsc.org/images/entities/i_char_0044_0302.gif) , as the ratio of solute diffusivity in the source and in the bulk. As such, we incorporate the effects of these parameters by determining
, as the ratio of solute diffusivity in the source and in the bulk. As such, we incorporate the effects of these parameters by determining  using eqn (12). Fig. 4(a) shows
using eqn (12). Fig. 4(a) shows  for different values of K and
for different values of K and ![[D with combining circumflex]](https://www.rsc.org/images/entities/i_char_0044_0302.gif) . As expected, the molar rate has a higher strength for a larger K value, and the decay is slower for a smaller value of
. As expected, the molar rate has a higher strength for a larger K value, and the decay is slower for a smaller value of ![[D with combining circumflex]](https://www.rsc.org/images/entities/i_char_0044_0302.gif) .
.
 . (a)
. (a)  as calculated by inverting eqn (12), for a finite-sized source of radius
as calculated by inverting eqn (12), for a finite-sized source of radius 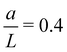 . K = 10, 1000 and
. K = 10, 1000 and ![[D with combining circumflex]](https://www.rsc.org/images/entities/i_char_0044_0302.gif) = 10−1, 10−3. (b) Φ(τ) for K = 100 and
= 10−1, 10−3. (b) Φ(τ) for K = 100 and ![[D with combining circumflex]](https://www.rsc.org/images/entities/i_char_0044_0302.gif) = 10−2, d = 1–8. (c) doptvs.
= 10−2, d = 1–8. (c) doptvs. ![[D with combining circumflex]](https://www.rsc.org/images/entities/i_char_0044_0302.gif) for K = 500. (d) doptvs. K for
for K = 500. (d) doptvs. K for ![[D with combining circumflex]](https://www.rsc.org/images/entities/i_char_0044_0302.gif) = 10−2.
= 10−2. determined by inverting eqn (12). We evaluate Φ(τ) for different values for K and
determined by inverting eqn (12). We evaluate Φ(τ) for different values for K and ![[D with combining circumflex]](https://www.rsc.org/images/entities/i_char_0044_0302.gif) . Fig. 4(b) shows Φ(τ) with
. Fig. 4(b) shows Φ(τ) with  and for different d values. Much like Fig. 3, we observe an optimal separation distance, dopt ≈ 5. This demonstrates that dopt is a generic feature of a time-dependent molar rate. We investigate the dependence of dopt on K and
and for different d values. Much like Fig. 3, we observe an optimal separation distance, dopt ≈ 5. This demonstrates that dopt is a generic feature of a time-dependent molar rate. We investigate the dependence of dopt on K and ![[D with combining circumflex]](https://www.rsc.org/images/entities/i_char_0044_0302.gif) using the optimization scheme described earlier. Fig. 4(c) shows the variation of dopt with
using the optimization scheme described earlier. Fig. 4(c) shows the variation of dopt with ![[D with combining circumflex]](https://www.rsc.org/images/entities/i_char_0044_0302.gif) for K = 500, where we observe that dopt is weakly dependent on
for K = 500, where we observe that dopt is weakly dependent on ![[D with combining circumflex]](https://www.rsc.org/images/entities/i_char_0044_0302.gif) . However, Fig. 4(d) shows that dopt is strongly dependent on K.
. However, Fig. 4(d) shows that dopt is strongly dependent on K.![[D with combining circumflex]](https://www.rsc.org/images/entities/i_char_0044_0302.gif) is surprising, as one would expect
is surprising, as one would expect ![[D with combining circumflex]](https://www.rsc.org/images/entities/i_char_0044_0302.gif) to impact the timescale of solute molar rate decay, which would ultimately impact the optimal separation distance. Therefore, we investigate this effect further. We note that there are two timescales for
to impact the timescale of solute molar rate decay, which would ultimately impact the optimal separation distance. Therefore, we investigate this effect further. We note that there are two timescales for  a short timescale, during which solute transport occurs over a small boundary layer within the source, and a longer timescale where concentration gradients inside of the source are fully developed. An expansion of eqn (12) around large s (small τ) shows that
a short timescale, during which solute transport occurs over a small boundary layer within the source, and a longer timescale where concentration gradients inside of the source are fully developed. An expansion of eqn (12) around large s (small τ) shows that
![[D with combining circumflex]](https://www.rsc.org/images/entities/i_char_0044_0302.gif) would be observed. Interestingly, an expansion of eqn (12) around small s yields
would be observed. Interestingly, an expansion of eqn (12) around small s yields
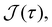 which primarily depends on K.
which primarily depends on K.
 , termed here as an octupole system, affects banding. Fig. 5(a) shows the four octupole arrangements we study. Case 1 refers to the arrangement where each source is nearest to two sinks and vice versa, i.e., a relatively symmetric arrangement. Case 4 refers to the most asymmetric scenario where four sources are arranged consecutively, followed by four sinks. Case 2 and Case 3 are in between, with Case 2 being more symmetric than Case 3. The shaded areas outlined by dashed lines represent the integration region that Φ(τ) is calculated over. Fig. 5(b and c) show simulation snapshots at τ = 100 for
, termed here as an octupole system, affects banding. Fig. 5(a) shows the four octupole arrangements we study. Case 1 refers to the arrangement where each source is nearest to two sinks and vice versa, i.e., a relatively symmetric arrangement. Case 4 refers to the most asymmetric scenario where four sources are arranged consecutively, followed by four sinks. Case 2 and Case 3 are in between, with Case 2 being more symmetric than Case 3. The shaded areas outlined by dashed lines represent the integration region that Φ(τ) is calculated over. Fig. 5(b and c) show simulation snapshots at τ = 100 for  with
with  (panel b) and
(panel b) and  (panel c). τ0 = 18.2 is used for all simulations.
(panel c). τ0 = 18.2 is used for all simulations.
 . (b and c) Simulation snapshots at τ = 100 with
. (b and c) Simulation snapshots at τ = 100 with  for
for  and
and  . (d)
. (d) 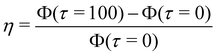 for Cases 1–4 with
for Cases 1–4 with  varying from 1–5.
varying from 1–5. i.e., the relative increase in Φ. Fig. 5(d) shows η for all four octupole arrangements, with
i.e., the relative increase in Φ. Fig. 5(d) shows η for all four octupole arrangements, with  varying from 1 to 5. For
varying from 1 to 5. For  Case 1 experiences the smallest increase in Φ(τ), while Case 4 experiences the largest increase. As
Case 1 experiences the smallest increase in Φ(τ), while Case 4 experiences the largest increase. As  increases from 1 to 5, this trend reverses and Case 1 experiences the largest increase in Φ(τ) while Case 4 experiences the smallest increase. To understand this trend, we invoke our understanding from the dipole arrangement. The octupole has multiple interpole diffusion timescales. The smallest timescale is associated with
increases from 1 to 5, this trend reverses and Case 1 experiences the largest increase in Φ(τ) while Case 4 experiences the smallest increase. To understand this trend, we invoke our understanding from the dipole arrangement. The octupole has multiple interpole diffusion timescales. The smallest timescale is associated with  and the longest timescale is associated with
and the longest timescale is associated with  . When
. When  the maximum
the maximum  . Therefore, all sources and sinks interact before the molar rate decays. In this scenario, the arrangement with the most geometric asymmetry, i.e., Case 4, has the largest η. Intuitively, in this case the source/sink screening is minimized, as the sources and sinks are collectively the furthest apart. When
. Therefore, all sources and sinks interact before the molar rate decays. In this scenario, the arrangement with the most geometric asymmetry, i.e., Case 4, has the largest η. Intuitively, in this case the source/sink screening is minimized, as the sources and sinks are collectively the furthest apart. When  the smallest
the smallest  implying that none of the sources and sinks interact. Case 1 performs best in this regime, as sources are able to benefit from a local increase in ñ(
implying that none of the sources and sinks interact. Case 1 performs best in this regime, as sources are able to benefit from a local increase in ñ(![[r with combining tilde]](https://www.rsc.org/images/entities/b_i_char_0072_0303.gif) ,τ) due to depletion from multiple nearby sinks. This effect is similar to the increase in performance for dipoles compared to a monopole observed earlier, see Fig. 2(h). Lastly, we note that η, for all four cases, increases with
,τ) due to depletion from multiple nearby sinks. This effect is similar to the increase in performance for dipoles compared to a monopole observed earlier, see Fig. 2(h). Lastly, we note that η, for all four cases, increases with  because dij also increases with
because dij also increases with  . As
. As  increases, the sinks and sources enrich particles for longer before interacting. We underscore that such complex banding patterns are unlikely to occur in one-dimensional diffusiophoretic systems as the motion of colloidal particles is restricted to one direction.
increases, the sinks and sources enrich particles for longer before interacting. We underscore that such complex banding patterns are unlikely to occur in one-dimensional diffusiophoretic systems as the motion of colloidal particles is restricted to one direction.![[D with combining circumflex]](https://www.rsc.org/images/entities/i_char_0044_0302.gif) into our molar rate profiles. We find that the optimal separation distance in this scenario depends primarily on K, with
into our molar rate profiles. We find that the optimal separation distance in this scenario depends primarily on K, with ![[D with combining circumflex]](https://www.rsc.org/images/entities/i_char_0044_0302.gif) only showing a weak effect. More importantly, we used the optimization of separation distance to elucidate that there are two timescales that impact the banding process. This discovery can be used to engineer complex systems with multiple sources and sinks. For instance, for an octupole arrangement of sources and sinks, we find that banding is also affected by geometric asymmetry. In fact, the optimal arrangement of sources and sinks is due to the interplay between multiple interpole diffusion timescales and the molar rate decay timescale.
only showing a weak effect. More importantly, we used the optimization of separation distance to elucidate that there are two timescales that impact the banding process. This discovery can be used to engineer complex systems with multiple sources and sinks. For instance, for an octupole arrangement of sources and sinks, we find that banding is also affected by geometric asymmetry. In fact, the optimal arrangement of sources and sinks is due to the interplay between multiple interpole diffusion timescales and the molar rate decay timescale.

 we can write eqn (18) as
we can write eqn (18) as
 dependence will yield a higher uDP around the sink. In contrast, uDP will decrease around a source. We anticipate the qualitative features will remain the same. We invite interested readers to explore this effect quantiatively in future studies.
dependence will yield a higher uDP around the sink. In contrast, uDP will decrease around a source. We anticipate the qualitative features will remain the same. We invite interested readers to explore this effect quantiatively in future studies.![[M with combining tilde]](https://www.rsc.org/images/entities/i_char_004d_0303.gif) = −0.5, we see that particles move from the source towards the sink, Fig. 6(b), similar to that observed in Fig. 6(a). Additionally, as shown by the streaklines, we observe particles moving towards the side of the sink farthest from the source, similar to that observed in Fig. 6(a). The observed qualitative agreement with experimental observations highlights the potential for our system to be used as a design tool in two-dimensional banding systems.
= −0.5, we see that particles move from the source towards the sink, Fig. 6(b), similar to that observed in Fig. 6(a). Additionally, as shown by the streaklines, we observe particles moving towards the side of the sink farthest from the source, similar to that observed in Fig. 6(a). The observed qualitative agreement with experimental observations highlights the potential for our system to be used as a design tool in two-dimensional banding systems.

![[M with combining tilde]](https://www.rsc.org/images/entities/i_char_004d_0303.gif) = −0.5. d = 3 and
= −0.5. d = 3 and  . Simulation results are for
. Simulation results are for ![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) ,ỹ ∈ [−10,10], but are zoomed in to
,ỹ ∈ [−10,10], but are zoomed in to ![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) ,ỹ ∈ [−3,3].
,ỹ ∈ [−3,3].

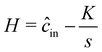 in eqn (20) and obtain
in eqn (20) and obtain





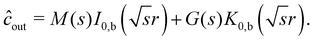








 at the interface between the inner and outer region as
at the interface between the inner and outer region as
 for dipole simulations with a constant molar rate
for dipole simulations with a constant molar rate for the dipole simulations with a constant molar rate; see Fig. 7. Initially the dipoles have larger
for the dipole simulations with a constant molar rate; see Fig. 7. Initially the dipoles have larger  however, eventually
however, eventually  starts to decay. We argue that the initial increase in
starts to decay. We argue that the initial increase in  is caused by enrichment at S1 due to depletion from the sink. We observe that
is caused by enrichment at S1 due to depletion from the sink. We observe that  decays later for larger d. As the decay at longer times is caused by interactions between the sources and sinks, dipoles separated farther apart screen each other later.
decays later for larger d. As the decay at longer times is caused by interactions between the sources and sinks, dipoles separated farther apart screen each other later.

 for
for
![[M with combining tilde]](https://www.rsc.org/images/entities/b_i_char_004d_0303.gif) = 0.5,
= 0.5,  .
.  for a monopole (black line) and dipoles with d = 1 − 6 for a constant molar rate
for a monopole (black line) and dipoles with d = 1 − 6 for a constant molar rate  .
.![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) approaches unity. However, the magnitudes of
approaches unity. However, the magnitudes of ![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) are significantly smaller away from the source and sink, and our mobility approximation remains valid in most of the region. We note the negative concentration values as the initial concentration was taken to be zero. The values can be offset simply by choosing a different initial condition. The results will remain unaffected since the particle velocities only rely on the difference of concentrations and are not influenced by the absolute value.
are significantly smaller away from the source and sink, and our mobility approximation remains valid in most of the region. We note the negative concentration values as the initial concentration was taken to be zero. The values can be offset simply by choosing a different initial condition. The results will remain unaffected since the particle velocities only rely on the difference of concentrations and are not influenced by the absolute value.










