Improving the efficiency of ternary organic solar cells by reducing energy loss†
Mengni
Wang
abc,
Yanan
Shi
ab,
Ziqi
Zhang
ab,
Yifan
Shen
ab,
Min
Lv
ab,
Yangjun
Yan
d,
Huiqion
Zhou
 ab,
Jianqi
Zhang
ab,
Jianqi
Zhang
 ab,
Kun
Lv
ab,
Yajie
Zhang
ab,
Kun
Lv
ab,
Yajie
Zhang
 *ab,
Hailin
Peng
e and
Zhixiang
Wei
*ab,
Hailin
Peng
e and
Zhixiang
Wei
 *ab
*ab
aChinese Academy of Sciences (CAS) key laboratory of nanosystem and hierarchical fabrication, National Center for Nanoscience and Technology, Beijing 100190, China. E-mail: zhangyj@nanoctr.cn; weizx@nanoctr.cn
bUniversity of Chinese Academy of Sciences, Beijing 100049, China
cAcademy for Advanced Interdisciplinary Studies, Peking University, Beijing 100871, People's Republic of China
dSchool of Science, Beijing Jiaotong University, Beijing 100044, China
eCenter for Nanochemistry, Beijing Science and Engineering Center for Nanocarbons, Beijing National Laboratory for Molecular Sciences, College of Chemistry and Molecular Engineering, Peking University, Beijing 100871, China. E-mail: hlpeng@pku.edu.cn
First published on 15th June 2023
Abstract
Effectively reducing the voltage loss in organic solar cells (OSCs) is critical to improving the power conversion efficiency (PCE) of OSCs. In this study, highly efficient ternary OSCs were constructed by adding a non-fullerene acceptor Qx2 with a high open-circuit voltage (VOC) and low energy loss (Eloss) into PM6:m-BTP-PhC6 based binary devices. The third component Qx2 shows slightly complementary absorption with m-BTP-PhC6 and also optimizes the molecular packing, orientation, and morphology of the active layer. Moreover, the incorporation of Qx2 reduced the energetic disorder and improved the electroluminescence quantum efficiency, which suppresses the Eloss and further leads to a higher VOC than the PM6:m-BTP-PhC6 binary blend. Consequently, synergetic enhancements of VOC, short circuit current (JSC), and fill factor (FF) are realized, resulting in the PCE of 18.60%. This work shows that the selection of the appropriate third component has positive implications for reducing Eloss and improving the PCE of OSCs.
New conceptsCompared with inorganic or perovskite solar cells, the open-circuit voltage (VOC) of OSCs is still low, owing to the relatively large energy loss (Eloss). It is necessary to effectively reduce Eloss to further improve the PCE of OSCs. Previously reported work has focused on molecule design to improve the electroluminescence yield or reduce the reorganization energies to reduce non-radiative Eloss. However, it could hardly simultaneously improve all photovoltaic characters. We present a straightforward strategy to construct high-efficiency ternary OSCs with low Eloss by incorporating a high VOC and low Eloss small molecule acceptor Qx2 into the PM6:m-BTP-PhC6 blend. The best PCE of 18.60% was achieved in the optimal ternary devices due to the synergistic enhancement of VOC of 0.871 V, JSC of 26.71 mA cm−2, and FF of 80.04%. The optimal ternary devices based on PM6:m-BTP-PhC6:Qx2 achieved a higher electroluminescence yield value than that of binary devices based on PM6:m-BTP-PhC6, corresponding to a lower non-radiative energy loss (ΔE3) and a higher VOC. This work demonstrated that the appropriate selection of the third component not only reduces the nonradiative energy loss of the device, further increasing VOC, but also realizes the simultaneous increase of JSC and FF. |
Introduction
Organic solar cells (OSCs) have attracted continuous attention as a promising clean energy technology due to their advantages of tunable molecular structures, solution processability, flexibility, lightweight properties, and low-cost large-area fabrication techniques.1–9 Benefiting from the most advanced non-fullerene acceptors, precise morphology manipulation, and interface engineering, the power conversion efficiency (PCE) of OSCs has exceeded 19% with the best fill factors (FF) over 80%, showing their promising application prospects.10–13The ternary blend strategy has been widely used as a practical and straightforward approach to improve the efficiency of OSCs.14–16 By incorporating a third component, the light-harvesting of blend films could be improved, effectively promoting the short-circuit current density (JSC).17–19 Since most advanced non-fullerene acceptors possess favorable light-harvesting capabilities, the scope for further improvement of the JSC is limited. Meanwhile, the open-circuit voltage (VOC) of the OSCs is mostly lower than 0.9 V, which is much lower than the VOC of perovskite and GaAs solar cells.20 The unsatisfactory VOC could be attributed to relatively large energy loss (Eloss). Compared with other high-efficiency solar cells, for instance, the GaAs solar cell has an Eloss of 0.29 eV and perovskite solar cells have an Eloss as low as 0.34 eV,21,22 most of the advanced OSCs still possess a large Eloss of higher than 0.5 eV,23,24 which shows a noticeable distance from the theoretical value of 0.25–0.30 eV derived from the Shockley–Queisser (SQ) limit.25 Therefore, suppressing the Eloss of OSC is the key to achieving higher VOC as well as further improving PCE.
With the “tilted” orientation of the hexyl chains relative to the molecular plane, m-BTP-PhC6 is an outstanding non-fullerene acceptor material that exhibits more ordered intermolecular packing, resulting in enhanced electron mobility and good efficiency.5 However, the relatively large energy loss of PM6:m-BTP-PhC6 based OSCs results in a non-ideal VOC. Compared to the structure of m-BTP-PhC6, Qx2 has a different molecular backbone and side chains. The introduction of Qx2 could form a slightly complementary absorption spectrum with the PM6:m-BTP-PhC6 blend. Moreover, although QX2 has a similar lowest unoccupied molecular orbital (LUMO) energy level to m-BTP-PhC6, the PM6:Qx2 based OSCs possessed a much higher VOC with an Eloss of less than 0.5 eV. Therefore, it is highly expected that Qx2 is a suitable third component for PM6:m-BTP-PhC6 based OSCs to increase the VOC and JSC simultaneously due to the lower Eloss of PM6:Qx2 binary devices.
In this contribution, we construct high-efficiency ternary OSCs with suppressed Eloss by incorporating the small molecule acceptor Qx2 into the PM6:m-BTP-PhC6 blends. The contact angle measurement confirmed that Qx2 is mainly located at the interface of PM6 and m-BTP-PhC6 as additional charge transport channels, leading to an ideal active layer morphology. The best PCE of 18.60% was achieved in the optimal ternary devices due to the synergistic enhancement of JSC of 26.71 mA cm−2, VOC of 0.871 V, and FF of 80.04%. The JSC improvement may be ascribed to the complementary absorption of m-BTP-PhC6 and Qx2, higher exciton dissociation probability, and suppressed recombination in the ternary blends. The increased FF is ascribed to the more balanced and efficient charge transport. The PM6:m-BTP-PhC6:Qx2 (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.98
0.98![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.42) based ternary devices gained a higher electroluminescence yield value of 1.94 × 10−4 than PM6:m-BTP-PhC6 based binary devices, corresponding to a decreased nonradiative energy loss (ΔE3) of 0.221 eV and a higher VOC.
0.42) based ternary devices gained a higher electroluminescence yield value of 1.94 × 10−4 than PM6:m-BTP-PhC6 based binary devices, corresponding to a decreased nonradiative energy loss (ΔE3) of 0.221 eV and a higher VOC.
Results and discussion
Molecular characterization
The chemical structures of the polymer donor PM6, and the small molecular acceptors BTP-m-PhC6 and Qx2 are illustrated in Fig. 1a. The normalized UV-vis absorption of these three materials (Fig. 1b) shows that the absorption spectrum of Qx2 is slightly complementary to those of PM6 and BTP-m-PhC6, which enhances the photon harvesting of the ternary blend film in contrast to the PM6-based binary blend films. The energy levels of PM6, m-BTP-PhC6, and Qx2 are presented in Fig. 1c. The highest occupied molecular orbital (HOMO) energy of Qx2 is −5.54 eV, which is marginally higher than the HOMO of m-BTP-PhC6 (−5.59 eV).5 The identical LUMO energies of Qx2 and m-BTP-PhC6 are all located at −3.86 eV.26 Interestingly, with the weight content of Qx2 in the acceptor mixture increasing, VOC shows a linear tendency to increase (Fig. 1d).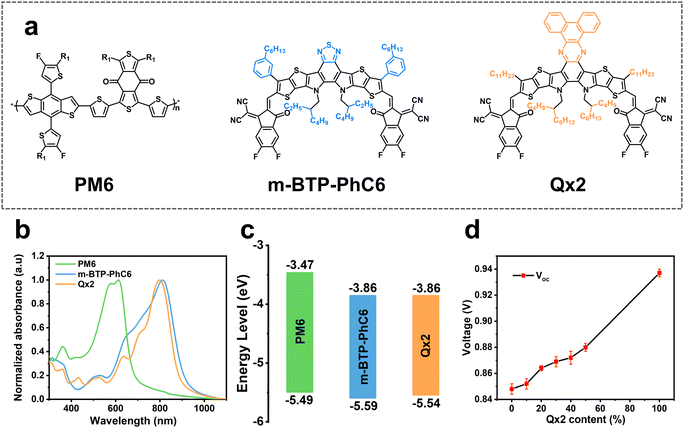 | ||
| Fig. 1 (a) Chemical structures and (b) normalized UV-vis spectra of PM6, m-BTP-PhC6 and Qx2 thin films. (c) Energy level alignment diagram of the studied materials5,26 (d) The change of the VOCs in ternary devices with different weight ratios of Qx2. | ||
Photovoltaic characteristics
The conventional device structure of indium tin oxide (ITO)/poly(3,4-ethylenedioxythiophene)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) poly(styrene sulfonate) (PEDOT
poly(styrene sulfonate) (PEDOT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
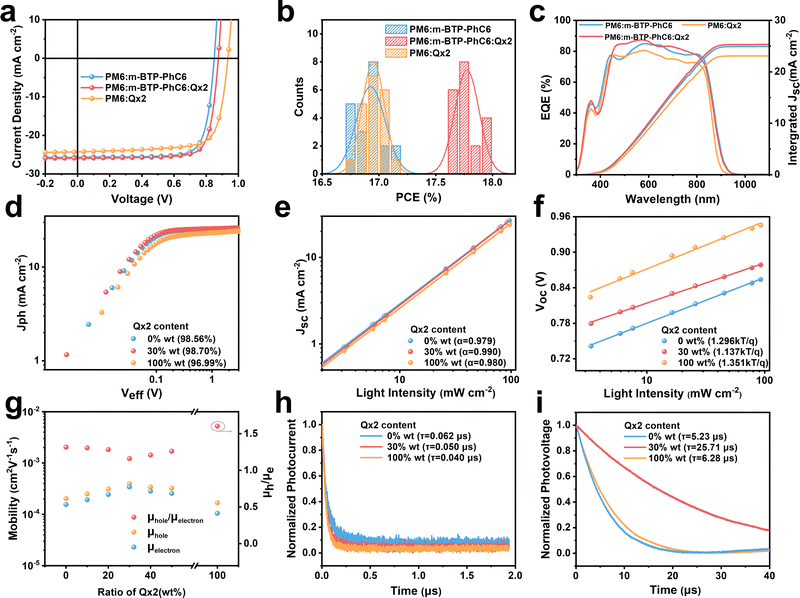
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) PSS)/active layer/PNDIT-F3N/Ag was utilized to fabricate OSCs for the evaluation of the photovoltaic performance. The donor and acceptor materials are dissolved in chloroform solution with 0.6 vol% 1-chloronaphthalene as the solvent additive. Detailed fabrication methods are demonstrated in the ESI.†Fig. 2a shows the representative current–voltage (J–V) characteristics of the optimized binary and ternary OSCs measured under simulated AM1.5G sun illumination (100 mW cm−2) and the corresponding photovoltaic characters are summarized in Table 1. For PM6:m-BTP-PhC6 binary OSCs, the best performance indicates a PCE of 17.12%, with a VOC of 0.850 V, a JSC of 25.69 mA cm−2, and an FF of 78.43%. Using PM6:Qx2 as the active layer, the device delivers a PCE of 17.11%, with a higher VOC of 0.935 V, a JSC of 24.28 mA cm−2, and an FF of 75.37%. With increasing Qx2 weight ratio in ternary blends, a linear increase in VOC is observed (Fig. 1d), and the optimized PCE of ternary OSCs is achieved with a 30% Qx2 weight ratio. The champion ternary OSC exhibits an outstanding PCE of 17.97% with an enhanced VOC of 0.875 V, a JSC of 25.91 mA cm−2, and an FF of 79.12%. When we used 2PACZ as the transport layer, the PCE was higher (18.62%), with an impressive JSC of 26.71 mA cm−2 and an outstanding FF of over 80%. Compared with the PM6:m-BTP-PhC6 binary system, the distinctly improved VOC does not sacrifice JSC and FF. The J–V curve of ternary devices with different weight ratios Qx2 and corresponding photovoltaic characters are summarized in Table S1 and Fig. S1a (ESI†). Since the optimal ternary devices keep the donor
PSS)/active layer/PNDIT-F3N/Ag was utilized to fabricate OSCs for the evaluation of the photovoltaic performance. The donor and acceptor materials are dissolved in chloroform solution with 0.6 vol% 1-chloronaphthalene as the solvent additive. Detailed fabrication methods are demonstrated in the ESI.†Fig. 2a shows the representative current–voltage (J–V) characteristics of the optimized binary and ternary OSCs measured under simulated AM1.5G sun illumination (100 mW cm−2) and the corresponding photovoltaic characters are summarized in Table 1. For PM6:m-BTP-PhC6 binary OSCs, the best performance indicates a PCE of 17.12%, with a VOC of 0.850 V, a JSC of 25.69 mA cm−2, and an FF of 78.43%. Using PM6:Qx2 as the active layer, the device delivers a PCE of 17.11%, with a higher VOC of 0.935 V, a JSC of 24.28 mA cm−2, and an FF of 75.37%. With increasing Qx2 weight ratio in ternary blends, a linear increase in VOC is observed (Fig. 1d), and the optimized PCE of ternary OSCs is achieved with a 30% Qx2 weight ratio. The champion ternary OSC exhibits an outstanding PCE of 17.97% with an enhanced VOC of 0.875 V, a JSC of 25.91 mA cm−2, and an FF of 79.12%. When we used 2PACZ as the transport layer, the PCE was higher (18.62%), with an impressive JSC of 26.71 mA cm−2 and an outstanding FF of over 80%. Compared with the PM6:m-BTP-PhC6 binary system, the distinctly improved VOC does not sacrifice JSC and FF. The J–V curve of ternary devices with different weight ratios Qx2 and corresponding photovoltaic characters are summarized in Table S1 and Fig. S1a (ESI†). Since the optimal ternary devices keep the donor![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) acceptor ratio of 1
acceptor ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.4, we also used this ratio to construct binary devices to exclude the influence of the change of the donor
1.4, we also used this ratio to construct binary devices to exclude the influence of the change of the donor![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) acceptor ratio on the device photovoltaic characters, and the corresponding results are in Table S2 (ESI†). The reproducibility of the optimized binary and ternary OSCs is also evaluated by the statistical distribution of efficiencies originating from 20 independent devices, as shown in Fig. 2b. The efficiencies of most optimized ternary devices are located around 17.8%, which confirms the effectiveness of this ternary strategy.
acceptor ratio on the device photovoltaic characters, and the corresponding results are in Table S2 (ESI†). The reproducibility of the optimized binary and ternary OSCs is also evaluated by the statistical distribution of efficiencies originating from 20 independent devices, as shown in Fig. 2b. The efficiencies of most optimized ternary devices are located around 17.8%, which confirms the effectiveness of this ternary strategy.
| Active layer combinations | Qx2 content [%] | V OC (V) | J SC (mA cm−2) | Fill factor (%) | Efficiencya (%) |
|---|---|---|---|---|---|
| a The average values with standard deviation were obtained from at least 10 individual devices. b The ternary devices utilize 2PACZ as the transport layer. | |||||
| PM6:m-BTP-PhC6 | 0 | 0.850 (0.848 ± 0.004) | 25.69 (25.48 ± 0.23) | 78.43 (78.37 ± 0.40) | 17.12 (16.92 ± 0.12) |
| PM6:m-BTP-PhC6:Qx2 | 30 | 0.875 (0.869 ± 0.004) | 25.91 (25.96 ± 0.26) | 79.12 (78.76 ± 0.72) | 17.97 (17.77 ± 0.10) |
| 30b | 0.871 (0.866 ± 0.006) | 26.71 (26.77 ± 0.14) | 80.04 (79.21 ± 0.87) | 18.62 (18.35 ± 0.17) | |
| PM6:Qx2 | 100 | 0.935 (0.937 ± 0.003) | 24.28 (24.34 ± 0.25) | 75.37 (74.29 ± 0.79) | 17.11 (16.95 ± 0.10) |
To investigate the internal causes of the JSC increase, the external quantum efficiency (EQE) curves are plotted in Fig. 2c and Fig. S1b (ESI†). Though the inevitable spectrum mismatch and nonlinear photocurrent response to light intensity lead to a difference between the JSC from EQE measurement and JSC from the J–V curve, the integrated JSC of the devices from the EQE spectra matched well with the JSC from the J–V curve with errors less than 5%. The introduction of Qx2 leads to a slight blue-shift in absorption edge, but higher ternary EQE values over almost the entire absorption range (450–800 nm).
The behavior of the exciton dissociation as well as the charge recombination mechanism were also analyzed. Various relevant measurements were performed, including the dependence of photocurrent density (Jph) extraction on the applied electric field and the dependence of JSC and VOC on the light intensity. The Jph is the difference between JL and JD, where the JL represents the light current density and the JD represents the dark current density. Veff is the difference between V0 (the voltage when Jph = 0) and V (the applied bias). Firstly, with the Veff > 2 V, the Jph of all devices approached saturation (Jsat), which means complete dissociation and charge collection. We utilize the ratio of Jph/Jsat to evaluate the exciton dissociation probability (P(E, T)).27 As shown in Fig. 2d, for the optimized PM6:m-BTP-PhC6 binary and PM6:m-BTP-PhC6:Qx2 ternary device, P(E, T) is 0.9856 and 0.9870, respectively. It turns out that ideal exciton dissociation results in high JSC and FF.28 Furthermore, the power law relationship between JSC and the light intensity (Plight) can be characterized as JSC ∝ (Plight)α, where α is the exponential factor describing the degree of charge recombination (Fig. 2e).29 Compared to the α value of the binary devices (0.979 and 0.980), the α value of the PM6:m-BTP-PhC6:Qx2 ternary device (0.990) is improved, demonstrating more efficient free charge collection with less biomolecular recombination within the PM6:m-BTP-PhC6:Qx2 devices.
As shown in Fig. 2f, the relationship of VOC dependence on Plight can be fitted by VOC ∝ n(kT/q) ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Plight, where k is the Boltzmann constant, T is the absolute temperature, and q is the elemental charge. The n value is utilized to evaluate the degree of trap-assisted recombination.30 The closer n is to 1, the more trap-assisted recombination is suppressed. Accordingly, the n values for PM6:m-BTP-PhC6, PM6:m-BTP-PhC6:Qx2, and PM6:Qx2 devices turn out to be 1.296, 1.137, and 1.351, respectively, demonstrating that the addition of Qx2 can effectively prevent the trap-assisted recombination in devices.31 And it could also be verified by the enhanced FF. Further detailed Jph–Veff curves, and the dependence of JSC and VOC on the light intensity of the two binary and ternary OSCs, are presented in Fig. S2 (ESI†).
Plight, where k is the Boltzmann constant, T is the absolute temperature, and q is the elemental charge. The n value is utilized to evaluate the degree of trap-assisted recombination.30 The closer n is to 1, the more trap-assisted recombination is suppressed. Accordingly, the n values for PM6:m-BTP-PhC6, PM6:m-BTP-PhC6:Qx2, and PM6:Qx2 devices turn out to be 1.296, 1.137, and 1.351, respectively, demonstrating that the addition of Qx2 can effectively prevent the trap-assisted recombination in devices.31 And it could also be verified by the enhanced FF. Further detailed Jph–Veff curves, and the dependence of JSC and VOC on the light intensity of the two binary and ternary OSCs, are presented in Fig. S2 (ESI†).
To investigate the dynamic charge transport process in the active layers, the space-charge limited current (SCLC) method was performed to measure the carrier mobilities. Fig. 2g and Table S3 (ESI†) show the hole mobility (μh) and electron mobility (μe) obtained by fitting the curves. In comparison with the two binary blends, both μh and μe of the ternary blends are increased, indicating a more balanced charge transport. Transient photocurrent (TPC) and transient photovoltage (TPV) measurements were also performed (Fig. 2h and i) to further explore the charge transport process. The photocurrent of the ternary device decays faster than that in the PM6:m-BTP-PhC6 device, indicating that the trap-state density of the ternary device is lower than that in the PM6:m-PhC6 based device.32 The reduced trap state density is one of the reasons that the trap-assisted recombination of the ternary device is inhibited after the incorporation of Qx2. Moreover, the charge extraction time of ternary OSCs (0.050 μs) is shorter than that of PM6:m-BTP-PhC6 based binary devices (0.062 μs). Likewise, the carrier lifetimes are 5.23 μs, 25.71 μs, and 6.28 μs for PM6:m-BTP-PhC6, PM6:m-BTP-PhC6:Qx2, and PM6:Qx2 OSCs, respectively. The reduced charge extraction time and increased carrier lifetime of the ternary OSCs are conducive to increased charge mobility and inhibited charge combination, which contributes to the improvement of JSC and FF.33–35
Energy loss
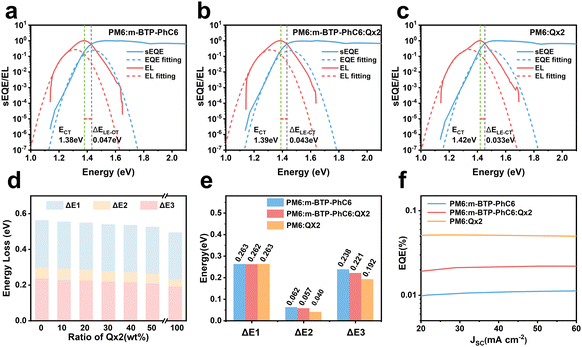
To reveal the underlying cause of the increase in VOC, we investigated the energy loss (Eloss = Eg − qVOC, where Eg is the bandgap) (Fig. 3a–c) of the devices, which can be quantified as the following equation:36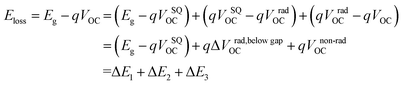 | (1) |
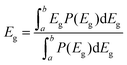 | (2) |
In eqn (1), ΔE1 originated from the mismatch between solid angle solar irradiation and omnidirectional blackbody radiation of the absorption above the optical gap. Therefore, ΔE1 is inevitable once the Eg is confirmed.38 ΔE2 is due to the radiative recombination below the bandgap of the active layer in bulk heterojunction OSCs, which is partly associated with the reorganization energy and the energetic disorder degree of the blends.37 ΔE3 is attributed to the nonradiative recombination at the donor/acceptor interfaces in OSCs, which can be calculated from:36
ΔE3 = kT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(EQEEL) ln(EQEEL) | (3) |
The bandgaps are calculated as 1.419 eV for the PM6:m-BTP-PhC6 binary blend, 1.420 eV for the optimized PM6:m-BTP-PhC6:Qx2 ternary blend, and 1.427 eV for the PM6:Qx2 binary blend. More detailed information on the Eloss is shown in Table 2 and Table S4 (ESI†). As shown in Fig. 3d, the energy loss shows a decreasing trend with increasing Qx2 content. Eloss of the optimized ternary device is 0.539 eV, lower than that of the PM6:m-BTP-PhC6 based device (0.560 eV). Profiting from the introduction of Qx2, the differences in energy loss principally originate from the decrease of ΔE2 and ΔE3, which can be attributed to the sharp absorption edge and the suppressive nonradiative recombination (Fig. 3e).
| Qx2 content [wt%] | E g (eV) | qV OC (eV) | qV SQOC (eV) | qV radOC (eV) | E loss (eV) | ΔE1 | ΔE2 | ΔE3 | EQEEL |
|---|---|---|---|---|---|---|---|---|---|
| 0 | 1.419 | 0.859 | 1.156 | 1.094 | 0.560 | 0.263 | 0.062 | 0.238 | 1.00E-4 |
| 30 | 1.420 | 0.881 | 1.157 | 1.100 | 0.539 | 0.262 | 0.057 | 0.221 | 1.94E-4 |
| 100 | 1.427 | 0.934 | 1.164 | 1.124 | 0.493 | 0.263 | 0.040 | 0.192 | 5.95E-4 |
As discussed in dedicated studies, active layer absorption edge and nonradiative recombination are related to the energetic disorder. We evaluated the degree of the energetic disorder in terms of an Urbach energy parameter (EU), which follows Urbach's rule:39
| α(E) = α0e(E−Eg)/EU | (4) |
For further analysis of ΔE3, we measured and contrasted the ECT (energy of charge transfer states) and electroluminescence quantum efficiency of the two binary and optimized ternary devices.18,19,40ECT could be obtained by Gaussian fitting of highly sensitive EQE and EL (electroluminescence) using Marcus equations:41
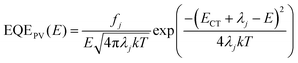 | (5) |
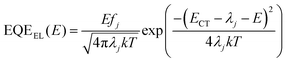 | (6) |
The results of the EQEEL measurement are presented in Fig. 3f and Table S4 (ESI†). The EQEEL of the optimized ternary device is 1.94 × 10−4, obviously higher than that of the PM6:m-BTP-PhC6 based binary device (1.00 × 10−4), and thus the ΔE3 of the optimized ternary device (0.221 eV) is lower than that of the binary device (0.238 eV). Accordingly, in comparison with the binary devices, the reduced ΔE2 and ΔE3 induced a suppressive total energy loss for PM6:m-BTP-PhC6:Qx2 based devices, which contributes to the increase of VOC.
Film morphology
To study the effects of the third component Qx2 on the morphology of the blend films, the miscibility was checked by contact angle measurement. As the miscibility of Qx2 with PM6 and m-BTP-PhC6 largely determines the distribution of Qx2 in the active layer, this is closely associated with the device performance. The surface energies of the pristine PM6, m-BTP-PhC6, and Qx2 films are 14.11, 20.10, and 16.86 mN m−1, respectively (Fig. 4 and Table S5, ESI†). Furthermore, the Flory-Huggins interaction parameter, which is calculated from the surface energy of a neat film, could be used to assess the degree of miscibility between the two molecules.44 Smaller χD–A (the Flory–Huggins interaction parameter between the donor and acceptor) values correspond to better miscibility, and vice versa.45,46 The χD–A value between PM6 and m-BTP-PhC6 turns out to be 0.53, much higher than the 0.12 between PM6 and Qx2, demonstrating the better miscibility between the two acceptors as well as the reduced mixing ability between PM6 and m-BTP-PhC6. With the incorporation of 30 wt% Qx2 into the film, the m-BTP-PhC6:Qx2 binary composite showed a reduced χD–A value of 0.30, certifying that Qx2 could be applicable to regulate the miscibility between PM6 and m-BTP-PhC6. To further confirm the thermodynamic position of the incorporated Qx2 in the ternary system (D: A1: A2), the wetting coefficient (ω) of the third ingredient A2 in the blends of host D and A1 was calculated by Young's equation:30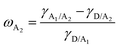 | (7) |
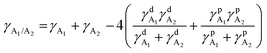 | (8) |
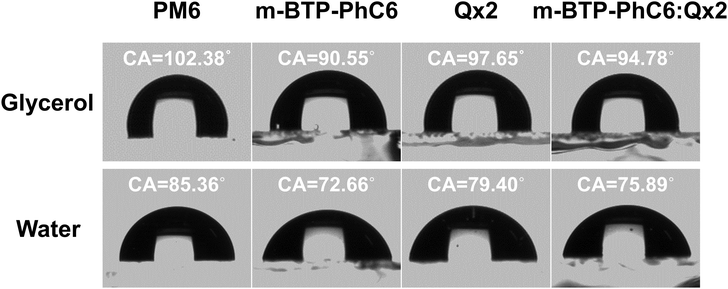 | ||
| Fig. 4 Contact angle images of PM6, m-BTP-PhC6, m-BTP-PhC6:Qx2, Qx2 films with water and glycerol droplets. | ||
For the PM6:m-BYP-PhC6:Qx2 ternary blend, the ωm-BTP-PhC6/Qx2 turns out to be 0.709, which is in the range of −1 and 1, implying that Qx2 is more inclined to locate at the interface between PM6 and m-BTP-PhC6. Therefore, the Qx2 introduction may promote molecular miscibility at the donor and acceptor interface, and this structure facilitates efficient separation and collection of charges, which benefits the JSC increase.
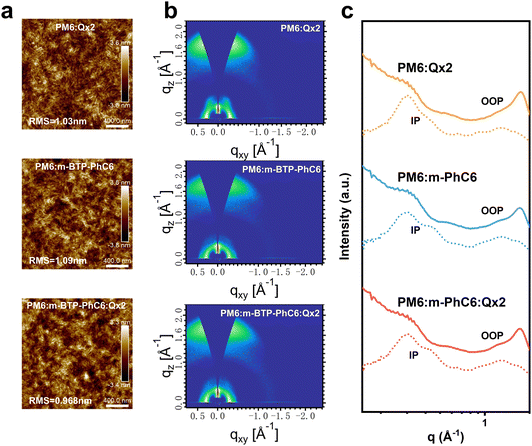
Atomic force microscopy (AFM) and grazing incident wide-angle X-ray diffraction (GIWAX) measurements were performed to further verify the morphology of the active layers. From the AFM height images of the blend films shown in Fig. 5a, we find that all the blends contain similar fibrous structures. The PM6:m-BTP-PhC6 blend reveals a root-mean-square (RMS) surface roughness value of 1.09 nm. By contrast, the PM6:m-BTP-PhC6:Qx2 blend with 30.0 wt% Qx2 has a smoother surface (RMS = 0.968 nm) than those of the PM6:m-BTP-PhC6 and PM6:Qx2 binary blends (RMS = 1.09 nm and 1.03 nm, respectively). This demonstrates that the excessive aggregation of the two acceptors in the ternary blends could be suppressed due to the good compatibility between m-BTP-PhC6 and Qx2, thus facilitating charge transport. GIWAXS analysis was also used to characterize the molecular packing of the active layers. Fig. 5b and c displays the two-dimensional GIWAXs (2D-GIWAXs) patterns and the corresponding in-plane (IP) and out-of-plane (OOP) intensity profiles of relevant binary and ternary blend films. By the evident lamellar stacking peaks in the IP-direction and π–π stacking peaks in the OOP direction, we confirmed that all the blended films are more inclined to face-on orientation, which improved the charge transfer capability in OSCs and indicated that the incorporation of Qx2 to construct ternary blended films has very little effect on the orientation of the molecules. The corresponding crystalline correlation lengths (CCL) correlated with the π–π stacking peaks in PM6:m-BTP-PhC6, PM6:Qx2, and ternary blends are 21.34 Å, 21.88 Å, and 21.62 Å, respectively. The CCL result indicates that the introduction of QX2 did not significantly affect the crystallinity of the ternary blend films and moderate domain sizes are conducive to charge transport and collection. The π–π stacking peaks in PM6:m-BTP-PhC6, PM6:Qx2, and ternary blends are 3.63 Å, 3.59 Å, and 3.65 Å, respectively. The increased π–π stacking distance in the ternary blends verifies the better miscibility at the interface of donor and acceptor phases.
Conclusion
In summary, high-performance ternary OSCs were realized by introducing a non-fullerene acceptor Qx2 with much lower energy loss into the PM6:m-BTP-PhC6 based OSCs, which achieves a synergistic improvement of JSC, VOC, and FF. The wetting coefficient value reveals that QX2 introduction not only has good compatibility with the m-BTP-PhC6 acceptor, but also promotes molecular miscibility at the donor and acceptor interface, which is conducive to exciton separation and charge transport and leads to an ideal morphology and molecular orientation in the ternary blend films. The increase in VOC could be partly due to the lower ΔE2 resulting from the decrease in energetic disorder. The reduced nonradiative recombination, which originates from the reduced ΔELE-CT and the higher electroluminescence quantum efficiency, contributed most of the reduced total energy loss. Therefore, the optimized PM6:m-BTP-PhC6:Qx2 ternary device, after incorporation of 30%wt Qx2, shows a best PCE of 18.62%, with a JSC of 26.71mA cm−2, a VOC of 0.871 V, and an FF of 80.04%. This work demonstrated that the appropriate selection of the third component not only reduces the nonradiative energy loss of the device, further increasing VOC, but also realizes the simultaneous increase of JSC and FF.Author contributions
Wang MN fabricated all the OSC devices, tested the device performance and wrote the original draft. Shi YN synthesized the small molecule acceptor Qx2. Zhang ZQ, Shen YF and Yan YJ helped the energy loss measurement. Lv M helped the contact angle measurement. Zhang JQ completed the GIWAXS measurement. Zhou HQ completed the TPC and TPV measurement. Zhang YJ and Wei ZX guided the idea and finalized the manuscript. All authors participated in general discussion and the manuscript revision.Conflicts of interest
The authors declare that they have no conflict of interest.Acknowledgements
The authors acknowledge the financial support from the National Natural Science Foundation of China (Grant No. 21975059, 22135001, 21721002), the Strategic Priority Research Program of the Chinese Academy of Sciences (No. XDB36000000).References
- J. Zhang, S. Luo, H. Zhao, X. Xu, X. Zou, A. Shang, J. Liang, F. Bai, Y. Chen, K. S. Wong, Z. Ma, W. Ma, H. Hu, Y. Chen and H. Yan, Angew. Chem., Int. Ed., 2022, 61, e202206930 CAS.
- J. Zhang, F. Bai, I. Angunawela, X. Xu, S. Luo, C. Li, G. Chai, H. Yu, Y. Chen, H. Hu, Z. Ma, H. Ade and H. Yan, Adv. Energy Mater., 2021, 11, 2102596 CrossRef CAS.
- J. X. Wang, C. Y. Han, J. H. Han, F. Z. Bi, X. K. Sun, S. G. Wen, C. P. Yang, C. M. Yang, X. C. Bao and J. H. Chu, Adv. Energy Mater., 2022, 12, 2201614 CrossRef CAS.
- X. Duan, W. Song, J. Qiao, X. Li, Y. Cai, H. Wu, J. Zhang, X. Hao, Z. Tang, Z. Ge, F. Huang and Y. Sun, Energy Environ. Sci., 2022, 15, 1563–1572 RSC.
- G. Chai, Y. Chang, J. Zhang, X. Xu, L. Yu, X. Zou, X. Li, Y. Chen, S. Luo, B. Liu, F. Bai, Z. Luo, H. Yu, J. Liang, T. Liu, K. S. Wong, H. Zhou, Q. Peng and H. Yan, Energy Environ. Sci., 2021, 14, 3469–3479 RSC.
- H. Lu, D. Li, G. Ran, Y.-N. Chen, W. Liu, H. Wang, S. Li, X. Wang, W. Zhang, Y. Liu, X. Xu and Z. Bo, ACS Energy Lett., 2022, 7, 3927–3935 CrossRef CAS.
- J. Li, Z. Zhang, G. Ran, X. Xu, C. E. Zhang, W. Liu, X. Zheng, D. Li, X. Xu, Y. Liu, Z. Tang, W. Zhang and Z. Bo, Small, 2022, 18, 2203454 CrossRef CAS PubMed.
- J. Guo, X. Xia, B. Qiu, J. Zhang, S. Qin, X. Li, W. Lai, X. Lu, L. Meng, Z. Zhang and Y. Li, Adv. Mater., 2023, 2211296 CrossRef CAS PubMed.
- H. Yang, W. Chen, Y. Yu, Y. Shen, H. Yang, X. Li, B. Zhang, H. Chen, Q. Cheng, Z. Zhang, W. Qin, J.-D. Chen, J.-X. Tang, Y. Li and Y. Li, Adv. Mater., 2023, 35, 2208604 CrossRef CAS PubMed.
- C. Li, J. Zhou, J. Song, J. Xu, H. Zhang, X. Zhang, J. Guo, L. Zhu, D. Wei, G. Han, J. Min, Y. Zhang, Z. Xie, Y. Yi, H. Yan, F. Gao, F. Liu and Y. Sun, Nat. Energy, 2021, 6, 605–613 CrossRef CAS.
- S. Bao, H. Yang, H. Fan, J. Zhang, Z. Wei, C. Cui and Y. Li, Adv. Mater., 2021, 33, e2105301 CrossRef PubMed.
- H. Wang, Y. Yang, Y. Zhang, S. Wang, Z. A. Tan, S. Yan, L. Wang, J. Hou and B. Xu, Adv. Funct. Mater., 2023, 33, 2213914 CrossRef CAS.
- H. Chen, S. Y. Jeong, J. Tian, Y. Zhang, D. R. Naphade, M. Alsufyani, W. Zhang, S. Griggs, H. Hu, S. Barlow, H. Y. Woo, S. R. Marder, T. D. Anthopoulos, I. McCulloch and Y. Lin, Energy Environ. Sci., 2023, 16, 1062–1070 RSC.
- M. Zhang, L. Zhu, T. Hao, G. Zhou, C. Qiu, Z. Zhao, N. Hartmann, B. Xiao, Y. Zou, W. Feng, H. Zhu, M. Zhang, Y. Zhang, Y. Li, T. P. Russell and F. Liu, Adv. Mater., 2021, 33, 2007177 CrossRef CAS PubMed.
- N. Y. Doumon, L. Yang and F. Rosei, Nano Energy, 2022, 94, 106915 CrossRef CAS.
- H. Lu, H. Wang, G. Ran, S. Li, J. Zhang, Y. Liu, W. Zhang, X. Xu and Z. Bo, Adv. Funct. Mater., 2022, 32, 2203193 CrossRef CAS.
- Y. Cai, C. Xie, Q. Li, C. Liu, J. Gao, M. H. Jee, J. Qiao, Y. Li, J. Song, X. Hao, H. Y. Woo, Z. Tang, Y. Zhou, C. Zhang, H. Huang and Y. Sun, Adv. Mater., 2023, 35, 2208165 CrossRef CAS PubMed.
- Y. Li, Y. Cai, Y. Xie, J. Song, H. Wu, Z. Tang, J. Zhang, F. Huang and Y. Sun, Energy Environ. Sci., 2021, 14, 5009–5016 RSC.
- Y. Cai, Y. Li, R. Wang, H. Wu, Z. Chen, J. Zhang, Z. Ma, X. Hao, Y. Zhao, C. Zhang, F. Huang and Y. Sun, Adv. Mater., 2021, 33, e2101733 CrossRef PubMed.
- G. Yang, H. Zhang, S. Li, Z. Ren, G. Fang, D. Lei and G. Li, SmartMat, 2022, 3, 513–521 CrossRef CAS.
- Z. Liu, L. Krückemeier, B. Krogmeier, B. Klingebiel, J. A. Márquez, S. Levcenko, S. Öz, S. Mathur, U. Rau, T. Unold and T. Kirchartz, ACS Energy Lett., 2019, 4, 110–117 CrossRef CAS.
- M. A. Green and A. W. Y. Ho-Baillie, ACS Energy Lett., 2019, 4, 1639–1644 CrossRef CAS.
- P. Cheng, G. Li, X. Zhan and Y. Yang, Nat. Photonics, 2018, 12, 131–142 CrossRef CAS.
- Q. An, J. Wang, X. Ma, J. Gao, Z. Hu, B. Liu, H. Sun, X. Guo, X. Zhang and F. Zhang, Energy Environ. Sci., 2020, 13, 5039–5047 RSC.
- M. Gruber, J. Wagner, K. Klein, U. Hörmann, A. Opitz, M. Stutzmann and W. Brütting, Adv. Energy Mater., 2012, 2, 1100–1108 CrossRef CAS.
- Y. Shi, Y. Chang, K. Lu, Z. Chen, J. Zhang, Y. Yan, D. Qiu, Y. Liu, M. A. Adil, W. Ma, X. Hao, L. Zhu and Z. Wei, Nat. Commun., 2022, 13, 3256 CrossRef CAS PubMed.
- J.-L. Wu, F.-C. Chen, Y.-S. Hsiao, F.-C. Chien, P. Chen, C.-H. Kuo, M. H. Huang and C.-S. Hsu, ACS Nano, 2011, 5, 959–967 CrossRef CAS PubMed.
- D. He, M. Zeng, Z. Zhang, Y. Bai, G. Xing, H.-M. Cheng and Y. Lin, SmartMat, 2023, e1176 CrossRef.
- M. Lenes, M. Morana, C. J. Brabec and P. W. M. Blom, Adv. Funct. Mater., 2009, 19, 1106–1111 CrossRef CAS.
- L. J. A. Koster, V. D. Mihailetchi, R. Ramaker and P. W. M. Blom, Appl. Phys. Lett., 2005, 86, 123509 CrossRef.
- S. Zeiske, O. J. Sandberg, N. Zarrabi, W. Li, P. Meredith and A. Armin, Nat. Commun., 2021, 12, 3603 CrossRef CAS PubMed.
- P. Bi, S. Zhang, Z. Chen, Y. Xu, Y. Cui, T. Zhang, J. Ren, J. Qin, L. Hong, X. Hao and J. Hou, Joule, 2021, 5, 2408–2419 CrossRef CAS.
- X. Zhang, L. Qin, J. Yu, Y. Li, Y. Wei, X. Liu, X. Lu, F. Gao and H. Huang, Angew. Chem., Int. Ed., 2021, 60, 12475–12481 CrossRef CAS PubMed.
- G. Zhang, K. Zhang, Q. Yin, X.-F. Jiang, Z. Wang, J. Xin, W. Ma, H. Yan, F. Huang and Y. Cao, J. Am. Chem. Soc., 2017, 139, 2387–2395 CrossRef CAS PubMed.
- H. R. Bai, Q. An, M. Jiang, H. S. Ryu, J. Yang, X. J. Zhou, H. F. Zhi, C. Yang, X. Li, H. Y. Woo and J. L. Wang, Adv. Funct. Mater., 2022, 32, 2200807 CrossRef CAS.
- J. Yao, T. Kirchartz, M. S. Vezie, M. A. Faist, W. Gong, Z. He, H. Wu, J. Troughton, T. Watson, D. Bryant and J. Nelson, Phys. Rev. Appl., 2015, 4, 014020 CrossRef.
- U. Rau, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 085303 CrossRef.
- D. He, F. W. Zhao, C. R. Wang and Y. Z. Lin, Adv. Funct. Mater., 2022, 32, 2111855 CrossRef CAS.
- S. Liu, J. Yuan, W. Deng, M. Luo, Y. Xie, Q. Liang, Y. Zou, Z. He, H. Wu and Y. Cao, Nat. Photonics, 2020, 14, 300–305 CrossRef CAS.
- X.-K. Chen, D. Qian, Y. Wang, T. Kirchartz, W. Tress, H. Yao, J. Yuan, M. Hülsbeck, M. Zhang, Y. Zou, Y. Sun, Y. Li, J. Hou, O. Inganäs, V. Coropceanu, J.-L. Bredas and F. Gao, Nat. Energy, 2021, 6, 799–806 CrossRef CAS.
- R. A. Marcus, J. Phys. Chem., 1989, 93, 3078–3086 CrossRef CAS.
- D. Qian, Z. Zheng, H. Yao, W. Tress, T. R. Hopper, S. Chen, S. Li, J. Liu, S. Chen, J. Zhang, X.-K. Liu, B. Gao, L. Ouyang, Y. Jin, G. Pozina, I. A. Buyanova, W. M. Chen, O. Inganäs, V. Coropceanu, J.-L. Bredas, H. Yan, J. Hou, F. Zhang, A. A. Bakulin and F. Gao, Nat. Mater., 2018, 17, 703–709 CrossRef CAS PubMed.
- V. Coropceanu, X.-K. Chen, T. Wang, Z. Zheng and J.-L. Brédas, Nat. Rev. Mater., 2019, 4, 689–707 CrossRef.
- L. Ye, W. Zhao, S. Li, S. Mukherjee, J. H. Carpenter, O. Awartani, X. Jiao, J. Hou and H. Ade, Adv. Energy Mater., 2017, 7, 1602000 CrossRef.
- L. Ye, H. Hu, M. Ghasemi, T. Wang, B. A. Collins, J.-H. Kim, K. Jiang, J. H. Carpenter, H. Li, Z. Li, T. McAfee, J. Zhao, X. Chen, J. L. Y. Lai, T. Ma, J.-L. Bredas, H. Yan and H. Ade, Nat. Mater., 2018, 17, 253–260 CrossRef CAS PubMed.
- M. Ghasemi, N. Balar, Z. Peng, H. Hu, Y. Qin, T. Kim, J. J. Rech, M. Bidwell, W. Mask, I. McCulloch, W. You, A. Amassian, C. Risko, B. T. O’Connor and H. Ade, Nat. Mater., 2021, 20, 525–532 CrossRef CAS PubMed.
- M. Sumita, K. Sakata, S. Asai, K. Miyasaka and H. Nakagawa, Polym. Bull., 1991, 25, 265–271 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3nh00122a |
| This journal is © The Royal Society of Chemistry 2023 |