The driving effects of common atmospheric molecules for formation of clusters: the case of sulfuric acid, nitric acid, hydrochloric acid, ammonia, and dimethylamine†
Received
28th July 2023
, Accepted 3rd September 2023
First published on 7th September 2023
Abstract
Understanding how secondary aerosols form in the atmosphere is one of the main uncertainties for a better understanding of global warming. Secondary aerosols form from gas-phase molecules that combine to create prenucleation complexes, which can then grow to form aerosols. The study of the formation of prenucleation complexes is difficult from both an experimental and theoretical point of view. Sulfuric acid has been linked to the formation of aerosols, yet the details of interactions are not understood. We have completed an exhaustive study of the formation of prenucleation complexes of three strong acids: sulfuric acid, nitric acid, and hydrochloric acid, combined with ammonia and dimethylamine bases, and three water molecules. By combining an evolutionary algorithm search routine with density functional geometry optimizations and single-point electronic energy calculations with complete basis set (CBS) extrapolations, we have completed an exhaustive search of the DLPNO-CCSD(T)/CBS//ωB97X-D/6-31++G** Gibbs free energy surface for this system. We have used previous work where the weaker formic acid replaces either nitric acid or hydrochloric acid to explore the details of how three acids combine with two bases and a few water molecules to make prenucleation clusters. As clusters grow, stabilizing effects of nitric acid, hydrochloric acid, and formic acid change in unique ways. This research adds to the body of work that illustrates that, depending on the system being studied, the acid/base strength of the monomers, the charge distribution within the clusters, and the detailed hydrogen bond topology have a subtle interplay that determines which cluster is most stable.
Environmental significance
The impact of aerosols on global climate is a major source of uncertainty in the understanding of global warming. Understanding the growth and formation of secondary aerosols is key to fully grasp the effect of aerosols on Earth's climate. The beginning stages in the formation of prenucleation complexes, that eventually lead to larger aerosols, cannot currently be investigated experimentally. Using robust computational chemistry methods, we have determined the lowest Gibbs free energy clusters and predicted equilibrium concentrations of the sulfuric acid–nitric acid–hydrochloric acid–ammonia–dimethylamine–water system. When compared to previously studied systems sulfuric acid–formic acid–hydrochloric acid–ammonia–dimethylamine–water and sulfuric acid–formic acid–nitric acid–ammonia–dimethylamine–water, we see that the stability of the nitric acid–hydrochloric acid is affected by the number and identity of surrounding monomers.
|
1 Introduction
Aerosols' impact on Earth's climate is one of the main sources of uncertainty for a better understanding of global warming.1 They affect the climate by scattering light, absorbing and emitting radiation, and as cloud condensation nuclei (CCN).2 CCN nucleate cloud droplets and ice particles, and thus dramatically influence the processes that lead to the formation of rain, snow, hail, and other forms of precipitation.3 Aerosols exert a net cooling of the atmosphere, but the uncertainties in our knowledge are larger than the cooling effects.1–4 Primary aerosols such as sea spray and dust enter the atmosphere directly and secondary aerosols form in the gas phase from precursor molecules.5 Secondary aerosols are estimated to account for 50% or more of all aerosol particles, and perhaps even all CCN-candidate particles.6,7 However, how secondary aerosols form is still not well understood, as experimental and theoretical approaches for learning how gaseous vapor from multiple molecular species combine to create the initial prenucleation clusters is a very difficult problem.8–14 Thus, an incredible amount of experimental and computational effort has been devoted to understanding which species are involved, and how they combine together, to form secondary aerosols.6,8–85 It is common in the field to work under the assumption that acids and bases grow into an ensemble that contains an equal number of both types of molecules.8–14 Yet, the tremendous number of potential compounds that can form prenucleation clusters is vast, and there is no experimental technique that can identify all of the different molecules in prenucleation complexes or small aerosols in the sub-nanometer (nm) to nm size range.12 Thus, this problem has been described as seeking a needle in a haystack.14 Our recent examination of prenucleation complexes which contain formic acid, a weaker acid compared to sulfuric acid, nitric acid, and hydrochloric acid, in clusters of unequal amounts of acids and bases, reveal that the detailed hydrogen bonding topology of a particular cluster is sometimes more important than traditional acid/base strength.65,67,72,86 In our previous work we have simulated how sulfuric acid (SA), formic acid (FA), ammonia (A), and water (W), form prenucleation complexes and discovered that FA is as effective as A at forming clusters with SA.65 We have also computed all the interactions between SA, A, and the amino acids glycine and serine, and found that the amino acids and A are practically interchangeable, and there is no easy way to predict which of the three molecules are protonated when SA loses its proton to one of those species. The acid/base reaction proceeds with all three species at specific instances that depend on the details of the molecular cluster.67 We next explored the role of three acids, two bases, and a handful of water molecules to form prenucleation complexes by computing all possible combinations of one SA, one FA, one nitric acid (NA), one A, and one dimethylamine (DMA) with five waters (W). We again found that the detailed geometries of each Gibbs free energy minimum is often more important than traditional acid or base strength.72 Addition of water to a dry cluster can enhance stabilization, as the (SA)(NA)(A)(DMA)(W) cluster has enhanced stability. NA is predicted to drive prenucleation almost as efficiently as SA.72 Most recently, we swapped NA for hydrochloric acid (HCl), and explored all possible combinations of SA, FA, HCl, A, DMA, and up to three W to probe the effects of this swap of one strong acid for another.86 This first detailed study of HCl interacting with two other acids and two bases revealed that NA forms stronger interactions in dry clusters than HCl, but sometimes as the clusters grow larger and are hydrated the sequential Gibbs free energies of clusters containing HCl become more favorable than those for NA.86 Overall this previous work adds to the body of evidence that reveals that hydrogen bond topology and the detailed structural interactions within a prenucleation cluster are as important as conventional ideas such as acid/base strength. Prenucleation clusters, held together by hydrogen bonding and other van der Waals forces, have free energies determined by the subtle interactions between enthalpy and entropy, which depend on the molecular structure of the complex. In this paper, we present the results for swapping FA with NA. This detailed exploration of the Gibbs free energy surface of (SA)(NA)(HCl)(A)(DMA)(W)0–3 allows us to compare all three systems, such that we have examined each combination of these three acids with these two bases where SA is one of the acids.
2 Methodology
Configurational sampling of clusters containing SA, NA, HCl, A, DMA, and up to three W was employed using the genetic-algorithm-based OGOLEM program,87,88 followed by semiempirical geometry optimizations with the GFN2-xTB semi-empirical method.89–91 An evolutionary algorithm in OGOLEM rearranges the initial configurations until reaching convergence on a final set of clusters in the designated pool. We used a pool size of 1000 and set the number of global GFN2-xTB optimizations to 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000. Because of the uncertainties associated with semi-empirical methods,58,92 all structures within 30 kcal mol−1 of the GFN2-xTB global minimum were then re-optimized at the ωB97X-D/6-31++G** level of theory93–98 using the Gaussian 16 Rev. B01 program,99 and duplicate structures were removed.100 All DFT structures within 8 kcal mol−1 of the ωB97X-D/6-31++G** electronic energy global minimum were recalculated using the domain-based local pair natural orbital coupled cluster (DLPNO-CCSD(T)) method101–108 with single, double, and semi-canonical perturbative triple excitations with three Dunning basis sets,109–112 cc-pVnZ (n = D, T, Q) using Orca 5.0.1.113 Estimates of the thermodynamic corrections for H°, S°, and G° were computed at a standard state of 1 atm pressure and temperatures of 216.65, 273.15, and 298.15 K using the THERMO.pl script114 from the National Institute of Science and Technology. These computations used the ωB97X-D/6-31++G** frequencies, which were scaled by a factor of 0.971 to partially account for anharmonicity.115,116 An inverse 4–5 polynomial complete basis set (CBS) extrapolation117 on the three CCSD(T)/cc-pVnZ (n = D, T, Q) electronic energies was used to obtain CBS electronic energies. The CBS energies were combined with the ωB97X-D/6-31++G** thermal corrections to obtain the final G° values. The complete methodology is outlined in Fig. 1. Once the final G° values were calculated for the individual clusters, ΔG°binding was calculated as follows:
000. Because of the uncertainties associated with semi-empirical methods,58,92 all structures within 30 kcal mol−1 of the GFN2-xTB global minimum were then re-optimized at the ωB97X-D/6-31++G** level of theory93–98 using the Gaussian 16 Rev. B01 program,99 and duplicate structures were removed.100 All DFT structures within 8 kcal mol−1 of the ωB97X-D/6-31++G** electronic energy global minimum were recalculated using the domain-based local pair natural orbital coupled cluster (DLPNO-CCSD(T)) method101–108 with single, double, and semi-canonical perturbative triple excitations with three Dunning basis sets,109–112 cc-pVnZ (n = D, T, Q) using Orca 5.0.1.113 Estimates of the thermodynamic corrections for H°, S°, and G° were computed at a standard state of 1 atm pressure and temperatures of 216.65, 273.15, and 298.15 K using the THERMO.pl script114 from the National Institute of Science and Technology. These computations used the ωB97X-D/6-31++G** frequencies, which were scaled by a factor of 0.971 to partially account for anharmonicity.115,116 An inverse 4–5 polynomial complete basis set (CBS) extrapolation117 on the three CCSD(T)/cc-pVnZ (n = D, T, Q) electronic energies was used to obtain CBS electronic energies. The CBS energies were combined with the ωB97X-D/6-31++G** thermal corrections to obtain the final G° values. The complete methodology is outlined in Fig. 1. Once the final G° values were calculated for the individual clusters, ΔG°binding was calculated as follows:| |  | (1) |
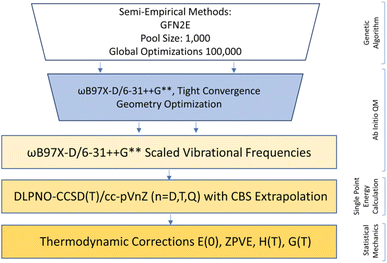 |
| | Fig. 1 Complete methodology used in this study. | |
The sequential binding energies for the addition of a monomer were computed using:
| | 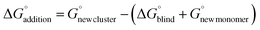 | (2) |
These addition energies, alongside initial concentrations for the monomers, were used to calculate the equilibrium concentrations of each cluster, assuming a closed system. Using a closed system accounts for monomer vapor depletion. These concentrations were calculated at 216.65 K and 298.15 K, which correspond to the top and bottom of the troposphere. We used a water concentration of 7.7 × 1017 cm−3 at 298 K and 9.9 × 1014 cm−3 at 217 K, which corresponds to 100% humidity at the bottom and top of the troposphere.5 Initial starting concentrations of the monomers were 5 × 107 cm−3 for SA, 9.8 × 1010 cm−3 for NA, 1 × 109 cm−3 for HCl, 2 × 1011 cm−3 for A, and 2 × 109 cm−3 for DMA at 298 K, which are relevant for each of the monomers over inland and urban areas.5,30,118–125 At 217 K, the monomer concentrations are decreased by three orders of magnitude to compensate for the reduction of condensable/nucleating/aerosol-forming vapors in the upper troposphere. This is a rough estimate based on the three orders of magnitude decrease in concentration of water, and we used this approximation since experimental concentrations of these monomers in the upper troposphere are difficult to measure. These results were combined with results from the previously studied (SA)(FA)(NA)(A)(DMA)(W)0–3 and (SA)(FA)(HCl)(A)(DMA)(W)0–3 clusters,72,86 allowing for a comparison of the different combinations of three different acids with the two different bases. We note that there are several limitations to our methodology.14 First, as we are unable to know if we have sampled the entirety of the semi-empirical potential energy surface (PES), there is always a possibility that minimum energy clusters were missed. Second, computing the CCSD(T) electronic energies on the DFT structures means we are making electron correlation corrections to the original DFT PES. Third, using the DLPNO approximation, and scaled frequencies from the rigid-rotor harmonic oscillator model generally leads to slightly more positive free energies. Finally, we note that we have previously investigated the effect of augmented bases sets (aug-cc-pVnZ) for the SA–A–glycine–serine system and found that the CBS extrapolation converged both results to within a half kcal mol−1.67 More work in this area is warranted. For more details about our methodology, we refer the reader to our recent review.14
3 Results and discussion
3.1 Trimers of two acids and one base
For the (SA)(NA)(HCl)(A)(DMA)(W)0–3 system, all monomers, dimers, and one acid-two base trimers have previously been discussed and are listed in the ESI (Tables T1–T5 and Fig. S1–S5†).72,86 We have not included the two acid dimers containing HCl, [(SA)(HCl)(W)0–3, (NA)(HCl)(W)0–3, and (FA)(HCl)(W)0–3] as previous results have shown these clusters are not atmospherically significant due to the lack of hydrogen bonding sites and bases present for deprotonation.72,86 The (SA)(NA)(HCl) trimer structure is included in the ESI† along with the energetics for the hydration of all the three acid clusters (Fig. S6 and Table T6†). We begin the discussion of the (SA)(NA)(HCl)(A)(DMA)(W)0–3 system with two acid-one base trimers. The structures and energies of the two acid-one base trimers are shown in Fig. 2 and Tables 1 & 2. In the figures, hydrogen bonds are marked in blue, and are defined as hydrogen-bonded distances of less than 2.2 Å and hydrogen bond angles between 140 and 180°. Red lines are used to denote van der Waals forces where either the bond angle encompassing the hydrogen is less than 140° or the hydrogen-bond distance is greater than 2.2 Å. The top half of Fig. 2 illustrates the Gibbs free energy minima (298 K) for HCl bound to one of the other acids (SA, FA, or NA), the ammonia base, and 0–3 waters, while the bottom half of the figure shows how these combinations of acids are complexed with the DMA base and water. Unsurprisingly, as displayed in Table 1, two acid–one base trimers with SA have the most negative energies of formation. The two acid–ammonia trimer with the most positive energy of formation is (NA)(HCl)(A) (Table 1). This is likely due to the dry cluster only forming two hydrogen bonds (Fig. 2). However, this cluster has a very large first sequential hydration energy of −5.30 kcal mol−1 at 217 K (Table 1), probably caused by a proton transfer and the addition of two new hydrogen bonds and one van der Waals interaction. The (NA)(HCl)(A)(W) cluster has the largest magnitude for the first hydration energy of any other complex that contains HCl (vide infra). The second sequential hydration energy is −3.88 kcal mol−1 at 217 K, which is the most negative second hydration energy of the two acid–ammonia trimers (Table 1). Similar to the one water cluster, HCl and A are in their charged forms with NA remaining neutral. (NA)(HCl)(A)(W)2 has five hydrogen bonds and one van der Waals interaction, gaining only one hydrogen bond upon the addition of the second water (Fig. 2). For the two acid–DMA trimers, (NA)(HCl)(base) again has the most positive energy of formation but also has the most negative sequential hydration energies. (NA)(HCl)(DMA) has only two hydrogen bonds and one van der Waals interaction. Upon first hydration, only one new hydrogen bond is formed, with the DMA donating a hydrogen bond to the water. Additional water molecules add to the previous water(s), forming a ring between the DMA, HCl, and waters and leaving the NA on the outside of the cluster in every scenario. These results agree with previous results where clusters with HCl have more negative energies of sequential hydration than other clusters.86
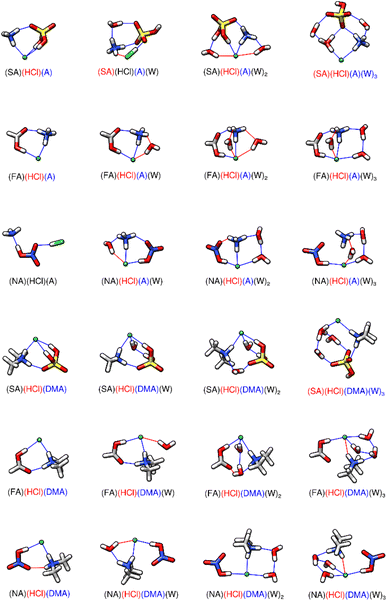 |
| | Fig. 2 DLPNO-CCSD(T)/CBS//ωB97X-D/6-31++G** minimum energy structures for the sequential hydration of hydrochloric acid with one acid and one base at 298 K. The molecule labels are colored according to charge as follows: blue = +1, black = 0, red = −1. Atoms are drawn in the following colors: hydrogen – white, carbon – grey, nitrogen – blue, oxygen – red, sulfur – yellow, chlorine – green. In the figures, hydrogen bonds are marked in blue, which have hydrogen-bonded distances of less than 2.2 Å and hydrogen bond angles between 140 and 180°. Red lines are used to denote van der Waals forces where either the bond angle encompassing the hydrogen is less than 140° or the hydrogen-bond distance is greater than 2.2 Å. | |
Table 1 DLPNO-CCSD(T)/CBS//ωB97X-D/6-31++G** Gibbs free energy changes (kcal mol−1) associated with the formation and sequential hydration of two acid and ammonia trimers at atmospherically relevant temperatures and 1 atm pressure. Values from a72 and b86
| Cluster |
216.65 K |
273.15 K |
298.15 K |
| SA + FA + A ⇌ (SA)(FA)(A)a |
−17.13 |
−13.39 |
−11.74 |
| (SA)(FA)(A) + W ⇌ (SA)(FA)(A)(W)a |
−4.65 |
−2.76 |
−1.93 |
| (SA)(FA)(A)(W) + W ⇌ (SA)(FA)(A)(W)2a |
−3.19 |
−1.36 |
−0.55 |
| (SA)(FA)(A)(W)2 + W ⇌ (SA)(FA)(A)(W)3a |
−3.23 |
−1.42 |
−0.62 |
| SA + NA + A ⇌ (SA)(NA)(A)a |
−15.74 |
−11.99 |
−10.40 |
| (SA)(NA)(A) + W ⇌ (SA)(NA)(A)(W)a |
−5.73 |
−4.04 |
−3.23 |
| (SA)(NA)(A)(W) + W ⇌ (SA)(NA)(A)(W)2a |
−3.83 |
−2.13 |
−1.38 |
| (SA)(NA)(A)(W)2 + W ⇌ (SA)(NA)(A)(W)3a |
−3.15 |
−1.51 |
−0.79 |
| SA + HCl + A ⇌ (SA)(HCl)(A)b |
−13.15 |
−9.52 |
−7.90 |
| (SA)(HCl)(A) + W ⇌ (SA)(HCl)(A)(W)b |
−3.92 |
−2.50 |
−1.88 |
| (SA)(HCl)(A)(W) + W ⇌ (SA)(HCl)(A)(W)2b |
−3.54 |
−1.39 |
−0.45 |
| (SA)(HCl)(A)(W)2 + W ⇌ (SA)(HCl)(A)(W)3b |
−3.69 |
−2.06 |
−1.33 |
| FA + NA + A ⇌ (FA)(NA)(A)a |
−8.42 |
−5.25 |
−3.87 |
| (FA)(NA)(A) + W ⇌ (FA)(NA)(A)(W)a |
−2.79 |
−0.32 |
0.78 |
| (FA)(NA)(A)(W) + W ⇌ (FA)(NA)(A)(W)2a |
−2.84 |
−0.96 |
−0.18 |
| (FA)(NA)(A)(W) 2 + W ⇌ (FA)(NA)(A)(W)3a |
−0.80 |
0.69 |
1.40 |
| FA + HCl + A ⇌ (FA)(HCl)(A)b |
−6.65 |
−3.04 |
−1.45 |
| (FA)(HCl)(A) + W ⇌ (FA)(HCl)(A)(W)b |
−4.41 |
−2.80 |
−2.10 |
| (FA)(HCl)(A)(W) + W ⇌ (FA)(HCl)(A)(W)2b |
−3.53 |
−1.82 |
−1.17 |
| (FA)(HCl)(A)(W)2 + W ⇌ (FA)(HCl)(A)(W)3b |
−3.31 |
−1.70 |
−0.88 |
| NA + HCl + A ⇌ (NA)(HCl)(A) |
−4.73 |
−1.99 |
−0.78 |
| (NA)(HCl)(A) + W ⇌ (NA)(HCl)(A)(W) |
−5.30 |
−3.06 |
−2.07 |
| (NA)(HCl)(A)(W) + W ⇌ (NA)(HCl)(A)(W)2 |
−3.88 |
−2.04 |
−1.23 |
| (NA)(HCl)(A)(W)2 + W ⇌ (NA)(HCl)(A)(W)3 |
−3.42 |
−1.85 |
−1.16 |
Table 2 DLPNO-CCSD(T)/CBS//DLPNO-CCSD(T)/CBS//ωB97X-D/6-31++G** Gibbs free energy changes (kcal mol−1) associated with the formation and sequential hydration of two acid and dimethylamine trimers at atmospherically relevant temperatures and 1 atm pressure. Values from a72 and b86
| Cluster |
216.65 K |
273.15 K |
298.15 K |
| SA + FA + DMA ⇌ (SA)(FA)(DMA)a |
−26.08 |
−22.19 |
−20.48 |
| (SA)(FA)(DMA) + W ⇌ (SA)(FA)(DMA)(W)a |
−3.31 |
−1.57 |
−0.80 |
| (SA)(FA)(DMA)(W) + W ⇌ (SA)(FA)(DMA)(W)2a |
−1.93 |
0.00 |
0.85 |
| (SA)(FA)(DMA)(W)2 + W ⇌ (SA)(FA)(DMA)(W)3a |
−1.21 |
0.50 |
1.25 |
| SA + NA + DMA ⇌ (SA)(NA)(DMA)a |
−25.19 |
−21.37 |
−19.69 |
| (SA)(NA)(DMA) + W ⇌ (SA)(NA)(DMA)(W)a |
−3.60 |
−1.66 |
−0.89 |
| (SA)(NA)(DMA)(W) + W ⇌ (SA)(NA)(DMA)(W)2a |
−2.95 |
−1.24 |
−0.42 |
| (SA)(NA)(DMA)(W)2 + W ⇌ (SA)(NA)(DMA)(W)3a |
−2.35 |
−0.62 |
0.16 |
| SA + HCl + DMA ⇌ (SA)(HCl)(DMA)b |
−23.69 |
−20.10 |
−18.50 |
| (SA)(HCl)(DMA) + W ⇌ (SA)(HCl)(DMA)(W)b |
−3.96 |
−1.97 |
−1.09 |
| (SA)(HCl)(DMA)(W) + W ⇌ (SA)(HCl)(DMA)(W)2b |
−2.75 |
−0.93 |
−0.13 |
| (SA)(HCl)(DMA)(W)2 + W ⇌ (SA)(HCl)(DMA)(W)3b |
−1.96 |
−0.24 |
0.52 |
| FA + NA + DMA ⇌ (FA)(NA)(DMA)a |
−15.58 |
−11.46 |
−9.65 |
| (FA)(NA)(DMA) + W ⇌ (FA)(NA)(DMA)(W)a |
−2.34 |
−0.71 |
0.00 |
| (FA)(NA)(DMA)(W) + W ⇌ (FA)(NA)(DMA)(W)2a |
−1.42 |
0.34 |
1.12 |
| (FA)(NA)(DMA)(W) 2 + W ⇌ (FA)(NA)(DMA)(W)3a |
−1.66 |
0.31 |
1.18 |
| FA + HCl + DMA ⇌ (FA)(HCl)(DMA)b |
−15.73 |
−12.09 |
−10.48 |
| (FA)(HCl)(DMA) + W ⇌ (FA)(HCl)(DMA)(W)b |
−2.68 |
−1.01 |
−0.28 |
| (FA)(HCl)(DMA)(W) + W ⇌ (FA)(HCl)(DMA)(W)2b |
−2.23 |
−0.16 |
0.75 |
| (FA)(HCl)(DMA)(W)2 + W ⇌ (FA)(HCl)(DMA)(W)3b |
−2.78 |
−1.08 |
−0.33 |
| NA + HCl + DMA ⇌ (NA)(HCl)(DMA) |
−14.50 |
−10.92 |
−9.34 |
| (NA)(HCl)(DMA) + W ⇌ (NA)(HCl)(DMA)(W) |
−4.06 |
−2.42 |
−1.70 |
| (NA)(HCl)(DMA)(W) + W ⇌ (NA)(HCl)(DMA)(W)2 |
−2.96 |
−1.23 |
−0.47 |
| (NA)(HCl)(DMA)(W)2 + W ⇌ (NA)(HCl)(DMA)(W)3 |
−2.86 |
−0.78 |
0.14 |
3.2 Tetramers of three acids and one base
The structures and energies of formation and hydration for the tetramers of three acids and one base are shown in Fig. 3, Tables 3 & 4. When the singular base is A, the (SA)(NA)(HCl)(A) cluster has the most positive formation energy. This is consistent with the trimers, in which the cluster containing NA, HCl, and A was also the least stable. The (SA)(NA)(HCl)(A) dry cluster contains four hydrogen bonds, two van der Waals interactions, and a proton transfer from the HCl to the A (Fig. 3). Despite the dry cluster being the least stable (−11.05 kcal mol−1 at 298 K), the (SA)(NA)(HCl)(A)(W)1–3 clusters have the most negative hydration energies. Due to these large negative hydration energies, (SA)(FA)(NA)(A)(W)3 is only 1.27 kcal mol−1 more stable than (SA)(NA)(HCl)(A)(W)3 at 298 K, as compared to their dry clusters, which have a free energy difference of 5.23 kcal mol−1 (Table 3). This emphasizes the hydrating power of HCl. When the base is DMA, all dry clusters have formation energies averaging roughly 9.5 kcal mol−1 more negative than their A counterparts (Table 4: the exact differences are −8.64 for SA–FA–NA; −8.72 for SA–FA–HCl; −10.84 for SA–NA–HCl at 217 K). While both (SA)(FA)(NA)(base) clusters remain the most stable in the dry state, the (SA)(FA)(HCl)(DMA) is the least stable. All dry clusters are di-ionic and contain five hydrogen bonds, except for (SA)(NA)(HCl)(DMA), which contains four hydrogen bonds and one van der Waals interaction (Fig. 3). The clusters containing HCl have more negative hydration energies than (SA)(FA)(NA)(DMA)(W)1–3, as seen in Table 4. In fact, these hydration energies are so much lower for the clusters containing HCl that (SA)(FA)(NA)(DMA)(W)3 is the least stable of the tertiary hydrated three acid–DMA clusters, despite being the most stable in the dry state. This is likely in part caused by the di-ionic nature of the (SA)(FA)(NA)(DMA)(W)3 cluster, which only has eight hydrogen bonds and one van der Waals interaction, whereas the other tertiary hydrated three acid–DMA clusters are tetra-ionic. These structures have nine hydrogen bonds and reveal a proton transfer to water forming a hydronium ion (Fig. 3). The more negative sequential hydration values for (SA)(NA)(HCl)(base)(W)2–3 hint that three stronger acids and one base can hydrate more effectively than two strong acids, one weak acid, and one base. This is illustrated by comparing the Gibbs free energy values for hydration of the second and third waters in Tables 3 and 4. The values for hydration of (SA)(NA)(HCl)(A)(W)2 and (SA)(NA)(HCl)(A)(W)3 are −3.80 and −3.53 kcal mol−1 at 217 K, respectively (Table 3). Substituting FA for NA in these clusters result in the next lowest hydration energies (−2.88 for W2; −3.05 for W3 at 217 K), and the most positive hydration energies are for the (SA)(FA)(NA)(A)(W)2–3 clusters. Table 4 shows that substituting DMA for W has the same exact trends, with (SA)(NA)(HCl)(DMA)(W)2–3 having the most negative hydration free energies (−3.29 and −2.43 kcal mol−1 at 217 K), followed by the clusters where FA substitutes for NA. While this may be related to structural factors, it may also highlight the effects that three acids together have on a singular base. It is possible that acid strength is more important as the clusters are hydrated, or it may reaffirm the stabilizing effects that HCl has in hydrating clusters.86
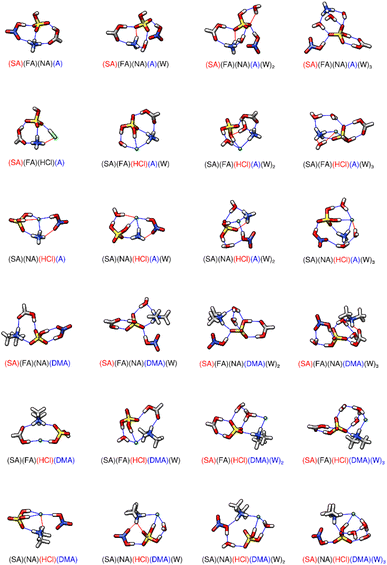 |
| | Fig. 3 DLPNO-CCSD(T)/CBS//ωB97X-D/6-31++G** minimum energy structures for the sequential hydration of three acids and one base. The molecule labels are colored according to charge as follows: blue = +1, black = 0, red = −1. Atoms are drawn in the following colors: hydrogen – white, carbon – grey, nitrogen – blue, oxygen – red, sulfur – yellow, chlorine – green. | |
Table 3 DLPNO-CCSD(T)/CBS//ωB97X-D/6-31++G** Gibbs free energy changes (kcal mol-1 associated with the formation and sequential hydration of three acid and ammonia tetramers at atmospherically relevant temperatures and 1 atm pressure. Values from a72 and b86
| Cluster |
216.65 K |
273.15 K |
298.15 K |
| SA + FA + NA + DMA ⇌ (SA)(FA)(NA)(DMA)a |
−33.41 |
−27.50 |
−24.90 |
| (SA)(FA)(NA)(DMA) + W ⇌ (SA)(FA)(NA)(DMA)(W)a |
−2.39 |
−0.48 |
0.36 |
| (SA)(FA)(NA)(DMA)(W) + W ⇌ (SA)(FA)(NA)(DMA)(W)2a |
−1.81 |
−0.01 |
0.78 |
| (SA)(FA)(NA)(DMA)(W)2 + W ⇌ (SA)(FA)(NA)(DMA)(W)3a |
−0.87 |
0.82 |
1.57 |
| SA + FA + HCl + DMA ⇌ (SA)(FA)(HCl)(DMA)b |
−28.92 |
−23.10 |
−20.59 |
| (SA)(FA)(HCl)(DMA) + W ⇌ (SA)(FA)(HCl)(DMA)(W)b |
−4.93 |
−3.06 |
−2.17 |
| (SA)(FA)(HCl)(DMA)(W) + W ⇌ (SA)(FA)(HCl)(DMA)(W)2b |
−2.69 |
−0.85 |
−0.03 |
| (SA)(FA)(HCl)(DMA)(W)2 + W ⇌ (SA)(FA)(HCl)(DMA)(W)3b |
−2.04 |
−0.34 |
0.42 |
| SA + NA + HCl + DMA ⇌ (SA)(NA)(HCl)(DMA) |
−29.60 |
−24.16 |
−21.76 |
| (SA)(NA)(HCl)(DMA) + W ⇌ (SA)(NA)(HCl)(DMA)(W) |
−4.06 |
−1.99 |
−1.11 |
| (SA)(NA)(HCl)(DMA)(W) + W ⇌ (SA)(NA)(HCl)(DMA)(W)2 |
−3.29 |
−1.47 |
−0.62 |
| (SA)(NA)(HCl)(DMA)(W)2 + W ⇌ (SA)(NA)(HCl)(DMA)(W)3 |
−2.43 |
−0.27 |
0.69 |
Table 4 DLPNO-CCSD(T)/CBS//ωB97X-D/6-31++G** Gibbs free energy changes (kcal mol−1) associated with the formation and sequential hydration of three acid and dimethylamine tetramers at atmospherically relevant temperatures and 1 atm pressure. Values from a72 and b86
| Cluster |
216.65 K |
273.15 K |
298.15 K |
| SA + FA + NA + DMA ⇌ (SA)(FA)(NA)(DMA)a |
−33.41 |
−27.50 |
−24.90 |
| (SA)(FA)(NA)(DMA) + W ⇌ (SA)(FA)(NA)(DMA)(W)a |
−2.39 |
−0.48 |
0.36 |
| (SA)(FA)(NA)(DMA)(W) + W ⇌ (SA)(FA)(NA)(DMA)(W)2a |
−1.81 |
−0.01 |
0.78 |
| (SA)(FA)(NA)(DMA)(W)2 + W ⇌ (SA)(FA)(NA)(DMA)(W)3a |
−0.87 |
0.82 |
1.57 |
| SA + FA + HCl + DMA ⇌ (SA)(FA)(HCl)(DMA)b |
−28.92 |
−23.10 |
−20.59 |
| (SA)(FA)(HCl)(DMA) + W ⇌ (SA)(FA)(HCl)(DMA)(W)b |
−4.93 |
−3.06 |
−2.17 |
| (SA)(FA)(HCl)(DMA)(W) + W ⇌ (SA)(FA)(HCl)(DMA)(W)2b |
−2.69 |
−0.85 |
−0.03 |
| (SA)(FA)(HCl)(DMA)(W)2 + W ⇌ (SA)(FA)(HCl)(DMA)(W)3b |
−2.04 |
−0.34 |
0.42 |
| SA + NA + HCl + DMA ⇌ (SA)(NA)(HCl)(DMA) |
−29.60 |
−24.16 |
−21.76 |
| (SA)(NA)(HCl)(DMA) + W ⇌ (SA)(NA)(HCl)(DMA)(W) |
−4.06 |
−1.99 |
−1.11 |
| (SA)(NA)(HCl)(DMA)(W) + W ⇌ (SA)(NA)(HCl)(DMA)(W)2 |
−3.29 |
−1.47 |
−0.62 |
| (SA)(NA)(HCl)(DMA)(W)2 + W ⇌ (SA)(NA)(HCl)(DMA)(W)3 |
−2.43 |
−0.27 |
0.69 |
3.3 Tetramers of two acids and two bases
The structures and energies of formation and hydration for the tetramers of two acids and two bases are displayed in Fig. 4 and Table 5. The left-hand side of the figure reveals that the dry clusters of the stronger acids are all tetra-ionic, but if FA replaces one of the stronger acids, the resulting complex is di-ionic. (SA)(HCl)(A)(DMA) is the most negative two acid–two base tetramer with a ΔG° value of −36.33 kcal mol−1 at 217 K (Table 5). When SA is replaced with NA to form (NA)(HCl)(A)(DMA), the ΔG° of formation becomes more positive by 11.96 kcal mol−1. Both (NA)(HCl)(A)(DMA) and (SA)(HCl)(A)(DMA) have four hydrogen bonds, with (SA)(HCl)(A)(DMA) also having one van der Waals interaction. The large energy difference between the two tetramers displays the driving effects of SA. However, if FA replaces NA, the ΔG° of binding is more positive than for (NA)(HCl)(A)(DMA) by 6.52 kcal mol−1. In fact, (FA)(HCl)(A)(DMA) is the least stable two acid–two base tetramer, with a ΔG° of formation of −17.85 kcal mol−1 at 217 K (Table 5). (FA)(HCl)(A)(DMA) has four hydrogen bonds, like the others, but (FA)(HCl)(A)(DMA) is di-ionic with a proton exchange between HCl and DMA (Fig. 4). The two acid–two base tetramers illustrate the competitive factors that contribute to the subtle stability of a pre-nucleation cluster: hydrogen bonding topology, protonation states, acid strength, and the driving effects of specific monomers. Upon hydration, the trimers with HCl have on average more negative energies of sequential hydration than those without. The primary exception to this pattern is (SA)(NA)(A)(DMA)(W), which has been previously noted for its special stability upon hydration.72 (SA)(HCl)(A)(DMA)(W) has the second most negative energy of first hydration, −4.26 kcal mol−1 at 217 K, followed closely by (NA)(HCl)(A)(DMA)(W) at −3.73 kcal mol−1 (Table 5). Both (SA)(HCl)(A)(DMA)(W) and (NA)(HCl)(A)(DMA)(W) have six hydrogen bonds and are tetra-ionic (Fig. 4). The 0.53 kcal mol−1 difference in first sequential hydration energy is likely a result of subtle hydrogen bonding topology differences. (SA)(HCl)(A)(DMA)(W)2 has the most negative second sequential hydration energy, followed again by (NA)(HCl)(A)(DMA)(W)2. Upon the third sequential hydration, all but one of the two acid–two base tetramers seem to have very similar energies, with no clear preference between clusters with or without HCl. Somewhat surprisingly, (NA)(HCl)(A)(DMA)(W)3 has the most positive third sequential hydration energy, with positive ΔG° values at atmospherically relevant temperatures. However, examining the structures reveals this is because the (NA)(HCl)(A)(DMA)(W)3 complex has only one more hydrogen bond than (NA)(HCl)(A)(DMA)(W)2 (Fig. 4). Nitric acid is a much worse contributor to hydrogen bonds in this system compared to sulfuric acid. The two acid–two base cluster results reaffirm the idea that hydrogen bonding topology is influential for cluster stability and energetics.
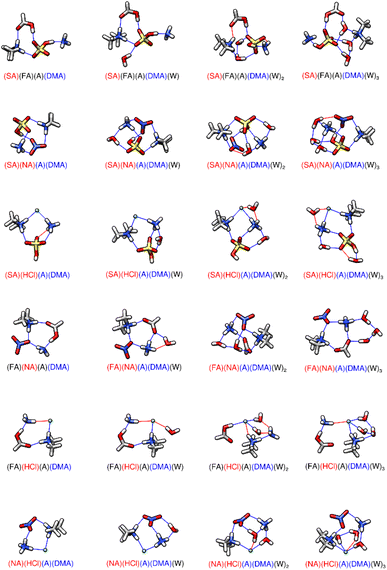 |
| | Fig. 4 DLPNO-CCSD(T)/CBS//ωB97X-D/6-31++G** minimum energy structures for the sequential hydration of two acids and two bases. The molecule labels are colored according to charge as follows: blue = +1, black = 0, red = −1. Atoms are drawn in the following colors: hydrogen – white, carbon – grey, nitrogen – blue, oxygen – red, sulfur – yellow, chlorine – green. | |
Table 5 DLPNO-CCSD(T)/CBS//ωB97X-D/6-31++G** Gibbs free energy changes (kcal mol−1) associated with the formation and sequential hydration of two acid and two base tetramers at atmospherically relevant temperatures and 1 atm pressure. Values from a72 and b86
| Cluster |
216.65 K |
273.15 K |
298.15 K |
| SA + FA + A + DMA ⇌ (SA)(FA)(A)(DMA)a |
−30.63 |
−24.98 |
−22.49 |
| (SA)(FA)(A)(DMA) + W ⇌ (SA)(FA)(A)(DMA)(W)a |
−2.25 |
−0.50 |
0.27 |
| (SA)(FA)(A)(DMA)(W) + W ⇌ (SA)(FA)(A)(DMA)(W)2a |
−1.07 |
1.10 |
1.99 |
| (SA)(FA)(A)(DMA)(W)2 + W ⇌ (SA)(FA)(A)(DMA)(W)3a |
−2.05 |
−0.48 |
0.28 |
| SA + NA + A + DMA ⇌ (SA)(NA)(A)(DMA)a |
−33.31 |
−27.23 |
−24.55 |
| (SA)(NA)(A)(DMA) + W ⇌ (SA)(NA)(A)(DMA)(W)a |
−6.79 |
−4.84 |
−3.99 |
| (SA)(NA)(A)(DMA)(W) + W ⇌ (SA)(NA)(A)(DMA)(W)2a |
−1.60 |
0.48 |
1.40 |
| (SA)(NA)(A)(DMA)(W)2 + W ⇌ (SA)(NA)(A)(DMA)(W)3a |
−1.62 |
0.22 |
1.04 |
| SA + HCl + A + DMA ⇌ (SA)(HCl)(A)(DMA)b |
−36.33 |
−30.87 |
−28.45 |
| (SA)(HCl)(A)(DMA) + W ⇌ (SA)(HCl)(A)(DMA)(W)b |
−4.26 |
−2.45 |
−1.66 |
| (SA)(HCl)(A)(DMA)(W) + W ⇌ (SA)(HCl)(A)(DMA)(W)2b |
−3.18 |
−1.56 |
−0.84 |
| (SA)(HCl)(A)(DMA)(W)2 + W ⇌ (SA)(HCl)(A)(DMA)(W)3b |
−2.14 |
−0.36 |
0.42 |
| FA + NA + A + DMA ⇌ (FA)(NA)(A)(DMA)a |
−19.35 |
−13.94 |
−11.57 |
| (FA)(NA)(A)(DMA) + W ⇌ (FA)(NA)(A)(DMA)(W)a |
−2.16 |
−0.32 |
0.50 |
| (FA)(NA)(A)(DMA)(W) + W ⇌ (FA)(NA)(A)(DMA)(W)2a |
−1.82 |
0.38 |
1.36 |
| (FA)(NA)(A)(DMA)(W)2 + W ⇌ (FA)(NA)(A)(DMA)(W)3a |
−2.73 |
−1.23 |
−0.66 |
| FA + HCl + A + DMA ⇌ (FA)(HCl)(A)(DMA)b |
−17.85 |
−12.63 |
−10.32 |
| (FA)(HCl)(A)(DMA) + W ⇌ (FA)(HCl)(A)(DMA)(W)b |
−2.50 |
−0.79 |
−0.04 |
| (FA)(HCl)(A)(DMA)(W) + W ⇌ (FA)(HCl)(A)(DMA)(W)2b |
−2.16 |
−0.10 |
0.81 |
| (FA)(HCl)(A)(DMA)(W)2 + W ⇌ (FA)(HCl)(A)(DMA)(W)3b |
−2.15 |
−0.74 |
−0.12 |
| NA + HCl + A + DMA ⇌ (NA)(HCl)(A)(DMA) |
−24.37 |
−18.73 |
−16.25 |
| (NA)(HCl)(A)(DMA) + W ⇌ (NA)(HCl)(A)(DMA)(W) |
−3.73 |
−1.97 |
−1.20 |
| (NA)(HCl)(A)(DMA)(W) + W ⇌ (NA)(HCl)(A)(DMA)(W)2 |
−2.49 |
−0.62 |
0.21 |
| (NA)(HCl)(A)(DMA)(W)2 + W ⇌ (NA)(HCl)(A)(DMA)(W)3 |
0.08 |
1.75 |
2.49 |
3.4 Pentamer of three acids and two bases
The structures and energies of formation and hydration for the pentamers of three acids and two bases are shown in Fig. 5 and Table 6. At 217 K, the ΔG° of formation for the dry pentamer (SA)(NA)(HCl)(A)(DMA) is 0.34 kcal mol−1 more positive than (SA)(FA)(HCl)(A)(DMA) (Table 6). Both dry pentamers are tetra-ionic, with SA and HCl donating protons to A and DMA. Additionally, both dry structures have six hydrogen bonds and display acid–base bridging between the charged species. A structural feature of (SA)(FA)(HCl)(A)(DMA) that may result in its slightly more negative energy is the presence of the SA–FA dimer, which Harold et al. showed to have exceptional stability (Fig. 5).65 (SA)(FA)(NA)(A)(DMA) is also tetra-ionic with six hydrogen bonds and has a ΔG° of binding 3.18 kcal mol−1 more positive than (SA)(NA)(HCl)(A)(DMA) at 217 K (Table 6). The dry three acid–two base pentamers with HCl have more negative ΔG° binding values than the pentamer without HCl. When the pentamers are hydrated with one water, the pentamers with HCl gain two hydrogen bonds, while (SA)(FA)(NA)(A)(DMA)(W) only gains one hydrogen bond and one van der Waals interaction. However (SA)(NA)(HCl)(A)(DMA) has the most positive energy of first sequential hydration by 1.52 kcal mol−1 relative to when FA replaces HCl (Table 6). (SA)(FA)(HCl)(A)(DMA)(W) has the most negative first sequential hydration energy, −4.35 kcal mol−1, nearly double that of (SA)(FA)(HCl)(A)(DMA)(W). In (SA)(NA)(HCl)(A)(DMA)(W), NA is loosely bound to the rest of the cluster through one hydrogen bond accepted by SA. The other two primary hydrated pentamers form the SA–FA dimer, which seems to have a stabilizing effect on the first hydration energy of the three acid–two base pentamers, in addition to hydrogen bonding topology. (SA)(FA)(HCl)(A)(DMA)(W)2 has the most positive second sequential hydration energy, despite forming one more hydrogen bond than (SA)(NA)(HCl)(A)(DMA)(W)2 and incorporating the SA–FA dimer. The (SA)(FA)(HCl)(A)(DMA)(W)3 cluster also maintains the SA–FA dimer, as well as gaining one hydrogen bond and one van der Waals interaction, yet has no additional stabilization at 217 K. The only tertiary sequential hydration that has negative ΔG° values is for (SA)(NA)(HCl)(A)(DMA)(W)3, which has a total of eleven hydrogen bonds and is the most stable three water pentamer. The three acid–two base pentamers demonstrate the stabilizing power of nitric acid combined with hydrochloric acid when sufficient bases are present.
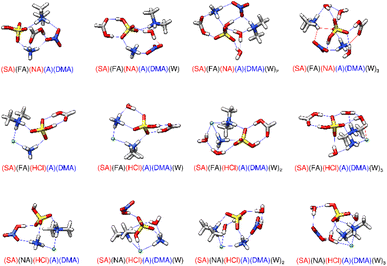 |
| | Fig. 5 DLPNO-CCSD(T)/CBS//ωB97X-D/6-31++G** minimum energy structures for the sequential hydration of three acids and two bases. The molecule labels are colored according to charge as follows: blue = +1, black = 0, red = −1. Atoms are drawn in the following colors: hydrogen – white, carbon – grey, nitrogen – blue, oxygen – red, sulfur – yellow, chlorine – green. | |
Table 6 DLPNO-CCSD(T)/CBS//ωB97X-D/6-31++G** Gibbs free energy changes (kcal mol−1) associated with the formation and sequential hydration of three acid and two base pentamers at atmospherically relevant temperatures and 1 atm pressure. Values from a72 and b86
| Cluster |
216.65 K |
273.15 K |
298.15 K |
| SA + FA + NA + A + DMA ⇌ (SA)(FA)(NA)(A)(DMA)a |
−39.56 |
−31.53 |
−28.00 |
| (SA)(FA)(NA)(A)(DMA) + W ⇌ (SA)(FA)(NA)(A)(DMA)(W)a |
−4.13 |
3.09 |
4.03 |
| (SA)(FA)(NA)(A)(DMA)(W) + W ⇌ (SA)(FA)(NA)(A)(DMA)(W)2a |
−4.07 |
−1.54 |
−0.64 |
| (SA)(FA)(NA)(A)(DMA)(W)2 + W ⇌ (SA)(FA)(NA)(A)(DMA)(W)3a |
1.16 |
3.69 |
4.58 |
| SA + FA + HCl + A + DMA ⇌ (SA)(FA)(HCl)(A)(DMA)b |
−43.08 |
−35.34 |
−32.02 |
| (SA)(FA)(HCl)(A)(DMA) + W ⇌ (SA)(FA)(HCl)(A)(DMA)(W)b |
−4.35 |
−2.67 |
−1.82 |
| (SA)(FA)(HCl)(A)(DMA)(W) + W ⇌ (SA)(FA)(HCl)(A)(DMA)(W)2b |
−2.85 |
−0.85 |
0.04 |
| (SA)(FA)(HCl)(A)(DMA)(W)2 + W ⇌ (SA)(FA)(HCl)(A)(DMA)(W)3b |
0.00 |
2.07 |
2.86 |
| SA + NA + HCl + A + DMA ⇌ (SA)(NA)(HCl)(A)(DMA) |
−42.74 |
−35.29 |
−32.00 |
| (SA)(NA)(HCl)(A)(DMA) + W ⇌ (SA)(NA)(HCl)(A)(DMA)(W) |
−2.61 |
−0.35 |
0.66 |
| (SA)(NA)(HCl)(A)(DMA)(W) + W ⇌ (SA)(NA)(HCl)(A)(DMA)(W)2 |
−3.67 |
−1.73 |
−0.86 |
| (SA)(NA)(HCl)(A)(DMA)(W)2 + W ⇌ (SA)(NA)(HCl)(A)(DMA)(W)3 |
−2.60 |
−0.80 |
−0.01 |
3.5 Equilibrium concentrations and pathways of formation
Equilibrium constants were calculated using the ΔG° values of the cluster at 216.65 and 298.15 K, corresponding to the top and bottom of the troposphere. Systems of equations adapted from Odbadrakh et al. were then used to calculate the equilibrium concentrations,57,72 assuming a closed system consisting of SA, NA, FA, HCl, A, DMA, and three W. In terms of kinetics, the ratio between formation and evaporation reactions is accounted for by the equilibrium constants. Other kinetic factors, such as the timescale to reach equilibrium and potential scavenging or sink reactions will only be important at very low vapor concentrations. We chose a water concentration of 7.7 × 1017 cm−3 at 298 K and 9.9 × 1014 cm−3 at 217 K, which corresponds to 100% humidity at the bottom and top of the troposphere.5 Initial starting concentrations of the monomers were 5 × 107 cm−3 for SA, 9.8 × 1010 cm−3 for NA, 1 × 109 cm−3 for HCl, 2 × 1011 cm−3 for A, and 2 × 109 cm−3 for DMA at 298 K, which are relevant for each of the monomers over inland and urban areas.5,30,118–125 At 217 K, the monomer concentrations are decreased by three orders of magnitude to account for atmospheric thinning at the top of the troposphere. This is a rough estimate based on the three orders of decrease in concentration of water, and we resort to this approximation since experimental concentrations of these monomers in the upper troposphere are difficult to measure. The calculated equilibrium concentrations of atmospherically relevant clusters are shown in Table 7, where we have defined atmospherically relevant as equilibrium concentrations above one cm−3 at either temperature. Among the atmospherically relevant dimers, the (SA)(DMA) dimer is the most abundant. The NA–base dimers are present in higher concentrations, for both dry and hydrated conditions, than the HCl–base dimers and the FA–base dimers discussed previously.72,86 The largest dry cluster in this simulation that is atmospherically relevant is (SA)(HCl)(A)(DMA), which is the most stable dry two acid–two base tetramer by 3 kcal mol−1 at 217 K. In comparison, the largest dry cluster with NA that is atmospherically relevant is the (SA)(NA)(DMA) trimer, indicating that NA might evaporate out of the clusters before they grow too large. When the system is hydrated, clusters with NA have larger equilibrium constants than those with HCl, similar to the dimer results. The largest hydrated cluster with HCl is (HCl)(DMA)(W)2, and the largest hydrated cluster with NA is (SA)(NA)(A)(DMA)(W). As previously noted (SA)(NA)(A)(DMA)(W) is exceptionally stable, explaining its appearance as the only hydrated tetramer.72 While clusters with HCl have more favorable Gibbs free energies of sequential hydration than those with NA, clusters with NA are more atmospherically relevant in their hydrated forms, likely due to their higher initial concentrations. This is because in our simulation the initial concentration of NA is about two orders of magnitude higher than the concentration of HCl. If the concentrations were the same, the hydrated HCl clusters would be more important. Under our simulation conditions there are no clusters containing both NA and HCl that have concentrations above one cm−3 at 217 K or 298 K. However, investigating the growth pathways to form the dry (SA)(NA)(HCl)(A)(DMA) pentamer can reveal driving effects of the different monomers. Therefore, in Table 8, we show the optimal growth pathways for the dry (SA)(NA)(HCl)(A)(DMA) pentamer using the most atmospherically relevant paths at 217 K and 298 K. The optimal pathway for growth begins with (SA)(DMA) at both temperatures. SA and DMA are both known to be strong drivers of nucleation, which will promote cluster growth. NA is added next, which has stabilizing effects.72 Ammonia and finally HCl are added to reach the dry pentamer. This mechanism is consistent with the usual alternate addition of acid and bases for other acid–base systems and leads to an approximately 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio of acid to bases in the growing clusters. The second-best pathway starts with (NA)(DMA) and then adds SA. Therefore, the first- and second-best pathways pass through the same trimer, (SA)(NA)(DMA), which is atmospherically relevant at both temperatures. The only difference between the first- and second-best pathways is the acid in the starting dimer. This discrepancy is likely due to the balance between thermodynamics and mass balance, as (SA)(DMA) is thermodynamically favored but NA is present in a much higher concentration than SA. In both of these pathways, HCl is the last molecule to be added to the cluster, likely because HCl has a much greater stabilizing effect on hydrated clusters than dry clusters. The third-best pathway also starts with (SA)(DMA), followed by the addition of HCl. (SA)(HCl)(DMA) is barely atmospherically relevant, present only at 298 K and in a very low concentration (Table 7). Ammonia is added to form the tetramer (SA)(HCl)(A)(DMA) and NA is added last. When the three systems (SA)(FA)(NA)(A)(DMA),72,86 (SA)(FA)(HCl)(A)(DMA),72,86 and (SA)(NA)(HCl)(A)(DMA) are compared, SA and DMA stand out as strong drivers of prenucleation due to their higher equilibrium concentrations. In this particular system, NA appears more in both dry and hydrated clusters than HCl does, likely caused by a higher initial concentration of NA than for HCl in our calculations. Many subtleties are at play in the beginning stages of pre-nucleation and these results cannot be attributed to only one factor. Hydrogen bonding topology and complex structural interactions appear to play an important role in structure energetics and atmospheric relevance.
1 ratio of acid to bases in the growing clusters. The second-best pathway starts with (NA)(DMA) and then adds SA. Therefore, the first- and second-best pathways pass through the same trimer, (SA)(NA)(DMA), which is atmospherically relevant at both temperatures. The only difference between the first- and second-best pathways is the acid in the starting dimer. This discrepancy is likely due to the balance between thermodynamics and mass balance, as (SA)(DMA) is thermodynamically favored but NA is present in a much higher concentration than SA. In both of these pathways, HCl is the last molecule to be added to the cluster, likely because HCl has a much greater stabilizing effect on hydrated clusters than dry clusters. The third-best pathway also starts with (SA)(DMA), followed by the addition of HCl. (SA)(HCl)(DMA) is barely atmospherically relevant, present only at 298 K and in a very low concentration (Table 7). Ammonia is added to form the tetramer (SA)(HCl)(A)(DMA) and NA is added last. When the three systems (SA)(FA)(NA)(A)(DMA),72,86 (SA)(FA)(HCl)(A)(DMA),72,86 and (SA)(NA)(HCl)(A)(DMA) are compared, SA and DMA stand out as strong drivers of prenucleation due to their higher equilibrium concentrations. In this particular system, NA appears more in both dry and hydrated clusters than HCl does, likely caused by a higher initial concentration of NA than for HCl in our calculations. Many subtleties are at play in the beginning stages of pre-nucleation and these results cannot be attributed to only one factor. Hydrogen bonding topology and complex structural interactions appear to play an important role in structure energetics and atmospheric relevance.
Table 7 Equilibrium concentrations of clusters that form at more than 1 cm−3 at 217 or 298 K. Initial concentrations of the monomers at 217 K were: SA = 5.00 × 104, NA = 9.80 × 107, HCl = 1.00 × 106, A = 2.00 × 108, DMA = 2.00 × 106 cm−3. Initial concentrations of the monomers at 298 K were: SA = 5.00 × 107, NA = 9.80 × 1010, HCl = 1.00 × 109, A = 2.00 × 1011, DMA = 2.00 × 109 cm−3. The water concentration is 9.90 × 1017 cm−3 at 217 K and 7.70 × 1014 cm−3 at 298 K. See text for details
| Cluster |
216.65 K |
298.15 K |
| SA |
2.96 × 101 |
1.48 × 107 |
| NA |
9.77 × 101 |
9.63 × 1010 |
| HCl |
1.00 × 106 |
9.99 × 108 |
| A |
2.00 × 108 |
2.00 × 1011 |
| DMA |
1.95 × 106 |
1.98 × 109 |
| (SA)(NA) |
6.50 × 10−6 |
2.10 |
| (SA)(A) |
9.50 × 10−2 |
5.99 × 103 |
| (SA)(DMA) |
2.53 × 104 |
1.14 × 107 |
| (NA)(A) |
2.69 × 102 |
2.16 × 105 |
| (NA)(DMA) |
1.89 × 102 |
2.23 × 104 |
| (HCl)(A) |
2.26 × 10−4 |
3.73 |
| (HCl)(DMA) |
4.39 × 10−3 |
4.24 |
| (SA)(NA)(DMA) |
1.26 × 102 |
1.26 × 103 |
| (SA)(HCl)(DMA) |
3.97 × 10−2 |
1.75 |
| (SA)(A)(DMA) |
2.51 × 10−3 |
1.05 |
| (SA)(HCl)(A)(DMA) |
1.32 |
2.80 × 10−1 |
| (SA)(W) |
2.48 × 101 |
1.50 × 107 |
| (SA)(W)2 |
3.41 |
2.90 × 106 |
| (SA)(W)3 |
7.48 × 10−2 |
1.45 × 105 |
| (NA)(W) |
3.19 × 105 |
1.73 × 109 |
| (NA)(W)2 |
3.04 × 102 |
1.33 × 107 |
| (NA)(W)3 |
3.11 × 10−2 |
1.50 × 104 |
| (HCl)(W) |
1.24 × 101 |
7.01 × 105 |
| (HCl)(W)2 |
3.79 × 10−4 |
3.39 × 102 |
| (HCl)(W)3 |
7.60 × 10−7 |
3.61 |
| (A)(W) |
6.57 × 103 |
3.79 × 108 |
| (A)(W)2 |
5.61 × 10−2 |
4.52 × 104 |
| (A)(W)3 |
1.88 × 10−5 |
1.03 × 102 |
| (DMA)(W) |
1.86 × 102 |
5.01 × 106 |
| (DMA)(W)2 |
1.04 × 10−2 |
3.76 × 103 |
| (DMA)(W)3 |
2.47 × 10−6 |
5.54 |
| (SA)(NA)(W) |
7.06 × 10−6 |
2.13 |
| (SA)(A)(W) |
6.65 × 10−3 |
5.61 × 102 |
| (SA)(A)(W)2 |
9.05 × 10−1 |
1.29 × 104 |
| (SA)(A)(W)3 |
3.82 × 10−4 |
6.31 × 101 |
| (SA)(DMA)(W) |
2.38 × 104 |
5.42 × 106 |
| (SA)(DMA)(W)2 |
7.38 × 102 |
3.06 × 105 |
| (SA)(DMA)(W)3 |
8.04 × 101 |
4.30 × 104 |
| (NA)(A)(W) |
9.48 × 10−3 |
1.28 × 102 |
| (NA)(DMA)(W) |
6.73 |
1.42 × 103 |
| (NA)(DMA)(W)2 |
1.38 × 10−1 |
6.54 × 101 |
| (NA)(DMA)(W)3 |
1.25 × 10−3 |
3.40 |
| (HCl)(DMA)(W) |
2.48 × 10−2 |
2.06 × 101 |
| (HCl)(DMA)(W)2 |
5.95 × 10−3 |
5.60 |
| (SA)(NA)(DMA)(W) |
1.58 × 101 |
1.77 × 102 |
| (SA)(NA)(DMA)(W)2 |
4.37 × 10−1 |
1.12 × 101 |
| (SA)(NA)(A)(DMA)(W) |
2.39 × 101 |
9.81 × 10−1 |
Table 8 Optimal pathways for growing the dry pentamer at 1 atm pressure according to equilibrium concentrations calculated using initial concentrations of [SA]0 = 5.00 × 107, [NA]0 = 9.80 × 1010, [HCl]0 = 1.00 × 109, [A]0 = 2.00 × 1011, and [DMA]0 = 2.00 × 109 cm−3 at 298 K. Concentrations were decreased by 3 orders of magnitude at 217 K. See text for details
|
|
216.65 K |
298.15 K |
| Optimal pathway |
SA + DMA ⇌ (SA)(DMA) + NA ⇌ (SA)(NA)(DMA) + A ⇌ (SA)(NA)(A)(DMA) + HCl ⇌ (SA)(NA)(HCl)(A)(DMA) |
SA + DMA ⇌ (SA)(DMA) + NA ⇌ (SA)(NA)(DMA) + A ⇌ (SA)(NA)(A)(DMA) + HCl ⇌ (SA)(NA)(HCl)(A)(DMA) |
| 2nd best pathway |
NA + DMA ⇌ (NA)(DMA) + SA ⇌ (SA)(NA)(DMA) + A ⇌ (SA)(NA)(A)(DMA) + HCl ⇌ (SA)(NA)(HCl)(A)(DMA) |
NA + DMA ⇌ (NA)(DMA) + SA ⇌ (SA)(NA)(DMA) + A ⇌ (SA)(NA)(A)(DMA) + HCl ⇌ (SA)(NA)(HCl)(A)(DMA) |
| 3rd best pathway |
SA + DMA ⇌ (SA)(DMA) + HCl ⇌ (SA)(HCl)(DMA) + A ⇌ (SA)(HCl)(A)(DMA) + NA ⇌ (SA)(NA)(HCl)(A)(DMA) |
SA + DMA ⇌ (SA)(DMA) + HCl ⇌ (SA)(HCl)(DMA) + A ⇌ (SA)(HCl)(A)(DMA) + NA ⇌ (SA)(NA)(HCl)(A)(DMA) |
4 Conclusions
For this system, sulfuric acid, nitric acid, hydrochloric acid, ammonia, dimethylamine, and three waters, we find that nitric acid is not stabilizing when paired with HCl in two acid–one base trimers. On the other hand, with two bases and an SA present, nitric acid is stabilizing when paired with HCl in the formation of three acid–two base pentamers. The charge on the monomers within clusters can be influential in the energetics, as the di-ionic and tetra-ionic two acid–two base tetramers illustrate. Acid strength is clearly important for hydrated clusters such as the three acid–one base tetramers. Complexes containing HCl tend to have more negative Gibbs free energies of hydration than those without HCl. Because deprotonated HCl simply leaves the chloride ion as a binding partner, clusters containing HCl tend to form more symmetric clusters, especially with water. This may explain the more negative Gibbs free energies of hydration for clusters containing HCl. This research adds to the body of work that illustrates that, depending on the system being studied, the acid/base strength of the monomers and the hydrogen bond topology of the resulting clusters have a subtle interplay that determines which cluster is most stable. In particular, sulfuric acid and dimethylamine excel at forming prenucleation complexes, and SA's ability to attract and bind additional molecules to the cluster drives growth. Other acids can't participate in as many hydrogen bonding events as bases add to a growing cluster.
Author contributions
The manuscript was written through contributions of all authors. All authors have given approval to the final version of the manuscript.
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
Funding for this work was provided by grants CHE-16626238, CHE-1903871, and CHE-2018427 from the National Science Foundation (GCS), the Arnold and Mabel Beckman Foundation Beckman Scholar Award (CJB), and the Barry M. Goldwater Scholarship (CJB). High-performance computing resources were provided by the Research Corporation for Science Advancement (27446) and the MERCURY Consortium (https://www.mercuryconsortium.org/).126,127 Molecular graphics and analyses performed with UCSF Chimera, developed by the Resource for Biocomputing, Visualization, and Informatics at the University of California, San Francisco, with support from NIH P41-GM103311. We thank the reviewers for helpful comments.
References
-
IPCC, Climate Change 2021: The Physical Science Basis. Contribution of Working Group I to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change, Cambridge University Press, Cambridge, United Kingdom and New York, NY, USA, 2021 Search PubMed.
- K. A. Prather, C. D. Hatch and V. H. Grassian, Analysis of atmospheric aerosols, Annu. Rev. Anal. Chem., 2008, 1, 485–514 CrossRef CAS PubMed.
- M. O. Andreae and D. Rosenfeld, Aerosol-cloud-precipitation interactions. Part 1. The nature and sources of cloud-active aerosols, Earth-Sci. Rev., 2008, 89, 13–41 CrossRef.
- M. E. Gonzalez, A. F. Corral, E. Crosbie, H. Dadashazar, G. S. Diskin, E. L. Edwards, S. Kirschler, R. H. Moore, C. E. Robinson, J. S. Schlosser, M. Shook, C. Stahl, K. L. Thornhill, C. Voigt, E. Winstead, L. D. Ziemba and A. Sorooshian, Relationships between supermicrometer particle concentrations and cloud water sea salt and dust concentrations: analysis of MONARC and ACTIVATE data, Environ. Sci.: Atmos., 2022, 2, 738–752 CAS.
-
J. H. Seinfeld and S. N. Pandis, in Ch. 10 Days in the Atmosphere, Wiley, 3rd edn, 2016 Search PubMed.
- J. Kontkanen, D. Stolzenburg, T. Olenius, C. Yan, L. Dada, L. Ahonen, M. Simon, K. Lehtipalo and I. Riipinen, What controls the observed size-dependency of the growth rates of sub-10 nm atmospheric particles?, Environ. Sci.: Atmos., 2022, 2, 449–468 CAS.
- A. A. Nair and F. Q. Yu, Quantification of Atmospheric Ammonia Concentrations: A Review of Its Measurement and Modeling, Atmosphere, 2020, 11, 1092 CrossRef CAS.
- A. Leonardi, H. M. Ricker, A. G. Gale, B. T. Ball, T. T. Odbadrakh, G. C. Shields and J. G. Navea, Particle formation and surface processes on atmospheric aerosols: A review of applied quantum chemical calculations, Int. J. Quantum Chem., 2020, 120, e26350 CrossRef CAS.
- J. Elm, J. Kubecka, V. Besel, M. J. Jaaskelainen, R. Halonen, T. Kurten and H. Vehkamaki, Modeling the formation and growth of atmospheric molecular clusters: A review, J. Aerosol Sci., 2020, 149, 105621 CrossRef CAS.
- X. Zhang, S. Tan, X. Chen and S. Yin, Computational chemistry of cluster: Understanding the mechanism of atmospheric new particle formation at the molecular level, Chemosphere, 2022, 308, 136109 CrossRef CAS PubMed.
- R. Zhang, A. Khalizov, L. Wang, M. Hu and W. Xu, Nucleation and growth of nanoparticles in the atmosphere, Chem. Rev., 2012, 112, 1957–2011 CrossRef CAS PubMed.
- J. N. Smith, D. C. Draper, S. Chee, M. Dam, H. Glicker, D. Myers, A. E. Thomas, M. J. Lawler and N. Myllys, Atmospheric clusters to nanoparticles: Recent progress and challenges in closing the gap in chemical composition, J. Aerosol Sci., 2021, 153, 105733 CrossRef CAS.
- C. Li and R. Signorell, Understanding vapor nucleation on the molecular level: A review, J. Aerosol Sci., 2021, 153, 105676 CrossRef CAS.
- J. Elm, D. Ayoubi, M. Engsvang, A. B. Jensen, Y. Knattrup, J. Kubecka, C. J. Bready, V. R. Fowler, S. E. Harold, O. M. Longsworth and G. C. Shields, Quantum chemical modeling of organic enhanced atmospheric nucleation: A critical review, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2023, e1662 Search PubMed.
- J. N. Smith, K. F. Moore, P. H. McMurry and F. L. Eisele, Atmospheric measurements of sub-20 nm diameter particle chemical composition by thermal desorption chemical ionization mass spectrometry, Aerosol Sci. Technol., 2004, 38, 100–110 CrossRef CAS.
- M. Kulmala, H. Vehkamaki, T. Petaja, M. Dal Maso, A. Lauri, V. M. Kerminen, W. Birmili and P. H. McMurry, Formation and growth rates of ultrafine atmospheric particles: a review of observations, J. Aerosol Sci., 2004, 35, 143–176 CrossRef CAS.
- M. Kulmala, I. Riipinen, M. Sipila, H. E. Manninen, T. Petaja, H. Junninen, M. D. Maso, G. Mordas, A. Mirme, M. Vana, A. Hirsikko, L. Laakso, R. M. Harrison, I. Hanson, C. Leung, K. E. Lehtinen and V. M. Kerminen, Toward direct measurement of atmospheric nucleation, Science, 2007, 318, 89–92 CrossRef CAS PubMed.
- C. Kuang, P. H. McMurry, A. V. McCormick and F. L. Eisele, Dependence of nucleation rates on sulfuric acid vapor concentration in diverse atmospheric locations, J. Geophys. Res.: Atmos., 2008, 113, D10209 CrossRef.
- J. L. Jimenez, M. R. Canagaratna, N. M. Donahue, A. S. Prevot, Q. Zhang, J. H. Kroll, P. F. DeCarlo, J. D. Allan, H. Coe, N. L. Ng, A. C. Aiken, K. S. Docherty, I. M. Ulbrich, A. P. Grieshop, A. L. Robinson, J. Duplissy, J. D. Smith, K. R. Wilson, V. A. Lanz, C. Hueglin, Y. L. Sun, J. Tian, A. Laaksonen, T. Raatikainen, J. Rautiainen, P. Vaattovaara, M. Ehn, M. Kulmala, J. M. Tomlinson, D. R. Collins, M. J. Cubison, E. J. Dunlea, J. A. Huffman, T. B. Onasch, M. R. Alfarra, P. I. Williams, K. Bower, Y. Kondo, J. Schneider, F. Drewnick, S. Borrmann, S. Weimer, K. Demerjian, D. Salcedo, L. Cottrell, R. Griffin, A. Takami, T. Miyoshi, S. Hatakeyama, A. Shimono, J. Y. Sun, Y. M. Zhang, K. Dzepina, J. R. Kimmel, D. Sueper, J. T. Jayne, S. C. Herndon, A. M. Trimborn, L. R. Williams, E. C. Wood, A. M. Middlebrook, C. E. Kolb, U. Baltensperger and D. R. Worsnop, Evolution of organic aerosols in the atmosphere, Science, 2009, 326, 1525–1529 CrossRef CAS PubMed.
- J. N. Smith and G. J. Rathbone, Carboxylic acid characterization in nanoparticles by thermal desorption chemical ionization mass spectrometry, Int. J. Mass Spectrom., 2008, 274, 8–13 CrossRef CAS.
- J. N. Smith, K. C. Barsanti, H. R. Friedli, M. Ehn, M. Kulmala, D. R. Collins, J. H. Scheckman, B. J. Williams and P. H. McMurry, Observations of aminium salts in atmospheric nanoparticles and possible climatic implications, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 6634–6639 CrossRef CAS PubMed.
- T. E. Morrell and G. C. Shields, Atmospheric implications for formation of clusters of ammonium and 1-10 water molecules, J. Phys. Chem. A, 2010, 114, 4266–4271 CrossRef CAS PubMed.
- J. Herb, A. B. Nadykto and F. Q. Yu, Large ternary hydrogen-bonded pre-nucleation clusters in the Earth's atmosphere, Chem. Phys. Lett., 2011, 518, 7–14 CrossRef CAS.
- J. Elm, M. Bilde and K. V. Mikkelsen, Assessment of binding energies of atmospherically relevant clusters, Phys. Chem. Chem. Phys., 2013, 15, 16442–16445 RSC.
- J. Elm, M. Bilde and K. V. Mikkelsen, Assessment of Density Functional Theory in Predicting Structures and Free Energies of Reaction of Atmospheric Prenucleation Clusters, J. Chem. Theory Comput., 2012, 8, 2071–2077 CrossRef CAS PubMed.
- C. Kuang, M. Chen, J. Zhao, J. Smith, P. H. McMurry and J. Wang, Size and time-resolved growth rate measurements of 1 to 5 nm freshly formed atmospheric nuclei, Atmos. Chem. Phys., 2012, 12, 3573–3589 CrossRef CAS.
- P. M. Winkler, J. Ortega, T. Karl, L. Cappellin, H. R. Friedli, K. Barsanti, P. H. McMurry and J. N. Smith, Identification of the biogenic compounds responsible for size-dependent nanoparticle growth, Geophys. Res. Lett., 2012, 39, L20815 CrossRef.
- D. E. Husar, B. Temelso, A. L. Ashworth and G. C. Shields, Hydration of the bisulfate ion: atmospheric implications, J. Phys. Chem. A, 2012, 116, 5151–5163 CrossRef CAS PubMed.
- B. Temelso, T. E. Morrell, R. M. Shields, M. A. Allodi, E. K. Wood, K. N. Kirschner, T. C. Castonguay, K. A. Archer and G. C. Shields, Quantum mechanical study of sulfuric acid hydration: atmospheric implications, J. Phys. Chem. A, 2012, 116, 2209–2224 CrossRef CAS PubMed.
- B. Temelso, T. N. Phan and G. C. Shields, Computational study of the hydration of sulfuric acid dimers: implications for acid dissociation and aerosol formation, J. Phys. Chem. A, 2012, 116, 9745–9758 CrossRef CAS PubMed.
- J. Almeida, S. Schobesberger, A. Kurten, I. K. Ortega, O. Kupiainen-Maatta, A. P. Praplan, A. Adamov, A. Amorim, F. Bianchi, M. Breitenlechner, A. David, J. Dommen, N. M. Donahue, A. Downard, E. Dunne, J. Duplissy, S. Ehrhart, R. C. Flagan, A. Franchin, R. Guida, J. Hakala, A. Hansel, M. Heinritzi, H. Henschel, T. Jokinen, H. Junninen, M. Kajos, J. Kangasluoma, H. Keskinen, A. Kupc, T. Kurten, A. N. Kvashin, A. Laaksonen, K. Lehtipalo, M. Leiminger, J. Leppa, V. Loukonen, V. Makhmutov, S. Mathot, M. J. McGrath, T. Nieminen, T. Olenius, A. Onnela, T. Petaja, F. Riccobono, I. Riipinen, M. Rissanen, L. Rondo, T. Ruuskanen, F. D. Santos, N. Sarnela, S. Schallhart, R. Schnitzhofer, J. H. Seinfeld, M. Simon, M. Sipila, Y. Stozhkov, F. Stratmann, A. Tome, J. Trostl, G. Tsagkogeorgas, P. Vaattovaara, Y. Viisanen, A. Virtanen, A. Vrtala, P. E. Wagner, E. Weingartner, H. Wex, C. Williamson, D. Wimmer, P. Ye, T. Yli-Juuti, K. S. Carslaw, M. Kulmala, J. Curtius, U. Baltensperger, D. R. Worsnop, H. Vehkamaki and J. Kirkby, Molecular understanding of sulphuric acid-amine particle nucleation in the atmosphere, Nature, 2013, 502, 359–363 CrossRef CAS PubMed.
- M. Kulmala, J. Kontkanen, H. Junninen, K. Lehtipalo, H. E. Manninen, T. Nieminen, T. Petaja, M. Sipila, S. Schobesberger, P. Rantala, A. Franchin, T. Jokinen, E. Jarvinen, M. Aijala, J. Kangasluoma, J. Hakala, P. P. Aalto, P. Paasonen, J. Mikkila, J. Vanhanen, J. Aalto, H. Hakola, U. Makkonen, T. Ruuskanen, R. L. Mauldin, 3rd, J. Duplissy, H. Vehkamaki, J. Back, A. Kortelainen, I. Riipinen, T. Kurten, M. V. Johnston, J. N. Smith, M. Ehn, T. F. Mentel, K. E. Lehtinen, A. Laaksonen, V. M. Kerminen and D. R. Worsnop, Direct observations of atmospheric aerosol nucleation, Science, 2013, 339, 943–946 CrossRef CAS PubMed.
- Y. Zhang, I. R. Turkmen, B. Wassermann, A. Erko and E. Ruhl, Structural motifs of pre-nucleation clusters, J. Chem. Phys., 2013, 139, 134506 CrossRef CAS PubMed.
- J. Elm, M. Fard, M. Bilde and K. V. Mikkelsen, Interaction of glycine with common atmospheric nucleation precursors, J. Phys. Chem. A, 2013, 117, 12990–12997 CrossRef CAS PubMed.
- D. J. Bustos, B. Temelso and G. C. Shields, Hydration of the sulfuric acid-methylamine complex and implications for aerosol formation, J. Phys. Chem. A, 2014, 118, 7430–7441 CrossRef CAS PubMed.
- K. Lehtipalo, L. Rondo, J. Kontkanen, S. Schobesberger, T. Jokinen, N. Sarnela, A. Kurten, S. Ehrhart, A. Franchin, T. Nieminen, F. Riccobono, M. Sipila, T. Yli-Juuti, J. Duplissy, A. Adamov, L. Ahlm, J. Almeida, A. Amorim, F. Bianchi, M. Breitenlechner, J. Dommen, A. J. Downard, E. M. Dunne, R. C. Flagan, R. Guida, J. Hakala, A. Hansel, W. Jud, J. Kangasluoma, V. M. Kerminen, H. Keskinen, J. Kim, J. Kirkby, A. Kupc, O. Kupiainen-Maatta, A. Laaksonen, M. J. Lawler, M. Leiminger, S. Mathot, T. Olenius, I. K. Ortega, A. Onnela, T. Petaja, A. Praplan, M. P. Rissanen, T. Ruuskanen, F. D. Santos, S. Schallhart, R. Schnitzhofer, M. Simon, J. N. Smith, J. Trostl, G. Tsagkogeorgas, A. Tome, P. Vaattovaara, H. Vehkamaki, A. E. Vrtala, P. E. Wagner, C. Williamson, D. Wimmer, P. M. Winkler, A. Virtanen, N. M. Donahue, K. S. Carslaw, U. Baltensperger, I. Riipinen, J. Curtius, D. R. Worsnop and M. Kulmala, The effect of acid-base clustering and ions on the growth of atmospheric nano-particles, Nat. Commun., 2016, 7, 11594 CrossRef CAS PubMed.
- J. Trostl, W. K. Chuang, H. Gordon, M. Heinritzi, C. Yan, U. Molteni, L. Ahlm, C. Frege, F. Bianchi, R. Wagner, M. Simon, K. Lehtipalo, C. Williamson, J. S. Craven, J. Duplissy, A. Adamov, J. Almeida, A. K. Bernhammer, M. Breitenlechner, S. Brilke, A. Dias, S. Ehrhart, R. C. Flagan, A. Franchin, C. Fuchs, R. Guida, M. Gysel, A. Hansel, C. R. Hoyle, T. Jokinen, H. Junninen, J. Kangasluoma, H. Keskinen, J. Kim, M. Krapf, A. Kurten, A. Laaksonen, M. Lawler, M. Leiminger, S. Mathot, O. Mohler, T. Nieminen, A. Onnela, T. Petaja, F. M. Piel, P. Miettinen, M. P. Rissanen, L. Rondo, N. Sarnela, S. Schobesberger, K. Sengupta, M. Sipila, J. N. Smith, G. Steiner, A. Tome, A. Virtanen, A. C. Wagner, E. Weingartner, D. Wimmer, P. M. Winkler, P. Ye, K. S. Carslaw, J. Curtius, J. Dommen, J. Kirkby, M. Kulmala, I. Riipinen, D. R. Worsnop, N. M. Donahue and U. Baltensperger, The role of low-volatility organic compounds in initial particle growth in the atmosphere, Nature, 2016, 533, 527–531 CrossRef CAS PubMed.
- J. Elm, C. N. Jen, T. Kurten and H. Vehkamaki, Strong Hydrogen Bonded Molecular Interactions between Atmospheric Diamines and Sulfuric Acid, J. Phys. Chem. A, 2016, 120, 3693–3700 CrossRef CAS PubMed.
- F. Bianchi, J. Trostl, H. Junninen, C. Frege, S. Henne, C. R. Hoyle, U. Molteni, E. Herrmann, A. Adamov, N. Bukowiecki, X. Chen, J. Duplissy, M. Gysel, M. Hutterli, J. Kangasluoma, J. Kontkanen, A. Kurten, H. E. Manninen, S. Munch, O. Perakyla, T. Petaja, L. Rondo, C. Williamson, E. Weingartner, J. Curtius, D. R. Worsnop, M. Kulmala, J. Dommen and U. Baltensperger, New particle formation in the free troposphere: A question of chemistry and timing, Science, 2016, 352, 1109–1112 CrossRef CAS PubMed.
- H. Gordon, K. Sengupta, A. Rap, J. Duplissy, C. Frege, C. Williamson, M. Heinritzi, M. Simon, C. Yan, J. Almeida, J. Trostl, T. Nieminen, I. K. Ortega, R. Wagner, E. M. Dunne, A. Adamov, A. Amorim, A. K. Bernhammer, F. Bianchi, M. Breitenlechner, S. Brilke, X. Chen, J. S. Craven, A. Dias, S. Ehrhart, L. Fischer, R. C. Flagan, A. Franchin, C. Fuchs, R. Guida, J. Hakala, C. R. Hoyle, T. Jokinen, H. Junninen, J. Kangasluoma, J. Kim, J. Kirkby, M. Krapf, A. Kurten, A. Laaksonen, K. Lehtipalo, V. Makhmutov, S. Mathot, U. Molteni, S. A. Monks, A. Onnela, O. Perakyla, F. Piel, T. Petaja, A. P. Praplan, K. J. Pringle, N. A. Richards, M. P. Rissanen, L. Rondo, N. Sarnela, S. Schobesberger, C. E. Scott, J. H. Seinfeld, S. Sharma, M. Sipila, G. Steiner, Y. Stozhkov, F. Stratmann, A. Tome, A. Virtanen, A. L. Vogel, A. C. Wagner, P. E. Wagner, E. Weingartner, D. Wimmer, P. M. Winkler, P. Ye, X. Zhang, A. Hansel, J. Dommen, N. M. Donahue, D. R. Worsnop, U. Baltensperger, M. Kulmala, J. Curtius and K. S. Carslaw, Reduced anthropogenic aerosol radiative forcing caused by biogenic new particle formation, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, 12053–12058 CrossRef CAS PubMed.
- J. Kirkby, J. Duplissy, K. Sengupta, C. Frege, H. Gordon, C. Williamson, M. Heinritzi, M. Simon, C. Yan, J. Almeida, J. Trostl, T. Nieminen, I. K. Ortega, R. Wagner, A. Adamov, A. Amorim, A. K. Bernhammer, F. Bianchi, M. Breitenlechner, S. Brilke, X. Chen, J. Craven, A. Dias, S. Ehrhart, R. C. Flagan, A. Franchin, C. Fuchs, R. Guida, J. Hakala, C. R. Hoyle, T. Jokinen, H. Junninen, J. Kangasluoma, J. Kim, M. Krapf, A. Kurten, A. Laaksonen, K. Lehtipalo, V. Makhmutov, S. Mathot, U. Molteni, A. Onnela, O. Perakyla, F. Piel, T. Petaja, A. P. Praplan, K. Pringle, A. Rap, N. A. Richards, I. Riipinen, M. P. Rissanen, L. Rondo, N. Sarnela, S. Schobesberger, C. E. Scott, J. H. Seinfeld, M. Sipila, G. Steiner, Y. Stozhkov, F. Stratmann, A. Tome, A. Virtanen, A. L. Vogel, A. C. Wagner, P. E. Wagner, E. Weingartner, D. Wimmer, P. M. Winkler, P. Ye, X. Zhang, A. Hansel, J. Dommen, N. M. Donahue, D. R. Worsnop, U. Baltensperger, M. Kulmala, K. S. Carslaw and J. Curtius, Ion-induced nucleation of pure biogenic particles, Nature, 2016, 533, 521–526 CrossRef CAS PubMed.
- J. Elm, Elucidating the Limiting Steps in Sulfuric Acid-Base New Particle Formation, J. Phys. Chem. A, 2017, 121, 8288–8295 CrossRef CAS PubMed.
- H.-B. Xie, J. Elm, R. Halonen, N. Myllys, T. Kurtén, M. Kulmala and H. Vehkamäki, The atmospheric fate of monoethanolamine: Enhancing new particle formation of sulfuric acid as an important removal process, Environ. Sci. Technol., 2017, 51, 8422–8431 CrossRef CAS PubMed.
- H. H. Chen, S. Chee, M. J. Lawler, K. C. Barsanti, B. M. Wong and J. N. Smith, Size resolved chemical composition of nanoparticles from reactions of sulfuric acid with ammonia and dimethylamine, Aerosol Sci. Technol., 2018, 52, 1120–1133 CrossRef CAS.
- M. J. Lawler, M. P. Rissanen, M. Ehn, R. L. Mauldin, N. Sarnela, M. Sipila and J. N. Smith, Evidence for Diverse Biogeochemical Drivers of Boreal Forest New Particle Formation, Geophys. Res. Lett., 2018, 45, 2038–2046 CrossRef.
- L. Pichelstorfer, D. Stolzenburg, J. Ortega, T. Karl, H. Kokkola, A. Laakso, K. E. J. Lehtinen, J. N. Smith, P. H. McMurry and P. M. Winkler, Resolving nanoparticle growth mechanisms from size- and time-dependent growth rate analysis, Atmos. Chem. Phys., 2018, 18, 1307–1323 CrossRef CAS.
- N. Myllys, T. Ponkkonen, S. Chee and J. Smith, Enhancing Potential of Trimethylamine Oxide on Atmospheric Particle Formation, Atmosphere, 2019, 11, 35 CrossRef.
- S. E. Waller, Y. Yang, E. Castracane, E. E. Racow, J. J. Kreinbihl, K. A. Nickson and C. J. Johnson, The Interplay Between Hydrogen Bonding and Coulombic Forces in Determining the Structure of Sulfuric Acid-Amine Clusters, J. Phys. Chem. Lett., 2018, 9, 1216–1222 CrossRef CAS PubMed.
- Y. Yang, S. E. Waller, J. J. Kreinbihl and C. J. Johnson, Direct Link between Structure and Hydration in Ammonium and Aminium Bisulfate Clusters Implicated in Atmospheric New Particle Formation, J. Phys. Chem. Lett., 2018, 9, 5647–5652 CrossRef CAS PubMed.
- Y. Yang and C. J. Johnson, Hydration motifs of ammonium bisulfate clusters of relevance to atmospheric new particle formation, Faraday Discuss., 2019, 217, 47–66 RSC.
- F. Ma, H. B. Xie, J. Elm, J. Shen, J. Chen and H. Vehkamaki, Piperazine Enhancing Sulfuric Acid-Based New Particle Formation: Implications for the Atmospheric Fate of Piperazine, Environ. Sci. Technol., 2019, 53, 8785–8795 CrossRef CAS PubMed.
- J. Shen, H. B. Xie, J. Elm, F. Ma, J. Chen and H. Vehkamaki, Methanesulfonic Acid-driven New Particle Formation Enhanced by Monoethanolamine: A Computational Study, Environ. Sci. Technol., 2019, 53, 14387–14397 CrossRef CAS PubMed.
- S. Chee, N. Myllys, K. C. Barsanti, B. M. Wong and J. N. Smith, An Experimental and Modeling Study of Nanoparticle Formation and Growth from Dimethylamine and Nitric Acid, J. Phys. Chem. A, 2019, 123, 5640–5648 CrossRef CAS PubMed.
- N. Myllys, S. Chee, T. Olenius, M. Lawler and J. Smith, Molecular-Level Understanding of Synergistic Effects in Sulfuric Acid-Amine-Ammonia Mixed Clusters, J. Phys. Chem. A, 2019, 123, 2420–2425 CrossRef CAS PubMed.
- N. Myllys, J. Kubecka, V. Besel, D. Alfaouri, T. Olenius, J. N. Smith and M. Passananti, Role of base strength, cluster structure and charge in sulfuric-acid-driven particle formation, Atmos. Chem. Phys., 2019, 19, 9753–9768 CrossRef CAS.
- M. Wang, W. Kong, R. Marten, X. C. He, D. Chen, J. Pfeifer, A. Heitto, J. Kontkanen, L. Dada, A. Kurten, T. Yli-Juuti, H. E. Manninen, S. Amanatidis, A. Amorim, R. Baalbaki, A. Baccarini, D. M. Bell, B. Bertozzi, S. Brakling, S. Brilke, L. C. Murillo, R. Chiu, B. Chu, L. P. De Menezes, J. Duplissy, H. Finkenzeller, L. G. Carracedo, M. Granzin, R. Guida, A. Hansel, V. Hofbauer, J. Krechmer, K. Lehtipalo, H. Lamkaddam, M. Lampimaki, C. P. Lee, V. Makhmutov, G. Marie, S. Mathot, R. L. Mauldin, B. Mentler, T. Muller, A. Onnela, E. Partoll, T. Petaja, M. Philippov, V. Pospisilova, A. Ranjithkumar, M. Rissanen, B. Rorup, W. Scholz, J. Shen, M. Simon, M. Sipila, G. Steiner, D. Stolzenburg, Y. J. Tham, A. Tome, A. C. Wagner, D. S. Wang, Y. Wang, S. K. Weber, P. M. Winkler, P. J. Wlasits, Y. Wu, M. Xiao, Q. Ye, M. Zauner-Wieczorek, X. Zhou, R. Volkamer, I. Riipinen, J. Dommen, J. Curtius, U. Baltensperger, M. Kulmala, D. R. Worsnop, J. Kirkby, J. H. Seinfeld, I. El-Haddad, R. C. Flagan and N. M. Donahue, Rapid growth of new atmospheric particles by nitric acid and ammonia condensation, Nature, 2020, 581, 184–189 CrossRef CAS PubMed.
- T. T. Odbadrakh, A. G. Gale, B. T. Ball, B. Temelso and G. C. Shields, Computation of Atmospheric Concentrations of Molecular Clusters from ab initio Thermochemistry, J. Visualized Exp., 2020, 158, e60964 Search PubMed.
- B. T. Ball, S. Vanovac, T. T. Odbadrakh and G. C. Shields, Monomers of Glycine and Serine Have a Limited Ability to Hydrate in the Atmosphere, J. Phys. Chem. A, 2021, 125, 8454–8467 CrossRef CAS PubMed.
- J. J. Kreinbihl, N. C. Frederiks and C. J. Johnson, Hydration motifs of ammonium bisulfate clusters show complex temperature dependence, J. Chem. Phys., 2021, 154, 014304 CrossRef CAS PubMed.
- J. Elm, Clusteromics I: Principles, Protocols, and Applications to Sulfuric Acid-Base Cluster Formation, ACS Omega, 2021, 6, 7804–7814 CrossRef CAS PubMed.
- J. Elm, Clusteromics II: Methanesulfonic Acid-Base Cluster Formation, ACS Omega, 2021, 6, 17035–17044 CrossRef CAS PubMed.
- S. H. Jathar, C. D. Cappa, Y. He, J. R. Pierce, W. Chuang, K. R. Bilsback, J. H. Seinfeld, R. A. Zaveri and M. Shrivastava, A computationally efficient model to represent the chemistry, thermodynamics, and microphysics of secondary organic aerosols (simpleSOM): model development and application to α-pinene SOA, Environ. Sci.: Atmos., 2021, 1, 372–394 CAS.
- S. Chee, K. Barsanti, J. N. Smith and N. Myllys, A predictive model for salt nanoparticle formation using heterodimer stability calculations, Atmos. Chem. Phys., 2021, 21, 11637–11654 CrossRef CAS.
- N. Myllys, D. Myers, S. Chee and J. N. Smith, Molecular properties affecting the hydration of acid-base clusters, Phys. Chem. Chem. Phys., 2021, 23, 13106–13114 RSC.
- S. E. Harold, C. J. Bready, L. A. Juechter, L. A. Kurfman, S. Vanovac, V. R. Fowler, G. E. Mazaleski, T. T. Odbadrakh and G. C. Shields, Hydrogen-Bond Topology Is More Important Than Acid/Base Strength in Atmospheric Prenucleation Clusters, J. Phys. Chem. A, 2022, 126, 1718–1728 CrossRef CAS PubMed.
- R. J. Zhang, J. W. Shen, H. B. Xie, J. W. Chen and J. Elm, The role of organic acids in new particle formation from methanesulfonic acid and methylamine, Atmos. Chem. Phys., 2022, 22, 2639–2650 CrossRef CAS.
- C. J. Bready, S. Vanovac, T. T. Odbadrakh and G. C. Shields, Amino Acids Compete with Ammonia in Sulfuric Acid-Based Atmospheric Aerosol Prenucleation: The Case of Glycine and Serine, J. Phys. Chem. A, 2022, 126, 5195–5206 CrossRef CAS PubMed.
- A. Afzalifar, G. C. Shields, V. R. Fowler and R. H. A. Ras, Probing the Free Energy of Small Water Clusters: Revisiting Classical Nucleation Theory, J. Phys. Chem. Lett., 2022, 13, 8038–8046 CrossRef CAS PubMed.
- Y. Liu, H. B. Xie, F. Ma, J. Chen and J. Elm, Amine-Enhanced Methanesulfonic Acid-Driven Nucleation: Predictive Model and Cluster Formation Mechanism, Environ. Sci. Technol., 2022, 56, 7751–7760 CrossRef CAS PubMed.
- Z. Fu, H. B. Xie, J. Elm, Y. Liu, Z. Fu and J. Chen, Atmospheric Autoxidation of Organophosphate Esters, Environ. Sci. Technol., 2022, 56, 6944–6955 CrossRef CAS PubMed.
- J. Elm, Clusteromics III: Acid Synergy in Sulfuric Acid-Methanesulfonic Acid-Base Cluster Formation, ACS Omega, 2022, 7, 15206–15214 CrossRef CAS PubMed.
- C. J. Bready, V. R. Fowler, L. A. Juechter, L. A. Kurfman, G. E. Mazaleski and G. C. Shields, The driving effects of common atmospheric molecules for formation of prenucleation clusters: the case of sulfuric acid, formic acid, nitric acid, ammonia, and dimethyl amine, Environ. Sci.: Atmos., 2022, 2, 1469–1486 CAS.
- Y. Knattrup and J. Elm, Clusteromics IV: The Role of Nitric Acid in Atmospheric Cluster Formation, ACS Omega, 2022, 7, 31551–31560 CrossRef CAS PubMed.
- F. R. Rasmussen, J. Kubecka and J. Elm, Contribution of Methanesulfonic Acid to the Formation of Molecular Clusters in the Marine Atmosphere, J. Phys. Chem. A, 2022, 126, 7127–7136 CrossRef CAS PubMed.
- A. B. Jensen, J. Kubecka, G. Schmitz, O. Christiansen and J. Elm, Massive Assessment of the Binding Energies of Atmospheric Molecular Clusters, J. Chem. Theory Comput., 2022, 18, 7373–7383, DOI:10.1021/acs.jctc.2c00825.
- B. Rosati, S. Isokaanta, S. Christiansen, M. M. Jensen, S. P. Moosakutty, R. W. de Jonge, A. Massling, M. Glasius, J. Elm, A. Virtanen and M. Bilde, Hygroscopicity and CCN potential of DMS-derived aerosol particles, Atmos. Chem. Phys., 2022, 22, 13449–13466 CrossRef CAS.
- D. Thomsen, L. D. Thomsen, E. M. Iversen, T. N. Bjorgvinsdattir, S. F. Vinther, J. T. Skonager, T. Hoffmann, J. Elm, M. Bilde and M. Glasius, Ozonolysis of alpha-Pinene and Delta 3-Carene Mixtures: Formation of Dimers with Two Precursors, Environ. Sci. Technol., 2022, 56, 16643–16651 CrossRef CAS PubMed.
- J. W. Xue, F. F. Ma, J. Elm, J. W. Chen and H. B. Xie, Atmospheric oxidation mechanism and kinetics of indole initiated by center dot OH and center dot Cl: a computational study, Atmos. Chem. Phys., 2022, 22, 11543–11555 CrossRef CAS.
- J. Kubecka, I. Neefjes, V. Besel, F. Qiao, H. B. Xie and J. Elm, Atmospheric Sulfuric Acid-Multi-Base New Particle Formation Revealed through Quantum Chemistry Enhanced by Machine Learning, J. Phys. Chem. A, 2023, 127, 2091–2103 CrossRef CAS PubMed.
- F. Ma, H. B. Xie, R. Zhang, L. Su, Q. Jiang, W. Tang, J. Chen, M. Engsvang, J. Elm and X. C. He, Enhancement of Atmospheric Nucleation Precursors on Iodic Acid-Induced Nucleation: Predictive Model and Mechanism, Environ. Sci. Technol., 2023, 57, 6944–6954 CrossRef CAS PubMed.
- T. Olenius, R. Bergstrom, J. Kubecka, N. Myllys and J. Elm, Reducing chemical complexity in representation of new-particle formation: evaluation of simplification approaches, Environ. Sci.: Atmos., 2023, 3, 552–567 CAS.
- D. Ayoubi, Y. Knattrup, J. Elm and V. Clusteromics, Organic Enhanced Atmospheric Cluster Formation, ACS Omega, 2023, 8, 9621–9629 CrossRef CAS PubMed.
- M. Farnik, Bridging Gaps between Clusters in Molecular-Beam Experiments and Aerosol Nanoclusters, J. Phys. Chem. Lett., 2023, 14, 287–294 CrossRef CAS PubMed.
- N. Myllys, The role of hydration in atmospheric salt particle formation, Phys. Chem. Chem. Phys., 2023, 25, 7394–7400 RSC.
- X. L. Shen, J. Y. Chen, G. Y. Li and T. C. An, A new advance in the pollution profile, transformation process, and contribution to aerosol formation and aging of atmospheric amines, Environ. Sci.: Atmos., 2023, 3, 444–473 CAS.
- O. M. Longsworth, C. J. Bready and G. C. Shields, The Driving Effects of Common Atmospheric Molecules for Formation of Clusters: The Case of Sulfuric Acid, Formic Acid, Hydrochloric Acid, Ammonia, and Dimethyl Amine, Environ. Sci.: Atmos., 2023, 3, 1335–1351 CAS.
- J. M. Dieterich and B. Hartke, OGOLEM: Global cluster structure optimisation for arbitrary mixtures of flexible molecules. A multiscaling, object-oriented approach, Mol. Phys., 2010, 108, 279–291 CrossRef CAS.
- B. Hartke, Global optimization, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2011, 1, 879–887 CAS.
- C. Bannwarth, S. Ehlert and S. Grimme, GFN2-xTB-An Accurate and Broadly Parametrized Self-Consistent Tight-Binding Quantum Chemical Method with Multipole Electrostatics and Density-Dependent Dispersion Contributions, J. Chem. Theory Comput., 2019, 15, 1652–1671 CrossRef CAS PubMed.
- S. Grimme, Exploration of Chemical Compound, Conformer, and Reaction Space with Meta-Dynamics Simulations Based on Tight-Binding Quantum Chemical Calculations, J. Chem. Theory Comput., 2019, 15, 2847–2862 CrossRef CAS PubMed.
- P. Pracht, F. Bohle and S. Grimme, Automated exploration of the low-energy chemical space with fast quantum chemical methods, Phys. Chem. Chem. Phys., 2020, 22, 7169–7192 RSC.
- L. A. Kurfman, T. T. Odbadrakh and G. C. Shields, Calculating Reliable Gibbs Free Energies for Formation of Gas-Phase Clusters that Are Critical for Atmospheric Chemistry: (H(2)SO(4))(3), J. Phys. Chem. A, 2021, 125, 3169–3176 CrossRef CAS PubMed.
- J. D. Chai and M. Head-Gordon, Systematic optimization of long-range corrected hybrid density functionals, J. Chem. Phys., 2008, 128, 084106 CrossRef PubMed.
- J. D. Chai and M. Head-Gordon, Long-range corrected hybrid density functionals with damped atom-atom dispersion corrections, Phys. Chem. Chem. Phys., 2008, 10, 6615–6620 RSC.
- R. Ditchfield, W. J. Hehre and J. A. Pople, Self-Consistent Molecular-Orbital Methods. IX. An Extended Gaussian-Type Basis for Molecular-Orbital Studies of Organic Molecules, J. Chem. Phys., 1971, 54, 724–728 CrossRef CAS.
- W. J. Hehre, R. Ditchfield and J. A. Pople, Self—Consistent Molecular Orbital Methods. XII. Further Extensions of Gaussian—Type Basis Sets for Use in Molecular Orbital Studies of Organic Molecules, J. Chem. Phys., 1972, 56, 2257–2261 CrossRef CAS.
- P. C. Hariharan and J. A. Pople, The influence of polarization functions on molecular orbital hydrogenation energies, Theor. Chim. Acta, 1973, 28, 213–222 CrossRef CAS.
- M. J. Frisch, J. A. Pople and J. S. Binkley, Self-consistent molecular orbital methods 25. Supplementary functions for Gaussian basis sets, J. Chem. Phys., 1984, 80, 3265–3269 CrossRef CAS.
-
M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, et al., Gaussian 16 Rev. B.01, Wallingford, CT, 2016 Search PubMed.
- B. Temelso, J. M. Mabey, T. Kubota, N. Appiah-Padi and G. C. Shields, ArbAlign: A Tool for Optimal Alignment of Arbitrarily Ordered Isomers Using the Kuhn-Munkres Algorithm, J. Chem. Inf. Model., 2017, 57, 1045–1054 CrossRef CAS PubMed.
- F. Neese, F. Wennmohs and A. Hansen, Efficient and accurate local approximations to coupled-electron pair approaches: An attempt to revive the pair natural orbital method, J. Chem. Phys., 2009, 130, 114108 CrossRef PubMed.
- F. Neese, A. Hansen and D. G. Liakos, Efficient and accurate approximations to the local coupled cluster singles doubles method using a truncated pair natural orbital basis, J. Chem. Phys., 2009, 131, 064103 CrossRef PubMed.
- F. Neese, Prediction of molecular properties and molecular spectroscopy with density functional theory: From fundamental theory to exchange-coupling, Coord. Chem. Rev., 2009, 253, 526–563 CrossRef CAS.
- C. Riplinger, P. Pinski, U. Becker, E. F. Valeev and F. Neese, SparseMaps - A systematic infrastructure for reduced-scaling electronic structure methods. II. Linear scaling domain based pair natural orbital coupled cluster theory, J. Chem. Phys., 2016, 144, 024109 CrossRef PubMed.
- C. Riplinger, B. Sandhoefer, A. Hansen and F. Neese, Natural triple excitations in local coupled cluster calculations with pair natural orbitals, J. Chem. Phys., 2013, 139, 134101 CrossRef PubMed.
- C. Riplinger and F. Neese, An efficient and near linear scaling pair natural orbital based local coupled cluster method, J. Chem. Phys., 2013, 138, 034106 CrossRef PubMed.
- A. Hansen, D. G. Liakos and F. Neese, Efficient and accurate local single reference correlation methods for high-spin open-shell molecules using pair natural orbitals, J. Chem. Phys., 2011, 135, 214102 CrossRef PubMed.
- M. Sparta, M. Retegan, P. Pinski, C. Riplinger, U. Becker and F. Neese, Multilevel Approaches within the Local Pair Natural Orbital Framework, J. Chem. Theory Comput., 2017, 13, 3198–3207 CrossRef CAS PubMed.
- A. K. Wilson, T. van Mourik and T. H. Dunning, Gaussian basis sets for use in correlated molecular calculations. VI. Sextuple zeta correlation consistent basis sets for boron through neon, J. Mol. Struct.: THEOCHEM, 1996, 388, 339–349 CrossRef CAS.
- K. A. Peterson, D. E. Woon and T. H. Dunning, Benchmark calculations with correlated molecular wave functions. IV. The classical barrier height of the H+H2→H2+H reaction, J. Chem. Phys., 1994, 100, 7410–7415 CrossRef CAS.
- D. E. Woon and T. H. Dunning, Gaussian basis sets for use in correlated molecular calculations. III. The atoms aluminum through argon, J. Chem. Phys., 1993, 98, 1358–1371 CrossRef CAS.
- T. H. Dunning, Gaussian basis sets for use in correlated molecular calculations. I. The atoms boron through neon and hydrogen, J. Chem. Phys., 1989, 90, 1007–1023 CrossRef CAS.
- F. Neese, F. Wennmohs, U. Becker and C. Riplinger, The ORCA quantum chemistry program package, J. Chem. Phys., 2020, 152, 224108 CrossRef CAS PubMed.
-
K. K. Irikura,THERMO.PL, NIST, 2002 Search PubMed.
- I. M. Alecu, J. Zheng, Y. Zhao and D. G. Truhlar, Computational Thermochemistry: Scale Factor Databases and Scale Factors for Vibrational Frequencies Obtained from Electronic Model Chemistries, J. Chem. Theory Comput., 2010, 6, 2872–2887 CrossRef CAS PubMed.
-
S. Kanchanakungwankul, J. L. Bao, J. Zheng, I. M. Alecu, B. J. Lynch and D. G. Truhlar, Database of frequency scale factors for electronic model chemistries, version 5, 2021 Search PubMed.
- T. Helgaker, W. Klopper, H. Koch and J. Noga, Basis-set convergence of correlated calculations on water, J. Chem. Phys., 1997, 106, 9639–9646 CrossRef CAS.
- S. Aloisio, P. E. Hintze and V. Vaida, The hydration of formic acid, J. Phys. Chem. A, 2002, 106, 363–370 CrossRef CAS.
- K. Acker, D. Moller, R. Auel, W. Wieprecht and D. Kalass, Concentrations of nitrous acid, nitric acid, nitrite and nitrate in the gas and aerosol phase at a site in the emission zone during ESCOMPTE 2001 experiment, Atmos. Res., 2005, 74, 507–524 CrossRef CAS.
- X. L. Ge, A. S. Wexler and S. L. Clegg, Atmospheric amines - Part II. Thermodynamic properties and gas/particle partitioning, Atmos. Environ., 2011, 45, 561–577 CrossRef CAS.
- X. L. Ge, A. S. Wexler and S. L. Clegg, Atmospheric amines - Part I. A review, Atmos. Environ., 2011, 45, 524–546 CrossRef CAS.
- B. J. Su, T. Wang, G. H. Zhang, Y. Liang, C. Lv, Y. H. Hu, L. Li, Z. Zhou, X. M. Wang and X. H. Bi, A review of atmospheric aging of sea spray aerosols: Potential factors affecting chloride depletion, Atmos. Environ., 2022, 290, 119365 CrossRef CAS.
- S. Solomon, K. Stone, P. Yu, D. M. Murphy, D. Kinnison, A. R. Ravishankara and P. Wang, Chlorine activation and enhanced ozone depletion induced by wildfire aerosol, Nature, 2023, 615, 259–264 CrossRef CAS PubMed.
- S. N. Behera, R. Betha and R. Balasubramanian, Insights into Chemical Coupling among Acidic Gases, Ammonia and Secondary Inorganic Aerosols, Aerosol Air Qual. Res., 2013, 13, 1282–1296 CrossRef CAS.
- S. Preunkert, M. Legrand, B. Jourdain and I. Dombrowski-Etchevers, Acidic gases (HCOOH, CH3COOH, HNO3, HCl, and SO2) and related aerosol species at a high mountain Alpine site (4360 m elevation) in Europe, J. Geophys. Res.: Atmos., 2007, 112, D23S12 CrossRef.
- G. C. Shields, The Molecular Education and Research Consortium in Undergraduate Computational Chemistry (MERCURY): Twenty Years of Exceptional Success Supporting Undergraduate Research and Inclusive Excellence, SPUR-Scholarship and Practice of Undergraduate Research, 2019, 3, 5–15 CrossRef.
- G. C. Shields, Twenty years of exceptional success: The molecular education and research consortium in undergraduate computational chemistry (MERCURY), Int. J. Quantum Chem., 2020, 120, e26274 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Figures of minimum energy structures, sequential hydration tables, DFT and DLPNO-CCSD(T) energy tables, optimized structures, derivation of CBS extrapolation formula, and example calculations of stepwise energies. See DOI: https://doi.org/10.1039/d3ea00118k |
|
| This journal is © The Royal Society of Chemistry 2023 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article ,
Conor J.
Bready
,
Conor J.
Bready
 ,
Macie S.
Joines
and
George C.
Shields
,
Macie S.
Joines
and
George C.
Shields
 *
*
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000. Because of the uncertainties associated with semi-empirical methods,58,92 all structures within 30 kcal mol−1 of the GFN2-xTB global minimum were then re-optimized at the ωB97X-D/6-31++G** level of theory93–98 using the Gaussian 16 Rev. B01 program,99 and duplicate structures were removed.100 All DFT structures within 8 kcal mol−1 of the ωB97X-D/6-31++G** electronic energy global minimum were recalculated using the domain-based local pair natural orbital coupled cluster (DLPNO-CCSD(T)) method101–108 with single, double, and semi-canonical perturbative triple excitations with three Dunning basis sets,109–112 cc-pVnZ (n = D, T, Q) using Orca 5.0.1.113 Estimates of the thermodynamic corrections for H°, S°, and G° were computed at a standard state of 1 atm pressure and temperatures of 216.65, 273.15, and 298.15 K using the THERMO.pl script114 from the National Institute of Science and Technology. These computations used the ωB97X-D/6-31++G** frequencies, which were scaled by a factor of 0.971 to partially account for anharmonicity.115,116 An inverse 4–5 polynomial complete basis set (CBS) extrapolation117 on the three CCSD(T)/cc-pVnZ (n = D, T, Q) electronic energies was used to obtain CBS electronic energies. The CBS energies were combined with the ωB97X-D/6-31++G** thermal corrections to obtain the final G° values. The complete methodology is outlined in Fig. 1. Once the final G° values were calculated for the individual clusters, ΔG°binding was calculated as follows:
000. Because of the uncertainties associated with semi-empirical methods,58,92 all structures within 30 kcal mol−1 of the GFN2-xTB global minimum were then re-optimized at the ωB97X-D/6-31++G** level of theory93–98 using the Gaussian 16 Rev. B01 program,99 and duplicate structures were removed.100 All DFT structures within 8 kcal mol−1 of the ωB97X-D/6-31++G** electronic energy global minimum were recalculated using the domain-based local pair natural orbital coupled cluster (DLPNO-CCSD(T)) method101–108 with single, double, and semi-canonical perturbative triple excitations with three Dunning basis sets,109–112 cc-pVnZ (n = D, T, Q) using Orca 5.0.1.113 Estimates of the thermodynamic corrections for H°, S°, and G° were computed at a standard state of 1 atm pressure and temperatures of 216.65, 273.15, and 298.15 K using the THERMO.pl script114 from the National Institute of Science and Technology. These computations used the ωB97X-D/6-31++G** frequencies, which were scaled by a factor of 0.971 to partially account for anharmonicity.115,116 An inverse 4–5 polynomial complete basis set (CBS) extrapolation117 on the three CCSD(T)/cc-pVnZ (n = D, T, Q) electronic energies was used to obtain CBS electronic energies. The CBS energies were combined with the ωB97X-D/6-31++G** thermal corrections to obtain the final G° values. The complete methodology is outlined in Fig. 1. Once the final G° values were calculated for the individual clusters, ΔG°binding was calculated as follows:
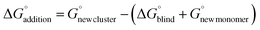
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio of acid to bases in the growing clusters. The second-best pathway starts with (NA)(DMA) and then adds SA. Therefore, the first- and second-best pathways pass through the same trimer, (SA)(NA)(DMA), which is atmospherically relevant at both temperatures. The only difference between the first- and second-best pathways is the acid in the starting dimer. This discrepancy is likely due to the balance between thermodynamics and mass balance, as (SA)(DMA) is thermodynamically favored but NA is present in a much higher concentration than SA. In both of these pathways, HCl is the last molecule to be added to the cluster, likely because HCl has a much greater stabilizing effect on hydrated clusters than dry clusters. The third-best pathway also starts with (SA)(DMA), followed by the addition of HCl. (SA)(HCl)(DMA) is barely atmospherically relevant, present only at 298 K and in a very low concentration (Table 7). Ammonia is added to form the tetramer (SA)(HCl)(A)(DMA) and NA is added last. When the three systems (SA)(FA)(NA)(A)(DMA),72,86 (SA)(FA)(HCl)(A)(DMA),72,86 and (SA)(NA)(HCl)(A)(DMA) are compared, SA and DMA stand out as strong drivers of prenucleation due to their higher equilibrium concentrations. In this particular system, NA appears more in both dry and hydrated clusters than HCl does, likely caused by a higher initial concentration of NA than for HCl in our calculations. Many subtleties are at play in the beginning stages of pre-nucleation and these results cannot be attributed to only one factor. Hydrogen bonding topology and complex structural interactions appear to play an important role in structure energetics and atmospheric relevance.
1 ratio of acid to bases in the growing clusters. The second-best pathway starts with (NA)(DMA) and then adds SA. Therefore, the first- and second-best pathways pass through the same trimer, (SA)(NA)(DMA), which is atmospherically relevant at both temperatures. The only difference between the first- and second-best pathways is the acid in the starting dimer. This discrepancy is likely due to the balance between thermodynamics and mass balance, as (SA)(DMA) is thermodynamically favored but NA is present in a much higher concentration than SA. In both of these pathways, HCl is the last molecule to be added to the cluster, likely because HCl has a much greater stabilizing effect on hydrated clusters than dry clusters. The third-best pathway also starts with (SA)(DMA), followed by the addition of HCl. (SA)(HCl)(DMA) is barely atmospherically relevant, present only at 298 K and in a very low concentration (Table 7). Ammonia is added to form the tetramer (SA)(HCl)(A)(DMA) and NA is added last. When the three systems (SA)(FA)(NA)(A)(DMA),72,86 (SA)(FA)(HCl)(A)(DMA),72,86 and (SA)(NA)(HCl)(A)(DMA) are compared, SA and DMA stand out as strong drivers of prenucleation due to their higher equilibrium concentrations. In this particular system, NA appears more in both dry and hydrated clusters than HCl does, likely caused by a higher initial concentration of NA than for HCl in our calculations. Many subtleties are at play in the beginning stages of pre-nucleation and these results cannot be attributed to only one factor. Hydrogen bonding topology and complex structural interactions appear to play an important role in structure energetics and atmospheric relevance.





