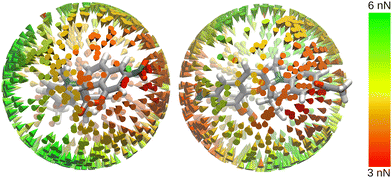Using oriented external electric fields to manipulate rupture forces of mechanophores
Tarek
Scheele
 a and
Tim
Neudecker
a and
Tim
Neudecker
 *abc
*abc
aUniversity of Bremen, Institute for Physical and Theoretical Chemistry, Leobener Straße 6, D-28359 Bremen, Germany. E-mail: neudecker@uni-bremen.de
bBremen Center for Computational Materials Science, University of Bremen, Am Fallturm 1, D-28359 Bremen, Germany
cMAPEX Center for Materials and Processes, University of Bremen, Bibliothekstraße 1, D-28359 Bremen, Germany
First published on 9th October 2023
Abstract
Oriented external electric fields (OEEFs) can facilitate chemical reactions by selectively weakening bonds. This makes them a topic of interest in mechanochemistry, where mechanical force is used to rupture specific bonds in molecules. Using electronic structure calculations based on density functional theory (DFT), we investigate the effect of OEEFs on the mechanical force required to activate mechanophores. We demonstrate that OEEFs can greatly lower the rupture force of mechanophores, and that the degree of this effect highly depends on the angle relative to the mechanical force at which the field is being applied. The greatest lowering of the rupture force does not always occur at the point of perfect alignment between OEEF and the vector of mechanical force. Using natural bond orbital analysis, we show that mechanical force amplifies the effect that an OEEF has on the scissile bond of a mechanophore. By combining methods to simulate molecules in OEEFs with methods applying mechanical force, we present an effective tool for analyzing mechanophores in OEEFs and show that computationally determining optimal OEEFs for mechanophore activation can assist in the development of future experimental studies.
1 Introduction
Oriented external electric fields (OEEFs) have increasingly become a focus of chemical research.1,2 OEEFs enable precise control over chemical selectivity and reactivity during a chemical reaction.1,3–7 By stabilizing polar transition states, they facilitate reactions that would otherwise be unfavourable.8,9 It has been shown that both the strength of the field and its orientation affect the outcome of a reaction.2,4,10 This has led to an increasing use of computational methods for studying chemical reactions3–5,11–15 as well as chemical properties16–18 of molecules in OEEFs.One field that has the potential to greatly benefit from the effects of OEEFs is mechanochemistry,19 the study of chemical reactions under mechanical stress. Mechanochemical research has made significant progress in recent decades, and interest in the field has consequently grown.20–24 Of particular interest for mechanochemists are the properties and reactions of mechanophores. Mechanophores are molecules that undergo structural changes when exposed to mechanical stress.20,25,26 They often have a particular bond, called the scissile bond, at which rupture occurs once the mechanical force is high enough, which is typically between 1 nN and 10 nN. When included in a polymer chain, mechanophores allow for selectively changing the structure of a polymer through mechanical action such as pulling, pressure, or ultrasound.20,25,27 These structural changes have a variety of applications ranging from changing the material's colour25,28 to releasing small molecules without causing material failure.26,29–31
As OEEFs polarize and weaken chemical bonds, one can expect that they will lower the rupture force of mechanophores. Of particular interest is the interaction between OEEFs and pulling force, a force applied from two opposing directions. Experimentally, pulling force is applied from the ends of a polymer chain that the mechanophore is embedded in. In experiments involving isolated polymer strands, for example using atomic force microscopy (AFM), the stretching of the polymer chain leads to the mechanophore having a known orientation, which is a prerequisite for the application of OEEFs to facilitate chemical reactions. Using a conductive AFM tip, it is possible to align the OEEF with the chain in such a setup, but OEEFs could also be applied from different orientations using a more complex setup with multiple conductors. The ability to precisely adjust the relative orientation of the mechanophore and OEEF in AFM experiments allows the combination of electric field strength, electric field direction, and pulling force as three external parameters that can alter the chemical reactivity of a mechanophore. However, it must be noted that experiments that guarantee a precise alignment of a molecule with an OEEF are scarce,3 given the practical difficulty of implementing such experiments.
Electronic structure calculations present themselves as a powerful tool for determining the optimal OEEF strength and direction required to lower the rupture force of a mechanophore. They have recently been used for determining optimal OEEFs for the purpose of lowering reaction barriers.32,33 Modelling the bond rupture of a mechanophore requires including mechanical force in the calculation, which can be done using a multitude of different approaches,34,35 but to the best of our knowledge, a thorough computational investigation of the behaviour of mechanophores in OEEFs using a combination of electric field and mechanical force models has not been done until now.
In this work, we investigate the effect of OEEFs on the force required to break the scissile bonds of mechanophores. Using computational electronic structure methods, we apply increasing stretching forces to mechanophores under the influence of an OEEF. This is performed for three different mechanophores representing three different bonding situations. We present a thorough investigation of the rupture behaviour of these mechanophores at different electric field strengths. We also show how the rupture behaviour changes when the OEEF is applied at different angles relative to the stretching coordinate, and we compare the effects on symmetric and asymmetric mechanophores. The goal of our research is to present a first look into the details of the rupture force behaviour of mechanophores in OEEFs, and to demonstrate that combining computational methods for applying OEEFs with methods for applying stretching force is a viable tool for finding the optimal parameters needed to activate a mechanophore.
The rest of this work is structured as follows: in Section 2, we present the methodology of our investigation, the molecules we investigated, and the computational methods we used. In Section 3, we present the rupture behaviour of the mechanophores at different electric field strengths, followed by the rupture behaviour when the OEEF is applied at different angles. Finally, we show the effect that combining OEEFs and mechanical force has on a mechanophore's scissile bond using natural bond orbital (NBO) analysis.
2 Computational details
For this work, three different molecules were investigated (Fig. 1). The three structures are meant to represent groups of known mechanophores that have been investigated in previous works.36 With a benzocyclobutene derivative (A), we investigated a high-symmetry mechanophore with a scissile C–C bond.37,38 The spiropyran (B), an asymmetric molecule with a scissile C–O bond, represents a group of mechanophores that has been thoroughly studied in literature.28,39 Finally, we decided to investigate a S–S bond rupture using a high-symmetry linear disulphide (C).40Electronic structure calculations were performed using Q-Chem 5.4.0.41 All electronic structure calculations were performed at the ωB97X-V/cc-pVDZ level of theory,42,43 which has been shown to provide good accuracy when calculating organic molecules in strong electric fields.44
We investigated the rupture force of each structure's scissile bond depending on the electric field strength. Electric fields were applied along the stretching coordinate indicated by arrows in Fig. 1 to match the alignment of the electric field with the direction of mechanical force. OEEFs were applied to molecules during the calculations using a custom routine that ensured the electric field always aligned with the marked bond during geometry optimizations. In Q-Chem, a positive electric field along an axis places the negative pole towards positive infinity and the positive pole towards negative infinity.
In this work, electric field strength is given in atomic units (1 a.u. ≈ 51.4 V Å−1). Electric field strengths between −0.06 a.u. and 0.06 a.u. in steps of 0.002 a.u. were tested. At each investigated field strength, the External Force is Explicitly Included (EFEI) approach45–47 as implemented in Q-Chem was used to apply a pulling force to the groups indicated by arrows in Fig. 1. Pulling forces applied ranged from 0 nN to 6 nN in steps of 0.05 nN.
For each electric field strength and pulling force, a geometry optimization was performed. The interatomic distances between the bond-forming atoms of the optimized geometries were checked to determine whether bond rupture has occurred. The rupture force of a molecule at a given field strength is considered to be the smallest pulling force at which bond rupture starts occurring. We determined bond rupture to have occurred when the distance between the two atoms forming the scissile bond became sufficiently high. Structures A and B form a new minimum geometry when the scissile bond breaks, whereas C separates and diverges.
To determine the effect of the electric field's angle on the rupture force, we performed further geometry optimizations of structure A. Here, the electric field was oriented at an angle rotated around either the scissile bond axis or one of its two orthogonal axes in steps of 10° (Fig. 2). Pulling force was applied in steps of 0.005 nN to better capture small differences. The pulling force was applied in the same way as in the previous calculations, from the groups marked in Fig. 1. Here, the direction of the OEEF and pulling force no longer coincide. This was done for electric field strengths between 0.01 a.u. and 0.05 a.u. in steps of 0.01 a.u.
 | ||
| Fig. 2 The axes in A around which the effect of the electric field's angle on the rupture force was investigated. The x axis is shown in blue, the y axis in red, and the z axis in yellow. | ||
The asymmetric spiropyran B has a more complex structure compared to the other two investigated molecules, and we chose to more generally investigate the effect of the electric field's direction on rupture force. The electric field was applied along 800 randomly chosen orientations while pulling force was applied in the same way as in the previous calculations, and the rupture force of the scissile bond was determined at a 0.5 nN resolution. This was performed using an electric field strength of 0.01 a.u., as it is within the order of magnitude used for applying OEEFs experimentally.3–5,48 With only few notable exceptions,3 it is not possible to experimentally specify the orientation of a molecule in an electric field with high precision, and experiments with OEEFs typically exhibit a random distribution in the alignment between OEEF and molecule. The random distribution used for these calculations allows us to model a more realistic scenario where the molecule might not always perfectly align with a field.
NBO analyses were performed using the NBO 7.0 program package.49 For each of the investigated mechanophores, we performed a natural population analysis (NPA) of the calculated natural localized molecular orbitals (NLMOs) to determine bond orders of the scissile bonds. This was done for geometries with electric field strengths between −0.02 a.u. and 0.02 a.u. in steps of 0.01 a.u. applied along the stretching coordinate, with no applied mechanical force as well as when mechanical force 0.05 nN below the molecule's rupture force is applied.
3 Results and discussion
The effect of electric fields on the rupture forces of the investigated molecules is shown in Fig. 3. As seen therein, the application of an electric field along the stretching coordinate lowers the force required to rupture the scissile bond, up to a point where the electric field alone will break the bond. As the three mechanophores are chemically very different, this is expected to apply generally. At no applied electric field, the rupture force may be compared with forces calculated by Klein et al. using the CoGEF method.36,50 Considering the difference in the applied level of theory, our calculated EFEI data is in agreement with the previously published CoGEF data, showing differences under 1 nN. Among the three investigated structures, C shows the lowest rupture force with no electric field, while B shows the highest. | ||
| Fig. 3 Rupture forces of the three mechanophores A (top), B (middle), and C (bottom) at different electric field strengths, calculated with EFEI. | ||
Structure A shows a symmetrical behaviour at negative and positive electric fields, which is expected of symmetrical molecules. The relation between rupture force and field strength in the figure resembles a parabola and the effect of the field on the rupture force increases as the field strength approaches the field-induced breaking point of the molecule. In contrast, structure B shows a steeper, but linear relation between field strength and rupture force. Structure C shows a similar behaviour to A, also being a symmetrical molecule. However, it shows similar robustness in electric fields as B; while A is still stable with no mechanical force applied at a field strength of ±0.05 a.u., B and C break around ±0.025 a.u. This difference in the field strength required to break the scissile bonds may be explained by the nature of the scissile bonds: the scissile C–C bond in A is stable and fully covalent despite the weakening from the cyclobutene ring strain, while B has a polar C–O bond and C a covalent, but long S–S bond.
Structure B as the only investigated structure without symmetry shows a difference in behaviour between positive and negative electric fields, having a slightly more pronounced lowering of the rupture force at negative fields compared to equivalent positive fields. This difference is small, and the behaviour at positive and negative fields is still similar. The electric field induced by the dipole moment along the polar scissile bond is small compared to the external electric field, and has little impact on the overall effect of the field on the molecule's rupture force.
We have investigated the effect of the electric field's angle relative to the scissile bond on the rupture force of a mechanophore using structure A. Fig. 4 shows the effect of applying the electric field from different directions by rotating around the scissile bond axis or two axes orthogonal to it (see Fig. 2). As seen in Fig. 4, the rupture force is strongly affected by the direction of the electric field, and specifically by how well the scissile bond aligns with the electric field. A stronger electric field amplifies this effect.
 | ||
| Fig. 4 Rupture forces of A with electric fields of differing strengths applied at different angles relative to the scissile bond, calculated with EFEI. The electric field is orthogonal to the x (top), y (middle), and z (bottom) axis as seen in Fig. 2, and the angle is a rotation around the respective axis (orange circle). An angle of 0° is indicated by the orange bar in the circle. | ||
When the electric field is aligned orthogonal to the scissile bond of A (Fig. 4, top), the effect of the electric field on the rupture force is minimal. Regardless of the angle around the bond axis, the rupture force stays close to the rupture force calculated without an applied electric field, dropping by up to 0.8 nN in strong electric fields when the electric field is parallel to the aromatic ring and the cyclobutadiene ring. Applying an electric field along the bonds near the scissile bond has an effect on the scissile bond's rupture force, albeit a small one compared to applying the field along the scissile bond itself.
Electric fields along the plane orthogonal to the y axis have a much more significant effect on the rupture force. In the middle graph of Fig. 4, the electric field is parallel to the scissile bond at angles of 0° and 180°. Notably, these are not the angles at which the rupture force is lowest. The lowest rupture forces are found at angles around 30° and 210°, when the electric field aligns with the stretching coordinate. Another observation is that the rupture force is higher than previously observed when the electric field is aligned orthogonal to the stretching coordinate, seen at angles around 120° and 300°. In these cases, the rupture force with an applied electric field is higher than the rupture force with no electric field. The change of rupture force with electric field angle displays cyclic behaviour, repeating after a rotation of 180° due to the rotational symmetry of structure A around the y axis.
Electric fields around the plane orthogonal to the z axis, largely aligned with the aromatic ring, also have a significant effect on the rupture force. As the electric field in this plane is never fully aligned with the stretching coordinate, the strongest lowering of the rupture force is found at angles around 0° and 180°, at which the electric field is aligned with the scissile bond. In this plane, no increase in rupture force above the value with no electric field is observed.
Due to the methodology used to determine the rupture point of molecular bonds, the change in rupture force with electric field angle is not smooth, and there are a number of outliers in Fig. 4, particularly in the case of the plane around the z axis. We assume these irregularities to be caused by numerical errors that caused specific structures to dissociate at lower rupture forces, and not by any physical effect.
Structure B is an asymmetric molecule with a complex structure, making the definition of perpendicular bond axes for the investigation difficult. Instead, we chose to investigate the effect of electric fields from arbitrary angles on the molecule's rupture force (Fig. 5). The three-dimensional data shows the directions from which an electric field has a significant impact on the rupture force of B. Red cones indicate OEEF directions through which maximum lowering of the rupture force is achieved.
On the benzopyran side of the spiropyran (l.h.s. of Fig. 5), strong lowering of the rupture force is achieved when the electric field is aligned with the aromatic benzopyran structure. Within the aromatic plane, the strongest effect on the rupture force occurs when the electric field is aligned with the NO2 group. A positive electric field in that direction pushes electron density out of the aromatic ring into the NO2 group, weakening the benzopyran structure.
On the indole side (r.h.s. of Fig. 5), the strongest lowering of the rupture force is achieved when the electric field is aligned with the stretching coordinate. This is similar to the behaviour of structure A. An electric field from this direction will weaken the scissile C–O bond more significantly than an electric field coming from the benzopyran side, as it aligns with the dipole moment of the bond, and the stretching leads to better alignment between the electric field, the stretching coordinate, and the scissile bond. As the polarity of the scissile bond works against the electric field when the electric field is applied from the benzopyran side, this effect is less pronounced, and the effect of the NO2 group becomes significant.
It should be noted that the areas where there is a strong effect on the rupture force can only be determined qualitatively using this methodology. Precisely determining the points of strongest electric field effect is made difficult by the molecule rotating slightly when stretching force is applied. The pronounced variation in rupture forces of B when applying electric fields from different angles highlights the high degree of sophistication required in experimental setups: if one is unable to precisely control the relative orientation of a mechanophore and the electric field, which is usually the case, tremendous variations in the yield of mechanophore activation are expected.
To better understand the effect that the combination of an OEEF and mechanical force has on the scissile bond of a mechanophore, we performed a set of NBO analyses on each mechanophore at different electric field strengths with and without applied mechanical force. We analyzed the calculated NLMO/NPA bond orders between the two atoms forming the scissile bond looking at changes in its covalent bond strength (Table 1). This type of bond order shows the covalent nature of the bond, with numbers lower than 1 indicating polarized or weakened bonds.
| Field (a.u.) | A | B | C | ||||||
|---|---|---|---|---|---|---|---|---|---|
| F = 0 | F ≈ Frup | F rup (nN) | F = 0 | F ≈ Frup | F rup (nN) | F = 0 | F ≈ Frup | F rup (nN) | |
| −0.02 | 0.94 | 0.85 | 4.30 | 0.50 | 0.45 | 1.00 | 0.94 | 0.77 | 3.90 |
| −0.01 | 0.97 | 0.91 | 4.75 | 0.57 | 0.51 | 3.60 | 0.99 | 0.85 | 4.35 |
| 0.00 | 1.00 | 0.97 | 4.90 | 0.60 | 0.56 | 5.55 | 1.02 | 1.00 | 4.60 |
| 0.01 | 0.97 | 0.91 | 4.75 | 0.62 | 0.65 | 3.65 | 0.99 | 0.85 | 4.35 |
| 0.02 | 0.94 | 0.85 | 4.30 | 0.66 | 0.70 | 1.55 | 0.94 | 0.77 | 3.90 |
Without an electric field or mechanical force, structure A shows a C–C bond order of close to 1.0, showing a perfectly symmetrical covalent single bond. Close to the rupture force of the molecule, the bond order drops only slightly, to 0.97. A greater effect is observed when applying a strong electric field. A field of 0.01 a.u. lowers the bond order to 0.97, with stronger fields lowering it further. Close to the rupture force at 0.01 a.u., the bond order drops to 0.9. We observe that the effects that electric fields and mechanical force have on the covalent bond order of the mechanophore greatly amplify each other. This trend continues, with the calculated bond order being significantly lower at stronger fields if mechanical force is applied.
Structure C behaves similarly, as it is also symmetrical. However, the amplifying effect is more pronounced. The S–S bond order drops at a similar rate as the C–C bond in A as the electric field strength is increased, but applying mechanical force results in a sharper drop in the bond order. At a field of 0.01 a.u., the calculated bond order is 0.98 without mechanical force and 0.85 close to the rupture point. The larger distance between atoms increases the effect that pulling the structure apart has on the bond's electronic structure, leading to mechanical force having a greater effect on the bond's stability. This is consistent with our earlier observations showing a greatly reduced rupture force for C (Fig. 3).
Structure B, being the only asymmetric molecule we investigated, shows different behaviour of its bond order. Without any force or electric field, the calculated bond order is 0.6 owing to the polarity of the C–O bond. In negative electric fields, the bond order decreases as the polarization of the bond is increased. Adding mechanical force shows the previously described amplifying effect, further reducing the bond order. Contrary to this, applying a positive electric fields shows an increase in the bond order. A positive electric field goes against the natural polarization of the C–O bond, reducing its polarity and increasing the covalent component of the bond. This has a stabilizing effect on the bond, as shown by the higher rupture force observed at positive electric fields compared to negative ones in Fig. 3. Applying mechanical force also amplifies this effect, further increasing the bond order. At +0.01 a.u., the bond order increases to 0.62 without mechanical force and to 0.65 close to the rupture point, while it drops to 0.57 and 0.51 at −0.01 a.u., respectively.
4 Conclusions and outlook
In conclusion, we used three mechanophores as examples to show that applying an oriented external electric field to a mechanophore generally lowers the rupture force needed to break the molecule's scissile bond significantly. Both the strength of the field and direction which the field is applied from affect the impact that the field has on the rupture force, with mechanophores showing differences in the relationship between rupture force and field strength. For symmetric molecules, aligning the field with the stretching coordinate leads to a greater lowering of the rupture force than aligning it with the scissile bond itself, and for asymmetric molecules, the field directions with strong effects may appear in more complex patterns. Applying mechanical force to a mechanophore in an electric field amplifies the effect that the field has on the bond, further increasing or reducing the bond's polarity.The research presented here shows that OEEFs are a viable tool for affecting rupture forces of mechanophores, and that computational methods to simulate molecules in OEEFs can be combined with methods applying mechanical force, enabling the computational study of mechanophores in electric fields. Experimental studies of molecules in OEEFs are difficult to perform, and computationally determining optimal field strengths and directions will help with the development of experimental setups to study mechanical properties of molecules in electric fields.
Data availability
The data that support the findings of this study are available from the corresponding author upon reasonable request.Conflicts of interest
The authors declare no conflicts of interest.Acknowledgements
Funding by the Deutsche Forschungsgemeinschaft is gratefully acknowledged (grant no. STA 1526/3-1, project no. 441071849). The authors gratefully acknowledge the computing time granted by the Resource Allocation Board and provided on the supercomputer Lise and Emmy at NHR@ZIB and NHR@Göttingen as part of the NHR infrastructure. The calculations for this research were conducted with computing resources under the project hbc00045.References
- S. Shaik, R. Ramanan, D. Danovich and D. Mandal, Structure and Reactivity/Selectivity Control by Oriented-External Electric Fields, Chem. Soc. Rev., 2018, 47, 5125–5145, 10.1039/C8CS00354H.
- S. Shaik, D. Danovich, J. Joy, Z. Wang and T. Stuyver, Electric-Field Mediated Chemistry: Uncovering and Exploiting the Potential of (Oriented) Electric Fields to Exert Chemical Catalysis and Reaction Control, J. Am. Chem. Soc., 2020, 142, 12551–12562, DOI:10.1021/jacs.0c05128.
- A. C. Aragonès, N. L. Haworth, N. Darwish, S. Ciampi, N. J. Bloomfield, G. G. Wallace, I. Diez-Perez and M. L. Coote, Electrostatic Catalysis of a Diels–Alder Reaction, Nature, 2016, 531, 88–91, DOI:10.1038/nature16989.
- S. Yu, P. Vermeeren, T. A. Hamlin and F. M. Bickelhaupt, HowOriented External Electric Fields Modulate Reactivity, Chem. – Eur. J., 2021, 27, 5683–5693, DOI:10.1002/chem.202004906.
- L. Zhang, E. Laborda, N. Darwish, B. B. Noble, J. H. Tyrell, S. Pluczyk, A. P. Le Brun, G. G. Wallace, J. Gonzalez, M. L. Coote and S. Ciampi, Electrochemical and Electrostatic Cleavage of Alkoxyamines, J. Am. Chem. Soc., 2018, 140, 766–774, DOI:10.1021/jacs.7b11628.
- B. Zhang, C. Schaack, C. R. Prindle, E. A. Vo, M. Aziz, M. L. Steigerwald, T. C. Berkelbach, C. Nuckolls and L. Venkataraman, Electric Fields Drive Bond Homolysis, Chem. Sci., 2023, 14, 1769–1774, 10.1039/D2SC06411A.
- L. Rincón, J. R. Mora, F. J. Torres and R. Almeida, On the Activation of σ-Bonds by Electric Fields: A Valence Bond Perspective, Chem. Phys., 2016, 477, 1–7, DOI:10.1016/j.chemphys.2016.08.008.
- Y. Zang, Q. Zou, T. Fu, F. Ng, B. Fowler, J. Yang, H. Li, M. L. Steigerwald, C. Nuckolls and L. Venkataraman, Directing Isomerization Reactions of Cumulenes with Electric Fields, Nat. Commun., 2019, 10, 4482, DOI:10.1038/s41467-019-12487-w.
- J. Lin, Y. Lv, K. Song, X. Song, H. Zang, P. Du, Y. Zang and D. Zhu, Cleavage of Non-Polar C(Sp2)–C(Sp2) Bonds in Cycloparaphenylenes via Electric Field-Catalyzed Electrophilic Aromatic Substitution, Nat. Commun., 2023, 14, 293, DOI:10.1038/s41467-022-35686-4.
- R. Meir, H. Chen, W. Lai and S. Shaik, Oriented Electric Fields Accelerate Diels–Alder Reactions and Control the Endo/Exo Selectivity, ChemPhysChem, 2010, 11, 301–310, DOI:10.1002/cphc.200900848.
- M. Zhang, H. Hou and B. Wang, Mechanistic and Kinetic Investigations on Decomposition of Trifluoromethanesulfonyl Fluoride in the Presence ofWater Vapor and Electric Field, J. Phys. Chem. A, 2023, 127, 671–684, DOI:10.1021/acs.jpca.2c07614.
- C. Wang, D. Danovich, H. Chen and S. Shaik, Oriented External Electric Fields: Tweezers and Catalysts for Reactivity in Halogen-Bond Complexes, J. Am. Chem. Soc., 2019, 141, 7122–7136, DOI:10.1021/jacs.9b02174.
- T. Stuyver, D. Danovich, F. De Proft and S. Shaik, Electrophilic Aromatic Substitution Reactions: Mechanistic Landscape, Electrostatic and Electric-Field Control of Reaction Rates, and Mechanistic Crossovers, J. Am. Chem. Soc., 2019, 141, 9719–9730, DOI:10.1021/jacs.9b04982.
- T. Stuyver, R. Ramanan, D. Mallick and S. Shaik, Oriented (Local) Electric Fields Drive the Millionfold Enhancement of the H-Abstraction Catalysis Observed for Synthetic Metalloenzyme Analogues, Angew. Chem., Int. Ed., 2020, 59, 7915–7920, DOI:10.1002/anie.201916592.
- M. T. Blyth and M. L. Coote, Manipulation of N-heterocyclic Carbene Reactivity with Practical Oriented Electric Fields, Phys. Chem. Chem. Phys., 2022, 25, 375–383, 10.1039/D2CP04507A.
- S. Sowlati-Hashjin and C. F. Matta, The Chemical Bond in External Electric Fields: Energies, Geometries, and Vibrational Stark Shifts of Diatomic Molecules, J. Chem. Phys., 2013, 139, 144101, DOI:10.1063/1.4820487.
- M. Li, X. Wan, X. He, C. Rong and S. Liu, Impacts of External Fields on Aromaticity and Acidity of Benzoic Acid: A Density Functional Theory, Conceptual Density Functional Theory and Information-Theoretic Approach Study, Phys. Chem. Chem. Phys., 2023, 25, 2595–2605, 10.1039/D2CP04557E.
- T. Clarys, T. Stuyver, F. D. Proft and P. Geerlings, Extending Conceptual DFT to Include Additional Variables: Oriented External Electric Field, Phys. Chem. Chem. Phys., 2021, 23, 990–1005, 10.1039/D0CP05277A.
- M. K. Beyer and H. Clausen-Schaumann, Mechanochemistry: The Mechanical Activation of Covalent Bonds, Chem. Rev., 2005, 105, 2921–2948, DOI:10.1021/cr030697h.
- J. N. Brantley, K. M. Wiggins and C. W. Bielawski, Polymer Mechanochemistry: The Design and Study of Mechanophores, Polym. Int., 2013, 62, 2–12, DOI:10.1002/pi.4350.
- S. L. James, et al., Mechanochemistry: Opportunities for New and Cleaner Synthesis, Chem. Soc. Rev., 2012, 41, 413–447, 10.1039/C1CS15171A.
- J. G. Hernández and C. Bolm, Altering Product Selectivity by Mechanochemistry, J. Org. Chem., 2017, 82, 4007–4019, DOI:10.1021/acs.joc.6b02887.
- K. J. Ardila-Fierro and J. G. Hernández, Sustainability Assessment of Mechanochemistry by Using the Twelve Principles of Green Chemistry, ChemSusChem, 2021, 14, 2145–2162, DOI:10.1002/cssc.202100478.
- P. F. McMillan, Chemistry at High Pressure, Chem. Soc. Rev., 2006, 35, 855–857, 10.1039/B610410J.
- M. Stratigaki and R. Göstl, Methods for Exerting and Sensing Force in Polymer Materials Using Mechanophores, ChemPlusChem, 2020, 85, 1095–1103, DOI:10.1002/cplu.201900737.
- H.-A. Klok, A. Herrmann and R. Göstl, Force Ahead: Emerging Applications and Opportunities of Polymer Mechanochemistry, ACS Polym. Au, 2022, 2, 208–212, DOI:10.1021/acspolymersau.2c00029.
- K. M. Wiggins, J. N. Brantley and C. W. Bielawski, Methods for Activating and Characterizing Mechanically Responsive Polymers, Chem. Soc. Rev., 2013, 42, 7130–7147, 10.1039/C3CS35493H.
- D. A. Davis, A. Hamilton, J. Yang, L. D. Cremar, D. Van Gough, S. L. Potisek, M. T. Ong, P. V. Braun, T. J. Martínez, S. R. White, J. S. Moore and N. R. Sottos, Force-Induced Activation of Covalent Bonds in Mechanoresponsive Polymeric Materials, Nature, 2009, 459, 68–72, DOI:10.1038/nature07970.
- M. B. Larsen and A. J. Boydston, Flex-Activated Mechanophores: Using Polymer Mechanochemistry To Direct Bond Bending Activation, J. Am. Chem. Soc., 2013, 135, 8189–8192, DOI:10.1021/ja403757p.
- M. B. Larsen and A. J. Boydston, Successive Mechanochemical Activation and Small Molecule Release in an Elastomeric Material, J. Am. Chem. Soc., 2014, 136, 1276–1279, DOI:10.1021/ja411891x.
- B. Cao, N. Boechler and A. J. Boydston, Additive Manufacturing with a Flex Activated Mechanophore for Nondestructive Assessment of Mechanochemical Reactivity in Complex Object Geometries, Polymer, 2018, 152, 4–8, DOI:10.1016/j.polymer.2018.05.038.
- J. M. Bofill, W. Quapp, G. Albareda, I. D. P. R. Moreira and J. Ribas-Ariño, Controlling Chemical Reactivity with Optimally Oriented Electric Fields: A Generalization of the Newton Trajectory Method, J. Chem. Theory Comput., 2022, 18, 935–952, DOI:10.1021/acs.jctc.1c00943.
- J. M. Bofill, M. Severi, W. Quapp, J. Ribas-Ariño, I. D. P. R. Moreira and G. Albareda, An Algorithm to Find the Optimal Oriented External Electrostatic Field for Annihilating a Reaction Barrier in a Polarizable Molecular System, J. Chem. Phys., 2023, 159, 114112, DOI:10.1063/5.0167749.
- T. Stauch and A. Dreuw, Advances in Quantum Mechanochemistry: Electronic Structure Methods and Force Analysis, Chem. Rev., 2016, 116, 14137–14180, DOI:10.1021/acs.chemrev.6b00458.
- J. Ribas-Arino and D. Marx, Covalent Mechanochemistry: Theoretical Concepts and Computational Tools with Applications to Molecular Nanomechanics, Chem. Rev., 2012, 112, 5412–5487, DOI:10.1021/cr200399q.
- I. M. Klein, C. C. Husic, D. P. Kovács, N. J. Choquette and M. J. Robb, Validation of the CoGEF Method as a Predictive Tool for Polymer Mechanochemistry, J. Am. Chem. Soc., 2020, 142, 16364–16381, DOI:10.1021/jacs.0c06868.
- C. R. Hickenboth, J. S. Moore, S. R. White, N. R. Sottos, J. Baudry and S. R. Wilson, Biasing Reaction Pathways with Mechanical Force, Nature, 2007, 446, 423–427, DOI:10.1038/nature05681.
- J. Wang, T. B. Kouznetsova, Z. Niu, M. T. Ong, H. M. Klukovich, A. L. Rheingold, T. J. Martinez and S. L. Craig, Inducing and Quantifying Forbidden Reactivity with Single-Molecule Polymer Mechanochemistry, Nat. Chem., 2015, 7, 323–327, DOI:10.1038/nchem.2185.
- H. Traeger, D. J. Kiebala, C. Weder and S. Schrettl, From Molecules to Polymers—Harnessing Inter- and Intramolecular Interactions to Create Mechanochromic Materials, Macromol. Rapid Commun., 2021, 42, 2000573, DOI:10.1002/marc.202000573.
- Y. Li, A. Nese, K. Matyjaszewski and S. S. Sheiko, Molecular Tensile Machines: Anti-Arrhenius Cleavage of Disulfide Bonds, Macromolecules, 2013, 46, 7196–7201, DOI:10.1021/ma401178w.
- E. Epifanovsky, et al., Software for the Frontiers of Quantum Chemistry: An Overview of Developments in the Q-Chem 5 Package, J. Chem. Phys., 2021, 155, 084801, DOI:10.1063/5.0055522.
- N. Mardirossian and M. Head-Gordon, ωB97X-V: A 10-Parameter, Range-Separated Hybrid, Generalized Gradient Approximation Density Functional with Nonlocal Correlation, Designed by a Survival-of-the-Fittest Strategy, Phys. Chem. Chem. Phys., 2014, 16, 9904–9924, 10.1039/C3CP54374A.
- T. H. Dunning, Gaussian Basis Sets for Use in Correlated Molecular Calculations. I. The Atoms Boron through Neon and Hydrogen, J. Chem. Phys., 1989, 90, 1007–1023, DOI:10.1063/1.456153.
- T. Scheele and T. Neudecker, Investigating the Accuracy of Density Functional Methods for Molecules in Electric Fields, J. Chem. Phys., 2023, 159, 124111, DOI:10.1063/5.0164372.
- J. Ribas-Arino, M. Shiga and D. Marx, Understanding Covalent Mechanochemistry, Angew. Chem., Int. Ed., 2009, 48, 4190–4193, DOI:10.1002/anie.200900673.
- M. T. Ong, J. Leiding, H. Tao, A. M. Virshup and T. J. Martínez, First Principles Dynamics and Minimum Energy Pathways for Mechanochemical Ring Opening of Cyclobutene, J. Am. Chem. Soc., 2009, 131, 6377–6379, DOI:10.1021/ja8095834.
- K. Wolinski and J. Baker, Theoretical Predictions of Enforced Structural Changes in Molecules, Mol. Phys., 2009, 107, 2403–2417, DOI:10.1080/00268970903321348.
- T. Lu and Q. Chen, Ultrastrong Regulation Effect of the Electric Field on the All-Carboatomic Ring Cyclo[18]Carbon, ChemPhysChem, 2021, 22, 386–395, DOI:10.1002/cphc.202000903.
- E. D. Glendening, J. K. Badenhoop, A. E. Reed, J. E. Carpenter, J. A. Bohmann, C. M. Morales, P. Karafiloglou, C. R. Landis and F. Weinhold, NBO 7.0, University of Wisconsin: Theoretical Chemistry Institute, Madison, WI, 2018 Search PubMed.
- M. K. Beyer, The Mechanical Strength of a Covalent Bond Calculated by Density Functional Theory, J. Chem. Phys., 2000, 112, 7307–7312, DOI:10.1063/1.481330.
| This journal is © the Owner Societies 2023 |