Exploring seebeck-coefficient fluctuations in endohedral-fullerene, single-molecule junctions

Abstract

For the purpose of creating single-molecule junctions, which can convert a temperature difference ΔT into a voltage ΔV via the Seebeck effect, it is of interest to screen molecules for their potential to deliver high values of the Seebeck coefficient S = −ΔV/ΔT. Here we demonstrate that insight into molecular-scale thermoelectricity can be obtained by examining the widths and extreme values of Seebeck histograms. Using a combination of experimental scanning-tunnelling-microscopy-based transport measurements and density-functional-theory-based transport calculations, we study the electrical conductance and Seebeck coefficient of three endohedral metallofullerenes (EMFs) Sc₃N@C₈₀, Sc₃C₂@C₈₀, and Er₃N@C₈₀, which based on their structures, are selected to exhibit different degrees of charge inhomogeneity and geometrical disorder within a junction. We demonstrate that standard deviations in the Seebeck coefficient σ_S of EMF-based junctions are correlated with the geometric standard deviation σ and the charge inhomogeneity σ_q. We benchmark these molecules against C₆₀ and demonstrate that both σ_q, σ_S are the largest for Sc₃C₂@C₈₀, both are the smallest for C₆₀ and for the other EMFs, they follow the order Sc₃C₂@C₈₀ > Sc₃N@C₈₀ > Er₃N@C₈₀ > C₆₀. A large value of σ_S is a sign that a molecule can exhibit a wide range of Seebeck coefficients, which means that if orientations corresponding to high values can be selected and controlled, then the molecule has the potential to exhibit high-performance thermoelectricity. For the EMFs studied here, large values of σ_S are associated with distributions of Seebeck coefficients containing both positive and negative signs, which reveals that all these EMFs are bi-thermoelectric materials.

---

New concepts

If high-thermoelectric-performance molecules could be identified, then they could be used as building blocks for organic thin-film materials able to convert waste heat into electricity. A key parameter governing thermoelectric performance is the Seebeck coefficient S, which determines the voltage generated when a temperature difference is applies to a single-molecule junction. In the literature, ensemble averaged values of S are typically reported. Here we demonstrate that the search for high-performance molecules can be accelerated by focussing attention on fluctuations in S. We study the electrical conductance and Seebeck coefficient of three endohedral metallofullerenes (EMFs) Sc₃N@C₈₀, Sc₃C₂@C₈₀, and Er₃N@C₈₀, which based on their structures, are selected to exhibit different degrees of charge inhomogeneity and geometrical disorder within a junction. These cause the molecules to exhibit a wide range of Seebeck coefficients, which means that if orientations corresponding to high values can be selected and controlled, then the molecules have the potential to exhibit high-performance thermoelectricity. Furthermore, the EMFs studied here exhibit distributions of Seebeck coefficients containing both positive and negative signs, which reveals that all these EMFs are bi-thermoelectric materials. The strategy of exploiting fluctuations is a new concept and will lead to new strategies for designing thermoelectric materials.

Introduction

During recent years, the search for non-toxic and easily processable thermoelectric materials has led several groups to explore the potential of molecular-scale devices for converting waste heat into electricity.^1–41 This is achieved via the Seebeck effect, which converts a temperature difference ΔT into a voltage ΔV = −SΔT, where the constant of proportionality is the Seebeck coefficient S. Measured values of S are currently too low to create an economically viable technology and therefore there is a need to develop strategies for rapidly assessing the ability of a given molecule to deliver high values of S. In the 1980s, studies of sample-to-sample variations in electrical conductance G of mesoscopic, phase-coherent solids led to remarkable discoveries such as universal conductance fluctuations (UCFs), in which the standard deviation σ_G in the conductance is σ_G = aG₀, where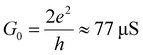 is the quantum of conductance.^42,43 In this expression, a is a number of order unity, which is independent of the average value of G, and depends only on the presence of an applied magnetic field or spin–orbit scattering. Since that time, the field of single-molecule electronics has been established, in which the electrical conductor is a single molecule located between electrodes separated by a few nanometres. However, even though many experiments have confirmed that transport through single molecules is phase coherent,^44–53 even at room temperature, information contained in fluctuations has been largely ignored. Here, our aim is to demonstrate that studies of fluctuations in single-molecule transport properties are of particular interest in the search for molecules with high thermoelectrical performance, because rare examples of junctions exhibiting extreme values of Seebeck coefficients are a proof of principle that such junctions can exhibit high thermopowers.

To demonstrate that fluctuations can be used to search for molecules with potential for high thermoelectric performance, we report a combined experimental and theoretical study of a family of endohedral metallofullerenes (EMFs), specifically chosen to exhibit large fluctuations. EMFs are chosen because they can form single-molecule junctions without the need for anchor groups, which in the literature, are often used to bind molecules to electrodes. Such anchor groups would restrict the number of binding configurations within a junction and reduce fluctuations, whereas in this study, we would like to explore the full phase space of molecular configurations within a junction.

EMFs represent a fascinating class of nanomaterials, whose optical,⁵⁴ electrochemical⁵⁵ or magnetic⁵⁶ properties are controlled by the type of metal atom(s) encapsulated by the fullerene cage. For example, erbium containing EMFs possess a characteristic 1520 nm emission associated with the erbium ion, which is of fundamental importance for telecommunication applications and the fabrication of erbium doped amplifiers.⁵⁷ Moreover, there is a broad spectrum of scandium-containing metallofullerenes, including the paramagnetic Sc@C₈₂ and Sc₃C₂@C₈₀, which can find applications as spin probes and quantum information processing components.⁵⁸ The latter exhibits a unique diamond shaped EPR, with respect to the three equivalent scandium atoms (see Fig. S4, ESI†). For the purpose of probing fluctuations in transport properties, these molecules are attractive, because they not only bind to electrodes with a range of different orientations, but also by making different choices for the encapsulated moiety, they can possess highly inhomogeneous charge distributions (for example as in the case of Sc₃C₂@C₈₀) or possess a relatively homogeneous charge distribution (as for C₆₀). Therefore, a study of their transport properties is expected to reveal how charge distributions and geometry are correlated with fluctuations in their Seebeck coefficients and their ability to exhibit high values of S.

To investigate correlations between Seebeck coefficient, geometry and charge inhomogeneity, our aim is to compare transport properties of Sc₃N@C₈₀ and C₆₀ (ref. 11), with those of two other trimetallic EMFs, namely, the paramagnetic Sc₃C₂@C₈₀ (see Fig. S4, ESI†) and a rare-earth-based EMF, Er₃N@C₈₀. Like Sc₃N@C₈₀, these EMFs are formed with the fullerene cage I_h–C₈₀, composed of 80 C atoms organised in an icosahedral structure (I_h symmetry also shared by C₆₀) (see Fig. 1a)^57–61 and their cages possess sizeable charge inhomogeneity. Our main result is that the standard deviations of Seebeck coefficients of these four molecules are strongly correlated with standard deviations in the charge distributions on their fullerene cages, thereby establishing a structure–function relationship between Seebeck fluctuations and charge inhomogeneity. Furthermore, molecules with high charge inhomogeneity exhibit rare examples of high thermopower, which means that if these rare junction configurations could be isolated and controlled, then such molecules have the potential to deliver high-performance thermoelectricity.

Fig. 1 Molecules studied and their STM characterization. (a) Schematic of the three endohedral metallofullerenes (EMFs) studied, namely, Sc₃N@C₈₀, Sc₃C₂@C₈₀, and Er₃N@C₈₀. (b) STM images of the new molecules investigated (top panel: Sc₃C₂@C₈₀; bottom panel: Er₃N@C₈₀) deposited on gold substrates. Image size: 8.8 × 8.8 nm² (top panel); 8 × 8 nm² (bottom panel). Bias voltage V_bias = 0.8 V and 0.5 V, respectively (tip grounded). (c and d) Two individual examples of simultaneous measurements of conductance G (in red) and Seebeck coefficient S (in blue) as a function of the tip displacement ΔZ for single-molecule Sc₃C₂@C₈₀ (c) and Er₃N@C₈₀ (d) junctions. Each example shows a complete approach-retraction cycle, as indicated by the arrows (approaches plotted in the top panels; retractions, in the bottom panels). Data points highlighted in yellow indicate the contact regime, that is, the tip displacement while the molecule is directly in contact with both electrodes. In both examples, V_bias = 0.01 V. G₀ = (2e²)/h is the quantum of conductance and ΔT is the temperature difference applied.

Results and discussion

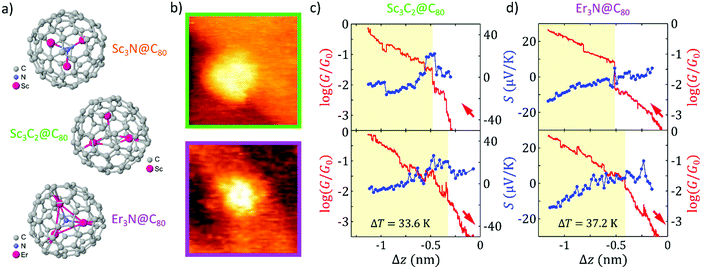
All molecules were deposited on gold (111) substrates by drop-casting from very dilute 1,2,4-trichlorobenzene (TCB) solutions of the corresponding EMF. The Au substrates were previously flame annealed to form atomically flat surfaces (see ESI† for more details on sample preparation). We perform our measurements in ambient conditions and at room temperature using a home-built scanning tunnelling microscope (STM) adapted to measure simultaneously the conductance G and Seebeck coefficient S of single-molecule junctions with our previously reported technique^4,11 (see ESI† for more details).

To localize individual molecules on the Au surface, we proceed by recording STM images of successively smaller areas.^4,11 Two typical STM images of individual scandium carbide and erbium nitride EMFs can be seen in Fig. 1b and additional images can be found in the ESI.† To form the molecular junction, the tip is then placed on top of the fullerene and is approached until a certain conductance threshold is reached. As the tip approaches, its motion is stopped every few picometers and a small voltage ramp (±10 mV) is applied, recording I–V curves (measured current I vs. applied voltage V). When a temperature difference of ΔT = 34–42 K is established between the tip and the substrate, I–V curves show a ΔT-dependent voltage offset at zero current, which is identified with the thermovoltage Vth of the fullerene junction and this one with the Seebeck coefficient S = V_th/ΔT. Furthermore, from the slope of the I–V curves, we obtain simultaneously the electrical conductance, G = I/V (see ESI† for a detailed description of the technique).

Two examples of simultaneous conductance G and Seebeck coefficient S approach-retraction cycles, as a function of the tip displacement ΔZ, are shown in Fig. 1c and d for single-molecule junctions of the new EMFs studied As the tip approaches the molecule (top panels in Fig. 1c and d, ΔZ decreases from zero; G plotted in red; S, in blue), the logarithmic conductance of the junction increases linearly with the distance (in semilogarithmic scale) until a physical contact is made with the corresponding EMF and a sudden jump in the signal is measured. The tip moves towards the fullerene for a further ∼ 0.7 nm, to establish a better tip-molecule contact (the contact regime during the tip approach in Fig. 1c and d has been shaded yellow for clarity). Simultaneous thermovoltage measurements allow us to obtain the thermopower of each single-molecule junction as it is formed. Fig. 1c shows an example of a junction with an initially positive Seebeck coefficient, while the junction in Fig. 1d has an initially negative Seebeck coefficient. A jump in Seebeck coefficient is also typically observed when physical contact is established (see Fig. 1c). Additionally, in the curves shown in Fig. 1c and d, we observe a clear correlation between small jumps observed in the conductance and the simultaneous thermopower signals once the contact is formed, showing that both magnitudes are sensitive to small changes in the junction geometry, such as atomic rearrangements in the electrodes.^62–64 During retraction, the curves remain almost the same, indicating that the junctions were unaltered (bottom panels in Fig. 1c and d). In particular, their conductance shows generally a change of the slope or a jump down, although some hysteresis is observed and the features of both G and S retraction traces are usually slightly shifted in ΔZ with respect to the approach curves, possibly due to elastic deformations of the Au atoms in the electrodes.^62–64 Further examples of individual junctions (see the ESI†) show both signs of the Seebeck coefficient in the case of the two EMFs analysed, demonstrating their bi-thermoelectric nature, with either positive or negative values of S depending on the single molecule studied. This behaviour is similar to the reported bi-thermoelectricity of Sc₃N@C₈₀ junctions and is in clear contrast to the consistently negative Seebeck coefficient values obtained for the C₆₀.¹¹

The bi-thermoelectric response of the scandium nitride, scandium carbide and erbium nitride are compared with the more conventional C₆₀ behaviour in Fig. 2a and b, which shows 2D histograms of the Seebeck coefficient S as a function of the conductance G (the data of C₆₀ and Sc₃N@C₈₀ junctions are those previously reported in ref. 11). While the histograms in Fig. 2a are formed with all the experimental data obtained from the complete approach traces (i.e. the whole tip movement from tunnelling until the selected conductance threshold), for the histograms in Fig. 2b, only G and S values at first-contact between the tip and molecule are collected, i.e. values measured within 0.1 nm after the contact in the G(ΔZ) curve, where pressure from the tip does not appreciably deform the fullerene-electrodes junction. These histograms, and especially those of first-contact values, show that Sc₃N@C₈₀ and Er₃N@C₈₀ present smaller G values than Sc₃C₂@C₈₀ and C₆₀ systems. Furthermore, these two trinitrate molecules present both positive and negative Seebeck coefficients mostly centred at zero. In contrast, the Seebeck coefficient of Sc₃C₂@C₈₀ junctions seems to be preferentially displaced towards negative values, despite also showing both signs and a considerable dispersion. C₆₀ junctions, as previously reported,^4,11 present only negative values of S.

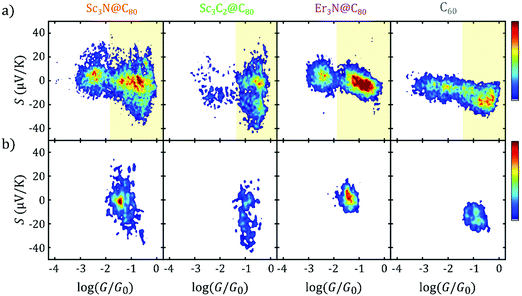Fig. 2 Conductance G and Seebeck coefficient S histograms of the monomers of EMFs and C₆₀. (a) S vs. G 2D histograms built with all the data from the I–V curves measured during the complete approach of the tip, from the noise level until close to the metallic contact. The area shadowed in yellow corresponds approximately to the contact regime (highlighted also in yellow in Fig. 1c and d). (b) S vs. G 2D histograms built with first-contact values, i.e., within 0.1 nm right after junction formation. In a and b, each column corresponds to one molecule, as indicated on top; from left to right: Sc₃N@C₈₀, Sc₃C₂@C₈₀, Er₃N@C₈₀ and the fullerene C₆₀. The colour scale accounts for the number of points in each histogram.

An additional striking feature of the histograms in Fig. 2b is the broad distribution of Seebeck coefficients obtained for Sc₃C₂@C₈₀ and Sc₃N@C₈₀, compared with the narrower distributions obtained for Er₃N@C₈₀ and C₆₀. This can be more easily observed in the 1D histograms of G and S shown in Fig. 3a and b for all four molecules. Fig. 3b and 2b show that all the EMFs present a bi-thermoelectric behaviour, signalled by the presence of both positive and negative values of S, in clear contrast with the empty fullerene C₆₀ that exhibits only negative Seebeck coefficients. The mean Seebeck coefficients S̄ of Sc₃N@C₈₀ and Er₃N@C₈₀ junctions are very small, while in the case of Sc₃C₂@C₈₀ (in green in Fig. 3b), two peaks appear in the 1D histogram, centred at 0 μV K⁻¹ and −20 μV K⁻¹, which means that it is equally likely to connect a molecule with a small value of S close to zero or with a negative value similar to that of C₆₀. Finally, Sc₃N@C₈₀ and Sc₃C₂@C₈₀ have a larger dispersion of S values than Er₃N@C₈₀. The Seebeck coefficient measurements of the latter are spread only over a range of approximately −20 μV K⁻¹ to +20 μV K⁻¹, whereas the range of values of the EMFs with three scandium atoms is twice as wide. The standard deviation σ_S in the Seebeck coefficients obtained from Fig. 3b for all the compounds are shown in column 6 of Table 1, (Note that the error in the determination of the thermopower is less than 0.9 μV K⁻¹).

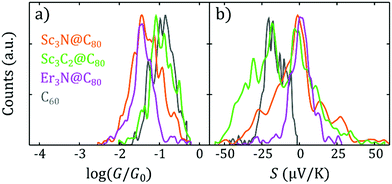Fig. 3 Experimental first-contact histograms of log (G/G₀) and S. G (a) and S (b) 1D histograms for all the molecules, showing only the values right after junction formation (at first contact). The data shown in these 1D histograms is the same as in Fig. 2b.

Table 1 Columns 2 and 3 show standard deviations σ of the distance d, associated with rotations about axes θ, Φ. Standard deviations of charge (columns 4 and 5) and Seebeck coefficients (columns 6 and 7) of Sc₃C₂@C₈₀, Sc₃N@C₈₀, Er₃N@C₈₀ and C₆₀. The sixth column shows experimental values for σ_S from the Seebeck distributions in Fig. 3b. The right-most column shows theoretical values for σ_S from Table S6 of the ESI. Computation of a theoretical value for σ_S of Er₃N@C₈₀ was not possible, due to the presence of f-electrons

Molecule	σ θ	σ Φ	σ q Hirshfeld	σ q Voronoi	σ S Exp. (μV K^−1)	σ S Theor. (μV K^−1)
Sc3C2@C80	1.47	1.09	113 × 10^−4	133 × 10^−4	19.2	36.0
Sc3N@C80	1.43	0.95	109 × 10^−4	119 × 10^−4	17.6	29.4
Er3N@C80	1.43	0.95	26 × 10^−4	27 × 10^−4	7.7	==
C60	==	==	5.7 × 10^−4	8.5 × 10^−4	6.8	2.44

---

To understand the origin of these differences in Seebeck fluctuations, we used density functional theory (DFT) to examine the binding energies of these junctions under various rotations. The basic theoretical principles of the method can be found in ref. 65 and 66. There are an infinite number of inequivalent orientations of the metallic moieties relative to their fullerene cage. Here we consider a selection of rotations about high-symmetry axes. Fig. 4 shows four axes of rotation θ, Φ, α and β considered below, while Fig. 5 shows how these axes pass through the metallic moieties. For each of the four axes of rotation, we investigate how the total energy varies with angle of rotation, both in presence and absence of the gold substrate. For each of these four axes, we consider one mode of rotation in the gas phase and three modes of rotation on a substrate.

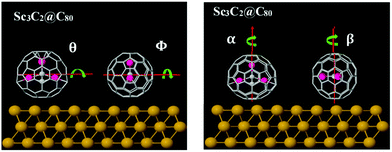Fig. 4 Illustration of the four rotation axes: θ and Φ are horizontal axes, α and β are vertical axes. This Figure shows how the axes pass through the I_h–C₈₀ cage + metallic moiety.

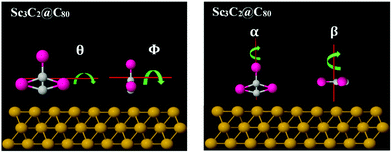Fig. 5 Illustration of how the four rotation axes θ, Φ, α and β, pass through the metallic moiety (in the absence of the cage).

In the gas phase, we consider rotation of the metallic moiety relative to a fixed fullerene cage. For this rotational mode, rotations about the β and Φ axes are equivalent, so in the gas phase, rotations about 3 distinct axes are investigated. In the presence of the gold substrate, we consider three modes of rotation about each of the four axes: rotation of the bare metallic moiety (in the absence of the cage), rotation of the metallic moiety in the presence of a fixed cage, and rotation of both the metallic moiety and cage, such that their relative orientation is fixed. This means that in total, on a substrate, 12 distinct cases are considered (4 axes x 3 modes of rotation). For simplicity of notation, in what follows, the same symbol (e.g. θ) is used to label both the rotation axis and the angle of rotation about the axis.

To quantify geometrical variations under rotation, it is convenient to define the distance d to be the smallest vertical distance between the top-most plane of the Au-substrate and the closest metal atom of the encapsulated moiety. Fig. S12 (ESI†) shows the variation of d with rotations about the above axes, while Table 1 (colums 2 and 3) shows the standard deviations σ_θ, σ_Φ in d under rotations about the axes θ, Φ. By symmetry σ_α = σ_β = 0 and therefore these follow the order σ_θ > σ_Φ > σ_α, σ_β. Furthermore, the values of both σ_θ and σ_Φ associated with Sc₃C₂@C₈₀ are higher than those associated with Sc₃N@C₈₀ and Er₃N@C₈₀ (for more detail see Table S2 in the ESI†).

To quantify the charge inhomogeneities associated with these molecules, we also computed the standard deviations σ_q of the charge distributions on their cages, using two different definitions of charge (Hirshfeld and Voronoi).^67,68 If the charge on atom i of the cage is |e|n_i|, then the standard deviation σ_q in the charge is defined by:

σ²_q = 〈< (n_i − 〈n_i〉)²〉

where angular brackets denote an average over all atoms on the cage. These are presented in Table 1 (columns 4 and 5) and reveal that Sc₃C₂@C₈₀ and Sc₃N@C₈₀ possess relatively high values of σ_q, followed by Er₃N@C₈₀. In contrast the charge distribution of C₆₀ is relatively uniform. Comparison between the experimental values for σ_S in the sixth column and the theoretical values for σ_S in the right-most column (obtained as described below and copied from Table S6 of the ESI†) shows that standard deviations in the Seebeck coefficients are strongly correlated with the structural and charge standard deviations σ_θ, σ_Φ and σ_q. Table 1 is a key result of our study and reveals the origin of the differences in Seebeck fluctuations between the four studied molecules. Interestingly, the experimental and theoretical values of σ_S for C₆₀ shown in Table 1 are comparable with those found for thiol-terminated oligophenylenes reported in ref. 69, which varied from 2.1 to 3.2 as the number of phenyl rings was increased from 1 to 3. They are higher than those found for thiol-terminated alkyl chains, which were found to be 0.3 ± 1 and almost independent of length.⁷⁰ Studies^71–74 have also shown that increasing the applied temperature difference can lead to additional fluctuations in the thermovoltage.

As a first step in the calculations leading to Table 1, energy barriers to rotation about the above axes were computed, to obtain the preferred angles of rotation, which minimise the total energy. σ_S was then obtained by computing Seebeck coefficients using an ensemble of angles and a distribution of Fermi energies E_F, as described in sections 5.7 to 5.15 of the ESI.†Table 2 shows the computed gas-phase energy barriers ΔE(θ), ΔE(Φ), ΔE(α) associated with rotations about θ, Φ, α of Sc₃C₂, Sc₃N and Sc₃N within the fixed I_h–C₈₀ cage, along with the preferred orientation angles for the three rotation axes (see Section 5.5 in the ESI†). This reveals that for all three axes, Sc₃C₂@C₈₀ possesses the highest energy barriers to rotation, followed by Sc₃N@C₈₀, with Er₃N@C₈₀ possessing the lowest barriers. These correlate closely with their values of σ²_q and furthermore, the highest energy barrier associated with Sc₃C₂@C₈₀ correlates with the high value of the standard deviation in d.

Table 2 Gas phase energy barriers ΔE(θ) > ΔE(Φ) > ΔE(α) associated with rotations about θ, Φ, α of Sc₃C₂, Sc₃N and Er₃N within the fixed I_h–C₈₀ cage, along with the preferred angles of rotation for the three rotation axes (according to Fig. S15, ESI)

EMF	ΔE(θ) (meV)	Preferred orientations (θ)	ΔE(Φ) (meV)	Preferred orientations (Φ)	ΔE(α) (meV)	Preferred orientations (α)
Sc3C2@C80	400	0°, 190° and 360°	350	0°, 110°, 180°, 210°, 270° and 360°	300	0°, 75°, 160°, 240° and 320°
Sc3N@C80	300	0°, 190° and 360°	250	10°, 95°, 200°, 280° and 340°	150	0°, 75°, 100°, 150°, 200° 250°, 300° and 350°
Er3N@C80	130	0°, 190° and 360°	100	0°, 120°, 250° and 350°	60	0°, 80°, 150°, 225°, 320°and 360°

---

Table 2 shows that for all EMFs, in the gas phase, the energy barriers to rotation follow the order ΔE(θ) > ΔE(Φ) > ΔE(α). Fig. S21 (ESI†) shows that on a gold surface, the binding energies are also higher for the θ and Φ axes and follow the order ΔE(θ)> ΔE(Φ)> ΔE(α) > ΔE(β). Furthermore the barriers are higher for Sc₃C₂@C₈₀ and lower for Er₃N@C₈₀. On a gold substrate, the energy barriers significantly increase to approximately 0.6 eV for Sc₃C₂@C₈₀, which means that the configurational degrees of freedom of the endofullerene relative to the electrode exhibit a small number of preferred orientations corresponding to minima in the total energy of the endofullerene/electrode complex as shown in Fig. S21 (ESI†) (for more detail see section 5.6 of the ESI†). The energy barrier for Sc₃N@C₈₀ is 0.3 eV and the lowest barrier of 0.1 eV is obtained for Er₃N@C₈₀ (see Fig. S18, ESI†). (Note: Fig. S21, ESI† shows the four rotation axes, while Fig. S18, ESI† shows only θ).

To obtain the theoretical values of σ_S in Table 1 from the above distribution of orientations, we used a combination of the quantum transport code Gollum⁷⁵ and the density functional theory (DFT) code SIESTA,⁷⁶ to calculate the transmission coefficient T(E) for electrons of energy E passing through the EMFs, when contacted to gold electrodes (a detailed description can be found in the ESI†). The energy dependence of transmissions curves for Sc₃C₂@C₈₀, Sc₃N@C₈₀ and C₆₀, and their Seebeck coefficients for all minimum-energy orientations, are shown in Fig. S23 to S44 (ESI†). Since the curves are rather smooth on the scale of k_BT at room temperature, their electrical conductance G is approximated by G ≈ T (E_F)G₀, where G₀ is the quantum of conductance, and 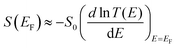⁶⁵ In the latter equation, if E is measured in units of electron volts, then S₀ = αT, which at T = 300 K, takes the value S₀ = 7.3 μV K⁻¹. Fig. S23 to S44 (ESI†) clearly show that rotations about the θ axis cause much more severe fluctuations in the transmission functions than rotations about the other axes. By sampling the transmission curves over a range of Fermi energies and preferred orientations (as described in the ESI†), we obtain the theoretical 2D histograms shown in Fig. S45, (ESI†) from which the theoretical values of σ_S in Table 1 were obtained. In general, depending on the value of E_F, the Seebeck coefficient can achieve high values when the distance d between the metallic moiety and the Au substrate is large (e.g., for θ = 90°, in Fig. S22, ESI†), whereas S tends to be lower when d is small (e.g., for θ = 0°, in Fig. S22, ESI†).

The high values of σ_S and the bi-thermoelectric response of these EMF junctions confirm our initial intuition that charge inhomogeneity leads to larger variability in the transport properties, compared with pristine C₆₀. This interesting behaviour is also observed in ref. 77, where Gd@C₈₂ and Ce@C₈₂ and the empty C₈₂ were reported to present mainly negative Seebeck coefficients, with occasional positive values that were attributed possibly to meta-stable configurations of the junctions. The values reported for the Seebeck coefficient show an enhancement in the endohedral fullerenes with respect to the C₈₂. Compared to our investigated EMFs, the main difference with the systems studied in ref. 77 is the total number of metal atoms inside the fullerene cage, which in the case of ref. 77 is just one atom placed out of centre.

Of particular interest for quantifying the thermoelectric performance of molecular junctions is the power factor GS². Fig. 6 shows a comparison between the experimental and theoretical power factor distributions. These possess comparable shapes and, in both cases, reveal that rare values corresponding to particular configurations of the junctions can lead to very high-power factors.

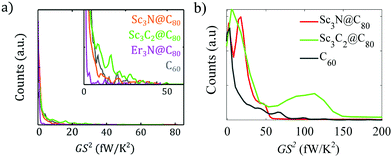Fig. 6 Power factor GS² analysis. a) Experimental 1D histograms of power factor at first contact, built with the data in Fig. 3. The inset zooms into the details of the main panel. b). Theoretical 1D histograms of power factor obtained from Fig. S46 of the ESI.†

Fig. 6 also shows that the high conductance and Seebeck coefficient values measured for the carbide EMF translate into quite high values of power factor GS², with the highest power factor values of Sc₃C₂@C₈₀ significantly exceeding those of C₆₀, both in value and probability.

Lee et al⁷⁷ noted that their EMF-based junctions possessed a high single molecule power factor of 16.2 fW K⁻² for Gd@C₈₂, which corresponds to around 4 × 10 μW K⁻² m⁻¹ for a thin-film device consisting of a monolayer of Gd@C₈₂, which at the time of publication was the largest power factor obtained for a single molecule device. From the first-contact data in Fig. 3, we find even higher values up to 50 fW K⁻² for Sc₃N@C₈₀ and Sc₃C₂@C₈₀ junctions, and even two examples of values up to 70–80 fW K⁻² (for these two EMFs). Statistically, we find larger values for the carbide compound (Sc₃C₂@C₈₀ junctions). Furthermore, considering all the measured conductance and Seebeck coefficient values (Fig. S9, ESI†), the power factor can be statistically increased when the junction becomes slightly compressed, because under compression, G increases and S becomes more negative.

Conclusions

Through a combination of experimental STM-based transport measurements and DFT-based transport calculations, we have studied the electrical conductance and Seebeck coefficient of three endohedral metallofullerenes (EMFs) Sc₃N@C₈₀, Sc₃C₂@C₈₀, and Er₃N@C₈₀, and found that all EMFs studied are bi-thermoelectric systems, exhibiting both positive and negative Seebeck coefficients, in contrast to the empty C₆₀. To understand the origin of these fluctuations in thermoelectric properties, DFT simulations of a selection of orientations were carried out, that allowed us to answer the following questions:

1) Can variations in the orientations of the fullerenes and their encapsulated moieties lead to fluctuations in Seebeck coefficients on the scale of those measured experimentally? DFT modelling shows that fluctuations on the scale of the measured values can indeed arise from variations in the orientations of the fullerenes and their encapsulated moieties and the degree of variation is characterised by the associated standard deviation σ, which is a purely geometric quantity. This is an important result, because it shows that such fluctuations are an intrinsic property of the junctions and not due to some unknown extrinsic effect.

2) Are there correlations between Seebeck fluctuations and the degree of charge inhomogeneity? To establish these correlations, in Fig. 4, 5 and Fig. S15, S21, Table S3, (ESI†) we explored a large number (360 × 3 axes in gas phase and 360 × 4 axes onto a gold surface) of different geometries and identified the most energetically favourable configurations, which are relevant experimentally. These calculations demonstrate a clear correlation between Seebeck fluctuations and the degree of charge inhomogeneity, which can be characterised by a standard deviation σ_q.

We found that standard deviations in the Seebeck coefficients σ_S of EMF-based junctions are correlated with the geometric standard deviation σ and the charge inhomogeneity σ_q. We benchmarked these molecules against C₆₀ and found that all of σ_q,σ_S are the largest for Sc₃C₂@C₈₀, all are the smallest for C₆₀ and for the other EMFs, they follow the order Sc₃C₂@C₈₀ >Sc₃N@C₈₀ > Er₃N@C₈₀ > C₆₀. This means that external measurements of fluctuations in the Seebeck coefficient provide insight into the internal structure and charge distribution of endohedral metallofullerenes.

This points the way to designs of molecular switches and bi-thermoelectric materials, because molecules with large values of σ_q possess large values of σ_S; the former is a sign that a molecule can switch between orientation-dependent electrical conductances, whereas the latter indicates that a molecule can exhibit a wide range of Seebeck coefficients with both positive and negative signs. If the orientation and Fermi energy of such molecules can be controlled, then high thermoelectric performance is possible. On the other hand, if the aim is to minimise fluctuations, then our study suggests that molecules with low values of σ and σ_q should be selected.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

P. D. acknowledges support from the Hellenic Foundation for Research and Innovation (Grant number: 1468). A. K. I. acknowledges the Leverhulme Trust for Early Career Fellowship ECF-2020-638. A. K. I and A. A are also grateful for financial assistance from Tikrit and Anbar Universities (Iraq), and the Iraqi Ministry of Higher Education (SL-20). T. A. is grateful for financial assistance from Al-Jouf University (Saudi Arabia), and the Saudi Ministry of Education. A. K. I and C. J. L. acknowledge financial support from the UK EPSRC, through Grant no. EP/M014452/1, EP/P027156/1 and EP/N03337X/1. This work was additionally supported by the European Commission is provided by the FET Open project 767187–QuIET. N. A. and G. R.-B. acknowledge the Spanish MINECO (grants MAT2014-57915-R, MAT2017-88693-R, and MDM-2014-0377, and the María de Maeztu Programme for Units of Excellence in R&D MDM-2014-0377 and CEX2018-000805-M) and Comunidad de Madrid (grants NANOFRONTMAG-CM, S2013/MIT-2850, and NANOMAGCOST-CM, P2018/NMT-4321). L. R.-G. acknowledges financial support from the Spanish MECD (Grant no. FPU14/03368). N. A. and L. R.-G. are also grateful for financial support from the Education and Research Council of the Comunidad de Madrid and the European Social Fund (Ref. PEJD-2019-POST/IND-16353).

References

1. F. Pauly, J. K. Viljas and J. C. Cuevas, Length-dependent conductance and thermopower in single-molecule junctions of dithiolated oligophenylene derivatives: A density functional study, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78(3), 035315.
2. D. Nozaki, H. Sevinçli, W. Li, R. Gutiérrez and G. Cuniberti, Engineering the figure of merit and thermopower in single-molecule devices connected to semiconducting electrodes, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81(23), 235406.
3. M. Bürkle, L. A. Zotti, J. K. Viljas, D. Vonlanthen, A. Mishchenko, T. Wandlowski, M. Mayor, G. Schön and F. Pauly, Ab initio study of the thermopower of biphenyl-based single-molecule junctions, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86(11), 115304.
4. C. Evangeli, K. Gillemot, E. Leary, M. T. Gonzalez, G. Rubio-Bollinger, C. J. Lambert and N. Agrait, Engineering the thermopower of C₆₀ molecular junctions, Nano Lett., 2013, 13(5), 2141–2145.
5. O. Karlström, M. Strange and G. C. Solomon, Understanding the length dependence of molecular junction thermopower, J. Chem. Phys., 2014, 140(4), 044315.
6. C. G. Péterfalvi, I. Grace, D. Z. Manrique and C. J. Lambert, Thermoelectric performance of various benzo-difuran wires, J. Chem. Phys., 2014, 140(17), 174711.
7. V. M. García-Suárez, C. J. Lambert, D. Z. Manrique and T. Wandlowski, Redox control of thermopower and figure of merit in phase-coherent molecular wires, Nanotechnology, 2014, 25(20), 205402.
8. A. K. Ismael, I. Grace and C. J. Lambert, Increasing the thermopower of crown-ether-bridged anthraquinones, Nanoscale, 2015, 7(41), 17338–17342.
9. H. Sadeghi, S. Sangtarash and C. J. Lambert, Oligoyne molecular junctions for efficient room temperature thermoelectric power generation, Nano Lett., 2015, 15(11), 7467–7472.
10. M. Bürkle, T. J. Hellmuth, F. Pauly and Y. Asai, First-principles calculation of the thermoelectric figure of merit for [2, 2] paracyclophane-based single-molecule junctions, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91(16), 165419.
11. L. Rincón-García, A. K. Ismael, C. Evangeli, I. Grace, G. Rubio-Bollinger, K. Porfyrakis, N. Agraït and C. J. Lambert, Molecular design and control of fullerene-based bi-thermoelectric materials, Nat. Mater., 2016, 15(3), 289–293.
12. C. Perroni, D. Ninno and V. Cataudella, Thermoelectric efficiency of molecular junctions, J. Phys.: Condens. Matter, 2016, 28(37), 373001.
13. D. Z. Manrique, Q. Al-Galiby, W. Hong and C. J. Lambert, A new approach to materials discovery for electronic and thermoelectric properties of single-molecule junctions, Nano Lett., 2016, 16(2), 1308–1316.
14. L. Rincón-García, C. Evangeli, G. Rubio-Bollinger and N. Agraït, Thermopower measurements in molecular junctions, Chem. Soc. Rev., 2016, 45(15), 4285–4306.
15. C. J. Lambert, H. Sadeghi and Q. H. Al-Galiby, Quantum-interference-enhanced thermoelectricity in single molecules and molecular films, C. R. Phys., 2016, 17(10), 1084–1095.
16. Y. Li, L. Xiang, J. L. Palma, Y. Asai and N. Tao, Thermoelectric effect and its dependence on molecular length and sequence in single DNA molecules, Nat. Commun., 2016, 7(1), 1–8.
17. L. Cui, R. Miao, C. Jiang, E. Meyhofer and P. Reddy, Perspective: Thermal and thermoelectric transport in molecular junctions. The, J. Chem. Phys., 2017, 146(9), 092201.
18. P. Gehring, A. Harzheim, J. Spiece, Y. Sheng, G. Rogers, C. Evangeli, A. Mishra, B. J. Robinson, K. Porfyrakis and J. H. Warner, Field-effect control of graphene–fullerene thermoelectric nanodevices, Nano Lett., 2017, 17(11), 7055–7061.
19. J.-C. Klöckner, R. Siebler, J. C. Cuevas and F. Pauly, Thermal conductance and thermoelectric figure of merit of C 60-based single-molecule junctions: electrons, phonons, and photons, Phys. Rev. B, 2017, 95(24), 245404.
20. Q. H. Al-Galiby, H. Sadeghi, D. Z. Manrique and C. J. Lambert, Tuning the Seebeck coefficient of naphthalenediimide by electrochemical gating and doping, Nanoscale, 2017, 9(14), 4819–4825.
21. X. Wang, T. L. Bennett, A. Ismael, L. A. Wilkinson, J. Hamill, A. J. White, I. M. Grace, O. V. Kolosov, T. Albrecht and B. J. Robinson, Scale-up of room-temperature constructive quantum interference from single molecules to self-assembled molecular-electronic films, J. Am. Chem. Soc., 2020, 142(19), 8555–8560.
22. A. Ismael, A. Al-Jobory, X. Wang, A. Alshehab, A. Almutlg, M. Alshammari, I. Grace, T. L. Benett, L. A. Wilkinson and B. J. Robinson, Molecular-scale thermoelectricity: as simple as ‘ABC’, Nanoscale Adv., 2020, 2(11), 5329–5334.
23. A. Ismael, X. Wang, T. L. Bennett, L. A. Wilkinson, B. J. Robinson, N. J. Long, L. F. Cohen and C. J. Lambert, Tuning the thermoelectrical properties of anthracene-based self-assembled monolayers, Chem. Sci., 2020, 11(26), 6836–6841.
24. X. Wang, A. Ismael, A. Almutlg, M. Alshammari, A. Al-Jobory, A. Alshehab, T. L. Bennett, L. A. Wilkinson, L. F. Cohen and N. J. Long, Optimised power harvesting by controlling the pressure applied to molecular junctions, Chem. Sci., 2021, 12(14), 5230–5235.
25. A. Harzheim, Thermoelectricity in single-molecule devices, Mater. Sci. Technol., 2018, 34(11), 1275–1286.
26. L. Algharagholy, T. Pope and C. Lambert, Strain-induced bi-thermoelectricity in tapered carbon nanotubes, J. Phys.: Condens. Matter, 2018, 30(10), 105304.
27. G. Yzambart, L. Rincón-García, A. A. Al-Jobory, A. K. Ismael, G. Rubio-Bollinger, C. J. Lambert, N. Agraït and M. R. Bryce, Thermoelectric Properties of 2, 7-Dipyridylfluorene Derivatives in Single-Molecule Junctions. The, J. Phys. Chem. C, 2018, 122(48), 27198–27204.
28. R. Miao, H. Xu, M. Skripnik, L. Cui, K. Wang, K. G. Pedersen, M. Leijnse, F. Pauly, K. Wärnmark and E. Meyhofer, Influence of quantum interference on the thermoelectric properties of molecular junctions, Nano Lett., 2018, 18(9), 5666–5672.
29. M. K. Al-Khaykanee, A. K. Ismael, I. Grace and C. J. Lambert, Oscillating Seebeck coefficients in π-stacked molecular junctions, RSC Adv., 2018, 8(44), 24711–24715.
30. L. Cui, R. Miao, K. Wang, D. Thompson, L. A. Zotti, J. C. Cuevas, E. Meyhofer and P. Reddy, Peltier cooling in molecular junctions, Nat. Nanotechnol., 2018, 13(2), 122–127.
31. M. Famili, I. M. Grace, Q. Al-Galiby, H. Sadeghi and C. J. Lambert, Toward high thermoelectric performance of thiophene and ethylenedioxythiophene (EDOT) molecular wires, Adv. Funct. Mater., 2018, 28(15), 1703135.
32. H. Khalatbari, S. I. Vishkayi and H. R. Soleimani, Effect of dopant nitrogen on the thermoelectric properties of C20 and C60 fullerene in graphene nanoribbon junction, Phys. E, 2019, 108, 372–381.
33. H. Chen, S. Sangtarash, G. Li, M. Gantenbein, W. Cao, A. Alqorashi, J. Liu, C. Zhang, Y. Zhang and L. Chen, Exploring the thermoelectric properties of oligo (phenylene-ethynylene) derivatives, Nanoscale, 2020, 12(28), 15150–15156.
34. A. K. Ismael and C. J. Lambert, Molecular-scale thermoelectricity: a worst-case scenario, Nanoscale Horiz., 2020, 5(7), 1073–1080.
35. M. Noori, H. Sadeghi, Q. Al-Galiby, S. W. Bailey and C. J. Lambert, High cross-plane thermoelectric performance of metallo-porphyrin molecular junctions, Phys. Chem. Chem. Phys., 2017, 19(26), 17356–17359.
36. S. Sangtarash, H. Sadeghi and C. J. Lambert, Connectivity-driven bi-thermoelectricity in heteroatom-substituted molecular junctions, Phys. Chem. Chem. Phys., 2018, 20(14), 9630–9637.
37. S. Naghibi, A. K. Ismael, A. Vezzoli, M. K. Al-Khaykanee, X. Zheng, I. M. Grace, D. Bethell, S. J. Higgins, C. J. Lambert and R. J. Nichols, Synthetic Control of Quantum Interference by Regulating Charge on a Single Atom in Heteroaromatic Molecular Junctions, J. Phys. Chem. Lett., 2019, 10(20), 6419–6424.
38. H. Dekkiche, A. Gemma, F. Tabatabaei, A. S. Batsanov, T. Niehaus, B. Gotsmann and M. R. Bryce, Electronic conductance and thermopower of single-molecule junctions of oligo (phenyleneethynylene) derivatives, Nanoscale, 2020, 12(36), 18908–18917.
39. P. Gehring, J. K. Sowa, C. Hsu, J. de Bruijckere, M. van der Star, J. J. Le Roy, L. Bogani, E. M. Gauger and H. S. van der Zant, Complete mapping of the thermoelectric properties of a single molecule, Nat. Nanotechnol., 2021, 16(4), 426–430.
40. K. Wang, E. Meyhofer and P. Reddy, Thermal and thermoelectric properties of molecular junctions, Adv. Funct. Mater., 2020, 30(8), 1904534.
41. S. Park, H. Kang and H. J. Yoon, Structure–thermopower relationships in molecular thermoelectrics, J. Mater. Chem. A, 2019, 7(24), 14419–14446.
42. E. Akkermans and G. Montambaux, Mesoscopic physics of electrons and photons. Cambridge university press, 2007.
43. S. Datta, Electronic transport in mesoscopic systems. Cambridge university press, 1997.
44. W. Hong, H. Valkenier, G. Mészáros, D. Z. Manrique, A. Mishchenko, A. Putz, P. M. García, C. J. Lambert, J. C. Hummelen and T. Wandlowski, An MCBJ case study: The influence of π-conjugation on the single-molecule conductance at a solid/liquid interface, Beilstein J. Nanotechnol., 2011, 2(1), 699–713.
45. G. Sedghi, V. M. García-Suárez, L. J. Esdaile, H. L. Anderson, C. J. Lambert, S. Martín, D. Bethell, S. J. Higgins, M. Elliott and N. Bennett, Long-range electron tunnelling in oligo-porphyrin molecular wires, Nat. Nanotechnol., 2011, 6(8), 517–523.
46. S. Ballmann, R. Härtle, P. B. Coto, M. Elbing, M. Mayor, M. R. Bryce, M. Thoss and H. B. Weber, Experimental evidence for quantum interference and vibrationally induced decoherence in single-molecule junctions, Phys. Rev. Lett., 2012, 109(5), 056801.
47. V. Kaliginedi, P. Moreno-García, H. Valkenier, W. Hong, V. M. García-Suárez, P. Buiter, J. L. Otten, J. C. Hummelen, C. J. Lambert and T. Wandlowski, Correlations between molecular structure and single-junction conductance: a case study with oligo (phenylene-ethynylene)-type wires, J. Am. Chem. Soc., 2012, 134(11), 5262–5275.
48. J. Chaste, A. Eichler, J. Moser, G. Ceballos, R. Rurali and A. Bachtold, A nanomechanical mass sensor with yoctogram resolution, Nat. Nanotechnol., 2012, 7(5), 301–304.
49. H. Vazquez, R. Skouta, S. Schneebeli, M. Kamenetska, R. Breslow, L. Venkataraman and M. Hybertsen, Probing the conductance superposition law in single-molecule circuits with parallel paths, Nat. Nanotechnol., 2012, 7(10), 663–667.
50. W. Hong, D. Z. Manrique, P. Moreno-Garcia, M. Gulcur, A. Mishchenko, C. J. Lambert, M. R. Bryce and T. Wandlowski, Single molecular conductance of tolanes: experimental and theoretical study on the junction evolution dependent on the anchoring group, J. Am. Chem. Soc., 2012, 134(4), 2292–2304.
51. C. R. Arroyo, S. Tarkuc, R. Frisenda, J. S. Seldenthuis, C. H. Woerde, R. Eelkema, F. C. Grozema and H. S. Van Der Zant, Signatures of quantum interference effects on charge transport through a single benzene ring, Angew. Chem., Int. Ed., 2013, 52(11), 3152–3155.
52. Y. Geng, S. Sangtarash, C. Huang, H. Sadeghi, Y. Fu, W. Hong, T. Wandlowski, S. Decurtins, C. J. Lambert and S.-X. Liu, Magic ratios for connectivity-driven electrical conductance of graphene-like molecules, J. Am. Chem. Soc., 2015, 137(13), 4469–4476.
53. M. H. Garner, H. Li, Y. Chen, T. A. Su, Z. Shangguan, D. W. Paley, T. Liu, F. Ng, H. Li and S. Xiao, Comprehensive suppression of single-molecule conductance using destructive σ-interference, Nature, 2018, 558(7710), 415–419.
54. Y. Ito, T. Okazaki, S. Okubo, M. Akachi, Y. Ohno, T. Mizutani, T. Nakamura, R. Kitaura, T. Sugai and H. Shinohara, Enhanced 1520 nm photoluminescence from Er³⁺ ions in di-erbium-carbide metallofullerenes (Er2C2)@ C82 (isomers I, II, and III), ACS Nano, 2007, 1(5), 456–462.
55. L. Dunsch and S. Yang, Metal nitride cluster fullerenes: their current state and future prospects, Small, 2007, 3(8), 1298–1320.
56. C.-H. Chen, D. S. Krylov, S. M. Avdoshenko, F. Liu, L. Spree, R. Yadav, A. Alvertis, L. Hozoi, K. Nenkov and A. Kostanyan, Selective arc-discharge synthesis of Dy 2 S-clusterfullerenes and their isomer-dependent single molecule magnetism, Chem. Sci., 2017, 8(9), 6451–6465.
57. C. D. Tran and G.-H. Gao, Characterization of an erbium-doped fiber amplifier as a light source and development of a near-infrared spectrophotometer based on the EDFA and an acoustooptic tunable filter, Anal. Chem., 1996, 68(13), 2264–2269.
58. M. Krause, M. Hulman, H. Kuzmany, O. Dubay, G. Kresse, K. Vietze, G. Seifert, C. Wang and H. Shinohara, Fullerene quantum gyroscope, Phys. Rev. Lett., 2004, 93(13), 137403.
59. A. Rodríguez-Fortea, A. L. Balch and J. M. Poblet, Endohedral metallofullerenes: a unique host–guest association, Chem. Soc. Rev., 2011, 40(7), 3551–3563.
60. A. Rodríguez-Fortea, S. Irle and J. M. Poblet, Fullerenes: formation, stability, and reactivity, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2011, 1(3), 350–367.
61. X. Aparicio-Anglès, N. R. Alegret, A. Clotet, A. Rodríguez-Fortea and J. M. Poblet, Endohedral metallofullerenes containing lanthanides: a robust yet simple computational approach, J. Phys. Chem. C, 2013, 117(24), 12916–12921.
62. N. Agrait, G. Rubio and S. Vieira, Plastic deformation of nanometer-scale gold connective necks, Phys. Rev. Lett., 1995, 74(20), 3995.
63. N. Agrait, G. Rubio and S. Vieira, Plastic deformation in nanometer scale contacts, Langmuir, 1996, 12(19), 4505–4509.
64. G. Rubio, N. Agrait and S. Vieira, Atomic-sized metallic contacts: mechanical properties and electronic transport, Phys. Rev. Lett., 1996, 76(13), 2302.
65. C. J. Lambert, Quantum Transport in Nanostructures and Molecules. IOP Publishing, 2021.
66. C. Lambert, Basic concepts of quantum interference and electron transport in single-molecule electronics, Chem. Soc. Rev., 2015, 44(4), 875–888.
67. F. Bickelhaupt and N. van Hommes, Organometallics, 1996, 15, 2923; C. Fonseca Guerra, J. W. Handgraaf, E. J. Baerends and F. Bickelhaupt, J. Comput. Chem., 2004, 25, 189.
68. H. Hirshfeld, Synthesis, Crystal structure, and Hirshfeld Surface Analysis of a New Mixed Ligand Copper(II) Complex, Theor. Chim. Acta, 1977, 44, 129–138.
69. P. Reddy, S.-Y. Jang, R. A. Segalman and A. Majumdar, Thermoelectricity in molecular junctions, Science, 2007, 315(5818), 1568–1571.
70. J. A. Malen, P. Doak, K. Baheti, T. D. Tilley, R. A. Segalman and A. Majumdar, Identifying the length dependence of orbital alignment and contact coupling in molecular heterojunctions, Nano Lett., 2009, 9(3), 1164–1169.
71. S. Park, N. Cho and H. J. Yoon, Two Different Length-Dependent Regimes in Thermoelectric Large-Area Junctions of n-Alkanethiolates, Chem. Mater., 2019, 31(15), 5973–5980.
72. S. Park, J. Jang and H. J. Yoon, Validating the Mott Formula with Self-Assembled Monolayer (SAM)-Based Large-Area Junctions: Effect of Length, Backbone, Spacer, Substituent, and Electrode on the Thermopower of SAMs. The, J. Phys. Chem. C, 2021, 125(36), 20035–20047.
73. S. Park, S. Kang and H. J. Yoon, Power factor of one molecule thick films and length dependence, ACS Cent. Sci., 2019, 5(12), 1975–1982.
74. S. Park and H. J. Yoon, New Approach for large-area thermoelectric junctions with a liquid eutectic gallium–indium electrode, Nano Lett., 2018, 18(12), 7715–7718.
75. J. Ferrer, C. J. Lambert, V. M. García-Suárez, D. Z. Manrique, D. Visontai, L. Oroszlany, R. Rodríguez-Ferradás, I. Grace, S. Bailey and K. Gillemot, GOLLUM: a next-generation simulation tool for electron, thermal and spin transport, New J. Phys., 2014, 16(9), 093029.
76. J. M. Soler, E. Artacho, J. D. Gale, A. García, J. Junquera, P. Ordejón and D. Sánchez-Portal, The SIESTA method for ab initio order-N materials simulation, J. Phys.: Condens. Matter, 2002, 14(11), 2745.
77. S. K. Lee, M. Buerkle, R. Yamada, Y. Asai and H. Tada, Thermoelectricity at the molecular scale: a large Seebeck effect in endohedral metallofullerenes, Nanoscale, 2015, 7(48), 20497–20502.

---

Footnotes

† Electronic supplementary information (ESI) available: Synthesis, purification and MALDI-TOF data of the EMFs, HPLC graphs demonstrating the purification process for the Sc₃N@C₈₀; Tauc plots and UV-Visible spectra for Er₃N@C₈₀ and Sc₃N@C₈₀; EPR of the Sc₃C₂@C₈₀; details on the experimental methods, further examples of individual measurements and complementary analysis of the results; details on the theoretical methods, and complementary results from the theoretical calculations are available free of charge via the internet. See DOI: https://doi.org/10.1039/d1nh00527h

‡ These authors contributed equally to this work.

---