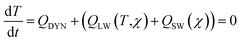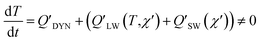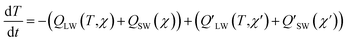Impacts of a near-future supersonic aircraft fleet on atmospheric composition and climate

Abstract

Supersonic aircraft will have environmental impacts distinct from those of subsonic aviation, and are once again being developed and bought. Assessments of supersonic aircraft emissions impacts over the last decade have focused on the ozone and climate impacts of nitrogen oxides and water vapor, but assumed zero-sulfur fuel, zero black carbon emissions, and neglect likely design constraints on near-future engine technology. We assess the impacts on atmospheric composition and non-CO₂ climate forcing of a near-future supersonic aircraft fleet with current-generation engine technology burning fossil-based kerosene fuel with current-day sulfur content. Using vehicle performance modeling, market demand projection and global atmospheric chemistry-transport modeling, we find that a supersonic fleet flying at Mach 1.6 and 15–17 km altitude, burning 19 Tg of fuel each year and emitting 170 Gg of NO_x would cause a 0.046% reduction in global column ozone. We estimate the radiative forcing (climate impact) from changes in atmospheric concentrations of ozone (2.9 mW m⁻²), water vapor (1.3 mW m⁻²), carbonaceous and inorganic aerosols (−6.6 mW m⁻²), and methane (−0.65 mW m⁻²), resulting in a net non-CO₂, non-contrail forcing of −3.5 mW m⁻² and varying from −3.0 to −3.9 mW per m² per year to year. We also show that the use of zero-sulfur fuel would halve net ozone depletion but increases the net non-CO₂ non-contrail forcing to +2.8 mW m⁻² due to the loss of a cooling effect from sulfate aerosols. A smaller fleet of Mach 2.2 aircraft flying at 18–20 km and burning 14 Tg of fuel but emitting twice as much NO_x per unit of fuel results in 17 times as much net ozone depletion. The net radiative forcing for this fleet is of uncertain sign, averaging −0.15 mW m⁻² but varying between −3.2 and +2.0 mW per m² per year to year. Our results show that assessments of near-future supersonic aviation must consider the effects of fuel sulfur and black carbon alongside emissions of water vapor, NO_x, and CO₂, and that the net environmental impacts will be a trade-off between competing environmental concerns.

---

Environmental significance

Airlines, aircraft manufacturers, and policy makers are again discussing supersonic aviation. Although the use of zero-sulfur, net-zero lifecycle carbon fuel has been proposed, it is not clear whether this will be used in practice. This study quantifies the environmental impacts of a modern fleet of supersonic airliners, powered by the sulfur-bearing fossil fuel available at almost all airports worldwide. Our results suggest that the sulfur and carbonaceous aerosol emissions from supersonic aircraft may cause climate cooling effects which exceed the warming resulting from changes in ozone, stratospheric water vapor, or CO₂. Sulfur emissions are also found to increase the global mean ozone depletion. Decision makers considering low-sulfur fuel must therefore consider a trade-off between decreasing global ozone depletion and increasing climate impacts.

Introduction

Environmental impacts associated with the operation of supersonic aircraft in the stratosphere have been an object of scientific interest since the 1970s when the first commercial supersonic airliners, the Tupolev Tu-144 and the Concorde, entered service. Because supersonic aircraft emit NO_x and water vapor at high altitudes, stratospheric ozone depletion has been a central subject of investigation.^1–6 Studies have also quantified climate impacts associated with supersonic aircraft including radiative forcing due to CO₂, water vapor, and changes in ozone.^2,6–12

Interest in supersonic passenger aircraft has been recently renewed, and several companies are actively developing new supersonic aircraft. The International Civil Aviation Organization (ICAO) Committee on Aviation Environmental Protection (CAEP) is considering the environmental impacts of supersonic aircraft as part of the CAEP/12 cycle and has stated that “it is anticipated that the certification of a supersonic aeroplane could occur in the 2020–2025 timeframe” with regards to landing and take-off noise.¹³ United Airlines also announced in June 2021 that they planned to purchase 15 Overture supersonic aircraft from Boom, designed to fly at a cruise speed of Mach 1.7 and a cruise altitude of 18 km, carrying up to 88 passengers and designed to burn sustainable aviation fuel (SAF).¹⁴ Most forms of SAF also contain almost no sulfur or aromatic compounds, and as such should have near-zero emissions of sulfur and significantly reduced emissions of soot (black carbon).^15–17 Since SAF is intended to result in lower emissions of CO₂, Boom have called their Overture aircraft “[the] most sustainable supersonic airliner”.¹⁸

However, the use of SAF will not address impacts resulting from NO_x emissions or water vapor. Supersonic aircraft typically cruise at higher altitudes than subsonic aircraft, and NO_x emissions at these higher altitudes are expected to result in depletion of the stratospheric ozone layer and a change in the radiative balance of the planet.^2,12,19 Water vapor emitted into the stratosphere can also have a warming effect, trapping outgoing longwave radiation. Using radiative forcing (RF) as a metric of climate impacts, past studies investigating supersonic aviation's effects on the environment have found that the RF resulting from changes in atmospheric ozone and water vapor could exceed those from CO₂ – and this remains true for water vapor even when considered on a 100 year timescale.^7,12 SAF also typically has greater hydrogen content and therefore water emissions, with paraffinic biofuels producing 11% more water per unit of fuel burned than is the case for conventional jet fuel.²⁰ Due to the greater fuel burn required to achieve the same distance, supersonic aircraft will also produce more emissions in absolute terms to ferry the same number of passengers the same distance compared to subsonic aircraft using the same fuel.

A commitment to purchase SAF, such as the commitment made by Boom, will also not necessarily mean that the supersonic aircraft will physically use 100% SAF. Under the currently active ASTM International standard specification for aviation turbine fuels (ASTM D1655, DOI: 10.1520/D1655-21C), currently certified SAF are only allowed to be used to a blend ratio of up to 50% in commercial aircraft.¹⁵ While these blending limits might change or could potentially be set differently for supersonic aircraft, they raise the question of whether a 100% SAF commitment for supersonic aircraft would in practice be achieved. Furthermore, for a 100% SAF commitment to be achieved, a separate SAF fueling infrastructure would be needed at airports served by supersonic jets. Until that time, instead of having some flights use SAF exclusively while others use conventional fuel, SAF would be blended with conventional fuel at the airport level, meaning that all aircraft departing from a specific location receive the same fuel. While such a setup would result in the same net CO₂ reduction, this implies the possibility that supersonic aircraft in service may be burning a blend of SAF and conventional jet fuel – meaning emissions of both sulfur and black carbon (soot) at the higher altitudes of supersonic aircraft.²

The impact of this choice has not been captured in recent work on supersonic aviation, since most studies to date have assumed that the sulfur and soot emissions of supersonic aircraft would be negligible. Several assessments did not include fuel sulfur or soot emissions, simulating only the emissions of NO_x and water vapor.^5,9,10,12 A multi-model assessment led by NASA in the late 1990s included an assumed 200 ppm sulfur by mass but assumed that sulfur and black carbon did not significantly contribute to the radiative forcing from supersonic aircraft, although this was subject to significant uncertainty regarding sulfate particle formation pathways.² A study by Rahmes et al. focused on soot, finding a radiative forcing of less than 1 mW m⁻² from supersonic aircraft black carbon emissions burning 77 Tg of fuel year.²¹ However, a later study of supersonic aviation's impacts by Grewe et al. under the European Union SCENIC project found radiative forcings from emitted black carbon and sulfur aerosols of +4.6 mW m⁻² and −11.4 mW m⁻² respectively for an annual fuel burn of 60 Tg, exceeding the radiative forcing from either CO₂ emissions or changes in ozone despite the use of a black carbon emissions index 75% lower than that used by Rahmes et al.^7,11 The presence or absence of fuel sulfur has also been found to significantly change the total ozone depletion resulting from supersonic aviation. Based on 2-D simulations, Weisenstein et al. found that a fuel sulfur content of 200 ppm by mass could make sulfur emissions “potentially more important than emissions of NO_x and H₂O in terms of ozone depletion”.⁶ Current jet fuel sulfur content averages around 600 ppm, although the standard permits – and spot testing has found – values as high as 3000 ppm.²² The effect of a change in background sulfur concentrations on the sensitivity to NO_x emissions has also been investigated, but does not address the question of how fuel sulfur emissions specifically will affect ozone.^2,5

Another under-studied component of supersonic aviation impacts is their effect on atmospheric chemistry through reduction of global concentrations of methane, a greenhouse gas. Changes in atmospheric ozone concentrations due to subsonic aviation NO_x have been shown to reduce global methane concentrations, with a direct cooling effect. This also has the indirect effect of decreasing the amount of tropospheric ozone produced from NO_x, as well as reducing the chemical source of water vapor to the stratosphere. When these feedbacks are allowed to reach a steady state, the combination of these effects offsets almost the entire RF resulting from short-lived increases in ozone due to subsonic aviation NO_x.²³ Capturing these feedbacks in global atmospheric models requires the specification of surface methane fluxes, and capturing even 70% of the effects of long-term feedbacks on atmospheric composition requires a spin-up period exceeding the decade or longer perturbation lifetime of methane.^24,25 However, most studies of supersonic aviation to date have relied on a fixed methane boundary condition which cannot capture these effects. The only quantification of the role of methane in supersonic aviation impacts used a simple scaling relationship, and only calculated the direct RF effect of a reduction in methane concentrations.⁷

Long-term simulations are also required to capture inter-annual variability in supersonic emissions impacts. A study of changes in stratospheric ozone concentrations due to a supersonic aircraft fleet found that the variability in ozone impacts within a seven year period was ∼50 ppbv, similar in magnitude to the inter-model variability for supersonic aircraft impacts found by the Intergovernmental Panel on Climate Change (IPCC)'s special report on aviation.^3,26 A sensitivity study as part of the NASA multi-model assessment also found that ozone depletion at mid-to-high Northern latitudes could vary by ±15% due to interannual variability in temperature alone. However, most studies of supersonic emissions impacts either used repeating meteorological data from a single climatological year^5,6,9 or did not report interannual variability in impacts.^4,10,12

This study estimates the radiative forcing and global ozone depletion resulting from two different supersonic aircraft fleets, with and without indirect methane feedbacks, and including the chemical and radiative impacts of sulfur and carbonaceous aerosols. We evaluate one subsonic and two supersonic aircraft fleet scenarios, all burning fossil-based kerosene fuel with current-day fuel sulfur content, in addition to a supersonic fleet burning zero-sulfur fuel. For each scenario we perform a 42 year simulation of atmospheric chemistry with annually-recurring emissions, of which the final 14 years are used to estimate mean impacts and interannual variability.

Method

The effects of sub- and supersonic aviation on atmospheric ozone and the climate in 2035 are simulated with the global atmospheric chemistry transport model GEOS-Chem. This model includes a detailed treatment of the photochemistry of O₃, HO_x, NO_x, SO_x, CO, CH₄, H₂O, and other species necessary to capture the aforementioned feedbacks, and of radiative transfer needed to model photolysis and compute RF.

Aviation emissions scenarios

Three aviation scenarios are considered: subsonic aviation projected to 2035 with no supersonic aircraft available (“Subsonic”); a fleet of 60 seat, Mach 1.6 supersonic civil airliners with a range of 4500 nmi (“SST 1.6”); and a fleet of 60 seat, Mach 2.2 supersonic airliners with a range of 3500 nmi (“SST 2.2”). Both supersonic fleets are assumed to be able to travel supersonically over land. Although key features are summarized below, additional details regarding the approaches used to estimate total demand, flight scheduling, routing, and emissions indices are provided in Speth et al.,²⁷ in which the SST 1.6 and SST 2.2 supersonic fleets are referred to as SST45-1.6-60 and SST35-2.2-60 respectively.

Aircraft emissions for subsonic aircraft are calculated with the Aviation Emissions Inventory Code (AEIC), using existing aircraft performance data.²⁸ For the two supersonic fleets, global fleet emissions are calculated by estimating performance parameters of the aircraft, determining the fuel requirement to achieve each possible global route, simulating market demand for that route, and then estimating the monthly mean fleet emissions as a 3-D global grid to be read by our atmospheric chemistry model.

Key aircraft performance parameters (cruise-speed thrust-specific fuel consumption, the lift-to-drag ratio, and operating empty weight) are estimated based on constraining relationships between aircraft characteristics and performance. These relationships are derived from data for two reference aircraft: the NASA Supersonic Technology Concept Aeroplane²⁹ and an updated version of the Concorde (the so-called “B” model) which was intended to incorporate newer technologies than the original “A” model.³⁰ Fuel burn during take-off, climb, cruise, descent, and landing are estimated based on these performance characteristics, prescribing the climb and descent profiles as developed for the NASA N+2 supersonic aircraft research project.³¹

When simulating a single flight, emissions indices for each flight segment are estimated using an engine cycle model developed with the Numerical Propulsion System Simulation software,^27,32 from which NO_x, carbon monoxide, and unburned hydrocarbon emissions are calculated using the p₃T₃ method.³³ For each supersonic fleet, we use the CFM56-5B/3 two-spool, mixed-flow turbofan engine as a reference design, with appropriate temperature limits and component polytropic efficiencies. However, fan diameter and compressor pressure ratio are chosen through an iterative process for each fleet to accommodate the maximum thrust requirement of the design mission (a flight at the aircraft's maximum range, following the NASA N+2 mission profile) while matching the total fuel burn calculated earlier for said mission to within 15%.

The calculation of market demand for each fleet on each route includes this data, evaluating the fraction of the projected flying population in 2035 who would be willing to pay the higher ticket price (due to higher capital costs and increased fuel costs) in return for a shorter trip. Based on this information, the number of flights in each month between each origin–destination pair of airports is estimated for the given supersonic fleet. This allows the global, monthly mean emissions from the fleet to be quantified.

The total fuel burned, fuel efficiency, and emissions indices differ between the fleets as shown in Table 1, with the SST 2.2 fleet burning 1.7 times as much fuel per seat-km travelled compared to SST 1.6, and 8.7 times as much compared to the subsonic fleet. SST 2.2 also emits 3.8 times as much NO_x per seat-km travelled as SST 1.6. Nitrogen oxide (NO_x) and volatile organic compound (VOC) emissions are speciated as described by Barrett et al.³⁵ Black and organic carbon (BC and OC) emissions are estimated by assuming a fixed emissions index for each of 30 mg kg⁻¹ fuel burned.

Table 1 Average emissions indices and key information for each fleet. All units are g per kg of fuel burn. Emissions of NO_x are given on an NO₂ mass basis. Emissions of VOCs are given on a CH₄ mass basis. Sulfur emissions are split between SO₂ and H₂SO₄ as described in the main text. Subsonic aircraft BC emissions are calculated for each flight using the FOX method.³⁴ *Indicates that a single fleet-wide emissions index is used during all flight phases

	Subsonic	SST 1.6	SST 2.2
NOx	15	8.8	19
CO	8.3	6.3	15
VOCs	1.0	1.6	10
BC	0.082	0.030*	0.030*
OC	0.020	0.030*	0.030*
Sulfur	0.6*	0.6*	0.6*
H2SO4	0.036*	0.036*	0.036*
H2O	1231*	1231*	1231*
Fuel (kg) per seat km	0.023	0.12	0.20
Total annual fuel burn (Tg)	426	19.3	14.9
Total annual NOx emitted (Gg)	6.5	0.17	0.28
Cruise altitude (km)	9–12	15–17	18–20
Cruise Mach no.	<1	1.6	2.2

---

Unless otherwise specified, a fuel sulfur content of 600 ppm by mass is assumed, typical of current-day jet fuel.²² 98% of sulfur is emitted as SO₂, with the remaining 2% emitted as H₂SO₄. We also simulate an “ultra-low sulfur” perturbation scenario (“SST 1.6 ULS”). This is identical to scenario SST 1.6 except that sulfur emissions from the supersonic fleet are set to zero, providing data on one of the potential effects of using sustainable aviation fuels which typically contain zero or near-zero sulfur.

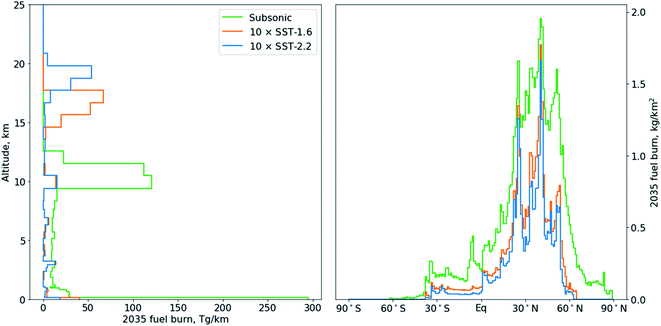
The vertical and horizontal (by latitude) distribution of fuel burn for each fleet are shown in Fig. 1. Although the majority of fuel burn for each SST fleet occurs within their cruise altitude range, there is an additional fuel burn peak at 10 km as this is the location of the constant-altitude acceleration from subsonic to supersonic prescribed by the N+2 mission profile.³¹ The horizontal distribution of fuel burn is similar to that of the subsonic fleet, with most fuel burn in the northern hemisphere. However, neither supersonic fleet flies polewards of 65°N.

Fig. 1 Global distribution of aviation fuel burn in 2035 by altitude (left) and latitude (right). The vertical distribution is shown after discretization onto the 72 vertical layers used by the GEOS-Chem model. Values for the supersonic fleets are multiplied by 10 for the sake of clarity.

For each supersonic fleet scenario we calculate both the induced demand for supersonic flight and the displacement of subsonic travel, resulting in a small decrease in subsonic emissions. Total impacts are estimated by simulating the atmosphere first with both the supersonic and reduced subsonic fleet emissions, and then subtracting results calculated with only the reduced subsonic fleet for that scenario. The impacts of subsonic fleet operations in 2035 are calculated by comparing a simulation which includes subsonic operations against one which does not.

Global atmospheric modeling

We use a modified version of the global CTM GEOS-Chem v11-02 (ref. 36) to simulate all scenarios, using the GEOS-Chem UCX unified tropospheric–stratospheric chemistry mechanism.³⁷ Simulations are performed using a global resolution of 4° × 5° (latitude × longitude) and with 72 non-uniform vertical layers, extending to a maximum altitude of around 80 km. Each simulation is integrated forwards in time for a total of 42 years. This is accomplished by using meteorological data from the NASA Global Modeling and Assimilation Office (GMAO) Modern Era Retrospective for Research and Analysis (MERRA) reanalysis dataset. We use data from the period January 1^st 2000 through December 31^st 2013, repeated twice to provide the full 42 year integration. This integration length ensures that long-term atmospheric responses mediated by methane are captured.

GEOS-Chem UCX has previously been evaluated against observations of stratospheric ozone depletion, stratospheric tracer–tracer correlations (both observed and as simulated by the Canadian Middle Atmosphere Model), and stratospheric lifetimes of long-lived gases³⁷ and has now been incorporated into the GEOS chemical composition forecast (GEOS-CF) used by NASA GMAO.^38,39 For this work, we also compared the simulated age of stratospheric air against observations.⁴⁰ As previously reported by Chabrillat et al., the simulated age of air is overestimated when using MERRA meteorology.⁴¹ Simulations at a resolution of 4° × 5° are also likely to simulate excessive horizontal mixing, resulting in a lower age of air at high latitudes.⁴² A comparison performed for this paper confirms these findings, but the age of air at 20 km all latitudes is within 6 months of the central estimate of the observed value and within the range of model estimates shown in Chabrillat et al.⁴¹ A 10 year model simulation at a finer resolution of 2° × 2.5° shows an increase in the stratospheric age of air outside of the tropics, improving the comparison against observations in the Southern Hemisphere (see ESI† for more details). Use of an updated meteorological dataset and a finer horizontal resolution may therefore provide an improvement in accuracy.

For these simulations, we replace GEOS-Chem's representation of stratospheric aerosol with a method implemented in the Whole Atmosphere Chemistry-Climate Model,⁴³ and use a gravitational settling scheme designed to more accurately capture settling of stratospheric aerosols with a log-normal size distribution.⁴⁴ In both the original and updated model, the surface area density and optical depth of stratospheric aerosol are calculated based on the mass concentration, causing direct radiative effects as well as indirect effects through heterogeneous chemistry on and within the aerosol.³⁷

Finally, we modify GEOS-Chem's treatment of stratospheric water vapor. The description by Eastham et al.³⁷ specifies that water vapor throughout the troposphere is prescribed to follow meteorological reanalysis, while water vapor in the stratosphere is allowed to evolve freely. However, this resulted in gradual accumulation of water in the stratosphere due to excessive water vapor entering from the tropical tropopause. We now force water vapor entering at the tropical tropopause (30°S–30°N) cold point to vary sinusoidally, between a minimum of 3.0 ppmv and 4.8 ppmv, with an offset of 155 days from the start of the year.⁴⁵ This results in steady sinusoidal variation in simulated stratospheric water vapor mixing ratios with an average trend of +0.0020% (+8.0 × 10⁻⁵ ppmv) per year in the tropics at 20 km altitude, replicating the observed “atmospheric tape recorder” of stratospheric water vapor.⁴⁶

The performance of the model when including these modifications was evaluated in Speth et al.²⁷ against 14 years of satellite observations. Comparisons to Microwave Limb Sounder readings show that the updated model reproduces zonal patterns of ozone, N₂O, H₂O, HNO₃, and HCl in the stratosphere, including seasonal variation. However vertical gradients of some long-lived species are steeper in the simulated stratosphere than is observed. This may be due to the coarse horizontal resolution of the simulation, which could result in artificially increased horizontal transport in the stratosphere.

Non-aviation emissions and boundary conditions

Non-aviation anthropogenic emissions are prescribed to annual mean values for 2035 based on the IPCC Representative Concentration Pathway (RCP) 4.5 projection.⁴⁷ Emissions of lightning NO_x, soil NO_x, mineral dust, sea salt, and biogenic emissions are calculated during the simulation based on the meteorological inputs.^48–52 Surface volumetric mixing ratios (VMRs) of long-lived species including N₂O and chlorofluorocarbons are also prescribed based on these projections, with the exception of methane for which a flux boundary condition is used.

Using a fixed methane boundary condition in simulations with changes to aviation emissions would prevent the effects of long-term methane feedbacks on atmospheric composition from being captured. Although methane feedback factors have been shown to provide a good approximation for the purposes of estimating changes in methane lifetime and burden,²⁵ they do not provide information on the resulting changes in the global distribution of ozone and other atmospheric constituents.⁵³ The feedback factor also varies between models, both in its value and in its relationship to background methane concentrations.²⁴

We instead simulate the surface flux of methane. Prior to any other simulations, a 42 year calibrating simulation is performed in which surface methane concentrations are prescribed to 1835 ppbv, the projected global surface mean volumetric mixing ratio (VMR) of methane for 2035 in RCP 4.5. This simulation includes all other emissions, including emissions from subsonic aviation as projected for 2035, but without any supersonic aircraft emissions. The methane fluxes which satisfy this fixed surface condition are archived, averaged by month and into four equal area latitude bands (90°S–30°S, 30°S–0°, 0°–30°N, and 30°N–90°N). The fluxes calculated from this “calibration” simulation are used in all subsequent simulations. This ensures that changes in methane loss due to changes in aviation emissions are captured and propagated, and unless otherwise stated, impacts are calculated with these effects included. The effect that these methane feedbacks have are quantified by comparing the results to a second set of simulations in which surface methane mixing ratios are prescribed.

Impact calculations

The atmospheric impacts of aviation are calculated using two metrics: change in global ozone, and non-CO₂, non-contrail climate impacts. Changes in atmospheric ozone are quantified as changes in the annual mean ozone column density in Dobson Units, or DU. Column density provides a metric of the total “overhead column loss”, a proxy for the expected increase in ultraviolet radiation reaching the surface due to ozone depletion.

We quantify non-CO₂, non-contrail climate impacts as the difference in radiative forcing when calculated in simulations with and without aviation emissions. We use the RRTMG radiative transfer model embedded in GEOS-Chem for these calculations.⁵⁴ Radiative forcing is calculated once every three hours during the first day of each month, and then all 12 days averaged to provide an estimate of annual radiative forcing. Similar to the Parallel Offline Radiative Transfer (PORT) tool used by CESM, which instead calculates radiative forcing on one out of every 73 time steps, this approach balances the need for accuracy against the need for computational efficiency.⁵⁵

For this study we modify GEOS-Chem's RRTMG implementation to include online calculation of RF due to water vapor and methane, at all altitudes from the surface to the stratopause. We also implement the calculation of stratospherically-adjusted radiative forcing, evaluating fluxes at the tropopause and using a fixed dynamical heating assumption.⁵⁶ A detailed description of this implementation is provided in Appendix A. RRTMG as implemented in GEOS-Chem includes the shortwave forcing from methane, identified by Etminan et al. as a significant component of the net radiative effect of methane.⁵⁷ Radiative forcing due to CO₂ is not calculated in this work as we do not explicitly simulate CO₂ emissions in GEOS-Chem.

For both ozone loss and radiative forcing, steady-state impacts are calculated based on the final 14 years of a 42 year simulation. Although true steady state cannot be achieved as the response is asymptotic, the mean ozone column change in the final 14 years is less than 7% different in magnitude than the response during the prior 14 years, and this change is exceeded by the interannual variability within the averaging period.

Results and discussion

We quantify changes in the global mean ozone column and in global mean radiative forcing for each of the two supersonic fleets. In each case we compare our results to prior analyses. A comprehensive spreadsheet comparing our results to those from the studies reviewed above is provided in the ESI.†

Changes to the global ozone distribution

Emissions from the SST 1.6 and SST 2.2 fleets result in the global mean ozone column changing by −0.046% and −0.77% respectively. This is shown relative to estimates from prior studies in Fig. 2. Except for the Dutta et al. 15–17 km aircraft, all results shown from external studies are for aircraft cruising at between 17 and 21 km. Studies in which sulfur emissions were included are shown as circles; those without sulfur emissions are shown as crosses. For our results, we also show the interannual variability as a vertical line. All results shown in the figure are also available in the ESI.†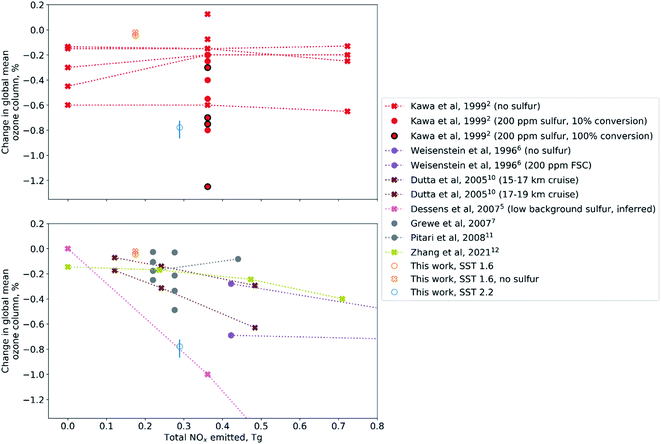

Fig. 2 Change in global mean ozone column as a function of total supersonic fleet NO_x emitted annually. Upper panel: results from the Kawa et al. multi-model assessment compared to our work. Lower panel: results from other studies compared to our work. Estimates in which sulfur emissions from supersonic aircraft were simulated are shown with circles, while those showing crosses include only NO_x and H₂O. If a study performed multiple simulations for identical fleets with different NO_x emissions indices, the estimates are connected by a dotted or dashed line. One color is used per study, apart from for this work where two are used to delineate the two aircraft. Results from this study include a vertical bar indicating the range of interannual variability. The vertical axis is truncated for clarity, removing two high-NO_x estimates from Dessens et al.⁵ and two from Weisenstein et al.⁶ All data plotted in this figure are provided in the ESI.†

There is no clear agreement regarding the effect of increasing NO_x emissions indices, indicated for individual studies in Fig. 2 by dashed lines. Some studies, including most contributors to the 1999 NASA² and IPCC²⁶ reports, have found either no sensitivity to increasing NO_x or a reduction in net ozone depletion with increasing NO_x as lower-altitude ozone production is increased. Others studies such as Dessens et al.⁵ and Dutta et al.¹⁰ instead find greater depletion with increasing NO_x emissions as stratospheric ozone depletion dominates. All studies find increasing impact with increased altitude. Although we do not directly evaluate the sensitivity of ozone to NO_x, dividing the global mean column ozone depletion by the total NO_x emitted for each of our simulated fleets results in an effective “sensitivity” of 0.003% ozone loss per Tg NO_x for SST 1.6, and 0.027% per Tg NO_x for SST 2.2. By comparison, our survey of the literature (see ESI†) shows a range of −0.003% loss (i.e. gain) per Tg NO_x to +0.035% loss per Tg NO_x, with the highest values inferred from simulations by Dessens et al. and in the results reported in Kawa et al. for the GSFC 2-D model. Dessens et al. suggested that the higher sensitivity to NO_x was due to updates to the NO_x chemistry mechanism used in their work, while Kawa et al. found that the sensitivity to NO_x was increased in a volcanically quiescent atmosphere. This may explain our greater sensitivity, since we also assume volcanically quiescent conditions. Large increases in background sulfur have been found to result in reduced sensitivity of stratospheric ozone concentrations to NO_x,⁶ but this finding is not consistent across studies⁵ and the effect on ozone RF has not yet been quantified.

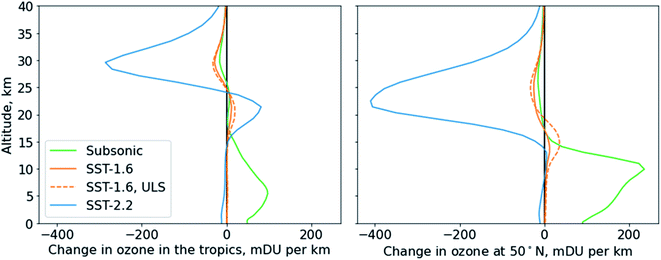
The annual mean net ozone depletion due to emissions from the SST 1.6 fleet varies by −21 to +25% relative to the 14 year average, compared to −6.5 to +11% for the SST 2.2 fleet. The greater variability for SST 1.6 is because of cancellation between ozone production at low altitudes and ozone depletion at higher altitudes. This is shown in Fig. 3, which plots the effect of subsonic fleets and both supersonic fleets on the vertical distribution of ozone.

Fig. 3 Change in the zonal mean vertical ozone distribution in the tropics (left), defined here as between 23.5°S and 23.5°N, and at 50°N (right). Both panels show results with variable surface methane mixing ratios (i.e. prescribed surface fluxes). Data are shown in units of milli-Dobson units per kilometer, meaning that the integrated value equals the total change in column ozone. All values correspond to the 14 year average. Axis limits are identical for both panels.

Both the subsonic and SST 1.6 fleet emissions cause a combination of increased ozone at lower altitudes and decreased ozone at higher altitudes. This is consistent with prior studies such as that by Köhler et al. which showed that NO_x emissions from subsonic aviation cause depletion of ozone above around 25 km altitude.⁵⁸ The “crossover point” at which the change is net zero varies by latitude, from 25 km in the tropics to 18 km at 50°N. This point is the same within 1.2 km between the subsonic and SST 1.6 fleets. However, the SST 1.6 fleet causes a larger ozone depletion at altitudes above the crossover point and a smaller ozone production below the crossover point, compared to the subsonic fleet. For example, at 50°N the ratio of the summed positive and negative perturbations is 11 (net positive) for subsonic aviation compared to 0.44 (net negative) for SST 1.6. Small changes in either the positive or negative perturbation therefore result in relatively large changes to the net value, resulting in greater interannual variability. For the SST 2.2 fleet, the negative perturbation at the same latitude is instead 250 times greater in magnitude than the positive perturbation. This is in part because the net effect of SST 2.2 on tropospheric ozone is a small decrease, rather than a net increase as in the case of subsonic aviation and SST 1.6. This tropospheric ozone loss is related to methane losses in the lower troposphere, which are discussed in more detail under “Effects of methane feedbacks and net forcing”.

Removal of sulfur from the fuel decreases the mean ozone depletion from SST 1.6 by 52% globally, illustrated in Fig. 3 with a dashed orange line. This is consistent with prior studies, which have found that inclusion of the effects of fuel sulfur can increase net ozone depletion from supersonic aircraft by up to a factor of 4.^2,6,11 Sulfur removal increases the altitude of the crossover point by 2 km at 50°N. It also increases the magnitude of the positive perturbation by 200% while increasing the negative perturbation by 5.7%. In the tropics the discrepancy is smaller, with a 70% increase in the positive perturbation compared to a 14% increase in the negative perturbation.

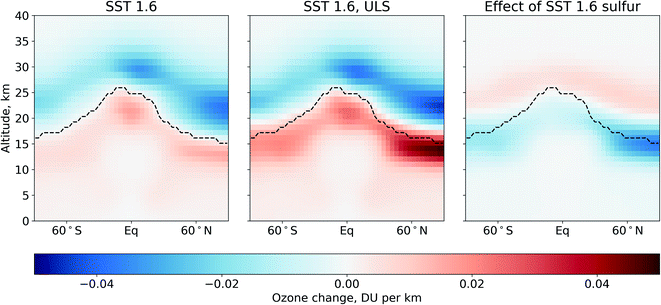
The effect of fuel sulfur on global ozone is illustrated for all latitudes and altitudes in Fig. 4. The crossover altitude shown on each plot is based on impacts from all SST 1.6 emissions as shown in the leftmost panel. Outside of the tropics, sulfur emissions result in ozone depletion around the crossover point and reduce the altitude at which this crossover occurs by 1–2 km. Sulfur-related depletion is greatest at northern mid- and high latitudes, at the SST 1.6 flight altitudes. At higher altitudes sulfur consistently results in an increase in ozone concentrations.

Fig. 4 Zonal mean ozone change resulting from SST 1.6 supersonic fleet emissions. Left: results including fuel sulfur emissions. Center: changes when fuel sulfur is set to zero. Right: the effect of fuel sulfur alone, taken as the difference between the left and center panels. The dashed line on each panel shows the crossover point as a function of latitude for the net impacts of SST 1.6.

Finally, the use of a fixed methane boundary condition reduces global mean ozone depletion by 13% and 5.9% for the SST 1.6 and SST 2.2 fleets respectively. For subsonic fleets, the effect is instead to increase the (positive) net ozone perturbation by 41%. The smaller sensitivity for supersonic emissions is because of the reduced role of tropospheric and lower-stratospheric ozone in determining the overall ozone column change, as shown in Fig. 3.

Radiative forcing due to ozone and water vapor

Fig. 5 shows the net non-CO₂, non-contrail radiative forcing resulting from each fleet's emissions, broken down by component. Each bar shows the 14 year average value, while error bars indicate the maximum and minimum annual mean RF over the same period. Results from simulations using a fixed methane boundary condition are shown in dark colors, while results from simulations in which methane is allowed to evolve freely (i.e. including methane feedbacks) are shown in paler colors. For SST 1.6, we also show results for the zero-sulfur case (ULS), which includes methane feedbacks. Results for the subsonic fleet in 2035 are also shown for comparison.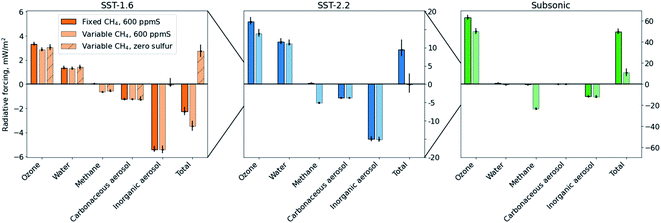

Fig. 5 Radiative forcing (RF) due to each aircraft fleet. Left: RF due to the SST 1.6 fleet emissions. Center: RF due to the SST 2.2 fleet emissions. Right: RF due to the subsonic fleet emissions in 2035. Dark colors show data from simulations using a fixed methane boundary condition, while paler colors show results from simulations with variable surface methane. Error bars shown the range of annual mean values over the 14 years used to determine the average value. Hatched bars show data from a simulation with zero fuel sulfur (SST 1.6 only). Colors are chosen to be consistent with those shown in Fig. 3. Error bars indicate interannual variability, showing the maximum range of annual mean values over the 14 year averaging period.

Our results show that water vapor emissions from SST 2.2 result in a net non-CO₂, non-contrail RF of 11 mW m⁻², or 0.60 mW m⁻² per Tg of water vapor emitted. This is consistent with prior studies of impacts from supersonic aircraft at similar altitudes which produced values ranging from 0.21 to 1.2 mW m⁻² Tg⁻¹ H₂O.^2,7,11,12 At lower altitudes, water vapor emissions produce a smaller radiative forcing due to their shorter lifetime.⁷ For the lower-altitude SST 1.6 we find a radiative forcing of 1.3 mW m⁻², or 0.055 mW m⁻² Tg⁻¹ H₂O emitted. The factor of 9 difference in forcing per unit emission is due to the longer effective lifetime of water vapor emitted at higher altitudes, with 14 times as much water vapor remaining in the stratosphere per unit emitted for SST 2.2 compared to SST 1.6. Emissions of water vapor from the SST 1.6 aircraft occur in the lowermost stratosphere, and vapor in this region passes into the troposphere through the extratropical tropopause.⁵⁹ Since tropospheric water vapor is prescribed in GEOS-Chem, this means that the effects of water vapor emissions at or near the tropopause are reduced. Simulations in which this boundary condition is relaxed or removed may find a greater radiative forcing for low-altitude emissions of water vapor.

Unlike previous studies, we find that the largest positive RF component is due to changes in ozone rather than water vapor. Ozone-attributable RF for the SST 1.6 fleet is 2.9 mW m⁻², or 0.15 mW m⁻² per Tg of fuel burned. This is 2.2 times as great as the RF due to water vapor accumulation. Removing sulfur from the fuel increases the net ozone RF by 7.0%, despite decreasing the overall ozone loss due to SST 1.6 by 52%. This contrasts with Pitari et al. who found that the inclusion of sulfur emissions caused a reduction in net ozone radiative forcing, although that assessment was for aircraft flying at higher altitudes.¹¹ For SST 1.6, it is possible that the loss of ozone at altitudes of 20–30 km when sulfur is removed has a disproportionate compensatory effect on RF compared to the additional ozone present at altitudes of 15–25 km.

Emissions from SST 2.2 result in a 4.8 times greater ozone RF of 14 mW m⁻², or 0.96 mW m⁻² per Tg of fuel burned emitted. The ozone RF is 25% greater than the 11 mW m⁻² RF from water vapor (i.e. 1.3 times as large, compared to 2.2 times for SST 1.6). The SST 2.2 engine also emits over twice as much NO_x per unit of fuel burned (19 g kg⁻¹ compared to 8.8 g kg⁻¹). Although prior studies have disagreed regarding the sensitivity of ozone RF to changes in the NO_x emissions index, the most recent analyses by Dessens et al. and Zhang et al. have found a near-linear relationship with greater NO_x emissions resulting in greater (positive) ozone RF.^5,12 Zhang et al. suggested that this may be due to increasing tropospheric ozone concentrations with increasing NO_x emissions, but we find the same increase in RF despite finding a small decrease in tropospheric ozone due to methane feedbacks (see Fig. 6). A possible alternate explanation is that SST 2.2 emits more NO_x than SST 1.6 and at higher altitudes, resulting in greater loss of ozone above 25 km altitude (see Fig. 3). Ozone at these altitudes induces a negative rather than positive radiative effect, such that ozone depletion results in a positive radiative forcing.^60–62

Fig. 6 Change in global mean ozone column (left) and global methane mixing ratios (right) as a result of emissions from each aircraft fleet. Simulations in which the surface methane mixing ratio is fixed are shown with dash-dotted lines (“Fixed CH₄). Simulations in which surface methane fluxes are prescribed are shown with solid lines (“Variable CH₄”).

Our study is the first to our knowledge to report a greater RF from ozone changes than from water vapor changes in response to SST emissions. This is likely the result of four factors. First, our lower-speed case, SST 1.6, flies at a cruise altitude lower than those of all recent analyses, resulting in less emitted water vapor remaining in the stratosphere. Second, our simulations show changes in column ozone which are at the high end of literature values per unit of NO_x emitted. The magnitude of the calculated ozone radiative forcing is the result of these large ozone changes, as the radiative forcings per Dobson unit of ozone column change (−20 mW m⁻² DU⁻¹ for SST 1.6 and −5.7 mW m⁻² DU⁻¹ for SST 2.2) are within the range of values reported in previous studies.^7,11,12 Third, the ozone radiative forcing is strongly dependent on the vertical structure of the change, since high-altitude ozone loss is warming whereas low-altitude ozone loss is cooling.^60–62 Finally, the NO_x emissions index for SST 2.2 is higher than that considered by most prior studies, at 19 g kg⁻¹ fuel burn – double that of SST 1.6. Given that the SST 2.2 ozone RF is 1.25 times its water vapor RF, compared to a factor of 2.2 for SST 1.6, a 50% reduction in the NO_x EI would likely result in the SST 2.2 water vapor RF exceeding the ozone RF.

Radiative forcing from sulfur and aerosol emissions

Fig. 5 shows that the positive RF contributions from ozone and water vapor for both SST 1.6 and SST 2.2 are opposed by negative RFs from inorganic (sulfate) and carbonaceous (black carbon) aerosol. Although carbonaceous aerosol also includes organic carbon aerosol, for which we use the same emissions index as black carbon, 80–81% of the SST 1.6 and SST 2.2 carbonaceous aerosol radiative forcing is the result of black carbon.

Carbonaceous aerosol emissions result in an RF of −1.2 and −3.8 mW m⁻² for SST 1.6 and SST 2.2 respectively. This is opposite in sign from the RF due to subsonic aviation per unit of fuel burned, due to the altitude of the emission. Absorbing aerosols emitted in the mid-stratosphere produce a negative RF by absorbing downwelling shortwave radiation before it can cross the tropopause, causing high altitude black carbon emissions to be investigated as a potential geoengineering strategy.⁶³ The carbonaceous aerosol RF from SST 1.6 and 2.2 is also 110 and 440 times greater respectively in magnitude than that of subsonic aviation, again per unit of fuel burned. This increase is due to the non-linear increase in lifetime for aerosols emitted at greater altitudes. A prior study of SST emissions by Pitari et al. found a positive RF of 4.6 mW m⁻² due to black carbon emissions, or 15 W per m² per Tg of carbon emitted (compared to −8.4 W m⁻² Tg_C⁻¹ for SST 2.2 and −2.1 W m⁻² Tg_C⁻¹ for SST 1.6).¹¹ The discrepancy in sign may be due to the location at which the RF is evaluated. If we calculate the RF at the top of the atmosphere instead of at the tropopause, we find a positive RF of 8.5 W m⁻² Tg_C⁻¹ for SST 2.2 (2.4 W m⁻² Tg_C⁻¹ for SST 1.6).

Inorganic aerosol forming as a consequence of aviation emissions result in an RF of −5.4 and −15 mW m⁻² for SST 1.6 and SST 2.2. Per unit of fuel burned, this is 9.9 and 36 times greater than the inorganic aerosol RF for subsonic aviation. As in the case of carbonaceous aerosol, the greater altitude of emission results in longer lifetimes and therefore a greater forcing per unit emitted. Since sulfate aerosol is predominantly optically scattering rather than absorbing, its effect is consistently to produce a net negative forcing by reflecting downwelling shortwave radiation back to space, regardless of altitude.

Combined, the net negative RF due to aerosols for SST 1.6 and SST 2.2 is −6.6 and −19 mW m⁻² respectively. Compared to the net positive RF from ozone and water vapor combined, the aerosol forcing is 1.6 and 0.76 times as large.

Per unit of atmospheric burden, the radiative forcings due to sulfate and black carbon aerosol produced by SST 2.2 are −0.65 W m⁻² Tg_S⁻¹ and −2.5 W m⁻² Tg_C⁻¹, respectively. The values for SST 1.6 are 5.7% and 13% smaller, respectively. The black carbon forcing per unit of atmospheric burden is lower than that reported by Kravitz et al. for simulations of stratospheric geoengineering involving the emission of large quantities of small black carbon particles at 16 or 25 km altitude (−8.5 or −5.7 W m⁻² Tg_C⁻¹ respectively),⁶³ but of the opposite sign to that reported by Pitari et al. of 6.0 W m⁻² Tg_C⁻¹.¹¹ The forcing per unit of atmospheric burden which we calculate for sulfate aerosol is 49–52% smaller than that which can be inferred from the results of Pitari et al.¹¹ (−1.3 W m⁻² Tg_S⁻¹) for a supersonic aircraft travelling at similar altitudes with a fuel sulfur content of 200 ppm. Again, these discrepancies may be partially attributable to differences in the location at which the RF is evaluated and in the simulated aerosol size distribution.

The large magnitude of the aerosol forcing from the SST 2.2 fleet is in part due to the long lifetime of the aerosol particles. Black carbon and sulfate particles produced from the SST 1.6 fleet have average lifetimes of 0.99 and 0.77 years respectively. This is consistent with estimates of aerosol lifetimes for small particles emitted in the lower stratosphere. For example, Kravitz et al. report a range of 1.4–3.8 years for a 16 km injection of black carbon particles, although this is for tropical emissions which maximize aerosol lifetime.⁶³ The SST 2.2 fleet black carbon and sulfate lifetimes are 3.4 and 2.6 years. The former value is again within the range reported by Kravitz et al. for black carbon but the latter value is at the high end of literature estimates of typical sulfate aerosol lifetimes in the stratosphere for background, volcanically-active, or geoengineered conditions.^64,65 However, the emission rate of sulfur considered in this study is several orders of magnitude lower than that considered for geoengineering and is likely to result in small, long-lived aerosols. For reference, the estimated black carbon and sulfate aerosol lifetimes from Pitari et al.¹¹ are 3.5 and 0.98 years respectively, based on the reported mean aerosol column densities (1.5 μg C per m²; and 53 μg SO₄ per m²), fuel burn (44 Tg per year), and emissions indices (0.005 g C per kg fuel; and 0.4 g SO₂ per kg fuel, or 200 ppm sulfur).

These factors combined result in a radiative forcing per unit of sulfur emitted from the SST 1.6 and SST 2.2 fleets which are 36–130% of that calculated for a supersonic fleet by Pitari et al.¹¹ Even if we conservatively reduce the aerosol radiative forcing by a factor of four, the net aerosol radiative forcing from SST 2.2 would still be approximately half that resulting from water vapor emissions. The broad conclusion that aerosol radiative forcing may be significant for supersonic aircraft is therefore robust to this uncertainty. Nevertheless, future work would benefit from the use of a size-resolving aerosol microphysics code which can more accurately estimate aerosol settling rates throughout the stratosphere.

Although we do not explicitly simulate emissions of CO₂ or their radiative forcing, estimates of long-term CO₂ forcing from other studies can provide some context regarding the magnitude of the aerosol forcing calculated here. Zhang et al. found a CO₂ RF of 4.1 mW m⁻² for a supersonic fleet burning 47 Tg of fuel each year¹² compared to the 19 and 15 Tg burned in this study by SST 1.6 and SST 2.2 respectively. The negative aerosol forcing we calculate is therefore larger in magnitude than the positive RF estimated for a larger fleet of supersonic aircraft in a separate study, and than the positive RF calculated in this work for with changes in either ozone or water vapor (although not the combined total in the case of SST 2.2). However, the precise balance between these terms will depend on the growth rate assumed for supersonic aviation and the time horizon considered.

Effects of methane feedbacks and net forcing

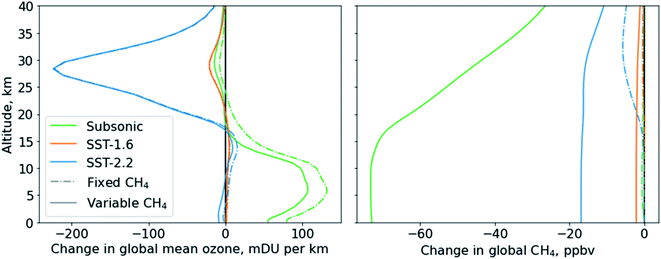
Fig. 6 shows the effect of methane feedbacks on both the ozone column and on methane mixing ratios. Subsonic aviation emissions cause the largest absolute change in methane, reducing mixing ratios by 73 ppbv (∼4%) at the surface. This reduction remains roughly constant to an altitude of approximately 15 km, as methane is well-mixed in the troposphere. Above this altitude the reduction decreases linearly, declining to 27 ppbv at 40 km altitude.

The net increase in ozone due to subsonic aviation is reduced by this loss of methane. This is because the majority of the change in ozone resulting from subsonic aviation is the result of NO_x producing ozone through chemical cycles involving ambient HO_x (OH and HO₂) and carbonaceous compounds, including methane and CO, although inclusion of methane feedbacks also increases ozone depletion in the lower and mid-stratosphere. We find that methane feedbacks reduce the change in global ozone column by 29% and in ozone RF by 21% relative to a simulation with fixed surface methane concentrations. The reduction in methane concentrations also results in a direct RF of −23 mW m⁻², offsetting 46% of the positive RF due to ozone changes. Including the reduction in ozone RF and assuming water vapor changes due to subsonic aviation are mostly due to methane oxidation, the net effect of methane feedbacks is to reduce the combined ozone, water vapor, and methane RF from subsonic aviation by 59%. This reduction is at the lower end of the range reported by a 2011 multi-model assessment of long-term methane feedbacks on RF for subsonic aviation.²³

For supersonic aviation the absolute change in methane concentration is again nearly constant from the surface to the tropopause, but is supplemented by additional depletion in the lower stratosphere. This may be due to the additional ozone (and therefore OH) at these altitudes which forms from increased O₂ photolysis enabled by mid-stratospheric ozone depletion (“self-healing”), as discussed by Prather and Hsu in the context of coupling between N₂O emissions and atmospheric methane.⁵³

The dominant factor in the net change in ozone column resulting from supersonic aircraft emissions is depletion at higher altitudes through catalytic reactions which are insensitive to methane abundance. This can be observed in Fig. 6 directly, where depletion of ozone above 20 km due to SST 2.2 is nearly identical with and without methane feedbacks. Changes in methane lifetime therefore reduce the lower-altitude production of ozone from supersonic aircraft but do not directly affect depletion at higher altitudes. Methane feedbacks increase the net depletion of ozone by SST 1.6 and SST 2.2 by 15% and 6.3%, respectively. Because the mechanism of impact is a reduction in the lower-altitude production of ozone, methane feedbacks still result in a reduction of net ozone RF by 14% and 20% respectively.

The net effect is that including methane feedbacks causes both a negative methane RF and a reduction in RF from other components. For SST 1.6, methane feedbacks result in an RF due to methane of −0.65 mW m⁻² (compared to −0.054 mW m⁻² without methane feedbacks) but the difference in net RF between a simulation with and without methane feedbacks is −1.2 mW m⁻². For SST 2.2, the methane RF is −5.2 mW m⁻² but the change in net RF due to feedbacks is −9.6 mW m⁻². Inclusion of methane feedbacks therefore results in a change in net RF for both SSTs which is 1.9 times the direct RF due to changes in the methane column alone, compared to a factor of 1.6 for subsonic aviation.

Due to the long perturbation lifetime of methane and the asymptotic nature of the methane response, our simulations cannot capture 100% of the steady-state change in atmospheric composition. Fitting an exponential decay curve to the change in methane due to aviation emissions in each scenario shows that the average change in global methane burden over the averaging period is 93–94% of the estimated equilibrium value (see ESI†). This suggests that methane feedbacks, including the resultant changes in ozone and water vapor, may grow by a further 6–8% if allowed to reach steady state.

Combined, we find that the 14 year average net, non-CO₂, non-contrail radiative forcing for SST 1.6 is −3.5 mW m⁻², with a range of −3.0 to −3.9 mW m⁻² in the annual average over this period. If zero-sulfur fuel is used, this increases to +2.8 mW m⁻² (2.2 to 3.2 mW m⁻²). For SST 2.2 using conventional jet fuel the sign of the net RF is uncertain, with an average value of −0.15 mW m⁻² (−3.2 to +2.0 mW m⁻²). This net forcing is smaller in magnitude than the forcing due to any single component, with the largest being ozone (+14 mW m²) and inorganic aerosol (−15 mW m⁻²).

Limitations

Further work is needed both to reduce the uncertainties highlighted by this work and to evaluate effects which are not considered here. For example, the RFs calculated here do not include cloud feedbacks, which may affect the overall impact of aviation at any altitude on the climate.⁶⁶ We also do not consider dynamical effects due to local heating by black carbon or its potential to darken arctic ice, both of which may have elevated significance for supersonic rather than subsonic aviation.⁶⁷ We also do not consider the possibility of condensation trails (“contrails”) forming behind supersonic aircraft. Although the RF due to contrails has been found to match or even exceed that due to CO₂ emissions for the subsonic aircraft fleet,⁶⁸ it is not yet known whether contrails would form regularly in the relatively dry conditions of the stratosphere or what their impacts would be. There is also limited confidence in model estimates of ice supersaturation in the upper troposphere and lower stratosphere, due in part to the difficulty of taking accurate measurements at these altitudes with radiosondes.^69,70

Our results are specific to the scenario considered, including methane and CFC boundary conditions derived from the RCP 4.5 scenario for 2035. If CFC concentrations change at a different rate than assumed under RCP 4.5, the impacts of supersonic NO_x emissions on ozone may be moderated or exacerbated due to their interactions with stratospheric chlorine. With regards to methane we assume a surface concentration of 1835 ppbv in 2035 consistent with the RCP 4.5 scenario,⁷¹ but this is at the low end of the range of 1690–2260 ppbv estimated for 2035 under the more recent Shared Socioeconomic Pathway (SSP) scenarios.⁷² The perturbation lifetime and “feedback factor” of methane are known to vary non-linearly with total methane burden,²⁴ suggesting that the methane feedbacks discussed in this study might take longer to respond and be of a different magnitude in a future with higher methane concentrations. While evaluation of the impacts of this assumption is outside of the scope of this paper, it should be considered in future studies of the likely long-term impacts of supersonic aviation on atmospheric composition and climate.

The modified GEOS-Chem UCX model uses the SNAP parameterization for aerosol microphysics,⁴⁴ and does not include size-resolved aerosols. It instead uses a log normal size distribution with variable modal radius,⁴³ estimating a mean settling rate and assuming optical properties consistent with stratospheric background aerosol. This is likely the cause of the high aerosol lifetimes calculated in this work. More accurate estimates of the impacts of supersonic aircraft-attributable aerosols may be possible through the use of size-resolving aerosol schemes. More broadly, the coarse horizontal resolution used in this study (4° × 5°) likely results in excessive horizontal mixing in the stratosphere, and future studies would benefit from using a finer horizontal resolution.⁴² However this need must be balanced against the additional computational cost, given the long integration times necessary to capture methane feedbacks.

Our results are also limited to evaluation of ozone change and RF. A full evaluation of climate impacts due to supersonic aviation is outside of the scope of this study, and would require multi-decade free-running global climate model simulations.

Conclusions

This study for the first time simultaneously considers ozone, water vapor, aerosols, and the long-term methane response in a single, coherent model of atmospheric chemistry and transport. We show that the sign of the net non-CO₂, non-contrail radiative forcing due to potential supersonic aviation may be uncertain at current levels of scientific understanding, and is subject not only to design choices such as the cruise altitude, but also to operational choices such as fuel composition. We find that the goal of minimizing ozone depletion may be in conflict with the goal of minimizing climate change when considering non-CO₂ emissions. Improving our understanding of this conflict is of urgent importance given that airlines, aircraft manufacturers, and international policy makers are considering deployment of a new supersonic aircraft within the next five to ten years.

The ideal fuel for an SST depends on the environmental objective. If seeking to minimize ozone depletion then this can be achieved by ensuring that fuel is sulfur free for supersonic aircraft specifically. If however the goal is to avoid positive radiative forcing, our work implies that reducing sulfur and black carbon emissions would remove a negative radiative forcing component which is comparable in magnitude to that arising from water vapor emissions or ozone. For a supersonic aircraft flying at 18–20 km with a NO_x emissions index of ∼20 g kg⁻¹, assuming no contrail production and the use of carbon offsets, aerosol forcing may determine whether that aircraft produces a net negative or net positive radiative forcing.

We also show that the effects of methane feedbacks on supersonic aircraft impacts are not consistent with those from subsonic aviation studies, due to the increased importance of stratospheric ozone depletion. We find that changes in methane alone can result in a direct negative radiative forcing up to 47% as large as the positive radiative forcing resulting from water vapor emissions, and can induce indirect changes in radiative forcing of the same magnitude as the direct methane forcing. This suggests that future evaluations of the impacts of supersonic aviation would be significantly improved by explicitly simulating long-term methane feedbacks.

Appendix A: Stratospherically adjusted radiative forcing

The standard RRTMG code as originally implemented in GEOS-Chem⁵⁴ calculated only the instantaneous RF and not the stratospherically-adjusted RF which has been recommended for calculations of climate-relevant forcing.^73,74 Stratospheric adjustment has been shown to change the net radiative forcing attributable to changes in stratospheric water vapor by around 50%, and may therefore be important to accurate calculation of the impacts of supersonic aviation.⁷⁵

To accomplish this, we use a time-marching method. We assume a quasi-steady state such that, in the baseline scenario with subsonic aviation only, stratospheric heating is in equilibrium. Following Maycock et al.⁷³ this can be expressed as

where Q_LW, Q_SW, and Q_DYN are the longwave radiative, shortwave radiative, and dynamical heating rates respectively, each with units of K per day. This approach assumes that dynamical heating is fixed, that shortwave heating changes as a function of species concentrations χ only with little sensitivity to small temperature changes, and that longwave heating changes as a function of both species concentration and temperature T.

In each of the non-baseline scenarios, the species concentrations will change from those in the baseline scenario, but the temperatures remain the same as they are prescribed from meteorological reanalysis data. This means that the net heating rate can become non-zero such that

implying a change in temperature over time. Under the fixed dynamical heating assumption, we assume that the dynamical heating is the same with and without the perturbation such that Q′_DYN = Q_DYN. We can then estimate the temperature tendency as
using the longwave and shortwave heating rates from the baseline simulation.

In each perturbation simulation, we calculate the temperature tendency and then integrate forwards in time using the Runge-Kutta 4^th order method with a time step of 12 hours. Only stratospheric grid cells are considered. For each calculation we allow only T to vary, and therefore only Q′_LW needs to be recalculated. The integration is performed independently for each model column to find the net temperature adjustment ΔT in each grid cell. Integration is stopped once the maximum temperature tendency anywhere in the stratospheric column is less than 1 mK per day, or if the integration time exceeds 150 simulation days. This latter condition is rare, typically occurring in less than 10 of the 3312 columns for each time step.

The temperature adjustment is calculated using radiative transfer calculations including all constituents. The radiative forcing due to each constituent in a single simulation is then calculated by repeating the longwave and shortwave radiative transfer calculations with that constituent excluded. For these “excluded-constituent” calculations, the temperature adjustment is not recalculated; instead the same temperature adjustment as was calculated for the “all-constituent” calculation is used.

Author contributions

Contributions are determined according to the CRediT role definitions (casrai.org/credit). SDE, FA, RLS, RGP, and SB conceptualized the study and acquired funding. SDE, FA, ISM, PP, and TF developed and tested software for the study, and performed the numerical experiments (investigation). SDE designed the methodology, analyzed and visualized the results, and wrote the original draft. All authors contributed to review and editing of the manuscript.

Acknowledgements

The authors would like to acknowledge Luke Kulik, Akshat Agarwal, and Irene Dedoussi, who were part of the MIT team investigating the impacts of supersonic aviation and provided valuable discussion and insight throughout. We would also like to thank Steve Baughcum and Susan Solomon for their suggestions and insights regarding stratospheric chemistry, supersonic emissions characterization, and model validation. Finally, we would like to thank Dr Simon Chabrillat for kindly providing their library of stratospheric age of air observational data. This work was partially supported by the National Aeronautics and Space Administration (NASA) under grant no. NNX14AT22A. It was also partially supported by the U.S. Federal Aviation Administration (FAA) Office of Environment and Energy through ASCENT, the FAA Center of Excellence for Alternative Jet Fuels and the Environment, projects 47 and 58 through FAA Award Number 13-C-AJFE-MIT under the supervision of László Windhoffer and Daniel Jacob. Any opinions, findings, conclusions or recommendations expressed in this material are those of the authors and do not necessarily reflect the views of either NASA or the FAA. The MERRA data used in this study have been provided by the Global Modeling and Assimilation Office (GMAO) at NASA Goddard Space Flight Center through the NASA GES DISC online archive.

References

1. D. M. Cunnold, F. N. Alyea and R. G. Prinn, Relative effects on atmospheric ozone of latitude and altitude of supersonic flight, AIAA J., 1977, 15, 337–345.
2. R. S. Kawa, S. L. Baughcum, C. A. Brock, W. H. Brune, R. C. Cohen, D. E. Kinnison, P. A. Newman, J. M. Rodriguez, R. S. Stolarski, D. Waugh and S. C. Wofsy, Assessment of the Effects of High-Speed Aircraft in the Stratosphere: 1998, NASA, 1999.
3. H. L. Rogers, M. P. Chipperfield, S. Bekki and J. A. Pyle, The effects of future supersonic aircraft on stratospheric chemistry modeled with varying meteorology, J. Geophys. Res., 2000, 105, 29359–29367.
4. S. Bekki and J. A. Pyle, Potential impact of combined NO_x and SO_x emissions from future high speed civil transport aircraft on stratospheric aerosols and ozone, Geophys. Res. Lett., 1993, 20, 723–726.
5. O. Dessens, H. L. Rogers and J. A. Pyle, A change in the calculated impact of supersonic aircraft NO_x emissions on the atmosphere, Aeronaut. J., 2007, 111, 311–314.
6. D. K. Weisenstein, M. K. W. Ko, N.-D. Sze and J. M. Rodriguez, Potential impact of SO₂ emissions from stratospheric aircraft on ozone, Geophys. Res. Lett., 1996, 23, 161–164.
7. V. Grewe, A. Stenke, M. Ponater, R. Sausen, G. Pitari, D. Iachetti, H. Rogers, O. Dessens, J. Pyle, I. S. A. Isaksen, L. Gulstad, O. A. Søvde, C. Marizy and E. Pascuillo, Climate impact of supersonic air traffic: an approach to optimize a potential future supersonic fleet–results from the EU-project SCENIC, Atmos. Chem. Phys., 2007, 5129–5145.
8. D. S. Lee, G. Pitari, V. Grewe, K. Gierens, J. E. Penner, A. Petzold, M. J. Prather, U. Schumann, A. Bais, T. Berntsen, D. Iachetti, L. L. Lim and R. Sausen, Transport impacts on atmosphere and climate: Aviation, Atmos. Environ., 2010, 44, 4678–4734.
9. D. E. Kinnison, P. S. Connell, J. M. Rodriguez, D. A. Rotman, D. B. Considine, J. Tannahill, R. Ramaroson, P. J. Rasch, A. R. Douglass, S. L. Baughcum, L. Coy, D. W. Waugh, S. R. Kawa and M. J. Prather, The Global Modeling Initiative assessment model: Application to high-speed civil transport perturbation, J. Geophys. Res., 2001, 106, 1693–1711.
10. M. Dutta, K. O. Patten and D. J. Wuebbles, Parametric Analyses of Potential Effects on Upper Tropospheric/Lower Stratospheric Ozone Chemistry by a Future Fleet of High Speed Civil Transport (HSCT) Type Aircraft, NASA, 2005.
11. G. Pitari, D. Iachetti, E. Mancini, V. Montanaro, N. De Luca, C. Marizy, O. Dessens, H. Rogers, J. Pyle, V. Grewe, A. Stenke and O. A. Søvde, Radiative forcing from particle emissions by future supersonic aircraft, Atmos. Chem. Phys., 2008, 8, 4069–4084.
12. J. Zhang, D. Wuebbles, D. Kinnison and S. L. Baughcum, Potential impacts of supersonic aircraft emissions on ozone and resulting forcing on climate: An update on historical analysis, J. Geophys. Res., 2021, 126(6) DOI:10.1029/2020jd034130.
13. ICAO CAEP, Supersonic Aircraft Noise Standards Development, https://www.icao.int/environmental-protection/Pages/Supersonic-Aircraft-Noise-Standards-Development.aspx, accessed June 26, 2021.
14. Boom Supersonic, 2021, https://boom-press-assets.s3.us-west-2.amazonaws.com/BoomFactSheet_220124.pdf.
15. R. H. Moore, K. L. Thornhill, B. Weinzierl, D. Sauer, E. D'Ascoli, J. Kim, M. Lichtenstern, M. Scheibe, B. Beaton, A. J. Beyersdorf, J. Barrick, D. Bulzan, C. A. Corr, E. Crosbie, T. Jurkat, R. Martin, D. Riddick, M. Shook, G. Slover, C. Voigt, R. White, E. Winstead, R. Yasky, L. D. Ziemba, A. Brown, H. Schlager and B. E. Anderson, Biofuel blending reduces particle emissions from aircraft engines at cruise conditions, Nature, 2017, 543, 411–415.
16. C. Voigt, J. Kleine, D. Sauer, R. H. Moore, T. Bräuer, P. Le Clercq, S. Kaufmann, M. Scheibe, T. Jurkat-Witschas, M. Aigner, U. Bauder, Y. Boose, S. Borrmann, E. Crosbie, G. S. Diskin, J. DiGangi, V. Hahn, C. Heckl, F. Huber, J. B. Nowak, M. Rapp, B. Rauch, C. Robinson, T. Schripp, M. Shook, E. Winstead, L. Ziemba, H. Schlager and B. E. Anderson, Cleaner burning aviation fuels can reduce contrail cloudiness, Commun. Earth Environ., 2021, 2, 1–10.
17. R. L. Speth, C. Rojo, R. Malina and S. R. H. Barrett, Black carbon emissions reductions from combustion of alternative jet fuels, Atmos. Environ., 2015, 105, 37–42.
18. Boom – Overture, https://boomsupersonic.com/overture, accessed June 26, 2021.
19. H. Johnson, The Effect of Supersonic Transport Planes on the Stratospheric Ozone Shield, Boston Coll. Environ. Aff. Law Rev., 1972, 735–781.
20. F. Caiazzo, A. Agarwal, R. L. Speth and S. R. H. Barrett, Impact of biofuels on contrail warming, Environ. Res. Lett., 2017, 12, 114013.
21. T. F. Rahmes, A. H. Omar and D. J. Wuebbles, Atmospheric distributions of soot particles by current and future aircraft fleets and resulting radiative forcing on climate, J. Geophys. Res., 1998, 103, 31657–31667.
22. J. I. Hileman, R. W. Stratton and P. E. Donohoo, Energy Content and Alternative Jet Fuel Viability, J. Propul. Power, 2010, 26, 1184–1196.
23. C. D. Holmes, Q. Tang and M. J. Prather, Uncertainties in climate assessment for the case of aviation NO, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 10997–11002.
24. C. D. Holmes, Methane Feedback on Atmospheric Chemistry: Methods, Models, and Mechanisms, J. Adv. Model. Earth Syst., 2018, 10, 1087–1099.
25. A. Khodayari, S. C. Olsen, D. J. Wuebbles and D. B. Phoenix, Aviation NO_x-induced CH₄ effect: Fixed mixing ratio boundary conditions versus flux boundary conditions, Atmos. Environ., 2015, 113, 135–139.
26. J. E. Penner, D. Lister, D. J. Griggs, D. J. Dokken and M. McFarland, Aviation and the Global Atmosphere: A Special Report of the Intergovernmental Panel on Climate Change, Cambridge University Press, Cambridge, England, 1999.
27. R. L. Speth, S. D. Eastham, T. M. Fritz, I. Sanz-Morere, A. Agarwal, P. Prashanth, F. Allroggen and S. R. H. Barrett, Global Environmental Impact of Supersonic Cruise Aircraft in the Stratosphere, NASA, 2021.
28. N. W. Simone, M. E. J. Stettler and S. R. H. Barrett, Rapid estimation of global civil aviation emissions with uncertainty quantification, Transp. Res. Part D Trans. Environ., 2013, 25, 33–41.
29. J. J. Berton, D. L. Huff, K. Geiselhart and J. Seidel, in AIAA Scitech 2020 Forum, American Institute of Aeronautics and Astronautics, 2020.
30. Roxburgh, Concorde SST: The Concorde B, http://www.concordesst.com/concordeb.html, accessed December 22, 2021.
31. J. Morgenstern, M. Buonanno, J. Yao, M. Murugappan, U. Paliath, L. Cheung, I. Malcevic, K. Ramakrishnan, N. Pastouchenko, T. Wood, S. Martens, P. Viars, T. Tersmette, J. Lee, R. Simmons, D. Plybon, J. Alonso, F. Palacios, T. Lukaczyk and G. Carrier, Advanced Concept Studies for Supersonic Commercial Transports Entering Service in the 2018-2020 Period Phase 2, NASA, 2015.
32. J. K. Lytle, The numerical propulsion system simulation: An overview, NASA, 2000.
33. D. DuBois and G. C. Paynter, “Fuel Flow Method2” for Estimating Aircraft Emissions, SAE Technical Paper, 2006.
34. M. E. J. Stettler, A. M. Boies, A. Petzold and S. R. H. Barrett, Global civil aviation black carbon emissions, Environ. Sci. Technol., 2013, 47, 10397–10404.
35. S. R. H. Barrett, M. Prather, J. Penner, H. Selkirk, A. Dopelheuer, G. Fleming, M. Gupta, R. Halthore, J. Hileman, M. Jacobson, S. Kuhn, R. Miake-lye, A. Petzold, C. Roof, U. Schumann, I. Waitz and R. Wayson, Guidance on the Use of AEDT Gridded Aircraft Emissions in Atmospheric Models, Massachusetts Institute of Technology, Cambridge, Massachusetts, 2010.
36. I. Bey, D. J. Jacob, R. M. Yantosca, J. A. Logan, B. D. Field, A. M. Fiore, Q. Li, H. Y. Liu, L. J. Mickley and M. G. Schultz, Global modeling of tropospheric chemistry with assimilated meteorology: Model description and evaluation, J. Geophys. Res., 2001, 106, 23073–23095.
37. S. D. Eastham, D. K. Weisenstein and S. R. H. Barrett, Development and evaluation of the unified tropospheric–stratospheric chemistry extension (UCX) for the global chemistry-transport model GEOS-Chem, Atmos. Environ., 2014, 89, 52–63.
38. C. A. Keller, K. E. Knowland, B. N. Duncan, J. Liu, D. C. Anderson, S. Das, R. A. Lucchesi, E. W. Lundgren, J. M. Nicely, E. Nielsen, L. E. Ott, E. Saunders, S. A. Strode, P. A. Wales, D. J. Jacob and S. Pawson, Description of the NASA GEOS composition forecast modeling system GEOS-CF v1.0, J. Adv. Model. Earth Syst., 2021, 13(4) DOI:10.1029/2020ms002413.
39. K. E. Knowland, P. Wales, L. Coy, K. Wargan, C. Keller, L. E. Ott, S. Pawson and S. D. Eastham, American Geophysical Union Fall Meeting, 2020, https://ui.adsabs.harvard.edu/abs/2020AGUFMA044.0002K/abstract.
40. A. E. Andrews, K. A. Boering, B. C. Daube, S. C. Wofsy, M. Loewenstein, H. Jost, J. R. Podolske, C. R. Webster, R. L. Herman, D. C. Scott, G. J. Flesch, E. J. Moyer, J. W. Elkins, G. S. Dutton, D. F. Hurst, F. L. Moore, E. A. Ray, P. A. Romashkin and S. E. Strahan, Mean ages of stratospheric air derived from in situ observations of CO₂, CH₄, and N₂O, J. Geophys. Res., 2001, 106, 32295–32314.
41. S. Chabrillat, C. Vigouroux, Y. Christophe, A. Engel, Q. Errera, D. Minganti, B. M. Monge-Sanz, A. Segers and E. Mahieu, Comparison of mean age of air in five reanalyses using the BASCOE transport model, Atmos. Chem. Phys., 2018, 18, 14715–14735.
42. S. E. Strahan and B. C. Polansky, Meteorological implementation issues in chemistry and transport models, Atmos. Chem. Phys., 2006, 6, 2895–2910.
43. T. Wegner, D. E. Kinnison, R. R. Garcia and S. Solomon, Simulation of polar stratospheric clouds in the specified dynamics version of the whole atmosphere community climate model, J. Geophys. Res., C: Oceans Atmos., 2013, 118, 4991–5002.
44. J.-P. Chen, I.-C. Tsai and Y.-C. Lin, A statistical–numerical aerosol parameterization scheme, Atmos. Chem. Phys., 2013, 13, 10483–10504.
45. J. P. McCormack and D. E. Siskind, Simulations of the quasi-biennial oscillation and its effect on stratospheric H₂O, CH₄, and age of air with an interactive two-dimensional model, J. Geophys. Res., C: Oceans Atmos., 2002, 107, 1–17.
46. P. W. Mote, K. H. Rosenlof, M. E. McIntyre, E. S. Carr, J. C. Gille, J. R. Holton, J. S. Kinnersley, H. C. Pumphrey, J. M. Russell and J. W. Waters, An atmospheric tape recorder: The imprint of tropical tropopause temperatures on stratospheric water vapor, J. Geophys. Res., 1996, 101, 3989.
47. A. M. Thomson, K. V. Calvin, S. J. Smith, G. P. Kyle, A. Volke, P. Patel, S. Delgado-Arias, B. Bond-Lamberty, M. A. Wise, L. E. Clarke and J. A. Edmonds, RCP4.5: a pathway for stabilization of radiative forcing by 2100, Clim. Change, 2011, 109, 77.
48. L. T. Murray, D. J. Jacob, J. A. Logan, R. C. Hudman and W. J. Koshak, Optimized regional and interannual variability of lightning in a global chemical transport model constrained by LIS/OTD satellite data, J. Geophys. Res., 2012, 117, D20307.
49. A. B. Guenther, X. Jiang, C. L. Heald, T. Sakulyanontvittaya, T. Duhl, L. K. Emmons and X. Wang, The model of emissions of gases and aerosols from nature version 2.1 (MEGAN2.1): An extended and updated framework for modeling biogenic emissions, Geosci. Model Dev., 2012, 5, 1471–1492.
50. L. Jaeglé, P. K. Quinn, T. S. Bates, B. Alexander and J. T. Lin, Global distribution of sea salt aerosols: New constraints from in situ and remote sensing observations, Atmos. Chem. Phys., 2011, 11, 3137–3157.
51. C. S. Zender, Mineral Dust Entrainment and Deposition (DEAD) model: Description and 1990s dust climatology, J. Geophys. Res., 2003, 108(D14) DOI:10.1029/2002jd002775.
52. R. C. Hudman, N. E. Moore, A. K. Mebust, R. V. Martin, A. R. Russell, L. C. Valin and R. C. Cohen, Steps towards a mechanistic model of global soil nitric oxide emissions: implementation and space based-constraints, Atmos. Chem. Phys., 2012, 12, 7779–7795.
53. M. J. Prather and J. Hsu, Coupling of nitrous oxide and methane by global atmospheric chemistry, Science, 2010, 330, 952–954.
54. C. L. Heald, D. A. Ridley, J. H. Kroll, S. R. H. Barrett, K. E. Cady-Pereira, M. J. Alvarado and C. D. Holmes, Contrasting the direct radiative effect and direct radiative forcing of aerosols, Atmos. Chem. Phys., 2014, 14, 5513–5527.
55. A. J. Conley, J.-F. Lamarque, F. Vitt, W. D. Collins and J. Kiehl, PORT, a CESM tool for the diagnosis of radiative forcing, Geosci. Model Dev., 2013, 6, 469–476.
56. S. B. Fels, J. D. Mahlman, M. D. Schwarzkopf and R. W. Sinclair, Stratospheric Sensitivity to Perturbations in Ozone and Carbon Dioxide: Radiative and Dynamical Response, J. Atmos. Sci., 1980, 37, 2265–2297.
57. M. Etminan, G. Myhre, E. J. Highwood and K. P. Shine, Radiative forcing of carbon dioxide, methane, and nitrous oxide: A significant revision of the methane radiative forcing, Geophys. Res. Lett., 2016, 43(24) DOI:10.1002/2016gl071930.
58. M. O. Köhler, G. Rädel, O. Dessens, K. P. Shine, H. L. Rogers, O. Wild and J. A. Pyle, Impact of perturbations to nitrogen oxide emissions from global aviation, J. Geophys. Res., 2008, 113, 1–15.
59. A. E. Dessler, E. J. Hintsa, E. M. Weinstock, J. G. Anderson and K. R. Chan, Mechanisms controlling water vapor in the lower stratosphere: “A tale of two stratospheres”, J. Geophys. Res., 1995, 100, 23167.
60. A. A. Lacis, D. J. Wuebbles and J. A. Logan, Radiative forcing of climate by changes in the vertical distribution of ozone, J. Geophys. Res., 1990, 95, 9971–9981.
61. P. M. d. F. Forster and K. P. Shine, Radiative forcing and temperature trends from stratospheric ozone changes, J. Geophys. Res., 1997, 102, 10841–10855.
62. F. Iglesias-Suarez, D. E. Kinnison, A. Rap, A. C. Maycock, O. Wild and P. J. Young, Key drivers of ozone change and its radiative forcing over the 21st century, Atmos. Chem. Phys., 2018, 18, 6121–6139.
63. B. Kravitz, A. Robock, D. T. Shindell and M. A. Miller, Sensitivity of stratospheric geoengineering with black carbon to aerosol size and altitude of injection, J. Geophys. Res., 2012, 117(D9) DOI:10.1029/2011jd017341.
64. P. J. Rasch, P. J. Crutzen and D. B. Coleman, Exploring the geoengineering of climate using stratospheric sulfate aerosols: The role of particle size, Geophys. Res. Lett., 2008, 35, 1–6.
65. SPARC Group, SPARC Report No. 4: Assessment of Stratospheric Aerosol Properties, Stratospheric Processes and their Role in Climate (SPARC), 2006.
66. M. Z. Jacobson, J. T. Wilkerson, A. D. Naiman and S. K. Lele, The effects of aircraft on climate and pollution. Part II: 20-year impacts of exhaust from all commercial aircraft worldwide treated individually at the subgrid scale, Faraday Discuss., 2013, 165, 369–382.
67. T. C. Bond, S. J. Doherty, D. W. Fahey, P. M. Forster, T. Berntsen, B. J. DeAngelo, M. G. Flanner, S. Ghan, B. Kärcher, D. Koch, S. Kinne, Y. Kondo, P. K. Quinn, M. C. Sarofim, M. G. Schultz, M. Schulz, C. Venkataraman, H. Zhang, S. Zhang, N. Bellouin, S. K. Guttikunda, P. K. Hopke, M. Z. Jacobson, J. W. Kaiser, Z. Klimont, U. Lohmann, J. P. Schwarz, D. Shindell, T. Storelvmo, S. G. Warren and C. S. Zender, Bounding the role of black carbon in the climate system: A scientific assessment, J. Geophys. Res., 2013, 118, 5380–5552.
68. D. S. Lee, D. W. Fahey, A. Skowron, M. R. Allen, U. Burkhardt, Q. Chen, S. J. Doherty, S. Freeman, P. M. Forster, J. Fuglestvedt, A. Gettelman, R. R. De León, L. L. Lim, M. T. Lund, R. J. Millar, B. Owen, J. E. Penner, G. Pitari, M. J. Prather, R. Sausen and L. J. Wilcox, The contribution of global aviation to anthropogenic climate forcing for 2000 to 2018, Atmos. Environ., 2020, 117834.
69. K. Gierens, S. Matthes and S. Rohs, How Well Can Persistent Contrails Be Predicted?, Aerospace, 2020, 7, 169.
70. S. Baughcum, M. Y. Danilin, L. M. Miloshevich and A. J. Heymsfield, in TAC-2 Proceedings, 2009, pp. 169–173.
71. M. Meinshausen, S. J. Smith, K. Calvin, J. S. Daniel, M. L. T. Kainuma, J.-F. Lamarque, K. Matsumoto, S. A. Montzka, S. C. B. Raper, K. Riahi, A. Thomson, G. J. M. Velders and D. P. P. van Vuuren, The RCP greenhouse gas concentrations and their extensions from 1765 to 2300, Clim. Change, 2011, 109, 213.
72. M. Meinshausen, Z. R. J. Nicholls, J. Lewis, M. J. Gidden, E. Vogel, M. Freund, U. Beyerle, C. Gessner, A. Nauels, N. Bauer, J. G. Canadell, J. S. Daniel, A. John, P. B. Krummel, G. Luderer, N. Meinshausen, S. A. Montzka, P. J. Rayner, S. Reimann, S. J. Smith, M. van den Berg, G. J. M. Velders, M. K. Vollmer and R. H. J. Wang, The shared socio-economic pathway (SSP) greenhouse gas concentrations and their extensions to 2500, Geosci. Model Dev., 2020, 13, 3571–3605.
73. a. C. Maycock, K. P. Shine and M. M. Joshi, The temperature response to stratospheric water vapour changes, Q. J. R. Meteorol. Soc., 2011, 137, 1070–1082.
74. IPCC, Climate Change 2007: Synthesis Report, 2007.
75. S. Solomon, K. H. Rosenlof, R. W. Portmann, J. S. Daniel, S. M. Davis, T. J. Sanford and G.-K. Plattner, Contributions of stratospheric water vapor to decadal changes in the rate of global warming, Science, 2010, 327, 1219–1223.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d1ea00081k

---