Open Access Article
Open Access ArticleNature of the surface space charge layer on undoped SrTiO3 (001)†
Hojoon
Lim‡
 a,
Chanyang
Song‡
a,
Minsik
Seo
a,
Chanyang
Song‡
a,
Minsik
Seo
 a,
Dongwoo
Kim
a,
Moonjung
Jung
a,
Dongwoo
Kim
a,
Moonjung
Jung
 a,
Habin
Kang
a,
Seunghwan
Kim
a,
Kyung-Jae
Lee
a,
Youngseok
Yu
a,
Habin
Kang
a,
Seunghwan
Kim
a,
Kyung-Jae
Lee
a,
Youngseok
Yu
 b,
Geonhwa
Kim
c,
Ki-Jeong
Kim
*c and
Bongjin Simon
Mun
b,
Geonhwa
Kim
c,
Ki-Jeong
Kim
*c and
Bongjin Simon
Mun
 *ad
*ad
aDepartment of Physics and Photon Science, Gwangju Institute of Science and Technology, Gwangju 61005, Republic of Korea. E-mail: bsmun@gist.ac.kr
bResearch Center for Materials Analysis, Korea Basic Science Institute, Daejeon 34133, Republic of Korea
cBeamline Research Division, Pohang Accelerator Laboratory, Pohang 37674, Republic of Korea. E-mail: kjkim@postech.ac.kr
dCenter for Advanced X-ray Science, Gwangju Institute of Science and Technology, Gwangju 61005, Republic of Korea
First published on 16th September 2021
Abstract
SrTiO3, an ABO3-type perovskite structure, has been a popular choice of substrate for many important heterostructures, e.g., ferroelectric thin films and superlattices. As numerous exotic physical phenomena are closely related to delicate electron/ion exchanges at the interfacial layer between the substrate and overlayer, precise characterization of surface/interfacial properties has become the center of many research studies. In most cases of SrTiO3 research, Nb-doping is applied on the SrTiO3 surface in order to characterize electrical properties with a negligible effect of contact potential between SrTiO3 and overlayer. On the other hand, the presence of doping can possibly interfere with a correct interpretation of the surface defect states, which become critical to apprehend the electrical properties of heterostructures. In this report, the undoped SrTiO3 (001) surface is investigated utilizing ambient-pressure XPS (AP-XPS) and low energy electron diffraction (LEED). We identified the complete chemical/structural/electronic states of O and Sr vacancies on the undoped SrTiO3 surface from ultra-high vacuum (UHV, <10−9 mbar) to O2 gas pressure of 0.1 mbar conditions. Under oxygen pressure conditions, chemically stable SrO1+x surface oxide with a c(6 × 2) superstructure is formed, generating electron depletion and band bending, i.e., the formation of a space charge layer underneath the surface. On the other hand, under UHV, the surface oxide comes from the O vacancy, which has different electronic properties from those of Sr vacancy-related oxides.
1. Introduction
Complex oxide heterostructures with an ABO3-type perovskite structure have shown remarkable physical phenomena, which include colossal magnetoresistance (CMR), metal–insulator transition (MIT), high Tc superconductivity, and two-dimensional electron gas (2DEG).1–7 Although the interfacial layers where different complex oxides form are mainly responsible for these exotic features, the exact functionality or working mechanism of oxides at the interface layer is yet fully understood.1–3,8–11 Having ABO3-type perovskite structures, SrTiO3 has suitable lattice mismatch for many overlayer oxides with ideal chemical/thermal stability from centrosymmetric cubic structures and has been a popular choice for many important heterostructures,12–15e.g., LaTiO3/SrTiO3 for quasi-two-dimensional electron gas systems, ZrO2:Y2O3/SrTiO3 for colossal ionic conductivity oxides, and CaCuO2/SrTiO3 for high temperature superconductors.7,16,17 From the results of many previous research studies on heterostructures with SrTiO3, most of the interfacial properties such as inter-diffusion, symmetry breaking, charge rearrangement, and interfacial strain, are known to have critical effects on the physical/chemical, mechanical, and electrical properties of the system.1–3,7,16,18 Consequently, the preparation and control of the interfacial layer with atomic level precision becomes critical to successful research on SrTiO3.1–3,8,19Among various interfacial properties listed above, the presence and roles of elemental vacancies become important to interpret the physical phenomena.20,21 For example, the O vacancy (VO) generated during pulsed laser deposition (PLD) growth is known as the source of increased conductivity.22 The PLD process below oxygen pressure of 10−6 mbar can generate VO on the substrate, which then converts SrTiO3, a wide band gap (∼3.2 eV) insulator, into a good conductor with a resistivity of <100 mΩ cm.12,23 On the other hand, the creation of Sr vacancies (VSr) is also known to occur under oxygen rich PLD conditions.2,24,25 Under the presence of oxygen species on the SrTiO3 surface, Sr atoms make surface migration to form SrO oxide at a cost of electrons in the subsurface region, i.e., formation of an electron depletion layer near the surface.2,24,26,27 In the case of VSr formation, the surface resistance increases, affecting the electrical properties of the interfacial layer. In fact, both types of VO or VSr can occur simultaneously during the PLD process in which an oxygen environment and elevated temperature are required.2,25 Thus, understanding the roles of these vacancies (VO and VSr), so-called “defect chemistry”, has become very important to achieve reliable functionality of SrTiO3 heterostructure systems.
Previously, the creation and role of VSr were investigated by many research groups. Marchewka et al. observed the presence of a depletion layer at the Fe:SrTiO3/Nb:SrTiO3 interface associated with acceptor-type interface defects, VSr.28 With the analysis of electron holography and numerical calculations, the creation of VSr and electron depletion layer were analyzed with changes in potential gradient at the interface. Also, with dynamic numerical simulations of high temperature MIT on n-type SrTiO3, Meyer et al. explained the relationship between the surface charge region and VSr.27 The simulation indicates that VSr plays an important role in connection of electrical conductivity of the n-SrTiO3 substrate. In the meantime, the role of VO has been also explored by many research groups. Kim et al. examined the correlation between structural phase transition (SPT) and VO state in the SrRuO3/SrTiO3 system using in situ X-ray diffraction (XRD) and ambient pressure X-ray photoelectron spectroscopy (AP-XPS).29 They demonstrated that the VO formed at the SrRuO3/SrTiO3 interface determines the structural phase of the overlayer SrRuO3 film. Moreover, with the application of isotope O18 on SrTiO3, Lippert et al. identified the correlation between oxygen distribution and conductivity, indicating the critical roles of VO at the LaAlO3/SrTiO3 interface.30 Recently, with the aim of controlling VO in SrTiO3, Kang et al. demonstrated a new idea of growing an epitaxial thin film utilizing a SrTiO3 substrate as an oxygen reservoir.31 By controlling the oxygen content from the pre-substrate annealing process, the distribution of VO concentration near the interfacial layer is optimized. That is, the SrTiO3 substrate is utilized to provide a tunable oxygen environment for overlayer film growth. In particular, they pointed out the importance of the chemical environment during thin film fabrication, emphasizing the role of chemical state of substrate in generating accurate stoichiometry to the overlayer. Overall, the access to well-defined defect states on the SrTiO3 substrate has become very important and critical to figure out the interfacial properties of complex oxide heterostructures based on SrTiO3. On the other hand, Basletic et al., from the spatial distribution of charge carriers on the LaAlO3/SrTiO3 interface layer with atomic force microscopy (AFM), showed that electron gas mobility is not affected by the degree of O vacancies, suggesting the alternate charge-transfer mechanism as a valid idea.32
In this report, to find out the role of the surface state of the substrate in the film growth process, i.e., the role of defect states, we investigate the chemical/structural/electronic properties of an undoped SrTiO3 (001) surface under film deposition conditions with application of AP-XPS and low energy electron diffraction (LEED). Previously, Andrä et al. utilized AP-XPS to investigate the chemical states of the electron depletion layer of the Nb-doped SrTiO3 surface.33,34 While their results show the evidence of the electron depletion layer due to the Sr segregation, the segregation of Sr is estimated by the presence of chemical shifts of XP spectra. In addition, Nb-doped SrTiO3 is used to provide an electron reservoir for necessary access to XPS measurements.35,36 However, it is previously reported that donor-doped SrTiO3 can generate modified effective mass for conductivity, which can possibly affect the formation of the depletion layer.37 In fact, it is a well-known fact that the doping process can make significant modification not only in the surface structure, but also in surface chemical/electronic properties. To avoid this uncertainty, an undoped SrTiO3 substrate is employed for the study of O and Sr vacancies under ultra-high vacuum (UHV, <10−9 mbar) to O2 gas pressure of 0.1 mbar condition. In the comparison of chemical composition and surface structure under various atmospheric conditions, the sign of both O and Sr vacancies is clearly observed. While both vacancies produce almost identical surface chemical states with similar depth distribution, the density of states near the Fermi level (EF) reveals the clear difference between the two vacancies, indicating different electronic states.
2. Experimental
Undoped SrTiO3 (001) single crystalline films (10 × 10 × 0.5 mm3, MaTeck GmbH) were grown by the flame fusion method. To achieve an atomically flat and TiO2 terminated surface, an acid-etchant-free technique, combination of deionized (DI) water leaching and annealing process, was employed.38 The film was annealed first at 1000 °C for 1 hour under atmospheric conditions and then rinsed with DI water for 30 sec at room temperature (RT) to dissolve the ionic bonded SrO layer.38 After two cycles of the process, the topography of prepared SrTiO3, using an AFM (XE-100, Park Systems), showed a step-terrace surface structure. (Fig. S1, ESI†) Later, an ordered surface of simple cubic (001) structure of SrTiO3 surface was verified with LEED measurements (ErLEED 150, Specs GmbH).Synchrotron-based AP-XPS measurements were carried out at PLS-II (8A2 beamline), Korea. The AP-XPS system consisting of the differentially pumped electrostatic lens and electron analyzer (PHOIBOS NAP 150, SPECS) allows the measurement of XP spectra up to a gas pressure of 25 mbar.39 To characterize the surface chemical states of the SrTiO3 (001) film at elevated temperature, in situ measurements were conducted during the thermal annealing process, up to 600 °C under both UHV and O2 gas pressure of 0.1 mbar conditions, which generated surface VO or VSr. An IR laser (dst11, OSTECH) was used for the annealing process.
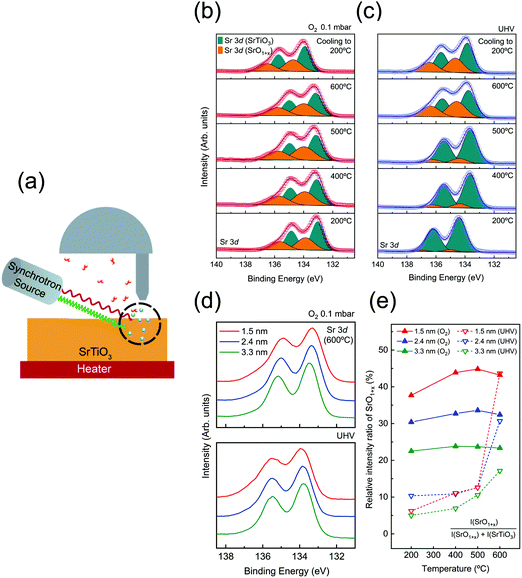
All characteristic core level spectra of SrTiO3 (O 1s, Ti 2p, and Sr 3d) were measured. In order to obtain depth profile information, i.e., distribution of the surface space charge layer, depth-resolved AP-XPS measurements with variable X-ray photon energies were performed for 3 inelastic mean-free paths (IMFPs, λ = 0.5, 0.8, and 1.1 nm). For each probing depth (3λ), 1.5, 2.4, and 3.3 nm, the formula of Tanuma, Powell, and Penn (TPP) 2M was used to define the photon energies.40 The photon energies used for each probing depth measurement are specified in Table S1 (ESI†). An experimental scheme of depth-resolved AP-XPS is displayed in Fig. 1(a).
It is to be noted that the X-ray-irradiated undoped SrTiO3 sample experiences the space-charge effect due to the electrically insulating characteristics of SrTiO3 near RT. In Table S2 (ESI†), the conductivity values of SrTiO3 at our experimental temperature are estimated based on previous literature values and conductivity formula, σ = CT−3/2exp(−Eg/2kBT),41–43 where C is a temperature-independent constant, T is the temperature, Eg is the band gap, and kB is a Boltzmann constant. In conventional XPS measurements, the space charge effect starts to occur when conductivity becomes less than 10−10 Ω−1 m−1.44 According to Table S2 (ESI†), it is clear that the space charge effect is fully compensated when the temperature of the SrTiO3 substrate reaches above 300 °C. Thus, all of our AP-XPS results above 300 °C are free from the charging problem. To analyze the XP spectra, the binding energy axis of all XP spectra was calibrated by the literature value of C 1s (284.5 eV) from intrinsic carbon species contained in the sample.45 The position of the C 1s peak before the energy calibration can be checked in Table S3 (ESI†). However, as C species no longer exist above 500 °C under an oxygen environment, an Au foil attached to the sample was utilized for the XPS calibration purpose. That is, the binding energy peak of Au 4f7/2 (84.0 eV) was used as a reference at 500 °C or above. In fact, under the condition in which charging is fully compensated while the carbon species remain on the surface, i.e., sample temperatures between 300 °C and 500 °C, both C 1s and Au 4f7/2 were utilized for calibration of binding energy, showing a consistent result with each other. The necessity and importance of careful assignment of binding energy to core levels can be further found in a previous report of Greczynski et al.46
3. Results and discussion
To begin with, AP-XPS measurements were performed during the annealing procedure, at 200, 400, 500, and 600 °C, and after cooling down (200 °C). All characteristic core level spectra under O2 0.1 mbar (red) and UHV (blue) conditions at a probing depth of 1.5 nm are displayed in Fig. S2 (ESI†). If there is any charging effect due to photoirradiation, the binding energy position of XP spectra will be shifted to the higher binding energy direction with a distorted line shape. However, the XP spectra in Fig. S2 (ESI†) show no apparent sign of the charging effect. At 200 °C, the binding energy of O 1s and Sr 3d is slightly shifted to a higher binding direction, yet the line shape of the spectra is identical to the rest of the spectra at higher temperature. As explained in Table S2 (ESI†), the charging effect was sufficiently compensated when the SrTiO3 film was annealed above 300 °C. Also, in Fig. S2(a–f) (ESI†), there are a couple of spectral dissimilarities between O2 pressure and UHV conditions. One is the difference in binding energy position between oxygen and UHV conditions, i.e., binding energy offset. The origin of the offset in binding energy will be discussed later. The other is the change of spectral line shape, particularly in Sr 3d spectra. When the temperature reaches 600 °C under UHV, the spectral weight of Sr 3d spectra at the higher binding energy side is significantly enhanced. In the case of annealing under O2 pressure, the broadening of Sr 3d spectra started to appear even at 200 °C. This feature in Sr 3d spectra will be also examined further later with discussion on the formation of VO and VSr.In order to characterize the variation of chemical composition during annealing, Sr 3d spectra are analyzed in Fig. 1(b and c). Each Sr 3d spectrum is obtained at a surface sensitive depth of 1.5 nm, under O2 pressure of 0.1 mbar [Fig. 1(b)] and UHV conditions [Fig. 1(c)]. The as-acquired spectra are plotted as red (blue) hollow symbols for the oxygen (UHV) environment. All spectra are de-convoluted with two doublets originating from SrTiO3 and SrO1+x components, respectively. The SrTiO3 component (cyan) indicates Sr bonding in the SrTiO3 lattice while the SrO1+x component (orange) indicates Sr oxide on the topmost surface.33,47,48 For the spectral fitting procedure, two Voigt doublets with a fixed branching ratio and spin orbit splitting are applied after the Shirley background is subtracted. The detailed fitting parameters are shown in Table S4 (ESI†).
In the case of the oxygen annealing process in Fig. 1(b), the presence of SrO1+x and SrTiO3 components can be found in all temperature regions. As 0.1 mbar of O2 gas is introduced, the surface oxide is formed on the SrTiO3 film surface even at a temperature as low as 200 °C. In contrast, under UHV conditions, the sign of SrO1+x surface oxide is very minimal at 200 °C, as shown in Fig. 1(c). This comparison of Sr 3d spectra between oxygen pressure and UHV implies that the formation of the SrO1+x component is not coming from air exposure of the sample. Rather, it indicates that introduced O2 gas molecules are dissociated and bound to Sr on the surface even at 200 °C. Fig. 1(b) shows that the SrO1+x surface oxide formed under oxygen pressure remains constant without much changes until 600 °C. In the case of UHV conditions, the formation of surface oxide starts to appear only at 600 °C, as shown in Fig. 1(c). Under both conditions, the surface oxide remains on the surface after the temperature is cooled down to 200 °C.
To compare the chemical states of Sr oxide with varied probing depth under oxygen and UHV environments, Sr 3d spectra (600 °C) at a probing depth of 1.5 (red), 2.4 (blue), and 3.3 nm (green), are plotted in Fig. 1(d). It clearly shows that both figures of Fig. 1(d) show the higher intensity of SrO1+x in the 1.5 nm region, indicating that the formation of surface oxide occurs at the surface. Furthermore, in order to have a quantitative comparison of SrO1+x surface oxide evolution, the relative intensity ratio of the SrO1+x component is plotted together as a function of annealing temperature, as shown in Fig. 1(e). The relative intensity ratio of the SrO1+x component [SrO1+x component area/total Sr 3d spectral area] is plotted on each fitted Sr 3d spectrum. Again, it is to be noted that chemical compositions are clearly different at the first annealing temperature step, 200 °C, between two different atmosphere conditions. In the 1.5 nm region, the relative intensity value of SrO1+x is ∼38% under oxygen conditions while that of UHV is only ∼6%. Under an O2 environment, the relative intensity ratio of SrO1+x remains similar throughout the entire temperature range, i.e., no sign of subsurface evolution to surface SrO1+x oxide. A closer look at Fig. 1(e) shows that the surface oxides in the 1.5 nm region continue to increase while the oxide components at 2.4 nm and 3.3 nm remain almost constant, revealing the sign of impeding oxygen diffusion. On the other hand, the intensity ratio of SrO1+x under UHV conditions shows no significant changes until the temperature reaches 600 °C. Under UHV conditions, a rapid increase of SrO1+x surface oxide from 6% (at 200 °C) to 45% (at 600 °C) was observed at 1.5 nm probing depth. An interesting point is that the relative intensity ratio of SrO1+x oxide of UHV conditions matches well with that of O2 environment conditions at 600 °C. In quantitative comparison of the SrO1+x spectra of O2 and UHV environments at 600 °C, relative amounts of SrO1+x are almost the same at a probing depth of 1.5 nm, i.e., ∼43%. While the other two probing depths show a slight difference, the difference is clearly reduced. To illustrate this point, Sr 3d spectra at a probing depth of 1.5 nm (T = 600 °C) from two conditions are plotted together in Fig. S3 (ESI†). Fig. S3 (ESI†) shows that the surface oxides formed under two different conditions, UHV and oxygen pressure, are having almost identical chemical states.
While the chemical states of the surface SrO1+x layer in Fig. S3 (ESI†) are similar, the formation process of oxides is very different. In the case of the oxygen annealing step, it can be interpreted that the stable SrO1+x passive layer is formed at topmost surface from the interaction of externally provided dissociated oxygen atoms with the surface migrated Sr atom from bulk, which in turn inhibits oxygen diffusion into the bulk side.27,49 On the other hand, the UHV annealing process, reducing condition for most of the metal oxide system, is expected to create oxygen defect states, as reported in many previous SrTiO3 studies.2,22,25 Until the temperature below 500 °C, no significant change in Sr 3d spectra is found across all depth ranges. However, when the temperature reaches 600 °C under UHV, a chemically stable SrO1+x surface oxide is formed on the topmost surface as shown in Sr 3d spectra in Fig. 1(c). The origin of the SrO1+x surface oxide will be provided later with the discussion of LEED. The VO feature can be also identified in Ti 2p and valence band (VB) spectra. The gray shaded area in Fig. S4(d) and S5 (ESI†) clearly reveals the enhancement of spectral weight as temperature increases, corresponding to emergence of Ti3+ component and formation of VO during the UHV annealing process. Overall, during the UHV annealing process, the TiO2 layer in SrTiO3 is gradually reduced and VO is left behind.50,51
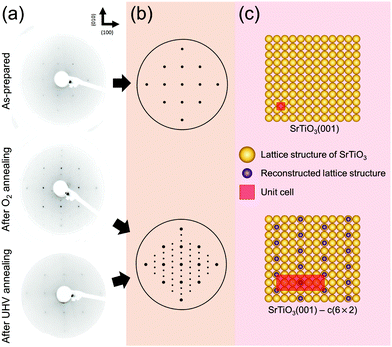
Next, in order to identify any changes in surface structural ordering after surface chemical rearrangement by the previous annealing procedure under both oxygen and UHV conditions, the measurements of LEED are carried out immediately after the AP-XPS measurements without the exposure to air, i.e., the measurement of in situ LEED. Fig. 2(a) displays the LEED patterns of the as-prepared, oxygen annealed, and UHV annealed SrTiO3 (001) surface. The annealing temperature is 600 °C. The characteristics of the (001) oriented cubic structure are explicitly identified in all patterns. Compared with the LEED pattern of the “as-prepared” SrTiO3 (001) surface, in principle both LEED patterns of “after O2 annealing” and “after UHV annealing” reveal the superstructure pattern, although the superstructure pattern is slightly blurred for the “after UHV annealing” image. For accurate structural analysis, all systematic distortions in LEED images in Fig. 2(a) are corrected and the patterns are simulated by the numerical fitting procedure as displayed in Fig. 2(b).52 Then, the lattice structures in real space are illustrated in Fig. 2(c)via inverse Fourier transform of Fig. 2(b). The yellow circles represent the basic lattice structure of SrTiO3 (001), and the purple circles represent the lattice structure of the reconstructed topmost surface from annealing. The unit cell is defined as a red square in Fig. 2(c).
As discussed before, SrO1+x surface oxide is formed on the SrTiO3 topmost surface during both O2 and UHV annealing at 600 °C. In the LEED pattern of “after O2 annealing”, there exist sub-patterns shown as low intensity spots between the strong (001) spots. The presence of new superstructure patterns shows that stable SrO1+x clusters form an ordered c(6 × 2) surface structure on SrTiO3 (001). Also, in the case of “after UHV annealing”, an identical c(6 × 2) superstructure pattern is formed on SrTiO3 (001). However, low intensity of the superstructure pattern in LEED indicates the presence of a less ordered surface structure during UHV annealing. In fact, it is well known that the concentration of surface defects increases under UHV annealing, which can blur the LEED image.
Previously, several numbers of surface reconstructions of SrTiO3 (001) have been reported, such as (1 × 1), (2 × 1), (4 × 4), c(4 × 2), c(4 × 4), and 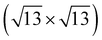 -R33.7°, including c(6 × 2).53,54 Many studies using surface sensitive techniques such as AFM, scanning tunneling microscopy (STM), reflection high-energy electron diffraction (RHEED) and density functional theory (DFT) were carried out to figure out these various reconstructed phases.55–60 Nevertheless, their conclusions are still unclear due to their instability and extreme sensitivity to thermodynamic conditions. In regard to the c(6 × 2) phase, the presence of c(6 × 2) reconstruction on SrTiO3 (001) from UHV and oxygen annealing was observed with RHEED and LEED study.60,61 Our Sr 3d LEED results clearly show the stable c(6 × 2) reconstruction taking place on the SrTiO3 (001) surface by both O2 (0.1 mbar) and UHV (<10−9 mbar) annealing at 600 °C, i.e., the formation of a nearly identical surface structure for both conditions. To our knowledge, no direct comparison of LEED patterns has been made between oxygen and UHV annealed SrTiO3 (001) surfaces.
-R33.7°, including c(6 × 2).53,54 Many studies using surface sensitive techniques such as AFM, scanning tunneling microscopy (STM), reflection high-energy electron diffraction (RHEED) and density functional theory (DFT) were carried out to figure out these various reconstructed phases.55–60 Nevertheless, their conclusions are still unclear due to their instability and extreme sensitivity to thermodynamic conditions. In regard to the c(6 × 2) phase, the presence of c(6 × 2) reconstruction on SrTiO3 (001) from UHV and oxygen annealing was observed with RHEED and LEED study.60,61 Our Sr 3d LEED results clearly show the stable c(6 × 2) reconstruction taking place on the SrTiO3 (001) surface by both O2 (0.1 mbar) and UHV (<10−9 mbar) annealing at 600 °C, i.e., the formation of a nearly identical surface structure for both conditions. To our knowledge, no direct comparison of LEED patterns has been made between oxygen and UHV annealed SrTiO3 (001) surfaces.
To look into the details of chemical states of surface oxide, the binding energy position of core level spectra of SrTiO3 is carefully monitored. Fig. 3(a) exhibits the characteristic binding energy values of the SrTiO3 lattice component during both oxygen and UHV thermal annealing processes. The probing depth of all spectra was 1.5 nm, providing the most surface sensitive information in our measurement. The binding energy positions of O 1s, Ti 2p3/2, and Sr 3d5/2 are plotted as black, red, and blue, respectively, and the solid (dotted) line indicates the binding energy positions under O2 (UHV) annealing conditions. The binding energy positions of each spectrum can be found in Table S5 (ESI†). In Fig. 3(a), the binding energy offset of all elements between oxygen and UHV environments can be noticed, as discussed with Fig. S2 (ESI†). Except for the case of 200 °C where the possible charging issues could occur, the binding energy positions of all elements under oxygen atmosphere are lower than those under UHV by as much as ∼0.54 eV in all temperature ranges, shown under the gray shaded area in Fig. 3(a). The identified values of the offset are shown in Table S5 (ESI†). As one example of this offset, Sr 3d spectra measured at 500 °C under two different conditions are compared in Fig. 3(b). Fig. 3(b) clearly shows that there exists not only a difference in spectral shape due to the difference in chemical composition, but the offset of binding energy position under two atmospheric conditions.
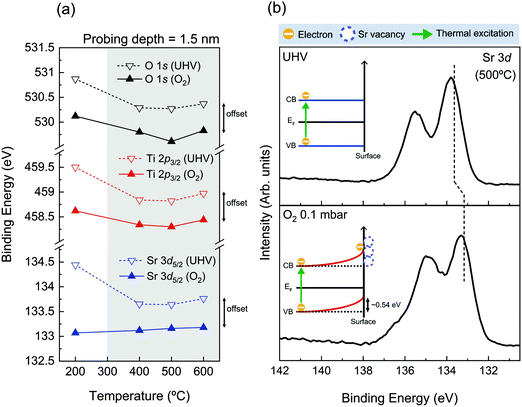 | ||
| Fig. 3 (a) Characteristic binding energy positions of the SrTiO3 lattice component as a function of annealing temperature. [Each core level O 1s, Ti 2p3/2, and Sr 3d5/2 is shown in black, red, and blue colors while the solid (dotted) line indicates the binding energy positions under O2 0.1 mbar (UHV) annealing conditions.] (b) Sr 3d spectra under UHV (up) and O2 (down) environments at 500 °C for the probing depth of 1.5 nm taken from Fig. 1(c and b). The dotted vertical lines in (b) indicate the binding energy positions of the SrTiO3 lattice component. The illustrations of band alignment under both annealing conditions are displayed in the inset of (b), respectively. | ||
In fact, the presence of the binding energy offset in the oxygen annealing process can be correlated with the formation of the space charge layer discussed in our introduction. According to the previous reports on space charge layer study on the Nb-doped SrTiO3 surface, VSr is generated while consuming electrons on the surface during the O2 annealing process,33,34 generating 0.55–0.60 eV core level shift in AP-XPS measurements. While the amount of this core level shift is almost identical to what is observed in Fig. 3, the origin is different. In the case of the Nb-doped SrTiO3 surface, the electron source for the surface charge layer, i.e. electron depletion layer, was provided from the substrate. Here, in the case of our undoped SrTiO3 system, electrons can be provided sufficiently by thermal excitation at temperature above 300 °C. In the O2 annealing process, thermally excited electrons are trapped by the VSr at the surface, which forms an electron depletion layer near the surface. Moreover, the mismatch of electron density between the surface electron depletion layer and bulk can create the VB bending near the Fermi level. The schematic of upward band bending during O2 annealing is illustrated in the inset of Fig. 3(b) in the rigid band model. Furthermore, this band bending phenomenon is identified by VB analysis in Fig. S6 (ESI†). The positions of the valence band maximum (VBM) under O2 conditions as a function of annealing temperature are displayed in Fig. S6 (ESI†). As annealing temperature increases from 200 °C up to 600 °C, the position of the VBM is gradually shifted up to ∼0.38 eV. Since a sufficient electron depletion layer has not yet formed due to less thermal electrons at 200 °C, the VB hardly moves. Then, the position of the VBM is shifted to a lower binding energy direction as temperature increases, indicating the onset of the surface space charge layer. At higher annealing temperature, the upward band bending becomes more pronounced. In the meantime, the important thing to be checked before the characterization of the space charge layer is the scale of Debye length. As can be found in Table S6 (ESI†), the length scale of the space charge layer is much smaller than Debye length in our condition, demonstrating that the above discussions on the nature of the space charge layer are valid.
On the other hand, the electron depletion and band bending could also occur under UHV conditions as our AP-XPS and LEED results confirm the formation of the SrO1+x surface under the UHV annealing process. However, as described before, when the temperature reaches 600 °C under UHV conditions, the TiO2 layer starts to get reduced and VO is formed as shown in Fig. S4(d) and S5 (ESI†). In this case, extra sources of electrons are generated, limiting the formation of the electron depletion layer and band bending at the surface. Overall, the presence of binding energy offset in Fig. 3 indicates that completely different surface electronic structures are formed in each annealing process. Up to now, we have shown that the chemical states and structures of surface SrO1+x oxide are very much similar in both UHV and oxygen annealing processes. Yet, the results of Fig. 3 clearly show that the difference of the electronic structures is an important parameter that can define the characteristics of surface defect states of SrTiO3 (001).
In Fig. 4, our understanding of surface reconstruction on SrTiO3 (001) during oxygen annealing is illustrated. Initially, O2 gas molecules (red circles) are dissociated on the SrTiO3 surface under oxygen atmosphere conditions. As the temperature increases, Sr atoms underneath the surface are pulled over to the outermost layer by external oxygen (Fig. 4(b) side view) and SrO1+x clusters are formed on the surface with c(6 × 2) surface ordering as shown in Fig. 4(b) top view. The surface chemical redox reaction is described at the top of Fig. 4(b) top view using Kröger–Vink notations. It should be noted that VSr is formed with SrO1+x surface oxide on the surface while consuming electrons under an oxygen atmosphere, implying the formation of a space charge layer. On the other hand, during UHV annealing, there is considerable SrO1+x formation only when the temperature reaches 600 °C. Again, during UHV annealing, SrO1+x surface oxide is formed on the topmost surface with a c(6 × 2) reconstruction phase, as explained through the LEED analysis in Fig. 2. Although a few models have been suggested, which focus on the formation of vacancies and their role in atomic rearrangement between Sr and O atoms during the annealing process, the exact understanding on the origin of surface reconstruction for SrTiO3 (001) under UHV conditions is still in debate.53,57,59–61 Our result from the UHV annealing process suggests that the surface reconstruction occurs as VO and Ti vacancies (VTi) interact with Sr atoms at the top surface, resulting in chemically stable SrO1+x surface oxide with a c(6 × 2) surface restructure.
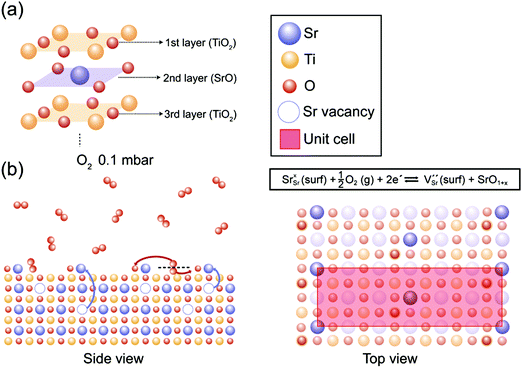 | ||
| Fig. 4 (a) The schematic illustration of the layer structure from the top surface of the as-prepared SrTiO3 (001). (b) The proposed surface redox process in side and top views during the annealing under O2 0.1 mbar. [Sr, Ti, and O atoms are indicated as blue, yellow and red circles, respectively, and each vacancy is expressed as a dotted circle of the corresponding color.] Top view displays the formation of SrO1+x with a c(6 × 2) superstructure confirmed by LEED analysis in Fig. 2(c). The surface redox reaction formula describes the formation of VSr and SrO1+x while consuming electrons under O2 annealing conditions. | ||
Finally, we would like to make comments on the doped-SrTiO3 system. Compared to the previous result of the Nb-doped SrTiO3 surface,43 our results on the undoped SrTiO3 surface show similar degrees of band bending effect, ∼0.54 eV, showing that the degree of the charge depletion layer is similar. However, in the case of Nb-doped SrTiO3, the previous group obtained the degree of band bending from the comparison of core level spectra of different probing depths. In our case of undoped SrTiO3, the degree of band bending is obtained from direct comparison between UHV and oxygen annealing conditions, which provides absolute pressure-dependent feature in AP-XPS. In addition, the core level positions of the Sr 3d peak of Nb-doped SrTiO3 show a gradual shift to a higher binding energy side as the probing depth increases while our undoped SrTiO3 surface shows almost constant binding energy in the entire spectra [Fig. 1], displaying a clear difference of chemical states from the surface to bulk layer.
4. Conclusions
With depth resolved AP-XPS and LEED analysis, we compared the chemical/structural/electronic states of the undoped SrTiO3 (001) surface under UHV and O2 pressure of 0.1 mbar conditions to identify the role of the surface state of the substrate. Our observations reveal that, under an oxygen environment, Sr elements are being pulled over to the outermost layer and chemically stable surface oxide, SrO1+x with a c(6 × 2) superstructure, is formed while forming an electron depletion layer underneath the surface. Furthermore, the modification of the electronic structure due to the electron depletion layer is confirmed as band bending near the Fermi level starts to appear. On the other hand, under UHV annealing conditions, the vacancy-related SrO1+x surface oxide formed at ∼600 °C. The SrO1+x surface oxide is chemically and structurally identical to those in the oxygen environment, yet the origin of oxide formation is different. Our findings suggest that the surface electronic structure of the substrate has a greater influence on the properties of complex oxide heterostructures than other parameters. This work provides a deeper understanding on the surface charge layer of undoped SrTiO3 (001), which can be useful for study of the SrTiO3-based complex oxide heterostructure.Author contributions
Hojoon Lim and Chanyang Song: conceptualization, experiment, data acquisition, formal analysis, and writing – original draft & editing. Minsik Seo, Dongwoo Kim, Moonjung Jung, Habin Kang, Seunghwan Kim, Kyung-Jae Lee, Youngseok Yu, and Geonhwa Kim: experiment and formal analysis. Ki-jeong Kim and Bongjin Simon Mun: supervision, writing – review & editing, formal analysis, funding acquisition, and project administration.Conflicts of interest
There are no conflicts to declare.Acknowledgements
Financial support was provided by the National Research Foundation of Korea (NRF-2019R1A2C2008052, NRF-2015R1A5A1009962) and the GIST Research Institute Grant funded by the Gwangju Institute of Science and Technology (GIST) GRI-2021. Experiments at PLS-II were supported in part by MSICT and POSTECH (NRF-2018R1D1A1B07048177, NRF-2019M3D1A1079309).References
- Y. Tokura, M. Kawasaki and N. Nagaosa, Nat. Phys., 2017, 13, 1056–1068 Search PubMed.
- J. Zhu, J. W. Lee, H. Lee, L. Xie, X. Pan, R. A. De Souza, C. B. Eom and S. S. Nonnenmann, Sci. Adv., 2019, 5, 1–10 Search PubMed.
- P. Zubko, S. Gariglio, M. Gabay, P. Ghosez and J. M. Triscone, Annu. Rev. Condens. Matter Phys., 2011, 2, 141–165 Search PubMed.
- C. H. Ahn, K. M. Rabe and J. M. Triscone, Science, 2004, 303, 488–491 CrossRef CAS PubMed.
- A. Brinkman, M. Huijben, M. Van Zalk, J. Huijben, U. Zeitler, J. C. Maan, W. G. Van Der Wiel, G. Rijnders, D. H. A. Blank and H. Hilgenkamp, Nat. Mater., 2007, 6, 493–496 CrossRef CAS PubMed.
- A. Gozar, G. Logvenov, L. F. Kourkoutis, A. T. Bollinger, L. A. Giannuzzi, D. A. Muller and I. Bozovic, Nature, 2008, 455, 782–785 CrossRef CAS PubMed.
- A. Ohtomo and H. Y. Hwang, Nature, 2004, 427, 423–426 CrossRef CAS PubMed.
- D. K. Bediako, M. Rezaee, H. Yoo, D. T. Larson, S. Y. F. Zhao, T. Taniguchi, K. Watanabe, T. L. Brower-Thomas, E. Kaxiras and P. Kim, Nature, 2018, 558, 425–429 CrossRef CAS PubMed.
- T. Kim, S. Fan, S. Lee, M.-K. Joo and Y. H. Lee, Sci. Rep., 2020, 10, 1–8 CrossRef PubMed.
- Y.-Y. Lu, C.-R. Guo, H.-L. Yeh, H.-W. Chen, C.-C. Kuo, J.-H. Hsu, J. Jhou, Y.-T. Huang, S.-H. Hsieh, C.-H. Chen, C.-H. Ho, R. Sankar and F.-C. Chou, ACS Appl. Nano Mater., 2020, 3, 11769–11776 CrossRef CAS.
- E. Pomerantseva and Y. Gogotsi, Nat. Energy, 2017, 2, 1–6 Search PubMed.
- Y. Y. Pai, A. Tylan-Tyler, P. Irvin and J. Levy, Rep. Prog. Phys., 2018, 81, 036503 CrossRef PubMed.
- O. F. Shoron, S. Raghavan, C. R. Freeze and S. Stemmer, Appl. Phys. Lett., 2017, 110, 232902 CrossRef.
- A. Verma, S. Raghavan, S. Stemmer and D. Jena, Appl. Phys. Lett., 2015, 107, 2–6 Search PubMed.
- C. S. Koonce, M. L. Cohen, J. F. Schooley, W. R. Hosler and E. R. Pfeiffer, Phys. Rev., 1967, 163, 380 CrossRef CAS.
- J. Garcia-Barriocanal, A. Rivera-Calzada, M. Varela, Z. Sefrioui, E. Iborra, C. Leon, S. J. Pennycook and J. Santamaria, Science, 2008, 321, 676–680 CrossRef CAS PubMed.
- D. Di Castro, C. Cantoni, F. Ridolfi, C. Aruta, A. Tebano, N. Yang and G. Balestrino, Phys. Rev. Lett., 2015, 115, 1–5 CrossRef PubMed.
- N. Nakagawa, H. Y. Hwang and D. A. Muller, Nat. Mater., 2006, 5, 204–209 CrossRef CAS.
- K. L. Tai, C. W. Huang, R. F. Cai, G. M. Huang, Y. T. Tseng, J. Chen and W. W. Wu, Small, 2020, 16, 1–10 Search PubMed.
- C. Xie, D. Yan, H. Li, S. Du, W. Chen, Y. Wang, Y. Zou, R. Chen and S. Wang, ACS Catal., 2020, 10, 11082–11098 CrossRef CAS.
- J. Maier, Angew. Chem., Int. Ed. Engl., 1993, 32, 313–335 CrossRef.
- F. Gunkel, D. V. Christensen, Y. Z. Chen and N. Pryds, Appl. Phys. Lett., 2020, 116, 120505 CrossRef CAS.
- S. A. Lee, H. Jeong, S. Woo, J. Y. Hwang, S. Y. Choi, S. D. Kim, M. Choi, S. Roh, H. Yu, J. Hwang, S. W. Kim and W. S. Choi, Sci. Rep., 2016, 6, 1–10 CrossRef CAS PubMed.
- M.-A. Rose, B. Šmid, M. Vorokhta, I. Slipukhina, M. Andrä, H. Bluhm, T. Duchoň, M. Ležaić, S. A. Chambers, R. Dittmann, D. N. Mueller and F. Gunkel, Adv. Mater., 2021, 33, 2004132 CrossRef CAS PubMed.
- P. P. Balakrishnan, M. J. Veit, U. S. Alaan, M. T. Gray and Y. Suzuki, APL Mater., 2019, 7, 011102 CrossRef.
- R. Meyer, R. Waser, J. Helmbold and G. Borchardt, Phys. Rev. Lett., 2003, 90, 105901 CrossRef PubMed.
- R. Meyer, A. F. Zurhelle, R. A. De Souza, R. Waser and F. Gunkel, Phys. Rev. B, 2016, 94, 1–19 Search PubMed.
- A. Marchewka, D. Cooper, C. Lenser, S. Menzel, H. Du, R. Dittmann, R. E. Dunin-Borkowski and R. Waser, Sci. Rep., 2014, 4, 1–6 Search PubMed.
- D. Kim, H. Lim, S. S. Ha, O. Seo, S. S. Lee, J. Kim, K. Kim, L. Perez Ramirez, J.-J. Gallet and F. Bournel, et al. , J. Chem. Phys., 2020, 152, 34704 CrossRef CAS PubMed.
- C. W. Schneider, M. Esposito, I. Marozau, K. Conder, M. Doebeli, Y. Hu, M. Mallepell, A. Wokaun and T. Lippert, Appl. Phys. Lett., 2010, 97, 2008–2011 CrossRef.
- K. T. Kang, B. Zhang, Y. Sharma, B. Paudel, H. Wang, P. Dowden and A. Chen, Appl. Phys. Lett., 2020, 117, 151601 CrossRef CAS.
- M. Basletic, J.-L. Maurice, C. Carrétéro, G. Herranz, O. Copie, M. Bibes, É. Jacquet, K. Bouzehouane, S. Fusil and A. Barthélémy, Nat. Mater., 2008, 7, 621–625 CrossRef CAS PubMed.
- M. Andrä, H. Bluhm, R. Dittmann, C. M. Schneider, R. Waser, D. N. Mueller and F. Gunkel, Phys. Rev. Mater., 2019, 3, 1–9 Search PubMed.
- M. Andrä, F. Dvořák, M. Vorokhta, S. Nemšák, V. Matolín, C. M. Schneider, R. Dittmann, F. Gunkel, D. N. Mueller and R. Waser, APL Mater., 2017, 5, 56106 CrossRef.
- A. Spinelli, M. A. Torija, C. Liu, C. Jan and C. Leighton, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 1–14 CrossRef.
- C. Rodenbücher, M. Luysberg, A. Schwedt, V. Havel, F. Gunkel, J. Mayer and R. Waser, Sci. Rep., 2016, 6, 1–8 CrossRef PubMed.
- W. Wunderlich, H. Ohta and K. Koumoto, Phys. B, 2009, 404, 2202–2212 CrossRef CAS.
- J. G. Connell, B. J. Isaac, G. B. Ekanayake, D. R. Strachan and S. S. A. Seo, Appl. Phys. Lett., 2012, 101, 98–101 CrossRef.
- G. Kim, Y. Yu, H. Lim, B. Jeong, J. Lee, J. Baik, B. S. Mun and K. Kim, J. Synchrotron Radiat., 2020, 27, 507–514 CrossRef CAS PubMed.
- S. Tanuma, C. J. Powell and D. R. Penn, Surf. Interface Anal., 1994, 21, 165–176 CrossRef CAS.
- N. G. Eror and U. Balachandran, J. Solid State Chem., 1982, 42, 227–241 CrossRef CAS.
- T. Bieger, J. Maier and R. Waser, Solid State Ionics, 1992, 53–56, 578–582 CrossRef CAS.
- W. D. Callister Jr. and D. G. Rethwisch, Materials Science and Engineering – An Introduction 10th Edition, 2018 Search PubMed.
- W. D. Callister Jr., D. G. Rethwisch, J. V. Sci, K. Artyushkova, H. Cohen, C. D. Easton, D. J. Morgan, M. Engelhard, T. R. Gengenbach, G. Greczynski, P. Mack and D. J. Morgan, J. Vac. Sci. Technol., A, 2020, 38, 031204 CrossRef.
- J. F. Moulder, W. F. Stickle, P. E. Sobol and K. D. Bomben, Handbook of X-ray Photoelectron Spectroscopy, United States of America, 1993 Search PubMed.
- G. Greczynski and L. Hultman, Sci. Rep., 2021, 11, 1–5 CrossRef PubMed.
- R. C. Hatch, M. Choi, A. B. Posadas and A. A. Demkov, J. Vac. Sci. Technol., B: Nanotechnol. Microelectron.: Mater., Process., Meas., Phenom., 2015, 33, 061204 CrossRef.
- G. M. Vanacore, L. F. Zagonel and N. Barrett, Surf. Sci., 2010, 604, 1674–1683 CrossRef CAS.
- R. A. De Souza, V. Metlenko, D. Park and T. E. Weirich, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 1–11 CrossRef.
- T. Nishimura, A. Ikeda, H. Namba, T. Morishita and Y. Kido, Surf. Sci., 1999, 421, 273–278 CrossRef CAS.
- A. R. Silva and G. M. Dalpian, J. Appl. Phys., 2014, 115, 33710 CrossRef.
- F. Sojka, M. Meissner, C. Zwick, R. Forker and T. Fritz, Rev. Sci. Instrum., 2013, 84, 015111 CrossRef PubMed.
- T. Kubo and H. Nozoye, Surf. Sci., 2003, 542, 177–191 CrossRef CAS.
- Y. Lin, A. E. Becerra-toledo, F. Silly, K. R. Poeppelmeier, M. R. Castell and L. D. Marks, Surf. Sci., 2011, 605, L51–L55 CrossRef CAS.
- Z. Wang, F. Li, S. Meng, J. Zhang, E. W. Plummer, U. Diebold and J. Guo, Phys. Rev. Lett., 2013, 111, 1–5 Search PubMed.
- T. Kubo, H. Orita and H. Nozoye, Phys. Chem. Chem. Phys., 2011, 13, 16516–16519 RSC.
- C. H. Lanier, A. Van De Walle, N. Erdman, E. Landree, O. Warschkow, A. Kazimirov, K. R. Poeppelmeier, J. Zegenhagen, M. Asta and L. D. Marks, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 1–9 CrossRef.
- N. Erdman, O. Warschkow, M. Asta, K. R. Poeppelmeier, D. E. Ellis and L. D. Marks, J. Am. Chem. Soc., 2003, 125, 10050–10056 CrossRef CAS PubMed.
- M. R. Castell, Surf. Sci., 2002, 505, 1–13 CrossRef CAS.
- M. Naito and H. Sato, Phys. C, 1994, 229, 1–11 CrossRef CAS.
- Q. D. Jiang and J. Zegenhagen, Surf. Sci., 1999, 425, 343–354 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available: Additional AP-XPS and AFM analyses. See DOI: 10.1039/d1tc03436g |
| ‡ Equally contribute to this work. |
| This journal is © The Royal Society of Chemistry 2021 |