Insights into the magnetism and phase transitions of organic radical-based materials
Mercè
Deumal
 *,
Sergi
Vela
*,
Sergi
Vela
 ,
Maria
Fumanal
,
Maria
Fumanal
 ,
Jordi
Ribas-Arino
,
Jordi
Ribas-Arino
 * and
Juan J.
Novoa
*
* and
Juan J.
Novoa
*
Departament de Ciència de Materials i Química Física and IQTCUB, Universitat de Barcelona, Martí i Franquès 1, E-08028, Barcelona, Spain. E-mail: merce.deumal@ub.edu; j.ribas@ub.edu; juan.novoa@ub.edu
First published on 10th June 2021
Abstract
Organic radicals have been consistently regarded as promising building blocks for the next generation of applied materials. Multiple radical families have been developed and characterized in the last decades, fostered by the ever-growing capabilities of organic synthesis. Thiazyl-, spiro-biphenalenyl-, 1,2,4-benzotriazinyl-, and nitroxide-based radicals have furnished striking examples of metal-free switchable materials, whose phase transitions are accompanied by changes in the magnetic, optical and/or electrical response. While similar in origin, their actual mechanism, driving force(s), and spin state stabilities often depict a different landscape. Fundamental knowledge on such aspects, as well as on the underlying network of spin exchange couplings and non-covalent interactions (including pancake bonding), are key to understand their spin transition, and the tailored modification of their properties. These complex features cannot be extracted based solely on experimental input, but rely on a computational interpretation. In this Perspective article, we discuss the insight gained from computational modelling into the magnetism and phase transitions of organic radical-based materials. We focus on the key importance of dynamic effects due to the labile nature of π-stack interactions assembling those materials, the structural distortions driven by spin changes, the coupling between electronic structure and order–disorder transitions, and the dependence of spin correlation upon temperature. All these phenomena uncovered by simulations should assist in the rational design of new dynamic organic crystals.
1. Introduction
Persistent organic radicals are receiving an ever growing interest in the field of materials science because they are very promising building blocks for magnetic materials, conductors, spintronic devices, organic light-emitting diodes, bistable memory devices, sensors, near-infrared dyes and spin probes.1–11 In this Perspective article, we will focus on organic magnets and on organic radical-based switchable materials.Purely organic magnets are an important class of materials within the family of molecule-based magnets. This type of magnets differs significantly from conventional metal (Fe, Co, Ni) or metal-oxide (e.g. CrO2) magnets in several ways. First of all, the structural building blocks are molecular in nature, and the unpaired electrons may be either localized on specific atoms, as in coordination complexes, or delocalized, as in purely-organic radicals. Another distinct feature is that molecule-based magnets are prepared via low-temperature solution-based techniques, which enables an exquisite degree of synthetic control at the molecular-level with the aim at tailoring their magnetic properties. For these reasons, molecular magnets have been conceived as promising candidates for applications in electronics, non-linear optics, and energy/memory storage devices.12–14
Molecule-based magnets derive their net moment from the cooperative effect of the spin-carrying molecular entities at the microscopic level, and can exhibit a variety of macroscopic magnetic properties such as ferromagnetism (FM), antiferromagnetism (AFM), spin canted response, or metamagnetism (MM). These depend on the relative arrangement of the spin-carrying units within the crystal, and its strength (JAB), which determines the critical temperature below which the magnetic order is shown.
Examples of purely organic molecule-based magnets are p-nitrophenyl nitronyl nitroxides,15 decamethylferrocenium tetracyanoethenide,16 mixed coordination compounds with bridging organic radicals,17 Prussian blue related compounds,18 and charge-transfer complexes.19
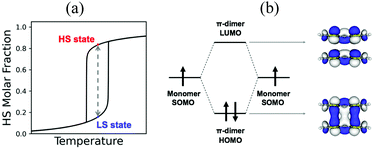
Beyond magnetism, molecular materials whose physical properties can be tuned by means of external stimuli (for instance, heat, pressure or light) hold great promise in the development of electronic switching and memory storage devices.13,20 These materials are particularly interesting for technological applications when they show bistability, which is the ability of a material to be observed in two different electronic states within a range of applied external perturbation (Fig. 1a).4 In the bistability region, the thermodynamically stable and metastable forms can coexist. To be used in memory devices, the bistability must be associated with a response function, such as optical, electrical or magnetic, that can reveal the state of the system. The most common example of molecular bistability is the spin-crossover (SCO) phenomenon, typically observed in transition metal complexes with a 3dn (4 ≤ n ≤ 7) electronic configuration. These complexes have the intrinsic possibility to show spin transitions between a low spin (LS) and a high spin (HS) state when they lie close in energy. In this regard, Fe(II)- and Fe(III)-based complexes are the largest family of studied SCO systems because of their ability to generate either spin state depending on the external conditions.21,22 Bistability has also been observed in purely-organic radicals. However the mechanism of spin transition is very different from that of transition metal complexes. In the latter, the spin transition can be explained by the local spin state change in the metal ion. In contrast, organic radicals usually exhibit a reversible spin transition between its monomeric form showing paramagnetic behaviour, and its dimeric form displaying a silent (or diminished) magnetic response. In both cases, a balance between the enthalpy loss and the entropy gain must be achieved.
In transition metals, the much larger entropy associated with the HS state is able to overcome enthalpy gaps within a window of 1–5 kcal mol−1.23,24 In organic radicals, the entropy gain is much smaller, and so is the dimerization enthalpy (can be less than 1 kcal mol−1). The balance between the dimerized and monomeric form is thus very subtle. If stronger, radicals are so reactive that they spontaneously and irreversibly dimerize. If weaker, the dimer is not formed, and the monomers behave as paramagnets without the possibility to show bistability. In between lie radicals that dimerize weakly and reversibly. Reversible dimerization is often shown between conjugated molecules featuring π-stacking interactions either in isolated dimers or extended columns. These allow the formation of long, multicentre bonds (otherwise known as pancake bonds)25,26 that are stable enough to be formed at low temperature, but weak enough to break into monomers upon temperature or light exposure. Pancake bonds have been spectroscopically and theoretically characterized (Fig. 1b) between a large variety of organic radicals, both neutral and ionic. They exhibit a large dependence upon the precise alignment of the two interacting planar π-radicals, in terms of both rotational and in-plane displacement, or in terms of slippage. For that reason, small changes in the geometry have large effects on the strength of the bond.27
In this Perspective article, we discuss the physical insights behind the magnetism and phase transitions of organic radical-based materials. In particular, we present our contribution in unravelling structure–property correlations, thermal effects and switchable properties in these systems by means of computational modelling, and how the outcomes of this work bring together a comprehensive picture of the main factors controlling their properties. This allows us to highlight the different phenomena observed in the most prominent families of organic radicals, and to connect them within the systems currently reported. This Perspective article consists of two sections: a section devoted to the interpretation/rationalization of the magnetic properties of organic radicals, and a section devoted to (i) the understanding of their structural properties, and (ii) the identification of the driving forces that trigger their spin- and phase-transitions.
2. Interpretation and rationalization of magnetic properties of molecule-based materials
The rationalization of magnetism in molecule-based materials is a non-trivial task. Empirical structure–property correlations connecting the micro- (JAB) and macroscopic magnetic (e.g. χ(T) and Cp(T)) properties have traditionally assisted the Material Science community to that end. This is typically done through the fitting of experimentally-measured macroscopic properties using analytical models (e.g. Bleaney–Bowers,28 Bonner–Fisher29). The result of these protocols is a set of JAB values, which accounts for the impact of multiple effects (e.g. temperature, long-range interactions, environment, motion). In this section, we will first tackle some ideas about the interpretation of magnetism largely accepted within the experimental community that proved to have flaws. Then, we review the First-Principles-Bottom-Up (FPBU) approach,30,31 an unbiased strategy to reproduce and interpret the magnetic response of molecular materials based on their crystal packing analysis and subsequent assessment of the significant magnetic interactions between radicals by means of first-principles calculations. Finally, we will devote some discussion to address the best approach to study the effect of temperature, since it has been disclosed to have a crucial role in the rationalization of molecule-based magnetism.2.1. On the interpretation of magnetism
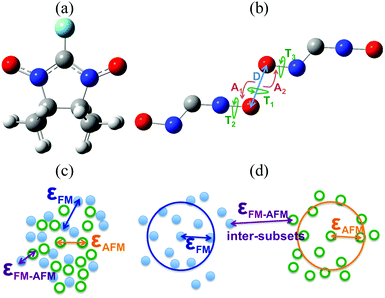
A systematic synthetic effort has provided different families of organic free radicals whose crystals present interesting magnetic properties, even bulk ferromagnetism (FM) in some cases although at low critical temperatures.1,32–37 The real challenge here lies in being able to rationally design materials using persistent radicals that have FM ordering at higher critical temperatures. This objective can only be achieved through the control of the crystal packing of the radicals and sound structure–magnetism relationships.One of the most extensively studied families of purely organic persistent radicals is the α-nitronyl nitroxide (or α-nitronyl aminoxyl) radicals38 (see Fig. 2a). The analysis of the magnetic properties and packing in the α-nitronyl nitroxide crystals shows that the presence of bulk ferromagnetism must be strongly related to the relative arrangement of the radicals within the crystal. Consequently, one of the most important points in this field is to recognize the relative arrangements of neighbouring molecules giving rise to intermolecular FM (or AFM) interactions.39–41 Increasing the strength of these interactions will make possible increasing the critical temperature of purely organic ferromagnets. Structural patterns found in radical crystals with dominant FM (AFM) interactions can be called FM-(AFM-)patterns. Since the exact geometries of these patterns are not known, a detailed inspection of the molecular packing of individual crystals led to several useful qualitative conclusions. For instance, short NO⋯ON contacts were associated with AFM patterns, while short NO⋯HC contacts were indicative of FM patterns.42–47 The existence of short repulsive N–O⋯O–N contacts in both FM and AFM crystals was thus taken as a consequence of the presence of short attractive C–H⋯O–N contacts.48,49
This approach had two major drawbacks: firstly, the structural information achieved on the magnetic patterns was very limited and, secondly, the conclusions were in many cases biased by preconceptions.50 In order to get clear insight into the matter, the packing of 47 α-nitronyl nitroxides crystals presenting either FM or AFM dominant response were systematically and quantitatively analysed to identify the presence of magnetic patterns by examining the geometry of the N–O⋯O–N, C(sp3)–H⋯ON and C(sp2)–H⋯ON contacts.51,52 The statistical differences in the relative spatial dispositions of these contacts within the FM and AFM subsets were investigated, searching for features which later on could be used as signatures for the presence of a type of magnetic interaction in other α-nitronyl nitroxide crystals.53 Using the database of 47 crystals (23 FM and 24 AFM), the total number of inter-radical contacts found was: (1) 1312 NO⋯ON contacts at O⋯O distances smaller than 10 Å, and (2) 6039 C(sp3)–H⋯O–N and 2286 C(sp2)–H⋯O–N contacts using a H⋯O cut-off of 3.8 Å. These three sets were large enough to allow a statistical analysis of the geometrical distribution of the parameters involved. The internal geometry of these groups was considered fixed, and the inter-contact arrangement was defined by means of six coordinates (see Fig. 2b).
Analysis of the geometry of the N–O⋯O–N contacts strikingly resulted in similar values of the D, A1, A2, T1, T2, and T3 parameters found in both FM and AFM subsets. For instance, the shortest value found in the FM and AFM subsets was 3.158 and 3.159 Å, respectively. This similarity was not an exception, but a general situation. Indeed, the number of short contacts is similar in the FM and AFM subsets (see Table 1). Thus, it follows that the two subsets (FM and AFM) present a similar packing efficiency for the N–O⋯O–N contacts. The angular distribution of the N–O⋯O–N contacts was also studied, revealing that the O atom is placed all over the space, with no clustering in particular regions, and that there is no difference between the spatial distribution of the FM and AFM contacts, i.e. for the same distance and angle values it is possible to find short N–O⋯O–N contacts in the FM and AFM subsets. Also, no differences were found in the geometrical distribution of the C–H⋯O–N contacts between the FM and AFM subsets.
| Distance range (Å) | # NO⋯ON contacts | # of contacts (percentage) | |
|---|---|---|---|
| FM | AFM | ||
| 0–3 | 0 | 0 (0%) | 0 (0%) |
| 3–4 | 24 | 10 (42%) | 14 (58%) |
| 4–5 | 68 | 26 (38%) | 42 (62%) |
| 5–6 | 112 | 54 (48%) | 58 (52%) |
| 6–7 | 174 | 77 (44%) | 97 (56%) |
| 7–8 | 230 | 107 (47%) | 123 (53%) |
| 8–9 | 293 | 142 (48%) | 151 (52%) |
| 9–10 | 411 | 195 (47%) | 216 (53%) |
| Mean value % | 45% | 55% | |
Following that study, one can wonder if the previous conclusions were just an artefact of the coordinate set selected for the analysis. To address this question, a factor analysis on the six internal coordinates defining the relative position of two ONCNO groups was carried out.54,55 This analysis indicated that six is the number of independent parameters necessary and sufficient to treat this problem, and that it is not possible to reduce this number. This conclusion also showed that the use of three or even two geometrical parameters, a common practice performed by some authors for analysing series of α-nitronyl nitroxide radicals, is not correct. In fact, a cluster analysis of the contact data for the FM and AFM subsets established that the two sets are nearly identical and interpenetrated, thus being completely indistinguishable (the criteria to define the cluster was the single linkage method,56 see Fig. 2c and d). One can then safely conclude that our main result, i.e. that there are no distinct geometrical trends for the FM subset, is not an artefact of the selected coordinate set, and the same conclusions would be obtained using other sets.48,49
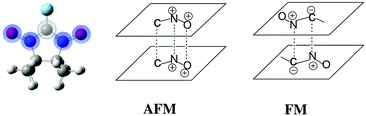
Since no specific geometrical parameter was found to explain why a material behaved as a ferromagnet, the magneto-structural correlation most widely used to qualitatively predict the magnetic coupling of any two given radicals was cross-examined in an attempt to rationalise the magnetic response of a molecular material. We refer to the McConnell-I model,57 which predicts the presence of intermolecular FM interactions between neighbouring radicals only when there are short contacts between atoms that have a considerable atomic spin population of opposite sign (otherwise, the interaction would be antiferromagnetic or negligible), irrespective of the orientation of those radicals. Due to the fact that most of the spin density is located in the ONCNO group (Fig. 3),58,59 it was long assumed that the intermolecular contacts relevant from the magnetic point of view in α-nitronyl nitroxide crystals were those involving the ONCNO groups. McConnell-I model predicts that short NO⋯ON contacts resulting from the direct overlap of two ONCNO groups can give rise to AFM or FM interactions, depending on the relative orientation of these ONCNO groups. When the dominant overlap comes from two NO subgroups, given the identical sign in their spins, the interaction is AFM (Fig. 3). However, it is possible that the dominant overlap is that between one NO subgroup and the central carbon, being then a FM interaction (Fig. 3).60–63 Also, accepting that the McConnell-I model could be extended to the C–H⋯O–N case, these H⋯O contacts are expected to give very weak magnetic interactions having a FM nature when the spin density on the H atoms is negative and AFM when it is positive. Owing to their weakness, this kind of contacts is not expected to be the determinant ones in defining the dominant magnetic interaction in the crystal, although if their number is large enough, they could compensate for the stronger ones.
The above rationale of the magnetic coupling between α-nitronyl nitroxide radicals was proven to be an oversimplification of the McConnell-I model.64 When the McConnell-I model makes the correct prediction of low and high spin stability it is only because the magnetic contributions from “closest contact” atoms that are not directly aligned is rather small. In systems where the alignment is not perfect, this fortuitous cancelation does not hold. In those cases, a qualitative prediction using the McConnell-I model is impossible without an a priori knowledge of the Jij magnetic coupling between i and j atoms carrying spin density from two interacting radicals. Further, it is clear that the Jij couplings have strong orientational and directional properties. Thus, the question of high spin (FM) versus low spin (AFM) stability will depend on subtle details of orientation manifested in the behaviour of the Jij coupling between atoms carrying significant spin density, which will belong to two close interacting radicals. The evaluation of atomic Jij couplings is not trivial. It is thus advised to resort to the assessment of the magnetic exchange coupling between pairs of radicals, JAB, which is an average measure of all atomic contributions. Therefore, contrary to common experimental belief, we concluded that the applicability of the McConnell-I magneto-structural correlation was not general: it had limited predictive value because orientational dependence of the model (via JAB exchange interactions) was never studied.
Summarizing, our data proved wrong the idea that short N–O⋯O–N contacts are indicative of a crystal being dominated by antiferromagnetic interactions, even when the angular orientation of these contacts is taken into account. Similarly, C–H⋯O–N contacts are not indicative of a crystal behaving as a ferromagnet. Consequently, this questions the validity of any magneto-structural correlation made looking at these contacts individually. At the same time, it indicates that the magneto-structural correlations present in the α-nitronyl nitroxide crystals must be collective, that is, associated with the relative disposition of all the magnetically active shortest contacts. It is clear that the intermolecular magnetic interaction depends on the relative orientation of the two radicals making the short contacts as a whole, and that too simple magneto-structural correlations must be called into question. These conclusions were a milestone of paramount importance in the path towards the theoretical and computational study of molecule-based magnets. Later research unveiled that, within a magnet, both FM and AFM interactions between radicals can coexist and it is their competition that will provide the overall macroscopic magnetic behaviour of a given material (see ref. 30 for a review).
2.2. First principles bottom-up working strategy
The resulting conclusions from our statistical analysis and from the study of the McConnell-I model were at odds with what was believed to be reliable. It became obvious that a general working strategy to reproduce but also rationalise the magnetic response of molecular materials was missing. An option to fill this void would be a strategy that could (1) use as input data the crystallographic X-ray or Neutron Diffraction information of the molecular material, (2) evaluate the JAB magnetic coupling between pairs of radicals and put forward the resulting magnetic topology, (3) calculate the macroscopic measured magnetic response, and (4) give insight into the correspondence between structure and magnetism. Our contribution is the FPBU working strategy30,31 to calculate macroscopic magnetic properties (e.g. χ(T) magnetic susceptibility, Cp(T) heat capacity, and M(H) magnetization) from the only knowledge of the crystal packing.Firstly, all possible magnetically relevant symmetry-unique pairs of radicals in the crystal have to be selected by analysing the crystal packing in terms of distances. Prior to this selection, the spin density of the radical to be studied is calculated in order to know which atoms will be more magnetically active, i.e. to learn over which atoms the spin density will be mainly delocalised. Pairs of radicals are then chosen in terms of the distance between those atoms carrying the most of the spin density. The distance threshold is usually calculated in terms of the van der Waals radii of the atoms involved in the interaction to be studied taking into account the exponential decay of JAB magnetic interaction with distance.65
Secondly, the radical⋯radical JAB interaction for each pair of radicals selected in the crystal has to be evaluated The microscopic JAB magnetic interaction is evaluated in terms of energy differences. Therefore, for the energy calculations, the neutral environment of any given radical must be well described. Direct observation of the crystal will hint at whether a radical pair model will be sufficient or, on the contrary, one will have to resort to 3-, 4-radical or larger models due to the presence of de facto biradicals in the crystal packing. Also the way the environment is taken into account needs some thought since it can be evaluated explicitly, by means of point charges, omitted, etc. Note that by environment we mean ligands, counterions, and solvent molecules. The energy calculations are usually performed at the DFT/UB3LYP level.66,67 However, depending on the system, one can resort to a variety of wave-function-based (e.g. CASSCF, RASSCF, DDCI).68–70 Also depending on the system, different schemes to obtain the numerical value of JAB magnetic coupling have to be explored: localized vs. delocalized, projected vs. un-projected, etc.71–80
Once all symmetry-unique JAB exchange couplings have been computed, one must propose the magnetic topology of the crystal in terms of all magnetically significant JAB interactions. This magnetic topology is then used to extract the minimal magnetic model space, which is the smallest set of JAB interactions whose extension along the crystallographic axes (a, b, c) would re-generate the entire magnetic topology. Having chosen the magnetic model, the matrix representation that contains all JAB values required to parameterize the Heisenberg Hamiltonian is built. The resulting parameterized matrix is then fully diagonalised on the space of spin functions of the minimal magnetic model. The energy eigenvalues and the corresponding spin quantum numbers obtained as a result of the full diagonalisation allow the calculation of magnetic susceptibility χ(T), heat capacity Cp(T) and magnetization M(H) data for each magnetic model using the corresponding expressions provided by Statistical Mechanics. Finally the calculated data are compared to the experimentally measured data to make sure that the FPBU procedure worked correctly. The FPBU approach is thus an integral strategy: through the analysis of an X-ray structure characterised at a given temperature we are able to calculate the magnetic properties of a molecule-based material.
The FPBU procedure meant an inflection point in the way one could approach the study of magnetism in molecule-based materials. Consequently, carefully-chosen prototypical magnetic molecular materials were studied and interpreted, namely, purely organic ferromagnets,81 purely organic co-crystal verdazyl antiferromagnet,82 low-dimensional magnetism (antiferromagnetic Heisenberg chain,83 spin-ladder,84 3D-to-quasi 2D antiferromagnet85–88), canting antiferromagnetism,89 role of ligands and counterions in 2D magnets,90 bistability (transition metal-based BDTA·Co(mnt)2,91 purely organic TTTA92), FM metal-radical coordination polymer TTTA·Cu(hfac)2,93 charge-transfer HMTTF·Ni(mnt)2,94 multi-orbital effect,95 metamagnetism.96
2.3. Effect of temperature
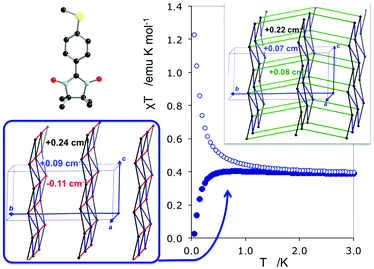
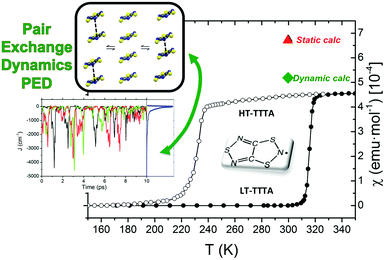
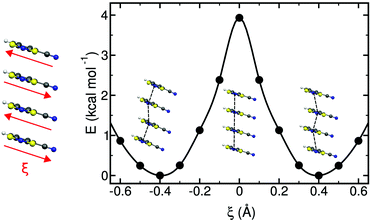
The study of some of these molecule-based materials revealed the exceedingly important role of the temperature at which those materials were characterized in order to adequately study their magnetism.81,89,92,97,98 In particular, the static study of the magnetism of para-(methylthio)phenyl nitronyl nitroxide purely organic molecular ferromagnet81 done at 298 K resulted in a 2D magnetic topology in which there is competition between FM (+0.24 and +0.09 cm−1) and AFM (−0.11 cm−1) interactions, while at 10 K the magnetic topology is 3D and purely FM (+0.11, +0.07 and +0.07 cm−1) (see Fig. 4). Experimentally, the material behaves as a bulk ferromagnet below 0.20 K. Clearly, only the computed χT(T) curve using the magnetic topology at 10 K is able to reproduce the whole temperature range (0–280 K) given that, at low-temperatures (T < 3 K, see Fig. 4), the computed χT(T) curves distinguish between a 2D magnetic topology presenting AFM interactions and a 3D FM topology. It was thus unveiled that the magnetic topology of a given magnet was temperature dependent. In order words, that the broadly-accepted static approach had flaws. Let us mention here that, for simulation purposes, a static study assumes that a molecule-based material can be described by a single X-ray structure all over the range of temperatures of interest. Therefore, in some cases it is not possible to rationalize the magnetic response of a compound only based upon the analysis of a single X-ray crystal structure.Further studies also encountered that the thermal expansion/contraction of the molecular crystal in π-labile systems (e.g. dithiazolyl99–106 and benzotriazinyl107 radicals) gives rise to significant changes in the magnetic response. Specifically, TTTA (1,3,5-trithia-2,4,6-triaza pentalenyl) bistable compound was chosen as a proof of concept108,109 since it had been extensively studied from an experimental point of view (see inset Fig. 5 for chemical formula). Our ab initio molecular dynamics AIMD110,111 studies concluded that the regular stacking motif of the high-temperature polymorph of TTTA does not correspond to a minimum in the potential energy surface (PES) of the system but it is the result of a fast intra-stack pair-exchange dynamics, whereby radicals continually exchange the adjacent neighbouring radical (upper or lower) with which they form an eclipsed π-dimer (see Fig. 5). This unique dynamics (labelled as pair-exchange dynamics PED) was found to be the source of significant vibrational entropy, which played a key role in driving the hysteretic phase transition of this material (see Fig. 1 and Section 3.3). The impact of PED on the magnetic properties of TTTA was investigated through the evaluation of the JAB values between the pairs of radicals of two different π-stacks for a large number of frames along the AIMD trajectories. For each of these frames, the magnetic susceptibility was computed by means of full diagonalizations of the Heisenberg Hamiltonian built from the previously evaluated JAB values (as usually done in the FPBU procedure, cf. Section 2.2). By averaging all these values of susceptibility we obtained the vibrationally-averaged magnetic susceptibility, i.e., the magnetic susceptibility averaged over all nuclear configurations sampled due to thermal fluctuations. As shown in Fig. 5, PED induces large fluctuations in the magnetic exchange interactions (JAB) between spins, up to 1000% of the average value (see J vs. time graphic), as they oscillate around their equilibrium positions. At 300 K, these deviations result in a ∼20% difference between the vibrationally-averaged magnetic susceptibility and that computed using the X-ray structure, the former being in better agreement with the experimental data (see red and green symbol, respectively, in Fig. 5). Our results thus showed that intermolecular vibrations due to temperature effects exert a notable impact on the magnetic behaviour of TTTA. The unveiled strong coupling between JAB interactions and intermolecular vibrations reveals that considering JAB as a constant value at a given temperature leads to a flawed description of the magnetism of TTTA. Instead, the physically relevant concept in this case is the statistical distribution of JAB values. It has been shown that PED is also exhibited by NCBDTA,112 and PDTA113–115 leading to a dynamic mechanism of stabilization of regular π-stacks. Thus, it is then likely that other systems also featuring labile π–π networks, as shown by TTTA, would also require the explicit consideration of the coupling between intermolecular vibrations and magnetic exchange interactions between spin centres. In this regard, the dithiazolyl DTA family of compounds allows to exhaustively exploring the effect of temperature in bistable materials.
The addition of molecular dynamics constituted a new turning point in the way to study magnetism and spin transitions in purely organic molecular materials. For the dithiazolyl DTA family, the AIMD data allowed to disclose which is the geometrical arrangement of radicals most likely to give rise to either a FM or AFM response.52 In particular, it was found that a drastic change in the magnetic response is always due to changes in the JAB magnetic interactions between adjacent radicals along the π-stacks of the crystal, which in turn are driven mostly by the changes in the interplanar distance and degree of lateral slippage, according to the interpretation of a series of magneto-structural correlation maps (see Fig. 6 for TTTA). Note that these two variables have been also successfully employed in magneto-structural correlations of other radicals.116–118 Furthermore, this magnetic fingerprint has been shown to be associated to the DTA-skeleton rather than to the DTA substituent. Specific geometrical dispositions have been recognized as a FM (AFM) fingerprint in such correlations (see Fig. 6). The different mechanisms for spin and phase transition in these systems are discussed in Section 3.3.
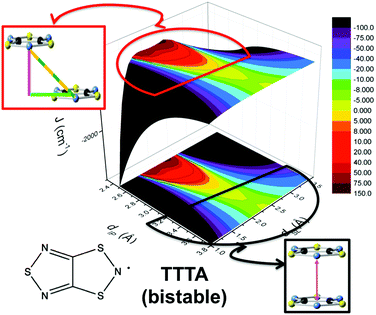 | ||
| Fig. 6 Magneto-structural correlation maps for TTTA (bistable). The FM and AFM fingerprint regions are shown in red and black, respectively. | ||
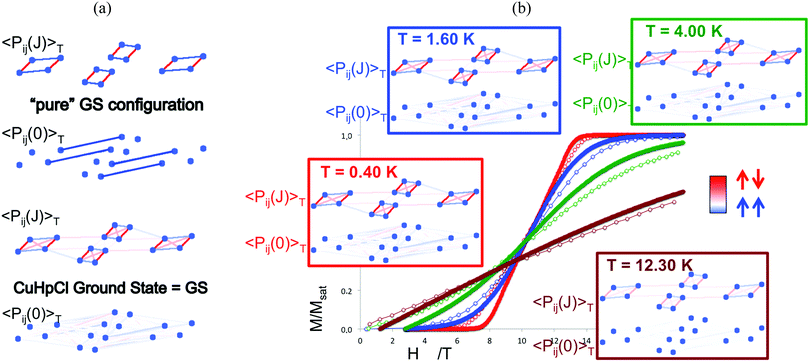
Finally, temperature effects were devoted to the thermal analysis of the magnetic wavefunction as provided by the FPBU procedure. This allows to quantify short and long-range spin correlation between radicals in a molecule-based material (and whether the main contribution is FM or AFM) as well as to calculate their magnetic transition temperature.119 Analysis in the region close to the magnetic transition regime is performed by monitoring all different contributions/weights of the magnetic coupling between radicals to the magnetic wavefunction as a function of temperature by means of a Valence Bond analysis. Accordingly, the spin alignment between radicals can be evaluated as a function of temperature in (1) each one of the eigenstates of the magnetic wavefunctions (e.g. ground state as well as any excited state configuration), and (2) in the magnetic wavefunction itself. For instance, in Cu2(1,4-diazacycloheptane)2Cl4 (CuHpCl) crystal,120 comparison between the short-range Pij(J)T and long-range Pij(0)T spin correlations of a pure singlet AFM ground state and the CuHpCl ground state shows that the singlet ground state is the collective result of singlet as well as higher multiplicity configurations (see Fig. 7a).121 The short-range and long-range spin correlation between magnetic units (see Pij(J)T and Pij(0)T, respectively, in Fig. 7b) were studied at 0.40 K, 1.60 K, 4.00 K, and 12.30 K in accordance with the magnetization experiments. This analysis revealed that the largest contribution from long-range spin correlation comes from the lowest 0.40 K temperature, being practically zero both short- and long-range ordering at 12.30 K. It thus follows that for CuHpCl the short-range magnetic correlation is the only meaningful contribution even at the lowest temperature, and that the long-range spin correlation can be neglected.
Altogether, within the framework of molecule-based magnetism, the FPBU approach combined with molecular dynamics aims at capturing the microscopic complexity of the molecular material to both attain an adequate understanding and reproduce the available experimental magnetic data. In contrast to other strategies that do not explicitly account for the electronic structure of the material and simply aim at fitting the experimental magnetic data to a parametric model that might (or not) resemble the crystal packing, computational chemistry can provide a sound insight into the nature and mechanism of the magnetic coupling. Therefore, the information furnished by quantum chemistry is exceedingly important in the Materials Science community since it can be envisaged as an exploratory tool for the design of new and complex multifunctional materials.
3. Understanding of structural properties and identification of driving forces in switchable materials based on organic radicals
Examples of the most studied organic radicals displaying spin transitions and bistability are spiro-biphenalenyls,122 benzotriazinyls123 and 1,3,2-dithiazolyl radicals.106 In the following, we discuss the mechanism and driving forces governing the phase transition in these three families of organic radicals. We highlight the role of computational analyses in unravelling the key factors behind their switchable magnetic properties, with special focus on the extreme sensitivity of the spin exchange coupling to small changes in the geometry of the radicals forming the pancake bonds.3.1. Spin transitions in π-dimers of spiro-biphenalenyl-based radicals
Phenalenyl (PLY) radicals are examples of open-shell graphene fragments known as the simplest non-Kekulé polynuclear benzenoid molecules or polycyclic aromatic hydrocarbons (PAHs).124 The spin density of the PLY radical is delocalised over the six carbons of its α positions (Fig. 8a), which enhances its stability and prevents the formation of σ-dimers.9 Since 1975,125 phenalenyl-based derivatives have been considered for the development of π-extended molecular spin devices.126,127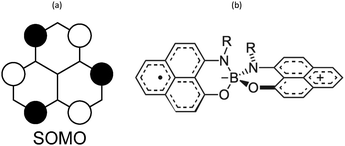 | ||
| Fig. 8 (a) Single occupied molecular orbital of phenalenyl (PLY) radical. (b) Scheme of a N- and O-functionalized spiro-bis(1,9-disubstitutedphenalenyl)boron radical (SPB). | ||
This type of compounds are currently intensively investigated because it is thought that they will feature improved performance over inorganic materials in spin-based information processing.128,129
Spiro-biphenalenyl-based (SBP) radicals are one of the most prominent families of organic radicals and one of the most prominent single-component radical conductors.11 They consist in two nearly perpendicular PLY units connected through a boron spiro-linker (Fig. 8b). As such, they are examples of organic-mixed valence compounds in which formally one PLY is a cation and the other PLY an open-shell neutral unit. DFT and multi-reference calculations (CASPT2 and NEVPT2) showed that N- and O-functionalized SBPs belong to the Robin-Day Class III of mixed-valence compounds130 in which the ground electronic state delocalises the positive charge and unpaired electron among both units.131 Notably, the calculations revealed that localising the charge in one PLY unit entails a very small energy penalty (1 kcal mol−1), thus explaining the diversity observed in the reported SBP crystals depending on their substituents and the crystal packing motif.
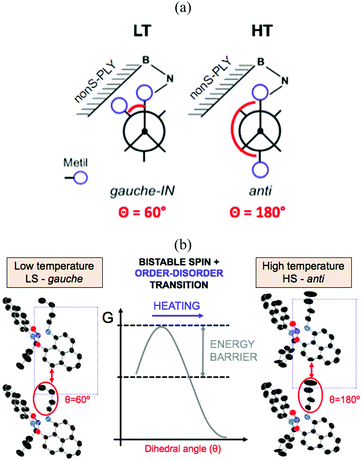
Indeed, several SBPs were reported as a result of different substitutions performed to the nitrogen atom. Ethyl-,132 propyl-,133 butyl-,122 pentyl-,134 octyl-135 and cyclooctyl-substitutions lead to the formation of π-dimers in the crystal structure, while hexyl-136 and benzyl-137 substitutions results in isolated monomers, and cyclohexyl- and cycloheptyl-SBPs form extended π-chains resulting in one-dimensional organic metals.138 Besides the remarkable conductive properties of materials based on spiro-biphenalenyl-based radicals, highly relevant was the discovery of two of these materials presenting a phase transition that simultaneously exhibits changes in three physico-chemical properties: electrical, optical, and magnetic. These are the ethyl- and butyl-substituted SBP, which were characterized by a spin transition between a diamagnetic and a paramagnetic phase at 140 K and 355 K, respectively.
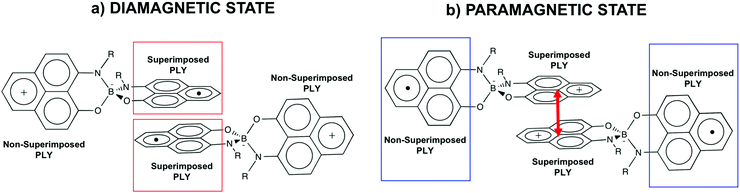
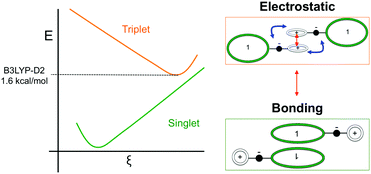
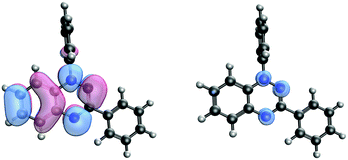
Such spin transitions add an extraordinary functionality to these materials to be exploited in memories and sensing applications. Several experimental139,140 and theoretical studies141–144 were devoted to the understanding of the key factors controlling the phase transition in these materials, which was ascribed to an intramolecular electron transfer between the superimposed and non-superimposed PLY within the π-dimers (Fig. 9). At low temperatures below the spin transition, the unpaired electrons are localised in the superimposed PLY resulting in a diamagnetic state (low spin LS) that arises from a very strong AFM coupling (Fig. 9a). This coupling originates from a long-multicentre (pancake) bond as a result of strong SOMO–SOMO orbital overlap. In contrast, at higher temperatures the material shows paramagnetic response (high spin HS), breaking the pancake bond and behaving as an open-shell system (Fig. 9b). Our calculations revealed that the configuration with the unpaired electrons localised on the non-superimposed PLY rings only exists as a stable minimum in the PES of the triplet state (Fig. 10). This scenario was also uncovered for the spin transition in the 1-phenyl-3-trifluoromethyl-1,4-dihydrobenzo[e][1,2,4]triazin-4-yl radical (see B3 in Section 3.2), thus suggesting that it can be a common feature in the mechanism of other purely organic spin-crossover (SCO) materials. Characterization of the intramolecular electron transfer accompanying the spin transition was performed by Haddon and coworkers based on a detailed bond length analysis of the LS and HS X-ray crystal structures. The reasons behind the stability of the paramagnetic π-dimers were however unclear considering that (1) the pancake bonding energy is zero, (2) the dispersion component is unfavorable and (3) two positive charges face each other in the superimposed PLY (Fig. 9b). Computational analysis was crucial to understand the origin of the counterintuitive stability of the HS state in these dimers, which was ascribed to the zwitterionic character of the SBP. An interaction energy decomposition analysis with B3LYP-D2 revealed that the electrostatic repulsion between the positively charged superimposed PLYs was counterbalanced by the electrostatic attraction between the negatively charged spiro-linkers and positively charged PLYs of the pairing SBP (Fig. 10), thus making the spin transition at low temperatures possible. This is closely related to the stability of supramolecular entities such as the (bis-TTF)-functionalised diphenyl glycoluril molecular clips, for which [TTF]˙+⋯[TTF]˙+ pancake bonds are stabilized in solution at room temperature by the appropriate charge distribution and structural arrangement.145
In addition to a higher transition temperature, the butyl-substituted SBP displays a 25 K wide hysteretic loop between 325 and 350 K. The fact that the phase transition occurs at around room temperature within a wide bistability window, and that the bistability is shown in three different physical channels (optical, electrical and magnetic) makes this material one of the most remarkable bistable molecule-based materials ever reported. Despite the similar crystal packing (π-dimers) between ethyl-SBP and butyl-SBP, little was known about the reasons behind the appearance of a hysteretic loop in the spin transition of butyl-SBP (and not in ethyl-SBP). Analysis of the crystal structures of the low-temperature (LT) and high-temperature (HT) phases of butyl-SBP pointed to the presence of a large energy barrier between the LT and HT phases that would explain the abrupt volume expansion and cooperativity not shown in ethyl-SBP. However the origin of this barrier was unknown. To address this question, we performed ab initio molecular dynamics simulations for the LT and HT phases of butyl-SBP. These revealed that the LS-to-HS spin transition in this material is accompanied by a gauche-to-anti conformational rearrangement of the butyl groups (Fig. 11a). At low temperatures, the most stable conformer is the gauche-IN conformer (Fig. 11a, left). This conformer stabilizes the LS state in the crystal by decreasing the π-stacking distance and shifts the transition temperature to higher values with respect to the ethyl-SBP. Heating above room temperature promotes the rotation of the butyl group towards the anti conformation (Fig. 11a). However the compact crystal packing prevents the free rotation of the butyl group and results in a large energy barrier that shifts the transition temperature to higher values (Fig. 11b). Overcoming this barrier allows the butyl groups to rotate and the unit cell expands in such an extent that triggers the intramolecular electron transfer promoting the HS state. In this way, the heating mode is controlled by the kinetics of the order–disorder expansion of the butyl groups, while the cooling mode follows the thermodynamic pathway.
The coupling between the intramolecular charge transfer and the conformational rearrangement of the butyl groups in butyl-SBP demonstrates that coupling a spin switch with a conformational switch is a promising strategy in the design of new bistable materials. In fact, it has been shown that bistability can be promoted in FeII and FeIII SCO complexes by order–disorder conformational changes in the counterion. One of the first reports of an order–disorder of anion leading to cooperative SCO was in [FeII(DAPP)(abpt)](ClO4)2, where DAPP = [bis(3-amino propyl)(2-pyridylmethyl)amine] and abpt = 4-amino-3,5-bis (pyridin-2-yl)-1,2,4-triazole.146 Similar order–disorder of the anion was found for a [FeII(H4L)2][ClO4]2·H2O·2(CH3)2CO complex based on bispyrazolylpyridine ligand,147 as well as for fac-[FeII(HL)3]Cl·PF6 where HL is 2-methylimidazol-4-yl-methylideneamino-n-propyl.148 A conformational change of the anion was found to trigger the spin transition in [FeIII(qsal-I)2]NTf2 (qsal-I = (N-8-quinolyl)-5-I-salicylaldiminate).147 While this is a common feature in inorganic SCO materials, recent work has also shown this phenomenon in other purely organic materials such as in benzotriazinyl radical cationic salts of 1-phenyl-3-(phenylamino)-1,2,4-benzotriazin-4-ium-1-ylium (see B7 in Section 3.2),149 and π-stacked dimers of N-(n-propyl) benzene triimide ([BTI-3C]) and its anionic radical ([BTI-3C]˙−).150 In these systems, changes in the π-stacking originate in entropy-driven conformational changes. In particular, bistability in BTI-3C dimers is ascribed to the anti/gauche isomerization observed in their propyl side chains following a very similar mechanism than that observed in butyl-SBP. Certainly, this strategy constitutes a facile synthetic route to promote bistability in organic systems by the structural modification of their skeletons to include bulky groups prone to isomerization.
2.2. Spin transitions in benzotriazinyl-based organic radicals
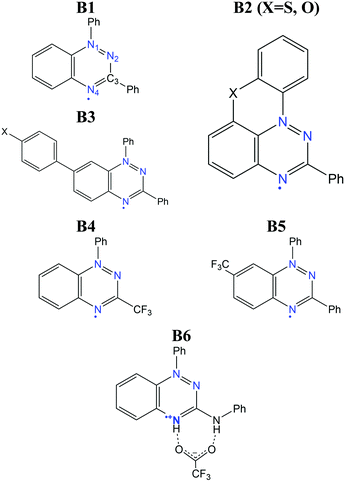
The benzo[e][1,2,4]triazinyl- or Blatter-radical (B1), first reported in 1968,151 is a highly-functionalizable core that gives rise to a family of purely-organic radicals with exceptional stability.152–154 Blatter radicals have attracted renewed interest in fundamental research155,156 and applications thanks to recent synthetic advances of Koutentis,157 Kaszynski,158 O’Donoghue159 and co-workers. Their high stability and versatility has enabled their use within the Metal-Radical approach,160–162 in which the Blatter radical is coordinated to a transition metal, as well as the synthesis of fused Blatter bi-radicals,163,164 which are of particular interest in modern applications.8 Beyond these exotic cases, a plethora of mono-radical purely-organic Blatter radicals have been reported, and their magnetism characterized, ranging from moderately-strong AFM, to FM.154,165–170 Such tuneable magnetic response stems from a significantly-delocalised spin density, that extends along the fused benzotriazinyl ring (see Fig. 12),107 and makes it sensitive to substituents. This fact, together with the relative molecular orientation in the crystals, results in tuneable dominant interactions and, thus, a variable magnetic response. The delocalised spin is indeed one of the ingredients that explains its exceptional stability (see Fig. 12). Another factor is the steric protection of the lone electron, fostered by large substituents. In particular, the aryl substituent at the N1 position arranges perpendicularly to the molecular plane, hindering π-dimerization (see atom labelling in Scheme 1). A notable exception is the planar Blatter radical reported by Kaszynski and co-workers,158,171,172 who succeeded at planarizing the N1 phenyl substituent through the formation of a chalcogen bond with S and O (B2 in Scheme 1, with X = S, O). This synthetic advance opened the possibility of exploiting σ- and π-dimerization as a mechanism to promote bistability, as in other radical families (e.g. DTA radicals discussed below).The computational modelling of Blatter radicals underwent the traditional difficulties associated with temperature effects and DFT methods. Initially, doubts were raised on the accuracy of DFT to correctly capture the ground state of these materials, and thus to evaluate the magnetic exchange interactions (JAB). These were based on a disagreement between the computed atom-based spin densities, and the ones estimated from EPR measurements.169,173 As a result, it was argued the need for a multi-configurational method, based on the existence of resonant forms with the unpaired electron localized in N1 and N2.173 In this work, it was mentioned that a better agreement could be reached with CASSCF computations107 for two Blatter radicals (B3 in Scheme 1, with X = H, F) displaying AFM interactions (−12.9 and −11.8 cm−1, respectively). Interestingly, both methods showed the same spin density distribution (both in slight disagreement with experiment), and described all orbital occupations close to 2.0 (occupied) and 0.0 (virtual), which prompted us to conclude that any potential discrepancy was not associated with the multi-configurational character of the radical's ground state.
Moreover, the numerical accuracy of B3LYP was further tested by comparison with DDCI,174,175 another multi-configurational method known for being highly accurate in the evaluation of JAB values, and the DFT method passed the test. Interestingly, both DDCI and B3LYP yielded very small JAB values (−1.2 and −4.4 cm−1 with B3LYP and −1.3 and −4.6 cm−1 with DDCI, for compounds B3(F) and B3(H) respectively), and the FPBU approach30,31 (see Discussion above) could not successfully model the low-temperature region. In the absence of low-temperature crystal structures, therein we employed variable-cell geometry optimizations, for the first time, to obtain a unit-cell structure more representative of the low-temperature region. On this optimized structure, the FPBU approach with B3LYP JAB values was finally able to reproduce the microscopic (AFM interactions) and macroscopic (χ vs. T curves) behaviour for both radicals.107 This example provided further evidence of the importance of thermal relaxation in the computational modelling of magnetism in organic radicals, and that its adequate modelling can often be more important than the electronic structure method employed.
One Blatter radical, the 1-phenyl-3-trifluoromethyl-1,4-dihydrobenzo[e][1,2,4]triazin-4-yl (B4), was shown to undergo an abrupt spin transition between a diamagnetic and a paramagnetic polymorph, thus demonstrating that benzotriazinyls can give rise to switchable materials.123 In this compound, a first-order phase-transition takes place at ca. 58(2) K, and proceeds via subtle changes of intra- and inter-stack interactions between two similar structural phases. The crystal structure of this benzotriazinyl radical has 1D π-slipped stacked columns (Fig. 13). The mean interplanar distance and the degree of slippage between adjacent radicals alternate along the stacking direction. The dominant JAB magnetic interactions in the LT phase were estimated to be −166 cm−1, with a Bleaney–Bowers model fitting, and −185 cm−1 at DFT level (B3LYP/6-311++G**). For the HT phase, DFT yielded JAB = +4.1 cm−1. Computations could complement the initial experimental interpretation of the phase transition mechanism,123 and identified it as a two-step process.176 The system starts at a low-temperature π-dimerized phase (LTLS). The first step consists of the population of the triplet state of this phase (② to ③, see Fig. 13), assisted by vibrational entropy (① to ②), and generating a meta-stable HS π-dimerized minimum (LTHS). The initial population of the LTHS phase is responsible for the gradual increase of magnetic response in the χ vs. T plots. At the transition temperature, the system has enough energy to overcome a small energy barrier connecting the LTHS and HTHS phase, and reach the π-slipped HS minimum (HTHS). Comparison between B4 and another member of the benzotriazinyl family (B5), which features a gradual increase of its magnetic response, revealed that the key factor explaining the existence of the HTHS minimum, and thus, of the abrupt spin transition of B4, was the large structural differences between the LS and HS minima, promoted by the comparatively-small π-surface of B4 in comparison with most Blatter radicals reported to date, which have a Ph substituent in C3. This subtle change in composition generates weaker inter-molecular interactions (mainly through a smaller dispersion-energy component), which leads to more important changes in the π-stacking upon LS-to-HS spin transition.
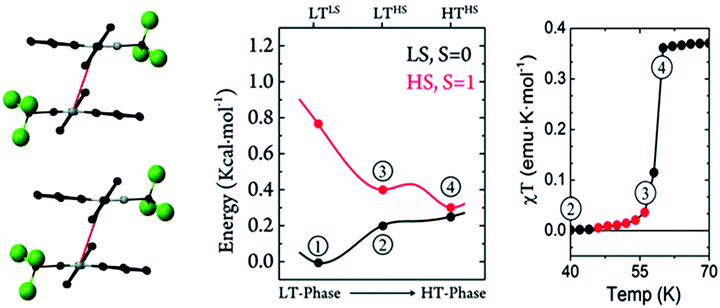 | ||
| Fig. 13 (left) HS- and LS-PES of dimers of B4 along the coordinate connecting the different minima. Energies are given per molecule. (right) Magnetic susceptibility curve of B4 around T1/2. In red, we highlight the points with χT ≠ 0 before the jump. The key steps of the phase transition are numbered in both plots, as discussed in the main text. Reprinted/adapted with permission from ref. 176. | ||
An important drawback associated with the bistability mechanism of B4 is the low-temperature at which the “bonded” dimer is broken. As we discussed above, the largest AFM interaction reported so far in Blatter radicals is in the range of −150 to −200 cm−1. This is only a fraction of the value reached in other radicals showing bistability as a result of a controlled (i.e. reversible) dimerization mechanism, as in the case of DTA radicals (see Section 3.3). Considering that the magnitude of the JAB values is related to the strength of the pancake-bonds, we can conclude that in Blatter radicals, the dimer is too weak to resist until moderately-large temperatures. As a result, the only reported case of an abrupt spin transition indeed occurs at ca. 60 K, far below other radical families. It is for this reason that the planar counterparts proposed by Kaszynski are more interesting towards the realisation of room-temperature bistability in Blatter radicals, provided that they can reach stronger JAB values in the dimerized form (as a result of a better π-stacking), while the dimerization mechanism still being reversible. In any case, B4 illustrates how difficult it is to induce a sufficiently-large structural change between the LS and HS minima that significantly modifies JAB and leads to an abrupt phase transition.
An alternative to the above mechanism is to couple the spin transition with an order–disorder (OD) transition of a magnetically-silent moiety in the unit-cell, as we have discussed in Section 3.1. In the context of Blatter radicals, the purpose of such an OD transition would be to bring an additional driving force to induce a significant change in the magnetic coupling between spin carriers. An example has been recently reported, in which a Blatter radical cation with trifluoroacetate counteranions (B6) showed an abrupt but small jump in the χ vs. T curves at around 120 K.149 That was ascribed to the sudden activation of an OD transition in the CF3 group of the trifluoroacetate, which leads to an enlargement of the radical–counterion and radical–radical (π⋯π stacking) distances upon heating. The OD could be identified experimentally and computationally by means of MD simulations. These proved the connection between the OD and the spin transition, due to a change in the distribution of magnetic exchange couplings (JAB) explored by the material upon vibration.149 The limitations of the OD strategy in terms of crystal-structure design are however clear. It is hardly possible to anticipate all the requirements of this mechanism to work. That is, the outcome of (1) the OD transition, (2) its sufficient impact on the radical–radical arrangement and (3) that such change in radical–radical arrangement is associated with a strong change in JAB. The latter seems a particular weak point in Blatter radicals, and thus it is not clear whether bistability can be reached even if crystal design is able to overcome (1) and (2).
3.3. Dynamic properties of regular π-stacks of planar dithiazolyl radicals
Planar 1,3,2-dithiazolyl (DTA) radicals are main actors within the family of organic spin-transition materials. Several radicals of this type have been reported to undergo phase transitions between a diamagnetic LT polymorph and a (weakly) paramagnetic HT polymorph.99,102–106,112 The phase transitions undergone by TDPDTA102, TTTA99,177,178 and PDTA105 radicals occur with thermal hysteresis, while the phase transitions of NCBDTA103,112 and CF3pyDTA104 occur without. The molecular structures of all these radicals, together with their phase transition temperatures are shown in Table 2 (the reader is also referred to ref. 103 and 179, where the spin-transition properties of these compounds is reviewed). The wide thermal hysteresis loops encompassing room temperature exhibited by TTTA and PDTA make these materials very interesting for data storage devices.The HT polymorphs of all the radicals displayed in Table 2 feature regular π-stacks with a uniform intermolecular spacing (⋯A⋯A⋯A⋯A⋯)n. In the cases of TTTA, PDTA and NCBDTA, each radical exhibits a notable degree of latitudinal slippage with respect to its adjacent neighbours along the π-stack, while the degree of longitudinal slippage is vanishingly small (see Fig. 14a). In the cases of TDPDTA and CF3pyDTA, each radical is both latitudinally and longitudinally slipped with respect to its adjacent neighbours along the π-stack (Fig. 14c). The LT polymorphs, in turn, consist of distorted π-stacks comprising slipped pairs of nearly eclipsed radicals (⋯A–A⋯A–A⋯)n (see Fig. 14b and d). The LT and HT polymorphs of TTTA and PDTA not only differ in the type of π-stacks (i.e., regular vs. dimerized) but also in some of the lateral contacts between stacks and the molecular plane orientations. Conversely, the single difference between the LT and HT polymorphs of NCBDTA and TDPDTA is the type of π-stack. As for the CF3pyDTA, the crystal structure of its LT phase has not yet been reported.
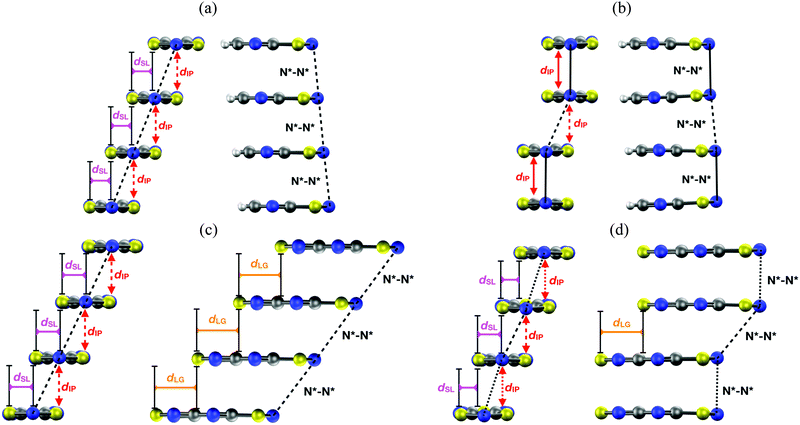 | ||
| Fig. 14 Two side views of a π-stack of the (a) HT and (b) LT polymorph of PDTA, and the (c) HT and (d) LT polymorph of TDPDTA. The dIP, dSL and dLG variables measure the interplanar distance between adjacent radicals, the degree of latitudinal slippage between adjacent radicals, and the degree of longitudinal slippage, respectively. As may be seen in the images, the latitudinal slippage measures the degree of slippage with respect to the symmetry plane that is perpendicular to the molecular plane. The longitudinal slippage refers to the slippage along an orthogonal direction. Although not shown in the images, the structure of the π-stacks of TTTA and NCBDTA is very similar to that of PDTA. Figure adapted with permission of ref. 114. | ||
The very small difference in lattice cohesive energies between the HT and LT phases of planar DTA radicals explains why these radicals undergo phase transitions. For instance, the computed energy difference between the HT and LT polymorphs of TTTA is 0.9 kcal mol−1 (given per TTTA molecule),115 which is in excellent agreement with the transition enthalpy of 0.6 kcal mol−1 measured in DSC experiments.180 The low dimerization enthalpies of planar DTA radicals are in line with these results and appear to be the reason for the tendency exhibited by DTA-based crystals to undergo spin transitions.179 According to our theoretical analysis, the drastic changes in the magnetic response of DTA materials upon spin transition are controlled by large changes in the magnetic exchange couplings (JAB) between adjacent radicals along the π-stacks. The diamagnetism of the LT phases was found to originate in the very strong AFM JAB's between spins of the radicals forming eclipsed dimers. The (weak) paramagnetism of the HT phases, in turn, originates in the moderately antiferromagnetic values for the JAB's between spins of adjacent slipped radicals (see Table 3).92,112,113
| DTA | LT phasea | HT phaseb |
|---|---|---|
| a In the LT polymorphs, the strongest magnetic exchange coupling corresponds to the eclipsed π-dimers. b In the HT polymorphs, the strongest magnetic exchange coupling corresponds to the slipped pairs of radicals along the regular π-stacks. | ||
| TDPDTA | −781 | −69 |
| TTTA | −1755 | −135 |
| PDTA | −1657 | −111 |
| NCBDTA | −1723 | −342 |
The structural relaxation calculations we carried out on the HT polymorphs of DTA radicals revealed surprising structural properties of their regular π-stacks. In the case of TTTA, NCBDTA and PDTA, it was shown that the structural relaxation results in an intrastack dimerization process (Fig. 15a). This process transformed the HT polymorph of NCBDTA into its LT polymorph.112 The dimerization occurred in the stacks of TTTA and PDTA, in turn, did not lead to the X-ray resolved LT polymorph because the lateral contacts and the molecular plane orientations of the optimized structures differ from those of the experimental structure.109,114 In stark contrast with the structural properties of TTTA, NCBDTA and PDTA, the regular π-stacks of the HT polymorph of TDPDTA were preserved upon structural relaxation114 (Fig. 15b). Therefore, our calculations showed that the regular π-stacking motif of TDPDTA is stable at 0 K (i.e., it corresponds to a minimum energy configuration), whereas the same motif is not stable for TTTA, NCBDTA and PDTA. This finding raises two key questions: (1) why do the X-ray resolved structures of the HT polymorphs of the latter three compounds exhibit a packing motif that is not associated with any minimum energy configuration? (2) why are the structural properties of the π-stacks of TDPDTA so different from those of TTTA, NCBDTA and PDTA? We will address these very questions in the following.
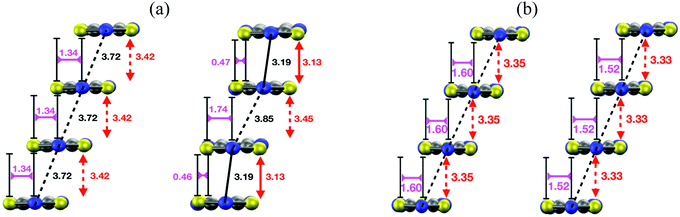 | ||
| Fig. 15 (a) Side view of a π-stack of the (left) X-ray-resolved structure at 323 K of the HT polymorph of PDTA and (right) the optimized structure at 0 K. Although not shown in the images, the structure of the π-stacks of TTTA and NCBDTA is very similar to that of PDTA. (b) Side views of a π-stack of the (left) X-ray-resolved structure at 293 K of the HT polymorph of TDPDTA and (right) the optimized structure at 0 K. The black, red, purple and orange values shown in the image mark the distances between the nitrogen atoms of the S–N–S moieties of adjacent radicals, the interplanar distance between adjacent radicals and the degree of latitudinal and longitudinal slippage between adjacent radicals, respectively. Figures adapted with permission of ref. 114. | ||
Concerning the regular π-stacks observed in X-rays, AIMD simulations performed on the HT polymorphs of these materials allow to reconciling theory with experiment. Specifically, thermal fluctuations of the radicals at finite temperatures were found to be the key ingredient behind the existence of uniform π-stacks. According to the AIMD simulations run at room temperature for the HT polymorphs, the TTTA, PDTA and NCBDTA radicals feature a so-called pair-exchange dynamics (PED), as mentioned in Section 2.3,109,112,114 which can be explained by means of a double-well potential model. The energy profile of Fig. 16 shows the variation of the potential energy of an isolated π-stack of NCBDTA radicals as a function of a collective sliding motion of its molecules. The energy profile has two degenerate minima, each of them associated with a dimerized configuration. The maximum energy configuration, in turn, corresponds to the regular stack. Hence, the energy profile computed for NCBDTA112 demonstrates that the regular π-stack configuration is actually a transition state configuration connecting two dimerized configurations. Although not shown in this article, the energy profiles for TTTA109 and PDTA114 are analogous to that of NCBDTA.
For PDTA, we even computed the minimum energy path for the interconversion of the two dimerized configurations through the nudged elastic band algorithm.114 The profile displayed in Fig. 16 clearly demonstrates that PED is a thermally activated process. Hence, PED is only operative when the radicals have enough thermal energy to overcome the barrier separating the two dimerized configurations.
Unravelling the PED mechanism allowed to understand not only the magnetism of the HT polymorph, but also the structure given that the average structures obtained from the AIMD simulations are almost identical to the crystallographic structures (Fig. 17a). The dynamics of the stacks of the HT polymorphs contrast with the dynamics of the stacks of the corresponding LT polymorphs, which showed that π-dimers are preserved throughout the entire AIMD trajectory (Fig. 17b). The absence of PED in the LT polymorphs is a consequence of not having enough thermal energy to overcome the energy barrier and results in smaller-amplitude thermal fluctuations of the radicals. It thus follows that the regular π-stacks observed in X-rays for the HT polymorphs of TTTA, NCBDTA and TDPDTA are actually the average of a dynamic process that interconverts two distorted stacks. It should be mentioned that the significant diffuse scattering detected in single-crystal X-ray diffraction experiments of TTTA at room temperature provided strong experimental support of the large thermal fluctuations observed in our simulations.109 In contrast with the dynamic properties of the regular stacks of TTTA, NCBDTA and PDTA, the π-stacks of the HT phase of TDPDTA were found not to exhibit any PED.114 This is not surprising, taking into account that the regular π-stacks of TDPDTA are minimum energy configurations. As the TDPDTA radicals do not undergo any PED, their thermal fluctuations have smaller amplitude than those of TTTA, NCBDTA and PDTA. This is reflected in the computed thermal ellipsoids of TDPDTA being significantly smaller than those of the other radicals.114 This result, which is consistent with the experimental thermal ellipsoids, means that the size of thermal ellipsoids may be taken as an indicator of whether or not a given regular π-stack of radicals features PED. The differences between the structural properties (both static and dynamic) of the stacks of the HT polymorph of TDPDTA and the HT stacks of the other radicals can be understood on the basis of the bonding properties of isolated π dimers of radicals. The 2D potential energy surface (PES) we computed114 for an isolated pair of TDPDTA radicals as a function of the latitudinal and longitudinal slippage is shown in Fig. 18a. Not surprisingly, the most stable minimum on the 2D-PES (point A) is associated with the structure of the π-dimers present in the LT polymorph of TDPDTA. Upon simultaneous increase of both types of slippage, a second minimum energy configuration emerges on the 2D-PES (point C). This new minimum corresponds to the structure of the slipped pairs of radicals in the HT phase. Therefore, the computed 2D-PES allowed us to conclude that the stability of the regular stacks of the HT polymorph arises from the fact that its latitudinally- and longitudinally-slipped pairs of radicals are locally stable configurations. The very small energy gap between the two different association modes of TDPDTA radicals (point A and C) explain why TDPDTA can undergo a phase transition and provides evidence that π-dimers of planar radicals are very useful building blocks for endowing molecular materials with switchable properties.
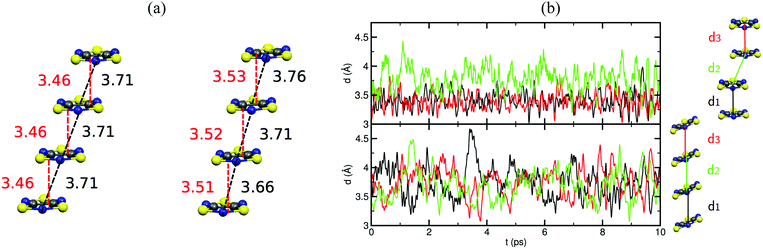 | ||
| Fig. 17 (a) Comparison between the structure of one stack of TTTA in the (left) X-ray resolved structure of the HT polymorph at 300 K and in the (right) average structure obtained from the AIMD simulations. The values marked in black and red refer to the N–N distance and the interplanar distance between adjacent radicals, respectively. (b) Time-resolved evolution of the distance between centroids of adjacent TTTA radicals in one of the stacks of the LT (top) and HT polymorph (bottom) of TTTA, as obtained from AIMD simulations run at 300 K. Figure adapted with permission of ref. 109. | ||
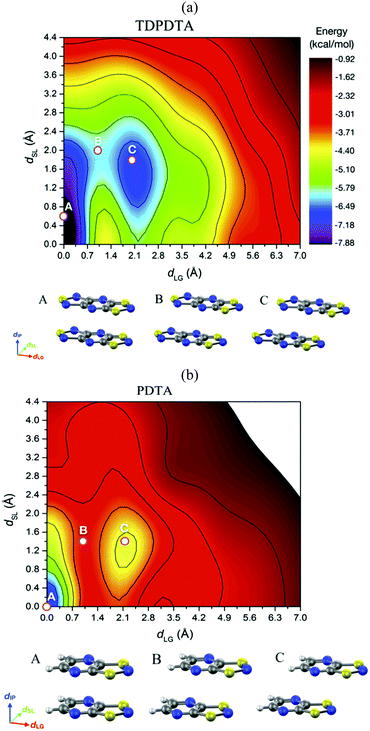 | ||
| Fig. 18 Potential energy surface of an (a) isolated π-dimer of TDPDTA radicals and (b) an isolated π-dimer of PDTA radicals as a function of the degree of latitudinal slippage (dSL) and the degree of longitudinal slippage (dLG), while keeping fixed the interplanar distance at values of 3.3 Å and 3.2 Å, respectively. The configurations associated with the A, B and C points marked on the color maps are displayed at the bottom of each color map. Figure adapted with permission of ref. 114. | ||
The analysis of the 2D-PES carried out for the isolated pair of TDPDTA radicals was also done for an isolated π-dimer of PDTA radicals, which is one of the examples of radicals whose regular stacks are not stable at 0 K. The resulting 2D-PES (Fig. 18b) also features two minima, but the energy difference between the latitudinally and longitudinally slipped pair of radicals and the eclipsed π-dimer is significantly higher than in the case of TDPDTA.114 This is consistent with the fact that no polymorph of PDTA comprises the latter type of π-dimers.
The 2D-PES of PDTA also shows that finite values of the latitudinal slippage while keeping a zero longitudinal slippage does not result in any alternative minimum energy configuration, thus explaining the instability of the regular π-stacks of PDTA against dimerization at 0 K. The results obtained from the exploration of the 2D-PESs demonstrate that the structural properties of π-stacks of planar DTA radicals mirrors the structural properties of isolated π-dimers. It thus follows that computational studies on the energy landscape of π-dimers of radicals would be a useful tool to screen DTA molecules for the design of new materials based on π-stacked architectures with the desired properties. This is similar to the conclusions we extracted from the interaction-energy analysis of a Blatter radical displaying an abrupt phase transition (B2, see Section 3.2). Overall, the calculations performed with the goal of investigating the evolution of the PED undergone by the TTTA, NCBDTA and PDTA radicals upon cooling offered valuable insights into the dynamics of its regular π-stacks. The evolution of the PED as a function of temperature was monitored through 2D probability distribution functions (PDFs) as a function of the interplanar distance and the degree of latitudinal slippage between adjacent radicals within a stack. These 2D-PDFs were obtained directly from the AIMD trajectories. Fig. 19 displays the 2D-PDFs of NCBDTA at different temperatures. The single peak observed at room temperature at values very close to those of the crystallographic structure means that the regular π-stack is the most probable configuration among all the configurations (including dimerized configurations) that are sampled along the AIMD simulation. Upon cooling, not only do the 2D-PDFs become more confined, but they gradually become bimodal. This reflects an important change in the dynamics of the crystal because a bimodal distribution means that a dimerized configuration is the most probable one. Therefore, the PED gradually slows down upon lowering the temperature and it ultimately freezes.112 The evolution of the dynamics of the stacks of TTTA109 and PDTA114 as a function of temperature is completely analogous to that of NCBDTA.
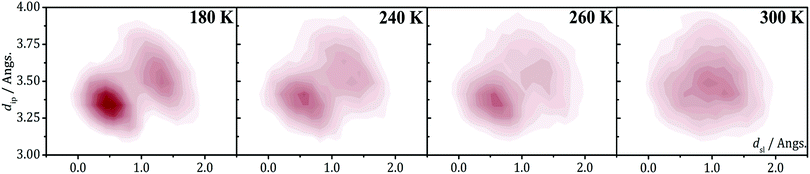 | ||
| Fig. 19 2D-PDF's associated with the interplanar distance (dip) and the relative latitudinal slippage (dsl) between adjacent NCBDTA radicals, as obtained from AIMD trajectories run at 180, 240, 260 and 300 K. Figure reprinted with permission of ref. 112. | ||
The evolution of the 2D-PDFs of Fig. 19 indicates that the thermal activation of the PED entails an order–disorder (OD) transition within the π-stacks of DTA radicals. As such, our calculations hinted at a second-order phase transition, i.e., a gradual transition without an abrupt release of thermal energy and without significant thermal hysteresis. The experimental verification of this hypothesis was not possible neither for TTTA nor for PDTA because in their phase transitions the transformation from dimerized stacks into regular stacks is accompanied by a rearrangement of the intermolecular interactions between stacks. The simultaneous occurrence of an intra-stack transformation and an inter-stack transformation in both TTTA and PDTA precludes any investigation of the nature of the former transformation. Conversely, the absence of any inter-stack rearrangement in NCBDTA renders this material an excellent platform for dissecting the nature of the OD transition of its constituent π-stacks. In differential scanning calorimetry experiments conducted on NCBDTA, a gradual release of thermal energy was observed in the 260–272 K range, thus demonstrating that the OD transition of the stacks entails a second-order phase transition.112 In line with these results, the change in the experimentally measured magnetic susceptibility of NCBDTA upon phase transition is smooth in the 260–272 K range.112
The thorough analysis on the phase transition of NCBDTA demonstrated that the initiation of a PED process provides a mechanism to prompt a spin transition in DTA-based materials by means of a second-order phase transition. Yet, this does not suffice to open a hysteresis loop and, thus, a temperature window of bistability. The phase transitions undergone by TTTA and PDTA demonstrate that a complementary rearrangement of intermolecular bonds between the π-stacks via a first-order phase transition is needed to generate hysteresis.112
The large-amplitude motions undergone by DTA radicals when PED is operative hints at a large vibrational entropy. To assess the importance of such vibrational entropy in driving the magnetic phase transitions in DTA materials, we calculated the variation of the vibrational entropy (ΔSvib) upon the LT → HT phase transition of TTTA. Note that LT, as opposed to HT, does not exhibit PED. Consequently, the difference in vibrational entropy between the two phases reflects the impact of PED on the vibrational entropy of HT. It was found that the TΔSvib value upon this phase transition at 310 K is ∼0.6 kcal mol−1. This represents approximately two thirds of the total entropic term, which also includes an electronic contribution, stemming from the fact that the LT phase is magnetically silent while the HT polymorph is a weak paramagnet. These results demonstrated that the vibrational entropy arising from PED is a major driving force for the LT → HT phase transition of TTTA.109 Accordingly, there is a parallelism with spin transitions of DTA radicals and spin transitions of Fe(II) complexes, where the vibrational entropy is by far the leading entropic contribution when it comes to clearing the enthalpic gap between high- and low-spin states. Let us mention that the methodology we employed to evaluate ΔSvib transcended the harmonic approximation commonly used. Specifically, we made use of a thermodynamic-integration-based technique, combined with AIMD simulations performed at different temperatures, to properly capture the important anharmonic effects associated with the PED.109
Overall, the computational work we have carried out over the last years has uncovered important aspects of the spin-Peierls-like transitions undergone by DTA radicals and the structural properties of their π-stacks. Our work has demonstrated that a regular π-stack of DTA radicals can be rendered stable, in a given range of temperatures, by means of two different mechanisms, namely a static mechanism and a dynamic mechanism. The underlying stabilization mechanism is static when the regular π-stacked configuration is associated with a locally stable minimum in the potential energy surface of the system (i.e., at 0 K). The stabilization mechanism is dynamic, in turn, when the regular stack arises from a dynamic interconversion between two degenerate dimerized configurations.
It is our belief that the discovery of these two stabilization mechanisms is relevant for several reasons. First, knowing which stabilization mechanism is operative in a given DTA material is important for the proper interpretation of its structural and physical properties. For instance, the results presented in Section 2.2 for TTTA have demonstrated that the magnetic properties of those regular stacks stabilized by the dynamic mechanism cannot be fully understood using exclusively the configuration provided by X-ray structures. It thus follows that, given a DTA material featuring regular stacks, it is crucial to identify whether or not these stacks are the result of a PED process. Besides computational tools, there are several experimental techniques (including DSC measurements, determination of thermal ellipsoids, searching for the presence of diffuse structure in the X-ray diffraction patterns and terahertz time-domain spectroscopy measurements181) that can provide most valuable information regarding the dynamics of a given regular stack. A gradual variation of the magnetic response of the material (like the one observed in NCBDTA112) can also hint at the presence of an order–disorder transition occurring within the π-stacks. In fact, the magnetic susceptibility curves of PyDTA182 and QDTA183 might signal an order–disorder transition taking place in the π-stacks of these DTA-based materials.
Second, the existence of two stabilization mechanisms for the regular π-stacks of DTAs entail two different ways of harnessing phase transitions between dimerized π-stacks and regular π-stacks for the development of new switchable DTA-based materials. If the regular stack is stable by means of the dynamic mechanism, the phase transition is brought about by the thermal promotion of a PED process within the stacks. In this case, the key parameter that needs to be controlled to engineer a spin transition is the energy barrier separating the two degenerate dimerized configurations. If, on the contrary, the regular stack is stable by means of a static mechanism, the key parameter to be controlled is the energy gap between the regular and dimerized configurations of the π-stacks. Note that the energy barrier between the two configurations might also play a role, for instance, by enabling a hysteresis loop. The single example of this type of spin transition reported thus far is that of TDPDTA. Given the hysteretic character of this spin transition, searching for other DTA radicals that undergo the same type of spin transition looks promising.
The results gathered so far appear to indicate that there is a correlation between the type of slippage exhibited by adjacent radicals and the type of stabilization mechanism of the regular stacks. When the radicals of a π-stack are both longitudinally and latitudinally slipped with respect to each other, the stabilization mechanism is static. When the radicals of a π-stack exhibit only a latitudinal slippage, the stabilization mechanism is dynamic. This correlation, together with the fact that the energy cost associated with the different degrees of slippage can be straightforwardly predicted using isolated pairs of radicals, should assist in the design of new switchable DTA-based materials with tailored properties. Finally, let us stress that the regular π-stacking motif is very common for other families of planar organic radicals not considered in this review,184 including tetrathiafulvalenes,185 tetracyanoquinodimethanes,186 semiquinones,187,188 verdazyls,189,190 metal bis(1,2-dithiolene) complexes.191,192 The findings we have reported for the stacks of planar DTAs might apply (at least partially) to the stacks of these alternative radicals.
4. Conclusions
In this Perspective article, we have shown how computational modelling is a most valuable tool to interpret the physical properties of molecular magnetic materials based on purely-organic radicals, including the study of their properties as magnetic switches.Firstly, we have discussed representative examples that demonstrate how theory and computations can disclose the macroscopic magnetic response of a material, from their magnetic topology and the relative arrangement of the spin-carrying centres. As an example, we have revised the case of the McConnell-I model, whose commonly accepted application was shown to be an oversimplification of no general validity. In addition, our studies proved wrong the idea that certain short atomic contacts were indicative of a crystal being dominated by either AFM or FM interactions. Consequently, any future magneto-structural correlation must consider the relative disposition of all the magnetically active shortest radical⋯radical contacts. Later research unveiled that, within a magnet, both FM and AFM interactions between radicals can coexist and it is their competition that will provide the overall macroscopic magnetic behaviour of a given molecule-based material. The study of short- and long-range spin correlation is also an excellent tool to monitor the evolution of the spin alignment upon temperature, i.e. of the competition between dominant opposing interactions.
Building upon our experience in modelling molecular magnetism, one must pay special attention to the calculations. The JAB magnetic interaction between radicals must be always evaluated. However, there is no model or method of general applicability to calculate the value of the JAB magnetic exchange coupling between two radicals. In some cases, not only the radicals establishing the interaction but also their environment (counterions, hydrogen bonding, solvent) must be considered. It will be also necessary to assess whether a DFT- or a wavefunction-based method is best to study a given radical. Given the large variety of issues one must tackle when choosing the correct model and method to evaluate JAB interactions for modelling magnetic properties in molecule-based materials, the “human factor” is a must to cross-examine and challenge computations before trusting any result.
An important aspect of many of these analyses, which we have thoroughly discussed along this manuscript, is the importance of temperature. Temperature impacts the modelling of molecular magnetism in two aspects: (1) the thermal contraction/expansion, and (2) thermal fluctuations. The former point implies that computations require good representative crystal structures, which can be obtained either from experiment (low-T crystal diffraction), or from computations (e.g. variable-cell optimizations). The latter point implies that, to evaluate/quantify/interpret the magnetism of organic radicals, it is often necessary to resort to molecular dynamics (MD) simulations. These are indeed necessary to characterize the main phase transitions (e.g. PED in DTA radicals), or order–disorder transitions concomitant to the spin transition (e.g. in SBP- or Blatter-radicals). In our research, MD simulations helped us to identify the driving forces that trigger phase transitions in SBP-, Blatter-, and DTA-based materials. Overall, these investigations, as well as recent discoveries from other groups worldwide, have taught us that it is necessary to think on organic radicals materials as dynamic objects, beyond the static structure depiction.
When possible, we have attempted an interpretation of solid-state properties based on the minimum working units, either molecule, or dimer, or column of radicals, with the aim at preserving a molecular- (or dimer-) based interpretation of the rich palette of magnetic properties displayed by organic radicals. Examples are the analysis of the SBP radicals, whose switchable magnetism can be explained on the basis of the subtle balance between pancake bonding and electrostatic effects in π-dimers, or the outcome of an abrupt phase transition in Blatter radicals, which we associated with the promotion of sufficiently-different HS and LS minima through the decrease of dimer interactions.
We have also shown that computations can occasionally promote new experimental investigations. In this sense, diffuse-scattering measurements carried out by Prof. Awaga and coworkers provided experimental support for our computational identification of the PED in TTTA. Furthermore, the DSC and magnetic susceptibility measurements carried by Prof. Turnbull, Prof. Jakobsche and coworkers corroborated our initial hypothesis that the initiation of the PED in NCBDTA entails a second-order phase transition.
To conclude, our investigations so far have been able to explain the properties (i.e. magnetism, spin transition mechanism, driving force, origin of hysteresis in phase transitions) of existing materials. In the future, our computations should lead to the prediction of novel materials: from the molecular level (magneto-structural correlations) to their crystal structure, and from magnetism to multifunctional materials. The prediction of new materials should embrace molecular crystals as well as 2D covalent organic radical frameworks, a class of recently emerged materials.193–196 To do so, new protocols should be conceived to facilitate the complex description of their phase- and spin-transitions using computations. In this sense, it is worth mentioning that spin transitions require some of the most-challenging tasks for computer simulations; such as the quantification of free-energy differences (which requires accurate evaluations of entropy197), or the simulation of phase transition processes, with the added difficulty of dealing with open-shell systems. Also, DFT approximations still suffer to balance the energetics of the pancake bonding, the strength of magnetic interactions (JAB), or the delocalization of the spin density. Finally, we should be able to integrate machine learning predictions to the field of spin transitions, with the aim to either discover new materials, or to reduce the computational burden. It is thus undeniable the potential contributions that computational chemistry still has to play in the field of molecule-based materials.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
MD, JRA, and JJN acknowledge financial support from MINECO (CTQ2017-87773-P/AEI/FEDER, UE), Spanish Structures Excellence María de Maeztu program (MDM-2017-0767), and Catalan DURSI (2017SGR348).References
- I. Ratera and J. Veciana, Chem. Soc. Rev., 2012, 41, 303–349 Search PubMed.
- M. Mas-Torrent, N. Crivillers, C. Rovira and J. Veciana, Chem. Rev., 2012, 112, 2506–2527 Search PubMed.
- R. G. Hicks, Org. Biomol. Chem., 2007, 5, 1321–1338 Search PubMed.
- R. G. Hicks, Nat. Chem., 2011, 3, 189–191 Search PubMed.
- T. Sugawara, H. Komatsu and K. Suzuki, Chem. Soc. Rev., 2011, 40, 3105–3118 Search PubMed.
- N. M. Gallagher, A. Olankitwanit and A. Rajca, J. Org. Chem., 2015, 80, 1291–1298 Search PubMed.
- S. M. Winter, S. Hill and R. T. Oakley, J. Am. Chem. Soc., 2015, 137, 3720–3730 Search PubMed.
- X. Hu, W. Wang, D. Wang and Y. Zheng, J. Mater. Chem. C, 2018, 6, 11232–11242 Search PubMed.
- B. Tang, J. Zhao, J.-F. Xu and X. Zhang, Chem. Sci., 2020, 11, 1192–1204 Search PubMed.
- L. Ji, J. Shi, J. Wei, T. Yu and W. Huang, Adv. Mater., 2020, 32, 1908015 Search PubMed.
- D. Yuan, W. Liu and X. Zhu, Chem, 2021, 7, 333–357 Search PubMed.
- Z. Zeng, X. Shi, C. Chi, J. T. López Navarrete, J. Casado and J. Wu, Chem. Soc. Rev., 2015, 44, 6578–6596 Search PubMed.
- O. Sato, Nat. Chem., 2016, 8, 644–656 Search PubMed.
- M. A. Halcrow, Spin-Crossover Materials: Properties and Applications, Wiley, Oxford, UK, 2013 Search PubMed.
- M. Tamura, Y. Nakazawa, D. Shiomi, K. Nozawa, Y. Hosokoshi, M. Ishikawa, M. Takahashi and M. Kinoshita, Chem. Phys. Lett., 1991, 186, 401–404 Search PubMed.
- S. Chittipeddi, K. R. Cromack, J. S. Miller and A. J. Epstein, Phys. Rev. Lett., 1987, 58, 2695–2698 Search PubMed.
- A. Caneschi, D. Gatteschi, R. Sessoli and P. Rey, Acc. Chem. Res., 1989, 22, 392–398 Search PubMed.
- S. Ferlay, T. Mallah, R. Ouahes, P. Veillet and M. Verdaguer, Nature, 1995, 378, 701–703 Search PubMed.
- J. S. Miller, A. J. Epstein and W. M. Reiff, Chem. Rev., 1988, 88, 201–220 Search PubMed.
- Z.-S. Yao, Z. Tang and J. Tao, Chem. Commun., 2020, 56, 2071–2086 Search PubMed.
- P. Gütlich, Y. Garcia and H. A. Goodwin, Chem. Soc. Rev., 2000, 29, 419–427 Search PubMed.
- D. J. Harding, P. Harding and W. Phonsri, Coord. Chem. Rev., 2016, 313, 38–61 Search PubMed.
- S. Vela, M. Fumanal, J. Cirera and J. Ribas-Arino, Phys. Chem. Chem. Phys., 2020, 22, 4938–4945 Search PubMed.
- K. P. Kepp, Inorg. Chem., 2016, 55, 2717–2727 Search PubMed.
- M. Kertesz, Chem. – Eur. J., 2019, 25, 400–416 Search PubMed.
- K. E. Preuss, Polyhedron, 2014, 79, 1–15 Search PubMed.
- E. M. Fatila, R. A. Mayo, M. Rouzières, M. C. Jennings, P. Dechambenoit, D. V. Soldatov, C. Mathonière, R. Clérac, C. Coulon and K. E. Preuss, Chem. Mater., 2015, 27, 4023–4032 Search PubMed.
- B. Bleaney and K. D. Bowers, Proc. R. Soc. London, Ser. A, 1952, 214, 451–465 Search PubMed.
- J. C. Bonner and M. E. Fisher, Phys. Rev., 1964, 135, A640–A658 Search PubMed.
- J. J. Novoa, M. Deumal and J. Jornet-Somoza, Chem. Soc. Rev., 2011, 40, 3182–3212 Search PubMed.
- M. Deumal, M. J. Bearpark, J. J. Novoa and M. A. Robb, J. Phys. Chem. A, 2002, 106, 1299–1315 Search PubMed.
- J. Ferrando-Soria, J. Vallejo, M. Castellano, J. Martínez-Lillo, E. Pardo, J. Cano, I. Castro, F. Lloret, R. Ruiz-García and M. Julve, Coord. Chem. Rev., 2017, 339, 17–103 Search PubMed.
- J. S. Miller, Mater. Today, 2014, 17, 224 Search PubMed.
- S. Kumar, Y. Kumar, S. K. Keshri and P. Mukhopadhyay, Magnetochemistry, 2016, 2, 42 Search PubMed.
- Molecular Magnetism – New Magnetic Materials, ed. K. Itoh and M. Kinoshita, Gordon & Breach Science Publishers, Amsterdam, 2000 Search PubMed.
- Molecular Magnetism: From Molecular Assemblies to Devices, ed. E. Coronado, P. Delhaes, D. Gatteschi and J.-S. Miller, Kluwer Academic, Dordretch, 1996 Search PubMed.
- Magnetism: A Supramolecular Function, ed. O. Kahn, Kluwer Academic, Dordretch, 1996 Search PubMed.
- α-Nitronyl nitroxide is the abbreviated name most widely employed, it is used here to indicate 4,5-dihydro-4,4,5,5-tetramethyl-3-oxido-1H-imidazol-3-ium-1-oxyl, the correct IUPAC name.
- M. C. Etter, Acc. Chem. Res., 1990, 23, 120–126 Search PubMed.
- J. Bernstein, R. E. Davis, L. Shimoni and N.-L. Chang, Angew. Chem., Int. Ed. Engl., 1995, 34, 1555–1573 Search PubMed.
- G. R. Desiraju, Angew. Chem., Int. Ed. Engl., 1995, 34, 2311–2327 Search PubMed.
- K. Awaga, T. Inabe, Y. Maruyama, T. Nakamura and M. Matsumoto, Chem. Phys. Lett., 1992, 195, 21–24 Search PubMed.
- K. Awaga, T. Inabe, T. Nakamura, M. Matsumoto and Y. Maruyama, Mol. Cryst. Liq. Cryst. Sci. Technol., Sect. A, 1993, 232, 69–78 Search PubMed.
- K. Awaga, T. Okuno, A. Yamaguchi, M. Hasegawa, T. Inabe, Y. Maruyama and N. Wada, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 3975–3981 Search PubMed.
- J. Veciana, J. Cirujeda, C. Rovira and J. Vidal-Gancedo, Adv. Mater., 1995, 7, 221–225 Search PubMed.
- J. Cirujeda, E. Hernàndez-Gasió, C. Rovira, J.-L. Stanger, P. Turek and J. Veciana, J. Mater. Chem., 1995, 5, 243–252 Search PubMed.
- M. M. Matsushita, A. Izuoka, T. Sugawara, T. Kobayashi, N. Wada, N. Takeda and M. Ishikawa, J. Am. Chem. Soc., 1997, 119, 4369–4379 Search PubMed.
- M. Deumal, J. Cirujeda, J. Veciana, M. Kinoshita, Y. Hosokoshi and J. J. Novoa, Chem. Phys. Lett., 1997, 265, 190–199 Search PubMed.
- J. J. Novoa and M. Deumal, Mol. Cryst. Liq. Cryst. Sci. Technol., Sect. A, 1997, 305, 143–156 Search PubMed.
- When no angular data are taken into account and only intermolecular distances are considered in a given magnetostructural correlation, one is always tempted to ascribe the observed FM intermolecular interaction to the contacts between atoms of the two interacting molecules that have opposite spin densities and are at the closest distances. However, in some molecular layouts there could be other atoms at longer distances that interact FM due to angular considerations.
- M. Deumal, J. Cirujeda, J. Veciana and J. J. Novoa, Adv. Mater., 1998, 10, 1461–1466 Search PubMed.
- M. Deumal, J. Cirujeda, J. Veciana and J. J. Novoa, Chem. – Eur. J., 1999, 5, 1631–1642 Search PubMed.
- The statistical analysis of those geometries was done using the CSD-module QUEST to locate the intermolecular contacts within each crystal, and the CSD-module VISTA for the visualization and a preliminary statistical treatment of the data. The factor and cluster analysis of the data were done with home-made computer programs.
- R. Barlow, Statistics, Wiley, Chichester, 1989 Search PubMed.
- E. R. Malinowski and D. G. Howery, Factor Analysis in Chemistry, Wiley Interscience, New York, 1980 Search PubMed.
- B. S. Everitt, Cluster Analysis, 3rd edn, Edward Arnold, London, 1993 Search PubMed.
- H. M. McConnell, J. Chem. Phys., 1963, 39, 1910 Search PubMed.
- A. Zheludev, V. Barone, M. Bonnet, B. Delley, A. Grand, E. Ressouche, P. Rey, R. Subra and J. Schweizer, J. Am. Chem. Soc., 1994, 116, 2019–2027 Search PubMed.
- J. J. Novoa, F. Mota, J. Veciana and J. Cirujeda, Mol. Cryst. Liq. Cryst. Sci. Technol., Sect. A, 1995, 271, 79–90 Search PubMed.
- C. Kollmar and O. Kahn, Acc. Chem. Res., 1993, 26, 259–265 Search PubMed.
- K. Yamaguchi, Y. Toyoda and T. Fueno, Chem. Phys. Lett., 1989, 159, 459–464 Search PubMed.
- K. Yoshizawa and R. Hoffmann, J. Am. Chem. Soc., 1995, 117, 6921–6926 Search PubMed.
- P. M. Lahti, ed. M. M. Turnbull, T. Sugimoto and L. K. Thompson, Molecule-Based Magnetic Materials, ACS Symp. Series, No. 644, 1996, ch. 14 Search PubMed.
- M. Deumal, J. J. Novoa, M. J. Bearpark, P. Celani, M. Olivucci and M. A. Robb, J. Phys. Chem. A, 1998, 102, 8404–8412 Search PubMed.
- C. Herring, in Direct Exchange between Well-Separated Atoms. In Magnetism, ed. G. T. Rado and H. Suhl, Academic Press, New York, 1966, vol. IIB, p. 5 Search PubMed.
- A. D. Becke, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 3098 Search PubMed.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789 Search PubMed.
- T. Helgaker, P. Jorgensen and J. Olsen, Molecular Electronic-structure Theory, 2000, Wiley, Chichester Search PubMed.
- C. de Graaf and R. Broer, Magnetic Interactions in Molecules and Solids, Springer, 2016 Search PubMed.
- P. A. Malmqvist, A. Rendell and B. O. Roos, J. Phys. Chem., 1990, 94, 5477–5482 Search PubMed.
- L. Noodleman, C. Y. Peng, D. A. Case and J. M. Mouesca, Coord. Chem. Rev., 1995, 144, 199–244 Search PubMed.
- L. Noodleman and E. R. Davidson, Chem. Phys., 1986, 109, 131–143 Search PubMed.
- L. Noodleman, J. Chem. Phys., 1981, 74, 5737–5743 Search PubMed.
- E. Ruiz, P. Alemany, S. Alvarez and J. Cano, J. Am. Chem. Soc., 1997, 119, 1297–1303 Search PubMed.
- R. Caballol, O. Castell, F. Illas, I. de, P. R. Moreira and J. P. Malrieu, J. Phys. Chem. A, 1997, 101, 7860–7866 Search PubMed.
- E. Ruiz, J. Cano, S. Alvarez and P. Alemany, J. Comput. Chem., 1999, 20, 1391–1400 Search PubMed.
- H. Nagao, M. Nishino, Y. Shigeta, T. Soda, Y. Kitagawa, T. Onishi, Y. Yoshioka and K. Yamaguchi, Coord. Chem. Rev., 2000, 198, 265–295 Search PubMed.
- F. Illas, I. P. R. Moreira, C. de Graaf and V. Barone, Theor. Chem. Acc., 2000, 104, 265–272 Search PubMed.
- I. d. P. R. Moreira and F. Illas, Phys. Chem. Chem. Phys., 2006, 8, 1645–1659 Search PubMed.
- F. Neese, Coord. Chem. Rev., 2009, 253, 526–563 Search PubMed.
- M. Deumal, M. J. Bearpark, M. A. Robb, Y. Pontillon and J. J. Novoa, Chem. – Eur. J., 2004, 10, 6422–6432 Search PubMed.
- J. Jornet, M. Deumal, J. Ribas-Ariño, M. J. Bearpark, M. A. Robb, R. G. Hicks and J. J. Novoa, Chem. – Eur. J., 2006, 12, 3995–4005 Search PubMed.
- J. Jornet-Somoza, M. Deumal, M. A. Robb, C. P. Landee, M. M. Turnbull, R. Feyerherm and J. J. Novoa, Inorg. Chem., 2010, 49, 1750–1760 Search PubMed.
- M. Deumal, G. Giorgi, M. A. Robb, M. M. Turnbull, C. P. Landee and J. J. Novoa, Eur. J. Inorg. Chem., 2005, 4673 Search PubMed.
- J. Jornet, L. Li, M. M. Turnbull, C. P. Landee, M. Deumal, J. J. Novoa and J. L. Wikaira, Inorg. Chem., 2007, 46, 11254–11265 Search PubMed.
- A. Shapiro, C. P. Landee, M. M. Turnbull, J. Jornet, M. Deumal, J. J. Novoa, M. A. Robb and W. Lewis, J. Am. Chem. Soc., 2007, 129, 952–959 Search PubMed.
- J. Jornet-Somoza, N. Codina-Castillo, M. Deumal, F. Mota, J. J. Novoa, R. T. Butcher, M. M. Turnbull, B. Keith, C. P. Landee and J. L. Wikaira, Inorg. Chem., 2012, 51, 6315–6325 Search PubMed.
- S. N. Herringer, M. Deumal, J. Ribas-Arino, J. J. Novoa, C. P. Landee, J. L. Wikaira and M. M. Turnbull, Chem. – Eur. J., 2014, 20, 8355–8362 Search PubMed.
- M. Deumal, J. M. Rawson, A. E. Goeta, J. A. K. Howard, R. C. B. Copley, M. A. Robb and J. J. Novoa, Chem. – Eur. J., 2010, 16, 2741–2750 Search PubMed.
- S. Vela, J. Jornet-Somoza, M. M. Turnbull, R. Feyerherm, J. J. Novoa and M. Deumal, Inorg. Chem., 2013, 52, 12923–12932 Search PubMed.
- S. Vela, M. Deumal, J. Ribas-Arino and J. J. Novoa, Inorg. Chem., 2012, 51, 8646–8648 Search PubMed.
- C. S. Clarke, J. Jornet-Somoza, F. Mota, J. J. Novoa and M. Deumal, J. Am. Chem. Soc., 2010, 132, 17817–17830 Search PubMed.
- S. Vela, A. Sopena, J. Ribas-Arino, J. J. Novoa and M. Deumal, Chem. – Eur. J., 2014, 20, 7083–7090 Search PubMed.
- S. Vela, M. Fumanal and M. Deumal, Dalton Trans., 2015, 44, 608–614 Search PubMed.
- M. Deumal and M. Fumanal, Phys. Chem. Chem. Phys., 2016, 18, 20738–20749 Search PubMed.
- C. Climent, S. Vela, J. Jornet-Somoza and M. Deumal, Phys. Chem. Chem. Phys., 2019, 21, 12184–12191 Search PubMed.
- J. Jornet-Somoza, M. Deumal, M. M. Turnbull and J. J. Novoa, Polyhedron, 2009, 28, 1965–1971 Search PubMed.
- J. Jornet-Somoza, M. Deumal, C. P. Landee, M. M. Turnbull and J. J. Novoa, Inorg. Chem., 2010, 49, 8017–8024 Search PubMed.
- W. Fujita and K. Awaga, Science, 1999, 286, 261–262 Search PubMed.
- K. Lekin, S. M. Winter, L. E. Downie, X. Bao, J. S. Tse, S. Desgreniers, R. A. Secco, P. A. Dube and R. T. Oakley, J. Am. Chem. Soc., 2010, 132, 16212–16224 Search PubMed.
- J. M. Rawson, A. Alberola and A. Whalley, J. Mater. Chem., 2006, 16, 2560–2575 Search PubMed.
- T. M. Barclay, A. W. Cordes, N. A. George, R. C. Haddon, M. E. Itkis, M. S. Mashuta, R. T. Oakley, G. W. Patenaude, R. W. Reed and J. F. Richardson, et al. , J. Am. Chem. Soc., 1998, 120, 352–360 Search PubMed.
- A. Alberola, R. J. Collis, S. M. Humphrey, R. J. Less and J. M. Rawson, Inorg. Chem., 2006, 45, 1903–1905 Search PubMed.
- A. Alberola, D. J. Eisler, L. Harvey and J. M. Rawson, CrystEngComm, 2011, 13, 1794–1796 Search PubMed.
- J. L. Brusso, O. P. Clements, R. C. Haddon, M. E. Itkis, A. A. Leitch, R. T. Oakley, R. W. Reed and J. F. Richardson, J. Am. Chem. Soc., 2004, 126, 14692–14693 Search PubMed.
- J. L. Brusso, O. P. Clements, R. C. Haddon, M. E. Itkis, A. A. Leitch, R. T. Oakley, R. W. Reed and J. F. Richardson, J. Am. Chem. Soc., 2004, 126, 8256–8265 Search PubMed.
- M. Fumanal, S. Vela, J. Ribas-Ariño and J. J. Novoa, Chem. – Asian J., 2014, 9, 3612–3622 Search PubMed.
- S. Vela, M. Deumal, M. Shiga, J. J. Novoa and J. Ribas-Arino, Chem. Sci., 2015, 6, 2371–2381 Search PubMed.
- S. Vela, F. Mota, M. Deumal, R. Suizu, Y. Shuku, A. Mizuno, K. Awaga, M. Shiga, J. J. Novoa and J. Ribas-Arino, Nat. Commun., 2014, 5, 4411 Search PubMed.
- D. Marx and J. Hutter, Ab Initio Molecular Dynamics: Basic Theory and Advanced Methods, Cambridge Univ. Press, 2009 Search PubMed.
- R. Car and M. Parrinello, Phys. Rev. Lett., 1985, 55, 2471–2474 Search PubMed.
- S. Vela, M. B. Reardon, C. E. Jakobsche, M. M. Turnbull, J. Ribas and J. J. Novoa, Chem. – Eur. J., 2017, 23, 3479–3489 Search PubMed.
- T. Francese, J. Ribas-Arino, J. J. Novoa, R. W. A. Havenith, R. Broer, C. de Graaf and M. Deumal, Phys. Chem. Chem. Phys., 2018, 20, 20406–20416 Search PubMed.
- T. Francese, S. Vela, M. Deumal, F. Mota, J. J. Novoa, M. F. Camellone, S. Fabris, R. W. A. Havenith, R. Broer and J. Ribas-Arino, J. Mater. Chem. C, 2020, 8, 5437–5448 Search PubMed.
- T. Francese, F. Mota, M. Deumal, J. J. Novoa, R. W. A. Havenith, R. Broer and J. Ribas-Ariño, Cryst. Growth Des., 2019, 19(4), 2329–2339 Search PubMed.
- A. A. Leitch, X. Yu, S. M. Winter, R. A. Secco, P. A. Dube and R. T. Oakley, J. Am. Chem. Soc., 2009, 131, 7112–7125 Search PubMed.
- J.-B. Rota, B. Le Guennic and V. Robert, Inorg. Chem., 2010, 49, 1230–1237 Search PubMed.
- M. Vérot, N. Bréfuel, J. Pécaut, C. Train and V. Robert, Chem. – Asian J., 2012, 7, 380–386 Search PubMed.
- J. Jornet-Somoza, M. Deumal, J. Borge and M. A. Robb, J. Phys. Chem. A, 2018, 122, 2168–2177 Search PubMed.
- J. Jornet-Somoza, F. Cosi, M. Fumanal and M. Deumal, Dalton Trans., 2021, 50, 1754–1765 Search PubMed.
- Note that the magnetic topology can be pictured as squared plaquettes formed by −3.88 cm−1 AFM and +2.30 cm−1 FM (and diagonal −0.29 in light blue) connected via AFM −1.05 and −1.38 cm−1) in an AFM 2D shape along the ab-layer that pile up antiferromagnetically along the c-axis to give rise to a 3D magnetic topology.
- M. E. Itkis, X. Chi, A. W. Cordes and R. C. Haddon, Science, 2002, 296, 1443–1445 Search PubMed.
- C. P. Constantinides, A. A. Berezin, G. A. Zissimou, M. Manoli, G. M. Leitus, M. Bendikov, M. R. Probert, J. M. Rawson and P. A. Koutentis, J. Am. Chem. Soc., 2014, 136, 11906–11909 Search PubMed.
- Y. Morita, S. Suzuki, K. Sato and T. Takui, Nat. Chem., 2011, 3, 197–204 Search PubMed.
- R. C. Haddon, Nature, 1975, 256, 394–396 Search PubMed.
- E. Coronado and A. J. Epstein, J. Mater. Chem., 2009, 19, 1670–1671 Search PubMed.
- T. Kubo, Molecules, 2019, 24, 665 Search PubMed.
- O. V. Yazyev, Rep. Prog. Phys., 2010, 73, 056501 Search PubMed.
- S. Mishra, D. Beyer, R. Berger, J. Liu, O. Gröning, J. I. Urgel, K. Müllen, P. Ruffieux, X. Feng and R. Fasel, J. Am. Chem. Soc., 2020, 142, 1147–1152 Search PubMed.
- M. B. Robin and P. Day, in Advances in Inorganic Chemistry and Radiochemistry, ed. H. J. Emeléus and A. G. Sharpe, Academic Press, 1968, vol. 10, pp. 247–422 Search PubMed.
- M. Fumanal, F. Mota, J. J. Novoa and J. Ribas-Arino, J. Am. Chem. Soc., 2015, 137, 12843–12855 Search PubMed.
- X. Chi, M. E. Itkis, K. Kirschbaum, A. A. Pinkerton, R. T. Oakley, A. W. Cordes and R. C. Haddon, J. Am. Chem. Soc., 2001, 123, 4041–4048 Search PubMed.
- X. Chi, M. E. Itkis, R. W. Reed, R. T. Oakley, A. W. Cordes and R. C. Haddon, J. Phys. Chem. B, 2002, 106, 8278–8287 Search PubMed.
- X. Chi, M. E. Itkis, F. S. Tham, R. T. Oakley, A. W. Cordes and R. C. Haddon, Int. J. Quantum Chem., 2003, 95, 853–865 Search PubMed.
- P. Liao, M. E. Itkis, R. T. Oakley, F. S. Tham and R. C. Haddon, J. Am. Chem. Soc., 2004, 126, 14297–14302 Search PubMed.
- X. Chi, M. E. Itkis, B. O. Patrick, T. M. Barclay, R. W. Reed, R. T. Oakley, A. W. Cordes and R. C. Haddon, J. Am. Chem. Soc., 1999, 121, 10395–10402 Search PubMed.
- S. K. Pal, M. E. Itkis, R. W. Reed, R. T. Oakley, A. W. Cordes, F. S. Tham, T. Siegrist and R. C. Haddon, J. Am. Chem. Soc., 2004, 126, 1478–1484 Search PubMed.
- S. K. Pal, M. E. Itkis, F. S. Tham, R. W. Reed, R. T. Oakley, B. Donnadieu and R. C. Haddon, J. Am. Chem. Soc., 2007, 129, 7163–7174 Search PubMed.
- S. K. Pal, P. Bag, A. Sarkar, X. Chi, M. E. Itkis, F. S. Tham, B. Donnadieu and R. C. Haddon, J. Am. Chem. Soc., 2010, 132, 17258–17264 Search PubMed.
- R. C. Haddon, A. Sarkar, S. K. Pal, X. Chi, M. E. Itkis and F. S. Tham, J. Am. Chem. Soc., 2008, 130, 13683–13690 Search PubMed.
- J. Huang and M. Kertesz, J. Am. Chem. Soc., 2003, 125, 13334–13335 Search PubMed.
- J. Huang and M. Kertesz, J. Phys. Chem. A, 2007, 111, 6304–6315 Search PubMed.
- T. Taniguchi, T. Kawakami and K. Yamaguchi, Polyhedron, 2005, 24, 2274–2279 Search PubMed.
- T. Mao, T. Takeshi, K. Takashi, K. Yasutaka, O. Mitsutaka and Y. Kizashi, Chem. Lett., 2007, 36, 1000–1001 Search PubMed.
- M. Fumanal, M. Capdevila-Cortada, J. S. Miller and J. J. Novoa, J. Am. Chem. Soc., 2013, 135(37), 13814–13826 Search PubMed.
- G. S. Matouzenko, A. Bousseksou, S. A. Borshch, M. Perrin, S. Zein, L. Salmon, G. Molnar and S. Lecocq, Inorg. Chem., 2004, 43, 227–236 Search PubMed.
- N. Phukkaphan, D. L. Cruickshank, K. S. Murray, W. Phonsri, P. Harding and D. J. Harding, Chem. Commun., 2017, 53, 9801–9804 Search PubMed.
- T. Fujinami, K. Nishi, D. Hamada, K. Murakami, N. Matsumoto, S. Iijima, M. Kojima and Y. Sunatsuki, Inorg. Chem., 2015, 54, 7291–7300 Search PubMed.
- A. Paul, R. Nasani, A. Mondal, S. Roy, S. Vela and S. Konar, Cryst. Growth Des., 2020, 20(10), 6296–6301 Search PubMed.
- D.-H. Tuo, C. Chen, H. Ruan, Q.-Q. Wang, Y.-F. Ao, X. Wang and D.-X. Wang, Angew. Chem., Int. Ed., 2020, 59, 14040–14043 Search PubMed.
- H. M. Blatter and H. Lukaszewski, Tetrahedron Lett., 1968, 9, 2701–2705 Search PubMed.
- Y. Ji, L. Long and Y. Zheng, Mater. Chem. Front., 2020, 4, 3433–3443 Search PubMed.
- F. J. M. Rogers, P. L. Norcott and M. L. Coote, Org. Biomol. Chem., 2020, 18, 8255–8277 Search PubMed.
- C. P. Constantinides, P. A. Koutentis, H. Krassos, J. M. Rawson and A. J. Tasiopoulos, J. Org. Chem., 2011, 76, 2798–2806 Search PubMed.
- L. L. Patera, S. Sokolov, J. Z. Low, L. M. Campos, L. Venkataraman and J. Repp, Angew. Chem., Int. Ed., 2019, 58, 11063–11067 Search PubMed.
- J. Z. Low, G. Kladnik, L. L. Patera, S. Sokolov, G. Lovat, E. Kumarasamy, J. Repp, L. M. Campos, D. Cvetko and A. Morgante, et al. , Nano Lett., 2019, 19, 2543–2548 Search PubMed.
- P. A. Koutentis and D. Lo Re, Synthesis, 2010, 2075–2079 Search PubMed.
- P. Kaszyński, C. P. Constantinides and V. G. Young, Angew. Chem., Int. Ed., 2016, 55, 11149–11152 Search PubMed.
- J. A. Grant, Z. Lu, D. E. Tucker, B. M. Hockin, D. S. Yufit, M. A. Fox, R. Kataky, V. Chechik and A. C. O’Donoghue, Nat. Commun., 2017, 8, 15088 Search PubMed.
- I. S. Morgan, A. Mansikkamäki, G. A. Zissimou, P. A. Koutentis, M. Rouzières, R. Clérac and H. M. Tuononen, Chem. – Eur. J., 2015, 21, 1–12 Search PubMed.
- I. S. Morgan, A. Peuronen, M. M. Hänninen, R. W. Reed, R. Clérac and H. M. Tuononen, Inorg. Chem., 2013, 53, 33–35 Search PubMed.
- R. Nasani, T. N. S. Sidharth, S. Roy, A. Mondal, J. M. Rawson and S. Konar, Dalton Trans., 2019, 48, 14189–14200 Search PubMed.
- Y. Zhang, Y. Zheng, H. Zhou, M.-S. Miao, F. Wudl and T.-Q. Nguyen, Adv. Mater., 2015, 27, 7412–7419 Search PubMed.
- Y. Zheng, M.-S. Miao, G. Dantelle, N. D. Eisenmenger, G. Wu, I. Yavuz, M. L. Chabinyc, K. N. Houk and F. Wudl, Adv. Mater., 2015, 27, 1718–1723 Search PubMed.
- C. P. Constantinides, A. A. Berezin, M. Manoli, G. M. Leitus, G. A. Zissimou, M. Bendikov, J. M. Rawson and P. A. Koutentis, Chem. – Eur. J., 2014, 20, 5388–5396 Search PubMed.
- C. P. Constantinides, A. A. Berezin, M. Manoli, G. M. Leitus, M. Bendikov, J. M. Rawson and P. A. Koutentis, New J. Chem., 2014, 38, 949–954 Search PubMed.
- C. P. Constantinides, E. Carter, D. M. Murphy, M. Manoli, G. M. Leitus, M. Bendikov, J. M. Rawson and P. A. Koutentis, Chem. Commun., 2013, 49, 8662–8664 Search PubMed.
- C. P. Constantinides, P. A. Koutentis and J. M. Rawson, Chem. – Eur. J., 2012, 18, 15433–15438 Search PubMed.
- C. P. Constantinides, P. A. Koutentis and J. M. Rawson, Chem. – Eur. J., 2012, 18, 7109–7116 Search PubMed.
- Y. Takahashi, N. Tsuchiya, Y. Miura and N. Yoshioka, New J. Chem., 2018, 42, 9949–9955 Search PubMed.
- A. A. Hande, P. Baylère, P. Kaszyński and A. Chrostowska, J. Phys. Chem. A, 2020, 124, 9777–9782 Search PubMed.
- P. Bartos, B. Anand, A. Pietrzak and P. Kaszyński, Org. Lett., 2020, 22, 180–184 Search PubMed.
- B. Yan, J. Cramen, R. McDonald and N. L. Frank, Chem. Commun., 2011, 47, 3201–3203 Search PubMed.
- N. Ben Amor and D. Maynau, Chem. Phys. Lett., 1998, 286, 211–220 Search PubMed.
- J. P. Malrieu, R. Caballol, C. J. Calzado, C. de Graaf and N. Guihéry, Chem. Rev., 2013, 114, 429–492 Search PubMed.
- M. Fumanal, S. Vela, J. J. Novoa and J. Ribas-Arino, Chem. Commun., 2015, 51, 15776–15779 Search PubMed.
- G. D. McManus, J. M. Rawson, N. Feeder, J. van Duijn, E. J. L. McInnes, J. J. Novoa, R. Burriel, F. Palacio and P. Oliete, J. Mater. Chem., 2001, 11, 1992–2003 Search PubMed.
- H. Matsuzaki, W. Fujita, K. Awaga and H. Okamoto, Phys. Rev. Lett., 2003, 91, 017403 Search PubMed.
- J. M. Rawson and J. J. Hayward, Book Chapter, 2013.
- W. Fujita, K. Awaga, H. Matsuzaki and H. Okamoto, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 65, 064434 Search PubMed.
- T. Kawano, I. Katayama, J. Ohara, M. Ashida and J. Takeda, J. Phys. Soc. Jpn., 2013, 83, 014713 Search PubMed.
- A. Alberola, O. P. Clements, R. J. Collis, L. Cubbitt, C. M. Grant, R. J. Less, R. T. Oakley, J. M. Rawson, R. W. Reed and C. M. Robertson, Cryst. Growth Des., 2008, 8, 155–161 Search PubMed.
- T. M. Barclay, A. Wallace Cordes, N. A. George, R. C. Haddon, R. T. Oakley, T. T. M. Palstra, G. W. Patenaude, R. W. Reed, J. F. Richardson and H. Zhang, Chem. Commun., 1997, 873–874, 10.1039/A700310B.
- K. Molcanov and B. Kojic-Prodic, IUCrJ, 2019, 6, 156–166 Search PubMed.
- E. Coronado and P. Day, Chem. Rev., 2004, 104, 5419–5448 Search PubMed.
- H. Endres in Extended Linear Chain Compounds, ed. J. S. Miller, Springer, Plenum Press, New York, 1983, vol. 3, pp. 263–312 Search PubMed.
- K. Molčanov, V. Stilinović, A. Šantić, N. Maltar-Strmečki, D. Pajić and B. Kojić-Prodić, Cryst. Growth Des., 2016, 16, 4777–4782 Search PubMed.
- K. Molčanov, Z. Mou, M. Kertesz, B. Kojić-Prodić, D. Stalke, S. Demeshko, A. Šantić and V. Stilinović, Chem. – Eur. J., 2018, 24, 8292–8297 Search PubMed.
- R. G. Hicks, M. T. Lemaire, L. Öhrström, J. F. Richardson, L. K. Thompson and Z. Xu, J. Am. Chem. Soc., 2001, 123, 7154–7159 Search PubMed.
- L. Norel, J.-B. Rota, L.-M. Chamoreau, G. Pilet, V. Robert and C. Train, Angew. Chem., Int. Ed., 2011, 50, 7128–7131 Search PubMed.
- A. Mizuno, H. Benjamin, Y. Shimizu, Y. Shuku, M. M. Matsushita, N. Robertson and K. Awaga, Adv. Funct. Mater., 2019, 29, 1904181 Search PubMed.
- Y. Le Gal, T. Roisnel, P. Auban-Senzier, N. Bellec, J. Íñiguez, E. Canadell and D. Lorcy, J. Am. Chem. Soc., 2018, 140, 6998–7004 Search PubMed.
- I. Alcón, R. Santiago, J. Ribas-Arino, M. Deumal, I. de P. R. Moreira and S. T. Bromley, Nat. Commun., 2021, 12, 1705 Search PubMed.
- S. Wu, M. Li, H. Phan, D. Wang, T. S. Herng, J. Ding, Z. Lu and J. Wu, Angew. Chem., Int. Ed., 2018, 57, 8007–8011 Search PubMed.
- Y. Jiang, I. Oh, S. H. Joo, O. Buyukcakir, X. Chen, S. H. Lee, M. Huang, W. K. Seong, J. H. Kim and J.-U. Rohde, et al. , ACS Nano, 2019, 13, 5251–5258 Search PubMed.
- I. Alcón, F. Viñes, I. de P. R. Moreira and S. T. Bromley, Nat. Commun., 2017, 8, 1957 Search PubMed.
- K. T. Butler, A. Walsh, A. K. Cheetham and G. Kieslich, Chem. Sci., 2016, 7, 6316–6324 Search PubMed.
| This journal is © The Royal Society of Chemistry 2021 |