Open Access Article
Open Access ArticleInduced fit activity-based sensing: a mechanistic study of pyrophosphate detection with a “flexible” Fe-salen complex†
Prerna
Yadav
a,
Olivier
Blacque
 a,
Andreas
Roodt
a,
Andreas
Roodt
 *b and
Felix
Zelder
*b and
Felix
Zelder
 *a
*a
aDepartment of Chemistry, University of Zurich, Winterthurerstrasse 190, CH-8057 Zurich, Switzerland. E-mail: felix.zelder@chem.uzh.ch; Fax: +4144 635 6803; Web: http://www.felix-zelder.net
bDepartment of Chemistry, University of the Free State, PO Box 339, Bloemfontein 9300, South Africa. E-mail: RoodtA@ufs.ac.za; Tel: +051 4012547 Web: http://www.ufs.ac.za/natagri/departments-and-divisions/chemistry-home/general/staff
First published on 8th June 2021
Abstract
Activity-based sensing of biological targets is attracting increasing attention. In this work, we report detailed UV-Vis and fluorescence mechanistic studies on an Fe-salen based probe, [FeIII{salenMeCl2(SO3)2}OH2]− for pyrophosphate (PPi) detection. In the presence of PPi as an analyte, the probe disassembles into its molecular subunits and releases a fluorescent signal. Our studies illustrate that the aqua form of the complex (1-OH2) is the active species and that upon substitution of Fe-coordinated H2O and an initial end-on coordination of HP2O73−, the “trapped” pyrophosphate species switches from a monodentate to a bidentate coordination mode (i.e. linkage isomerism) via a probable equilibrium process. The elusive intermediate is further stabilized by a hydrogen bonding interaction that activates the probe for the subsequent final irreversible rate-limiting step, and allows selective discrimination between the other pyrophosphate (H2P2O72− and P2O74−) species in favour of the HP2O73−. The flexible mode of molecular recognition and binding of HP2O73− by the tetradentate probe 1-OH2 is unexpected and most effective at physiological pH, and has precedence in enzymatic catalysis (i.e. induced fit principle). These binding properties explain the previously observed outstanding selectivity of 1-OH2 for pyrophosphate over other (poly)oxophosphates and potentially competing analytes.
Introduction
Activity-based sensing (ABS) attracts increasing attention for elucidating the roles and importance of chemical species in biological systems.1,2In this context, enormous progress has been observed in the development and application of chemosensors for detecting small reactive molecules of the carbon-,3,4 oxygen-,5,6 nitrogen-5–7 and sulfur families.6,8,9 In contrast to these developments, chemical methods for sensing phosphorus containing compounds in biological environments are scarce.10–13 Phosphates are ubiquitous in biological systems and play pivotal structural and functional roles ranging from its occurrence in the skeleton to signal transduction and energy storage processes.14,15 These biologically important anions are present in multiple facets and phosphates are encountered in different protonated forms of inorganic mono- and polyanions or as covalently bound building blocks of natural products such as pyrophosphate (PPi),16 adenosine triphosphate (ATP) or vitamin B12.17,18 For example, H4P2O7 is a four-proton donor with pKa values of 0.85, 1.96, 6.60 and 9.41![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 19 and hence, at physiological pH of 7.40, PPi is encountered as a mixture of HP2O73− (86%) and H2P2O72− (14%).11,20
19 and hence, at physiological pH of 7.40, PPi is encountered as a mixture of HP2O73− (86%) and H2P2O72− (14%).11,20
The Zelder group and others are interested in the development of activity-based probes to detect and study the roles of phosphates in biological systems, in the environment and in foodstuff.11,21–23 For this purpose, fluorescent probes are advantageous, but selective sensing of the target analyte in the presence of a pool of related bioavailable, competing phosphates is highly challenging.24–27 Genetically encoded and aptamer based systems offer interesting opportunities,28–30 whereas cost-effective small-molecular chemical systems are still rare. Important examples of the latter include a boronic acid functionalized rhodamine derivative for detecting mitochondrial ATP as well as Zn-terpyridine system for sensing cellular PPi.27,31 Two of us introduced Fe-salen complexes for selectively detecting PPi in cancer cells and in foodstuff.11,21,23 The FeIII complex 1-OH2 (Fig. 1A) exhibits a square pyramidal coordination geometry and is composed of four (i–iv) subunits:23 a central FeIII-ion (i), a 1,2-propanediamine backbone (6) (ii), two 3-chloro-5-sulfosalicylaldehyde moieties (4) (iii) and an apical water ligand (iv; Fig. 1A).23 Upon interaction with PPi, the metal complex disassembles and unleashes the fluorescent signaling unit 4 (Fig. 1A).23 Importantly, discrimination between PPi and other anions including related phosphates such as inorganic phosphate, ATP and ADP was demonstrated.23 Mechanistic details on the nature of the active species, the molecular recognition and the binding event as well as the irreversible disassembly process have however not been studied so far.
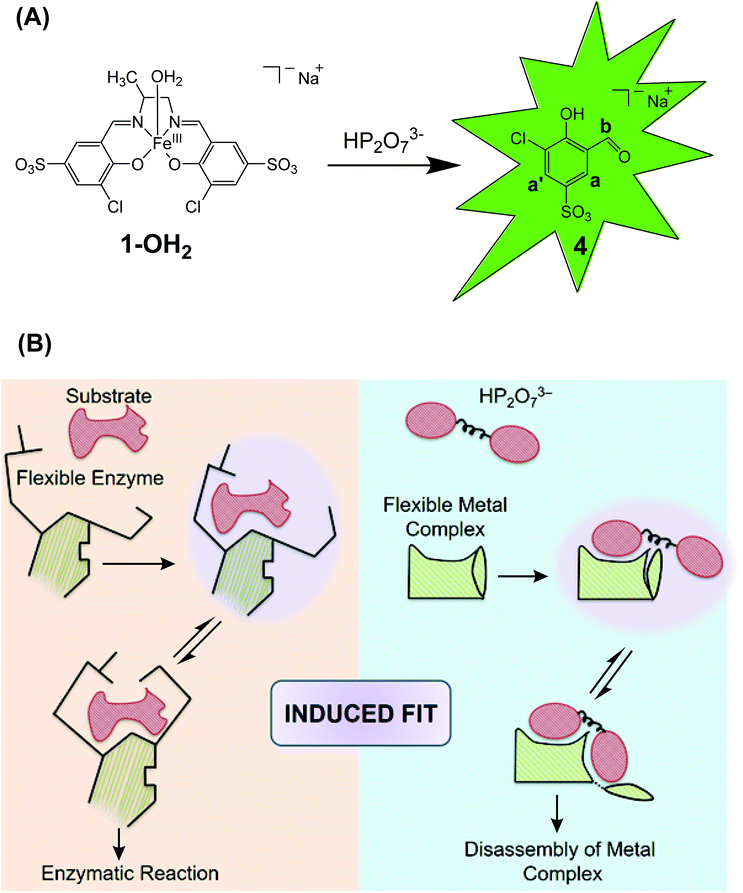 | ||
| Fig. 1 A: Liberation of the signaling unit 4 upon disassembly of the Fe-complex 1-OH2 with HP2O73−. B: Schematic comparison of the induced fit mechanism in enzymatic catalysis32 with the analyte-triggered disassembly of a “flexible” metal complex as described in this study for the reaction between 1-OH2 and HP2O73−. | ||
Thus, herein we present a detailed kinetic-mechanistic study on the structurally “flexible” probe 1-OH2 for the fluorometric detection of pyrophosphate (Fig. 1). In particular, we unravel an unprecedented reorganization of the FeIII-active site of 1-OH2 upon binding of the analyte (i.e. HP2O73−; Fig. 1B right). This PPi-induced structural change of the iron binding site of 1-OH2 is a pre-requisite for triggering the subsequent decomposition of the probe and liberation of the fluorescent signaling unit 4. The initial recognition and binding process of PPi by 1-OH2 is reminiscent to the induced fit binding of substrates by “flexible” enzymes such as phosphoglucomutase described with Koshland's induced fit theory (Fig. 1B left).32,33
Experimental section
Materials
Complex 1-OH2 was synthesized as its sodium salt as reported earlier.23 Sodium salts of PPi and F− were used in the kinetic studies. Unless otherwise stated, all chemicals were of reagent grade and purchased from Sigma-Aldrich-Merck, Fluka, Apollo Scientific or Alfa Aesar. Solvents for reactions were of p.a. grade. Stock solutions for kinetic experiments were prepared in Milli-Q H2O.Instrumentation
pH: Metrohm 827 pH meter equipped with pH sensitive electrode was employed. UV-Vis spectra: Cary Series Spectrophotometer (Agilent technologies); λmax in nm. UV spectra were recorded between 230 and 800 nm at 1.2 nm resolution and 20 points per s. Fluorescence spectra: Luminescence spectrometer, PerkinElmer, LS 50B. Unless stated, the slit-widths for the fluorescence experiments were kept at 10 nm (excitation) and 10 nm (emission) and the excitation wavelength was set at 385 nm. Unless stated, a UV Fused Silica Metallic Neutral Density Filter (FSQ-ND05) with optical density of 0.5 (from Newport) was used for fluorescence studies. 1H-NMR spectra in D2O; Bruker AV-401 (400 MHz) or Bruker AV2-500 (500 MHz); d in ppm rel. to TMS (d 0.00), J in Hz.Kinetic studies and data treatment
All UV-Vis and fluorescence kinetic experiments were carried out in a quartz cuvette (3.5 mL, 10 mm) without protection from air under pseudo first-order reaction conditions. Unless otherwise stated, all kinetic experiments were carried out with complex 1-OH2 (16 μM) at pH 7.35 ([Tris buffer] = 10 mM) at five different temperatures (12, 18, 25, 32 and 38 °C) and in presence of seven different concentrations of PPi (0.16, 0.24, 0.32, 0.48, 0.56, 0.64 and 0.80 mM). pH studies were performed at thirteen different pH values: 4.50, 5.00, 5.36, 5.71, 6.02, 6.33, 6.70, 7.00, 7.35, 7.67, 8.12, 8.42 and 9.40 ([Britton Robinson buffer] = 10 mM). Absorption and emission traces were collected over time until completion of reaction indicated by saturation. Origin 2020 and Micromath Scientist34 were used for fitting the kinetic traces and other specific functions. The observed pseudo first-order rate constants were obtained from least-squares (L.S.) fits of absorbance at 385 nm and emission at 500 nm (λex = 385 nm) vs. time traces to an appropriate first-order exponential,35 as described previously and illustrated in Fig. 3 and ESI.†![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 36–41 In Fig. 3–6, the solid lines indicate the L.S. fits/simulations of the respective experimental data (shown as individual points) to appropriate functions (details shown in the ESI†).
36–41 In Fig. 3–6, the solid lines indicate the L.S. fits/simulations of the respective experimental data (shown as individual points) to appropriate functions (details shown in the ESI†).
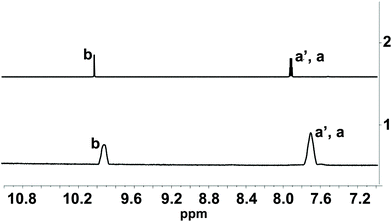 | ||
| Fig. 2 Line 1: 1H NMR spectra of 1-OH2* (2 mM) in the presence of PPi (10 equiv.; 20 mM; incubation time: 30 min) at pD 7.35 (D2O, [Tris buffer] = 10 mM). Line 2: 1H NMR spectra of pure signaling aldehyde 4 in D2O. Characteristic protons are indicated in Fig. 1A. * The 1H NMR spectrum of 1-OH2 did not show any signal in this region due to the paramagnetism of the probe. | ||
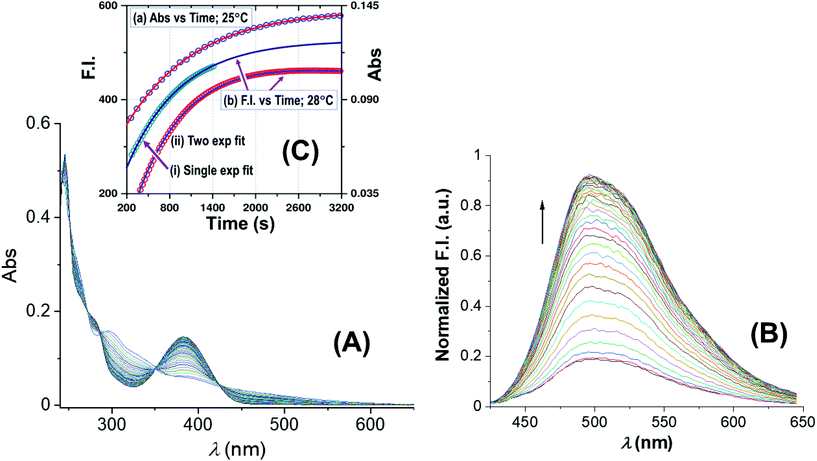 | ||
| Fig. 3 Spectral changes of the reaction between 1-OH2 (16 μM) and PPi (30 equiv.; 0.48 mM) with time at pH 7.35 ([Tris buffer] = 10 mM) at 25 °C: (A) absorbance vs. time scans; (B) fluorescence vs. time scans at 28 °C; inset (C): associated time traces of changes in absorbance at 385 nm and fluorescence emission at 500 nm (λex = 385 nm) illustrating similar kinetics, L.S. fitted to a typical first-order exponential (see text), yielding values for (a) kobs(Abs) = (1.025 ± 0.008) × 10−3 s−1, and (b) for kobs(Flu) = (1.30 ± 0.03) × 10−3 (single exponential) and kobs(Flu) = (1.280 ± 0.006) × 10−3 (two exponential) s−1, respectively (text; ESI Fig. S5†). Note that for clarity the y-axis of the single exponential F.I. trace indicated by (i) has been shifted by ca. +100 F.I. units to ensure no overlap with trace (ii) in the illustration. | ||
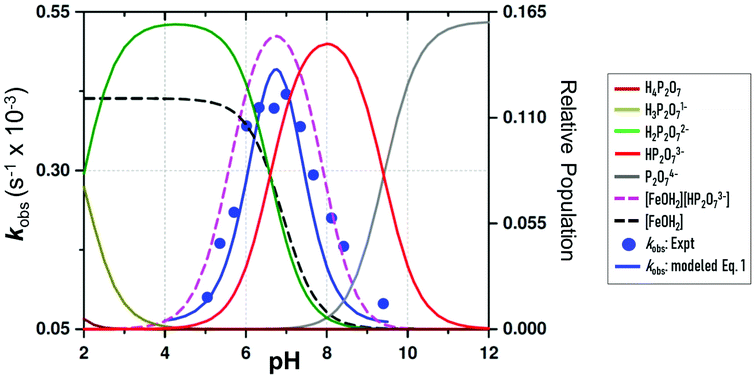 | ||
| Fig. 4 pH dependence of the observed pseudo first-order rate constant (kobs) (blue points) for the reaction between 1-OH2 (16 μM) and PPi (10 equiv.; 0.16 mM) at 25 °C. The line (blue curve) shows a modeled fit from all data at 25 °C, including those obtained from the fluorescence traces at 28 °C to the overall total rate law expression, eqn (1). This was obtained using kPPi = 3.1 × 10−3 s−1; and Keq = 2700 M−1, as well as a slow reaction concurrent to kPPi, as intercept, k22 = 6.0 × 10−5 s−1, to model the best visual fit [restrained to within the large relative standard deviations as expected: (i) due to the complexity of the system and model utilised, and (ii) having two dependent variables simultaneously] for the parameters kPPi and Keq. Also shown are relative speciation curves of PPi vs. pH, correlated to the pH dependency of kobs, as well as the pH speciation of 1-OH2 (black). These are all compared to the product of the populations of 1-OH2 and HP2O73− (pink). | ||
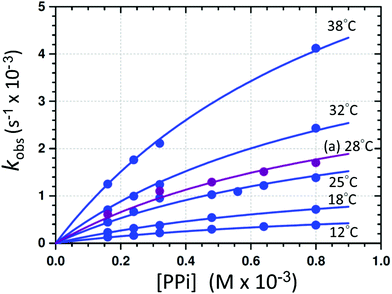 | ||
| Fig. 5 Individual L.S. fits of kobsvs. [PPi]tot (eqn (1)) at different temperatures and pH 7.35 ([Tris buffer] = 10 mM). (a) The purple line indicates the profile obtained from the F.I. vs. time traces at 28 °C. A global fit was additionally performed to determine the activation parameters (sections S1.1, S4, and Fig. S6†). | ||
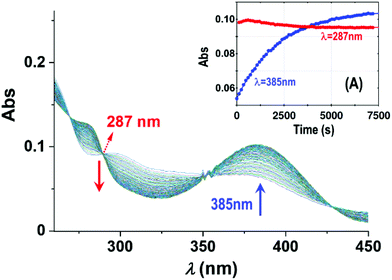 | ||
| Fig. 6 Absorbance changes of 1-OH2 (16 μM) around the isosbestic point (287 nm) with time in the presence of PPi (10 equiv.; 0.16 mM) at pH 7.35 ([Tris buffer] = 10 mM) and 12 °C illustrating the presence of earlier reactions. Inset (A): L.S. fits of Abs vs. time at 287 nm (red) and 385 nm (blue), respectively, showing the small absorbance changes of the first reactions (induction period) and underlining the small absorbance changes therewith, not influencing the individual fits and kinetic data as illustrated in the kobsvs. [PPi]tot graph in Fig. 3 and 5. | ||
Computational details
Density functional theory (DFT) calculations were carried out using the Gaussian 09 program package.42 The hybrid functional B3LYP43 was chosen in association with the standard 6-31G(d) basis set44 and the conductive polarizable continuum model (CPCM)45,46 for the solvent effects (water). The optimized ground state structures were obtained by unrestricted calculations and confirmed to be potential energy minima by vibrational frequency calculations at the same level of theory (no negative frequency).Results and discussion
PPi-triggered disassembly of complex 1-OH2
The PPi-triggered disassembly of 1-OH2 into the signaling unit 3-chloro-5-sulfosalicylaldehyde (4), 1,2-propanediamine (6) and Fe(PPi)n (5) (Scheme 1) was established previously based on the following observations.23 Firstly, upon addition of PPi (10 equiv.; 0.16 mM) to an aq. soln. of 1-OH2 (16 μM), the formation of a new absorption band at 385 nm was observed in the UV-Vis spectrum and a simultaneous 3.5-fold enhanced emission at 500 nm was observed with fluorescence spectroscopy (see also Fig. 3).23 These characteristic spectroscopic changes were unambiguously attributed to the liberation of 4 from complex 1-OH2.23 Moreover, these observations were supported by mass spectrometric and 1H NMR studies.23 In the latter experiments, formation of 4 from 1-OH2 (2 mM) was observed within 30 min at pD 7.35 ([Tris buffer] = 10 mM) after the addition of PPi (10 equiv.; 20 mM). Remarkably, we did not obtain any evidence for the intermediate formation of the metal-free salen ligand from disassembly experiments in deuterated H2O (Fig. 2).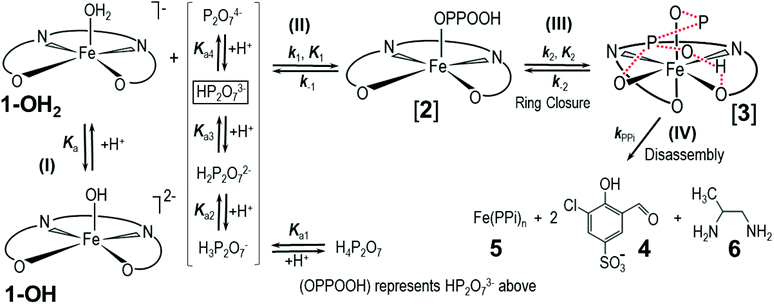 | ||
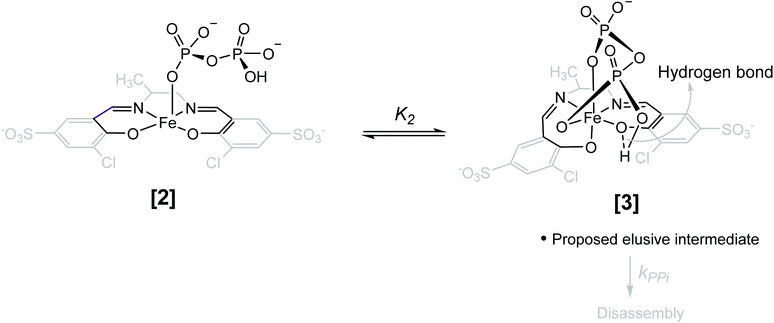
| Scheme 1 Simplified reaction scheme for the disassembly as studied kinetically, with reactant species 1-OH2 and 1-OH (interrelated by the acid dissociation constant Ka, and with [1]tot47). Compounds [2] and [3] are assumed reactive intermediates, 5 = final Fe(PPi)n species and 4 = 3-chloro-5-sulfosalicylaldehyde. [PPi]tot = total pyrophosphate concentration, of which the parent tetra-acid exhibits four pKa values, denoted by Ka1, Ka2, Ka3 and Ka4. | ||
Kinetic studies of the disassembly mechanism
Fig. 3A reports UV-Vis spectral changes for the reaction between complex 1-OH2 (16 μM) and PPi (30 equiv.; 0.48 mM) at pH 7.35 ([Tris buffer] = 10 mM) and 25 °C as a function of time. Changes of absorbance at 385 nm indicate the release of the signaling unit 4 and depict a first-order behavior with a rate constant of kobs(Abs) = (1.025 ± 0.008) × 10−3 s−1 and a half-life of ca. 600 s (approx. 10 min) (Fig. 3 inset). Also shown in Fig. 3 is the concurrent fluorescence changes at 500 nm (λex = 385 nm) with time (at 28 °C), which is clearly very similar to that observed from the absorbance measurements with kobs(Flu) = (1.30 ± 0.03) × 10−3 (single exponential) and kobs(Flu) = (1.280 ± 0.006) × 10−3 (two exponential) s−1, respectively, taking into account the slight temperature increase.Five isosbestic points were observed in the Abs vs. time spectra at 253, 265, 287, 350 and 420 nm, (Fig. 3), potentially indicating a clean conversion to the final product(s).
The absorbance vs. time traces under the selected experimental conditions showed clear first-order changes, although preceded by earlier reactions, which exhibit corresponding small absorbance/fluorescence changes. Following the principal reaction, an additional process (more prominent at higher [PPi]) on the fluorescence traces is observed, indicative of interaction of the signaling unit 4 with PPi. This necessitated treatment of the F.I. vs. time data to a two-exponential function (Fig. 3; ESI, Fig. S5†) although a single exponential function, when used for the early parts of the reaction, also adequately described the reaction process. Although it was not possible to critically evaluate the exact pH and entering nucleophile dependencies of these reactions with the required accuracy, these could nevertheless be interpreted as confirmation of the preceding equilibria K1 and K2 as indicated in Scheme 1.
It is expected that the rate law for the overall process should display pH dependent behavior since, as indicated above, the pyrophosphoric acid exhibits four successive pKa values,19 while 1-OH2 has one pKa value, forming the doubly charged anionic hydroxido species, 1-OH.23 Moreover, it is further a logic conclusion that 1-OH2, upon reacting with the PPi, is expected to show at least a first-order dependence on the PPi as entering nucleophilic species. Finally, the overall reaction is expected to be a multi-step process, as depicted in Scheme 1 (vide infra).
Subsequently, the influence of pH on the reaction rate with fixed concentration of [PPi]tot and [1]tot47 was studied at 25 °C between pH 4.50 and 9.40 and the results are illustrated in Fig. 4 and the ESI (Fig. S1, Table S1†).
The pseudo first-order rate constants (kobs) as a function of pH48 depict a quite well-defined bell-shaped curve with a maximum around pH 7.00 (Fig. 4 blue line and blue data points) resembling a similar shape as the speciation curve of HP2O73− with a pKa3 of 6.60.23 (Fig. 4; red line). However, the pH at which the maximum value of the pseudo first-order rate constant is reached deviates from the pH value at which the maximum distribution of the HP2O73− is found (i.e. ∼pH 8.00). This behavior is nicely explained by considering only the aqua species (1-OH2) being the primary active entity to capture the HP2O73− analyte. In fact, the maximum selectivity between pH 7.00 and 7.50 agrees very well with the pH where the total population of [1-OH2] × [HP2O73−] reaches its maximum (Fig. 4: pink line). This behavior clearly confirms the specificity of the system to selectively accommodate only the tri-anionic pyrophosphate species (HP2O73−). Apparently, neither H3P2O7− (pKa1 = 0.85) nor H2P2O72− (pKa2 = 1.96)19 are sufficiently nucleophilic for substituting the aqua ligand in complex 1-OH2 (pKa = 6.90)19 as indicated by the rapid decrease of the reaction rates at more acidic pH values (<pH 6.00). This underlines the novel ability of 1-OH2 to selectively discriminate between the H2P2O72−/P2O74− anions (both present in significant amounts in the pH range studied) in favor of HP2O73−. Moreover, it agrees with the fact that at more basic pH values, even the presence of the highly charged P2O74− species (pKa4 = 9.41)19 does not trigger the disassembly reaction of 1-OH2, which might in turn suggests that hydrogen bonding in the ring closing step is important (see further below). It should be noted that there is an indication of a slow parallel reaction (data points at ca. pH 8.00–9.00), although it clearly does not significantly affect neither the specificity nor the selectivity of 1-OH2.
Having determined the aqua form of Fe-complex (1-OH2) and HP2O73− as the active species in the disassembly reaction, we studied the influence of increasing concentration of [PPi]tot on the reaction rate at the pH where the capturing of the HP2O73− is the most effective. Variations of [PPi]tot at pH 7.35 and 25 °C (Fig. 5 blue graph) provide evidence of faster, preceding reactions, i.e., saturation kinetics with a rate-limiting dependence on [PPi]tot. The saturation kinetics provides excellent support for concluding preceding reactions, as postulated in Fig. 1 and Scheme 1.49,50 This behavior is thus supporting a rapid overall pre-equilibrium reaction, denoted by Keq and within this report indicated to be the net of initial coordination (K1) followed by a linkage isomerism (K2) succeeded by a final rate limiting first-order formation of products 4 and 5 (Scheme 1), denoted by kPPi. Based on these observations and the detailed study of the following systematic kinetic experiments, we summarize the mechanism of the PPi-triggered disassembly of Fe-salen complex 1-OH2 into its molecular building blocks 4, 5 and 6 in Scheme 1.
The total rate law may be derived from Scheme 1, yielding the complete expression of the pseudo first-order rate constant in eqn (1), which describes all the observations made in this study related to the total process.
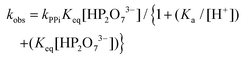 | (1) |
In eqn (1), the concentration of the tri-anionic species HP2O73− is given by eqn (2).
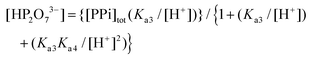 | (2) |
In particular, the net total reactivity and specificity of 1-OH2 towards the tri-anionic HP2O73− species is well addressed in eqn (1), when [PPi] ≫ [1]tot, and clearly describes
(a) The total acid–base behavior of both the PPi and the 1-OH2 species (Fig. 4);
(b) The plateau reached at high [PPi]tot (Fig. 5);51
(c) The simultaneous net changes in absorbance and fluorescence induced (Fig. 3).
(d) The small, potential concurrent reaction (k22, Fig. 4; caption) to the final step kPPi gives a value of zero within standard deviation, not justifying inclusion, see Fig. 5 and 6.
Finally, it should be noted that in eqn (1) and (2), only Ka3, Ka4 and the acid dissociation constant of the 1-OH2 species (Ka) are included, since at the pH values evaluated (pH > 4) the total PPi equals the concentration of the di-anionic species, H2P2O72−, which then dissociates further as the pH increases. Additional and detailed information relevant to the complete derivation of eqn (1) is given in the ESI† (sections S1.1 and S2).
Based on Scheme 1, and on the observation that virtually identical pseudo first-order rate constants are obtained from the absorbance/fluorescence vs. time data (Fig. 3), we proceeded to study the effect of a variation of [PPi] on both these properties in more detail. This is illustrated in Fig. 5 and confirms that similar individual rate constants are obtained, and that the same kobsvs. [PPi] profile is observed from both the absorbance/fluorescence vs. time data, yielding limiting kinetics as predicted by eqn (1).
The disassembly reactions of 1-OH2 and PPi were performed at six different temperatures and different concentrations of [PPi]tot (Fig. 5; Fig. S2–S4, Table S2†). As expected, the individual pseudo first-order rate constants increase with increasing temperatures (Fig. 5) and a least-squares (L. S.) fit analysis resulted in the determination of the equilibrium constant Keq of (4300 ± 400) M−1 and the first-order rate constant at 25 °C kPPi of (3.2 ± 0.2) × 10−3 s−1 (Table 1). This agrees very well with that obtained from the global fit (Table 1; Fig. S6†), as well as from the pH fit reported in Fig. 4. The latter defines the rate-determining step in reaction (IV) (Scheme 1), that is the formation of the signaling unit 4, and 5. We assume that the latter is a Fe-pyrophosphate species in agreement with previous investigations (Scheme 1).52 Results of the rate determining reaction (IV) were obtained by extended UV-Vis studies and are summarized in Fig. 5 and Table 1.
| Parameter | Temperature (°C) | Value |
|---|---|---|
a ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Fig. 5.
b Fig. 5.
b ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Fig. 4; eqn (1), using all kobs values at 25 °C (both variation of pH and [PPi] used).
c Fluorescence data, see Fig. 5.
d Average from six temperatures: 12, 18, 25, 32, 38 °C (abs vs. time) and 28 °C (F.I. vs. time).
e Global fit, see ESI, Fig. S6.† Fig. 4; eqn (1), using all kobs values at 25 °C (both variation of pH and [PPi] used).
c Fluorescence data, see Fig. 5.
d Average from six temperatures: 12, 18, 25, 32, 38 °C (abs vs. time) and 28 °C (F.I. vs. time).
e Global fit, see ESI, Fig. S6.†
|
||
| k PPi (s−1) | 12 | (9.09 ± 0.10) × 10−4 |
| 18 | (1.66 ± 0.13) × 10−3 | |
| 25 | (3.2 ± 0.2) × 10−3 | |
| 25b | (3.5 ± 0.7) × 10−3 | |
| 28c | (4.1 ± 0.2) × 10−3 | |
| 32 | (5.5 ± 0.3) × 10−3 | |
| 38 | (9.4 ± 0.5) × 10−3 | |
| K eq (M−1)a | 4300 ± 400 | |
| 25e | 4300 ± 400 | |
| 25b | 3500 ± 1100 | |
ΔH‡![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) e (kJ mol−1) e (kJ mol−1) |
— | 62 ± 1 |
ΔS‡![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) e (J K−1 mol−1) e (J K−1 mol−1) |
— | −86 ± 4 |
In an attempt to investigate the rapid pre-equilibrium (Keq) of the reaction between 1-OH2 and [PPi] in more detail, we analyzed deviations at the isosbestic point at 287 nm in the UV-Vis spectra in more detail (Fig. 6). We selected the lowest reaction temperature (12 °C) in an attempt to slow these down as much as possible to ensure accurate analysis thereof.
The subtle changes at this wavelength were observed early in the reaction at 12 °C but could hardly be detected at higher temperatures. The principal changes of absorbance vs. time at this wavelength correlate with reaction (IV) (Scheme 1; Fig. 6), following an “induction period” of <10 min. The latter is assumed to consist of preceding reactions which are attributed to two successive rapid equilibria (reactions (II) and (III); Scheme 2) as postulated in Scheme 1.
Based on this experimental proof, we assign the overall equilibrium constant Keq to the combination of the two equilibria with individual equilibrium constants K1 and K2 (Keq = K1K2) (Schemes 1 and 2). It thus defines the overarching equilibrium from 1-OH2 to [3]via[2], whereafter the disassembly is triggered. We assume that HP2O73− first substitutes the aqua ligand of 1-OH2 forming [2], in which the pyrophosphate entity acts as a monodentate ligand (Schemes 1 and 2). This binding mode preorganizes the other phosphate subunit of the Fe-bound PPi ligand for chelation via a postulated hydrogen bonding, and hence the PPi switches from a monodentate to a bidentate coordination mode (i.e. linkage isomerism) as depicted in the octahedral complex [3] (Schemes 1 and 2).50,53–55 Both intermediates have been confirmed by DFT calculations and intermediate [3] was found to be stabilized by 34.1 kcal mol−1 compared to the initial monocoordinated intermediate [2] (Fig. S7 and S8, section S5†). This is in agreement with the equilibrium also lying towards [3] compared to [2]. Such bidentate coordination mode has been recently observed in a FeIII-phenanthroline-PPi complex.56 Some precedence for strong hydrogen bonding at the O-donor atoms in tetradentate ligands is also found in the commercial 99mTc-radiopharmaceutical imaging agent, Ceretec, utilizing the multidentate hexamethylpropylene amine oxime ligand.57,58
It is therefore postulated that intermediate [3] is activated for the irreversible disassembly into its molecular building blocks by a hydrogen bond between the κ2-O,O′ pyrophosphate entity (HP2O73−) and the equatorial phenolato group of the salen ligand (Scheme 2). In fact, hydrogen bonds from hydrogen donors to the phenolate oxygen unit of metal–salen complexes are common structural features.59,60
This hypothesis was supported by accompanying fluorescence kinetic studies as performed and described herein. In particular, we followed the increase of emission intensity at 500 nm during the PPi-triggered disassembly reaction of 1-OH2, and as demonstrated earlier, this signal is univocally attributed to the liberation of the signaling unit 4 (Scheme 1) during the disassembly reaction. In the fluorescence studies, we collected fluorescence scans at 500 nm with time at different concentrations of [PPi]tot at 28 °C and pH 7.35 (Fig. S5†). The generation of fluorescence correlates exactly with reaction (IV), following the “induction period” of only a few minutes (Fig. 6; see also Fig. 3(C)). The respective kobs values at different [PPi] are summarized in Table S3† and illustrated in Fig. 5.
In summary it is concluded that although the “induction period” is clearly observed in the very early parts of the reaction in both the UV-Vis and the fluorescence kinetic studies, the spectral changes were too small and the associated relative standard deviations too large to allow for accurate analysis and was not pursued further.
However, in an attempt to further evaluate the initial substitution of the aqua ligand of complex 1-OH2 (Scheme 2; reaction (II)), we tested a monodentate nucleophile, namely, F− (0.16 mM) in kinetic studies at 12 °C and pH 7.35 and in the absence of PPi. These studies resulted only in a slow reaction that we assign to a background hydrolysis of the complex without significant observed coordination of the monodentate ligand to the iron center (Fig. S9†). In addition, utilization of the large excess of F− (8.00 mM) in combination with PPi did not lead to substantial changes in the pseudo first-order rate constant of the PPi-triggered disassembly reaction of complex 1-OH2 (Fig. S10†), although some changes in the total absorbance changes were indeed observed. This experiment suggests limited competition in the substitution of the aqua axial ligand in 1-OH2 by F− ions. Nevertheless, since the yield in absorbance was reduced, it indicates that there is some coordination by F− nucleophile in a probable parallel process, potentially trapping small amounts of 1-OH2 (Fig. S9†). However, since the experiments were performed under pseudo first-order conditions ([PPi] ≫ [1]tot), variations in [1-OH2] are not expected to influence the total kinetics observed. Moreover, as indicated for the preceding reactions with PPi (Fig. 6), small absorbance changes and large estimated standard deviations in traces with a monodentate nucleophile such as F− ions also rendered further accurate evaluation thereof unreliable and was not pursued further.
The initial steps of the disassembly process of the PPi selective probe 1-OH2 resemble the “induced fit” binding of a substrate to a protein during enzymatic catalysis,61 wherein the process is associated with a conformational change of the enzyme–substrate complex.32,61 In the disassembly of probe 1-OH2, the initial binding of HP2O73− is followed by a switch of the monodentate (κ1-O pyrophosphate) to a “bidentate” coordination mode (κ2-O,O′ pyrophosphate; Schemes 1 and 2). Based on kinetic evidence, we propose that this configurational change of the complex is associated with large conformational variations (also in agreement with the activation parameters, vide infra) that trigger the PPi-induced demetallation and subsequent release of signaling unit 4.
In contrast to observations with 1-OH2, most activity-based probes (ABP) follow the “key-lock” principle of molecular recognition for triggering a chemical irreversible reaction after binding of the analyte.1 We expand this concept herein to “induced fit” ABP that requires a large configurational and/or conformational change upon initial analyte binding (“induced fit” binding) for triggering the disassembly and signal transduction process.
Finally, the activation parameters of ΔS‡ = −86 ± 4 J K−1 mol−1 and ΔH‡ = 62 ± 1 kJ mol−1 for the disassembly reaction of 1-OH2 induced by PPi were obtained from a global fit analysis (section S1.1 and S6†) of the reactions monitored at different concentrations of [PPi]tot and temperatures as discussed in detail above (Fig. S2–S4 and S6†). The significant negative activation entropy associated with the final, rate-determining step is puzzling since the formation of both 4 and 5 overall might suggest a dissociative process. However, the significant structural changes required for the reorganization of intermediate [2] to [3] for triggering the disassembly (reaction (IV); Scheme 1), which in itself is a multi-step process, is assumed to be the origin of this behavior.
Conclusions
In recent years, the development of activity-based probes for biological analytes has attracted increasing attention. Despite enormous progress, mechanistic studies on the mode of analyte detection are still rare. Herein, we report a detailed kinetic-mechanistic evaluation on the detection of PPi with an Fe-salen activity-based probe following a disassembly reaction. The data presented herein illustrate that the aqua form of the complex (1-OH2) is the active species and that upon substitution of the Fe-coordinated aqua ligand and an initial end-on coordination of HP2O73− forms [2]. The tri-anionic pyrophosphate species is therefore selectively “trapped” following the switching from a monodentate to a bidentate coordination mode (i.e. linkage isomerism). The elusive intermediate [3] is further stabilized by an additional hydrogen bond, which activates the probe for the subsequent irreversible disassembly reaction and release of the fluorescent signal. The initial binding isomerism of pyrophosphate by the probe is unexpected and illustrates a structural flexible nature of the tetradentate FeIII-salen complex in the presence of HP2O73−. This unusual binding property nicely explain the previously observed outstanding selectivity of the probe for HP2O73−. Other analytes such as orthophosphate are however potentially too small and/or lack the chelating capability (e.g. F−), or are sterically too demanding (e.g. ATP) for inducing the required structural changes. Alternatively, they might lack the correct geometry and flexibility coupled with appropriate hydrogen donor capability within the metal complex to trigger the disassembly of the metal-analyte complex. This also explains the inability of the di- or tetra-anions of pyrophosphate (H2P2O72− and P2O74−) to significantly compete in the overall reaction. It is noteworthy that the mode of initial analyte binding and recognition by the “flexible” metal complex resembles the induced-fit principle in enzymatic catalysis. We anticipate that induced fit binding of anions and molecules to “flexible” metal complexes is not restricted to the combination of pyrophosphate species and Fe-salen complexes. Therefore, we envisage that flexible metal complexes will find interesting applications in analytical chemistry, but also catalysis, medicinal chemistry, material science and related areas in the near future.Conflicts of interest
The authors declare no competing financial interest.Acknowledgements
We acknowledge financial and general support by the Department of Chemistry of the University of Zurich. This work was financially supported by a grant of the Swiss National Science Foundation (F. Z.: grant-no.: 200021_169216). AR acknowledges financial assistance from the South African National Research Foundation (NRF), and Research Fund of the University of the Free State. This includes funding under the Swiss-South Africa joint research program (SSAJRP) from the SA NRF (AR: UID: 107802) as well as from the Competitive Program for Rated Researchers of the SA NRF (AR: UID 111698). Opinions, findings, conclusions, or recommendations expressed in this material are those of the authors and do not necessarily reflect the views of the NRF nor the SNF.Notes and references
- K. J. Bruemmer, S. W. M. Crossley and C. J. Chang, Activity-Based Sensing: A Synthetic Methods Approach for Selective Molecular Imaging and Beyond, Angew. Chem., 2020, 59, 13734–13762 Search PubMed.
- Y. Yang, Q. Zhao, W. Feng and F. Li, Luminescent Chemodosimeters for Bioimaging, Chem. Rev., 2013, 113, 192–270 Search PubMed.
- Y. Tang, Y. Ma, J. Yin and W. Lin, Strategies for designing organic fluorescent probes for biological imaging of reactive carbonyl species, Chem. Soc. Rev., 2019, 48, 4036–4048 Search PubMed.
- K. J. Bruemmer, T. F. Brewer and C. J. Chang, Fluorescent probes for imaging formaldehyde in biological systems, Curr. Opin. Chem. Biol., 2017, 39, 17–23 Search PubMed.
- X. Chen, X. Tian, I. Shin and J. Yoon, Fluorescent and luminescent probes for detection of reactive oxygen and nitrogen species, Chem. Soc. Rev., 2011, 40, 4783–4804 Search PubMed.
- X. Jiao, Y. Li, J. Niu, X. Xie, X. Wang and B. Tang, Small-Molecule Fluorescent Probes for Imaging and Detection of Reactive Oxygen, Nitrogen, and Sulfur Species in Biological Systems, Anal. Chem., 2018, 90, 533–555 Search PubMed.
- B. Dong, X. Kong and W. Lin, Reaction-Based Fluorescent Probes for the Imaging of Nitroxyl (HNO) in Biological Systems, ACS Chem. Biol., 2018, 13, 1714–1720 Search PubMed.
- M. C. Y. Chang, A. Pralle, E. Y. Isacoff and C. J. Chang, A selective, cell-permeable optical probe for hydrogen peroxide in living cells, J. Am. Chem. Soc., 2004, 126, 15392–15393 Search PubMed.
- J. Chan, S. C. Dodani and C. J. Chang, Reaction-based small-molecule fluorescent probes for chemoselective bioimaging, Nat. Chem., 2012, 4, 973–984 Search PubMed.
- H. J. Jessen, Phosphate Labeling and Sensing in Chemical Biology, Springer International Publishing, Switzerland, 2017 Search PubMed.
- P. Yadav and F. Zelder, Metal-Salen-based Probes for the Selective Detection of Phosphates via a Disassembly Approach, Chimia, 2020, 74, 252–256 Search PubMed.
- J. Wongkongkatep, A. Ojida and I. Hamachi, Fluorescence Sensing of Inorganic Phosphate and Pyrophosphate Using Small Molecular Sensors and Their Applications, Top. Curr. Chem., 2017, 375, 30 Search PubMed.
- S. Pal, T. K. Ghosh, R. Ghosh, S. Mondal and P. Ghosh, Recent advances in recognition, sensing and extraction of phosphates: 2015 onwards, Coord. Chem. Rev., 2020, 405, 213128 Search PubMed.
- A. E. Hargrove, S. Nieto, T. Zhang, J. L. Sessler and E. V. Anslyn, Artificial Receptors for the Recognition of Phosphorylated Molecules, Chem. Rev., 2011, 111, 6603–6782 Search PubMed.
- L. Stryer, Biochemistry, W. H., Freeman and Company, New York, 3rd edn, 1988 Search PubMed.
- “PPi” is the general term used for pyrophosphate, wherein no specific species are defined. When specific species of pyrophosphate are involved, the chemical formula with appropriate charge is used.
- F. Zelder, Recent trends in the development of vitamin B12 derivatives for medicinal applications, Chem. Commun., 2015, 51, 14004–14017 Search PubMed.
- J. K. Heinonen, Biological role of inorganic pyrophosphate, Kluwer Academic Publishers, Boston, 2001 Search PubMed.
- R. B. Stockbridge and R. Wolfenden, Enhancement of the Rate of Pyrophosphate Hydrolysis by Nonenzymatic Catalysts and by Inorganic Pyrophosphatase, J. Biol. Chem., 2011, 286, 18538–18546 Search PubMed.
- H. N. Po and N. M. Senozan, The Henderson-Hasselbalch Equation: Its History and Limitations, J. Chem. Educ., 2001, 78, 1499 Search PubMed.
- N. Kumari, H. Huang, H. Chao, G. Gasser and F. Zelder, A Disassembly Strategy for Imaging Endogenous Pyrophosphate in Mitochondria by Using an FeIII–salen Complex, ChemBioChem, 2016, 17, 1211–1215 Search PubMed.
- N. Kumari and F. Zelder, Detecting biologically relevant phosphates with locked salicylaldehyde probes in water, Chem. Commun., 2015, 51, 17170–17173 Search PubMed.
- P. Yadav, M. Jakubaszek, B. Spingler, B. Goud, G. Gasser and F. Zelder, FeIII-Salen-Based Probes for the Selective and Sensitive Detection of E450 in Foodstuff, Chem. – Eur. J., 2020, 26, 5717–5723 Search PubMed.
- D. H. Vance and A. W. Czarnik, Real-Time Assay of Inorganic Pyrophosphatase Using a High-Affinity Chelation-Enhanced Fluorescence Chemosensor, J. Am. Chem. Soc., 1994, 116, 9397–9398 Search PubMed.
- H. K. Cho, D. H. Lee and J.-I. Hong, A fluorescent pyrophosphate sensor via excimer formation in water, Chem. Commun., 2005, 13, 1690–1692 Search PubMed.
- D. H. Lee, S. Y. Kim and J.-I. Hong, A Fluorescent Pyrophosphate Sensor with High Selectivity over ATP in Water, Angew. Chem., Int. Ed., 2004, 43, 4777–4780 Search PubMed.
- S. Bhowmik, B. N. Ghosh, V. Marjomaki and K. Rissanen, Nanomolar Pyrophosphate Detection in Water and in a Self-Assembled Hydrogel of a Simple Terpyridine-Zn2+ Complex, J. Am. Chem. Soc., 2014, 136, 5543–5546 Search PubMed.
- H. Imamura, K. P. H. Nhat, H. Togawa, K. Saito, R. Iino, Y. K. Yamada, T. Nagai and H. Noji, Visualization of ATP levels inside single living cells with fluorescence resonance energy transfer-based genetically encoded indicators, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 15651 Search PubMed.
- J. Berg, Y. P. Hung and G. Yellen, A genetically encoded fluorescent reporter of ATP:ADP ratio, Nat. Methods, 2009, 6, 161–166 Search PubMed.
- T. Morii, M. Hagihara, S. Sato and K. Makino, In Vitro Selection of ATP-Binding Receptors Using a Ribonucleopeptide Complex, J. Am. Chem. Soc., 2002, 124, 4617–4622 Search PubMed.
- L. Wang, L. Yuan, X. Zeng, J. J. Peng, Y. Ni, J. C. Er, W. Xu, B. K. Agrawalla, D. D. Su, B. Kim and Y. T. Chang, A Multisite-Binding Switchable Fluorescent Probe for Monitoring Mitochondrial ATP Level Fluctuation in Live Cells, Angew. Chem., Int. Ed., 2016, 55, 1773–1776 Search PubMed.
- D. E. Koshland Jr., The Key–Lock Theory and the Induced Fit Theory, Angew. Chem., Int. Ed. Engl., 1995, 33, 2375–2378 Search PubMed.
- J. A. Yankeelov Jr. and D. E. Koshland Jr., Evidence for conformation changes induced by substrates of phosphoglucomutase, J. Biol. Chem., 1965, 240, 1593–1602 Search PubMed.
- MicroMath Scientist for Windows, Version 2.01, Copyright © 1986–1995, MicroMath, Inc., Utah, USA Search PubMed.
- {Aobs = A∞ − (A∞ − A0)e(−kobs.t)}.
- S. Otto, O. T. Alexander and A. Roodt, Observed structural and reactivity relationships in trans- [PtPh (L)2Cl] during the displacement reaction of Cl- by I- after alteration of the phosphine, arsenic and stibine ligands (L), S. Afr. J. Sci. Technol., 2019, 38, 180–194 Search PubMed.
- A. Brink, H. G. Visser and A. Roodt, Activation of Rhenium(I) Toward Substitution in fac-[Re(N,O′-Bid)(CO)3(HOCH3)] by Schiff-Base Bidentate Ligands (N,O′-Bid), Inorg. Chem., 2013, 52, 8950–8961 Search PubMed.
- A. Roodt, J. G. Leipoldt, L. Helm and A. E. Merbach, Equilibrium behavior and proton transfer kinetics of the dioxotetracyanometalate complexes of molybdenum(IV), tungsten(IV), technetium(V), and rhenium(V): carbon-13 and oxygen-17 NMR study, Inorg. Chem., 1994, 33, 140–147 Search PubMed.
- W. Purcell, A. Roodt, S. S. Basson and J. G. Leipoldt, Kinetic study of the reaction between trans-tetracyanodioxorhenate(V) and thiocyanate ions, Transition Met. Chem., 1989, 14, 224–226 Search PubMed.
- J. G. Leipoldt, R. V. Eldik, S. S. Basson and A. Roodt, Kinetics and mechanism of the reaction between trans-dioxotetracyanotungstate(IV) and azide in aqueous solution, Inorg. Chem., 1986, 25, 4639–4642 Search PubMed.
- A. Muller, S. Otto and A. Roodt, Rapid phosphorus(III) ligand evaluation utilising potassium selenocyanate, Dalton Trans., 2008, 650–657 Search PubMed.
- M. J. Frisch, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, T. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision D.01, Gaussian, Inc., Wallingford CT, 2013 Search PubMed.
- A. D. Becke, Density–functional thermochemistry. III. The role of exact exchange, J. Chem. Phys., 1993, 98, 5648–5652 Search PubMed.
- R. Ditchfield, W. J. Hehre and J. A. Pople, Self–Consistent Molecular–Orbital Methods. IX. An Extended Gaussian–Type Basis for Molecular–Orbital Studies of Organic Molecules, J. Chem. Phys., 1971, 54, 724–728 Search PubMed.
- M. Cossi, N. Rega, G. Scalmani and V. Barone, Energies, structures, and electronic properties of molecules in solution with the C-PCM solvation model, J. Comput. Chem., 2003, 24, 669–681 Search PubMed.
- R. Bauernschmitt and R. Ahlrichs, Treatment of electronic excitations within the adiabatic approximation of time dependent density functional theory, Chem. Phys. Lett., 1996, 256, 454–464 Search PubMed.
- [1] tot = [1-OH2] + [1-OH].
- D. A. Baldwin, D. M. R. de Sousa and R. M. A. von Wandruszka, The effect of pH on the kinetics of iron release from human transferrin, Biochim. Biophys. Acta, Gen. Subj., 1982, 719, 140–146 Search PubMed.
- C. J. Carrano and K. N. Raymond, Ferric ion sequestering agents. 2. Kinetics and mechanism of iron removal from transferrin by enterobactin and synthetic tricatechols, J. Am. Chem. Soc., 1979, 101, 5401–5404 Search PubMed.
- C. E. Brook, W. R. Harris, C. D. Spilling, W. Peng, J. J. Harburn and S. Srisung, Effect of Ligand Structure on the Pathways for Iron Release from Human Serum Transferrin, Inorg. Chem., 2005, 44, 5183–5191 Search PubMed.
- A. Roodt, H. G. Visser and A. Brink, Structure/reactivity relationships and mechanism from X-ray data and spectroscopic kinetic analysis, Crystallogr. Rev., 2011, 17, 241–280 Search PubMed.
- D. Winkler, S. Banke and P. Kurz, Fluorimetric Detection of Phosphates in Water Using a Disassembly Approach: A Comparison of FeIII-, ZnII-, MnII- and MnIII-salen Complexes, Z. Anorg. Allg. Chem., 2020, 646, 933–939 Search PubMed.
- T. J. Egan, D. C. Ross, L. R. Purves and P. A. Adams, Mechanism of iron release from human serum C-terminal monoferric transferrin to pyrophosphate: kinetic discrimination between alternative mechanisms, Inorg. Chem., 1992, 31, 1994–1998 Search PubMed.
- S. Hochreuther, S. T. Nandibewoor, R. Puchta and R. V. Eldik, Thermodynamic and kinetic behaviour of [Pt(2-methylthiomethylpyridine)(OH2)2]2+, Dalton Trans., 2012, 41, 512–522 Search PubMed.
- R. Romeo, L. M. Scolaro, M. R. Plutino, A. Romeo, F. Nicolo’ and A. D. Zotto, Ring Closure Kinetics of Bidentate Hemilabile P,N and P,S Ligands on a Platinum(II) Complex, Eur. J. Inorg. Chem., 2002, 2002, 629–638 Search PubMed.
- T. J. Greenfield, M. M. Turnbull, J. Zubieta and R. P. Doyle, Synthesis and structural and magnetic characterization of an Iron(III) pyrophosphate complex with 1,10′-phenanthroline, Inorg. Chim. Acta, 2019, 498, 119084 Search PubMed.
- S. Jurisson, D. Berning, W. Jia and D. Ma, Coordination compounds in nuclear medicine, Chem. Rev., 1993, 93, 1137–1156 Search PubMed.
- S. S. Jurisson and J. D. Lydon, Potential Technetium Small Molecule Radiopharmaceuticals, Chem. Rev., 1999, 99, 2205–2218 Search PubMed.
- C.-Y. Wong, W.-L. Man, C. Wang, H.-L. Kwong, W.-Y. Wong and T.-C. Lau, Proton-Bridged Dinuclear (salen)Ru Carbene Complexes: Synthesis, Structure, and Reactivity of {[(salchda)Ru
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C(OR)(CH
C(OR)(CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CPh2)]2·H}+, Organometallics, 2008, 27, 324–326 Search PubMed.
CPh2)]2·H}+, Organometallics, 2008, 27, 324–326 Search PubMed. - Y. Miyazato, K. Imaizumi, R. Tanaka, T. Wada and N. Matsushita, Preparation and Characterization of a μ-P2O7-μ-HPO4 Dinuclear Fe2(III, III) Complex, Bull. Chem. Soc. Jpn., 2018, 91, 787–789 Search PubMed.
- D. E. Koshland, Application of a Theory of Enzyme Specificity to Protein Synthesis, Proc. Natl. Acad. Sci. U. S. A., 1958, 44, 98 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1qi00209k |
| This journal is © the Partner Organisations 2021 |