 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Long-range exciton diffusion in non-fullerene acceptors and coarse bulk heterojunctions enable highly efficient organic photovoltaics†
Muhammad T. Sajjad *ab,
Arvydas Ruseckas
*ab,
Arvydas Ruseckas a,
Lethy Krishnan Jagadammaa,
Yiwei Zhanga and
Ifor D. W. Samuel
a,
Lethy Krishnan Jagadammaa,
Yiwei Zhanga and
Ifor D. W. Samuel *a
*a
aOrganic Semiconductor Centre, SUPA, School of Physics and Astronomy, University of St Andrews, St. Andrews, KY16 9SS, UK. E-mail: idws@st-andrews.ac.uk
bLondon Centre for Energy Engineering, School of Engineering, London South Bank University, 103 Borough Rd, London, SE1 0AA, UK. E-mail: sajjadt@lsbu.ac.uk
First published on 21st July 2020
Abstract
We investigated singlet exciton diffusion in three ITIC derivatives used as electron acceptors in organic photovoltaics (OPVs) by time-resolved photoluminescence volume quenching and exciton–exciton annihilation. The exciton diffusion coefficient was found to be in the range of 0.003–0.007 cm2 s−1 which leads to a three-dimensional exciton diffusion length of up to 31 nm. We fabricated solar cells using bulk heterojunctions of these acceptors with the electron donor PTB7-Th which showed ∼7% efficiency and large scale phase separation. Our results show that long range exciton diffusion and large domains offer significant advantages for OPVs.
The use of abundant and clean solar power to generate electricity is a very promising direction for renewable power. Organic photovoltaics (OPVs) are expected to play a major role in future power generation because of their simple fabrication enabling the deposition of solar cells on flexible substrates by printing from solution or spray-coating. Recently, the development of non-fullerene electron acceptors (NFAs), which replace fullerene derivatives, has led to important advances in both efficiency and stability.1,2 In contrast to fullerene derivatives, the absorption of NFAs extends over the visible spectral range and so improves light harvesting. The ionisation potentials and electron affinities of NFAs can be adjusted to achieve lower losses of open-circuit voltage (Voc).1,3 Organic solar cells using NFAs in binary and ternary blends to form bulk heterojunctions (BHJ) have reached power conversion efficiencies (PCE) of more than 17%.4,5 The use of NFAs also significantly increases the stability of solar cells with projected lifetimes up to 20 years.6
With high efficiency and other desirable properties such as light weight, low production cost, tuneable bandgaps and mechanical flexibility, OPVs offer low energy payback time compared to other photovoltaic technologies such as commercially available silicon. The energy payback time of OPVs with PCEs of 15% is predicted to be 0.5 weeks compared to 0.5 years for silicon.7 The bandgap tuneability of NFAs has led to the development of near-infrared absorbers8 which enable the production of semi-transparent or even fully transparent cells for their possible integration into buildings.9 Furthermore, OPVs are made from “green” materials compared to other solution or spray coated photovoltaic materials such as lead-containing hybrid perovskites.
The length-scale of phase separation between donor and acceptor is an important consideration in BHJ solar cells. Large scale phase separation is helpful for efficient charge extraction, as it reduces the area of the BHJ and so reduces charge recombination losses.10 However, this needs to be balanced against the need for efficient exciton harvesting (charge generation), which requires that the length-scale of phase separation should be comparable to the exciton diffusion length (LD) which is typically less than 10 nm in many solution-processed OPV materials.10,11 Increasing exciton diffusion length is very desirable because it provides a way of overcoming this trade-off by enabling efficient exciton harvesting in larger domains.
BHJs made from NFAs have shown large donor and acceptor domains (20–50 nm) and high domain purity.12 Despite these large domains, efficient exciton dissociation is observed in BHJs with NFAs which suggests that exciton diffusion lengths in NFAs are on a length-scale comparable to these domains. Despite the rapid development of materials and device engineering, photophysical investigations of NFAs are less developed, with only a couple of reports of measurements of exciton diffusion in NFAs (abbreviated names IDIC, INIC and its fluorinated derivative FINIC) using exciton–exciton annihilation measurements.13,14
Here we investigated exciton diffusion in a family of efficient NFA materials shown in Fig. 1 (abbreviated names ITIC,15ITIC-Th16 and IT-4F17). Time-resolved photoluminescence (PL) volume quenching and exciton–exciton annihilation measurements gave consistent values of exciton diffusion coefficient in all three materials investigated, which leads to three-dimensional exciton diffusion lengths between 18 and 31 nm. We fabricated solar cells using blends of these NFAs with the widely used donor polymer PTB7-Th which showed PCEs of more than 7%, consistent with previous reports.15,18 The analysis of PL decays measured in these photovoltaic blends suggests large and pure NFA domains of up to 32 nm in diameter.
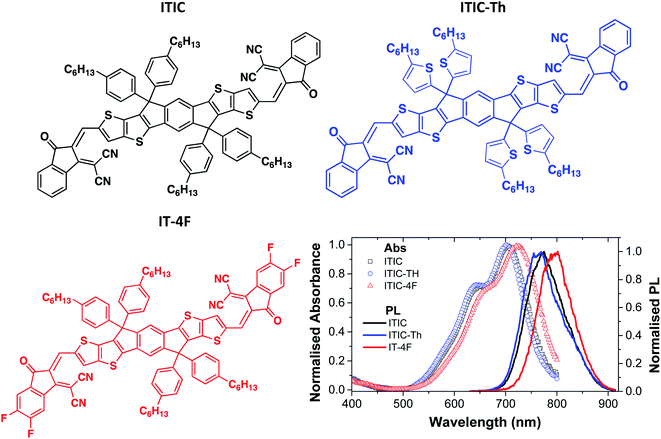 | ||
| Fig. 1 Chemical structures of ITIC derivatives used in this study and their absorption and photoluminescence (PL) spectra. | ||
Absorption and PL spectra of neat films of the three electron acceptors studied are shown in Fig. 1. ITIC has an absorption peak around 707 nm which corresponds to a 0–0 vibronic transition and a shoulder around 642 nm which can be attributed to a vibronic 0–1 transition. The absorption of ITIC-Th is slightly blue-shifted compared to ITIC with a strong 0–0 peak at around 703 nm whilst absorption of IT-4F is red-shifted with a 0–0 peak around 723 nm and a 0–1 shoulder around 659 nm. All these molecules show a single emission peak in thin films: ITIC emits around 772 nm, ITIC-Th around 763 nm and IT-4F around 795 nm.
First we investigated singlet exciton diffusion in films of these electron acceptors using PL quenching by DR3TBDTT molecules dispersed at low concentrations in the volume of electron acceptor films. The resulting fluorescence decays are plotted in Fig. S1.† For accurate measurement of exciton diffusion, homogenous dispersion of the quencher is required. To check this, we measured a range of quencher concentrations and determine the rate of quenching for each concentration (as shown in Fig. S2†). The rate of quenching shows a linear dependence at low concentration of quencher and deviates from the linear regime at high concentration. For exciton diffusion measurement, we only use the linear regime.
At low concentration, PL quenching is controlled by exciton diffusion to the quencher. For a given concentration, PL will decay faster if exciton diffusion is faster, so the decay can be used to measure exciton diffusion. As there is a finite spectral overlap of the PL spectra of the studied electron acceptors with the absorption of DR3TBDTT, therefore, Förster resonance energy transfer (FRET) to dispersed DR3TBDTT molecules can occur followed by electron transfer from DR3TBDTT to the electron acceptor which results in PL quenching (Fig. 2). For analysis it is convenient to take a ratio of the PL decay in films with a quencher to the PL decay without a quencher to account for the natural exciton decay in neat electron acceptor films. At high concentrations of dispersed DR3TBDTT molecules the direct FRET to the quencher dominates and the natural logarithm of the PL ratio is proportional to the square root of time as explained in ESI and has been observed before.19,20 This allows us to estimate the Förster radius R0 for FRET from electron acceptors to DR3TBDTT.
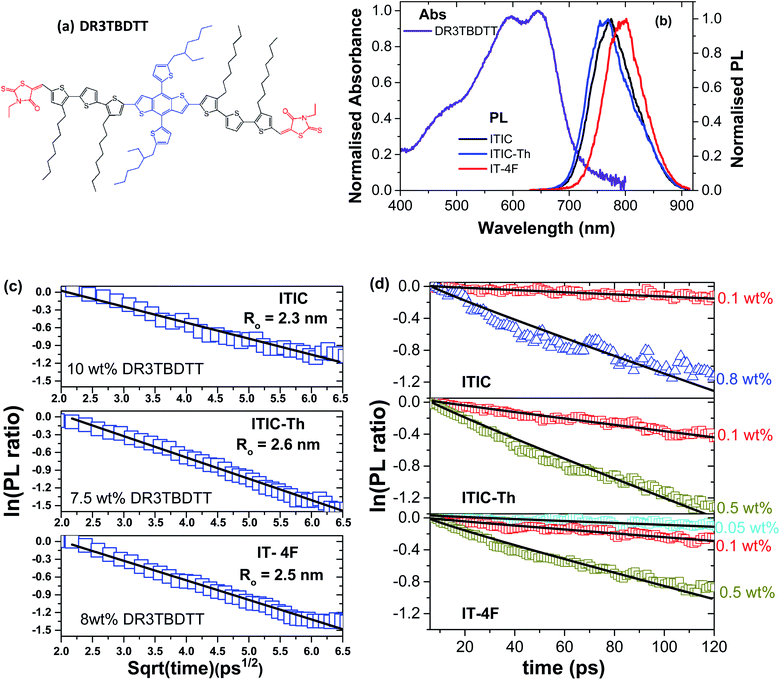 | ||
| Fig. 2 (a) Chemical structure of DR3TBDTT molecule used as a dispersed volume quencher of PL in NFA films. (b) Absorption spectrum of a neat DR3TBDTT film spin-coated from chlorobenzene solution and photoluminescence spectra of neat NFA films. (c and d) The natural logarithm of the ratio of the PL decays in films of ITIC derivatives doped with different concentrations of the quencher to the PL of the neat films without a quencher plotted vs. square root of time (c) and on a linear time axis (d). The lines are the fits with a sum of quenching rates representing direct Förster resonance energy transfer to the quencher (FRET) and diffusion-mediated quenching with the Förster radius R0 and diffusion coefficient D as fitting parameters (details described in ESI†). | ||
After determining R0, the diffusion coefficient is fitted to the PL decays (Fig. 2d) using the formula developed by Gösele et al. for the case of diffusion mediated FRET to quenchers21,22 as described further in ESI.† From this fitting we obtain exciton diffusion coefficients of (3.4 ± 0.8) × 10−3 cm2 s−1 for ITIC, (7.0 ± 2.0) × 10−3 cm2 s−1 for ITIC-Th and (4.5 ± 0.8) × 10−3 cm2 s−1 for IT-4F.
To verify these results we investigated exciton diffusion using singlet–singlet exciton annihilation. Excitons diffuse in the films and when two excitons approach each other one exciton transfers its energy onto the other which goes into a higher excited state. The higher energy state usually relaxes to the lowest excited state and one exciton is lost per annihilation event. We used time-resolved PL measured at different initial excitation densities to study this process and the results are shown in Fig. 3. PL intensity is proportional to the density of singlet excitons N and described by the rate equation
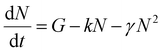 | (1) |
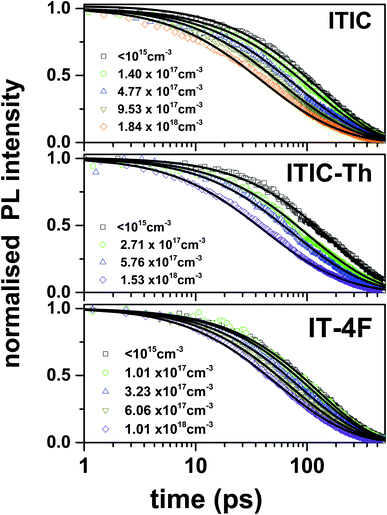 | ||
| Fig. 3 Singlet–singlet annihilation measurements showing PL decays in neat films of ITIC derivatives measured at different initial excitation densities given in the legend. Solid lines are the numerical fits using eqn (1) with a time-independent γ as a fitting parameter given in Table 1. | ||
| Material | D (×10−3 cm2 s−1) | γ (×10−8 cm3 s−1) | R a (nm) | d 100 (nm) | τ (ps) | L 3D (nm) |
|---|---|---|---|---|---|---|
| ITIC | 3.4 ± 0.8 | 1.0 ± 0.2 | 2.4 ± 0.3 | 1.50 | 163 ± 10 | 18 ± 2 |
| ITIC-Th | 7.0 ± 2.0 | 1.4 ± 0.3 | 1.5 ± 0.4 | 1.34 | 223 ± 10 | 31 ± 3 |
| IT-4F | 4.5 ± 0.8 | 1.0 ± 0.2 | 1.8 ± 0.3 | 1.79 | 132 ± 10 | 19 ± 2 |
The kinematic model of diffusion-limited exciton–exciton annihilation in unrestricted three-dimensional space relates the annihilation constant γ to the exciton diffusion coefficient D as
| γ = 4πDRa | (2) |
The obtained values of diffusion coefficient are more than an order of magnitude higher than for the widely used fullerene derivative PC71BM (D = 1.6 × 10−4 cm2 s−1) measured using volume quenching.31 It is interesting to note that ITIC-Th has been reported to show about five times higher electron mobility as compared to ITIC and 1.4 times higher than IT-4F32 suggesting a possible correlation between exciton diffusivity and electron mobility. It is very likely that both are enhanced by the large (010) coherence length in ITIC-Th along the π–π stacks up to 4 nm measured using GIWAXS.33
Normally, the lower value of exciton diffusion coefficient (D) in solution-processed organic semiconductors is associated with energetic disorder that is typically larger than thermal energy at room temperature, thus reducing the available density of states for exciton hopping.10,11 In the case of highly disordered materials, dispersive exciton transport is observed where the distribution of energy states has a strong influence on the rate of hopping i.e. exciton diffusion will be faster initially while relaxing within the density of states and become slower at longer time due to the unavailability of energetically accessible sites. Experimentally it leads to strong time-dependent PL quenching.34 However, in the case of NFAs, we observed a time-independent rate of PL quenching both in exciton–exciton annihilation (where a single time-independent gamma is used to describe the decay) and volume quenching measurements (at low quencher concentration where exciton diffusion is the dominant process). This indicates that fast exciton diffusion in NFAs is due to their higher energetic and structural order.
The charge generation efficiency depends on the ability of each exciton to reach a heterojunction which in turn depends on the exciton diffusion length and the donor and acceptor domain sizes. In BHJ geometry, three-dimensional exciton diffusion length is relevant, therefore, we estimated the three-dimensional exciton diffusion length using 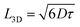 . Here τ is the exciton decay time in the absence of annihilation. The PL decays were non-exponential even for the low excitation density so we took τ to be the time taken for PL to fall to 1/e of its initial value in our estimation of exciton diffusion length. The 1/e decay times were 163 ps for ITIC, 223 ps for ITIC-Th and 132 ps for IT-4F. This leads to values of the three-dimensional diffusion length of 18 ± 2 nm for ITIC, 31 ± 3 nm for ITIC-Th and 19 ± 2 nm for IT-4F (Table 1).
. Here τ is the exciton decay time in the absence of annihilation. The PL decays were non-exponential even for the low excitation density so we took τ to be the time taken for PL to fall to 1/e of its initial value in our estimation of exciton diffusion length. The 1/e decay times were 163 ps for ITIC, 223 ps for ITIC-Th and 132 ps for IT-4F. This leads to values of the three-dimensional diffusion length of 18 ± 2 nm for ITIC, 31 ± 3 nm for ITIC-Th and 19 ± 2 nm for IT-4F (Table 1).
We also measured singlet exciton diffusion in PTB7-Th films using PL quenching by dispersed low concentrations of ITIC or IT-4F molecules. This gives the values of (1.0 ± 0.1) × 10−3 cm2 s−1 for exciton diffusion coefficient and 12 nm for the 3D diffusion length in PTB7-Th (details are given in ESI†).
To investigate the effect of exciton diffusion on the photovoltaic device performance, we fabricated solar cells using these NFAs as acceptors. We followed a simple protocol for device fabrication without any extra processing (e.g. thermal or solvent vapor annealing) or additives. For all three NFAs, we used the same donor: acceptor blend weight ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
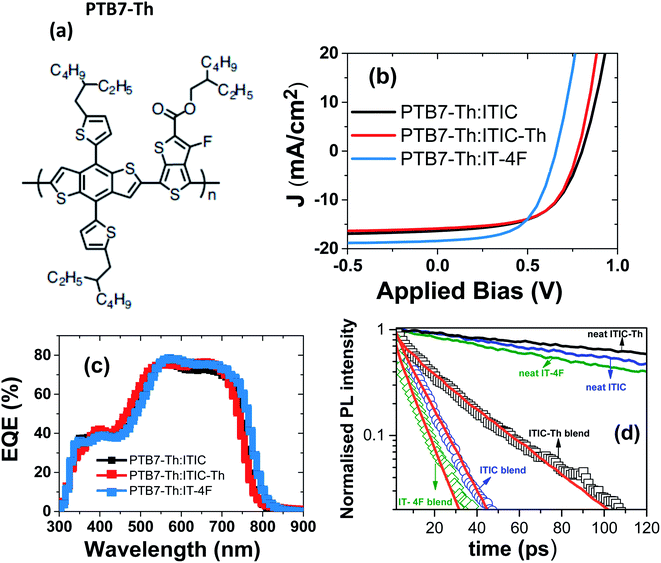
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.3, (with a total concentration of 23 mg mL−1) for easy comparison between the exciton diffusion length and solar cell device performance. For donor, we selected the widely used polymer PTB7-Th, whose molecular structure is shown in Fig. 4a. The photovoltaic J–V characteristics are shown in Fig. 4b and the external quantum efficiency (EQE) spectra are shown in Fig. 4c. All the photovoltaic performance parameters are given in Table 2. Our solar cell efficiencies are comparable to previously reported values using PTB7-Th as donor and ITIC as acceptor.15,18 Though all the three PTB7-Th:NFA blends showed power conversion efficiency (PCE) close to 7%, the blend, PTB7-Th:ITIC-Th showed the highest average (7%) and champion efficiency of 7.45%. The illuminated current density–voltage curve given in Fig. 4b shows that the blend with IT-4F has a higher short circuit current (JSC) density. This is due to enhanced absorption of this molecule in the region between 550 nm and 850 nm compared to the other two as shown in the absorption spectra in Fig. 1. The extended absorption range of this blend, PTB7-Th:IT-4F, is further reflected in the EQE spectra shown in Fig. 4c. Overall the blends with these three NFAs show an EQE of more than 70% in the region between 550 nm and 750 nm. The blends PTB7-Th:ITIC, and PTB7-Th:ITIC-Th show higher open circuit voltage (Voc) of ∼0.78 V compared to 0.65 V in IT-4F due to the wider HOMO–LUMO difference between the donor PTB7-Th and the corresponding NFAs (energy levels of NFAs along with PTB7-Th are given in the ESI, Fig. S9†). Among the three blends, the OPVs with PTB7-Th:ITIC-Th blend showed the highest fill factor (FF) of ∼62%. To estimate the contribution of reduced recombination to the higher FF of the PTB7-Th:ITIC-Th blend compared to the other two blends, the ideality factor (n) was estimated for the three blends. To obtain the value of n, we fitted the I–V curves (Fig. S10†) using the equation below.
1.3, (with a total concentration of 23 mg mL−1) for easy comparison between the exciton diffusion length and solar cell device performance. For donor, we selected the widely used polymer PTB7-Th, whose molecular structure is shown in Fig. 4a. The photovoltaic J–V characteristics are shown in Fig. 4b and the external quantum efficiency (EQE) spectra are shown in Fig. 4c. All the photovoltaic performance parameters are given in Table 2. Our solar cell efficiencies are comparable to previously reported values using PTB7-Th as donor and ITIC as acceptor.15,18 Though all the three PTB7-Th:NFA blends showed power conversion efficiency (PCE) close to 7%, the blend, PTB7-Th:ITIC-Th showed the highest average (7%) and champion efficiency of 7.45%. The illuminated current density–voltage curve given in Fig. 4b shows that the blend with IT-4F has a higher short circuit current (JSC) density. This is due to enhanced absorption of this molecule in the region between 550 nm and 850 nm compared to the other two as shown in the absorption spectra in Fig. 1. The extended absorption range of this blend, PTB7-Th:IT-4F, is further reflected in the EQE spectra shown in Fig. 4c. Overall the blends with these three NFAs show an EQE of more than 70% in the region between 550 nm and 750 nm. The blends PTB7-Th:ITIC, and PTB7-Th:ITIC-Th show higher open circuit voltage (Voc) of ∼0.78 V compared to 0.65 V in IT-4F due to the wider HOMO–LUMO difference between the donor PTB7-Th and the corresponding NFAs (energy levels of NFAs along with PTB7-Th are given in the ESI, Fig. S9†). Among the three blends, the OPVs with PTB7-Th:ITIC-Th blend showed the highest fill factor (FF) of ∼62%. To estimate the contribution of reduced recombination to the higher FF of the PTB7-Th:ITIC-Th blend compared to the other two blends, the ideality factor (n) was estimated for the three blends. To obtain the value of n, we fitted the I–V curves (Fig. S10†) using the equation below.
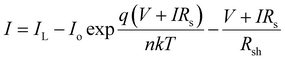 | (3) |
 | ||
| Fig. 4 Device characteristics of PTB7-Th:NFAs (ITIC, ITIC-Th and IT-4F) blends: (a) molecular structure of PTB7-Th, (b) current density–voltage (J–V) curves, (c) external quantum efficiency (EQE) of devices, (d) PL decays in the blends of electron acceptors with PTB7-Th which were used to make solar cells (symbols) and in neat electron acceptor films (solid lines). Solid red lines are the fits using eqn (4) which were used to estimate the average domain sizes of acceptors. | ||
| Blend | D![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) A ratio (wt%) A ratio (wt%) |
J sc (mA cm−2) | V oc (V) | FF (%) | PCE avg. (%) | PCE best (%) | Domain size (nm) | Φ gen |
|---|---|---|---|---|---|---|---|---|
| PTB7-Th:ITIC | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.3 1.3 |
15.6 ± 0.7 | 0.789 ± 0.008 | 54.9 ± 1.7 | 6.76 ± 0.56 | 7.38 | 17 nm | 0.91 |
| PTB7-Th:ITIC-Th | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.3 1.3 |
14.5 ± 0.3 | 0.773 ± 0.007 | 62.7 ± 1.9 | 7.0 ± 0.3 | 7.45 | 32 nm | 0.90 |
| PTB7-Th:IT-4F | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.3 1.3 |
17.2 ± 1.1 | 0.649 ± 0.014 | 55.6 ± 3.4 | 6.20 ± 0.51 | 6.99 | 14 nm | 0.93 |
The values of n obtained are 1.53 ± 0.41 for PTB7-Th:ITIC, 1.43 ± 0.34 for PTB7-Th:ITIC-Th and 1.55 ± 0.39 for PTB7-Th:IT-4F. The n value of the PTB7-Th:ITIC-Th blend is lowest, suggesting lower recombination losses in this blend than the other two. For the blends of PTB7-Th:ITIC and PTB7-Th:IT-4F, the estimated n values are similar and this is in agreement with their similar FF values shown in Table 2. To understand the contribution of mobility in the high FF for the blend with ITIC-Th, the electron mobility of the three NFAs was also considered. Previous studies have reported electron mobilities of 1.10 × 10−4 cm2 V−1 s−1 for ITIC, 6.10 × 10−4 cm2 V−1 s−1 for ITIC-Th, and 4.37 × 10−4 cm2 V−1 s−1 for IT-4F.32 The higher electron mobility of ITIC-Th NFA compared to the other two will also be contributing to the higher FF for the blend containing this NFA.
The higher FF in the PTB7-Th:ITIC-Th blend also indicates improved dissociation of charge transfer states in competition with geminate recombination and better charge extraction. A previous study has established a positive correlation between the device FF, the coherence length of π–π stacking of ITIC-Th molecules and electron mobility.33 We observed a higher exciton diffusion coefficient in ITIC-Th films than the other derivatives. It is very likely that exciton diffusivity and electron mobility both increase as a result of the improved coherence length in ITIC-Th. Non-geminate recombination is more severe in finely mixed BHJs with large area of the donor–acceptor interface. To investigate this hypothesis we measured the domain size in the blends using time-resolved PL spectroscopy.
We can estimate the average domain size of non-fullerene acceptors assuming that the PL quenching in the blends is limited by exciton diffusion in acceptor domains to the boundary with PTB7-Th using a procedure previously described by Hedley et al.31 and Jagadamma et al.35 For this purpose we measured the PL decays in the blends of electron acceptors with PTB7-Th which were used to make solar cells and normalised them to the PL decays in neat electron acceptor films to account for the natural exciton decay in non-fullerene acceptors (Fig. 4d). This approach is justified by good agreement of PL spectra measured in the blends and in neat acceptor films which all are substantially red-shifted relative to the PTB7-Th spectrum (Fig. S11†). Time-resolved PL spectra of the blends show a red-shift within 10 ps after excitation which can be attributed to energy transfer from PTB7-Th to electron acceptors (Fig. S12†). This suggests that PTB7-Th domains are much smaller than L3D in PTB7-Th of 12 nm or that these have some admixture of electron acceptor. The AFM image (Fig. S13†) shows that at least on the surface the domains are approximately round rather than elongated, therefore, in order to estimate their size we assumed that they have spherical shape. Previous studies of PTB7-Th blends with ITIC derivatives deposited by one-step spin-coating also showed fine granular morphology with roughly round grains.35,36 Recent reports show that high efficiency can also be achieved in sequentially deposited donor acceptor layers which may have very different needle-like morphology.37,38
Hence, assuming that acceptor domains have a spherical shape with a radius r, the ratio g(t) of the PL decay in a blend to the PL decay in a neat acceptor film is described by
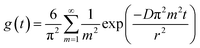 | (4) |
The radius of the sphere r is the only fitting parameter in this case as the exciton diffusion coefficient D was determined for each non-fullerene acceptor in the annihilation and volume quenching measurements described above. For the fitting, eqn (4) was multiplied by the fluorescence intensity in the absence of quencher and then used to fit the PL decays of the blends. A domain size of approximately 17 nm was obtained for ITIC, 32 nm for ITIC-Th and 14 nm for IT-4F. Large domains in the case of ITIC-Th are consistent with the higher fill factor observed. These results can be compared to the long-period (domain spacing) which was measured at around 95 nm in PTB7-Th:ITIC-Th blend using R-SoXS.33 Our method gives us a size estimate of pure acceptor domains because any mixture of the donor polymer would give faster PL quenching as compared to quenching solely at the domain boundaries. According to R-SoXS results, the domain purity in PTB7-Th:ITIC-Th blend is not the highest among other blends, hence, we consider our findings compatible with the reported R-SoXS results.
However, large domains could limit exciton harvesting as excitons have further to diffuse to a heterojunction. We therefore estimated the charge generation efficiency in these blends using the PL decays in the presence and absence of quencher as 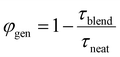 , where τblend is the lifetime of blend and τneat is the lifetime of neat acceptor film. We made an assumption here that every exciton that is quenched generates a charge. PL decays of blends and neat films are non-exponential, therefore we used 1/e lifetimes for our estimation. A generation efficiency of ∼91% was obtained for ITIC, ∼90% for ITIC-Th and ∼93% for IT-4F. Efficient charge generation (90%) in the blend of PTB7-Th:ITIC-Th even with large domains (>30 nm) indicates that most of the photogenerated excitons reach the interface due to large exciton diffusion length (>30 nm).
, where τblend is the lifetime of blend and τneat is the lifetime of neat acceptor film. We made an assumption here that every exciton that is quenched generates a charge. PL decays of blends and neat films are non-exponential, therefore we used 1/e lifetimes for our estimation. A generation efficiency of ∼91% was obtained for ITIC, ∼90% for ITIC-Th and ∼93% for IT-4F. Efficient charge generation (90%) in the blend of PTB7-Th:ITIC-Th even with large domains (>30 nm) indicates that most of the photogenerated excitons reach the interface due to large exciton diffusion length (>30 nm).
Conclusions
In conclusion, we measured the exciton diffusion coefficient in a family of fused ring non-fullerene acceptors and found values of exciton diffusion coefficient that are higher than many OPV materials, including fullerene derivatives. Furthermore, we found that exciton diffusion is time-independent, suggesting that there is less energetic and structural disorder in these materials. The high exciton diffusion coefficient leads to three-dimensional diffusion lengths of up to 31 nm, which allow blends with large domain sizes to be made using these NFAs. Our measurement of large exciton diffusion length along with large domains gives further understanding of why NFAs are such attractive materials for organic solar cells.Experimental section
Absorption measurements
Materials for this study were purchased from 1-Material. The absorption of films were measured using a Cary 300 UV-Vis spectrophotometer. Film thicknesses of 40–50 nm were used for these measurements.Time-resolved PL measurements
Time-resolved PL decays were measured with Hamamatsu C6860 streak camera in synchroscan mode. In the volume quenching and low excitation density measurements of neat films, the excitation was with 100 fs pulses at an excitation wavelength of 515 nm and a repetition rate of 80 MHz. For exciton–exciton annihilation measurements, the films were excited using 200 fs pulses at 640 nm with 100 kHz repetition rate generated by an optical parametric amplifier pumped by Pharos regenerative amplifier.For exciton–exciton annihilation measurements films of thickness 40–50 nm were used, so that the excitation density was close to uniform throughout the film. The thickness of photovoltaic blends used in time resolved study was around 100 nm as optimised for the best device efficiency.
For volume quenching measurement, the solutions of NFAs and donor (DR3TBDTT) was prepared separately using chlorobenzene and were kept overnight at 60 °C inside the glovebox. These solutions were mixed together and films were made by spin-coating the solution at 2000 rpm for 60 s inside the glovebox.
Device fabrication and characterisation
Inverted organic solar cells were fabricated on pre-patterned ITO-coated glass. The ITO-coated glass substrates were cleaned in detergent (Hellmanex, Sigma Aldrich), successively ultrasonicated in deionized water, acetone, and isopropyl alcohol, and exposed to an oxygen plasma for 3 minutes. The blend solutions of PTB7-Th:NFAs were prepared by dissolving the components in a ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.3 (by weight), with a total concentration of 23 mg mL−1 in chlorobenzene. The solution was kept stirring at 60 °C for ∼8 hours before spin-coating.
1.3 (by weight), with a total concentration of 23 mg mL−1 in chlorobenzene. The solution was kept stirring at 60 °C for ∼8 hours before spin-coating.
In all the inverted organic solar cells fabricated, the electron transporting layer was amorphous ZnO (a-ZnO) thin film having a thickness of ∼25 nm and was prepared according to a previous report.39 The active layer was deposited by spin-coating (at 1500 rpm for 45 s) on glass/ITO/a-ZnO substrates inside a nitrogen filled glove box. The samples were then transferred to a thermal evaporator (1 × 10−6 mbar base pressure) in the glove box and the hole transporting layer of MoOx (7 nm) and anode Ag (100 nm) deposited through a shadow mask. The active area of the device was 0.07 cm2.
After the electrode deposition, the devices were encapsulated with an UV optical adhesive and a glass coverslip. The current–voltage characteristics were determined under an illumination intensity of 100 mW cm−2 in air using an air mass 1.5 global (AM 1.5 G) Sciencetech solar simulator and a Keithley 2400 source-measure unit. The illumination intensity was verified with a calibrated mono-silicon detector and a KG-5 filter. The external quantum efficiency (EQE) measurements were performed at zero bias by illuminating the device with monochromatic light supplied from a xenon arc lamp in combination with a Bentham TMc300 monochromator. The number of photons incident on the sample was calculated for each wavelength by using a silicon photodiode calibrated by the National Physical Laboratory (NPL).
Conflicts of interest
There are no conflicts to declare.Acknowledgements
We acknowledge support from the European Commission (European Research Council grant 321305) and Marie Sklodowska-Curie Individual Fellowship grant 745776. We are also grateful to EPSRC for support from grants (EP/L017008/1 and EP/L012294/1).Notes and references
- J. Hou, O. Inganäs, R. H. Friend and F. Gao, Nat. Mater., 2018, 17, 119–128 CrossRef CAS PubMed.
- P. Cheng, G. Li, X. Zhan and Y. Yang, Nat. Photonics, 2018, 12, 131–142 CrossRef CAS.
- C. Yan, S. Barlow, Z. Wang, H. Yan, A. K.-Y. Jen, S. R. Marder and X. Zhan, Nat. Rev. Mater., 2018, 3, 1–19 CrossRef.
- Y. Lin, B. Adilbekova, Y. Firdaus, E. Yengel, H. Faber, M. Sajjad, X. Zheng, E. Yarali, A. Seitkhan, O. M. Bakr, A. El-Labban, U. Schwingenschlögl, V. Tung, I. McCulloch, F. Laquai and T. D. Anthopoulos, Adv. Mater., 2019, 31, 1902965 CrossRef CAS PubMed.
- Y. Cui, H. Yao, J. Zhang, K. Xian, T. Zhang, L. Hong, Y. Wang, Y. Xu, K. Ma and C. An, Adv. Mater., 2020, 32, 1908205 CrossRef CAS PubMed.
- X. Xu, J. Xiao, G. Zhang, L. Wei, X. Jiao, H.-L. Yip and Y. Cao, Sci. Bull., 2020, 65, 208–216 CrossRef CAS.
- S. B. Darling and F. You, RSC Adv., 2013, 3, 17633–17648 RSC.
- J. Lee, S.-J. Ko, H. Lee, J. Huang, Z. Zhu, M. Seifrid, J. Vollbrecht, V. V. Brus, A. Karki and H. Wang, ACS Energy Lett., 2019, 4, 1401–1409 CrossRef CAS.
- V. V. Brus, J. Lee, B. R. Luginbuhl, S. J. Ko, G. C. Bazan and T. Q. Nguyen, Adv. Mater., 2019, 31, 1900904 CrossRef PubMed.
- G. J. Hedley, A. Ruseckas and I. D. W. Samuel, Chem. Rev., 2017, 117, 796–837 CrossRef CAS PubMed.
- O. V. Mikhnenko, P. W. Blom and T.-Q. Nguyen, Energy Environ. Sci., 2015, 8, 1867–1888 RSC.
- Y. Lin, F. Zhao, S. K. Prasad, J. D. Chen, W. Cai, Q. Zhang, K. Chen, Y. Wu, W. Ma, F. Gao, J.-X. Tang, C. Wang, W. You, J. M. Hodgkiss and X. Zhan, Adv. Mater., 2018, 30, 1706363 CrossRef PubMed.
- S. Chandrabose, K. Chen, A. J. Barker, J. J. Sutton, S. K. Prasad, J. Zhu, J. Zhou, K. C. Gordon, Z. Xie, X. Zhan and J. M. Hodgkiss, J. Am. Chem. Soc., 2019, 141, 6922–6929 CrossRef CAS PubMed.
- S. Dai, J. Zhou, S. Chandrabose, Y. Shi, G. Han, K. Chen, J. Xin, K. Liu, Z. Chen, Z. Xie, W. Ma, Y. Yi, L. Jiang, J. M. Hodgkiss and X. Zhan, Adv. Mater., 2020, 32, 2000645 CrossRef CAS PubMed.
- Y. Lin, J. Wang, Z. G. Zhang, H. Bai, Y. Li, D. Zhu and X. Zhan, Adv. Mater., 2015, 27, 1170–1174 CrossRef CAS PubMed.
- Y. Lin, F. Zhao, Q. He, L. Huo, Y. Wu, T. C. Parker, W. Ma, Y. Sun, C. Wang, D. Zhu, A. J. Heeger, S. R. Marder and X. Zhan, J. Am. Chem. Soc., 2016, 138, 4955–4961 CrossRef CAS PubMed.
- W. Zhao, S. Li, H. Yao, S. Zhang, Y. Zhang, B. Yang and J. Hou, J. Am. Chem. Soc., 2017, 139, 7148–7151 CrossRef CAS PubMed.
- R. S. Gurney, W. Li, Y. Yan, D. Liu, A. J. Pearson and T. Wang, J. Energy Chem., 2019, 37, 148–156 CrossRef.
- A. J. Ward, A. Ruseckas and I. D. W. Samuel, J. Phys. Chem. C, 2012, 116, 23931–23937 CrossRef CAS.
- M. T. Sajjad, A. J. Ward, A. Ruseckas, A. K. Bansal, S. Allard, U. Scherf and I. D. W. Samuel, Phys. Status Solidi RRL, 2019, 13, 1800500 Search PubMed.
- U. Gösele, M. Hauser, U. Klein and R. Frey, Chem. Phys. Lett., 1975, 34, 519–522 CrossRef.
- U. Klein, R. Frey, M. Hauser and U. Gösele, Chem. Phys. Lett., 1976, 41, 139–142 CrossRef CAS.
- R. Kepler, V. Valencia, S. Jacobs and J. McNamara, Synth. Met., 1996, 78, 227–230 CrossRef CAS.
- A. Ruseckas, M. Theander, L. Valkunas, M. Andersson, O. Inganäs and V. Sundström, J. Lumin., 1998, 76, 474–477 CrossRef.
- M. A. Stevens, C. Silva, D. M. Russell and R. H. Friend, Phys. Rev. B, 2001, 63, 165213 CrossRef.
- M. T. Sajjad, O. Blaszczyk, L. K. Jagadamma, T. J. Roland, M. Chowdhury, A. Ruseckas and I. D. W. Samuel, J. Mater. Chem. A, 2018, 6, 9445–9450 RSC.
- M. T. Sajjad, Y. Zhang, P. B. Geraghty, V. D. Mitchell, A. Ruseckas, O. Blaszczyk, D. J. Jones and I. D. W. Samuel, J. Mater. Chem. C, 2019, 7, 7922–7928 RSC.
- P. E. Shaw, A. Ruseckas and I. D. W. Samuel, Adv. Mater., 2008, 20, 3516–3520 CrossRef CAS.
- J. Mai, Y. Xiao, G. Zhou, J. Wang, J. Zhu, N. Zhao, X. Zhan and X. Lu, Adv. Mater., 2018, 30, 1802888 CrossRef PubMed.
- R. Ma, Y. Chen, T. Liu, Y. Xiao, Z. Luo, M. Zhang, S. Luo, X. Lu, G. Zhang, Y. Li, H. Yan and K. Chen, J. Mater. Chem. C, 2020, 8, 909–915 RSC.
- G. J. Hedley, A. J. Ward, A. Alekseev, C. T. Howells, E. R. Martins, L. A. Serrano, G. Cooke, A. Ruseckas and I. D. W. Samuel, Nat. Commun., 2013, 4, 2867 CrossRef PubMed.
- A. Wadsworth, M. Moser, A. Marks, M. S. Little, N. Gasparini, C. J. Brabec, D. Baran and I. McCulloch, Chem. Soc. Rev., 2019, 48, 1596–1625 RSC.
- H. Hu, K. Jiang, P. C. Chow, L. Ye, G. Zhang, Z. Li, J. H. Carpenter, H. Ade and H. Yan, Adv. Energy Mater., 2018, 8, 1701674 CrossRef.
- M. T. Sajjad, A. J. Ward, C. Kastner, A. Ruseckas, H. Hoppe and I. D. W. Samuel, J. Phys. Chem. Lett., 2015, 6, 3054–3060 CrossRef CAS PubMed.
- L. K. Jagadamma, M. T. Sajjad, V. Savikhin, M. F. Toney and I. D. W. Samuel, J. Mater. Chem. A, 2017, 5, 14646–14657 RSC.
- Y. Tang, H. Sun, Z. Wu, Y. Zhang, G. Zhang, M. Su, X. Zhou, X. Wu, W. Sun, X. Zhang, B. Liu, W. Chen, Q. Liao, H. Y. Woo and X. Guo, Adv. Sci., 2019, 6, 1901773 CrossRef CAS PubMed.
- R. Sun, J. Guo, Q. Wu, Z. Zhang, W. Yang, J. Guo, M. Shi, Y. Zhang, S. Kahmann, L. Ye, X. Jiao, M. A. Loi, Q. Shen, H. Ade, W. Tang, C. J. Brabec and J. Min, Energy Environ. Sci., 2019, 12, 3118–3132 RSC.
- L. Ye, Y. Xiong, Z. Chen, Q. Zhang, Z. Fei, R. Henry, M. Heeney, B. T. O'Connor, W. You and H. Ade, Adv. Mater., 2019, 31, 1808153 CrossRef PubMed.
- L. K. Jagadamma, M. Abdelsamie, A. El Labban, E. Aresu, G. O. N. Ndjawa, D. H. Anjum, D. Cha, P. M. Beaujuge and A. Amassian, J. Mater. Chem. A, 2014, 2, 13321–13331 RSC.
- M. T. Sajjad, A. Ruseckas, L. K. Jagadamma, Y. Zhang and I. D. W. Samuel, Dataset, University of St Andrews Research Portal, 2020, DOI:10.17630/7bfdb2ad-def7-482b-82a8-4756b0d029c1.
Footnote |
| † Electronic supplementary information (ESI) available: The research data supporting this publication can also be accessed in ref. 40. See DOI: 10.1039/d0ta06017h |
| This journal is © The Royal Society of Chemistry 2020 |
