Room temperature demonstration of a sodium superionic conductor with grain conductivity in excess of 0.01 S cm⁻¹ and its primary applications in symmetric battery cells

Abstract

The lack of suitable candidate electrolyte materials for practical application limits the development of all-solid-state Na-ion batteries. Na_3+xZr₂Si_2+xP_1−xO₁₂ was the very first series of NASICONs discovered some 40 years ago; however, separation of bulk conductivity from total conductivity at room temperature is still problematic. It has been suggested that the effective Na-ion conductivity is ∼10⁻⁴ S cm⁻¹ at room temperature for Na_3+xZr₂Si_2+xP_1−xO₁₂ ceramics; however using a solution-assisted solid-state reaction for preparation of Na_3+xZr₂Si_2+xP_1−xO₁₂, a total conductivity of 5 × 10⁻³ S cm⁻¹ was achieved for Na_3.4Zr₂Si_2.4P_0.6O₁₂ at 25 °C, higher than the values previously reported for polycrystalline Na-ion conductors. A bulk conductivity of 1.5 × 10⁻² S cm⁻¹ was revealed by high frequency impedance spectroscopy (up to 3 GHz) and verified by low temperature impedance spectroscopy (down to −100 °C) for Na_3.4Zr₂Si_2.4P_0.6O₁₂ at 25 °C, indicating further the potential of increasing the related total conductivity. A Na/Na_3.4Zr₂Si_2.4P_0.6O₁₂/Na symmetric cell showed low interface resistance and high cycling stability at room temperature. A full-ceramic cell was fabricated and tested at 28 °C with good cycling performance.

---

Introduction

Although Li-ion batteries (LIBs) still dominate the global market of energy storage devices today, the application of Na-ion batteries (NIBs) has been extensively explored and discussed.^1–6 Since the Na ion is heavier (23.0 g mol⁻¹versus 6.9 g mol⁻¹), and has a lower ionization potential (−2.7 V versus −3.06 V) than the Li ion, NIBs are slightly inferior to LIBs both in terms of energy density and power density; however, sodium possesses the advantage of higher elemental abundance (23 000 ppm versus 20 ppm in the Earth's crust) and lower costs for raw materials and resulting compounds. Therefore in stationary applications such as storage of renewable energy, NIBs have the potential to outperform LIBs as energy production costs along with battery life are more important than energy and power density.^1–6

Since LIBs with liquid or polymer electrolytes have intrinsic problems due to flammability, complex reactions at the solid/liquid or solid/polymer interface, thermal instability, etc., LIBs in the all-solid-state (non-liquid/polymer-contained) design are becoming increasingly significant today.^7–11 Theoretically, an LIB with a solid-state electrolyte is not only able to overcome the disadvantages mentioned above, but also achieve both higher energy and power densities.^10,11 The above concept also applies to NIBs because of the high similarities between NIBs and LIBs.

Na_3+xZr₂Si_2+xP_1−xO₁₂ (NZSPx) was discovered some 40 years ago to be a Na-ion conductor.^12,13 Its structure exhibits high tolerance and flexibility for cation-substitution, leading to the foundation of the whole NASICON (Na Super-Ionic CONductors).^14,15 Together with β/β′′-aluminas,^16,17 they were regarded as the most promising candidates for possible solid electrolytes of NIBs because of their relatively high total ionic conductivities (σ_total, including bulk (σ_b) and grain-boundary (σ_gb) conductivity). Comparatively, β/β′′-aluminas are superior in σ_total (1–2 × 10⁻³ S cm⁻¹versus ∼10⁻⁴ S cm⁻¹ at room temperature,^14–16 as a standard, liquid electrolytes normally have conductivities of 5–10 × 10⁻³ S cm⁻¹ at room temperature¹⁸), while NASICONs show benefits of processing temperatures (∼1200 °C versus ∼1600 °C).^14,15,17 More than 400 publications have discussed NASICONs as Na-ion conductors (ESI Fig. S1†). However, until now even the separation of σ_b from σ_total of NASICONs at room temperature was problematic. In the published literature, only σ_total has generally been reported largely due to difficulty in observing the high frequency response in available instruments. The possible reasons for the inadequate understanding of NASICONs are: (1) in the past, NASICONs were mainly considered as electrolyte materials for high-temperature sodium batteries. Thus, the performance of NASICONs at temperatures of 200–300 °C was mainly targeted (ESI Fig. S1†). The literature discussing the properties of the NASICONs at room temperature is quite limited. (2) When Hong et al. discovered NZSPx 40 years ago,^12,13 they believed that the highest σ_total of the series occurs at −0.2 ≤ x ≤ 0.2 (i.e. Na content range from 2.8 to 3.2 mol per formula unit of the NASICONs). In the following 40 years, most research studies concentrated on a similar composition range and achieved similar values of σ_total.^14,15 The range of composition studied still seems deficient.

In the present study, the detailed investigation of NZSPx (with 0 ≤ x ≤ 0.6) using a more systematic substitution strategy and a more advanced processing method reveals that the σ_total of NZSPx, or even of NASICONs is largely underestimated. The σ_b of the samples is clearly distinguished from the σ_total. In particular, Na_3.4Zr₂Si_2.4P_0.6O₁₂ (NZSP0.4) is found to exhibit the highest σ_total among all polycrystalline Na-ion conductors. Together with sodium metal as electrodes, symmetric cells show high cycling stability at room temperature. Together with Na₃V₂P₃O₁₂ (NVP, which also has a NASICON structure) as an electrode material (both as positive and negative electrodes), full-NASICON-ceramic NIBs based on this superior NZSP0.4 electrolyte were developed. An all-solid-state NIB was successfully operated at room temperature.

Results

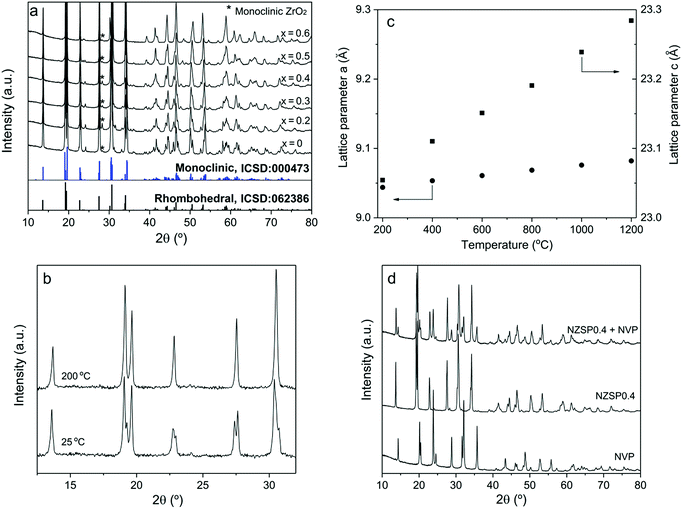
Properties of powders

The NZSPx powders were prepared using a solution-assisted solid-state reaction method (SA-SSR),^19–21 which is adaptable to large-scale preparation and guarantees low costs of the product. A relative density of >95% can be easily obtained for all the samples from NZSP0 to NZSP0.6 by conventional uniaxial pressing and conventional sintering at 1250–1300 °C for 5 h.

At room temperature, the NZSPx samples exhibit the NASICON structure, as a monoclinic phase (NZSP0 and 0.2), as a rhombohedral phase (NZSP0.6), or as a mixture of both (NZSP0.3–NZSP0.5). Evidently, from NZSP0 to NZSP0.6, the crystal structure of the samples at room temperature gradually changes from monoclinic to rhombohedral (Fig. 1a). Rietveld analysis yields that NZSP0.3, NZSP0.4 and NZSP0.5 are mixed by two phases with quantitative weight ratios of rhombohedral over monoclinic at 37 : 63, 48 : 52 and 66 : 34, respectively (ESI Fig. S2†). A slight secondary phase of monoclinic ZrO₂ is observed in all compositions.^20,21 Fortunately, their concentration is so small and has no apparent influence on σ_total of the samples.

Fig. 1 (a) Room temperature XRD patterns of NZSPx (x = 0–0.6) sintered at 1250–1300 °C. (b) Comparison of XRD patterns of NZSP0 measured at room temperature and 200 °C. (c) The lattice parameter a (circles) and c (squares) as a function of temperature for NZSP0. (d) Comparison of XRD patterns of NVP sintered at 750 °C in Ar/2% H₂, NZSP0.4 sintered at 1260 °C in air, and 60 wt% NVP (with carbon) with 40 wt% NZSP0.4 co-sintered at 900 °C in Ar/2% H₂.

All compositions exhibit the rhombohedral phase at >200 °C.²² A phase transformation from the rhombohedral to monoclinic structure occurs for samples of NZSP0–NZSP0.5 when the temperature decreases from 200 °C to 100 °C. An example of NSZP0 is shown in Fig. 1b (other compositions are shown in the ESI Fig. S3†). The XRD pattern of the monoclinic structure is quite similar to that of the rhombohedral structure, because it is merely a slightly twisted rhombohedral structure. Nevertheless, they can be easily distinguished by splitting the diffraction peaks of the monoclinic phase. The lattice parameters a and c of the rhombohedral NZSPx change differently when the temperature increases from 200 to 1200 °C. Compared to a, parameter c expands more on heating the samples, as shown in Fig. 1c (NZSP0 is shown as an example, the rest of the compositions are shown in the ESI Fig. S4†) resulting in the differences in thermal expansion coefficient (TEC) values, shown in Table 1. The TEC value of the a-axis is obviously much smaller than that of the c-axis. Similar results were reported for other NASICONs and defined as thermal-expansion anisotropy (TEA).²³ In the present study, the TEC of a decreases with the x value in NZSPx, while that of c increases, thus indicating that the anisotropy continuously increases with the x value.

Table 1 Thermal expansion coefficient (TEC) value of lattice parameters a and c for rhombohedral NZSPx in the temperature range of 200–1200 °C

	NZSP0	NZSP0.2	NZSP0.3	NZSP0.4	NZSP0.5	NZSP0.6
TEC a (10^−6 K^−1)	4.2	3.6	3.5	3.5	3.2	3.2
TEC c (10^−6 K^−1)	9.8	9.7	10.4	10.7	11.5	12.7

---

The primary particles of the NZSPx powder exhibit a favorable morphology. They are small (<100 nm), homogeneous, and almost spherical in shape (ESI Fig. S5†). They are important prerequisites for the further processing of the final ceramic product.

The NVP samples reveal a pure rhombohedral phase when sintered at 750 °C in Ar containing 2% H₂ (Fig. 1d), in agreement with previous results.²⁴ In addition, according to XRD patterns, NVP and NZSP0.4 do not exhibit detectable reactions after co-sintering up to 900 °C in Ar containing 2% H₂ (Fig. 1d). The chemical compatibility of NVP and NZSP0.4 is a necessary requirement for fabricating a full ceramic cell.

Properties of the sintered samples

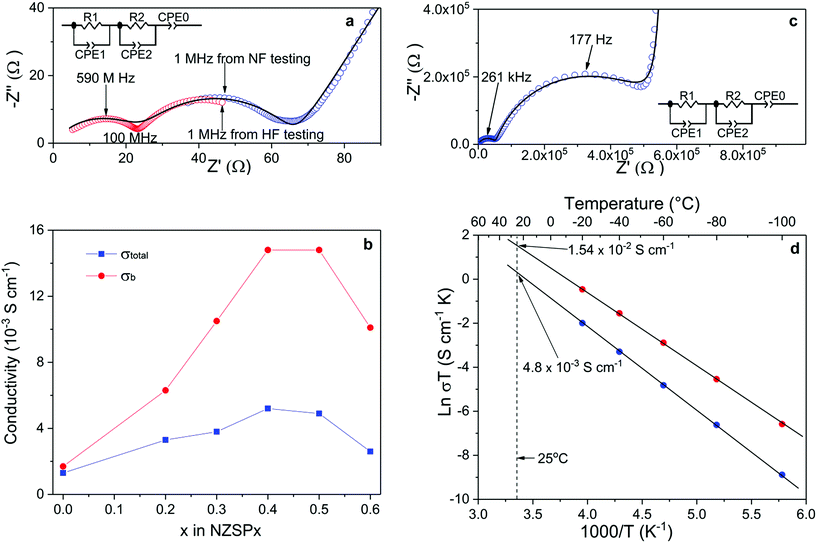
The σ_total and σ_b of the sintered samples are determined by fitting Nyquist plots of the impedance spectra, as shown in Fig. 2a. The equivalent circuit is shown as an inset of Fig. 2a, where R and CPE indicate the resistance and constant phase element (CPE), respectively. A number of key parameters of the equivalent circuit are shown in Table 2. Since the capacitance values of CPE1, CPE2 and CPE0 fit well to the characteristic capacitance²⁵ from the contribution of the bulk (high-frequency semi-cycle), the grain-boundary (middle-frequency semi-cycle) and the interface between electrolyte and electrodes (low-frequency line), respectively, R₁ and R₂ are attributed to the bulk and grain-boundary resistances (R_b and R_gb), respectively. It is quite common to discuss the conductivity of NASICON materials using Nyquist plots.^{20,21,26–32} However, limited by the frequency range of common impedance spectroscopy systems (up to 20 MHz), they usually show only one (or even half of one) semi-circle in the plots at room temperature. Therefore, it is difficult to separate R_b and R_gb contributions. Only the total resistance (R_total, which equals to R_b + R_gb) can be determined from such plots. In the present study, two impedance spectroscopy systems were used in combination to solve this problem, with frequency ranges from 3 GHz to 1 MHz and from 3 MHz to 0.01 Hz. As shown in Fig. 2a, the Nyquist plot of NSZP0.4 shows almost two complete semi-circles, starting very close from the origin of both the x and y axis. Nyquist plots of other samples are shown in the ESI Fig. S6.†

Fig. 2 (a) Experimental Nyquist plot of the impedance spectra recorded at 25 °C with gold electrodes using a high-frequency (HF) analyzer (red circle) and a normal-frequency (NF) analyzer (blue circle), together with the simulated data (solid line) for NZSP0.4 (diameter of 0.678 cm and thickness of 0.124 cm). (b) Experimental data of conductivity of σ_total (blue) and σ_b (red) of NZSPx measured at 25 °C. (c) Experimental Nyquist plot of the impedance spectra recorded at −100 °C using a normal-frequency analyzer (blue cycle) together with the simulated data (solid line) for NZSP0.4 (diameter of 0.666 cm and thickness of 0.137 cm). (d) Arrhenius plot of σ_total (blue) and σ_b (red) of the sample in (c).

Table 2 Some key parameters of the equivalent circuit shown in Fig. 2

	R 1 (Ω)	R 2 (Ω)	CPE1 (F)	CPE2 (F)	CPE0 (F)
Derived from Fig. 2a	23.1	42.9	1.3 × 10^−11	2.4 × 10^−9	8.6 × 10^−6
Derived from Fig. 2c	4.9 × 10^4	4.4 × 10^5	1.2 × 10^−11	2.0 × 10^−9	8.0 × 10^−7

---

Fig. 2b shows the conductivity data of the σ_total and σ_b of NZSPx measured at 25 °C, derived from the same method as in Fig. 2a. With increasing amounts of the x value, the σ_total of the NZSPx samples increases until x = 0.4, reaching a peak value of 5.2 × 10⁻³ S cm⁻¹. σ_b exhibits a similar dependence on the x value, reaching 1.49 × 10⁻² S cm⁻¹. When x ≥ 0.5, both σ_total and σ_b decrease with increasing x value. Experimental σ_b data of NASICONs at room temperature were never reported before, and such a value is unexpectedly high, even significantly higher than that of liquid-based Na-ion conductors.¹⁸ Moreover, it is also observed that R_b shows less contribution to R_total with increasing amounts of the x value, i.e. R_gb becomes more and more significant in R_total.

The σ_b of NZSPx can also be determined by normal-frequency impedance spectroscopy at low temperatures, since the time constant (τ) of the parallel RC element (R₁ and CPE1) representing the bulk component is shifted to the normal-frequency range because of the increased resistance of the samples at low temperatures.²⁵ An example is shown in Fig. 2c. At −100 °C, two complete semi-circles are observed for a sintered NZSP0.4 sample by impedance spectroscopy with a maximum frequency of 10 MHz. The capacitance values of CPE1, CPE2 and CPE0 in Fig. 2c also fit well to the characteristic capacitance²⁵ from the contribution of bulk, grain-boundary and the interface between electrolyte and electrodes (Table 2), indicating that R₁ and R₂ are attributed to R_b and R_gb, respectively. Nyquist plots of the sample tested at other temperatures are shown in the ESI Fig. S7.† Until −20 °C, at least part of the semi-circle representing the bulk component can be recognized using the Nyquist plot. σ_b and σ_total at these temperatures are then determined and the Arrhenius plots which are shown in Fig. 2d. Both plots of σ_b and σ_total show ideally linear behavior, with the activation energy of 0.28 and 0.32 eV, respectively. The fitted Arrhenius plot lines can be extended to the room-temperature range, where the σ_b and σ_total are determined indirectly to be 1.54 × 10⁻² and 4.8 × 10⁻³ S cm⁻¹ at 25 °C, respectively, which fit well with the results tested directly at 25 °C by the combination of the high and normal-frequency impedance spectroscopy systems (Fig. 1a). Since σ_b is the intrinsic property of the composition and is the upper limit that σ_total can reach (in an ideal situation when R_gb could be reduced to 0), the superior σ_b reported in the present work indicates further potential of increasing the related σ_total when the microstructure of the samples is further optimized in the future.

Based on the above analysis, with respect to the influences of the parameters on the σ_total of NZSPx samples, the following explanations are given: firstly, theoretically σ_b is directly proportional to the amount of charge carriers,³³ indicating that the increasing Na-ion occupancy in the structure also causes σ_b to increase, which may be the reason for the increasing σ_b in NZSPx up to x = 0.4 or 0.5. However, at the same time, it is important that some Na-ion vacancies are present in the structure to allow the motion of Na-ions. Otherwise, when all possible Na ion positions are occupied, it is not possible for Na-ions to hop from one site to another due to the lack of vacancies. The maximum Na ion occupation in one unit cell of NZSPx is 4,²⁰ which means that the best ratio between occupied and vacant Na-ion sites is about 3.4 : 0.6 or 3.5 : 0.5. It should be emphasized that this ratio mainly influences σ_b and does not necessarily relate to σ_gb.

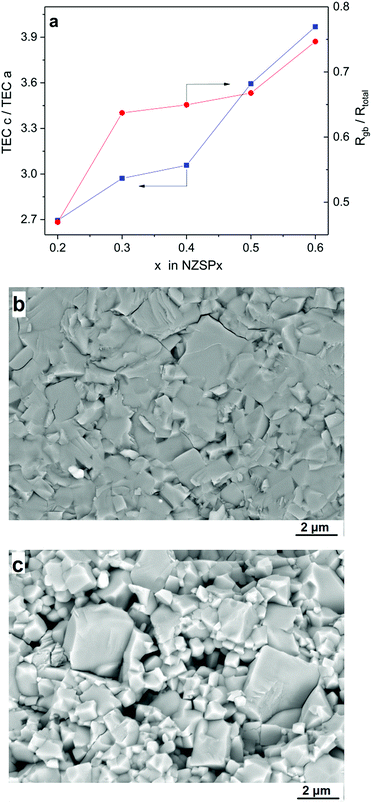
Secondly, the TEA (see Table 1) leads to differential contraction during cooling after sintering and the contact between the grains may be degraded, and R_gb is thusly increased. Fig. 3a compares the TEA, i.e. the ratio of TECs along lattice parameters c and a (derived from Table 1) and the ratio of R_gb divided by R_total (derived from Fig. S6†), both as a function of the x value in NZSPx. They both increase with the x value and also show a similar slope, indicating the influence of TEA on σ_gb and accordingly on σ_total. When the TEA increases, more contact losses occur and even micro-cracking along grain boundaries may be induced, leading to an apparent higher contribution of R_gb in R_total. The influence of TEA on σ_gb is further proved by the microstructure of the samples. Fig. 3b and c compare the microstructure of sintered NZSP0.4 and NZSP0.6 samples, with a relative density of 97% and 95%, respectively. Clearly, the contact of the grains of NZSP0.4 is tight, with only a few micro-cracks along the grain boundaries, while the contact of the grains of NZSP0.6 shows less adhesive bonding with much more micro-cracks because of the higher TEA (see Table 1 and Fig. 3a).

Fig. 3 (a) The comparison of TEA (expressed as TEC of lattice parameter c divided by TEC of lattice parameter a, blue squares) and contribution of R_gb to R_total (tested at 25 °C, expressed as R_gb divided by R_total, red circles) as a function of the x value in NZSPx. (b) Microstructure of NZSP0.4 sintered at 1260 °C. (c) Microstructure of NZSP0.6 sintered at 1280 °C.

In comparison, other reported NASICONs have been extensively investigated by means of scanning electron-microscopy (SEM).^29,34–38 They typically exhibit more severe cracks, poor contact between grains, and lower relative density due to the inappropriate processing technology. This explains why NASICONs have previously exhibited inferior σ_total and the value of σ_total scattered greatly even for the same composition at room temperature.^14,15 The R_gb was significantly higher and more uncontrollable. Moreover, this also explains why despite most subsequent research studies^14,15 having accepted the composition range from Hong et al. (−0.2 ≤ x ≤ 0.2, i.e. Na content range from 2.8 mol to 3.2 mol per formula unit of the NASICONs)^12,13 as the best composition for σ_total, several research studies in the last two years reported that the highest σ_total at room temperature appears at a Na content near 3.4 mol per formula unit of the NASICONs.^20,24,32,39 The enhanced processing technology decreases the R_gb and the σ_total is then significantly influenced by the σ_b of the sample, as shown in the present study.

Thirdly, a phase transition from a rhombohedral structure to a monoclinic structure exists for the samples of NZSP0–NZSP0.5 when the temperature decreases from 200 °C to 100 °C (Fig. 1b and ESI Fig. S3†). The transition should be accompanied by both a pathway change of Na-ion conduction in the lattice and a dimensional change of the grains in different directions, influencing both the R_b and R_gb of the samples accordingly. Other parameters like secondary phases existing in the grain boundaries, their conductivity, the volume ratio and distribution of grain-boundaries in the sintered sample etc. also influence the conductivity of NZSPx. Further experiments are needed to analyze these dependencies in detail.

The σ_total of a typical NZSP0.4 is compared with other NASICON materials, as shown in Fig. 4a.^{13,20,24,26,34,37,40} In general, early studies paid more attention to Na content range from 2.8 mol to 3.2 mol per formula unit of the NASICONs, and normally exhibited σ_total under 1 × 10⁻³ S cm⁻¹ at room temperature.^14,15 In the last two years, NASICON materials attracted great interest with Na_3.4Sc_0.4Zr₂Si₂PO₁₂ (ref. 20) and Na_3.3La_0.3Zr_1.7Si₂PO₁₂ (ref. 24) showing reasonably good σ_total of 2–4 × 10⁻³ S cm⁻¹ at 25 °C. In the present study, 5.2 × 10⁻³ S cm⁻¹ was obtained at 25 °C for a rare-earth free composition, which permits high performance and low cost simultaneously.

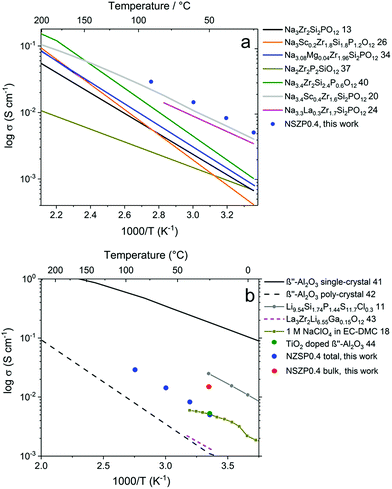Fig. 4 Temperature dependence of σ_total for NZSP0.4 and comparison with (a) other NASICON materials and (b) other Na and Li conductors.

The conductivity of NZSP0.4 is also compared with other Na and Li-ion conductors (Fig. 4b).^{11,18,41–44} Single-crystalline β′′-alumina exhibits the highest conductivity of all Na-ion conducting solid electrolytes, which reaches 0.16 S cm⁻¹ at 25 °C.⁴¹ However, since β′′-alumina exhibits two-dimensional Na-ion migration,^16,17 the σ_total for polycrystalline β′′-alumina is only 1–2 × 10⁻³ S cm⁻¹ at room temperature due to the unavoidably high R_gb caused by a mismatch in the conducting direction of different grains.⁴² The σ_total of NZSP0.4 is even comparable with common liquid electrolytes of NIBs, e.g. 1 M NaClO₄ in the mixture of ethylene carbonate and dimethyl carbonate (EC–DMC).¹⁸ Moreover, a wide window for electrochemical stability (from 0 up to 9 V versus Na/Na⁺) of the NASICON materials was also proven,^20,39 which is much higher than the liquid based electrolyte (lower than 5 V). The only comparable poly-crystalline Na-ion conductor is TiO₂ doped β′′-alumina reported in 2018, which has a room-temperature conductivity of 5.4 × 10⁻³ S cm⁻¹.⁴⁴ When compared to the best solid-state Li-ion conductors, NZSP0.4 shows a lower σ_total than that of Li_9.54Si_1.74P_1.44S_11.7Cl_0.3 (2.5 × 10⁻² S cm⁻¹ at 25 °C).¹¹ However, the application of sulfide is problematic because this material is very air-sensitive and unstable,⁴⁵ while NZSPx can be processed directly in ambient air. In addition to the sulfides, the most favored solid-state electrolyte for LIBs is La₃Zr₂Li₇O₁₂-based materials, of which La₃Zr₂Li_6.55Ga_0.15O₁₂ exhibits the best reported σ_total (1.3 × 10⁻³ S cm⁻¹ at 24 °C).⁴³ The higher σ_total of NZSP0.4 compared to Li₇La₃Zr₂O₁₂-based materials could play an important role in the further development of NIBs and LIBs in all-solid-state designs.

Na/NZSP0.4/Na symmetric cells

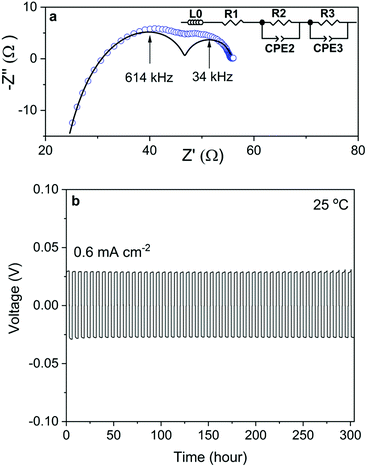
The Nyquist plot of the impedance spectra of a Na/NZSP0.4/Na symmetric cell is shown in Fig. 5a, which is also fitted by the equivalent circuit shown as an inset of the figure, where L₀ indicates the inductance induced by conductive parts in the measurement setup, R and CPE indicate the resistance and constant phase element, respectively. The sum of R₁ and R₂ is attributed to R_total of NZSP0.4 because their relative conductivity is calculated to be 4.8 × 10⁻² S cm⁻¹ at 25 °C, which fits well to the σ_total of NZSP0.4 itself. Then R₃ and CPE3 are reasonably attributed to the contribution of interface resistance (R_int) between Na and NZSP0.4. The calculated R_int (per interface) is 4.1 Ω cm² at 25 °C. As reference, Ma et al.²⁰ got >100 Ω cm² for Sc substituted NASICON at 25 °C, while the current best R_int between Li metal and Li-conducting ceramic is 2 Ω cm² at room temperature.⁴⁶ The cycling behavior of the Na/NZSP0.4/Na symmetric cell is shown in Fig. 5b. The cell was cycled for 300 h at ±0.6 mA⁻² cm at 25 °C, with 3 h per charge or discharge process, i.e. 1.8 mA h cm⁻² per charge or discharge. No apparent polarization was observed during the operation, and so was the dendrite formation. In comparison, Zhou et al.⁴⁷ reported a Na/NASICON/Na symmetric cell that only a reached current density of 0.25 mA cm⁻² and areal charge density of 0.25 mA h cm⁻², at 65 °C. Another example for Li/Li-ceramic conductor/Li symmetric cell⁴⁶ shows a current density of 0.2 mA cm⁻² and areal charge density of 0.2 mA h cm⁻², at 25 °C. The above cited references are both among the current best level of interfaces between Na (Li) and a ceramic electrolyte. The results in this work are a step forward. The parameters influence the R_int and the cycle-performance of the symmetric cells need more intensive investigations. However, a high σ_total of NZSP0.4 is definitely one of the most important reasons for the low R_int and high cycle stability of the symmetric cells.

Fig. 5 (a) Experimental Nyquist plot (blue circle) of the impedance spectra recorded at 25 °C with a sodium electrode normal-frequency analyzer, together with the simulated data (solid line) for NZSP0.4 (diameter of 1.03 cm and thickness of 0.185 cm). (b) Galvanostatic cycling of Na/NZSP0.4/Na at 0.6 mA cm⁻² for 300 h at 1.8 mA h cm⁻² per charge (discharge).

All ceramic sodium-ion batteries

All-NASICON-ceramic cells with sintered NZSP0.4 as the electrolyte and a mixture of NVP–NZSP0.4–carbon (54 : 40 : 6 in weight ratio) as both positive and negative electrodes were fabricated by sintering electrodes on the electrolyte at 750 °C in Ar containing 2% H₂. NVP and their fluorine-containing variant Na₃V₂P₂O₈F₃ have been extensively investigated and considered as promising candidates for NIBs. Conventional NIBs based on them and liquid electrolytes have already delivered impressive performances,.^48–52 It is known that the electrochemical extraction of Na⁺ from NVP to NaV₂P₃O₁₂ occurs after a two-phase reaction at 3.4 V versus Na/Na⁺, and the V³⁺ ions in NVP can also be reduced to V²⁺ through the insertion of one Na-ion towards Na₄V₂P₃O₁₂ at 1.6 V versus Na/Na⁺. Therefore NVP can be used as a positive as well as a negative electrode in a Na-ion battery and offers the possibility of assembling symmetrical cells (NVP/electrolyte/NVP) capable of delivering 1.8 V.^31,49,50,53 The microstructure of a typical prepared cell is shown in Fig. 6a and b. NZSP0.4 and NVP both form their network for Na-ion conduction and exchange, guaranteeing the processes of electrochemical reactions in the electrodes. Since NVP powder was prepared by Pechini's method,⁵⁴ which means NVP particles are first coated with organics and then sintered in Ar containing 2% H₂, each NVP particle in the electrodes is covered by a carbon “shell”. Under the observation of SEM, only carbon with certain agglomeration can be seen (Fig. 6a). While under the examination of a scanning transmission electron microscope (STEM) with an energy-dispersive X-ray spectroscope (EDS), the carbon “shell” can be observed for all NVP particles (a typical image is shown in the ESI Fig. S8†), thus ensuring electronic conduction within the electrodes. The interface between the grains of NZSP0.4 and NVP of a prepared electrode is sharp and neat (Fig. 6c–f), indicating that the co-sintering (750 °C) of the two materials did not induce any obvious solid-state reactions or diffusions between NZSP0.4 and NVP, in accord with XRD patterns (Fig. 1d). In addition, the presence of carbon “shell” on NVP particles is proved again (Fig. 6f). While the signal of carbon on NZSP0.4 is weak and can almost be regarded as background noise. This fits well with the expectation because NZSP0.4 is first sintered at 1260 °C and then mixed with NVP prepared by Pechini's method. No carbon "shell" is supposed to cover NZSP0.4 particle.

Fig. 6 The microstructure of NVP and NZSP0.4 grains in the electrode. (a and b) Cross sectional view by SEM. (c–f) STEM observation and the elemental distribution maps acquired by EDS.

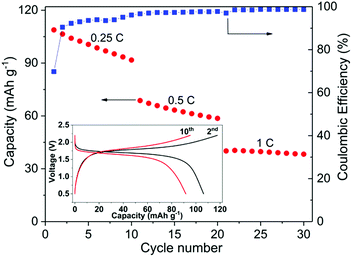
Fig. 7 shows the cycling performance of a typical all-NASICON-ceramic battery operating at 28 °C. The battery was running at 0.25C, 0.5C and 1C for 10 cycles each, respectively. During the first charge up to 2.2 V at 0.25C, an extra capacity (about 30% higher than the theoretical capacity) is observed and disappears upon further cycling, which may be the result of side-reactions of the electrodes, and also observed and discussed in previous reports on all-solid-state NIBs and LIBs.^53,55,56 A discharge capacity of 108.8 mA h g⁻¹ is obtained for the first cycle, which reaches 92.5% of the theoretical capacity of the battery. Degradation in the capacity and increase in polarization occur during each cycle in which the fixed C-rate is observed, especially for the low C-rate. At 0.25C, the discharge capacity decreases for 16% after 10 cycles. It is possible that the fading of the capacity comes from the dimensional change of NVP during charging and discharging.²⁴ The corresponding impedance spectrum supports this explanation (ESI Fig. S9†). However, further experiments are needed to better understand this process in detail. The coulombic efficiency of the cell starts at 70% for the first cycle due to the side-reactions, increases with the cycle number and C-rate, and reaches 99% after 30 cycles. According to the analysis of STEM-EDS (ESI Fig. S10†), the cell-operating processes also induce no obvious solid-state reactions or diffusions between NZSP0.4 and NVP, which further proves the electrochemical compatibility of the two materials.

Fig. 7 Cycling performance of the full-ceramic battery operated at 28 °C. The inset displays the charge and discharge curves of the 2^nd and 10^th cycle at a current rate of 0.25C. The capacity in the figure indicates the specific discharge capacity of the positive electrode.

Compared to conventional NIBs with a liquid electrolyte, the above performance is rather moderate. As an example, batteries in similar configuration, i.e. NVP/liquid electrolyte/NVP can cycle up to 100C and have a cycle life of 2000 (at 10C), both at room temperature.^49,50 Because NVP and liquid electrolyte have full and “soft” contact, interface problems can be neglected. In comparison, NVP and NZSP0.4 have insufficient and rigid contact, which is problematic when Na-ions have to cross the interface of NVP and NZSP0.4. However, the performance of the present study is acceptable for such a new concept as a rechargeable battery. In this battery, all the interfaces are between rigid ceramics. No liquid or polymer components are used at all. In comparison, Lalère et al.⁵³ reported a similar full-ceramic NIB composed of NVP–NZSP0–carbon/NZSP0/NVP–NZSP0–carbon. The cell was tested at 200 °C, but the degradation is much faster than the cell reported in the present study. Zhang et al.²⁴ also reported a ceramic half-cell with sodium metal as the negative electrode, which was based on Na_3.57Zr_1.72La_0.21Si_2.08P_0.92O₁₂ as an electrolyte material and ran at 80 °C. The charge–discharge performance is comparable to the performance in Fig. 7. Inoishi et al.⁵⁷ also announced full-ceramic NIBs operating at room temperature. Their batteries only contain one single material of Na_2.6V_1.6Zr_0.4P₃O₁₂, which serves as the material for Na-ion storage, Na-ion conduction and electric conduction at the same time. In that case, although the material has a much smaller conductivity (∼1 × 10⁻⁴ S cm⁻¹ at room temperature), the battery has no interface problems because it contains only one material. In the case of this work, although NSZP0.4 has a much higher conductivity, the interface between NZSP0.4 and NVP is a potential transport barrier because of the much lower Na-ion conductivity of NVP (<10⁻⁷ S cm⁻¹ at room temperature⁵⁷) and the rigid contact with NSZP0.4. The advanced fabrication method can bring better performances. Kehne et al.⁵⁸ applied the pulsed laser deposition method to deposit the Na_xCoO₂ cathode onto Na_3.4Sc_0.4Zr_1.6Si₂PO₁₂ ceramic electrolyte. With sodium metal as the anode material, the assembled thin-film NIB had only 25% performance degradation after 100 cycles under 0.15C and at room temperature. Some oxide-ceramic LIBs with lithium metal as the negative electrode were also reported in recent years.^56,59,60 However, their operating temperature was even higher than the NIBs mentioned above,²⁴ and cell performance was even worse. As mentioned above, the better performance of NIBs is due to the better electrolyte material with its higher conductivity at room temperature. In the present study, the high σ_total of the electrolyte, high chemical stability between the electrolyte and electrode, and favorable microstructure of both electrolyte and electrode lead to the desired performance of the full-ceramic battery operated at room temperature, thus indicating a promising future for full-ceramic NIBs.

Conclusions

NZSPx (x = 0–0.6) were prepared by means of SA-SSR synthesis. The synthesis method has the potential for use in industrial mass production. Benefiting from the optimized primary powders, NZSPx ceramics exhibit an optimized microstructure after sintering and result in high σ_total. The σ_total of NZSPx increases from x = 0 to x = 0.4, and decreases from x = 0.4 to x = 0.6, which may result from the combined influences of the ratio between the occupied and vacant Na ion sites, TEA between lattice parameters a and c, and the phase transition between the rhombohedral and monoclinic phase at 200 °C–100 °C. The σ_b and σ_total of the samples can be separated at 25 °C by combining two impedance spectroscopy systems with different frequency ranges. At 25 °C, NZSP0.4 exhibits a σ_b of 1.5 × 10⁻² S cm⁻¹ and a σ_total of 5 × 10⁻³ S cm⁻¹, which is the best value of all reported polycrystalline Na-ion conductors, and are comparable to common liquid electrolytes of NIBs. A Na/NZSP0.4/Na symmetric cell showed a low interface resistance of 4.1 Ω cm² and a high cycling performance of 1.8 mA h cm⁻² per charge or discharge process, both at 25 °C. The superior σ_total of NZSP0.4, high chemical stability between the NZSP0.4 electrolyte and NVP electrode, and favorable microstructure of both electrolyte and electrode lead to a full-ceramic cell of NVP–NZSP0.4–carbon/NZSP0.4/NVP–NZSP0.4–carbon which was successfully tested at 28 °C with reasonable cycling performances.

Experimental

Preparation of NZSPx and NVP powders

NZSPx (x = 0–0.6) powders can be prepared on a laboratory scale (10 g–1 kg) using a solution-assisted solid-state reaction method (SA-SSR).^19–21 NaNO₃ (VWR, 99.7%), ZrO(NO₃)₂ (Aldrich, 99%), Si(OCH₂CH₃)₄ (Merck, 99%) and NH₄H₂PO₄ (Merck, 99%) were used as starting materials. Corresponding amounts of NaNO₃, and ZrO(NO₃)₂ were dissolved into deionized water. A stoichiometric amount of Si(OCH₂CH₃)₄ was also added to the solution while stirring. When Si(OCH₂CH₃)₄ was hydrolyzed, the corresponding amount of NH₄H₂PO₄ was added to the system while also stirring. The homogeneous aqueous system then changed to a mixture of a colloidal sol and precipitates of complex zirconium oxyphosphate compounds.

The whole mixture was dried at 85 °C. The dried powder was calcined at 800 °C for 3 h. After calcination, a white powder was obtained. The calcined powder was then milled in ethanol with zirconia balls on a milling bench for 48 h, and dried at 70 °C for 12 h.

NVP powders were prepared by using the Pechini's method.⁴⁷ NaH₂PO₄ (Sigma-Aldrich, 99%) and NH₄VO₃ (Merck, 99%) were applied as starting materials. Corresponding amounts of NaH₂PO₄ and NH₄VO₃ were dissolved into deionized water. Double the amount of moles (sum of NaH₂PO₄ and NH₄VO₃) of citric acid was also dissolved into the same solution, before subsequently adding the same amount of ethylene glycol. The solution was dried at 200 °C while stirring, and calcined at 400 °C for 5 h. The calcined powder was then milled in ethanol with zirconia balls on a milling bench for 24 h, and dried at 70 °C for 12 h. The NVP powder has a rhombohedral structure after reduction at 750 °C for 8 h in Ar containing 2% H₂, with 10 wt% of carbon remaining in the powder, which comes from the incomplete combustion of citric acid and ethylene glycol. The carbon content was determined by heating the powder at 650 °C in air, where carbon was burnt out, while NVP was also decomposed because of its instability in air at high temperature. The decomposed NVP was then heated up at 750 °C in Ar containing 2% H₂ again. Pure phase NVP was obtained again. The weight difference of the final achieved powder and the original powder is regarded as the carbon content.

Fabrication of specimens and single cells

For conductivity testing, the milled NZSPx powders were put into a cylindrical pressing mold with a diameter of 8–13 mm and pressed with a uniaxial pressure of 100 MPa at room temperature. The pressed pellets were then sintered at 1250 °C–1300 °C for 5 h. The pellets had obtained a diameter of 6.5–10.5 mm and thickness of about 1 mm. For the preparation of electrolytes of the single cells, the procedure is just like above, but specifically only with NZSP0.4 powder, using a cylindrical pressing mold with a diameter of 13 mm and sintered at 1260 °C for 5 h. The pellets obtained had a diameter of about 10 mm and thickness of about 1 mm.

Some of the milled NZSP0.4 powder was sintered at 1260 °C for 5 h, then ground and ball-milled again on a milling bench for 48 h. The sintered NZSP0.4 powder obtained was mixed with the milled NVP powder with a NZSP0.4 : NVP (with carbon) = 40 : 60, i.e. NZSP0.4 : NVP : C weight ratio of 40 : 54 : 6. The mixed powder was then screen-printed on both sides of the sintered NZSP0.4 pellets as negative and positive electrodes, followed by co-sintering at 750 °C for 8 h in Ar containing 2% H₂. The single cells subsequently had a positive electrode weight of 0.1–1 mg. The weight of the negative electrode was adjusted to reach about 210% of the positive electrodes. The prepared single cells were then sealed inside aluminum pouch-bags, with Ni-metal pellets 12 mm in diameter as the current-collector for both anode and cathode sides.

Characterization

The XRD patterns of the sintered samples of NZSPx and/or NVP were recorded using a Bruker D4 ENDEAVOR diffractometer with Cu K_α radiation in the temperature range of 25–1200 °C. The lattice parameters and the quantitative phase analysis of the samples were determined by the Pawley and Rietveld refinement method using the TOPAS program (Bruker AXS GmbH). The microstructure of the powders or sintered samples was analyzed using a scanning electron microscope Zeiss Ultra55.

The prepared dense pellets of NSZSPx (x = 0–0.6) were sputtered with gold on both sides. The impedance spectra of the samples were measured at 25 °C using two commercial electrochemical systems (Keysight E4991B and Biologic VMP-300), with an AC frequency range from 3 GHz to 1 MHz and from 3 MHz to 1 Hz, respectively. The results were adjusted according to the dimension of the samples by multiplying with the conducting area and dividing with the thickness of the samples and fitted using software “Z-view” (Scribner Associates Inc.). The temperature was controlled using a climate chamber (Vötsch, VT4002). The temperature-dependent impedance of the NZSPx sample was measured between −100 °C and 90 °C using another commercial electrochemical system (Novocontrol Alpha-A, with normal frequency range of 10 MHz–0.01 Hz) including a temperature-controlling system, a liquid-nitrogen contained cooling system and a furnace.

The charge–discharge behavior of the all ceramic single cells was tested using an electrochemical system (Biologic VMP-300) with controlled temperature in a climate chamber (Vötsch, VT4002). A uniaxial pressure of about 100 MPa was applied during testing, while the samples were sealed in the pouch-bags and clipped between the two Ni-metal current collectors. The microstructure of the cells was analyzed by SEM (ZEISS Merlin) together with an Ar-cross-section polisher (JEOL, SM-09010). The scanning transmission electron microscopy (STEM) experiments were performed on an FEI Titan 80–200 Chemi-STEM equipped with a Super-X energy-dispersive X-ray spectroscopy (EDS) detector system.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors thank Dr D. Grüner (IEK-2) and Dr D. Sebold (IEK-1) for SEM investigations, and also Dr Y. J. Sohn (IEK-1) for XRD investigations. Partial financial support from the German Federal Ministry of Education and Research (BMBF) in the frame of the BenchBatt project (reference number 03XP0047B) is gratefully acknowledged.

Notes and references

1. H. Pan, Y.-S. Hu and L. Chen, Energy Environ. Sci., 2013, 6, 2338–2360.
2. V. Palomares, M. Casas-Cabanas, E. Castillo-Martínez, M. H. Han and T. Rojo, Energy Environ. Sci., 2013, 6, 2312–2337.
3. M. D. Slater, D. Kim, E. Lee and C. S. Johnson, Adv. Funct. Mater., 2013, 23, 947–958.
4. N. Yabuuchi, K. Kubota, M. Dahbi and S. Komaba, Chem. Rev., 2014, 114, 11636–11682.
5. M. Sawicki and L. L. Shaw, RSC Adv., 2015, 5, 53129–53154.
6. D. Larcher and J.-M. Tarascon, Nat. Chem., 2015, 7, 19–29.
7. A. Aboulaich, R. Bouchet, G. Delaizir, V. Seznec, L. Tortet, M. Morcrette, P. Rozier, J.-M. Tarascon, V. Viallet and M. Dollé, Adv. Energy Mater., 2011, 1, 179–183.
8. N. Kamaya, K. Homma, Y. Yamakawa, M. Hirayama, R. Kanno, M. Yonemura, T. Kamiyama, Y. Kato, S. Hama, K. Kawamoto and A. Mitsui, Nat. Mater., 2011, 10, 682–686.
9. K. Takada, Acta Mater., 2013, 61, 759–770.
10. A. L. Robinson and J. Janek, MRS Bull., 2014, 39, 1046–1047.
11. Y. Kato, S. Hori, T. Saito, K. Suzuki, M. Hirayama, A. Mitsui, M. Yonemura, H. Iba and R. Kanno, Nat. Energy, 2016, 1, 16030.
12. H. Y. P. Hong, Mater. Res. Bull., 1976, 11, 173–182.
13. J. B. Goodenough, H. Y. P. Hong and J. A. Kafalas, Mater. Res. Bull., 1976, 11, 203–220.
14. K.-D. Kreuer, H. Kohler and J. Maier, High conductivity ionic conductors: Recent trends and application, ed. T. Takahashi, 1986, pp. 242–279.
15. M. Guin and F. Tietz, J. Power Sources, 2015, 273, 1056–1064.
16. J. W. Fergus, Solid State Ionics, 2012, 227, 102–112.
17. X. Lu, G. Xia, J. P. Lemmon and Z. Yang, J. Power Sources, 2010, 195, 2431–2442.
18. A. Bhide, J. Hofmann, A. K. Dürr, J. Janek and P. Adelhelm, Phys. Chem. Chem. Phys., 2014, 16, 1987–1998.
19. Q. Ma, F. Tietz, S. Naqash and O. Guillon, Ger. Pat., DE102015013155, 2015.
20. Q. Ma, M. Guin, S. Naqash, C.-L. Tsai, F. Tietz and O. Guillon, Chem. Mater., 2016, 28, 4821–4827.
21. S. Naqash, Q. Ma, F. Tietz and O. Guillon, Solid State Ionics, 2017, 302, 83–91.
22. U. von Alpen, M. F. Bell and W. Wichelhaus, Mater. Res. Bull., 1979, 14, 1317–1322.
23. T. Oota and I. Yamai, J. Am. Ceram. Soc., 1986, 69, 1–6.
24. Z. Zhang, Q. Zhang, J. Shi, Y. S. Chu, X. Yu, K. Xu, M. Ge, H. Yan, W. Li, L. Gu, Y. S. Hu, H. Li, X. Q. Yang, L. Chen and X. Huang, Adv. Energy Mater., 2106, 6, 1601196.
25. J. T. S. Irvine and D. C. Sinclair, Adv. Mater., 1990, 2, 132–138.
26. M. A. Subramanian, P. R. Rudolf and A. Clearfield, J. Solid State Chem., 1985, 60, 172–181.
27. R. O. Fuentes, F. M. Figueiredo, M. R. Soares and F. M. B. Marques, J. Eur. Ceram. Soc., 2005, 25, 455–462.
28. J. S. Lee, C. M. Chang, Y. Lee, J. H. Lee and S. H. Hong, J. Am. Ceram. Soc., 2004, 87, 305–307.
29. A. Ahmad, T. A. Wheat, A. K. Kuriakose, J. D. Canaday and A. G. Mcdonald, Solid State Ionics, 1987, 24, 89–97.
30. J. Gulens, B. W. Hildebrandt, J. D. Canaday, A. K. Kuriakose, T. A. Wheat and A. Ahmad, Solid State Ionics, 1989, 35, 45–49.
31. Y. Noguchi, E. Kobayashi, L. S. Plashnitsa, S. Okada and J.-I. Yamaki, Electrochim. Acta, 2013, 101, 59–65.
32. M. Guin, F. Tietz and O. Guillon, Solid State Ionics, 2016, 293, 18–26.
33. A. R. West, Solid state chemistry and its applications, Wiley, 1987.
34. T. Takahashi, K. Kuwabara and M. Shibata, Solid State Ionics, 1980, 1, 163–175.
35. H. Perthuis and P. Colomban, Ceram. Int., 1986, 12, 39–52.
36. J. H. Kim, T. S. Oh, M. S. Lee, J. G. Park and Y. H. Kim, J. Mater. Sci., 1993, 28, 1573–1577.
37. N. Gasmi, N. Gharbi and H. Zarrouk, J. Sol-Gel Sci. Technol., 1995, 4, 231–237.
38. A. Ignaszak, P. Pasierb, R. Gajerski and S. Komornicki, Thermochim. Acta, 2005, 426, 7–14.
39. S. Song, H. M. Duong, A. M. Korsunsky, N. Hu and L. Lu, Sci. Rep., 2016, 6, 32330.
40. J. A. Kafalas and R. J. Cava, Fast ion transport in solids, ed. P. Vashishta, J. N. Mundy and G. K. Shenoy, North-Holland, Amsterdam, 1979.
41. J. L. Briant and G. C. Farrington, J. Solid State Chem., 1980, 33, 385–390.
42. W. I. Archer, R. D. Armstrong, D. P. Sellick, W. G. Burden and J. H. Duncan, J. Mater. Sci., 1980, 15, 2066–2072.
43. C. Bernuy-Lopez, W. Manalastas Jr, J. M. Lopez del Amo, A. Aguadero, F. Aguesse and J. A. Kilner, Chem. Mater., 2014, 26, 3610–3617.
44. E. Yi, E. Temeche and R. M. Laine, J. Mater. Chem. A, 2018, 6, 12411–12419.
45. Y. Wang and W.-H. Zhong, ChemElectroChem, 2015, 2, 22–36.
46. A. Sharafi, E. Kazyak, A. L. Davis, S. Yu, T. Thompson, D. J. Siegel, N. P. Dasgupta and J. Sakamoto, Chem. Mater., 2017, 29, 7961–7968.
47. W. Zhou, Y. Li, S. Xin and J. B. Goodenough, ACS Cent. Sci., 2017, 3, 52–57.
48. Q. Liu, D. Wang, X. Yang, N. Chen, C. Wang, X. Bie, Y. Wei, G. Chen and F. Du, J. Mater. Chem. A, 2015, 3, 21478–21485.
49. Y. Zhang, H. Zhao and Y. Du, J. Mater. Chem. A, 2016, 4, 7155–7159.
50. C. Zhu, P. Kopold, P. A. van Aken, J. Maier and Y. Yu, Adv. Mater., 2016, 28, 2409–2416.
51. E. Gu, S. Liu, Z. Zhang, Y. Fang, X. Zhou and J. Bao, J. Alloys Compd., 2018, 767, 131–140.
52. Y. Fang, X. Xu, Y. Du, X. Zhu, X. Zhou and J. Bao, J. Mater. Chem. A, 2018, 6, 11244–11251.
53. F. Lalère, J. B. Leriche, M. Courty, S. Boulineau, V. Viallet, C. Masquelier and V. Seznec, J. Power Sources, 2014, 247, 975–980.
54. M. P. Pechini, US Pat., 3330697, 1967.
55. G. Oh, M. Hirayama, O. Kwon, K. Suzuki and R. Kanno, Chem. Mater., 2016, 28, 2634–2640.
56. K. Park, B.-C. Yu, J.-W. Jung, Y. Li, W. Zhou, H. Gao, S. Son and J. B. Goodenough, Chem. Mater., 2016, 28, 8051–8059.
57. A. Inoishi, T. Omuta, E. Kobayashi, A. Kitajou and S. Okada, Adv. Mater. Interfaces, 2017, 6, 1600942.
58. P. Kehne, C. Guhl, Q. Ma, F. Tietz, L. Alff, R. Hausbrand and P. Komissinskiy, J. Power Sources, 2019, 409, 86–93.
59. T. Kato, S. Iwasaki, Y. Ishii, M. Motoyama, W. C. West, Y. Yamamoto and Y. Iriyama, J. Power Sources, 2016, 303, 65–72.
60. J. van den Broek, S. Afyon and J. L. M. Rupp, Adv. Energy Mater., 2016, 6, 1600736.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c9ta00048h

---