Cavity-enhanced cantilever-enhanced photo-acoustic spectroscopy

Abstract

We have improved the sensitivity of a state-of-the-art cantilever-enhanced photo-acoustic trace gas sensor by combining it with an optical power build-up cavity. The build-up cavity enhances the photo-acoustic signal by a factor of ∼100, resulting in an exceptionally good normalised noise equivalent absorption (NNEA) value of 1.75 × 10⁻¹² W cm⁻¹ Hz^−1/2. We demonstrate the sensor platform in the 1530 nm wavelength range with a simple distributed feedback diode laser, achieving 75 ppt sensitivity for C₂H₂ with a 10 s integration time.

---

Introduction

Lasers in conjunction with photo-acoustic spectroscopy (PAS) have long proven to be a highly sensitive and selective method for trace gas analysis in industry as well as in research and environmental monitoring.¹ Similarly to most optical methods, laser-based PAS is non-intrusive, allows in situ real-time monitoring and does not require sample preparation.² This method is selective, because narrow-line width lasers allow probing of spectral lines in high resolution, and sensitive because of the high brightness of the laser light. The brightness is especially beneficial in photo-acoustics as the signal strength depends on the amount of modulated optical radiation being absorbed in the sample. The radiation deposits energy into the gas. Collisional processes convert the energy to local heat, creating a pressure (sound) wave that is detected by the analyser. In cantilever-enhanced photo-acoustic spectroscopy (CEPAS), one of the most sensitive variants of PAS,³ the pressure wave is detected by measuring the movement of a mm-size cantilever with a laser based method, such as interferometry^4–6 or beam-deflection,^7,8 similarly to atomic force microscopy. CEPAS is suitable for broadband spectroscopy, as it does not require operation in an acoustic resonance of the cell nor the cantilever to reach high sensitivity.^9,10 Moreover, CEPAS has demonstrated a large linear dynamic range of at least six orders of magnitude, and its noise performance has reached the ultimate limit of the Brownian noise from the thermal movement of gas molecules.¹¹

CEPAS analysers with parts-per-trillion (ppt, volume mixing ratio) level sensitivity have been demonstrated using high-power lasers in several applications.^3,5,12,13 However, high-power lasers are rarely as compact, robust, easy to use, or inexpensive as diode and quantum cascade lasers (QCL), which would be essential for portable field instruments. Another approach, instead of using a high-power laser, is to enhance the PA signal by building up the optical power in a passive optical cavity.^14–18 A build-up cavity can be applied to any single frequency laser with sufficient beam quality, vastly extending the range of molecules that can be detected at very low concentrations. As an example, in this work, we use a highly reliable and inexpensive distributed feedback diode laser (DFB laser) from the telecommunications industry. The laser operates in the near-infrared (NIR) region where the probed absorption lines are two orders of magnitude weaker than the fundamental ro-vibration lines in the mid-infrared (MIR) region. Yet, we are able to achieve a very high detection sensitivity comparable to typical results obtained in the MIR range.

The optical cavity approach has already proved successful for another sensitive photo-acoustic technique called quartz-enhanced photo-acoustic spectroscopy (QEPAS).¹⁹ In the work by Patimisco et al.¹⁸ the authors use a high-finesse optical cavity to build up the optical power, and periodically scan the laser wavelength over a resonance mode of the cavity to create amplitude modulated (AM) laser light. The resulting pressure wave is detected using a resonant quartz tuning fork. Here, we report a detailed description of a new spectroscopic technique called cavity-enhanced CEPAS (CE-CEPAS), which combines CEPAS with an optical enhancement cavity. The technique employs wavelength modulation instead of amplitude modulation, which avoids any background signal from, for example, the cell windows, which is typical of the alternative AM approach. In this article, we also present a comparison of the new CE-CEPAS with a standard CEPAS sensor, which is operated under the same experimental conditions. Using the CE-CEPAS technique, we achieve an unprecedented normalised noise equivalent absorption (NNEA) value of 1.75 × 10⁻¹² W cm⁻¹ Hz^−1/2, which results in ppt-level detection sensitivities of HCN and C₂H₂ with the NIR laser. The technique has potential for sub-ppt level sensitivity when applied to the MIR wavelength range.

Instrumentation

Enhancement cavity

Optical cavities are mostly used in such spectroscopic techniques as cavity-enhanced absorption spectroscopy (CEAS) and cavity ring-down spectroscopy (CRDS),²⁰ where the interest is not as much in the optical power as it is in the interaction path length. An optical cavity consists of highly reflective mirrors, which reflect light repeatedly leading to many round-trips ranging from a few round-trips up to hundreds of thousands. At certain well-defined frequencies, called longitudinal cavity modes, a resonance condition is met such that the reflected electromagnetic wave reproduces itself after each round-trip. The fundamental resonance modes occur every so-called free-spectral range (FSR) expressed as c/L, where c is the speed of light and L is the cavity round-trip length. The modes are not monochromatic, but have a certain linewidth (Δν_c) (full width at half maximum, FWHM), which is related to the FSR by a parameter called finesse (F) as F = FSR/Δν_c. The finesse can also be written as F = 2π/(1 − R(1 − A)), which shows that it is fully defined by the total cavity round-trip losses 1 − R(1 − A), where R is the power reflectivity of the input coupling mirror, and A is the loss coefficient for all other cavity losses.

An efficient injection of laser light into an optical cavity requires that (1) the linewidth of the laser power spectrum (Δν_l) is comparable to or narrower than the linewidth of the cavity modes, (2) the cavity mirrors are chosen to satisfy the impedance matching condition, i.e., the input mirror transmission equals the sum of all other cavity round-trip losses, and (3) the laser beam is mode matched to the cavity, i.e., the beam matches in the size and waist position with the transversal mode profile of the cavity.²⁰ Assuming a perfect mode matching condition, the power build-up factor, defined as the circulating power divided by the input power, is²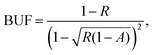¹

In the case of Δν_c < Δν_l, the enhancement factor is scaled down²⁰ by Δν_c/Δν_l. The maximum of BUF is BUF_max = 1/(1 − R) = F/π, when R = 1 − A and Δν_c ≥ Δν_l.

A typical quantum cascade laser in the MIR, or a distributed feedback diode laser in the NIR, has a linewidth in the range of 1–10 MHz. It is useful to consider this as a practical limit for the cavity enhancement. Assuming a short cavity of 10 cm in length (20 cm round-trip length) and a 5 MHz laser linewidth, the maximum practical power build-up factor is ∼100 as calculated by setting the cavity linewidth equal to that of the laser. Methods for narrowing the laser linewidth exist, such as the use of optical feedback,^15,16,22 or the use of a fast electronic feedback loop.²³ However, these are not well suited for wavelength modulation or out-of-the-lab instrumentation. Moreover, they increase the complexity of the instrument.

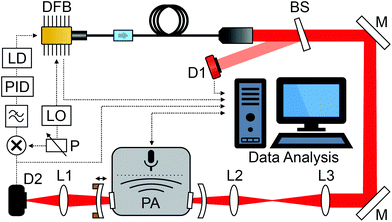
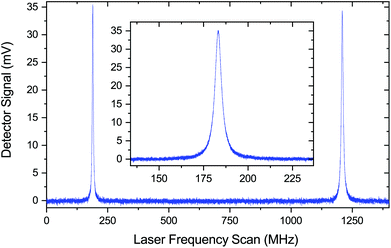
The laser used in our PA experiment is an inexpensive Avanex A1905LMI DFB laser, which operates around 6529 cm⁻¹ with a specified maximum linewidth of 5 MHz. According to the aforementioned estimation, the expected enhancement factor of the photo-acoustic signal is in the order of 100. The cavity, together with the rest of the setup, is depicted in Fig. 1. It consists of two spherical concave-convex mirrors, with dielectric coatings for the resonant wavelength. The linear cavity design is suitable in the near-infrared region, where inexpensive optical isolators (boxed arrow in Fig. 1) are available to prevent optical feedback to the laser. The input and output mirrors of the cavity have a radius of curvature of 75 mm and 100 mm, and reflectivity of >97% and >99.9%, respectively. The geometric length of the cavity is 14.7 cm (FSR = 1.02 GHz), just enough to accommodate the photo-acoustic cell with anti-reflection coated windows (Thorlabs WG10530-C) between the mirrors. The round-trip loss from the windows is 5.6 × 10⁻³ according to the specifications. The performance of the cavity was characterised by measuring its transmission spectrum, shown in Fig. 2, with a fast photodetector (Thorlabs DET08CFC/M) and a narrow linewidth external cavity diode laser (New Focus, Velocity 6328, a 50 kHz short-term linewidth). A fast detector and a narrow linewidth laser were required to avoid their contribution to the transmission spectrum. Knowing the cavity FSR, linear laser current tuning can be converted to an optical frequency. The transmission spectrum allows us to calculate the finesse of the cavity to be ∼200. Although the cavity is not impedance matched (R ≠ 1 − A), we can calculate the expected power build-up factor using eqn (1). We find that BUF ≈ 100, where we have assumed A according to specifications (window plus end mirror losses) and solved R such that the calculated finesse matches the measured one.

Fig. 1 Schematic picture of the CE-CEPAS instrument. DFB: distributed feedback laser, BS: beam sampler, M: mirror, LD: laser driver, PID: feedback controller, LO: local-oscillator, P: phase control, D: photodetector, L: lens, PA: photo-acoustic analyser.

Fig. 2 Cavity transmission spectrum over two longitudinal cavity modes as a function laser frequency scan. The spectrum was measured with a narrow linewidth laser and a fast photodetector. Inset: Zoom over a cavity mode.

Cavity locking

The laser beam is mode matched to a cavity resonance using lenses L2 and L3, shown in Fig. 1. Lens L1 is for focusing the laser beam on the InGaAs photodetector D2 (Thorlabs PDA20C), which provides the cavity transmission signal used for locking the laser wavelength to the centre of the cavity resonance mode. We performed the locking using the dither-and-lock method, where the laser frequency is slightly modulated by adding a sinusoidal voltage signal from a signal generator (LO, 5 MHz oscillation frequency) to the laser diode through a bias-T. Frequency modulation of the laser produces an amplitude modulated signal at the cavity output (D2 in Fig. 1), which is demodulated with a phase controlled (P) LO signal, low pass filtered for harmonic rejection (100 kHz bandwidth), and fed to a feedback-controller (PID), which outputs a control signal to the laser current driver (LD).

The achieved cavity lock is robust, which is essential for the experiment as the photo-acoustic measurement is performed in a wavelength modulation mode: the sinusoidal wavelength modulation at 30 Hz frequency is generated by moving the end mirror of the cavity to change its resonance frequency. As the laser is continuously locked to the cavity, the laser will follow the modulation. The feedback-controller (Toptica mFALC 110) has high gain in the low-frequency range (50 Hz corner frequency of the first integrator, 1.4 kHz for the second) to be able to follow the cavity length modulation over four FSRs, which is limited by the maximum scan range of the piezo actuators that move one of the cavity mirrors. The wavelength modulation frequency was chosen by looking for an interference free frequency, including the harmonics, in the acoustic noise spectrum of the cantilever.³ For the cantilever, the non-resonant modulation frequencies are low, typically between 10 and 100 Hz, making it easier to implement the wavelength modulation.

Photo-acoustic detection

The cantilever-enhanced photo-acoustic detection system (PA in Fig. 1), manufactured by Gasera Ltd, is the same as the one used in our previous work.³ It is equipped with a 95 mm long, 4 mm in diameter PA cell made of aluminium with gold coated surfaces. The cell temperature is stabilised to 30 °C and isolated from environmental mechanical noise by the air-suspension system of the optical table the instrument is constructed on. In later work, the air-suspension could be replaced by a spring suspension, common for CEPAS instruments in field applications. The PA detection system is connected to a measurement computer via a USB link. The connection is used for full control over the PA system, including a PA signal read-out at 1 Hz rate, a gas exchange routine, and wavelength modulation via moving of the cavity mirror. The computer used for the measurements also reads the temperature and current of the laser diode, signal level at the detector D2, and output power of the laser sampled by a CaF₂ beam sampler (BS in Fig. 1). The output power of the DFB laser, after beam sampling, available for the PA experiment is about 7.5 mW. For comparison measurements in the standard CEPAS configuration with a single pass of the laser beam through the PA cell, the cell is placed aside the cavity, and the laser beam intersected with a flip-mirror before the mode matching optics to guide it through the cell.

Experimental results

The demonstration of the new CE-CEPAS experiment was performed in the near-infrared region, which is rich in overtone bands of molecules of interest. Within the tuning range of the DFB laser (6525–6534 cm⁻¹), there exist relatively strong and isolated transitions of HCN (ν₀ = 6528.2 cm⁻¹, S = 3.787 × 10⁻²¹ cm⁻¹/(molecules cm⁻²)) and C₂H₂ (6529.2 cm⁻¹, 1.165 × 10⁻²⁰ cm⁻¹/(molecules cm⁻²)),²⁴ which show good promise for the trace gas detection. In this article, we focus mainly on the detection performance of C₂H₂ as it is a well-known spectroscopic reference gas in the near-infrared region and also of interest in environmental monitoring,²⁵ whereas HCN has interesting applications, for example, in human breath analysis.^26,27 In addition, H₂O and CO₂ have lines suitable for trace gas detection in this range, although with two orders of magnitude lower line strengths.

Our objective is first to characterise the performance of our new CE-CEPAS method. We have certified mixtures of HCN and C₂H₂ in N₂ at 5 ppm and 1 ppm mixing ratios, respectively. The mixtures are diluted with N₂ using mass flow controllers to desired mixing ratios. A total gas flow rate of approximately 1–2 l min⁻¹ is used. An automatic gas exchange system pumps the sample through the PA cell from a bypass flow when a gas exchange is initiated. The PA signal is recorded with a closed cell, which poses a limit for the continuous measurement period if the sample gas is reactive, such as HCN, and starts to desorb or adsorb on the walls of the cell. Common solutions to reduce these effects include selection of suitable inert surface materials,²⁸ heating the wetted surfaces and performing rapid gas exchange cycles.²⁹ With inert gases, such as C₂H₂, there is no such problem and therefore repeated reproducible measurements are easy to make.

The measurements are performed in the wavelength modulation mode with the detection of the peak of the second harmonic of the demodulated PA signal (peaks in Fig. 3). A potential problem using wavelength modulation in conjunction with cavity enhanced PAS is that the pressure generated by the moving cavity mirror may couple to the microphone. In our case, this problem is avoided as the PA cell is sealed with windows separate from the cavity. We observe only a small constant background at the modulation frequency of 30 Hz, caused by a residual amplitude modulation from the current modulation of the laser, which is amplified in the cavity and coupled to the PA signal through window absorption. Nevertheless, the second harmonic of the demodulated PA signal is background free (as seen in Fig. 3), which we are only interested in.

Fig. 3 Measured and simulated 2^nd harmonic spectra with the optical build-up cavity for the PA signal enhancement.

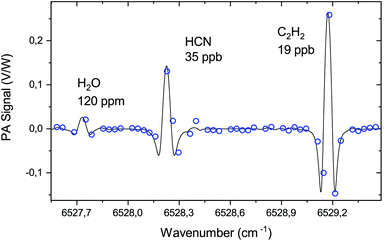
The PA cell can be operated at sample gas pressures in the range of 150 to 1000 mbar. At high pressures, the optimal modulation amplitude for wavelength modulation is large, as it is proportional to the absorption linewidth.³⁰ At low pressure, the linewidth approaches the Doppler limit and the peak height starts to reduce, resulting in weaker signals. By considering possible pressure and modulation amplitude ranges, as well as interference from nearby absorption lines, we have chosen 200 mbar as the optimal pressure for the experiment. At 200 mbar, we obtain the strongest 2^nd harmonic signal for the C₂H₂ line with a 0.04 cm⁻¹ (1.2 GHz) modulation amplitude as shown in Fig. 4, including simulation of the signal behaviour using the HITRAN 2016 database²⁴ and Voigt line profile. The measurement follows closely the simulation, showing that the wavelength modulation with the build-up cavity works normally.

Fig. 4 Measured and simulated photo-acoustic 2^nd harmonic peak signal levels for a C₂H₂ line at 200 mbar.

We identify the targeted absorption line by performing a spectral scan of a known sample gas, by tuning the temperature of the laser, which allows a wider tuning range than scanning the drive current. Since a high spectral resolution is unnecessary to identify a transition, the scan is performed step-wise by hopping from one cavity mode to another. The spectrum is recorded with a sample gas containing H₂O (residual, measured with a Vaisala DMT143 dewpoint transmitter), HCN and C₂H₂ (from gas cylinders). The result is shown in Fig. 3 together with a simulated spectrum, which was obtained using the HITRAN database and the 2^nd harmonic of the Voigt line profile. The wavenumber axis was calibrated by matching the line centres and fixing the cavity FSR to 0.034 cm⁻¹.

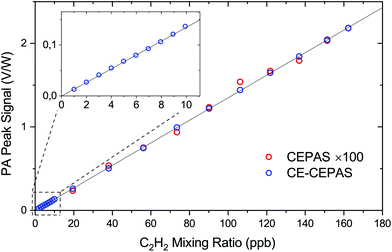
Having identified the spectral lines, the DFB temperature is fixed, and only the peak of the 2^nd harmonic of the target transition is recorded. For sensor calibration, the mixing ratio of the target gas is varied by changing the flow rates of the mass flow controllers, while recording the peak value of a transition. The calibration is performed both with CE-CEPAS and standard CEPAS with the same laser power of 7.5 mW. The result is shown in Fig. 5. In the case of standard CEPAS, the data are noisier, since the mixing ratios were close to the detection limit. A scaling factor of 100 was found to equate the CEPAS and CE-CEPAS results, which rigidly shows that the build-up factor and the PA signal enhancement of the CE-CEPAS technique are 100, as expected based on the cavity design and characterisation.

Fig. 5 CE-CEPAS and CEPAS 2^nd harmonic peak values as a function of the target gas mixing ratio.

In the presented calibration curve, we did not account for the fact that the absorbance of the sample gas will add to the cavity losses A and non-linearly decrease BUF, as is apparent from eqn (1). For the highest measured volume mixing ratio of 160 ppb, the BUF has decreased by only 0.9%. As examples of higher C₂H₂ concentrations, the BUF decreases 5.5% and 31% for volume mixing ratios of 1 ppm and 10 ppm, respectively. This effect does not result in false measurements if accounted for. In fact, it extends the dynamic range of the instrument as the signal strength is reduced at high mixing ratios.

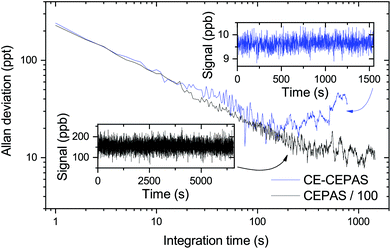
Finally, in order to determine the sensitivity and stability of both CE-CEPAS and CEPAS sensors, we performed an Allan variance analysis for a long series of data, measured with the PA cell filled with a low mixing ratio of the target gas. The results are shown in Fig. 6. The noise equivalent mixing ratio of C₂H₂ for CE-CEPAS is found to be 240 ppt for a 1 s integration time, which improves to 24 ppt with a 100 s integration time. The NNEA value for CE-CEPAS with the 7.5 mW input power is calculated to be 1.75 × 10⁻¹² W cm⁻¹ Hz^−1/2, which scales directly with respect to the build-up factor and is, to the best of our knowledge, better than any values for PAS reported before.³¹ The corresponding values for standard CEPAS are worse by the amount of the build-up factor.

Fig. 6 Allan deviation of the 2^nd harmonic peak values of CE-CEPAS and CEPAS in the case of a small amount of the target gas (C₂H₂). CEPAS values have been divided by the enhancement factor BUF = 100 for comparison.

In both cases of CE and standard CEPAS, the ultimate stability was most likely limited by the leak rate of the PA cell as the measurements were performed without a gas exchange. The CE-CEPAS measurement starts drifting sooner than the CEPAS one because the frequency of the cavity resonance was not actively stabilised and, therefore, it slowly drifts away from the transition peak centre. The Allan deviations of CEPAS and CE-CEPAS coincide for short integration times, meaning that the cavity does not introduce any extra noise at low signal levels. At high signal levels, we noted that the CE-CEPAS signal starts to drift already around 30 s due to random power fluctuations. However, it was possible to correct the drift by monitoring the transmitted or input power.

Discussion and conclusions

The new CE-CEPAS technique and the instrument discussed here provide excellent performance in trace gas detection. Yet, we note that the instrument is in its early demonstration phase. Some of the features required for a convenient out-of-lab operation, such as an automatic locking to the cavity resonance mode, and integration to a portable form, have not yet been implemented. Adding an erbium doped fibre amplifier (EDFA) to the setup would provide relatively inexpensively 10 to 100 times more optical power, and an equal improvement in the sensitivity. With such an amplifier, it would be interesting to investigate what the highest optical power practical for a PA signal generation would be without degrading the stability or noise performance of the instrument.

To conclude, we have demonstrated the first use of an optical power enhancement cavity with CEPAS, and the first optical power enhancement cavity operating in the wavelength modulation mode for photo-acoustic spectroscopy. We have verified a signal enhancement factor of about 100 by a rigorous comparison between CEPAS and CE-CEPAS by comparing both the response to different target gas mixing ratios and the noise performance. The realised optical power build-up factor is optimal for most of the single frequency diode lasers on the market, as the cavity resonance peaks remain wide enough not to limit the cavity input coupling, allowing for a simple experimental configuration and yet significant performance improvement. The achieved NNEA of 1.75 × 10⁻¹² W cm⁻¹ Hz^−1/2 is, to our knowledge, the best reported PAS NNEA so far, surpassing previous CEPAS results by two orders of magnitude.³ For comparison, the reported NNEA values of similar cavity-enhanced photo-acoustic techniques are 3.2 × 10⁻¹⁰ W cm⁻¹ Hz^−1/2 for intra-cavity QEPAS,¹⁸ 2.6 × 10⁻¹¹ W cm⁻¹ Hz^−1/2 for optical feedback cavity-enhanced resonant PAS (OF-CERPAS),¹⁵ and 1.1 × 10⁻¹¹ W cm⁻¹ Hz^−1/2 for another OF-CERPAS.¹⁶ Yet, the NNEA of our work is a subject to further improvement if a cavity of a higher finesse and a laser of a narrower linewidth are used. The noise equivalent concentration achieved in our work is comparable to typical state-of-the-art results in the mid-infrared region, although the experiments here were performed in the near-infrared region, where the first overtone absorption band lines are typically two orders of magnitude weaker than the fundamental ro-vibrational lines in the mid-infrared region. The result is of high practical importance, since the near-infrared lasers and optical components, especially those used in the telecommunications industry, are more reliable and less expensive than their mid-infrared counterparts.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We acknowledge the following funding sources: CHEMS doctoral program of the University of Helsinki, Jenny and Antti Wihuri Foundation and The Academy of Finland (grants 294752, 314363).

References

1. A. Elia, P. M. Lugarà, C. Di Franco and V. Spagnolo, Sensors, 2009, 9, 9616–9628.
2. J. Hodgkinson and R. P. Tatam, Meas. Sci. Technol., 2013, 24, 012004.
3. T. Tomberg, M. Vainio, T. Hieta and L. Halonen, Sci. Rep., 2018, 8, 1848.
4. V. Koskinen, J. Fonsen, J. Kauppinen and I. Kauppinen, Vib. Spectrosc., 2006, 42, 239–242.
5. K. Chen, Q. Yu, Z. Gong, M. Guo and C. Qu, Sens. Actuators, B, 2018, 268, 205–209.
6. S. Zhou, M. Slaman and D. Iannuzzi, Opt. Express, 2017, 25, 17541–17548.
7. R. A. Coutu, I. R. Medvedev and D. T. Petkie, Sensors, 2016, 16, 251.
8. W. Li, Z. Wang, C. Feng, Q. Li and H. Yu, Sens. Actuators, A, 2019, 285, 300–307.
9. T. Mikkonen, C. Amiot, A. Aalto, K. Patokoski, G. Genty and J. Toivonen, Opt. Lett., 2018, 43, 5094–5097.
10. I. Sadiek, T. Mikkonen, M. M. Vainio, J. Toivonen and A. Foltynowicz, Phys. Chem. Chem. Phys., 2018, 20, 27849–27855.
11. V. Koskinen, J. Fonsen, K. Roth and J. Kauppinen, Vib. Spectrosc., 2008, 48, 16–21.
12. J. Peltola, M. Vainio, T. Hieta, J. Uotila, S. Sinisalo, M. Metsälä, M. Siltanen and L. Halonen, Opt. Express, 2013, 21, 10240–10250.
13. J. Peltola, T. Hieta and M. Vainio, Opt. Lett., 2015, 40, 2933–2936.
14. A. Rossi, R. Buffa, M. Scotoni, D. Bassi, S. Iannotta and A. Boschetti, Appl. Phys. Lett., 2005, 87, 041110.
15. M. Hippler, C. Mohr, K. A. Keen and E. D. McNaghten, J. Chem. Phys., 2010, 133, 044308.
16. A. Kachanov, S. Koulikov and F. K. Tittel, Appl. Phys. B: Lasers Opt., 2013, 110, 47–56.
17. S. Borri, P. Patimisco, I. Galli, D. Mazzotti, G. Giusfredi, N. Akikusa, M. Yamanishi, G. Scamarcio, P. De Natale and V. Spagnolo, Appl. Phys. Lett., 2014, 104, 091114.
18. P. Patimisco, S. Borri, I. Galli, D. Mazzotti, G. Giusfredi, N. Akikusa, M. Yamanishi, G. Scamarcio, P. De Natale and V. Spagnolo, Analyst, 2015, 140, 736–743.
19. A. A. Kosterev, Y. A. Bakhirkin, R. F. Curl and F. K. Tittel, Opt. Lett., 2002, 27, 1902–1904.
20. G. Gagliardi and H.-P. Loock, Cavity-enhanced spectroscopy and sensing, Springer, 2014.
21. L.-S. Ma, J. Ye, P. Dubé and J. L. Hall, J. Opt. Soc. Am. B, 1999, 16, 2255–2268.
22. B. Dahmani, L. Hollberg and R. Drullinger, Opt. Lett., 1987, 12, 876–878.
23. R. Drever, J. L. Hall, F. Kowalski, J. Hough, G. Ford, A. Munley and H. Ward, Appl. Phys. B: Photophys. Laser Chem., 1983, 31, 97–105.
24. I. Gordon, L. Rothman, C. Hill, R. Kochanov, Y. Tan, P. Bernath, M. Birk, V. Boudon, A. Campargue, K. Chance, B. Drouin, J.-M. Flaud, R. Gamache, J. Hodges, D. Jacquemart, V. Perevalov, A. Perrin, K. Shine, M.-A. Smith, J. Tennyson, G. Toon, H. Tran, V. Tyuterev, A. Barbe, A. Császár, V. Devi, T. Furtenbacher, J. Harrison, J.-M. Hartmann, A. Jolly, T. Johnson, T. Karman, I. Kleiner, A. Kyuberis, J. Loos, O. Lyulin, S. Massie, S. Mikhailenko, N. Moazzen-Ahmadi, H. Müller, O. Naumenko, A. Nikitin, O. Polyansky, M. Rey, M. Rotger, S. Sharpe, K. Sung, E. Starikova, S. Tashkun, J. V. Auwera, G. Wagner, J. Wilzewski, P. Wcisło, S. Yu and E. Zak, J. Quant. Spectrosc. Radiat. Transfer, 2017, 203, 3–69.
25. F. M. Schmidt, O. Vaittinen, M. Metsälä, P. Kraus and L. Halonen, Appl. Phys. B: Lasers Opt., 2010, 101, 671–682.
26. F. M. Schmidt, M. Metsälä, O. Vaittinen and L. Halonen, J. Breath Res., 2011, 5, 046004.
27. M. Metsälä, J. Breath Res., 2018, 12, 027104.
28. O. Vaittinen, M. Metsälä, S. Persijn, M. Vainio and L. Halonen, Appl. Phys. B: Lasers Opt., 2014, 115, 185–196.
29. N. O. B. Lüttschwager, A. Pogány, J. Grodde, O. Werhahn and V. Ebert, Imaging and Applied Optics, 2016, vol. 2016, p. LM3G.3.
30. P. Kluczynski, J. Gustafsson, Å. M. Lindberg and O. Axner, Spectrochim. Acta, Part B, 2001, 56, 1277–1354.
31. P. Patimisco, A. Sampaolo, L. Dong, F. K. Tittel and V. Spagnolo, Appl. Phys. Rev., 2018, 5, 011106.

---