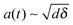Controlling and predicting droplet size of nanoemulsions: scaling relations with experimental validation†
Ankur
Gupta
a,
H. Burak
Eral
b,
T. Alan
Hatton
a and
Patrick S.
Doyle
*a
aMassachusetts Institute of Technology, Cambridge, MA, USA. E-mail: pdoyle@mit.edu; Fax: +31 617 324 0066; Tel: +31 617 253 4534
bDelft University of Technology, The Netherlands
First published on 26th November 2015
Abstract
Nanoemulsions possess powerful nano-scale properties that make them attractive for diverse applications such as drug delivery, food supplements, nanoparticle synthesis and pharmaceutical formulation. However, there is little knowledge in nanoemulsion literature about controlling and predicting droplet size. In this article, we propose a scaling relation to predict the dependence of nanoemulsion droplet size with physical properties such as viscosity of the droplet phase and continuous phase, and process parameters such as input power density. We validate our proposed scaling with a wide range of droplet size data from nanoemulsions prepared with high pressure homogenization and ultrasonication. Our proposed scaling also compares favorably with experimental data from literature. The scaling relation can serve as a guiding principle for rational design of nanoemulsions.
1 Introduction
Nanoemulsions consist of droplets on the order of 100 nm stabilized by an emulsifier. There are primarily two types of nanoemulsions: oil-in-water (O/W) and water-in-oil (W/O). Due to their exceptional properties such as high surface area per unit volume, long shelf life, transparent appearance and tunable rheology, nanoemulsions have been an active area of research over the past decade or so.1–4 Nanoemulsions have been used in drug delivery research as a medium to transport hydrophobic drugs dissolved in the oil phase.5–8 In the food industry, nanoemulsions have been used to develop smart drinks which consist of healthy hydrophobic components like β-carotene and circumin in the oil phase.9–11 Nanoemulsions have also been explored for other research areas like nanoparticle synthesis12–14 and pharmaceutical crystallization.15Two widely used high energy methods to prepare nanoemulsions are high pressure homogenization (HPH) and ultrasonication (Fig. 1). In HPH, a mixture of oil, water and surfactant is pushed through a small gap where droplets experience extreme shear and elongational stress.16 The gap height is typically on the order of 1–10 μm and therefore the pressure drop (ΔP) across HPH can reach a few thousand bars.16–18 Due to high level of stress inside the homogenizer, droplets deform and break into smaller droplets (Fig. 1(a)). The mixture is typically passed multiple times through the homogenizer until the droplet size is roughly constant2,17,19 (referred as number of passes, N). In ultrasonication, electrical signals are converted into mechanical vibrations. These mechanical vibrations create sinusoidal pressure variations in the surrounding medium. During one of the low pressure cycles, cavitation results in formation of bubbles. These bubbles contract and expand until implosion, creating disturbance in the local flow field which ultimately breaks the droplet20–22 (Fig. 1(b)). Like homogenization, ultrasonication is also continued for sufficient time until the droplet size is roughly constant.19,23 Low energy methods to prepare nanoemulsions like emulsion inversion point,24 phase inversion temperature25 and bubble bursting at an oil/water interface26 have also been developed. However, in this article, we will restrict the discussion to high energy methods.
There is a rich theoretical understanding about the prediction of droplet size of macroemulsions, i.e. emulsions with droplet size on the order of 10 μm or larger. The macroemulsion literature mostly uses either Taylor's theory27 or Hinze's theory28 to predict the droplet size. Taylor's theory was developed for low Reynolds number (Re) flow with simple flow fields.27 On the other hand, Hinze's theory was built on the assumption that during emulsification, the flow is completely turbulent.28 Though these theories represent completely different flow regimes and were developed for macroemulsions, many modern nanoemulsion studies have referred to Taylor's theory as well as Hinze's theory to explain trends observed in droplet size.2,17,18,20,23,29–37 However, few studies also acknowledge that the agreement with Taylor's and Hinze's theory is only qualitative at best and that these theories should be used only for an order of magnitude estimation of droplet size.17,23 Further, there are also experimental studies on nanoemulsion which do not use any theoretical prediction and fit their droplet size data using empirical power law correlations.19,37–40 For instance, experimental studies have shown that nanoemulsion size increases with increase in droplet viscosity (μd) and decreases with increase in continuous phase viscosity (μc).29,37,40 Hence, this article focuses on bridging the gap between experimental observations and theoretical predictions for nanoemulsion droplet size.
In this article, we first review the theories proposed by Taylor27 and Hinze28 and argue that the correlations developed for macroemulsions cannot be directly used for nanoemulsions. We then modify Hinze's theory28 based on more appropriate hydrodynamic light scales to accurately predict the droplet size of nanoemulsions. We also validate our proposed scaling by generating a wide range of experimental data, as well as comparing to existing data from literature. The new scaling relation is able to quantitatively predict droplet size variation with physical properties and hence enables rationale design of nanoemulsions prepared by high energy methods.
2 Theory
We review the classical work of Taylor27 that describes the relationship between the fluid flow and the droplet size of macroemulsions. Taylor performed experimental and theoretical analysis on a single droplet being deformed by laminar flow field. Taylor suggested that a droplet will not break unless the applied stress (τapplied) deforming the droplet exceeds the interfacial stress holding the droplet in the same shape. Hence, Taylor defined a critical capillary number,
holding the droplet in the same shape. Hence, Taylor defined a critical capillary number, 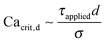 below which the droplet will not break. Mathematically, Taylor's criteria for droplet breakup can be expressed as:
below which the droplet will not break. Mathematically, Taylor's criteria for droplet breakup can be expressed as:| Cacrit,d = C1 | (1) |
![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) , where, μc is the continuous phase viscosity,
, where, μc is the continuous phase viscosity, ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) is the shear rate in the continuous phase. Hence, the droplet size can be defined as:
is the shear rate in the continuous phase. Hence, the droplet size can be defined as: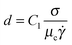 | (2) |
 .41,42 However, nanoemulsion literature has referred to Taylor's theory in the form of eqn (2) and hence, we will use the same form.2,17,18,20,23
.41,42 However, nanoemulsion literature has referred to Taylor's theory in the form of eqn (2) and hence, we will use the same form.2,17,18,20,23
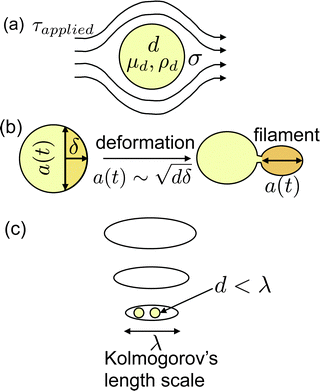
While Taylor's theory provides a very intuitive understanding of droplet deformation, it is not applicable to the turbulent flow produced inside a homogenizer and ultrasonicator used in industrial applications.43 The most widely used theory for predicting droplet size in industrially prepared macroemulsions was developed by Hinze.28 Hinze suggested that if a droplet of viscosity μd, density ρd, interfacial tension with outer phase σ, is deformed by the outer phase with a stress τapplied (Fig. 2(a)), two dimensionless numbers that govern the problem are the critical Weber number:
 | (3) |
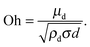 | (4) |
| Wecrit,d = C2(1 + f(Oh)) | (5) |
 | (6) |
Since nanoemulsions are typically prepared through a homogenizer or an ultrasonicator (where the flow is turbulent), we decided to build upon the work of Hinze. If we assume typical values for nanoemulsions of d ≈ 100 nm, μd ≈ 10 cP, ρd ≈ 1000 kg m−3, σ ≈ 10 mN m−1, we calculate that Oh ≈ 10. Therefore, one cannot assume f(Oh) ≈ 0 and we need to define a new criteria of critical Weber number for the large Oh regime.
An overview of the proposed mechanism for nanoemulsion formation is provided in Fig. 2. We propose that prior to droplet breakup, a filament extrudes out from the parent droplet due to an instability at the surface. Similar to literature on the impact of droplet on a solid surface, we propose that for a droplet to break, the inertial stress of the filament extruding from the parent droplet has to exceed the interfacial stress.44,45 Let us assume that an instability of length δ ∼ udt has penetrated inside the parent droplet, where ud is the velocity scale inside the droplet given by Hinze28 as  and t is the propagation time of the instability (Fig. 2(b)). Conservation of mass dictates that volume of the filament and the hypothetical cap formed by the instability are equal. Upon geometrical calculations, we find that the diameter of the base of the spherical cap scales as
and t is the propagation time of the instability (Fig. 2(b)). Conservation of mass dictates that volume of the filament and the hypothetical cap formed by the instability are equal. Upon geometrical calculations, we find that the diameter of the base of the spherical cap scales as  . Hence, the volume of this spherical cap scales as Vs,cap ∼ a(t)2δ ∼ dδ2. We can also define the velocity scale inside the filament as
. Hence, the volume of this spherical cap scales as Vs,cap ∼ a(t)2δ ∼ dδ2. We can also define the velocity scale inside the filament as  .
.
Now, we will do a general derivation to define the criteria for droplet breakup. This derivation reduces to Hinze's result for low values of Ohnesorge number. However, for large Ohnesorge number (a regime relevant to nanoemulsions), we obtain a completely different result. To arrive at a droplet breakup criteria, we need to evaluate the filament properties when the droplet breaks. For the regime of Oh ≪ 1, since the viscous effects inside the droplet are negligible, the droplet breakup time scale (t ∼ tbreakup) is dominated by the convective time scale. In other words, the droplet break up time scale is simply given by 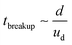 . Hence, for the Oh ≪ 1, at t ∼ tbreakup one has δ ∼ a ∼ d and ua ∼ ud. On the other hand, for Oh > 1, the viscous stresses inside the drop would start to play an important role and hence the droplet breakup time scale would be dominated by the diffusive time scale
. Hence, for the Oh ≪ 1, at t ∼ tbreakup one has δ ∼ a ∼ d and ua ∼ ud. On the other hand, for Oh > 1, the viscous stresses inside the drop would start to play an important role and hence the droplet breakup time scale would be dominated by the diffusive time scale  . In this regime, we can also think of droplet breakup time scale as
. In this regime, we can also think of droplet breakup time scale as  , where Red is the droplet Reynolds number given as
, where Red is the droplet Reynolds number given as  . Therefore, for Oh > 1, at t ∼ tbreakup, δ ∼ dRed−1, a ∼ dRed−0.5 and ua ∼ udRed0.5. We observe that in large Oh regime, since the viscous stresses inside the droplet are important, a and ua are strongly dependent on Red. Now, we can mathematically define the breakup criteria of the filament:
. Therefore, for Oh > 1, at t ∼ tbreakup, δ ∼ dRed−1, a ∼ dRed−0.5 and ua ∼ udRed0.5. We observe that in large Oh regime, since the viscous stresses inside the droplet are important, a and ua are strongly dependent on Red. Now, we can mathematically define the breakup criteria of the filament:
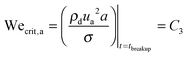 | (7) |
 | (8) |
 | (9) |
| Wecrit,d = C4Oh2/5 | (10) |
τ
applied is governed by the flow dynamics of the continuous phase around the droplet. Although flow in a homogenizer and ultrasonicator is turbulent in bulk (see ESI† for more details), the flow around droplets is still viscous. This can be seen by the relative values of the smallest eddy size (or the Kolmogorov's length scale), λ and the droplet size, d (Fig. 2(c)). The value of λ is given by  .46,47 Assuming the value of μc ≈ 1 cP, ρc ≈ 1000 kg m−3 and ε ≈ 108 W kg−1,43 we get, λ ≈ 300 nm. Since, d ≈ 100 nm, nanoemulsions are on the similar length scale as the smallest eddy and hence, the flow around them is viscous. Therefore, τapplied should be given by the stress inside the smallest eddy, or,
.46,47 Assuming the value of μc ≈ 1 cP, ρc ≈ 1000 kg m−3 and ε ≈ 108 W kg−1,43 we get, λ ≈ 300 nm. Since, d ≈ 100 nm, nanoemulsions are on the similar length scale as the smallest eddy and hence, the flow around them is viscous. Therefore, τapplied should be given by the stress inside the smallest eddy, or,  . This regime is called the viscous turbulent regime and has been recently validated experimentally.46,47 This has also been recognized by Nazarzadeh et al. where authors mentioned nanoemulsion droplets are smaller than the smallest eddy.36 However, they did not recognize that nanoemulsions lie in the large Oh regime. Hence, using
. This regime is called the viscous turbulent regime and has been recently validated experimentally.46,47 This has also been recognized by Nazarzadeh et al. where authors mentioned nanoemulsion droplets are smaller than the smallest eddy.36 However, they did not recognize that nanoemulsions lie in the large Oh regime. Hence, using  in eqn (3) and (10), we get:
in eqn (3) and (10), we get:
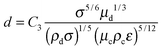 | (11) |
| d ∼ μd1/3 | (12) |
| d ∼ μc−5/12 | (13) |
| d ∼ ε−5/12 | (14) |
3 Results and discussion
We prepared O/W nanoemulsions using both high pressure homogenizer (HPH) and ultrasonication. We systematically varied the oil phase viscosity to encompass a wide range of Oh. We prepared nanoemulsions with the following composition: 1% (v/v) oil–175 mM sodium dodecyl sulphate (SDS)–water. The values of physical properties of the oil phase are summarized in Table 1 (details in ESI†). The interfacial tension given here is measured in the presence of surfactant well above its critical micelle concentration. We chose SDS as the surfactant in order to avoid emulsifier-size effects.29,40 In HPH experiments, we homogenized each nanoemulsion system for 4 different pressure drops with 20 passes each. In ultrasonication experiments, we sonicated each nanoemulsion system at 3 different sonication amplitudes for 20 minutes each. The size and polydispersity was measured using dynamic light scattering (DLS). The details of size and polydispersity calculations from raw DLS data are provided in ESI.†| Oil | μ d (cP) | ρ d (kg m−3) | σ (mN m−1) |
|---|---|---|---|
| Hexadecane | 3 | 764 | 4.9 |
| Silicone oil | 4 | 914 | 7.6 |
| 75–25 silicone mixture | 12 | 916 | 8.8 |
| 50–50 silicone mixture | 22 | 928 | 9.0 |
| Mineral | 24 | 840 | 7.4 |
| 25–75 silicon mixture | 46 | 938 | 7.9 |
| Viscous silicone oil | 97 | 958 | 8.7 |
Fig. 3(a) shows the droplet size variation for silicone oil nanoemulsions obtained from HPH. As expected, the droplet size decreases with pressure drop (ΔP) and number of passes (N). This is consistent with the observations from the literature.2,18,19 Also, the droplet size follows an exponentially decaying function with N (shown by solid lines in Fig. 3(a)). This is a classic signature of a system that has no coalescence and is dominated by droplet breakage. Polydispersity remains practically constant (≈25%) suggesting that the average size of the droplet is a good representative of the distribution. Since we are in interested in validating Wecrit,d, we assume that the diameter after 20 passes (d20) will not change significantly on further emulsification. The variations of d20 with ΔP for all the nanoemulsion systems prepared using HPH are shown in Fig. 3(b). Experimental results clearly show that d20 is dependent of μd as well as ΔP. As μd increases, droplet size increases and as ΔP increases, droplet size decreases.
The results for droplet size variations for silicone oil nanoemulsions obtained from ultrasonication are shown in Fig. 3(c and d). Similar to the dependence of droplet size with number of passes in HPH, the droplet size variation with ultrasonication time decays exponentially. The variation of d20 (size after 20 minutes of sonication) for all the nanoemulsion systems prepared using ultrasonicator are shown in Fig. 3(d). One immediately observes while comparing Fig. 3(b) and (d) that the size range of nanoemulsions obtained from the homogenizer and ultrasonicator is almost identical. Also, the effect of μd on d20 follows the same trend for both HPH and ultrasonication. However, unlike the effect of ΔP on d20 in HPH, change in ultrasonication amplitude does not change d20 significantly. This effect has also been observed in literature.19,23 We explain the reason behind this observation later.
For converting the raw data to Wecrit,d, we estimated the value of ε for both the homogenizer (εh) and ultrasonicator (εs). We estimate that  where Q is the flowrate and Vhomogenizer is the volume of the homogenizer.37,48 For the homogenizer used in our experiments, Q ≈ 10−6 m3 s−1, ΔP ≈ 108 Pa, ρc ≈ 103 kg m−3, Vhomogenizer ≈ 10−9 m3 and hence, εh ≈ 108 W kg−1. Since Q is constant for our homogenizer, εh ∼ ΔP (please see ESI† for more details). εs was estimated using the correlation,
where Q is the flowrate and Vhomogenizer is the volume of the homogenizer.37,48 For the homogenizer used in our experiments, Q ≈ 10−6 m3 s−1, ΔP ≈ 108 Pa, ρc ≈ 103 kg m−3, Vhomogenizer ≈ 10−9 m3 and hence, εh ≈ 108 W kg−1. Since Q is constant for our homogenizer, εh ∼ ΔP (please see ESI† for more details). εs was estimated using the correlation,  , where Pb is the average cavitation collapse pressure, Patm is the atmospheric pressure, τb is the bubble collapse time scale.22 Using the correlations mentioned in the literature,22Pb ≈ 105 Pa, τb ≈ 1 μs, ρc ≈ 1000 kg m−3 and hence, εs ≈ 108 W kg−1. The dependence of εs is non-monotonic since an increase in the amplitude increases both Pb and τb (please see ESI† for more details). Some observations can be made from the estimated values of εh and εs. First, both εh and εs are on similar order of magnitude which corroborates the observation that size range from nanoemulsion for both HPH and ultrasonication is similar (Fig. 3(b and d)). The variation of εh ∼ ΔP supports the observation that size decreases as ΔP increases (Fig. 3(b), eqn (14)). Similarly, since εs is insensitive to change in ultrasonication amplitude, the droplet size does not show a significant variation with amplitude (Fig. 3(d), eqn (14)). Finally, since εh and εs are on the order of 108 W kg−1, we can assume that nanoemulsion formation takes place in the viscous turbulent regime.
, where Pb is the average cavitation collapse pressure, Patm is the atmospheric pressure, τb is the bubble collapse time scale.22 Using the correlations mentioned in the literature,22Pb ≈ 105 Pa, τb ≈ 1 μs, ρc ≈ 1000 kg m−3 and hence, εs ≈ 108 W kg−1. The dependence of εs is non-monotonic since an increase in the amplitude increases both Pb and τb (please see ESI† for more details). Some observations can be made from the estimated values of εh and εs. First, both εh and εs are on similar order of magnitude which corroborates the observation that size range from nanoemulsion for both HPH and ultrasonication is similar (Fig. 3(b and d)). The variation of εh ∼ ΔP supports the observation that size decreases as ΔP increases (Fig. 3(b), eqn (14)). Similarly, since εs is insensitive to change in ultrasonication amplitude, the droplet size does not show a significant variation with amplitude (Fig. 3(d), eqn (14)). Finally, since εh and εs are on the order of 108 W kg−1, we can assume that nanoemulsion formation takes place in the viscous turbulent regime.
We fitted the Wecrit,dvs. Oh data (Fig. 4) with a two parameter power law model and the fits to the experimental data yield scalings very close to the proposed scaling of Wecrit,d ∼ Oh2/5. There are some conclusions one can draw from Fig. 4. First, we observe that nanoemulsion synthesis indeed lies in the large Oh regime. Also, we can clearly see that the proposed scaling is able to capture the variation of μd for both homogenizer and ultrasonicator data. Interestingly, the similarity in predicted exponents and pre-exponential factor for both the homogenizer and ultrasonicator suggests a universal collapse of data for nanoemulsions prepared through different two different methods (see ESI†). This shows the merit of approaching droplet size prediction using dimensionless analysis. However, there is some scatter in the data around the predicted values within the same oil phase. We believe that this scatter is due to error present in the estimation of εh and εs. Since homogenization and ultrasonication involve complex and dynamic processes, there is high uncertainty in the estimation of power density.
To validate the predicted trend of droplet size on μc, we replotted the experimental data from Wooster et al.29 (Fig. 5(a)) where researchers added PEG to water phase for O/W nanoemulsions to vary μc. As noted previously, we predict a scaling of d ∼ μc−5/12 as mentioned in eqn (13). Taylor's theory predicts a scaling of d ∼ μc−1 (eqn (2)) whereas Hinze's theory predicts a scaling of d ∼ μ0c (eqn (6)). There is excellent agreement between experimental data predicted with our proposed scaling. However, Taylor's theory over predicts the variation of droplet size of μc whereas Hinze's theory under predicts the variation of droplet size with μc. Modern nanoemulsion literature has incorrectly extrapolated Taylor's and Hinze's theory2,17,18,20,23,29–37 to explain the trends in nanoemulsion droplet size.
 | ||
| Fig. 5 Validation of proposed scaling with experimental data from literature. (a) The data has been taken from Wooster et al.29 where the authors increased the continuous phase viscosity. As shown, our proposed scaling of d ∝ μc−5/12 agrees well with the experimental data. On the other hand, modern nanoemulsion studies2,17,18,20,23,29–37 have incorrectly extrapolated the theories of Taylor27 and Hinze28 to predict nanoemulsion droplet size. (b) The data has been taken from Seekkuarachchi et al.37 where the authors varied both dispersed phase viscosity as well as continuous phase viscosity. Our proposed scaling is in good agreement with the experimental data. | ||
We also validated our scaling relation with the data from Seekkuarachchi et al.37 We re-plotted the size data for nanoemulsion systems prepared at the same homogenization condition but with wide range of μd and μc. Since the variations in ρd and σ were negligible across different formulations, we plotted the variation of d with our predicted scaling in Fig. 5(b) (eqn (12) and (13)). We obtain excellent agreement from our scaling relation with an extensive set of experimental data.
To conclude, in this article, we proposed a scaling relation to predict nanoemulsion droplet size based on the fundamentals of filament breakup. Our proposed scaling, Wecrit,d = C4Oh2/5, is able to quantitatively predict the droplet size of nanoemulsions. The strongest aspect of our proposed scaling is its ability to predict the trends in droplet size with droplet viscosity as well as continuous phase viscosity. Our scaling relation fits a large range of experimental data obtained for completely different nanoemulsion systems and prepared through different techniques. Also, the dimensionless form of scaling can be used as a guiding principle to identify critical parameters and enable rational design of nanoemulsions.
4 Material and methods
Materials
Hexadecane, silicone oil (5 cSt, 100 cSt), mineral oil and SDS are products from Sigma Aldrich.Methods
Pre-emulsion for HPH and ultrasonication was prepared by mixing 175 mM SDS aqueous solution with 1% (v/v) oil phase using a magnetic stirrer bar for 30 minutes at 700 rpm. 30 mL of pre-emulsion was homogenized in Avestin C-3 homogenizer with four different pressure drops (5, 10, 15, 20 kPsi) and 20 passes each. 2 mL pre-emulsion was ultrsonicated at three different amplitudes (20, 30, 40%) in an ultrasonicator with a 24 mm horn diameter (from Cole Parmer) at a frequency of 20 kHz. The prepared nanoemulsion was diluted 10 times in DI water and then used as a sample for dynamic light scattering (DLS). 3 independent measurements were taken for each sample. Each DLS measurement involved 10 acquisitions of 5 seconds each. Size and polydispersity were extracted from raw DLS data using second order cumulant analysis (details in the ESI†).Acknowledgements
The authors would like to thank Eni SPA for providing funds for this project. We acknowledge The Biophysical Instrumentation Facility at MIT for providing us with the DLS support (NSF-0070319). We also acknowledge the contribution of Bavand Keshavarz for helping us out with the theoretical understanding of droplet splash.References
- A. Gupta, H. E. Burak, T. A. Hatton and P. S. Doyle, Soft Matter, 2015 Search PubMed , under review.
- T. G. Mason, S. M. Graves, J. N. Wilking and M. Y. Lin, Condens. Matter Phys., 2006, 9, 193–199 CrossRef.
- T. Tadros, P. Izquierdo, J. Esquena and C. Solans, Adv. Colloid Interface Sci., 2004, 108–109, 303–318 CrossRef CAS PubMed.
- C. Solans, P. Izquierdo, J. Nolla, N. Azemar and M. Garciacelma, Curr. Opin. Colloid Interface Sci., 2005, 10, 102–110 CrossRef CAS.
- M. Kumar, A. Misra, A. K. Babbar, A. K. Mishra, P. Mishra and K. Pathak, Int. J. Pharm., 2008, 358, 285–291 CrossRef CAS PubMed.
- D. Sarker, Curr. Drug Delivery, 2005, 2, 297–310 CrossRef CAS.
- C. Lovelyn, J. Biomater. Nanobiotechnol., 2011, 02, 626–639 CrossRef CAS.
- F. Shakeel, S. Baboota, A. Ahuja, J. Ali, M. Aqil and S. Shafiq, AAPS PharmSciTech, 2007, 8, E104 CrossRef PubMed.
- D. J. McClements and J. Rao, Crit. Rev. Food Sci. Nutr., 2011, 51, 285–330 CrossRef CAS PubMed.
- D. J. McClements, Soft Matter, 2011, 7, 2297–2316 RSC.
- J. Rao and D. J. McClements, Food Hydrocolloids, 2011, 25, 1413–1423 CrossRef CAS.
- N. Anton, J.-P. Benoit and P. Saulnier, J. Controlled Release, 2008, 128, 185–199 CrossRef CAS PubMed.
- K. Landfester, Angew. Chem., Int. Ed., 2009, 48, 4488–4507 CrossRef CAS PubMed.
- J. M. Asua, Prog. Polym. Sci., 2002, 27, 1283–1346 CrossRef CAS.
- H. B. Eral, V. López-Mejías, M. O'Mahony, B. L. Trout, A. S. Myerson and P. S. Doyle, Cryst. Growth Des., 2014, 14, 2073–2082 CAS.
- J. Floury, J. Bellettre, J. Legrand and A. Desrumaux, Chem. Eng. Sci., 2004, 59, 843–853 CrossRef CAS.
- T. G. Mason, J. N. Wilking, K. Meleson, C. B. Chang and S. M. Graves, J. Phys.: Condens. Matter, 2006, 18, R635–R666 CrossRef CAS.
- M. E. Helgeson, S. E. Moran, H. Z. An and P. S. Doyle, Nat. Mater., 2012, 11, 344–352 CrossRef CAS PubMed.
- S. Y. Tang, P. Shridharan and M. Sivakumar, Ultrason. Sonochem., 2013, 20, 485–497 CrossRef CAS PubMed.
- T. S. H. Leong, T. J. Wooster, S. E. Kentish and M. Ashokkumar, Ultrason. Sonochem., 2009, 16, 721–727 CrossRef CAS PubMed.
- S. Abbas, K. Hayat, E. Karangwa, M. Bashari and X. Zhang, Food Eng. Rev., 2013, 5, 139–157 CrossRef CAS.
- T. J. Mason and J. P. Lorimer, Applied Sonochemistry, Wiley-VCH, 2002 Search PubMed.
- T. Delmas, H. Piraux, A.-C. Couffin, I. Texier, F. Vinet, P. Poulin, M. E. Cates and J. Bibette, Langmuir, 2011, 27, 1683–1692 CrossRef CAS PubMed.
- A. Forgiarini, J. Esquena, C. Gonzalez and C. Solans, Langmuir, 2001, 17, 2076–2083 CrossRef CAS.
- P. Izquierdo, J. Esquena, T. F. Tadros, C. Dederen, M. Garcia, N. Azemar and C. Solans, Langmuir, 2002, 18, 26–30 CrossRef CAS.
- J. Feng, M. Roché, D. Vigolo, L. N. Arnaudov, S. D. Stoyanov, T. D. Gurkov, G. G. Tsutsumanova and H. A. Stone, Nat. Phys., 2014, 10, 606–612 CrossRef CAS.
- G. I. Taylor, Proc. R. Soc. London, Ser. A, 1932, 138, 41–48 CrossRef CAS.
- J. O. Hinze, AIChE J., 1955, 1, 289–295 CrossRef CAS.
- T. J. Wooster, M. Golding and P. Sanguansri, Langmuir, 2008, 24, 12758–12765 CrossRef CAS PubMed.
- K. Meleson, S. Graves and T. G. Mason, Soft Mater., 2004, 2, 109–123 CrossRef CAS.
- V. Ghosh, A. Mukherjee and N. Chandrasekaran, Ultrason. Sonochem., 2013, 20, 338–344 CrossRef CAS PubMed.
- S. Kotta, A. W. Khan, K. Pramod, S. H. Ansari, R. K. Sharma and J. Ali, Expert Opin. Drug Delivery, 2012, 9, 585–598 CrossRef CAS PubMed.
- Z. Han, B. Yang, Y. Qi and J. Cumings, Ultrasonics, 2011, 51, 485–488 CrossRef CAS PubMed.
- S. M. Graves and T. G. Mason, J. Phys. Chem. C, 2008, 112, 12669–12676 CAS.
- J. Schmidt, C. Damm, S. Romeis and W. Peukert, Chem. Eng. Sci., 2013, 102, 300–308 CrossRef CAS.
- E. Nazarzadeh and S. Sajjadi, AIChE J., 2010, 56, 2751–2755 CrossRef CAS.
- I. N. Seekkuarachchi, K. Tanaka and H. Kumazawa, Ind. Eng. Chem. Res., 2006, 45, 372–390 CrossRef CAS.
- F. Dons, M. Sessa and G. Ferrari, Ind. Eng. Chem. Res., 2012, 51, 7606–7618 CrossRef.
- T. Gothsch, J. H. Finke, S. Beinert, C. Lesche, J. Schur, S. Büttgenbach, C. Müller-Goymann and a. Kwade, Chem. Eng. Technol., 2011, 34, 335–343 CrossRef CAS.
- C. Qian and D. J. McClements, Food Hydrocolloids, 2011, 25, 1000–1008 CrossRef CAS.
- G. Taylor, Proc. R. Soc. London, Ser. A, 1934, 501–523 CrossRef CAS.
- B. J. Bentley and L. G. Leal, J. Fluid Mech., 1986, 167, 241 CrossRef CAS.
- J. Davies, Chem. Eng. Sci., 1987, 42, 1671–1676 CrossRef CAS.
- J. C. Bird, S. S. H. Tsai and H. A. Stone, New J. Phys., 2009, 11, 063017 CrossRef.
- C. Josserand and S. Zaleski, Phys. Fluids, 2003, 15, 1650 CrossRef CAS.
- R. Shinnar, J. Fluid Mech., 1961, 10, 259–275 CrossRef.
- J. A. Boxall, C. A. Koh, E. D. Sloan, A. K. Sum and D. T. Wu, Langmuir, 2012, 28, 104–110 CrossRef CAS PubMed.
- F. Innings and C. Trägårdh, Exp. Therm. Fluid Sci., 2007, 32, 345–354 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c5sm02051d |
| This journal is © The Royal Society of Chemistry 2016 |