Traction force microscopy in physics and biology

Abstract

Adherent cells, crawling slugs, peeling paint, sessile liquid drops, bearings and many other living and non-living systems apply forces to solid substrates. Traction force microscopy (TFM) provides spatially-resolved measurements of interfacial forces through the quantification and analysis of the deformation of an elastic substrate. Although originally developed for adherent cells, TFM has no inherent size or force scale, and can be applied to a much broader range of mechanical systems across physics and biology. In this paper, we showcase the wide range of applicability of TFM, describe the theory, and provide experimental details and code so that experimentalists can rapidly adopt this powerful technique.

---

1 Introduction

Traction Force Microscopy (TFM) is a powerful technique for measuring the forces that objects exert on surfaces on which they rest, adhere or move. Measuring these traction forces is important, as they often reveal key physical or biological processes. TFM works by attaching an object of interest to an elastic substrate and imaging the induced substrate deformations. From a knowledge of the mechanical properties of the substrate, the measured deformations can be converted into traction forces.

TFM has several key advantages: (i) it is relatively straightforward to set up and perform, as we describe below. (ii) It has no inherent size or force scale, so a wide range of length and force scales are accessible simply by adjusting the substrate stiffness and the imaging technique. (iii) It has the ability to measure spatially-resolved interfacial forces across extended objects. This ease-of-use and versatility differentiates TFM from other approaches for measuring interfacial forces. For example, atomic force microscopy,¹ optical tweezers^2,3 and magnetic tweezers⁴ provide precise measurements of interfacial forces averaged over areas in the nanometre to micrometre range. The surface forces apparatus⁵ and cantilever/plate bending measurements⁶ similarly measure interfacial forces, but typically averaged over more macroscopic scales.

We have two main aims for this review. Firstly, we aim to showcase the broad range of science to which TFM can be applied. TFM was originally developed in cell biology, and this is where it is most widely used. However recent work has shown that it is much more widely applicable. By reviewing this work, we hope to encourage scientists who can potentially make use of this powerful technique. We note that this paper is not intended to be an exhaustive review of all the previous work performed using TFM.^7–10 Secondly, we aim to make TFM accessible to experimentalists. TFM is conceptually simple, but optimal results rely on several steps of experimental design, data collection, and computational analysis. Here we facilitate the process of getting started with TFM by reviewing the basic theory, detailing experimental procedure for each step, and providing example code.

2 Applications of traction force microscopy

TFM has been applied to diverse problems in biology, physics, and engineering (Fig. 1). Although these problems span over four orders of magnitude in length and stress scales, we shall see that the potential range of TFM is far more extensive, and that there are many promising areas where it can provide novel insights.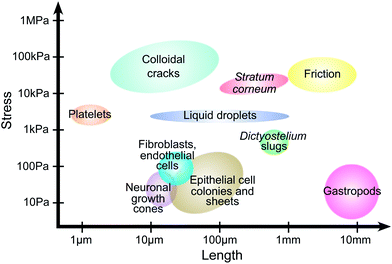

Fig. 1 Traction force microscopy across scales. Approximate length and stress scales from published reports. Platelets;¹¹ colloidal cracks;^12,13stratum corneum;¹⁴ friction;¹⁵ liquid droplets;^16,17dicty slugs;^18,19 neuronal growth cones;^20,21 fibroblasts and endothelial cells;^22,23 epithelial cell colonies and sheets;^24,25 gastropods.²⁶

2.1 Cellular TFM

TFM was originally developed to measure single-cell traction forces,^27–30 and this is still its most common application.^7–10 Cells are typically on the order of 10–100 μm in diameter, and their reported stresses range from [scr O, script letter O] (10 Pa) in neuronal growth cones^20,21 to [scr O, script letter O] (1 kPa) for platelets.¹¹ This makes cell-associated stresses among the smallest reported in the TFM literature (Fig. 1). Cellular TFM has given a detailed understanding of cell tractions and the intra- and inter-cellular structures contributing to force generation.

In vivo, cells generate traction forces to drive processes like migration,³¹ morphogenesis,^32,33 and extracellular matrix remodelling.^34,35 Cells generate tractions by anchoring themselves to neighbouring objects and contracting.^10,31 Anchoring occurs on protein networks in the extracellular environment (known as extracellular matrix), and on neighbouring cells via membrane-spanning protein complexes. Contraction in eukaryotic cells is typically driven by networks of actin filaments and myosin motors. In highly-contractile cells, contraction is usually produced by stress fibres – ordered bundles of actin filaments resembling muscle fibres.^36,37 However, other types of cytoskeletal architecture can also generate contraction.^38,39

Traction forces can be observed in isolated cells on flexible substrates coated with adhesion-stimulating proteins.^9,40–45 The magnitude and spatial distribution of these tractions vary widely with cell type. Cells typically pull on the substrate near their edges, with contraction indicated by inwardly-directed traction forces. In migrating cells, traction forces are often polarised according to the direction of motion.^{42–44,46,47} Recent work has probed the connection between cytoskeleton, adhesion and force dynamics by combining these traction measurements with techniques such as the fluorescent labelling of cellular proteins.^48,49 Cells on planar substrates usually spread out so they are very thin. Therefore, cellular tractions are predominantly in-plane. However, recent studies have suggested that cortical tension, nuclear compression, and focal-adhesion rotation can cause significant out-of-plane forces on the substrate.^23,50–52

2.2 Multicellular systems

Multicellular systems are inherently more complicated than single-cell systems because of intercellular adhesion and all of its downstream signalling.⁵³ Recently TFM has begun to be applied to multicellular systems, advancing understanding of cooperative phenomena in cell mechanics.

One of the first multicellular applications of TFM measured intercellular forces and showed how cells move at the edge of advancing epithelial-cell sheets.²⁴ This study showed that collective motion is not driven by leader cells at the sheet edge, but by cells distributed throughout the sheet. The authors also introduced a key force-balance concept for calculating cell–cell forces with TFM, as illustrated in Fig. 2a and b with a tug-of-war analogue. This approach for calculating internal forces is well-established in studies of the mechanics of thin films, where it is known as the “shear-lag model”.^54–56 For simple geometries, the intercellular tension is given by the integral of the traction forces from the edge of the cell colony (Fig. 2c and d). This technique has been extended to generate 2-dimensional maps of intercellular stresses in large sheets of cells.⁵⁷

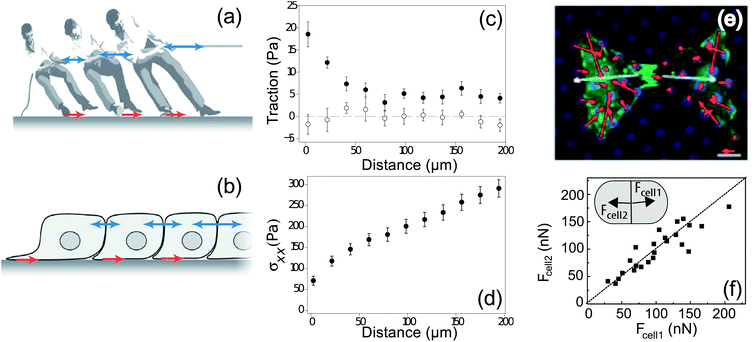Fig. 2 Balance of forces in multicellular systems. (a) The game of tug-of-war involves balance of forces between the tugging on the rope and the force transmitted to the ground through the players' feet.⁵⁸ From this force balance, we can determine the inter-person forces (blue arrows) if we know the traction forces (red arrows). (b) Intercellular forces can similarly be calculated from cellular traction forces.⁵⁸ (c) The average in-plane traction stress perpendicular to the leading edge of migration of a sheet of MDCK cells cultured on a soft substrate decays slowly with distance from the edge (filled symbols), whereas the average in-plane traction stress parallel to the leading edge is negligible and independent of the distance from the edge (open symbols).²⁴ (d) Tension within the cell sheet, given by the integral of traction, increases as a function of distance from the leading edge of a sheet of MDCK cells.²⁴ (e) Tugging forces (white), given as the vector sum of tractions (red) on an individual cell in a pair of two endothelial cells cultured on an array of PDMS posts (blue).⁵⁹ (f) Net force exerted by cell 2 on cell 1, F_cell1, as a function of the force exerted by cell 1 on cell 2, F_cell2, for two MDCK cells in a doublet on a flat, PAA substrate. Dashed line indicates a slope of one. (Inset) schematic of a cell pair depicting F_cell1 and F_cell2.⁶⁰

Force balance has also been applied to smaller cellular systems to measure cell–cell adhesion forces (Fig. 2e). For example, human pulmonary artery endothelial cells (HPAECs) have been shown to tug on each other with force ranging from 20–60 nN, with higher forces when the area of the cell–cell junction is larger.⁵⁹ A similar study using doublets of Madin-Darby Canine Kidney (MDCK) cells shows that these epithelial cells are stronger, typically pulling on their neighbours with forces of 50–200 nN (Fig. 2f). However, in this case, there is no correlation between pulling force and the size of the cell–cell junction.⁶⁰

Recent results have highlighted the power of TFM as a technique for understanding the collective behaviour of cells. TFM studies of keratinocyte colonies with strong intercellular adhesions show that traction forces localise at the edge of a colony. For large colonies, the total force exerted by the colony scales with its colony perimeter, suggesting the emergence of an effective surface tension.²⁵ Perturbation of cadherin-based intercellular adhesions reveals that these adhesions organise the spatial distribution of traction force in epithelial cells; in the absence of E-cadherin, the surface-tension analogy breaks down.⁶¹ In another example, force measurements show how cardiac myocytes mature into electromechanical syncitia – demonstrated by the transfer of force from the cell–matrix interface to the adherens junction over the course of 4 days.⁶²

2.3 Emerging applications of TFM in biology

Recently, biological traction force studies have expanded to investigate traction forces at the molecular, tissue and organism scales. TFM was used in conjunction with conventional rheology to investigate the non-linear response of collagen networks to shear strain, illustrating the unique way that TFM can be used to study heterogeneities in cellular aggregates and tissues by providing a spatially-resolved measure of polymer network stress.⁶³ TFM has revealed heterogenous drying stresses in the outer epidermal barrier,¹⁴ and been used to examine the force around quiescent engineered 3D epithelial tissues embedded in a collagen network.⁶⁴

Dictyostelium discoideum is an excellent model for studying how cells coordinate to generate multicellular behaviour. This unicellular amoeba undergoes aggregation under starvation conditions to form a migrating “slug”. Several recent traction force studies have addressed how the aggregated slug generates concerted motion.^18,19,65 Frictional forces opposing motion are found at the leading front of the slug, whereas propulsive traction forces are measured posterior to this region under the slug body and are associated with a sub-population of cells (Fig. 3). Out-of-plane forces have also been observed, and these are attributed to tension in a secreted slime sheath.¹⁹ At a much larger length scale, gastropod slugs show a more complex pattern with periodic waves of muscle contraction propagating from the tail to the head. In this case, propulsive traction force is generated in the interwave zones that are in contact with the substrate.²⁶ These studies reveal two distinct mechanisms of propulsion for crawling animals and may help guide the design of biomimetic devices. The use of TFM to study organismic behaviour is in its infancy, and offers great opportunities to understand how animals grow and move.

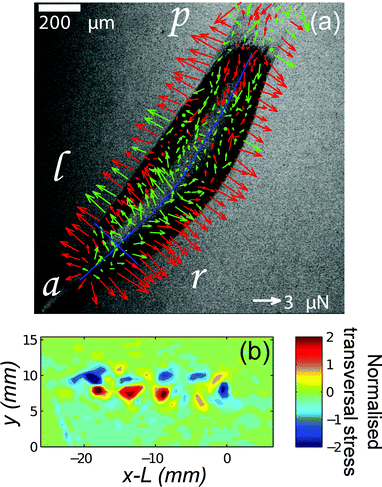Fig. 3 TFM reveals two mechanisms of propulsion in crawling animals. (a) Dictyostelium slugs apply frictional drag forces near the anterior tip and propulsive forces under the body (a = anterior, p = posterior, l = left, r = right). Arrows represent the in-plane component of the force. Red arrows correspond to force vectors with an upward vertical component and green arrows to vectors with a downward vertical component. ‘Shell tension’ creates an upward force at the slug's sides.¹⁹ (b) TFM of a migrating garden snail shows periodic patterns of stress perpendicular to the direction of motion.²⁶

2.4 Emerging applications of TFM in physics

TFM has recently been adopted in the realm of physics for studying problems such as wetting, fracture, adhesion, and friction.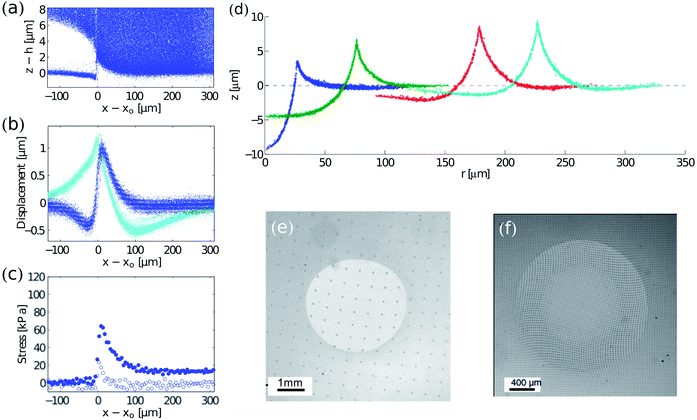

2.4.1 Mechanics of films. TFM is a useful tool for the analysis of fracture and measurement of material properties in thin films. For instance, TFM has recently been used to analyse the drying of colloidal suspensions, which are generally too fragile for measurement by conventional experimental techniques.^12,13 Initial work measured stress intensity factors during delamination from an underlying substrate, and quantified stress fields around crack tips (Fig. 4a–c).¹² More recently, bulk properties such as Young's modulus and critical tensile stress were measured by analysing in-plane, channeling cracks.¹³ TFM should be particularly well-suited to the analysis of cracks in composite and layered materials. Basic investigations into the deformation of materials at the microscale would benefit from the correlation of microstructural rearrangements and local stresses.

Fig. 4 Examples of TFM in the physical sciences. (a–c) Cracking in drying colloidal suspensions (modified from 12): (a) side view of tracer particle locations in a drying colloidal coating. The colloidal coating has delaminated from a silicone elastomer surface at z ≈ 0. (b) Displacements at the surface of the elastomer. The crack tip is at x = x₀. In-plane and out-of-plane displacements are cyan and blue respectively. (c) In-plane (blue) and out-of-plane stresses (white) near the crack tip. (d) Wetting on soft, silicone substrates. Radial profiles of substrates under glycerol droplets measured by confocal microscopy. From left to right, drops of radii of 26.8, 74.5, 176.7 and 225.5 μm. The dashed line through z = 0 corresponds to the initial surface profile before droplet deposition. The substrate is 50 μm thick.¹⁷ (e and f) Contact mechanics on soft substrates: surface displacements under sliding (unpublished image from experiments in ref. 66, courtesy of Antoine Chateauminois) and twisting⁶⁷ spherical indenters shown by the deformation of regular patterns (a grid and an array of dots respectively). Fig. 4f is reprinted with permission from A. Chateauminois, C. Fretigny and L. Olanier, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2010, 81, 026106. Copyright (2010) by the American Physical Society.

2.4.2 Wetting. A droplet is perhaps the simplest example of an object that exerts forces on an surface. The droplet's surface tension pulls up at the contact line, while its internal pressure pushes downwards. On soft materials this can cause substantial surface deformations (Fig. 4d).^16,68–73

Analysis of surface profiles under droplets has yielded one of the first techniques for direct measurement of solid surface stresses—or surface tensions—in soft materials.¹⁷ The technique only requires measurement of the surface tension of the droplet and the angles between interfaces at the contact line. Sufficiently close to the contact line, elasticity becomes unimportant, and there is a force balance between the solid surface stresses and the liquid–vapour surface tension.^16,74 Thus the two solid surface stresses can be calculated using Neumann's triangle.⁷⁵

Solid surface stress, γ_s is important to account for when using TFM at small scales; it can strongly affect the deformation response of the substrate when the characteristic length scale of interfacial forces are small relative to the system elastocapillary length γ_s/E. Here E is the Young modulus of the substrate. Typical elastocapillary lengths are O (μm) for gels in air and O (nm) for elastomers in air.^17,76 For hydrogels in water, surface stresses are very low, and so elastocapillary lengths will be much smaller. Accounting for solid surface stress in TFM only requires a small modification to the algorithm that converts surface displacement to stress.^16,71

2.4.3 Contact mechanics, friction and adhesion. The previous examples highlighted TFM measurement for micrometric processes. TFM has also been put to elegant use at larger scales in studying contact, friction and adhesion of indenters on soft substrates. In these experiments, centimetric, rigid indenters are pushed into a soft solid, and then either twisted or slid along the solid surface (Fig. 4e and f).^15,67 Markings at the surface of the solid allow displacements to be tracked, and subsequent calculation of interfacial stresses.

Contact experiments have allowed detailed investigation of the friction between a surface and a sliding indenter,^15,66 the adhesion and failure of a twisting contact,⁶⁷ high-speed stick-slip motion between sliding contacts,⁷⁷ and the effect of surface roughness on contact.⁷⁸ A great advantage of TFM, relative to typical indentation studies, is that it reveals the details of the stress distribution at solid–solid contacts, and thus allows development and testing of quantitative models for friction and adhesion. Recently, TFM methods have been applied to study the adhesion of particles and liposomes at a more microscopic scale.^76,79

2.4.4 TFM at different scales. TFM could be extended to an even larger range of materials and length scales by using other measurement techniques. The examples above have all used optical microscopy to measure displacements. However, this places limits on the size of displacements that can be measured. Imaging techniques with higher resolution, such as electron microscopy, would allow for the measurement of forces on stiffer materials. Similarly, there is no reason why TFM cannot be used to measure displacements and forces at macroscopic length scales – for example in measuring load distributions of large objects on flat surfaces.

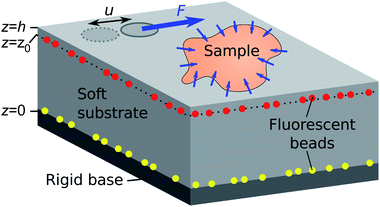
3 How TFM works

The idea of TFM is to measure forces by observing how a sample deforms an elastic substrate (Fig. 5). This is closely related to measuring the force on a spring by observing its extension, δ, and using Hookes law F = kδ.⁸⁰ Consider the patch of substrate (dark grey circle) shown in Fig. 5. If we exert a force F on the patch, it will be displaced by a distance u. Here the spring constant will depend on the patch size, and substrate properties such as stiffness, thickness and compressibility. However, typical samples do not exert discrete forces like this, but distributions of forces, as in the contractile sample in Fig. 5. These forces are best described in terms of traction stress σ_iz – the force per unit area applied by the sample on the surface.

Fig. 5 Schematic diagram of a TFM substrate. A soft substrate (light grey) is bonded to a rigid base (dark grey). Fluorescent beads (yellow, red) are embedded at the substrate base, and near its surface. A discrete force, F, is applied to a finite patch (dark grey circle) of the substrate displacing it a distance u. A continuous stress distribution is applied by a contractile sample.

In TFM, one measures displacements by tracking the movement of tracer particles embedded in the substrate. Then one calculates the traction stresses by solving a boundary-value problem. We assume that the substrate is a linear-elastic solid, so stresses σ(x) are related to displacements u(x) by the tensorial version of Hooke's law,

where I is the identity tensor, and ν is Poisson's ratio.⁸¹ Mechanical equilibrium requires that ∇·σ = 0,⁸¹ so

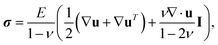(1 − 2ν)∇²u + ∇(∇·u) = 0 (2)

The substrate geometry is shown in Fig. 5. It is rigidly attached to a stiff base at z = 0, and has a free surface at z = h. Traction stresses at the surface can be calculated if the displacement field is known on a horizontal plane located at or below the surface (i.e., for some z = z₀ ≤ h).¹² Stress features with a length scale less than h − z₀ can not be accurately resolved, so the finest spatial resolution is achieved when the displacement field is measured at the free surface (z₀ = h). In the following, we assume that this is the case, so the system boundary conditions are u(z = h) = u*(x, y) and u(z = 0) = 0, with u*(x, y) being the measured deformation field at the substrate surface.

Eqn (2) can be solved by applying Fourier transforms in x and y.^12,29,82,83 This gives an ordinary differential equation in z for the Fourier transforms û(k_x, k_y, z) of u, with k_x and k_y being the x- and y – wavenumbers, respectively. Evaluating the result at the substrate surface, one finds that the Fourier transforms of the traction stresses, [small sigma, Greek, circumflex], are linearly related to û:

[small sigma, Greek, circumflex]_iz(k_x, k_y, z = h) = Q_ij(k_x, k_y; h)û_j(k_x, ky, z = h), (3)

with summation over repeated indices.¹² Two- and three-dimensional versions of the matrix Q, and MATLAB code for calculating two- and three-dimensional traction stresses, are given in the ESI.†

Thus the basic procedure for calculating surface traction stresses from the surface displacement field is: (i) calculate the in-plane Fourier transform of the displacements. (ii) For each wavenumber pair k_x, k_y, calculate the matrix Q(k_x, k_y; h). (iii) Apply Q to the displacement data for each wavenumber to give the Fourier transform of the traction stress. (iv) Calculate the traction stress via inverse Fourier transformation.

Alternative approaches exist to convert displacements into stresses. For example finite element methods can be used to solve the elastic problem in place of the Fourier technique.²³ If tracer particles are distributed and imaged throughout the substrate, rather than only at the surface, stresses can be calculated directly from the full, three-dimensional displacement field viaeqn (1).^23,84,85 This approach is particularly useful for measuring tractions of objects embedded in 3D matrices.

4 Substrate fabrication and characterisation

It is important to select an appropriate substrate material. In particular, the substrate should be sufficiently soft that deformations caused by the traction stresses can be accurately measured. At the same time, the substrate should also be sufficiently stiff that strains do not exceed its linear-response regime, so that linear-elastic theory can be applied.

Common materials for flat TFM substrates are polyacrylamide (PAA) gels and polydimethylsiloxane silicone (PDMS) gels and elastomers. These have tuneable stiffnesses spanning a wide range of Young's moduli. PAA gels can typically be made between E ∼ 100 Pa to 100 kPa. Commercially available silicones have stiffnesses ranging from E ∼ 3 kPa for PDMS gels (Dow Corning Toray, CY 52-276 A/B) to E ∼ 2 MPa for PDMS elastomers (Dow Corning, Sylgard 184).^86–91 Substrate stiffness is normally controlled by varying the amount of crosslinker in the polymer network, but it can also vary with curing temperature. PAA gels span an excellent range of stiffnesses for studying cell tractions, but they can have some nonlinear effects⁹² and can swell if not osmotically balanced with the sample.⁹³ Silicone-based materials have a high refractive index, and this has the advantage of allowing Total Internal Reflection Fluorescence (TIRF) microscopy.^94,95

Flat TFM substrates generally consist of a thin layer of a transparent and deformable elastic material embedded with fluorescent tracer beads bonded to a rigid, glass coverslip (Fig. 5). We provide our protocol for fabricating silicone TFM substrates by spin-coating in the ESI.† In brief, preparation of a silicone TFM substrate typically involves deposition of (i) fluorescent tracer beads on a glass slide, (ii) a uniform layer of silicone, (iii) fluorescent tracer beads, and (iv) an optional thin layer of silicone.^12,71 Thorough details of PAA substrate fabrication can be found in previous work.⁹⁶

While we focus on flat substrates here, there are alternative substrate designs. TFM studies can also be performed on arrays of elastic posts, which bend as samples exert forces on them.^97,98 The posts are simple cantilevers, so the traction forces are proportional to the deflection of the post tips. However this approach cannot measure out-of-plane forces, and requires posts and inter-post spacings to be much smaller than length scales of interest in the sample. A few recent studies have also examined tractions caused by cells embedded in a 3D matrix, made from modified polyethylene glycol diacrylate⁸⁵ or collagen I.⁹⁹ Stresses are measured by using fluorescent tracer beads spread throughout the 3D matrix.

To calculate traction stresses, we need to know the material properties of the substrate: i.e. Young's modulus, Poisson's ratio, and the size of the substrates linear-elastic response regime. If the substrate stiffness E ≳ 100 kPa, so that the material can support its own weight, this can be done with a tensile test on a thin rod of the substrate material. For softer materials like gels, we can characterise mechanical properties in shear with a rheometer. We provide details of mechanical testing in the ESI† along with examples of rheometry on a soft silicone gel.

Substrates also need appropriate surface properties for the sample to adhere to, or slide across. In some cases, samples naturally stick to substrates, as in studies of stratum corneum tissue¹⁴ and colloidal coatings.¹² However, in most cellular studies, it is necessary to coat the substrate with an extracellular-matrix (ECM) protein such as fibronectin, collagen, gelatin, or laminin to promote cell–substrate adhesion.^88,100 For wetting experiments, substrates made out of materials such as silicone are relatively hydrophobic, so water will not spread easily on them.¹⁷ Plasma treatment can temporarily increase hydrophilicity, but can also create a stiff oxide layer on the surface. This will modify the mechanical properties of the substrate, and in extreme cases, leads to cracking.^101,102

5 Experimental protocol

5.1 Imaging

The key requirement of imaging for TFM is to accurately measure the centroid positions of fluorescent tracer beads embedded in the substrate. To accurately track beads, images must be acquired with good contrast between the beads and the background, and with no image saturation. Images should be oversampled so that the point spread functions of individual beads are spread across multiple pixels, allowing sub-pixel accuracy when tracking bead positions. When there are only in-plane tractions – a good approximation for many cells⁵⁰ – we only need to track in-plane bead motion, so standard bright-field and epifluorescence microscopy is sufficient. However, for 3-dimensional tractions, confocal microscopy is required to measure the out-of-plane bead positions. We take images in an out-of-plane stack of at least five planes through the span of the image of the beads.

Care must be taken when measuring traction stresses at the edge of a field of a view (FOV). If part of a sample lies outside of a FOV, then it can cause nearby surface displacements inside the FOV. The elastic calculation will then ascribe these displacements to fictional traction stresses inside, and near the edge of the FOV. Thus, generally, it is advisable to acquire images with the sample in the middle of the FOV and surrounded by an area of bare substrate, so that surface displacements decay to zero at the edge of the FOV. If the sample is too large to fit in a single image, multiple overlapping images can be stitched together – ideally overlapping by ∼25%. Accurate stitching can be achieved by comparing tracked bead positions in overlapping regions. If stitching is not a possibility, the stress calculation can still be performed, but stresses near the edge of the FOV may not be reliable.

5.2 Reference state

An image of the substrate in a stress-free reference state is generally required to measure absolute substrate displacements – and thus to calculate absolute values of traction forces. The exception is when using regularly patterned beads or markers (e.g.Fig. 4e and f).^15,87 It is generally easiest to measure the reference state by imaging the stress-free substrate after completely detaching the sample. For cells, this can often be done with detergents or enzymes like trypsin, proteinase K, Triton X-100, or SDS.¹⁰³ Taking a reference state pre-attachment is challenging, because the sample then needs to be precisely placed in the middle of the imaged reference area. A solution for cell studies is to micropattern ECM onto the substrate, restricting regions of cell attachment.^59,97 In some experiments only relative values of traction stresses will be needed. Then, any time point can be used as the reference state. The reference state images should include images of beads on the rigid bottom of the substrate (Fig. 5). Comparison of the position of these bottom beads between timepoints allows for precise quantification of drift in the imaging system. This drift can then be subtracted when calculating the displacements of the top beads.

Reference states can be used to check that TFM substrates do not exhibit creep. Comparison of images before sample attachment, and after removal should reveal no displacement of fluorescent beads beyond measurement noise. This is a useful control, as irreversible displacements will lead to systematic errors in the calculation of traction forces.

6 Data analysis

Having imaged the sample, one can calculate the traction stresses. This involves (i) tracking fluorescent bead movement to calculate surface displacements, (ii) correcting for drift, (iii) removing bad displacement data, (iv) interpolating and filtering the displacements onto a regular grid for Fourier transforming, and (v) using theory to calculate the traction stresses. We provide step-by-step details of our stress-calculation protocol in the ESI.† Our ESI† also includes an example data set and MATLAB software for calculating traction stresses. Here, we outline three key procedures: tracking, low-pass filtering, and calculating traction stresses.

6.1 Tracking fluorescent beads

The 3-dimensional displacements of embedded fluorescent beads can be tracked in images using single particle tracking or correlation tracking (see ESI†). Particle tracking follows individual beads between images.¹⁰⁴ Correlation tracking, also known as digital image correlation¹⁰⁵ or particle image velocimetry,¹⁰⁶ tracks constellations of particles rather than individual particles. They each have strengths and weaknesses but can be combined to give powerful hybrid techniques – useful when high-resolution spatial displacements are required, but particle movement between frames is too large for particle tracking.¹⁰⁷

6.2 Low-pass filter for displacements

Traction stresses calculated from the displacement data can depend sensitively on the noise in the measured displacements since Q ∼ k for large k, so high-frequency noise is significantly amplified in the stress calculation (eqn (3)). We avoid this problem by removing high-frequency noise in the displacement data with a low-pass filter. Specifically, we use an exponential low-pass filter with a tuneable cut-off wavelength.¹⁰⁸ We make the cut-off wavelength as small as possible. When the cut-off wavelength is too small, ringing or rippling occurs in the stress field due to noise amplification. When the cut-off wavelength is too long, the fine features of the stress field become obscured.

6.3 Converting displacements into stresses

Once the displacement data is interpolated onto a regular grid, the traction stresses can be calculated using elastic theory. The first step is to calculate the Fourier transform, û(k_x, k_y, h), of the displacement data u(x, y, h) on a regular grid of wavenumbers (k_x, k_y). Secondly, one calculates Q_ij(k_x, k_y, h) for each pair of wavenumbers, and then use eqn (3) to determine the Fourier transform of the stresses, [small sigma, Greek, circumflex](k_x, k_y, h), from Q and û. Finally one takes the inverse Fourier transform of [small sigma, Greek, circumflex] to obtain the traction stresses σ.

7 Concluding remarks

Traction force microscopy is a powerful technique for measuring forces at interfaces. Although it involves several detailed experimental and computational steps, TFM is relatively straightforward to implement. In this review, we have detailed all of the necessary steps, from designing experiments through to the analysis of results. We have also showcased the potential of TFM for use across a much broader range of applications in biology, and for a variety of emerging applications in physics. TFM is particularly useful because it is a scale-free technique: it can be applied at any stress or length-scale. Current applications, using optical microscopy, have measured traction stresses from 1 Pa to 1 MPa, over length scales from 1 μm to 1 cm. In the future, we hope to see the application of TFM to new materials and processes.

Acknowledgements

We gratefully acknowledge support from Unilever and the National Science Foundation (DBI-0619674).

References

1. G. Binnig, C. F. Quate and C. Gerber, Phys. Rev. Lett., 1986, 56, 930–933.
2. A. Ashkin, J. Dziedzic, J. Bjorkholm and S. Chu, Opt. Lett., 1986, 11, 288–290.
3. E. R. Dufresne and D. G. Grier, Rev. Sci. Instrum., 1998, 69, 1974–1977.
4. C. Gosse and V. Croquette, Biophys. J., 2002, 82, 3314–3329.
5. J. N. Israelachvili and P. M. McGuiggan, J. Mater. Res., 1990, 5, 2223–2231.
6. M. Elbestawi, in Mechanical Variables Measurement: Solid, Fluid, and Thermal, ed. J. G. Webster, CRC Press, 2000, pp. 4.1–4.16.
7. U. Schwarz and M. Gardel, J. Cell Sci., 2012, 125, 3051–3060.
8. C. Kraning-Rush, S. Carey, J. Califano and C. Reinhart-King, in Methods Cell Biol., ed. A. R. Asthagiri and A. P. Arkin, Academic Press, 2012, vol. 110, pp. 139–178.
9. C. Mierke, D. Rosel, B. Fabry and J. Brabek, Eur. J. Cell Biol., 2008, 87, 669–676.
10. M. L. Gardel, I. C. Schneider, Y. Aratyn-Schaus and C. M. Waterman, Annu. Rev. Cell Dev. Biol., 2010, 26, 315–333.
11. S. Schwarz Henriques, R. Sandmann, A. Strate and S. Köster, J. Cell Sci., 2012, 125, 3914–3920.
12. Y. Xu, W. C. Engl, E. R. Jerison, K. J. Wallenstein, C. Hyland, L. A. Wilen and E. R. Dufresne, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 14964–14967.
13. Y. Xu, G. K. German, A. F. Mertz and E. R. Dufresne, Soft Matter, 2013, 9, 3735–3740.
14. G. K. German, W. C. Engl, E. Pashkovski, S. Banerjee, Y. Xu, A. F. Mertz, C. Hyland and E. R. Dufresne, Biophys. J., 2012, 102, 2424–2432.
15. A. Chateauminois and C. Fretigny, Eur. Phys. J. E, 2008, 27, 221–227.
16. R. W. Style and E. R. Dufresne, Soft Matter, 2012, 8, 7177–7184.
17. R. W. Style, R. Boltyanskiy, Y. Che, J. S. Wettlaufer, L. A. Wilen and E. R. Dufresne, Phys. Rev. Lett., 2013, 110, 066103.
18. J.-P. Rieu, C. Barentin, Y. Maeda and Y. Sawada, Biophys. J., 2005, 89, 3563–3576.
19. J.-P. Rieu and H. Delanoë-Ayari, Phys. Biol., 2012, 9, 066001.
20. T. Betz, D. Koch, Y. B. Lu, K. Franze and J. A. Käs, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 13420–13425.
21. D. Koch, W. Rosoff, J. Jiang, H. Geller and J. Urbach, Biophys. J., 2012, 102, 452–460.
22. R. Krishnan, D. D. Klumpers, C. Y. Park, K. Rajendran, X. Trepat, J. Van Bezu, V. W. M. Van Hinsbergh, C. V. Carman, J. D. Brain, J. J. Fredberg, J. P. Butler and G. P. Van Nieuw Amerongen, Am. J. Physiol.: Cell Physiol., 2011, 300, C146–C154.
23. W. R. Legant, C. K. Choi, J. S. Miller, L. Shao, L. Gao, E. Betzig and C. S. Chen, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 881–886.
24. X. Trepat, M. R. Wasserman, T. E. Angelini, E. Millet, D. A. Weitz, J. P. Butler and J. J. Fredberg, Nat. Phys., 2009, 5, 426–430.
25. A. F. Mertz, S. Banerjee, Y. Che, G. K. German, Y. Xu, C. Hyland, M. C. Marchetti, V. Horsley and E. R. Dufresne, Phys. Rev. Lett., 2012, 108, 198101.
26. J. Lai, J. del Alamo, J. Rodrguez-Rodrguez and J. Lasheras, J. Exp. Biol., 2010, 213, 3920–3933.
27. A. Harris, P. Wild and D. Stopak, Science, 1980, 208, 177–179.
28. M. Dembo and Y.-L. Wang, Biophys. J., 1999, 76, 2307–2316.
29. J. P. Butler, I. M. Tolić-Nųrrelykke, B. Fabry and J. J. Fredberg, Am. J. Physiol.: Cell Physiol., 2002, 282, C595–C605.
30. O. Du Roure, A. Saez, A. Buguin, R. H. Austin, P. Chavrier, P. Siberzan and B. Ladoux, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 2390–2395.
31. A. Huttenlocher and A. Horwitz, Cold Spring Harbor Perspect. Biol., 2011, 3, 1–16.
32. E. Farge, Curr. Top. Dev. Biol., 2011, 95, 243–265.
33. T. Mammoto and D. Ingber, Development, 2010, 137, 1407–1420.
34. A. Czirok, E. A. Zamir, M. B. Filla, C. D. Little and B. J. Rongish, Curr. Top. Dev. Biol., 2006, 73, 237–258.
35. S. L. Dallas, Q. Chen and P. Sivakumar, Curr. Top. Dev. Biol., 2006, 75, 1–24.
36. S. Kumar, I. Maxwell, A. Heisterkamp, T. Polte, T. Lele, M. Salanga, E. Mazur and D. Ingber, Biophys. J., 2006, 90, 3762–3773.
37. B. Alberts, A. Johnson, J. Lewis, M. Raff, K. Roberts and P. Walter, Molecular Biology of the Cell, Garland Science, 5th edn, 2007.
38. Y. Aratyn-Schaus, P. W. Oakes and M. L. Gardel, Mol. Biol. Cell, 2011, 22, 1330–1339.
39. K. A. Beningo, M. Dembo, I. Kaverina, J. V. Small and Y. L. Wang, J. Cell Biol., 2001, 153, 881–888.
40. C. Lemmon, C. Chen and L. Romer, Biophys. J., 2009, 96, 729–738.
41. M. Tsujioka, K. Yoshida and K. Inouye, EMBO J., 2004, 23, 2216–2225.
42. S. Munevar, Y. Wang and M. Dembo, Biophys. J., 2001, 80, 1744–1757.
43. S. Munevar, Y. L. Wang and M. Dembo, Mol. Biol. Cell, 2001, 12, 3947–3954.
44. M. F. Fournier, R. Sauser, D. Ambrosi, J. J. Meister and A. B. Verkhovsky, J. Cell Biol., 2010, 188, 287–297.
45. V. Peschetola, V. Laurent, A. Duperray, R. Michel, D. Ambrosi, L. Preziosi and C. Verdier, Cytoskeleton, 2013, 70, 201–214.
46. K. Burton, J. H. Park and D. L. Taylor, Mol. Biol. Cell, 1999, 10, 3745–3769.
47. B. G. Ricart, M. T. Yang, C. A. Hunter, C. S. Chen and D. A. Hammer, Biophys. J., 2011, 101, 2620–2628.
48. M. L. Gardel, B. Sabass, L. Ji, G. Danuser, U. S. Schwarz and C. M. Waterman, J. Cell Biol., 2008, 183, 999–1005.
49. Y. Aratyn-Schaus and M. L. Gardel, Curr. Biol., 2010, 20, 1145–1153.
50. H. Delanoë-Ayari, J. P. Rieu and M. Sano, Phys. Rev. Lett., 2010, 105, 248103.
51. S. Hur, Y. Zhao, Y.-S. Li, E. Botvinick and S. Chien, Cell. Mol. Bioeng., 2009, 2, 425–436.
52. D. T. Tambe, U. Croutelle, X. Trepat, C. Y. Park, J. H. Kim, E. Millet, J. P. Butler and J. J. Fredberg, Nat. Mater., 2013, 10, 469–475.
53. M. Perez-Moreno, C. Jamora and E. Fuchs, Cell, 2003, 112, 535–548.
54. M. Hu and A. Evans, Acta Metall., 1989, 37, 917–925.
55. J. Beuth and N. Klingbeil, J. Mech. Phys. Solids, 1996, 44, 1411–1428.
56. M. Yanaka, Y. Tsukahara, N. Nakaso and N. Takeda, J. Mater. Sci., 1998, 33, 2111–2119.
57. D. T. Tambe, H. C. Corey, T. E. Angelini, K. Rajendran, C. Y. Park, X. Serra-Picamal, E. H. Zhou, M. H. Zaman, J. P. Butler, D. A. Weitz, J. J. Fredberg and X. Trepat, Nat. Mater., 2011, 10, 469–475.
58. X. Trepat and J. J. Fredberg, Trends Cell Biol., 2011, 21, 638–646.
59. Z. J. Liu, J. L. Tan, D. M. Cohen, M. T. Yang, N. J. Sniadecki, S. A. Ruiz, C. M. Nelson and C. S. Chen, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 9944–9949.
60. V. Maruthamuthu, B. Sabass, U. S. Schwarz and M. L. Gardel, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 4708–4713.
61. A. F. Mertz, Y. Che, S. Banerjee, J. M. Goldstein, K. A. Rosowski, S. F. Revilla, C. M. Niessen, M. C. Marchetti, E. R. Dufresne and V. Horsley, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 842–847.
62. M. L. McCain, H. Lee, Y. Aratyn-Schaus, A. G. Kléber and K. K. Parker, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 9881–9886.
63. R. C. Arevalo, J. S. Urbach and D. L. Blair, Chaos, 2011, 21, 041102.
64. N. Gjorevski and C. M. Nelson, Biophys. J., 2012, 103, 152–162.
65. J.-P. Rieu, T. Saito, H. Delanoë-Ayari, Y. Sawada and R. R. Kay, Cell Motil. Cytoskeleton, 2009, 66, 1073–1086.
66. D. Nguyen, P. Paolino, M. Audry, A. Chateauminois, C. Fretigny, Y. Le Chenadec, M. Portigliatti and E. Barthel, J. Adhes., 2011, 87, 235–250.
67. A. Chateauminois, C. Fretigny and L. Olanier, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2010, 81, 026106.
68. M. Shanahan and P.-G. de Gennes, C. R. Acad. Sci., Ser. II: Mec., Phys., Chim., Sci. Terre Univers, 1986, 302, 517.
69. R. Pericet-Camara, A. Best, H.-J. Butt and E. Bonaccurso, Langmuir, 2008, 24, 10565–10568.
70. R. Pericet-Camara, G. K. Auernhammer, K. Koynov, S. Lorenzoni, R. Raiteri and E. Bonaccurso, Soft Matter, 2009, 5, 3611–3617.
71. E. R. Jerison, Y. Xu, L. A. Wilen and E. R. Dufresne, Phys. Rev. Lett., 2011, 106, 186103.
72. R. W. Style, Y. Che, S. J. Park, B. M. Weon, J. H. Je, C. Hyland, G. K. German, M. Power, L. A. Wilen, J. S. Wettlaufer and E. R. Dufresne, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 12541–12544.
73. A. Marchand, S. Das, J. H. Snoeijer and B. Andreotti, Phys. Rev. Lett., 2012, 108, 094301.
74. J. Olives, J. Phys.: Condens. Matter, 2010, 22, 085005.
75. F. Neumann, Vorlesungen über die Theorie der Capillarität, ed. B. G. Teubner, Leipzig, 1894.
76. R. W. Style, C. Hyland, R. Boltyanskiy, J. S. Wettlaufer and E. R. Dufresne, Nat. Commun., 2013, 4, 2728.
77. M. C. Audry, C. Fretigny, A. Chateauminois, J. Teissere and E. Barthel, Eur. Phys. J. E, 2012, 35, 1–7.
78. D. Nguyen, S. Ramakrishna, C. Fretigny, N. Spencer, Y. Le Chenadec and A. Chateauminois, Tribol. Lett., 2013, 49, 135–144.
79. M. P. Murrell, R. Voituriez, J. F. Joanny, P. Nassoy, C. Sykes and M. L. Gardel, Nat. Phys., 2014, 10, 163–169.
80. L. D. Landau and E. M. Lifshitz, Course of Theoretical Physics, Theory of Elasticity, Pergamon Press, 3rd edn, 1986, vol. 7.
81. L. D. Landau and E. M. Lifshitz, Course of Theoretical Physics, Mechanics, Butterworth-Heinemann, 3rd edn, 1976, vol. 1.
82. J. C. del Álamo, R. Meili, B. Alonso-Latorre, J. Rodríguez-Rodríguez, A. Aliseda, R. A. Firtel and J. C. Lasheras, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 13343–13348.
83. J. C. del Alamo, R. Meili, B. Alvarez-Gonzalez, B. Alonso-Latorre, E. Bastounis, R. Firtel and J. C. Lasheras, PLoS One, 2013, 8, e69850.
84. S. A. Maskarinec, C. Franck, D. A. Tirrell and G. Ravichandran, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 22108–22113.
85. W. Legant, J. Miller, B. Blakely, D. Cohen, G. Genin and C. Chen, Nat. Methods, 2010, 7, 969–971.
86. D. Armani, C. Liu and N. Aluru, Proceedings of the IEEE Micro Electro Mechanical Systems (MEMS), 1999, pp. 222–227.
87. C. M. Cesa, N. Kirchgeßner, D. Mayer, U. S. Schwarz, B. Hoffmann and R. Merkel, Rev. Sci. Instrum., 2007, 78, 034301.
88. R. Merkel, N. Kirchgeßner, C. M. Cesa and B. Hoffmann, Biophys. J., 2007, 93, 3314–3323.
89. M. Ochsner, M. R. Dusseiller, H. M. Grandin, S. Luna-Morris, M. Textor, V. Vogel and M. L. Smith, Lab Chip, 2007, 7, 1074–1077.
90. D. Fuard, T. Tzvetkova-Chevolleau, S. Decossas, P. Tracqui and P. Schiavone, Microelectron. Eng., 2008, 85, 1289–1293.
91. L. Chen, G. K. Auernhammer and E. Bonaccurso, Soft Matter, 2011, 7, 9084–9089.
92. T. Boudou, J. Ohayon, C. Picart, R. I. Pettigrew and P. Tracqui, Biorheology, 2009, 46, 191–205.
93. H. H. Hooper, J. P. Baker, H. W. Blanch and J. M. Prausnitz, Macromolecules, 1990, 23, 1096–1104.
94. Y. Iwadate and S. Yumura, BioTechniques, 2008, 44, 739–750.
95. E. Gutierrez, E. Tkachenko, A. Besser, P. Sundd, K. Ley, G. Danuser, M. H. Ginsberg and A. Groisman, PLoS One, 2011, 6, e23807.
96. Y. Aratyn-Schaus, P. W. Oakes, J. Stricker, S. P. Winter and M. L. Gardel, J. Vis. Exp., 2010, 46, e2173.
97. J. Tan, J. Tien, D. Pirone, D. Gray, K. Bhadriraju and C. Chen, Proc. Natl. Acad. Sci. U. S. A., 2003, 100, 1484–1489.
98. L. Trichet, J. Le Digabel, R. Hawkins, S. Vedula, M. Gupta, C. Ribrault, P. Hersen, R. Voituriez and B. Ladoux, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 6933–6938.
99. T. M. Koch, S. Münster, N. Bonakdar, J. P. Butler and B. Fabry, PLoS One, 2012, 7, e33476.
100. A. A. Boulton, G. B. Baker and W. Walz, Practical cell culture techniques, Springer, 1992, vol. 23.
101. S. Béfahy, P. Lipnik, T. Pardoen, C. Nascimento, B. Patris, P. Bertrand and S. Yunus, Langmuir, 2010, 26, 3372–3375.
102. K. L. Mills, X. Zhu, S. Takayama and M. D. Thouless, J. Mater. Res., 2008, 23, 37–48.
103. M. Jamur and C. Oliver, in Immunocytochemical Methods and Protocols, ed. C. Oliver and M. C. Jamur, Humana Press, 2010, vol. 588, pp. 63–66.
104. D. L. Blair and E. R. Dufresne, The Matlab Particle Tracking Code Repository, http://physics.georgetown.edu/matlab/.
105. T. Chu, W. Ranson and M. Sutton, Exp. Mech., 1985, 25, 232–244.
106. C. Willert and M. Gharib, Exp. Fluids, 1991, 10, 181–193.
107. E. A. Cowen, S. G. Monismith, E. A. Cowen and S. G. Monismith, Exp. Fluids, 1997, 22, 199–211.
108. S. T. Bow, Pattern recognition and image preprocessing, CRC Press, 2002.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c4sm00264d

‡ Present address: Department of Bioengineering, Binghamton University, P.O. Box 6000, Binghamton, NY, 13902-6000, USA.

§ Present address: Department of Engineering Science, University of Oxford, Parks Road, Oxford, OX1 3PJ, UK.

---