Nonlinear microrheology of an aging, yield stress fluid using magnetic tweezers
Jason P.
Rich
a,
Jan
Lammerding
b,
Gareth H.
McKinley
*c and
Patrick S.
Doyle
*a
aMassachusetts Institute of Technology, Department of Chemical Engineering, Cambridge, MA, USA. E-mail: pdoyle@mit.edu; Fax: +1 617-324-0066; Tel: +1 617-253-4534
bCardiovascular Division, Department of Medicine, Brigham and Women's Hospital, Harvard Medical School, Cambridge, MA, USA
cMassachusetts Institute of Technology, Department of Mechanical Engineering, Hatsopoulos Microfluids Laboratory, Cambridge, MA, USA. E-mail: gareth@mit.edu; Fax: +1 617-258-8559; Tel: +1 617-258-0754
First published on 25th August 2011
Abstract
The large deformation mechanical response of complex fluids and soft materials provides fundamental insight into their underlying microstructure and dynamics. Additionally, associated yielding and flow processes are often central to industrial processing and end-use. By probing nonlinear rheological properties at the microscopic scale, microstructural dynamics and flow mechanisms can be more directly elucidated. In the current work, we present a simple magnetic tweezer technique for probing the nonlinear microrheology of complex fluids and soft materials. The setup is characterized in terms of the accessible stresses, the applied magnetic fields, and the measurable viscosities and shear rates. Further, we report the first use of magnetic tweezers to determine yield stresses at the microscopic scale, as well as the first comparison between bulk and micro-scale yield stress measurements. The capabilities of the technique are demonstrated on an aqueous dispersion of Laponite®: an aging, thixotropic colloidal clay of considerable scientific and practical interest. Probe trajectories in this material reflect the yield stress and strong shear-thinning behaviour observed on the bulk scale, and for sufficient clay concentrations we find good agreement for the shear yield stress obtained from bulk rheology and magnetic tweezer measurements. These unforeseeable observations illuminate the nature of the dispersion microstructure, including the characteristic size of microstructural features.
1 Introduction
Microrheology has become an important tool for understanding and characterizing soft materials.1 The field encompasses various methods in which rheological properties are extracted from the motions of embedded microscopic probe particles.2 It is especially suited for situations where bulk rheometry is not feasible, such as for rare materials or in vivo studies of biological fluids,3 and can provide insight into materials with complex microstructure, which may exhibit different rheological behaviour at bulk and microscopic length scales.4,5 Techniques for probing both linear (small deformation and deformation rate) and nonlinear (large deformation and/or deformation rate) microrheology have been developed, with the nonlinear case necessarily involving active techniques in which external forces are applied to probes.2,4,6 While linear microrheology has received the most attention, nonlinear microrheology plays a key role in the flow properties of numerous important microstructured materials, such as colloidal glasses,7 electrorheological and magnetorheological fluids,8 and polymer-colloid mixtures.9 The bulk response and proper function of these materials is highly dependent on shear-thinning and yield stress phenomena at microscopic length scales. For example, in magnetorheological suspensions, microscopic iron-containing particles are often dispersed in viscoplastic carrier fluids, whose rheological properties prevent particle sedimentation and influence field-responsive self-assembly.10Because of its significance in understanding the properties of structured fluids, recent work in the field has begun to investigate nonlinear microrheology for several canonical materials, and has explored relationships with bulk properties. A number of studies have examined the micro-scale viscosity of colloidal dispersions,11–14 the nature of forced microstructural rearrangements and shear melting near the colloidal glass transition,7 and an active microrheological method for measuring normal stress coefficients.15 Additionally, yield stress measurements at the microscopic length scale were first reported by Wilking and Mason, who examined gelatin solutions using optical tweezers that were modified to exert torques on an embedded microdisk.16
In the current work, we present a magnetic tweezer technique for measuring nonlinear microrheological properties of complex fluids. The motion of embedded magnetic microparticles has been used for many years to probe such phenomena as the mechanical properties of cell protoplasm,17 the elasticity of gels,18 the stretching behaviour of macromolecules,19 and the mechanotransduction of cells.20 Here we employ the single-pole design from Lammerding,21 which can apply forces on the order of 10 nN on 4.5 μm superparamagnetic particles. The dynamic range of the instrument is characterized and probe trajectories are analyzed to extract effective viscosity measurements. Additionally, we report the first use of magnetic tweezers to determine yield stresses at the microscopic scale, affording advantages to optical tweezer techniques because of simpler design and implementation. The technique is demonstrated on a typical thixotropic, aging, yield stress material,22 an aqueous dispersion of the synthetic clay Laponite®.23 Often used as a rheological modifier in commercial soft materials, Laponite® clay consists of nanometric disks that undergo progressive structural arrest over time when dispersed in water at concentrations as low as about 1 wt%.24–27 The microstructural development results in complex and time-dependent rheology.28–32 Previous work has addressed the bulk rheology and linear microrheology of aqueous Laponite® dispersions; for more thorough reviews of the current understanding of the phase behaviour, structure, and rheology, see Ruzicka et al.33 and Rich et al.34 We note that while the local nonlinear rheology of aqueous Laponite® dispersions has also been studied,35 only probes with sizes on the order of 1 mm were used. The current work therefore presents the first truly micro-scale nonlinear rheological study of this material, as well as the first comparison to bulk nonlinear properties. We observe that the effective viscosity is strongly shear-thinning, obeying similar power-law behaviour at both the bulk and microscopic scales. Additionally, the yield stress grows approximately logarithmically with age time, exhibiting quantitative agreement between bulk and microscopic scales for concentrations ≥ 2 wt%.
2 Experimental
The magnetic tweezer device used in the present work was designed and described by Lammerding.21 A rod of high magnetic permeability iron (CMI-C, CMI Specialty Products, Bristol, CT) is machined to a sharp tip of width ≈ 200 μm, as shown in Fig. 1, and subsequently annealed according to the manufacturer's specifications. The highly pointed geometry results in large magnetic field gradients, leading to relatively large forces on magnetic probe particles.36,37 The core metal is wrapped with about 300 turns of AWG 19 copper magnet wire over a length of 7.2 cm, leading to a wire turn density n of about n ≈ 4200 m−1. The assembly is then mounted on a manual micromanipulator (MX110, Siskiyou, Grants Pass, OR) alongside an inverted microscope (Axiovert 40 CFL, Carl Zeiss AG, Oberkochen, Germany) and the wires are connected to a DC power supply (GPS-2303, GWInstek, Taipei, Taiwan). Experiments are conducted at room temperature, T ≈ 22.5 °C. For a current of 1.5 A, the temperature of the tip does not rise more than about 1 °C over the time scale of a measurement (∼ 1 min).21 We therefore consider electrical resistance heating of the tip to be negligible. Gaussmeter measurements at the back of the core indicate that the magnetic field stabilizes within 1 s of applying a current. | ||
| Fig. 1 The magnetic tweezer setup used for nonlinear microrheology experiments. (a) The magnetic tweezer device is mounted on a micromanipulator adjacent to the stage of an inverted microscope. The iron core is machined to a sharp tip, which is dipped directly into the fluid of interest. The flattened tip design, which is shown in detail in the inset, leads to locally horizontal forces when the device is held at an angle of 45° to the horizontal.21 (b) Microscope view frame of the magnetic tweezer experiment. The point of the tip is flattened to a width of about 200 μm, providing an approximately unidirectional magnetic force in the vicinity of the tip. Upon magnetization of the core, superparamagnetic probe particles (diameter d = 4.5 μm) move towards the tip with a velocity U. The distance from a probe to the surface is given by x, while y defines the distance along the surface of the tweezer device. | ||
Laponite RD® powder was obtained from Rockwood Additives. To prepare the clay dispersion, dry Laponite® powder is added to an aqueous buffer of pH ≈ 10 consisting of 1.8 mM NaOH and 4.1 mM NaHCO3. The purpose of the buffer is to maintain the dispersion pH and fix the solvent ionic strength at 5.9 mM. The dispersion is mixed vigorously for at least 1.5 h and subsequently passed through a 0.8 μm filter, breaking apart most of the remaining aggregates with a strong shear.38 This filtration marks the reference point for subsequent aging studies, in accordance with previous work on Laponite® dispersions,39 and structuring of the clay progressively increases as the system ages. Petit et al.40 demonstrated that about 7% of the initial Laponite® concentration is lost when dispersions of about 3 wt% Laponite® are passed through 0.45 μm filters. However, since the present study uses filters with larger pores (0.8 μm), it is assumed that filtration does not change the nominal concentration of Laponite®.
Immediately following filtration, superparamagnetic microparticles of diameter d = 4.5 μm (M-450 Dynabeads, Invitrogen Life Technologies, Carlsbad, CA) are added at a concentration of about ϕ ≈ 0.4 vol%. The magnetic particle concentration is chosen to achieve a large number of measureable particle trajectories with approximately non-interacting particles. After vortex mixing for about 15 s, the magnetic particles are randomly dispersed in the sample. The additional rejuvenation of the sample due to vortex mixing is minimal since it is conducted immediately after filtering. A small petri dish is filled with the dispersion and placed on the microscope stage for visualization with a 20× objective (N.A. = 0.5). By adjusting the micromanipulator, the tip of the magnetic tweezer device is dipped directly into the dispersion and brought arbitrarily close to magnetic probe particles, maximizing the accessible forces on probes.36 The tip is machined such that approximately horizontal magnetic fields are locally obtained when the device is positioned at a 45° angle to the horizontal, as pictured in Fig. 1a. The directionality of the force is confirmed by checking that particles remain in focus as they move towards the tip.
Movies of probe particle dynamics are captured with a CCD camera (KP-M1A, Hitachi, Tokyo, Japan) having a variable shutter speed between 1/60 s and 1/10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 s set to frame integration mode. Scion Image software is used to record movies at a rate of 30 frames s−1. Each video frame consists of two interlaced fields (the odd or even rows of the CCD matrix) that are exposed 1/60 s apart, requiring each frame to be de-interlaced during the movie analysis. The interlacing also results in a loss of spatial resolution in the direction perpendicular to the interlacing;41 thus, particle displacements in this study are only examined in the horizontal direction (the x-direction), which is the predominant direction of motion. Movies are analyzed to obtain particle trajectories using publicly available software developed by Crocker and Grier.41† Any particles that chain or cluster together are neglected in the analysis.
000 s set to frame integration mode. Scion Image software is used to record movies at a rate of 30 frames s−1. Each video frame consists of two interlaced fields (the odd or even rows of the CCD matrix) that are exposed 1/60 s apart, requiring each frame to be de-interlaced during the movie analysis. The interlacing also results in a loss of spatial resolution in the direction perpendicular to the interlacing;41 thus, particle displacements in this study are only examined in the horizontal direction (the x-direction), which is the predominant direction of motion. Movies are analyzed to obtain particle trajectories using publicly available software developed by Crocker and Grier.41† Any particles that chain or cluster together are neglected in the analysis.
Bulk rheology measurements are made using a stress-controlled rheometer (ARG-2, TA Instruments, New Castle, DE) with a 40 mm diameter aluminium plate geometry and a 0.5 mm gap. Adhesive-backed 600 grit sandpaper (McMaster-Carr, Elmhurst, IL, RMS roughness ≈ 6.0 μm), is attached to each surface to minimize wall-slip. The Laponite® dispersion is prepared in the same way as in the microrheology experiments, and is introduced between the plates immediately after filtering, which is again marked as the time of zero age, tw = 0. To help ensure a reproducible initial condition, the sample is then pre-sheared at a shear rate of ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) = 250 s−1 for 30 s. Though the pre-shear may keep aggregates from forming and partially rejuvenate the fluid,42 we find this additional rejuvenating effect to be negligible when the pre-shear is performed immediately subsequent to the filtration step. After the dispersion is allowed to age at a constant temperature T = 22.5 °C, continuous ramp tests are performed to explore the yielding and shear-thinning behaviour. Starting from a value below the static yield stress, the applied shear stress is increased continuously until the dispersion has yielded, allowing the extraction of the flow curve and viscosity behaviour during yielding. The stress is ramped linearly at a rate of about 1 Pa s−1 over a time of 2 min, which is small compared to the age of the dispersion. We note that this protocol estimates the static yield stress, which is the stress required to induce flow from rest, in contrast to the dynamic yield stress, which is estimated by decreasing the shear rate and extrapolating the resulting shear stresses to
= 250 s−1 for 30 s. Though the pre-shear may keep aggregates from forming and partially rejuvenate the fluid,42 we find this additional rejuvenating effect to be negligible when the pre-shear is performed immediately subsequent to the filtration step. After the dispersion is allowed to age at a constant temperature T = 22.5 °C, continuous ramp tests are performed to explore the yielding and shear-thinning behaviour. Starting from a value below the static yield stress, the applied shear stress is increased continuously until the dispersion has yielded, allowing the extraction of the flow curve and viscosity behaviour during yielding. The stress is ramped linearly at a rate of about 1 Pa s−1 over a time of 2 min, which is small compared to the age of the dispersion. We note that this protocol estimates the static yield stress, which is the stress required to induce flow from rest, in contrast to the dynamic yield stress, which is estimated by decreasing the shear rate and extrapolating the resulting shear stresses to ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) = 0 s−1.43
= 0 s−1.43
3 Results and discussion
3.1 Calibration of magnetic tweezers
The force and the stress applied by the magnetic tweezer device on probe particles are calibrated by tracking particle motion in Trimethylsiloxy-terminated Polydimethylsiloxane (DMS-T43, Gelest, Morrisville, PA), a Newtonian liquid with kinematic viscosity ν = 30,000 cSt (dynamic viscosity η = 29.5 Pa s). The reported viscosity was confirmed using bulk rheology measurements. The stress applied by the tweezer device is a function of both the distance from the tip surface, x, and the current in the copper wire, I. About 30 particle trajectories xi(t) are obtained at a given current and an average trajectory is calculated by applying a least-squares fit. The most suitable fit for the calibration experiments is provided by functions of the form ts,i − t = Pm(x), where ts,i is the time at which the ith particle reaches the tip and Pm is a polynomial of order m (m = 3–6). By taking a time derivative of the fit, an expression for the average particle velocity, U(x), is obtained, allowing calculation of the shear rate![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) (x) = 3|U(x)|/2a and the stress
(x) = 3|U(x)|/2a and the stress  , where a is the probe radius. The resulting stress calibration curves for three different values of the current are plotted in Fig. 2. Here it is seen that the instrument can impose stresses on probe particles up to about 230 Pa, which provides an upper limit for measureable yield stress values. Additionally, the stress depends only weakly on I over the range explored in the present work, increasing by 10–27% (depending on x) from I = 1.50 A to I = 2.50 A. The inset of Fig. 2 shows a typical probe trajectory in the Newtonian calibration fluid at a current of 2.00 A. A smooth acceleration towards the surface is observed, with d2x/d2t < 0 for all x, as a result of the constant viscosity and the continually increasing stress on the particle. The magnetic tweezer technique therefore provides a micro-scale analogy to the bulk continuous stress ramp described in the previous section. In Section 3.2.1, we contrast the shape of this trajectory with that in the non-Newtonian case, where effects of shear-thinning behaviour become apparent.
, where a is the probe radius. The resulting stress calibration curves for three different values of the current are plotted in Fig. 2. Here it is seen that the instrument can impose stresses on probe particles up to about 230 Pa, which provides an upper limit for measureable yield stress values. Additionally, the stress depends only weakly on I over the range explored in the present work, increasing by 10–27% (depending on x) from I = 1.50 A to I = 2.50 A. The inset of Fig. 2 shows a typical probe trajectory in the Newtonian calibration fluid at a current of 2.00 A. A smooth acceleration towards the surface is observed, with d2x/d2t < 0 for all x, as a result of the constant viscosity and the continually increasing stress on the particle. The magnetic tweezer technique therefore provides a micro-scale analogy to the bulk continuous stress ramp described in the previous section. In Section 3.2.1, we contrast the shape of this trajectory with that in the non-Newtonian case, where effects of shear-thinning behaviour become apparent.
 | ||
Fig. 2 Calibration curves for the stress applied by the magnetic tweezers as a function of the distance from the tip. Results for I = 1.50 A, 2.00 A, and 2.50 A are shown. The stress increases as the tip is approached and stresses up to about 230 Pa are accessible close to the tip. For x < 20 μm, the computed stress values are highly sensitive to the order of the polynomial fit to trajectory data. The stress exhibits only weak dependence on current, suggesting that either the core or the probe particles are approaching magnetic saturation. The inset shows a typical probe trajectory in the Newtonian calibration fluid, which has a kinematic viscosity of ν = 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cSt (η = 29.5 Pa s). 000 cSt (η = 29.5 Pa s). | ||
By combining the stress calibration with the limitations of the optical and particle-tracking setup, we construct an operating diagram of the accessible shear rates and viscosities that can be measured by the magnetic tweezer technique. This diagram is shown in Fig. 3, in which the range of accessible shear rates is bounded by the dotted lines. Assuming thermal forces are negligible compared to magnetic forces, the lower bound ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) min is given by the spatial resolution (here about 90 nm, as determined from the apparent displacement of immobilized particles at 20× magnification44) divided by the duration of the experiment, which in the present work is 1 min. The upper bound
min is given by the spatial resolution (here about 90 nm, as determined from the apparent displacement of immobilized particles at 20× magnification44) divided by the duration of the experiment, which in the present work is 1 min. The upper bound ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) max = 3|Umax|/2a is limited by the maximum frame rate of the camera (30 frames s−1, or 60 interlaced fields s−1), which allows particles to be accurately tracked at velocities up to about |Umax| ≈ 20 μm s−1 under 20× magnification. This highlights a potential modification that could extend the dynamic range of future realizations of the technique through the use of a high-speed camera. The range of measurable viscosities is given by the stress calibration in Fig. 2, using the relation
max = 3|Umax|/2a is limited by the maximum frame rate of the camera (30 frames s−1, or 60 interlaced fields s−1), which allows particles to be accurately tracked at velocities up to about |Umax| ≈ 20 μm s−1 under 20× magnification. This highlights a potential modification that could extend the dynamic range of future realizations of the technique through the use of a high-speed camera. The range of measurable viscosities is given by the stress calibration in Fig. 2, using the relation 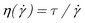 . The dark gray area shows the dynamic range demonstrated in the present work, while the lighter region, which corresponds to smaller shear stresses, is accessible at lower currents than used here. At very low currents, the applied stress becomes comparable to the characteristic Brownian stress
. The dark gray area shows the dynamic range demonstrated in the present work, while the lighter region, which corresponds to smaller shear stresses, is accessible at lower currents than used here. At very low currents, the applied stress becomes comparable to the characteristic Brownian stress  . In this limit, particle diffusion out of the area of focus generally makes continual tracking of particle trajectories impossible, so that
. In this limit, particle diffusion out of the area of focus generally makes continual tracking of particle trajectories impossible, so that 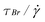 corresponds to an ultimate lower limit to the measurable viscosities.
corresponds to an ultimate lower limit to the measurable viscosities.
 | ||
Fig. 3 Operating diagram for the magnetic tweezer setup showing the range of accessible shear rates and viscosities. The maximum shear rate ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) max = 3|Umax|/2a is limited primarily by the frame rate of the camera (30 frames s−1 or 60 interlaced fields s−1), which enables particles with diameter 2a = 4.5 μm to be tracked at velocities up to about |Umax| ≈ 20 μm s−1 under 20× magnification. The minimum shear rate max = 3|Umax|/2a is limited primarily by the frame rate of the camera (30 frames s−1 or 60 interlaced fields s−1), which enables particles with diameter 2a = 4.5 μm to be tracked at velocities up to about |Umax| ≈ 20 μm s−1 under 20× magnification. The minimum shear rate ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) min is given by dividing the spatial resolution (here about 90 nm) by the time over which the magnetic field is applied (here 1 min). The stress calibration in Fig. 2 allows calculation of the corresponding accessible viscosities. The dynamic range demonstrated in the present work is given by the dark shaded region, with min is given by dividing the spatial resolution (here about 90 nm) by the time over which the magnetic field is applied (here 1 min). The stress calibration in Fig. 2 allows calculation of the corresponding accessible viscosities. The dynamic range demonstrated in the present work is given by the dark shaded region, with  = 225 Pa and = 225 Pa and  = 30 Pa, while the lighter region is accessible at lower currents than used here. Eventually, Brownian stresses become significant, providing an ultimate lower limit to the measurable viscosities. Here this limit is calculated using the characteristic Brownian stress = 30 Pa, while the lighter region is accessible at lower currents than used here. Eventually, Brownian stresses become significant, providing an ultimate lower limit to the measurable viscosities. Here this limit is calculated using the characteristic Brownian stress  at T = 22.5 °C on a particle with radius a = 2.25 μm. at T = 22.5 °C on a particle with radius a = 2.25 μm. | ||
Further insight into the capabilities of the technique can be gained by considering the magnetic field applied by the tweezers and the resulting magnetization of the probe particles. While it is difficult to accurately measure the magnetic field, B, at distances of 10–100 μm away from the tip, it can be estimated by combining the calibration data with a suitable model for the particle magnetization, M. We use the Fröhlich–Kennelly equation:45
 | (1) |
 | (2) |
| Fdrag(x) = −6πηaU(x) = 6πηaAα−1αx(α−1)/α | (3) |
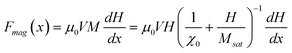 | (4) |
 | (5) |
Using the condition that H → 0 as x → ∞, eqn (5) can be integrated to obtain an expression that is explicit in x but implicit in H.
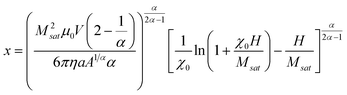 | (6) |
This expression is plotted in Fig. 4 (black line) in terms of the magnetic field B(x) = μ0H(x) for I = 1.50 A. Within 100 μm of the tip, the magnetic field acting on magnetizable probe particles is of the order ∼1 T, which is consistent with the magnetization properties of the CMI-C core metal shown in the inset. The magnetic field decays with increasing distance from the tip, dropping by about 35% over a distance from x = 20 μm to x = 100 μm. This field gradient leads to a magnetic force on the probe particles according to eqn (4). The resulting probe particle magnetization values, calculated from eqn (1), are 28.6–29.1 kA m−1, so that M ≈ Msat = 30 kA m−1. This near-saturation provides an explanation for the marginal difference between stress calibration curves at different currents shown in Fig. 2. If M → Msat, the particle force balance results in a simpler relation between H and x.
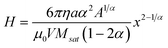 | (7) |
 | ||
| Fig. 4 Calculation of the magnetic field as a function of distance from the tip at a current of I = 1.50 A. The black line presents the result obtained from eqn (6), which uses the Fröhlich–Kennelly relation in eqn (1) to model the particle magnetization. The strength of the field is attributed to the magnetization properties of the CMI-C core metal, shown in the inset with data provided by the manufacturer. The dotted lines bound the range of H values in our experiment, where H = nI and n ≈ 4200 m−1 is the wire turn density of the coil. As a result of the field strengths on the order ∼1 T, the magnetization of probe particles is calculated from eqn (1) to be 28.6–29.1 kA m−1, which is very close to saturation. The gray line shows the calculation of the field using the approximation of probe particle saturation M = Msat from eqn (7). The result is about 15–20% lower than the values obtained using the Fröhlich–Kennelly relation, though the trend is the same. | ||
Eqn (7) is shown by the gray line in Fig. 4. Though this expression provides physical insight, Fig. 4 shows that it is not as suitable for quantitative analysis since it underestimates the field by about 15–20% compared to eqn (6). These calculations imply that larger stresses could be achieved by using probe particles with a higher saturation magnetization.
A final important consideration is the variation in the applied stress across the lateral plane of the tip (see Fig. 1b). Roughness and edge effects on the microscopic scale could lead to significant deviations at different values of y, especially when the probes are very close to the tip at small values of x. Because the coefficient of variation for the probe size is less than 5% (manufacturer information), and it has been claimed that deviations in magnetic properties are largely due to size polydispersity,46 these irregularities in tip geometry are expected to be the primary source of variations in the applied stress. To explore this effect, probe particles are binned according to their position along the y-axis, as shown in the inset in Fig. 5a. For each bin j, an average trajectory is obtained by applying a least-squares fit to a polynomial as described above, allowing calculation of an average velocity function Uj(x) and a shear stress-distance calibration curve,  . At least 5 individual trajectories are averaged per bin. The calibration curves for I = 2.00 A are shown in Fig. 5a, and we find that the variation across the lateral plane of the tip becomes increasingly significant at closer distances. This is also seen in Fig. 5b, where the applied stress is plotted as a function of y at various values of x. Beyond a distance of x ≈ 40 μm, the applied shear stress is essentially constant across the tip. In particular, the coefficient of variation at x = 20 μm is about 10%, and so we limit our quantitative experiments to distances beyond this value. This calibration indicates that improvements on this technique could be achieved by decreasing the variation across the tip through more precise micro-machining. This would increase the upper bound of practically accessible stresses while maintaining the experimental error within reasonable limits.
. At least 5 individual trajectories are averaged per bin. The calibration curves for I = 2.00 A are shown in Fig. 5a, and we find that the variation across the lateral plane of the tip becomes increasingly significant at closer distances. This is also seen in Fig. 5b, where the applied stress is plotted as a function of y at various values of x. Beyond a distance of x ≈ 40 μm, the applied shear stress is essentially constant across the tip. In particular, the coefficient of variation at x = 20 μm is about 10%, and so we limit our quantitative experiments to distances beyond this value. This calibration indicates that improvements on this technique could be achieved by decreasing the variation across the tip through more precise micro-machining. This would increase the upper bound of practically accessible stresses while maintaining the experimental error within reasonable limits.
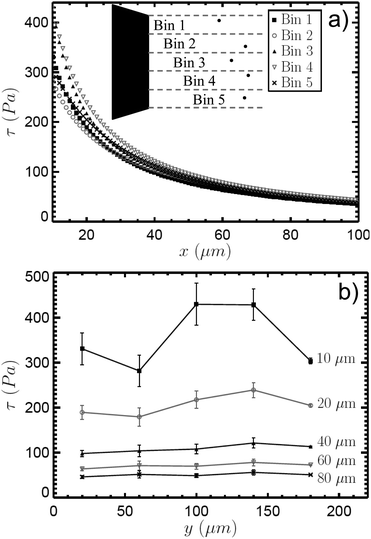 | ||
| Fig. 5 Lateral variation in the applied stress across the surface of the tweezer device. (a) Stress calibration data is plotted at I = 2.00 A with particle trajectories partitioned into five bins according to their positions along the y-axis, as shown in the inset. Though the applied stress becomes approximately uniform far from the tip, local variations in the tip geometry lead to deviations in the stress as the tip is approached. This is clarified in (b), where the applied stress is re-plotted as a function of y at five distances from the tip. Error bars represent the standard error between individual trajectories. In order to neglect non-uniformities in the stress across the surface, we limit our analysis to distances beyond x = 20 μm, where the coefficient of variation is less than 10%. | ||
3.2 Nonlinear microrheology of an aging colloidal clay
Having discussed the instrument calibration and associated considerations, we now apply this magnetic tweezer device to the examination of the nonlinear microrheology of an aging, thixotropic, microstructured yield stress material: a colloidal clay composed of an aqueous dispersion of Laponite®. The nonlinear rheology of aqueous Laponite® dispersions has been studied at the bulk scale,30,31 but has never been examined at scales below ∼ 1 mm.35 In addition to shear-thinning behaviour, we present the first magnetic tweezer measurements of yield stresses at the microscopic scale. Since microstructural length scales are expected to be on the order of the probe size,47 it is unclear a priori whether micro-scale yield stress results will match those obtained from bulk rheology.5,48
Fig. 6a shows five typical probe trajectories in a 2.0 wt% Laponite® dispersion at an age time of tw = 2 h. The current is I = 2.00 A. The trajectories are generally consistent with the expectations described above, with a few additional features that merit explanation. We first note that the bottom three trajectories do reach the tip surface (x = 0); however, some data is lost because for x ≤ 22 μm, the particles move too fast to be tracked at 30 frames s−1. Therefore, some probe particles reach the tip surface during the experiment and others, which generally begin farther away, do not. The most prominent feature of the “mobile” trajectories is their rapid acceleration toward the tip upon reaching a critical separation (or stress), which in this case is about x = 32 μm (corresponding to a stress of about  = 135 Pa). This observation is in agreement with our expectations as described above, and is in contrast to the smooth trajectories observed in the Newtonian calibration fluid. Prior to this rapid acceleration there is a region in which d2x/dt2 > 0, indicating a slight slowing of the probe velocity. Though this behaviour is not explored in detail in this communication, our present contention is that it is a result of effective “jamming” of the dispersion microstructure, while d2x/dt2 < 0 indicates a Newtonian or shear-thinning response. The “immobile” trajectories, while never reaching the tip surface, do exhibit measurable displacement. This slow creep and eventual plateau toward the end of the experiment indicates an elastic response and may also be a result of microstructural jamming. Whether or not creeping probes eventually break the yield stress and accelerate rapidly toward the tip depends on the balance between the stress on the particle, which slowly increases as the particle creeps, and the rheological aging process, which results in a continual increase in the static yield stress and the effective viscosity of the unyielded state.42,51 Spatial heterogeneity in the dispersion rheological properties may also play a role.34 Since the material properties of the dispersion evolve with age time, it is expected that changes will be observed in the probe trajectories as the material undergoes aging. This is demonstrated in Fig. 6b, where typical trajectories of mobile particles are shown for a 1.5 wt% Laponite® dispersion at four different age times and a current of I = 2.00 A. As the material ages and the microstructure develops, the static yield stress is expected to increase. As a result, we observe that the separation distance at which probes accelerate rapidly towards the surface decreases with age. Or equivalently, the critical stress of rapid acceleration increases with age, here going from about 30 Pa at tw = 30 min to about 60 Pa at tw = 1.5 h.
= 135 Pa). This observation is in agreement with our expectations as described above, and is in contrast to the smooth trajectories observed in the Newtonian calibration fluid. Prior to this rapid acceleration there is a region in which d2x/dt2 > 0, indicating a slight slowing of the probe velocity. Though this behaviour is not explored in detail in this communication, our present contention is that it is a result of effective “jamming” of the dispersion microstructure, while d2x/dt2 < 0 indicates a Newtonian or shear-thinning response. The “immobile” trajectories, while never reaching the tip surface, do exhibit measurable displacement. This slow creep and eventual plateau toward the end of the experiment indicates an elastic response and may also be a result of microstructural jamming. Whether or not creeping probes eventually break the yield stress and accelerate rapidly toward the tip depends on the balance between the stress on the particle, which slowly increases as the particle creeps, and the rheological aging process, which results in a continual increase in the static yield stress and the effective viscosity of the unyielded state.42,51 Spatial heterogeneity in the dispersion rheological properties may also play a role.34 Since the material properties of the dispersion evolve with age time, it is expected that changes will be observed in the probe trajectories as the material undergoes aging. This is demonstrated in Fig. 6b, where typical trajectories of mobile particles are shown for a 1.5 wt% Laponite® dispersion at four different age times and a current of I = 2.00 A. As the material ages and the microstructure develops, the static yield stress is expected to increase. As a result, we observe that the separation distance at which probes accelerate rapidly towards the surface decreases with age. Or equivalently, the critical stress of rapid acceleration increases with age, here going from about 30 Pa at tw = 30 min to about 60 Pa at tw = 1.5 h.
 | ||
| Fig. 6 Probe trajectories in Laponite® dispersions. (a) Five typical trajectories are shown in 2.0 wt% Laponite® at an age time of tw = 2 h with current I = 2.00 A. Some particles, generally those beginning closer to the tip, accelerate rapidly toward the surface (“mobile” particles), moving too fast to be tracked for small x. Others remain at a finite separation over the course of the experiment (“immobile” particles). The initial slowing of both populations of probes is suggested to be a result of “jamming” of the dispersion microstructure, while the eventual rapid acceleration of mobile particles is a result of strong shear-thinning behaviour upon yielding. (b) Typical trajectories of mobile particles are shown for different age times in 1.5 wt% Laponite®. As the material ages and undergoes structural arrest, the critical separation at which the particles accelerate rapidly towards the surface decreases, indicating that the critical value of the local stress required to induce flow increases with age. | ||
![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) (x) = 3|U(x)|/2a. Combining this with the calibration for the stress
(x) = 3|U(x)|/2a. Combining this with the calibration for the stress 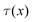 allows calculation of an effective micro-scale viscosity, ηmicro:
allows calculation of an effective micro-scale viscosity, ηmicro: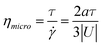 | (8) |
The shear rate dependence of the effective viscosity for a 1.5 wt% dispersion is shown at three different age times in Fig. 7. The applied current is I = 2.00 A. Here magnetic tweezer microrheology results (solid symbols) are compared directly with bulk rheology data (open symbols) obtained from continuous stress ramp tests. At both bulk and microscopic length scales, the effective viscosity exhibits a power law dependence on the shear rate, ηeff(![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) ) ∝
) ∝ ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) p. The material is very strongly shear-thinning, with pmicro ≈ −0.89 and pbulk ≈ −0.95. This result may reflect the open microstructure of the dispersion. At 1.5 wt% (≈ 0.6 vol%), the dispersion is mostly water, so that when the microstructure is disrupted and the material begins to flow, the viscosity is expected to decrease sharply and approach that of water. The power law exponents at both length scales are essentially independent of age time, an observation we attribute to the common microstructural states realized during the aging-rejuvenation process and the (age time)–(shear stress) superposition described by Joshi et al.30 That is, when a dispersion at long age times undergoes shear melting, it passes through many of the same states during rejuvenation as a dispersion at shorter age times.
p. The material is very strongly shear-thinning, with pmicro ≈ −0.89 and pbulk ≈ −0.95. This result may reflect the open microstructure of the dispersion. At 1.5 wt% (≈ 0.6 vol%), the dispersion is mostly water, so that when the microstructure is disrupted and the material begins to flow, the viscosity is expected to decrease sharply and approach that of water. The power law exponents at both length scales are essentially independent of age time, an observation we attribute to the common microstructural states realized during the aging-rejuvenation process and the (age time)–(shear stress) superposition described by Joshi et al.30 That is, when a dispersion at long age times undergoes shear melting, it passes through many of the same states during rejuvenation as a dispersion at shorter age times.
 | ||
Fig. 7 Effective viscosity as a function of shear rate for 1.5 wt% Laponite® at three age times. Results from bulk stress ramp tests (open symbols, with lines added to guide the eye) and microrheology (solid symbols) are shown, with both exhibiting strong shear-thinning behaviour. A current of I = 2.00 A is used for the magnetic tweezer experiments. The effective viscosity follows approximately a power law dependence on shear rate, ηeff∝ m![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) p, and the observed power law exponents are essentially independent of age time, having values of pmicro ≈ −0.89 and pbulk ≈ −0.95. The correspondence between the power law exponents at bulk and microscopic scales suggests commonality in the nature of the shear melting process. The magnitude of the viscosity increases with age time, but is consistently 2 to 6 times smaller on the microscopic scale, in qualitative agreement with previous work comparing the linear viscoelastic moduli of Laponite® dispersions from bulk- and micro-rheology measurements.32,34 p, and the observed power law exponents are essentially independent of age time, having values of pmicro ≈ −0.89 and pbulk ≈ −0.95. The correspondence between the power law exponents at bulk and microscopic scales suggests commonality in the nature of the shear melting process. The magnitude of the viscosity increases with age time, but is consistently 2 to 6 times smaller on the microscopic scale, in qualitative agreement with previous work comparing the linear viscoelastic moduli of Laponite® dispersions from bulk- and micro-rheology measurements.32,34 | ||
The correspondence between the power law exponents for bulk and micro-scale measurements is consistent with calculations that reveal similar shear-thinning behaviour between the micro- and macroviscosity in colloidal dispersions of spherical particles.11 Additionally, it indicates that the nature of the shear melting process in Laponite® dispersions is similar at bulk and microscopic length scales. In both cases, the interactions between Laponite®platelets result in an arrested microstructure that must be disrupted, either locally or globally, for the material to flow. The observation that pmicro ≈ pbulk is in spite of fundamental differences between the character of the two flows. The bulk viscosity measurement is extracted from a viscometric shear flow between parallel plates, whereas the micro-scale viscosity is obtained from flow past a sphere. Despite the similarity between p values across length scales, the magnitude of the effective bulk scale viscosity, ηbulk, is about 2 to 6 times ηmicro for all shear rates and age times. This observation is qualitatively consistent with linear rheological measurements in aqueous Laponite® dispersions, which indicate a weaker gel (lower viscoelastic moduli and longer gelation times) at microscopic length scales.32,34 As in the linear case, the discrepancy is likely due to microstructural features in the dispersion, such as pores or clay particle clusters, that exhibit characteristic sizes similar to the probe size, so that microrheology reflects the mechanical properties of a slightly different structure than bulk measurements.
Before leaving this discussion, it is important to address the unsteady nature of the flows from which the viscosity data in Fig. 7 is extracted. Because the stress is continually increasing in both the bulk and micro-scale experiments, it may be inappropriate to consider the viscosity values as steady-state measurements. For similar Laponite® systems, the stress relaxation time scale, λ, was measured to be on the order of ∼ 100 s,52 which is large compared to the current shearing time scale 1/![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) . In other words, the Deborah number, De, is large for the experiments in Fig. 7: De = λ
. In other words, the Deborah number, De, is large for the experiments in Fig. 7: De = λ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) ≫ 1. For this aging system with continually evolving microstructure and rheological properties, however, it is unclear how to measure bulk steady-state viscosity values in the traditional sense. In particular, if such an experiment could even reach steady-state it would likely take significant time, prohibiting the study of age-time dependence. This was demonstrated by Abou et al.,31 who performed bulk creep tests on Laponite® dispersions of similar concentration and ionic strength as in the present study. They found that reaching steady state requires exceeding a critical shear stress and shearing for times on the order of hours. With this method, they measured steady-state viscosities over the range of shear rates 50 s−1 ≤
≫ 1. For this aging system with continually evolving microstructure and rheological properties, however, it is unclear how to measure bulk steady-state viscosity values in the traditional sense. In particular, if such an experiment could even reach steady-state it would likely take significant time, prohibiting the study of age-time dependence. This was demonstrated by Abou et al.,31 who performed bulk creep tests on Laponite® dispersions of similar concentration and ionic strength as in the present study. They found that reaching steady state requires exceeding a critical shear stress and shearing for times on the order of hours. With this method, they measured steady-state viscosities over the range of shear rates 50 s−1 ≤ ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) ≤ 5000 s−1 and found a shear-thinning power law of p ≈ −0.6, which is clearly not as strongly shear-thinning as the data in Fig. 7. This discrepancy further suggests that effects of the unsteady nature of the flows may be present, and so we qualify our results as “effective” viscosities. However, because of the continuous ramping of the shear stress in both cases, the bulk and micro-scale measurements reported in Fig. 7 are still considered to be analogous to each other.
≤ 5000 s−1 and found a shear-thinning power law of p ≈ −0.6, which is clearly not as strongly shear-thinning as the data in Fig. 7. This discrepancy further suggests that effects of the unsteady nature of the flows may be present, and so we qualify our results as “effective” viscosities. However, because of the continuous ramping of the shear stress in both cases, the bulk and micro-scale measurements reported in Fig. 7 are still considered to be analogous to each other.
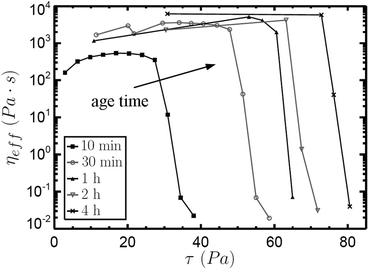 | ||
| Fig. 8 Effective viscosity as a function of applied shear stress from bulk continuous stress ramp tests on 2 wt% Laponite®. Results are shown at five different age times. At a critical stress, the viscosity exhibits a sharp drop over several orders of magnitude, a phenomenon associated with a yield stress on the bulk scale. This critical stress increases with the age time. We note that because the stress in each test is ramped continuously over 2 min, the reported viscosity values do not correspond directly to steady-state measurements. | ||
Magnetic tweezer measurements of the yield stress at the microscopic scale are based upon the distinction between “mobile” and “immobile” probe particles as described in Section 3.2.1. Mobile particles break the yield stress and cause shear-thinning of the surrounding fluid, eventually reaching the tip. Immobile particles exhibit a slow creep, but their trajectories plateau and they remain separated from the tip. The x value that separates the shear-thinning region from the creep region can be considered a yield surface. More specifically, the yield stress,  , is bounded by the minimum stress on mobile particles and the maximum stress on immobile particles. That is, if xmobile is the farthest distance from the tip for mobile particles and ximmobile is the shortest distance from the tip for immobile particles, then
, is bounded by the minimum stress on mobile particles and the maximum stress on immobile particles. That is, if xmobile is the farthest distance from the tip for mobile particles and ximmobile is the shortest distance from the tip for immobile particles, then  and
and  are bounds on
are bounds on  and we take
and we take  as the average of
as the average of  and
and  . One would expect that xmobile < ximmobile, so that based on the calibration in Fig. 2,
. One would expect that xmobile < ximmobile, so that based on the calibration in Fig. 2,  >
>  . However, we typically observe xmobile > ximmobile as a result of the creeping of immobile particles over the course of a measurement. This is demonstrated in Fig. 6a, in which one of the immobile particles eventually creeps past the initial position of a mobile particle, and yet remains far from the tip. This observation is likely a result of a small amount of aging during a single measurement, as well as spatial heterogeneity in the dispersion rheological properties. Another consequence of the creep behaviour is that the experimental time (i.e., the time over which the current is applied) must be kept constant; otherwise immobile particles may creep varying distances for different experiments, resulting in inconsistent calculations of
. However, we typically observe xmobile > ximmobile as a result of the creeping of immobile particles over the course of a measurement. This is demonstrated in Fig. 6a, in which one of the immobile particles eventually creeps past the initial position of a mobile particle, and yet remains far from the tip. This observation is likely a result of a small amount of aging during a single measurement, as well as spatial heterogeneity in the dispersion rheological properties. Another consequence of the creep behaviour is that the experimental time (i.e., the time over which the current is applied) must be kept constant; otherwise immobile particles may creep varying distances for different experiments, resulting in inconsistent calculations of  . We maintain the experimental time at 1 min.
. We maintain the experimental time at 1 min.
Yield stress measurements as a function of age time are plotted in Fig. 9 for three Laponite® concentrations. Bulk rheology data (gray open symbols) and magnetic tweezer measurements (black solid symbols) are directly compared. The reproducibility of the data is demonstrated by the error bars, which represent the standard error of measurements on three different samples at each age time. In agreement with previous work on the rheology of Laponite® dispersions,29,35 as well as other microstructured aging materials,54,55 the yield stress grows approximately logarithmically with age time according to the function
 | (9) |
 | ||
| Fig. 9 Comparison of yield stress measurements at bulk and microscopic scales. The age-time dependence of the observed yield stress is shown for Laponite® concentrations of (a) 1.5 wt%, (b) 2.0 wt%, and (c) 2.5 wt%. Error bars represent the standard error of measurements on three different samples at each age time. For all concentrations, the yield stress measured at both length scales grows approximately logarithmically with age time according to eqn (9), although this is a somewhat poor approximation for the micro-scale data at 1.5 wt% (R2 = 0.72 for 1.5 wt% micro-scale data). Fits to this functional form are shown by lines in black (micro) and gray (bulk). While there is good agreement between the bulk and raw microrheology data for the lowest concentration up to tw = 200 min, the raw micro-scale data provides higher values for the yield stress compared to measurements from bulk shear for 2.0 and 2.5 wt% Laponite®. However, by treating the pre-yielded material as a linear elastic solid and approximating the shear contribution to the applied stress for the microrheology experiments, quantitative agreement with the bulk yield stress measured in shear can be recovered for concentrations c ≥ 2.0 wt%. This approximate shear component of the micro-scale applied stress is π/4 times (78.5%) the measured average stress based on the total force and the probe surface area in the magnetic tweezer experiment and is given by the dashed black line. The characteristic time scales tm, which are related to microstructural development and are extracted by fitting the bulk and micro-scale data to eqn (9), decrease exponentially with Laponite® concentration, as shown in (d). | ||
While quantitative agreement between bulk and micro-scale yield stress data is observed for the lowest Laponite® concentration of 1.5 wt% up to tw = 200 min, the micro-scale data systematically provides higher values for the yield stress compared to measurements from bulk shear for higher concentrations. To interpret these results, it is important to consider the differences between the flow kinematics for the bulk and micro-scale experiments.57 Only shear stresses are applied in the bulk plate-plate experiment, while the fluid experiences both shear and normal stresses at the surface of magnetic probe particles. Since yield stress materials generally exhibit resistance to both shear and normal stresses, it is reasonable that an elevated yield stress might be observed from magnetic tweezer measurements. A more appropriate comparison of the data can be achieved by considering only the shear component of the stress. Without knowledge of the flow kinematics, however, an exact expression for the shear stress in the micro-scale experiment is unavailable. As an approximation, we treat the pre-yielded fluid as a linear elastic medium. In this case, the Rayleigh analogy between viscous flow and the linear elastostatics of isotropic, incompressible solids dictates that the stress distribution around the probe sphere is the same as that for Newtonian creeping flow past a sphere,58,59 for which the shear stress distribution is
 | (10) |
 , which is π/4 times (78.5%) the average stress based on the total force (Stokes drag, |F| = 6πηa|U|) divided by the sphere surface area,
, which is π/4 times (78.5%) the average stress based on the total force (Stokes drag, |F| = 6πηa|U|) divided by the sphere surface area, 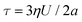 . Using this result from linear elastic kinematics to approximate the contribution of shear stresses, we therefore shift the logarithmic fits to the micro-scale data down by a factor of π/4. These shifted results, shown as black dashed lines in Fig. 9, exhibit closer agreement with bulk shear yield stress data and a β value of βshear = 18.2 Pa. However, the correspondence between bulk and micro-scale data at 1.5 wt% Laponite® breaks down when considering only the shear contribution to the stress; the apparent agreement of the black dotted line with the bulk measurements is an artefact of the questionable fit of the magnetic tweezer data to eqn (9) at this concentration.
. Using this result from linear elastic kinematics to approximate the contribution of shear stresses, we therefore shift the logarithmic fits to the micro-scale data down by a factor of π/4. These shifted results, shown as black dashed lines in Fig. 9, exhibit closer agreement with bulk shear yield stress data and a β value of βshear = 18.2 Pa. However, the correspondence between bulk and micro-scale data at 1.5 wt% Laponite® breaks down when considering only the shear contribution to the stress; the apparent agreement of the black dotted line with the bulk measurements is an artefact of the questionable fit of the magnetic tweezer data to eqn (9) at this concentration.
We note briefly that the problem of a sphere moving through the simplest model yield stress fluid, a Bingham plastic, was previously considered by Beris et al. using finite element analysis.61 In this work, an expression is proposed that relates the yield stress to the critical applied force, F, necessary to induce flow:  . Applying this expression to our magnetic tweezer data results in micro-scale yield stresses that are about 40–50% of bulk measurements. This discrepancy is not necessarily surprising, however, since the Laponite® dispersion does not strictly obey the Bingham model, but exhibits both pre-yield elastic deformation and post-yield shear-thinning and ‘rejuvenation’ (see Fig. 6 and 7).
. Applying this expression to our magnetic tweezer data results in micro-scale yield stresses that are about 40–50% of bulk measurements. This discrepancy is not necessarily surprising, however, since the Laponite® dispersion does not strictly obey the Bingham model, but exhibits both pre-yield elastic deformation and post-yield shear-thinning and ‘rejuvenation’ (see Fig. 6 and 7).
The correspondence, or lack thereof at low concentrations, between bulk and micro-scale rheology is related to the characteristic size of microstructural features in the dispersions, such as pores and other microstructural heterogeneities, as compared to the length scale that is probed. For dispersions of similar concentration and ionic strength, Pignon et al. studied the physical structure of Laponite® dispersions by combining small-angle X-ray and neutron scattering with static light scattering.47,62 With this method, they obtained the scattering curve over five orders of magnitude in length scale. Their results indicate that the microstructure consists of a fractal network of loosely-connected clusters having a characteristic size of about 5 μm. At larger length scales, the dispersion appears homogeneous. We therefore expect that probing at length scales significantly larger than 5 μm would result in data that match bulk measurements. Results for smaller probes will primarily reflect the rheological properties on the length scale of the probe size. Since the largest microstructural length scale is on the same order of magnitude as the probe size in the present work, we do not necessarily anticipate that bulk rheology and microrheology results will match, though we might expect them to be close. It is reasonable to expect that the characteristic pore size will shrink as the dispersion concentration is increased. Such a trend in the size of microstructural features may account for the fact that better agreement is observed between the bulk and the appropriately shear-corrected magnetic tweezer measurements for the more concentrated dispersions of 2.0 wt% and 2.5 wt%. Multiple particle tracking linear microrheology experiments in aqueous Laponite® dispersions have also suggested that the characteristic pore size decreases with age time, based on the delay in the apparent gelation time observed with decreasing probe particle size.34 This could provide an explanation for the eventual increase in the micro-scale yield stress for the 1.5 wt% dispersion at the longest age time, at which point the shear contribution to the stress corresponds reasonably well with the bulk measurement.
4 Conclusions
Nonlinear rheology is critical to the processing and end-use of many industrially relevant materials, as well as in numerous settings in nature and biology. In many of these situations, micro-scale dynamics play a key role; however, methods for quantitatively probing nonlinear microrheology are only recently being developed. In the present work, we have discussed a simple magnetic tweezer technique for studying the nonlinear microrheology of complex fluids. The instrument can apply magnetic fields on the order of ∼ 1 T, leading to stresses up to about 230 Pa on 4.5 μm superparamagnetic probe particles. Shear rates up to about 10 s−1 and viscosities up to about 105 Pa s can be measured. The experimental error is controlled by limiting measurements to probe separations beyond 20 μm, where the variability in the magnetic force across the tip of the tweezer device is less than 10%. Improvements to the technique and the experimental setup could be achieved through more precise machining and the use of a high-speed camera.The technique has been demonstrated on an industrially and scientifically relevant aging and thixotropic yield stress fluid: an aqueous dispersion of the synthetic clay Laponite®. “Mobile” and “immobile” probe trajectories were observed, reflecting a distinction between probes that overcome the yield stress of the material and those that experience insufficient stress to cause flow. By analyzing “mobile” probe trajectories, the effective micro-scale viscosity was determined as a function of the shear rate. The Laponite® dispersion was found to exhibit strong shear-thinning behaviour, a feature extracted from the rapid acceleration of probes towards the tip and associated with microstructural disruption and shear melting. The shear-thinning behaviour was corroborated by bulk measurements, which exhibited similar power law results despite differences in viscosity values by a factor of about 2 to 6. Furthermore, the distinction between “mobile” and “immobile” probe trajectories has provided a basis for the first use of magnetic tweezers to directly and quantitatively measure yield stresses at the microscopic scale. When the approximate shear contribution to microrheology results is isolated, bulk and micro-scale yield stress measurements were found to agree quantitatively for Laponite® concentrations of 2.0 wt% or higher, with both exhibiting an approximately logarithmic growth with age time. The age-time dependence of the yield stress has revealed a time scale associated with microstructural development, which we have found to decrease with Laponite® concentration.
It is expected that nonlinear bulk and micro-scale rheology results will agree if probe particles are large compared to the characteristic length scale of microstructural features in the dispersion.5 An interesting problem for future work would be to determine the probe size at which the bulk-micro agreement observed in Fig. 9b and 9c breaks down. This would provide insight into the microstructural length scales in those dispersions. Further, does agreement break down at all age times, or might the measurements coincide at long enough age times? Our current contention is that measurements with smaller probes in 2.0 or 2.5 wt% Laponite® would likely follow similar behaviour as the data in Fig. 9a, and that a concentration–(probe-size) superposition would exist, as in the linear rheology case.34
The methods and tools presented here will aid in the micro-scale characterization of complex fluids and soft materials, providing new insight into the microstructure and mechanical response of such materials as polymer gels, colloidal glasses, and biological tissues. Additionally, this work will enable a more complete rheological characterization of materials that are difficult to obtain in large quantities, like certain biofluids. Finally, the results of this article will further the understanding of aqueous Laponite® dispersions, which have become important model thixotropic materials in industry and in academic studies.
The authors would like to express thanks to the reviewers of this paper; their insightful comments ultimately led to significant improvements. Acknowledgement is also made to the Donors of the American Chemical Society Petroleum Research Fund (grant ACS-PRF #49956-ND9) for support of this research.
References
- P. Cicuta and A. M. Donald, Soft Matter, 2007, 3, 1449 RSC.
- M. L. Gardel, M. T. Valentine and D. A. Weitz, in Microscale Diagnostic Techniques, ed. K. S. Breuer, Springer Verlag, New York, 2005, pp. 1 Search PubMed.
- D. Wirtz, Annu. Rev. Biophys., 2009, 38, 301 CrossRef CAS.
- T. A. Waigh, Rep. Prog. Phys., 2005, 68, 685 CrossRef.
- J. Liu, M. L. Gardel, K. Kroy, E. Frey, B. D. Hoffman, J. C. Crocker, A. R. Bausch and D. A. Weitz, Phys. Rev. Lett., 2006, 96, 118104 CrossRef CAS.
- L. G. Wilson and W. C. K. Poon, Phys. Chem. Chem. Phys., 2011, 13, 10617 RSC.
- P. Habdas, D. Schaar, A. C. Levitt and E. R. Weeks, Europhys. Lett., 2004, 67, 477 CrossRef CAS.
- M. Parthasarathy and D. J. Klingenberg, Mater. Sci. Eng., R, 1996, 17, 57 CrossRef.
- R. G. Larson, The Structure and Rheology of Complex Fluids, Oxford University Press, New York, 1999 Search PubMed.
- P. J. Rankin, A. T. Horvath and D. J. Klingenberg, Rheol. Acta, 1999, 38, 471 CrossRef CAS.
- T. M. Squires and J. F. Brady, Phys. Fluids, 2005, 17, 21 CrossRef.
- A. Meyer, A. Marshall, B. G. Bush and E. M. Furst, J. Rheol., 2006, 50, 77 CrossRef CAS.
- I. C. Carpen and J. F. Brady, J. Rheol., 2005, 49, 1483 CrossRef CAS.
- I. Sriram, A. Meyer and E. M. Furst, Phys. Fluids, 2010, 22, 10 CrossRef.
- A. S. Khair and T. M. Squires, Phys. Rev. Lett., 2010, 105, 4 CrossRef.
- J. N. Wilking and T. G. Mason, Phys. Rev. E, 2008, 77, 055101 CrossRef.
- W. Seifriz, Br. J. Exp. Biol., 1924, 2, 1 Search PubMed.
- M. Gordon, S. C. Hunter, J. A. Love and T. C. Ward, Nature, 1968, 217, 735 CrossRef.
- C. Haber and D. Wirtz, Rev. Sci. Instrum., 2000, 71, 4561 CrossRef CAS.
- J. Lammerding, A. R. Kazarov, H. Huang, R. T. Lee and M. E. Hemler, Proc. Natl. Acad. Sci. U. S. A., 2003, 100, 7616 CrossRef CAS.
- J. Lammerding, PhD Thesis, Dept of Biological Engineering, Massachusetts Institute of Technology, 2004 Search PubMed.
- H. A. Barnes, J. Non-Newtonian Fluid Mech., 1997, 70, 1 CrossRef CAS.
- Rockwood Additives: Southern Clay Products, Laponite product information, (http://www.scprod.com/pdfs/Laponite%20brochure%20EN.pdf).
- A. Mourchid, A. Delville, J. Lambard, E. LeColier and P. Levitz, Langmuir, 1995, 11, 1942 CrossRef CAS.
- B. Ruzicka, L. Zulian and G. Ruocco, Phys. Rev. Lett., 2004, 93, 258301 CrossRef CAS.
- B. Ruzicka, L. Zulian and G. Ruocco, Langmuir, 2006, 22, 1106 CrossRef CAS.
- S. Jabbari-Farouji, H. Tanaka, G. H. Wegdam and D. Bonn, Phys. Rev. E, 2008, 78, 061405 CrossRef CAS.
- S. Cocard, J. F. Tassin and T. Nicolai, J. Rheol., 2000, 44, 585 CrossRef CAS.
- A. S. Negi and C. O. Osuji, Phys. Rev. E, 2010, 82, 031404 CrossRef.
- Y. M. Joshi and G. R. K. Reddy, Phys. Rev. E, 2008, 77, 021501 CrossRef.
- B. Abou, D. Bonn and J. Meunier, J. Rheol., 2003, 47, 979 CrossRef CAS.
- F. K. Oppong, P. Coussot and J. R. de Bruyn, Phys. Rev. E, 2008, 78, 10 CrossRef.
- B. Ruzicka and E. Zaccarelli, Soft Matter, 2011, 7, 1268 RSC.
- J. P. Rich, G. H. McKinley and P. S. Doyle, J. Rheol., 2011, 55, 273 CrossRef CAS.
- C. Wilhelm, F. Elias, J. Browaeys, A. Ponton and J.-C. Bacri, Phys. Rev. E, 2002, 66, 021502 CrossRef CAS.
- A. R. Bausch, F. Ziemann, A. A. Boulbitch, K. Jacobson and E. Sackmann, Biophys. J., 1998, 75, 2038 CrossRef CAS.
- P. Kollmannsberger and B. Fabry, Rev. Sci. Instrum., 2007, 78, 6 CrossRef.
- D. Bonn, H. Kellay, H. Tanaka, G. Wegdam and J. Meunier, Langmuir, 1999, 15, 7534 CrossRef CAS.
- B. Abou, D. Bonn and J. Meunier, Phys. Rev. E, 2001, 64, 021510 CrossRef CAS.
- L. Petit, C. Barentin, J. Colombani, C. Ybert and L. Bocquet, Langmuir, 2009, 25, 12048 CrossRef CAS.
- J. C. Crocker and D. G. Grier, J. Colloid Interface Sci., 1996, 179, 298 CrossRef CAS.
- D. Bonn, P. Coussot, H. T. Huynh, F. Bertrand and G. Debrégeas, Europhys. Lett., 2002, 59, 786 CrossRef CAS.
- Q. D. Nguyen and D. V. Boger, Annu. Rev. Fluid Mech., 1992, 24, 47 CrossRef.
- T. Savin and P. S. Doyle, Biophys. J., 2005, 88, 623 CrossRef CAS.
- R. M. Bozorth, Ferromagnetism, Wiley - IEEE Press, 1993 Search PubMed.
- F. Ebert, P. Dillmann, G. Maret and P. Keim, Rev. Sci. Instrum., 2009, 80, 083902 CrossRef CAS.
- F. Pignon, A. Magnin, J. M. Piau, B. Cabane, P. Lindner and O. Diat, Phys. Rev. E, 1997, 56, 3281 CrossRef CAS.
- M. T. Valentine, P. D. Kaplan, D. Thota, J. C. Crocker, T. Gisler, R. K. Prud'homme, M. Beck and D. A. Weitz, Phys. Rev. E, 2001, 64, 061506 CrossRef CAS.
- R. Ewoldt, C. Clasen, A. E. Hosoi and G. H. McKinley, Soft Matter, 2007, 3, 634 RSC.
- P. Coussot, Q. D. Nguyen, H. T. Huynh and D. Bonn, Phys. Rev. Lett., 2002, 88, 175501 CrossRef.
- P. Coussot, Q. D. Nguyen, H. T. Huynh and D. Bonn, J. Rheol., 2002, 46, 573 CrossRef CAS.
- R. Bandyopadhyay, P. H. Mohan and Y. M. Joshi, Soft Matter, 2010, 6, 1462 RSC.
- P. C. F. Møller, A. Fall and D. Bonn, Europhys. Lett., 2009, 87, 6 Search PubMed.
- T. S. Chow, Polymer, 1993, 34, 541 CrossRef CAS.
- K. Chen and K. S. Schweizer, Phys. Rev. E, 2008, 78, 031802 CrossRef.
- R. G. D. Steel and J. H. Torrie, Principles and Procedures of Statistics, 2 edn, McGraw-Hill, New York, 1980 Search PubMed.
- T. M. Squires, Langmuir, 2007, 24, 1147 CrossRef.
- J. W. S. Rayleigh, The Theory of Sound, 2 edn, Dover, 1945 Search PubMed.
- W. B. Russel and P. R. Sperry, Prog. Org. Coat., 1994, 23, 305 CrossRef CAS.
- W. M. Deen, Analysis of Transport Phenomena, Oxford University Press, New York, 1998 Search PubMed.
- A. N. Beris, J. A. Tsamopoulos, R. C. Armstrong and R. A. Brown, J. Fluid Mech., 1985, 158, 219 CrossRef CAS.
- F. Pignon, J.-M. Piau and A. Magnin, Phys. Rev. Lett., 1996, 76, 4857 CrossRef CAS.
Footnote |
| † http://www.physics.emory.edu/%7Eweeks/idl/, “Particle Tracking Using IDL”, site maintained by Eric Weeks |
| This journal is © The Royal Society of Chemistry 2011 |
