Open Access Article
Open Access ArticleState-of-the-art local correlation methods enable affordable gold standard quantum chemistry for up to hundreds of atoms†
Péter R.
Nagy
 *abc
*abc
aDepartment of Physical Chemistry and Materials Science, Faculty of Chemical Technology and Biotechnology, Budapest University of Technology and Economics, Műegyetem rkp. 3., H-1111 Budapest, Hungary
bHUN-REN-BME Quantum Chemistry Research Group, Műegyetem rkp. 3., H-1111 Budapest, Hungary
cMTA-BME Lendület Quantum Chemistry Research Group, Műegyetem rkp. 3., H-1111 Budapest, Hungary. E-mail: nagy.peter@vbk.bme.hu
First published on 28th August 2024
Abstract
In this feature, we review the current capabilities of local electron correlation methods up to the coupled cluster model with single, double, and perturbative triple excitations [CCSD(T)], which is a gold standard in quantum chemistry. The main computational aspects of the local method types are assessed from the perspective of applications, but the focus is kept on how to achieve chemical accuracy (i.e., <1 kcal mol−1 uncertainty), as well as on the broad scope of chemical problems made accessible. The performance of state-of-the-art methods is also compared, including the most employed DLPNO and, in particular, our local natural orbital (LNO) CCSD(T) approach. The high accuracy and efficiency of the LNO method makes chemically accurate CCSD(T) computations accessible for molecules of hundreds of atoms with resources affordable to a broad computational community (days on a single CPU and 10–100 GB of memory). Recent developments in LNO-CCSD(T) enable systematic convergence and robust error estimates even for systems of complicated electronic structure or larger size (up to 1000 atoms). The predictive power of current local CCSD(T) methods, usually at about 1–2 order of magnitude higher cost than hybrid density functional theory (DFT), has become outstanding on the palette of computational chemistry applicable for molecules of practical interest. We also review more than 50 LNO-based and other advanced local-CCSD(T) applications for realistic, large systems across molecular interactions as well as main group, transition metal, bio-, and surface chemistry. The examples show that properly executed local-CCSD(T) can contribute to binding, reaction equilibrium, rate constants, etc. which are able to match measurements within the error estimates. These applications demonstrate that modern, open-access, and broadly affordable local methods, such as LNO-CCSD(T), already enable predictive computations and atomistic insight for complicated, real-life molecular processes in realistic environments.
1 Introduction
Systematically improvable wave function approaches, especially the coupled cluster (CC) methods,1,2 are among the most reliable and accurate quantum modeling tools, which has been repeatedly corroborated at least for smaller molecules.3–10 Aside from strong correlation situations, the CC model with single and double excitations (CCSD) augmented with perturbative triples correction [CCSD(T)]11 is considered one of the “gold standard” methods of quantum chemistry, often providing chemical accuracy (ca. 1 kcal mol−1 uncertainty). The major drawbacks of CCSD(T) are its steep, seventh- and fourth-power-scaling operation and data requirements, which limit the applicability of even its advanced, parallel implementations.12–22 The largest conventional CCSD(T) computations with a reliable basis set convergence can reach 20–30 atoms,22 and this limit can be roughly doubled by using natural orbital (NO) based cost-reduction approaches.23–25At this size range, one can also exploit the relatively short-range nature or locality of dynamical electron correlation, leading to the local correlation approaches. Their extensive development, especially in combination with various NO-based basis compression ideas yielded a substantial improvement for local methods up to the CCSD(T) level.26–29 The combination of orbital pair specific NOs (PNOs) with recent local correlation methods was pioneered by Neese and co-workers in the domain-based local pair natural orbital (DLPNO) family of approaches26,30–35 and was also adopted by other groups.27,28,36–41 Alternatively, the local NO (LNO) methods construct NOs specifically for each localized orbital; this LNO idea was initially proposed by Kállay and co-workers,42,43 and has also been extensively developed by the author and his co-workers since 2015.29,44–49
Here, we review the recent advances and capabilities of these state-of-the-art local correlation methods focusing on their utility and potential from the perspective of applications. As second-order Møller–Plesset (MP2) perturbation theory is part of the local CC computations, the possibilities for MP2 (and hence double-hybrid DFT methods) will be implicitly covered, but the main topic is local correlation methods available up to the CCSD(T) level. Reviews of related local correlation methods, most recently from around 2017–2019,27,50–57 traditionally focus on a single family of local methods often from the theoretical and algorithmic point of view, while the broader comparison of multiple approaches from the perspective of applications remains scarce.51 Thus, we also summarize the current state of local correlation methods in general to put the developments and applications related to our LNO local correlation methods29,44–49 into the broader perspective. Therefore, besides the capabilities of the LNO methods in the MRCC suite of quantum chemistry programs,58,59 existing comparisons with other advanced methods and codes are also overviewed. Selecting the DLPNO method (as implemented in the ORCA package60) as the primary reference point appears to be the most broadly relevant for multiple reasons. For example, the DLPNO methods are currently the most widely known and used, and the largest number of implementations, features, and performance benchmarks are also available for those.26,31–35,52 However, regarding other aspects defining the state-of-the-art, such as the accuracy of the local approximations and the efficiency of large-scale computations, we demonstrate that LNO-CCSD(T) consistently outperforms DLPNO-CCSD(T).
To better explain the benefits and drawbacks of various local correlation approaches, we start in Section 2 with a general theoretical introduction to the three major groups of local methods. The focus is kept on the main similarities and differences between the popular local approximations at a level sufficient from the perspective of applications up to local CCSD(T) energies. Thus, deeper theoretical and technical details, as well as extensive but somewhat less mature developments toward excited states,49,53,61–68 derivative molecular properties,69–81 multi-reference (MR) methods82–86etc. are beyond the scope of this review. Then, we place the LNO method into this broader context in Sections 2.2 and 2.3, highlighting its advanced or often unique theoretical and algorithmic properties, which enable its outstanding accuracy over cost performance.
The systematic convergence of LNO-CCSD(T) toward the conventional or local approximation free (LAF) and the complete basis set (CBS) limit of CCSD(T) is demonstrated in practice in Sections 3.2 and 3.3. Chemically relevant examples are used, including also relatively straightforward, average, and challenging cases of intermolecular interactions and catalytic reaction steps up to ca. 100 atoms. A key point is that default LNO approximations settings and suitable (triple- to quadruple-ζ) basis sets usually provide good accuracy over cost performance for most practical purposes. Moreover, especially for handling the examples with more complicated electronic structure, additional tools are developed to provide robust CCSD(T)/CBS estimates. For example, the systematic improvability along the basis set and local approximations also enables extrapolation and composite schemes (Section 3.4) to accelerate the convergence toward CCSD(T)/CBS. Furthermore, we developed robust error measures to estimate the remaining local and basis set errors. In a tutorial-style demonstration of these powerful tools (not available, e.g., for non-ab initio methods), we show how to select reliable and efficient settings for large-scale LNO-CCSD(T) applications while prioritizing the retention of the intrinsic accuracy of CCSD(T). It is useful to incorporate such a convergence test or comparisons to benchmark studies for a representative example of an extensive computational project. This enables us to safely determine local correlation and basis settings that can be used in an automated, practically black-box manner for a large set of molecules, reaction steps, conformers, etc.
We also highlight potential pitfalls that are often not properly handled in current local CCSD(T) applications and ways to overcome them. For example, practical experience obtained with DFT or wave function methods on small systems does not necessarily translate into the application of local CCSD(T) applications on larger molecules. In particular, systems with more complicated electronic structure or properties scaling with the system size could require tighter local approximations settings. Additionally, commonly employed double- or triple-ζ-sized basis sets, often suitable for DFT computations, can cause sizable basis set superposition and incompleteness errors.
This practical demonstration is followed by an extensive statistical analysis of the LNO and DLPNO local approximation errors compared to conventional CCSD(T) references for 14 compilations, covering ca. 1000 entries in a wide range of chemical processes (Section 4). These tests show that at least for up to 40–60 atoms, the average LNO errors are mostly well below 0.5 kcal mol−1 and the maximum errors rarely surpass 1 kcal mol−1, and these errors are substantially smaller than those with the DLPNO approach. The timing and data requirement benchmarks of Section 5 demonstrate that well-converged LNO-CCSD(T) and basis set settings are feasible even for up to a few hundred atoms using routinely accessible resources (a few 10s to 100 GB of memory and days of wall time on a single, mid-range CPU). Additionally, robust LNO-based CCSD(T)/CBS estimates can be obtained even for very complicated cases, or uniquely up to 1000 atoms, as demonstrated, e.g., in a few biochemical applications.
The practical utility of such reliable and widely accessible CCSD(T) energies is illustrated in Sections 6 and 7 covering advanced PNO-based CCSD(T) as well as more than 50 LNO-CCSD(T) applications. Real-life systems are gathered, including molecule sizes above 100 atoms or 100s of structures with reliable local correlation and basis set settings. These studies targeted molecular interactions, main group and transition metal reactions, and complex processes including solvent, crystal, or biochemical environments. Finally, we summarize our experience in Section 8, based on the theoretical and algorithmic design, as well as the benchmark and production applications. General trends and corresponding practical advice are discussed to assist future applications, where, e.g., we arrange chemical processes into groups of relatively simple and more challenging from the perspective of local CCSD(T) applications. The main point is that, at least for the average cases, current and open-accessible local CCSD(T) methods provide a relatively simple and widely affordable way for the computational community to achieve gold standard accuracy even for complex molecular processes with realistic environments, catalysts, etc.
2 Introduction to local correlation methods
The main goal of the approximate correlation methods is to accelerate the computation of costly MP, configuration interaction (CI), CC, etc. approaches while retaining their intrinsic accuracy. For example, for 1 kcal mol−1 accuracy commonly labeled as chemical accuracy, around 99.9–99.99% accuracy is needed in the approximated correlation energies. This figure originates from the about 1–10 hartree or up to 6275 kcal mol−1 correlation energy of molecules up to 100 atoms and the assumption that not all atoms play an important role, e.g., in the chemical transformation. Thus, even if some cancellation of errors occurs, a 3–4 significant digit accuracy should be targeted in the correlation energy, highlighting the difficulty of achieving considerable cost reduction.2.1 Main approaches in local correlation methods
Let us start with a theoretical introduction to the current and frequently employed local correlation methods, whose properties are also summarized in Table 1. While the field of local correlation methods is very diverse, most of them take advantage of the relatively fast decay of the electron correlation with a leading, inverse sixth-power dependence on the distance (in non-metallic systems). This is usually exploited by working in a localized molecular orbital (LMO)26–51,57,91–114 [or atomic orbital (AO)115–122] basis and by computing the correlation energy from the contributions of spatially close parts. These parts (indexed with K in eqn (1)) can be fragments of the molecule, atoms or atom groups, orbitals or orbital pairs/groups, etc. This decomposition to parts is possible, since both the exact and most popular correlation methods' correlation energy can be expressed as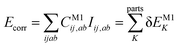 | (1) |
| Type | Fragmentation-based | Coupled (direct) | Uncoupled |
|---|---|---|---|
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||
| Description | Partitioned into (non-bonded) subsystems | Coupled equations for wave function (wfn) parameters | Subsystem wfn equations are uncoupled |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||
| Benefit | Simpler implementation & parallelization, ability to reuse canonical codes | Exact HF; all CI & CC wfn parameters can couple to all others in the entire system | Exact HF; retains naturally uncoupled nature of MP, (T) & (Q) wfn parameters |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||
| Drawback | Large, overlapping fragments lead to redundancy & high cost (above MP2 level) | Unnecessary coupling in MP & (T), redundant virtual orbitals, most complicated of the 3 groups | Approximate decoupling in CI & CC, redundant CI & CC wfn equations |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||
| Available | HF, DFT, MP2–4, CCSD(T)… | MP2-3, up to CCSD(T), MR-PT2 | MP2–3, general order CC, CI, QMC87 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||
| Methods | MBE,54 FMO,55 MIM,88 MTA,56 GEBF89… | DLPNO,33 PNO-L,27 PNO39… | LNO,29 DC,90 DEC,91 CIM,57… |
The efficiency gain comes from approximations, which usually restrict the summations in the above expression:
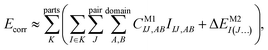 | (2) |
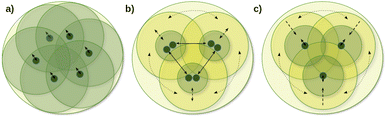
One of the main local correlation method groups employs fragmentation-type approximations (summarized in the first column of Table 1). Here, the entire system is divided into smaller parts, if needed, e.g., via bond cutting and capping, so that the smaller part (fragment) becomes tractable with conventional quantum chemistry methods (Fig. 1a).50,51,123–125 Their significant benefits are the ability to use conventional codes and relatively simple parallelization for the independent fragment computations, which also accelerated the implementation of a large set of features besides energies. While several fragment-based methods are available up to the CCSD(T) level,54,96–101 the fragment sizes in general have to be relatively large to minimize the neglected or approximated inter-fragment interactions. Currently, this makes conventional CC methods for the fragment computations too expensive, at least for large 3D systems connected with primary bond types.
To overcome this bottleneck, local correlation methods can also take advantage of the sparsity of wave functions not only in the 3D space or atomic coordinates but also in their orbital expansion. This is achieved by employing a compressed unoccupied orbital space that is expressed in some sort of natural orbital (NO, indices A, B in eqn (2)).26,27,29,39 All of the above (i.e., pair, domain, NO, etc.) approximations are often compensated for by more cost-efficient, but lower-, M2-level corrections (that is, ΔEM2I(J…) of eqn (2)). Local correlation methods employing such combination of approaches do not fragment the molecule into smaller subsystems (at least not at the HF level). To categorize these methods, let us note that they differ at the solution of the wave function equations. The equations yielding these CM1IJ…,AB… parameters are coupled in the conventional form of the CI and CC methods for the entire molecule, that is, the values of all CI/CC wave function parameters depend on all other CI/CC parameters. Compared to that, for example, conventional MP wave function parameters can be obtained independently from each other (in the canonical MO basis).
The coupled (often also called direct) local correlation methods aim to retain the interaction between the CI/CC parameters (middle column of Table 1 and Fig. 1b). In turn, working in the non-canonical LMO basis couples the conventionally independent equations of perturbative approaches as well [e.g., for MPn (n = 2, 3, …) or the (T) term of CCSD(T)]. Advanced methods in this coupled (or direct) category construct LMO pair specific NOs (PNOs), that is a separate set of NOs for each occupied orbital pair. The use of PNOs was reintroduced in the context of modern local methods via the (D)LPNO approaches, developed extensively by Neese, Valeev, Riplinger, Guo, and co-workers,26,30–35 and then were taken over also by Werner, Ma, and co-workers27,36–38 as well as by Hättig and Tew.28,39 The main advantages of PNOs are their compactness and their decreasing number with the distance of the LMO pairs. The drawback appears to be the redundancy and the large total number of the different PNOs generated separately for all LMO pairs which is explained further in Section S1 of the ESI.† Consequently, memory, disk, and/or network bottlenecks can occur for converged basis sets and large molecules (above ca. 100–200 atoms) despite the relatively low operation count demand of current PNO-based CC implementations.26,27,39
The third group of uncoupled local methods (last column of Table 1) utilizes the fact that the expressions for the wave function parameters of perturbative approaches [such as MPn, or (T) and (Q) of CC methods] are independent, i.e., not coupled. In turn, uncoupled methods introduce approximations to uncouple the interdependent (CI and mostly) CC equations for distant molecular parts (Fig. 1c).§ The wave function parameters are usually determined for one or a group of orbitals at a time, which are coupled to the surrounding but not all distant parts of the molecule. On the one hand, the decoupling approximation helps to eliminate data storage and communication bottlenecks and to have excellent parallel scaling. On the other hand, it introduces a (linear-scaling) redundancy in the M1 equations solved for each decoupled part. Thus, the simple reuse of conventional M1 codes for the uncoupled equations often leads to execution time bottlenecks in this category. However, additional approximations (Section 2.2) can mitigate the drawbacks of overlapping uncoupled parts.
The variety of this third group of methods developed up to the CC level includes the cluster-in-molecule (CIM) method of Li, Li, Piecuch, Guo, and their co-workers,57,102–104 the divide-expand-consolidate (DEC) scheme of Jørgensen et al.,91 and the divide-and-conquer (DC) method of Li and Li105 and Kobayashi and Nakai.106,107 In the related LNO methods of ours,29,42–48 discussed in Sections 2.2 and 2.3, we exploited the beneficial properties of the uncoupled MP2, (T), etc. perturbative equations and extensively developed local, NO, and other approximations as well as algorithmic improvements to mitigate the drawbacks of overlapping computations, e.g., at the CCSD level.
2.2 Local natural orbital (LNO) methods: introduction
The LNO family of methods includes at the M1 level of theory MP2,44,47 random phase approximation (RPA)114 (as well as the corresponding spin-component scaled and double-hybrid DFT methods utilizing local MP2 or RPA), CCSD(T),29,43,45,46,48 and general order CC methods29,42,48 (as implemented in the MRCC quantum chemistry suite58,59). All of their correlation energies can be expressed in terms of the individual correlation energy contributions of LMOs (I, J) as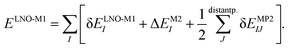 | (3) |
Without approximations, the sum of the first, δELNO-M1I orbital specific correlation energy contributions recovers the exact M1 level correlation energy, e.g., the M1 = CCSD(T) result and the last two correction terms of eqn (3) vanish. However, the contribution of distant LMO pairs can be included much more effectively via approximate MP2 expressions (δEMP2IJ).44,46 The benefit is that the more costly δELNO-M1I and ΔEM2I terms of eqn (3) are only evaluated for an asymptotically linear-scaling list of strong LMO pairs.
Aiming for the target 99.9–99.99% correlation energy accuracy, the LMOs are represented in our LNO method with at least 99.99% accuracy after all LMO truncation steps. Even for well-localized orbitals (e.g., corresponding to C–C or C–H σ-bonds, lone pairs, etc.) LMOs represented with at least 99.99% accuracy entail relatively long tails and encompass a considerable volume, as shown in Fig. 2. Consequently, even localized MOs can have many strongly interacting LMO pairs (up to 50–100 per LMO for 3D molecules), with some strong pair LMOs located surprisingly far from each other.29,44,46,48 Thus, the LNO methods include several additional approaches to accelerate the evaluation of the high-level δELNO-M1I terms for these more strongly correlated orbitals. The unique properties and algorithmic features of the LNO methods, as well as their corresponding practical benefits are summarized in Table 2, discussed in brief as follows and further detailed in Section S2 of the ESI.†
| Approach/algorithm/feature of LNO methods | Corresponding theoretical/computational benefit |
|---|---|
| Theoretical and algorithmic properties for accuracy and efficiency | |
| Molecule (orbital, wave function, operator) dependent local approximations (no fragmentation or bond breaking, no real space cutoff) | All approximations adapt to the wave function complexity enabling a systematically convergable LNO setting hierarchy: loose, normal, tight, very tight… & extrapolation to LAF limit |
| Uncoupled perturbative approaches [MP2, (T)] also in the LMO basis | Redundancy-free & efficient [MP1 and (T)] amplitude computation |
| NOs for occupied & virtual spaces, NAFs, specialized CCSD & (T) codes | Record-sized LNO-CCSD(T) applications at CBS up to 1000 atoms |
| Outstanding memory, disk, and network-economic implementation | Routinely applicable on standard hardware (few 10 GB memory & disk) |
| Energy contributions obtained in a quasi-canonical local NO basis | Enables also LNO-based MP, RPA & general order CC methods |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|
| Functionality and features | |
| Restricted open-shell intermediates & long-range spin polarization approximation | Open-shell LMP2 & LNO-CCSD(T) benefit from closed-shell efficiency |
| Up to 4-level embedding into local correlation, DFT, & MM environments | LNO-CCSD(T)/LMP2/DFT/MM for protein, solvent, crystal environment |
| Independent (uncoupled) energy contribution computations | Frequent checkpointing, restartable jobs, parallelization |
| Treatment of quasi-redundant AO basis sets | Enables the use of large, diffuse AO basis sets needed for CBS |
| Treatment of non-Abelian point group symmetry | Speedup comparable to the point group rank |
The approximations in the LNO method are designed to adapt to the properties of the molecule, i.e., they are determined by the orbitals, complexity of the wave function, the size of the ERIs and pair energies. Thus, techniques representative of fragmentation methods (fragmentation to subsystems, bond cutting, capping, etc.) or any other real space based or systems independent cutoffs are avoided. Pair correlation energy estimates determine the distant and strong LMO pair lists of eqn (3). Then, orbital completeness criteria govern the domain approximations, where the domain specific NOs are selected based on robust NO occupation number criteria. Then, the most expensive M1, e.g., CCSD(T), part is computed in the compressed occupied and virtual LNO bases. Finally, the MP2 level energy correction of eqn (3), that is δEM2I = δEM2I − δELNO-M2I is added to compensate for the truncation of the LNO approximations. Additionally, an accurate local MP2 energy emerges as a byproduct by combining the δEM2I and the pair energy terms (see eqn (1) of Section S2).
2.3 LNO methods: algorithm and features
The LNO-CCSD(T) computation steps are summarized in Fig. S1 of the ESI.† To accelerate the M1, e.g., the CCSD(T) computations in the LNO basis, we extensively utilize density-fitting (DF) approaches, a unique compression approach for the DF basis set yielding natural auxiliary functions (NAFs),23,126 as well as state-of-the-art CCSD22 and (T)45 implementations, which we specifically optimized also for the conditions in LNO computations (as detailed in Section S2 of the ESI†).Moreover, the Laplace-transform127 based MP2 (ref. 44 and 47) and (T)45,48 expressions of the LNO methods enable the redundancy-free (uncoupled) evaluation of the corresponding amplitudes for the domain local MP2 and LNO-(T) energies (i.e., δEMP2I and δELNO-(T)I), respectively. The efficiency gained is particularly important for the rate-determining (T) term. Besides the low operation count of the LNO methods, we reported the lowest memory, disk, and network traffic requirements29,44,46 (see Sections 3.2, 3.3, and 5 for examples). This enables large-scale LMP2 and LNO-CCSD(T) computations relatively affordably on routinely accessible computational hardware containing 10s–100 GB memory and even network file systems (i.e., without a local hard drive). To further improve the applicability of the LNO method from the practical perspective, we introduced additional unique features, which include frequent checkpointing and restartability, treatment of quasi-redundant AO basis sets commonly occurring for large molecules and (diffuse) basis sets, utilization of (non-Abelian) point group symmetry,29,46 and up to 4-layer embedding128,129 (see Section 2.4).
Regarding open-shell systems, the development of efficient methods using unrestricted (U) CC formalisms is even more challenging because of the solution of about 3–4 times as many equations and storage of 3–4 times as many wave function parameters as for the restricted CC counterparts. Therefore, only a handful of open-shell local CCSD(T) methods have been reported,35,38,48,130,131 including our recent restricted open-shell (RO) based LNO-CCSD(T) implementation.48 The open-shell LNO-CCSD(T) code is already equipped with almost all of the features listed in Table 2. Additionally, techniques are implemented to get the demand of open-shell LNO-CCSD(T) closer to that of the closed-shell case (e.g., RO integral-transformation and a unique long-range spin polarization approximation).47,48
2.4 Multi-level and embedding with local methods
When large and complicated systems are studied, especially involving condensed phase, surface, biochemical, etc. environments, it is often not necessary to model all parts equally at the CCSD(T) level. That is, the CCSD(T) treatment can be focused on the most relevant, chemically active part and lower-cost models can be utilized for the environment. The main embedding frameworks can employ classical environments via molecular mechanics (MM) in the well-known QM/MM approach, as well as quantum embedding into DFT environment40,128,129,132,133 or multi-layer local correlation approaches.128,129,134–140 The variety of multi-level and embedding approaches available for local CC methods in the MRCC package58,59 are summarized in Fig. 3.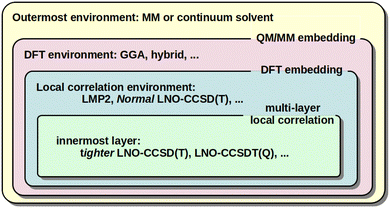 | ||
| Fig. 3 Illustration of the QM/MM, DFT, and multi-layer local correlation embedding variations available in the MRCC58,59 package. | ||
One form of DFT embedding methods, relevant also in the local CC context, includes the Huzinaga-embedding128,129,141 and the numerically similar projection-based embedding40,132,133 methods. Both are formally exact for DFT-in-DFT embedding when using the same functional for both subsystems, and both are applicable for DFT-in-DFT and local CC-in-DFT embedding. The lower-level DFT solution is obtained for the entire system in both methods. Then, the high-level DFT or wave function model is solved only for the chemically active electrons while keeping the embedded orbitals exactly (or up to a high precision) orthogonal to the environment orbitals via the Huzinaga (or projection-based) embedding methods. The implementation and applications were presented for DLPNO-CCSD(T0)-in-DFT within the projection-based scheme by Bensberg and Neugebauer40,135 and for (local) wave function-in-DFT, e.g., with our LMP2, LNO-CCSD(T), LNO-CCSDT(Q), …series of methods using the Huzinaga-embedding128,129 (see Fig. 3).
In comparison, the multi-layer local correlation approaches use local wave function methods for both the embedded and the environment subsystems. The division of the correlation energy into contributions of parts (e.g., orbitals or orbital pairs), as shown in eqn (2), offers a straightforward way to define such multi-level approaches. One can employ a higher-level wave function method for the chemically most relevant orbitals and a more efficient model for the orbitals assigned to the environment.128,129,134–140 Efficient combinations include [local CCSD(T)]-in-[local MP2] or [tighter local CC]-in-[looser local CC], which are available for the DLPNO,134,136 LNO,128,129 and other coupled and uncoupled type local correlation methods.137–140 For very high accuracy, the LNO-CCSDT(Q)-in-LNO-CCSD(T) option can also be of utility.29,128 Both (hybrid) DFT and lower-cost local correlation models have limitations for large systems above the 1000 atom range. Thus, a third, MM layer can be added to, e.g., both the DLPNO142,143 and LNO128,144 methods, yielding [local CC]-in-[DFT or local CC]/MM type 3-layer QM/MM models (see Fig. 3). In this context, the availability of up to 4-layer [LNO-CC]-in-[LNO-CC or LMP2]-in-DFT/MM type models could also be of interest,128,129 but in practice mostly 2 (or 3) layers are sufficient.
3 Systematic convergence with local wave function methods
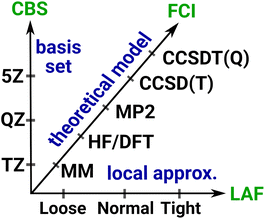
Systematically improvable approaches, when affordable, are highly reliable and successful in getting converged correlation energies and corresponding error estimates. Systematic convergence is enabled by the single particle AO basis set hierarchies (e.g., using X-tuple-ζ basis sets with X = D, T, Q, 5, …) and the MP, CI, CC, … wave function Ansatz hierarchies (e.g., using increasingly higher levels, that is, single, double, triple, quadruple, … excitations). Fig. 4 illustrates the setup of these systematically converging series toward the complete basis set (CBS) limit regarding the AO basis and toward the practically complete wave function expansion of the electronic structure problem [labeled as FCI (that is full CI) in Fig. 4]. Additionally, the convergence can be accelerated, e.g., by using standard CBS extrapolation expressions. For example, here we employ two-point CBS(X, X + 1) extrapolation computed from X–ζ and (X + 1)–ζ basis set results separately for the HF145 and correlation energy146 terms (see details in Section S11 of the ESI†). Additionally, to accelerate the convergence toward the FCI and CBS limits, various composite (or focal point) and embedding approaches can focus the use of high-level approaches for the (chemically) most important contributions and add lower-level corrections for the remaining basis set, correlation, or environment effects.This robust, systematically converging approach demonstrated great success for smaller (<10–15 atoms) molecules, e.g., by providing thermochemical or spectroscopic properties at a quality comparable to experiments.2–10 With conventional methods, the main difficulty in reaching convergence is the significant computational cost increase associated with taking a single step along the hierarchies. For example, the cost of HF, MP2, CCSD, CCSD(T), etc. can increase by 1–2 orders of magnitude at each step, while increasing the basis set size by one cardinal number also takes ca. 10× or more time. One practical difficulty is thus the too large jumps between the steps along both series, which can be substantially improved by using local correlation, NO, and if needed, multi-level approaches. Besides the overall cost reduction benefit, one can set the parameters of the local and NO approximations in a much finer resolution, which govern the convergence along both the wave function and basis set hierarchies. This leads to much smaller steps of manageable size and thus more points can be used to determine the level of convergence. As demonstrated below, these advantages enable the realization of systematic convergence for large systems with accessible resources.
3.1 Systematic convergence of local approximations
Compared to the wave function and basis set aspects, it is often not emphasized enough that systematic convergence should also be achieved along the third axis, that is, the local approximations. To illustrate this point, the “local approx.” axis of Fig. 4 collects the increasingly better local approximation settings tending toward the local approximation free (LAF) limit. For this purpose, a few including the DLPNO,31 PNO-L,27 and the LNO29 family of methods offer multiple pre-defined, user-friendly composite local approximation setting combinations. For the LNO methods, the threshold combinations are labeled Loose, Normal (the default), Tight, veryTight (or vTight),29etc., and a similar series of LoosePNO, NormalPNO, TightPNO, or VeryTightPNO settings were introduced for the DLPNO-based methods too.31 The composite local approximation settings combine a set of thresholds, which form a systematically convergent series separately for each approximation. Together, these setting combinations usually provide systematic improvement toward the canonical (i.e., the LAF) correlation energy. Although the monotonic convergence property of the individual local and NO approximations is not necessarily inherited by the composite thresholds in all cases, in practice, we usually find systematically improving energy series through the Loose, Normal, Tight, etc. LNO settings. Naturally, the individual approximations can also be controlled one-by-one, but that level of detail is usually not required for the applications.Recently, approaches were also introduced to accelerate the convergence with respect to (some or all of) the local and NO approximations via extrapolation.24,29,147,148 To that end, we proposed a rather cautious extrapolation expression toward the LAF limit, assuming only that monotonic convergence occurs in the threshold series.29 In practice, an extrapolated energy estimate is formed from the two tightest available local correlation results, supposing that the subsequent step in the local approximation setting series will be smaller than the last step. This is equivalent to assuming systematic convergence, that is monotonically decreasing difference between the best two results. Thus, the estimate extrapolated from the last two steps is placed in the middle of the interval assuming a smaller forthcoming step in the series (see Fig. S2† for an illustration). The step size is also utilized as an uncertainty estimate, that can be employed to monitor the convergence. For instance, the extrapolation using Normal and Tight settings will give a Normal–Tight (N–T) LNO correlation energy result of
| EN–TLAF = ETight + 0.5(ETight − ENormal) ± 0.5(ETight − ENormal), | (4) |
In addition, we designed the latest Loose, Normal, Tight, etc. LNO settings to work in accord with this LAF extrapolation.29 In general, the result extrapolated toward the LAF limit can be written as
| ELAFS−(S+1) = ES+1 + 0.5(ES+1 − ES) ± 0.5(ES+1 − ES), | (5) |
3.2 Practical systematic convergence examples
Next, demonstrative examples (summarized in Table 3) show how to approach the CBS and LAF limits with LNO-CCSD(T), including simpler and more complicated systems. Comparison to the most recent DLPNO-CCSD(T1)26 variation is also provided when those computations were feasible on the accessible hardware. A common difficulty with the highlighted examples (Fig. 5–7 and S4–S9) is that the largest species involved is formed (via dimerization or reaction) from multiple smaller molecules of similar size. In such cases, a notable basis set superposition error (BSSE) can often occur, slowing the convergence to the CBS limit. Here, counterpoise corrections153 are only employed for the dimer interaction energies (acetic acid and coronene) to overcome some of the BSSE, while such BSSE corrections can be problematic for reactions with multiple elementary steps. An additional problem is that one cannot rely on substantial cancellation of local errors, as the local approximations affect the largest species disproportionately compared to the smaller species. Namely, some local approximations affecting the correlation energy components of more distant electrons are not or only moderately active for the smaller systems of ca. 10–30 atoms. Moreover, most of the inter-/intramolecular interactions in the largest systems are not present in the smaller reactants or monomers, excluding the possibility of corresponding error compensation in these interaction components.| System | No. of atoms | Subsystems | Basis set | Figure | ΔECBS(T,Q),TN–T LNO-CCSD(T) |
|---|---|---|---|---|---|
| Acetic acid dimer IE151 | 18 | 2 | haug-cc-pVXZ, X = T, Q, 5 | S4 | 0.08 |
| OMCB RE29 | 36 | 2 | cc-pVXZ, X = T, Q | 5 | 0.23 |
| Androstendion RE29 | 61 | 2 | aug-cc-pVXZ, X = D, T, Q, 5 | S5 | 0.03 |
| Halocyclization barrier149 | 63 | 3 | aug-cc-pV(X + d)Z, X = T, Q, 5 | 6 | 0.32 |
| Coronene dimer IE152 | 72 | 2 | aug-cc-pVXZ, X = T, Q, 5 | S8 | 0.09 |
| Lanosterol isomerization29 | 81 | 1 | aug-cc-pVXZ, X = D, T, Q | S9 | 0.03 |
| Phenylalanine r. trimer IE152 | 87 | 2 | aug-cc-pVXZ, X = T, Q, 5 | S6 | 0.29 |
| Michael-addition barrier29 | 90 | 4 | aug-cc-pVXZ, X = T, Q | 7 | 0.50 |
| Michael-a. diff. of barriers | 90 | 1 | aug-cc-pVXZ, X = D, T, Q | S7 | 0.09 |
In contrast, we find a more rapid convergence of energy differences in relatively local chemical processes (e.g., reactions localized mainly to a functional group).29 This is partly explained by the comparable effect of the local approximations when the reactant and product molecules are similar (see, e.g., Fig. S5 and S7 of the ESI†). Some of the examples provided in Section 3.3 are relatively complicated to illustrate the capabilities of current methods, while typical practical applications converge considerably faster. Here, we focus on the convergence of energy differences, while the corresponding correlation energy errors and their analysis are given in Section S6 of the ESI.†
First, the interaction energy of the acetic acid dimer (Fig. S4†) and the reaction energy for the formation of octamethylcyclobutane (OMCB, Fig. 5) are studied. Reaching the CBS limit for the acetic acid dimer of the S66 set154 is relatively complicated even with BSSE corrections,151 while the OMCB reaction is the largest and one of the most complex test cases in the compilation of Neese, Wennmohs, and Hansen (NWH) introduced for the accuracy assessment of (D)LPNO methods.30 For these medium-sized systems, we can also compare local CCSD(T) results to the known conventional CCSD(T) reference (denoted by horizontal lines with colors matching that of the local CCSD(T) results). The 18- and 36-atom acetic acid dimer and OMCB are close to the limits where conventional CCSD(T) is feasible with 5-ζ and Q-ζ basis sets, respectively.22
Regarding the acetic acid dimer interaction energies (Fig. S4†), both the basis set and the Loose–vTight series of LNO-CCSD(T) thresholds indicate excellent, sub-0.1 kcal mol−1 convergence with respect to the CBS limit and the conventional CCSD(T) references. Additionally, the LAF extrapolations further decrease the LNO errors by about 50–60%, while the corresponding LNO error estimates tightly envelope the conventional CCSD(T) results. Compared to each other the NormalPNO and TightPNO DLPNO-CCSD(T1) results also show the expected improvement, and are found to be close to the Loose and Tight (or L–N extrapolated) LNO-CCSD(T) interaction energies, respectively.
The case of the OMCB dimerization (Fig. 5) is similar in terms of the formation of many new interaction contributions in addition to the two broken π- and two formed σ-C–C bonds. The LNO-CCSD(T) results again converge relatively rapidly to their LAF limit [cf. the ca. 0.2 kcal mol−1 error already Normal LNO-CCSD(T).¶ In such cases of fast convergence, e.g., the N–T extrapolation can overshoot the LAF limit, indicating that the convergence with the LNO threshold sets and the LAF extrapolation is not always strictly monotonic at the few tenths of a kcal mol−1 scale. Regarding DLPNO-CCSD(T1), the NormalPNO errors are again comparable to those with Loose LNO-CCSD(T) (with an opposite sign), while a somewhat smaller improvement is observed with the TightPNO settings. Nevertheless, both sets of DLPNO-CCSD(T1) results provide chemical accuracy.
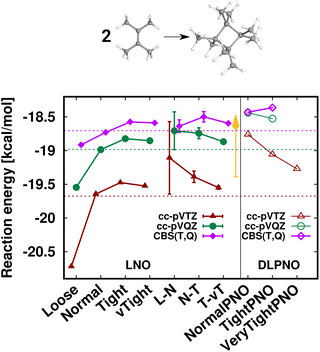 | ||
| Fig. 5 Reaction energy of octamethylcyclobutane (OMCB) dimerized from 2,3-dimethylbut-2-ene of the NWH reaction compilation.30 The plot shows LNO-CCSD(T) (left), LAF extrapolated LNO-CCSD(T) according to eqn (5) (middle) and DLPNO-CCSD(T1) (right) results compared to the horizontal lines corresponding to the conventional CCSD(T) results. The Normal LNO-CCSD(T)/ΔCBS(T,Q) basis set correction to Normal–Tight LNO-CCSD(T)/haTZ in the composite ECBS(X,X+1),XLAF CCSD(T) approach of eqn (7) is depicted as an orange vertical arrow. | ||
While these two examples of 18–36 atoms are smaller than the average targets in local CCSD(T) applications, it is instructive to see the performance of the convergence tools in practice when the conventional CCSD(T) reference is still available. We provide five additional convergence examples and their analysis in Section S7 of the ESI† for the larger systems listed in Table 3. Two of these examples having a more representative size (ca. 60–90 atoms) show similar or even faster convergence with especially the LNO approximations (formation of androstendione from its precursor29 in Fig. S5† and interaction energy of phenylalanine residue trimer152 in Fig. S6†). The fast convergence can be attributed to the relatively similar structures on the two sides of the formed energy differences. While such cases occur often in practice and thus compensation of some of the local and basis set errors can be expected on average, we leave the more detailed analysis of the relatively flat convergence curves to Section S7 of the ESI.†
3.3 Systematic convergence for more complicated cases
A transition state (TS) of a halocyclization reaction149,150 is shown in Fig. 6, exhibiting the difficulties of forming a molecular complex (63 atoms) of the reactants with the catalyst, as well as multiple (6) simultaneous bond formation and breaking steps. Here, the agreement of the CBS(T,Q) and CBS(Q,5) LNO-CCSD(T) energies is again compelling from the perspective of basis set convergence. The Normal LNO-CCSD(T)/aug-cc-pVTZ barrier does not appear to be chemically accurate yet, differing by ca. 1.3 kcal mol−1 from the veryTight–veryveryTight (vT–vvT) LAF extrapolated LNO-CCSD(T) result. This somewhat slower convergence can be attributed to the trimer formation in the transition state. However, the Tight and N–T LAF extrapolated results are within 0.7 and 0.4 kcal mol−1 of the best reference, also indicated by the N–T LNO error bar of 0.3 kcal mol−1. While it is rarely warranted in practice, for demonstrative purposes we evaluated the veryveryTight LNO-CCSD(T) and the VeryTightPNO DLPNO-CCSD(T1) barriers too. Convincingly, the shift in the LNO-CCSD(T)/aug-cc-pVTZ energies going toward tighter settings appears to decrease to the 0.1 kcal mol−1 scale. However, at this point it is complicated to understand better the 1.5 kcal mol−1 disagreement of the vT–vvT LNO-CCSD(T) and the VeryTightPNO DLPNO-CCSD(T1) barriers. In such unclear cases, one may inspect the convergence of the local CCSD(T) correlation energies, which show much more convincing trends for LNO-CCSD(T) (for the results and demonstrative analysis see Table S4 and Section S6 of the ESI†). Finally, let us note the sizable, ca. 7 kcal mol−1 basis set incompleteness even with the aug-cc-pVTZ basis, which, however, can be efficiently overcome via Normal or Tight LNO-CCSD(T)/CBS(T,Q) basis set corrections (see details in Section 3.4).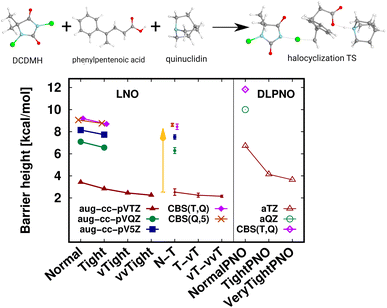 | ||
| Fig. 6 Transition state (63 atoms) barrier height of a halocyclization reaction comparing LNO-CCSD(T) (left) and DLPNO-CCSD(T1) (right) barrier height energies.149,150 The CBS(T,Q) and CBS(Q,5) LNO-CCSD(T) results are slightly shifted along the x-axis to increase visibility. | ||
The largest system covered here in detail is the 90-atom transition state structure for the carbon–carbon bond formation step of an organocatalytic Michael-addition reaction (Fig. 7).29,155 Here, besides the breaking of two carbon–carbon π-bonds and the formation of two new σ-bonds, the complex formation from the two reactants, catalyst, and co-catalyst poses an additional challenge from the perspective of substantial intermolecular interactions. Thus, we again find a large, ca. 7 kcal mol−1 basis set incompleteness deviation between the triple-ζ and the CBS(T,Q) barrier heights. Compared to that, the convergence of the LNO approximation errors is much faster, achieving about 0.2–0.3 kcal mol−1 uncertainty already with the Normal LNO settings both with the triple- and quadruple-ζ basis sets.29 The agreement between the Normal LNO-CCSD(T) and NormalPNO DLPNO-CCSD(T1) barrier heights within ca. 1.3 kcal mol−1 is consistent with the examples above.
Compared to the relatively slow convergence of this barrier height, let us note on the much faster convergence found often for the difference of energy differences. For example, the energy difference of this Michael-addition TS (Fig. 7) with a similar TS leading to a competing stereoisomer product is analyzed in detail in the ESI (Fig. S7).† In brief, about 0.1–0.2 kcal mol−1 level convergence can be reached for the difference of the barrier heights already with Normal LNO-CCSD(T)/aug-cc-pVTZ and even the Loose and/or aug-cc-pVDZ level results provide chemical accuracy. In general, even for relatively large and complicated systems, such difference of energy differences can considerably benefit from compensation of (both local and basis set) errors and thus can be computed very accurately and efficiently with local CCSD(T) methods.
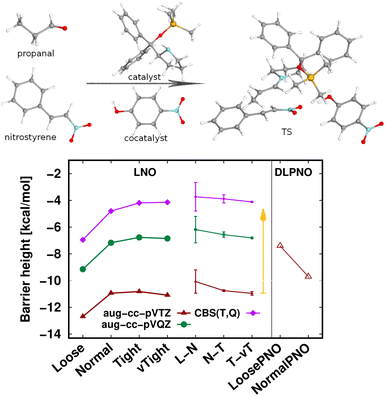 | ||
| Fig. 7 Transition state barrier height of an organocatalytic Michael-addition reaction comparing LNO-CCSD(T) (left) and DLPNO-CCSD(T1) (right) energies.29 | ||
Finally, we note on two additional examples which are considerably more challenging than the average local CCSD(T) applications. The coronene dimer (Fig. S8†) of the popular L7 molecular complex compilation156 is one of the most complicated examples studied with multiple high-quality wave function methods.27,34,152,157–161 Its highly delocalized π-systems and the impossibility of local error compensation in the intermolecular interaction energy terms represent a challenge for all local correlation methods. Moreover, practically all of the 72 atoms contribute importantly to its relatively large interaction energy of ca. 20 kcal mol−1. Thus, here, the interaction energy is not only roughly proportional to the area of the interacting surface but scales with the total system size. Additionally, we show a net reaction energy taken from the biosynthesis of cholesterol (Fig. S9†).162 Here, the lanosterol educt and (S)-2,3-oxidosqualene product are markedly different and separated by many elementary steps of the net reaction. Therefore, all 81 atoms play an important role and limited error compensation can be expected. These examples aim to illustrate the difficulty of modeling size-extensive properties with local correlation methods, such as interaction between large surfaces, atomization or cluster formation energies, net reactions of many elementary steps and so on. While leaving the detailed analysis to Section S7 of the ESI,† all in all, CBS extrapolation and (very)veryTight LNO-CCSD(T) computations were still feasible at this size range, which provide 0.1–0.2 kcal mol−1 LNO uncertainties also for these complicated cases. For practical purposes, Tight or N–T LNO-CCSD(T) with some form of CBS extrapolation or correction also falls within chemical accuracy.
3.4 Approaching CCSD(T)/CBS via composite methods
The correlation energy convergence with respect to the AO basis set saturation of different wave function methods can often be similar. These trends can also be observed in Fig. 5–7 and S4–S9 for the close parallelity of the local approximation convergence curves obtained with different basis sets, which can be exploited by forming composite energy expressions. The most common approach is to obtain an energy value from a high-level (HL) but demanding wave function method [e.g., CCSD(T)] with a moderate basis set combined with a CBS correction obtained with a lower-level (LL) method (often MP2).3,4,152,163 While we provide more details and a general approach in Section S4 of the ESI,† here we just formulate the above-noted common practice example as:| ECBSCCSD(T) ≈ ECBS(X+1,X),XCCSD(T),MP2 = EXCCSD(T) + ΔECBS(X+1,X),XMP2, | (6) |
| ECBS(X,X+1),XN–TLNO-CCSD(T) = EXN–T LNO-CCSD(T) + ΔECBS(X,X+1),XNormal LNO-CCSD(T). | (7) |
A key point is that, while such detailed convergence studies are feasible, apparently, one can select cost-effective composite approaches performing at a similar accuracy level. That is, for the production calculations, costly very tight or sometimes even tight, as well as 5-ζ and often also Q-ζ computations are not necessary. Besides this robust ΔECBS(T,Q),TN–T LNO-CCSD(T) variant, if the type of application allows, one can consider even more efficient composite expressions, which we discuss in detail in Section S4 of the ESI.† In Section S4† we also present advice on how to obtain reliable and representative local and basis set error estimates.
4 Accuracy of local approximations: statistical analysis
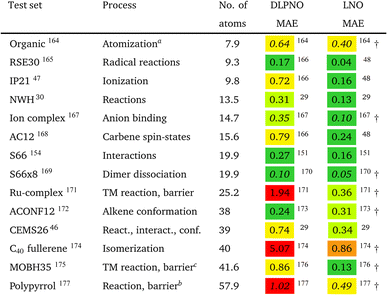
Multiple tools exist for the broader accuracy assessment of the local correlation approximations. The most straightforward way is to compare against conventional CCSD(T) results for representative benchmark sets, which can provide exact local approximation error statistics. The main difficulty is that conventional CCSD(T) benchmarks with a reliable (triple-ζ or larger) basis set are limited to about 20–30 atoms22 and can be moderately extended in special cases (such as with a high level of spatial symmetry).46 Consequently, most of the early benchmark sets had to gather smaller molecules and/or use small basis sets (see Table 4 and Fig. 8).| a Obtained with an early, 2017 version of LNO-CCSD(T) with the tighter settings in ref. 45 and the 2013 version of DLPNO-CCSD(T0) with TightPNO settings.178 b Extended π-systems including a few borderline multireference examples. c Reactions 17–20 and 24–25 were omitted due to their size, and 8–9 were recommended to be omitted due to their multireference character in ref. 176. The MAX local errors are larger for complexes 8 and 9, namely 2.41 kcal mol−1 for LNO-CCSD(T) and 14.96 kcal mol−1 for DLPNO-CCSD(T1). |
|---|
|
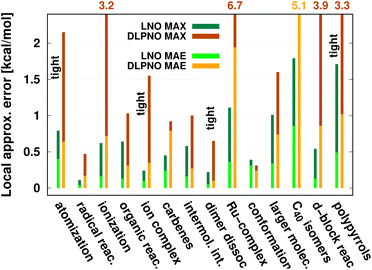 | ||
| Fig. 8 Mean absolute error (MAE) and maximum error [in kcal mol−1] of default (or when labeled explicitly, tight) LNO-CCSD(T) (left bars) and DLPNO-CCSD(T1) (right bars) against canonical CCSD(T) for various energy difference properties. The average system size increases from left to right. MAE or MAX values above 2.2 kcal mol−1 are given at the top of the figure to improve visibility. The numerical values and additional details are collected in Table 4 and S1.† | ||
However, the statistics reported for molecules below ca. 20–30 atoms could underestimate local CCSD(T) errors for typical use cases, as some of the local approximations are inactive for such compact systems. Moreover, benchmarks employing small basis sets (below the triple-ζ level) may underestimate the effect of natural orbital approximations because the size of the NO basis usually can be compressed with reasonable accuracy to only about double-ζ size. To mitigate these limitations, we compiled the correlation energies of medium-sized systems (CEMS26) set, containing 26 molecules of 30–63 atoms and 12 corresponding energy differences using at least triple-ζ basis sets.46 While the CEMS26 compilation is probably one of the most complicated and realistic sets for the assessment of local CCSD(T) methods against canonical CCSD(T), such efforts should be considerably extended in the future in terms of system size and number as well as complexity of the electronic structure.
While being aware of these limitations, all existing benchmark studies available for both LNO and DLPNO are summarized in Table 4 and S1.† The 14 compilations together cover a wide range of properties, including about 1000 reaction, interaction, conformation, isomerization, etc. energies of organic and transition metal (TM) containing systems with both closed- and open-shell electronic structure. The test sets in Table 4 are arranged to have an increasing average number of atoms from the top (7.9 atoms) to the bottom (57.9 atoms). Out of the 14 benchmark studies, 8 were reported independently from the developers of the LNO or DLPNO methods (labeled by † symbols at the end of the rows). Four of the independent studies reported only Tight LNO and TightPNO DLPNO results (italicized), while error measures with the default settings are collected in Table 4 for the other 10 compilations. The colors are assigned to assess the quality of the deviations with respect to the conventional CCSD(T) results. The different expectations on the accuracy of the default and tighter settings are taken into account in the color coding of Table 4. The LNO and DLPNO mean absolute (MAE) and maximum errors are also depicted via histograms in Fig. 8.
The most apparent trend in the results of Table 4 (from top to bottom) and Fig. 8 (from left to right) is the increasing local approximation errors with system size and with the complexity of the computed properties. Generally good performance is found for the smaller systems (up to ca. 30 atoms) and for the more straightforward (mostly size-intensive) reaction and interaction energies (cf. sets 2–7 of Fig. 8 and rows RSE30 to S66x8 of Table 4). For these cases, e.g., the MAE and maximum errors with LNO-CCSD(T) are confidently in the few tenths of a kcal mol−1 and below 0.6 kcal mol−1, respectively. In the next group of test cases one of the complicating circumstances appear. Namely, one faces increasing system size (ACONF12, CEMS26), more complicated electronic structure (delocalized π-systems, not strictly single reference character, or TM complexes, e.g., in rows ‘Ru-complexes’ and MOBH35), or size-extensive properties (e.g., atomization in the first row). Here, about 0.5 kcal mol−1 MAE and up to about 1 kcal mol−1 maximum errors can be expected from Normal LNO-CCSD(T) computations. Finally, the largest errors are found for the combination of these complexities (C40 isomers and polypyrrole reactions), where the mean (maximum) absolute LNO error is 0.5–1 (2) kcal mol−1.
In comparison to LNO-CCSD(T), the performance of the DLPNO-CCSD(T1) results in Fig. 8 and in Table 4 is similar (for ACONF12) or a factor of 1.5–3 worse for the simpler systems. However, for the larger and more complicated Ru-complexes, C40, MOBH35, and polypyrrole compilations, the 1–2 kcal mol−1 MAE and 3–6 kcal mol−1 maximum DLPNO-CCSD(T1) errors in Tables 4 and S1† are perhaps too high for most practical applications. In such cases, tighter settings can be recommended for both the LNO and DLPNO methods. A detailed analysis of these test sets could provide valuable insight toward the further improvement of local approximations in future studies. Additionally, for the C40, MOBH35, and polypyrrole tests, only small, double-ζ quality basis sets were employed due to the 40–60 atom system size. As the double-ζ basis set is usually insufficient for accurate correlated computations, local CCSD(T) methods are developed for use with at least triple-ζ basis sets. Thus, the double-ζ benchmarks may not be entirely representative of practical applications with larger basis sets due to the markedly different behavior of the natural orbital approximations for such small basis sets.
For 10 of the 14 benchmark compilations listed in Table 4, the accuracy of the local approximated correlation energies can also be inspected (Table S5 of the ESI†). In brief, for most sets (8 out of the 10 available), the mean (maximum) absolute correlation energy error measures are in the 0.02–0.04% (0.05–0.1%) range for LNO-CCSD(T). The largest deviations are found for the more complicated CEMS26 and polypyrrole test sets (ca. 0.065% MAE and up to 0.145% at maximum). Thus, the aimed 99.9% or better accuracy is mostly satisfied already with the default (Normal) LNO-CCSD(T) settings. Compared to the same canonical CCSD(T) reference, the DLPNO-CCSD(T1) average and maximum correlation energy deviations are ca. 2–6 and 2–3 times higher than the corresponding LNO-CCSD(T) error measures. The case of the MOBH35 set is notably different, where probably due to the small double-ζ basis set, 0.5% average and in some cases above 1% DLPNO-CCSD(T1) errors were reported.176 This, however, can be considerably decreased with tighter DLPNO settings and CPS extrapolation.176 Thus, the relative correlation energy error trends are consistent with those in the energy differences. Namely, more accurate correlation energies and better error compensation in energy differences affecting only a size-independent number of atoms translate into better energy differences. On the other hand, less converged correlation energies or the lack of error cancellation in size-extensive properties pose difficulties for local approximations. A more detailed local correlation energy error analysis is given in Section S6 of the ESI.†
An additional important message is that, depending on the applications, local correlation methods exhibit different levels of accuracy, e.g., with their default settings. Thus, in practice, one can determine an acceptable level of accuracy specifically for the application at hand, at least for a few representative examples, and then find suitable local correlation threshold settings. To that end, we recommend performing a convergence test with respect to the local approximation settings as introduced in Fig. 5–7 and S4–S9.† Next, we briefly show that the systematic convergence of the local CCSD(T) results is maintained also from the statistical point of view for three representative examples (NWH reaction energies in Fig. S3 of the ESI† as well as S66 interaction energies and CEMS26 mixed energy differences in Fig. 9). For all three compilations, both the LNO- and DLPNO-based results improve reliably by about a factor of 2–3 when switching to one step tighter settings (e.g., from default to tight). However, the absolute errors depend on the system size and computed property. For example, all settings provide chemical accuracy29 for the interaction energies (covering a ca. 18 kcal mol−1 range) of the relatively small S66 dimers (Fig. 9 top panel). Compared to that, a similar but slightly slower convergence is observed for the more complicated NWH reactions (Fig. S4† of the ESI). Due to the ca. 102 kcal mol−1 wide range of NWH reaction energies, more outliers are found with Loose LNO and NormalPNO DLPNO settings. In contrast to the S66 and NWH sets, the errors notably increase for the ca. twice as large systems in the CEMS26 compilation (Fig. 9 bottom panel). Here, only the results with at least Normal LNO and TightPNO DLPNO settings fall completely within chemical accuracy.
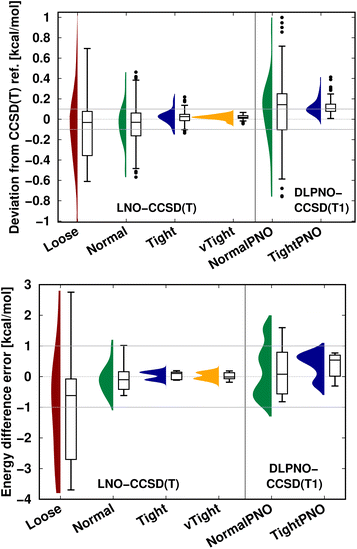 | ||
| Fig. 9 LNO-CCSD(T) (left) and DLPNO-CCSD(T1) (right) energy deviations against the DF-CCSD(T) reference for the S66 (ref. 154) interaction energy compilation in the haug-cc-pVTZ basis set151 (top panel) and the CEMS26 compilation29 (bottom panel). (Half) violin curves show the distribution of the signed errors, where the height of the curve (along the horizontal axis) indicates the frequency of the signed errors corresponding to an error value on the vertical axis. The horizontal lines of the boxes indicate the lower, median, and upper quartiles, respectively. Whiskers extend to the most distant data point whose error value lies within 1.5 times of the difference between the lower and upper quartiles. Outliers beyond the whiskers, if any, are represented by dots. The numerical data is from Tables 3 and S2 of ref. 29. | ||
While comparison to conventional CCSD(T) in general is limited to a few dozen atoms, obtaining well converged local CCSD(T) results, for example, with LAF extrapolation and error estimates (as shown in Section 3) is accessible for up to hundreds of atoms.29,152 The practical utility of using the best converged LNO-CCSD(T) as a reference to assess the local approximations is illustrated also in Section S6 of the ESI.† Moreover, we can also employ local approximation free DF-MP2 references to characterize come of the local approximations, since efficient DF-MP2 implementations can scale up to a few hundred atoms. Therefore, reference DF-MP2 results can be compared to local MP2, where none (or not all) of the natural orbital approximations, but some of the most relevant (domain and pair) approximations are already present. For example, our local MP2 (LMP2) approach44,47 employs the same pair and domain approximations as LNO-CCSD(T), hence LMP2 energies are obtained free as a by-product of an LNO-CCSD(T) computations. Moreover, our LMP2 results were found to be at least 99.9% accurate for systems of ca. 100–600 atoms already with a slightly looser threshold than those in the current Normal settings (cf. Table 7 of ref. 44 and the crambin protein result in Table III of ref. 103). Thus, such comparisons at the MP2 level indicate the reliability of the domain and pair approximations used also in LNO-CCSD(T) up to hundreds of atoms. However, importantly, such tests do not include any information about the error of the NO basis truncation.
The reliability of local MP2 results is also useful to accelerate double-hybrid (DH) DFT methods. Moreover, the second-order component of the DH-DFT approaches is often significantly scaled down in the functional definition (e.g., by 0.27 in B2PLYP). Consequently, the local approximation error is also proportionally smaller in the local approximated DH-DFT results than in local MP2.44,179
Finally, inspecting the correlation energies and their differences in Fig. 9, S3, and S10 of the ESI, one can also observe a difference in the naming choices of the LNO and DLPNO threshold combinations. Namely, the performance of NormalPNO DLPNO is closer to Loose LNO than to Normal LNO and TightPNO DLPNO results are closer to Normal LNO than to Tight LNO. This is simply a difference in the labeling, as for example, the same strong pair energy threshold (10−5 hartree) is used with both the TightPNO DLPNO and the Normal LNO settings. More importantly, both the DLPNO and LNO approaches reliably converge to the LAF limit of CCSD(T) when all thresholds are systematically tightened.
5 Computational requirements and accessible system size
Shifting our focus on the efficiency, here we argue that the computation of local CCSD(T) energies converged within chemical accuracy (in terms of both the local approximations and basis set) has become possible using widely accessible hardware for molecules of a (few) hundred atoms. Clearly, the upper size limit depends on the complexity of the investigated chemical process or molecular property, target accuracy, hardware, etc. Thus, first, we illustrate the current possibilities of convergence studies up to very tight local approximations and close to the CBS limit for representative systems of 60–90 atoms (Fig. 10 and S11†). As shown in Fig. 5–7 and S4–S9,† results with tight settings and quadruple-ζ basis sets (with the corresponding LAF and CBS extrapolations) are also great for most practical purposes, and this level can be afforded up to a few hundred atoms and is reachable also for 1000-atom proteins (cf.Table 5 and Fig. 11).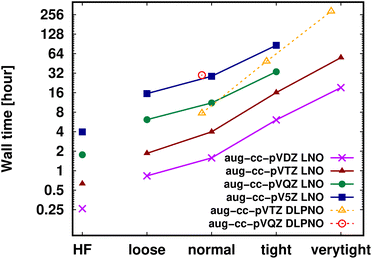 | ||
| Fig. 10 DF-HF, LNO-CCSD(T) (solid lines) and DLPNO-CCSD(T1) (dashed and slightly shifted) wall time measurements [on a logarithmic scale in hours] on 16 cores for the 63-atom TS of the halocyclization reaction of Fig. 6 with various basis set choices. For simplicity, similarly named (e.g., Normal LNO and NormalPNO DLPNO) timings are plotted with the same (e.g., ‘normal’) x-axis label. | ||
Fig. 10 and the similar Fig. S11† show the wall-time requirements (on a logarithmic scale) of DF-HF, DLPNO-CCSD(T1) and LNO-CCSD(T) for the 63-atom TS of the halocyclization reaction (Fig. 6) and the 90-atom TS of the Michael-addition reaction (Fig. 7), representing typical system sizes when modeling catalytic reaction mechanisms. These two sets of timing measurements can also identify some generally observed trends. Namely, at this size range, local CCSD(T) computations with the loose settings are only about 2–4 times longer than efficient DF-HF computations. This can be explained by the still 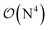 -scaling of DF-HF and the reduced, but not yet linear-scaling of the local CCSD(T) methods in this 50–100 atom range. For smaller than ca. 50-atom systems, the scaling of the local CCSD(T) approaches is not completely decreased from the original
-scaling of DF-HF and the reduced, but not yet linear-scaling of the local CCSD(T) methods in this 50–100 atom range. For smaller than ca. 50-atom systems, the scaling of the local CCSD(T) approaches is not completely decreased from the original 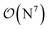 to linear, and thus their relative cost compared to DF-HF could be higher (with, of course, affordable absolute time requirements). A related observation reported by Liakos and Neese is that if the HF (or hybrid DFT) computation is not accelerated, e.g., via DF, then the local CCSD(T) runtime could become comparable to that of HF algorithms using four-center ERIs already for smaller molecules.32 Around 100 atoms, about
to linear, and thus their relative cost compared to DF-HF could be higher (with, of course, affordable absolute time requirements). A related observation reported by Liakos and Neese is that if the HF (or hybrid DFT) computation is not accelerated, e.g., via DF, then the local CCSD(T) runtime could become comparable to that of HF algorithms using four-center ERIs already for smaller molecules.32 Around 100 atoms, about  -scaling44,181 and above several 100 atoms even asymptotically linear-scaling HF algorithms182–184 can be employed in combination with local CCSD(T). However, as the decrease in the scaling of the local CCSD(T) component is faster than that of DF-HF, a crossover can occur between the cost of (reduced-scaling) DF-HF and local CCSD(T) for large systems of several 100 atoms.29,46
-scaling44,181 and above several 100 atoms even asymptotically linear-scaling HF algorithms182–184 can be employed in combination with local CCSD(T). However, as the decrease in the scaling of the local CCSD(T) component is faster than that of DF-HF, a crossover can occur between the cost of (reduced-scaling) DF-HF and local CCSD(T) for large systems of several 100 atoms.29,46
Let us continue with the cost of the CCSD(T) correlation energy computations in Fig. 10 and in S11† as the function of the local correlation thresholds. There, a consistent, ca. 2–4 times cost increase is found when the thresholds are tightened by one step, with a somewhat steeper increase for the compact 3D system of the Michael-addition TS. Regarding the dependence of the wall-times on the basis set size, one again finds a quite representative factor of ca. 3–4 cost increase when using a basis set of one cardinal number higher (e.g., triple-ζ to quadruple-ζ). This is a considerably smaller increase than expected from the formal  -scaling of conventional CCSD(T) with respect to the basis set size, which would lead to a factor of 10–20 cost increase without LNO/DLPNO approximations. The moderate scaling with the AO basis size can be explained by the higher effectiveness of the natural orbital based compression for larger basis sets. These trends apply quite similarly for both the DLPNO-CCSD(T)31 and LNO-CCSD(T)29 methods, which can be attributed to the related domain, pair, and natural orbital approximations employed in both approaches. Regarding the absolute times, the DLPNO-CCSD(T) computations of Fig. 10 and S11† took 2–10 times longer than LNO-CCSD(T) with the similarly named settings and same hardware (see more Computational details in Section S10 of the ESI†).
-scaling of conventional CCSD(T) with respect to the basis set size, which would lead to a factor of 10–20 cost increase without LNO/DLPNO approximations. The moderate scaling with the AO basis size can be explained by the higher effectiveness of the natural orbital based compression for larger basis sets. These trends apply quite similarly for both the DLPNO-CCSD(T)31 and LNO-CCSD(T)29 methods, which can be attributed to the related domain, pair, and natural orbital approximations employed in both approaches. Regarding the absolute times, the DLPNO-CCSD(T) computations of Fig. 10 and S11† took 2–10 times longer than LNO-CCSD(T) with the similarly named settings and same hardware (see more Computational details in Section S10 of the ESI†).
The practical consequences of the above are as follows: at the size range of around 100 atoms, it is now possible to perform LNO-CCSD(T) with the default settings at ca. 5–10 times the cost of the HF computation (at the same basis set). As the basis set requirement of CCSD(T) is usually higher than that of HF (or DFT) and one might also need tighter local settings, well-converged LNO-CCSD(T) results could take 10–20 or more times the cost of hybrid DFT (computed with a smaller basis set). Therefore, chemically accurate local CCSD(T) electronic energies can already be an affordable part of computational chemistry protocols including structure (and harmonic frequency) computations with medium-sized basis sets and (above rung-3) DFT methods used for the optimization or free energy corrections.
From a practical point of view, it is interesting to consider the computational cost required for a targeted level of accuracy compared to the approximation free CCSD(T)/CBS result. Here, we review general experience and add a specific example for the halocyclization TS in Fig. S12 of the ESI.† Clearly, a balanced description of both the local approximations and the basis set convergence is important. Both in Fig. S12† and in general, for larger molecules and for properties which are simpler for local approximations, the basis set incompleteness, below ca. the CBS(T,Q) level can dominate the total error with respect to CCSD(T)/CBS. In turn, for properties more sensitive to local approximations (combined, e.g.,. with BSSE corrections, e.g., for the coronene dimer in Fig. S8†), the local errors could become higher. Considering both aspects, for example, the ECBS(T,Q),TN–T LNO-CCSD(T) composite approach of Section 3.4 offers a good balance. It often provides reliable accuracy and requires roughly a day for the (somewhat flat) 63-atom TS and a week for the 90-atom TS with a single processor (and 6–16 cores).
While detailed parallelization scaling studies are not available for either the DLPNO or the LNO methods, practical experience shows appreciable scaling up to 1–2 dozen processor cores with currently released implementations (while involved parallelization developments are in progress for both the LNO and DLPNO methods). The largest system reported with one step better converged (i.e., veryTight and aug-cc-pV5Z) LNO-CCSD(T) results is the 132-atom buckyball-in-a-ring type supramolecular complex,152 where, however, the extensive delocalized π-system caused a significant cost increase. While often unnecessary, highly-converged computations should be feasible up to a few hundred atoms for somewhat simpler, e.g., organic or biochemical systems.
The performance of the local CCSD(T) methods for larger (bio)molecules (e.g., of Fig. 11) with the more relevant triple- and quadruple-ζ level is illustrated in Table 5. Results obtained with diffuse basis sets are scarce in the 100+ atom range due to the apparent cost increase of the local approximations compared to the basis sets without the spatially more spread diffuse orbitals. The largest NormalPNO DLPNO-CCSD(T1)/quadruple-ζ computation reported so far for the 176-atom vancomycin glycopeptide26 shows that basis set convergence can be achieved with both the DLPNO and LNO methods at least up to this point. Here, the wall-times are actually not very long, but the memory and disk space requirements of the DLPNO implementation can become a bottleneck.26
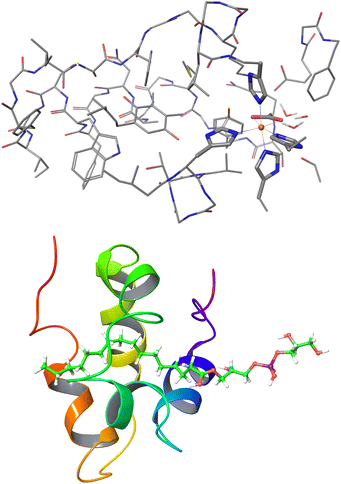 | ||
| Fig. 11 Largest systems where local CCSD(T) computations were feasible. Top: Open-shell LNO-CCSD(T)/def2-TZVP for the 565-atom photosystem II bicarbonate protein model.48 Bottom: Closed-shell LNO-CCSD(T)/def2-QZVP for the 1023-atom lipid transfer protein complex.29 | ||
| System | Figure | No. of atoms | Basis set | No. of AOs | DLPNO-CCSD(T1) | LNO-CCSD(T) | |||
|---|---|---|---|---|---|---|---|---|---|
| Cores | Time [h] | Cores | Time [h] | Memory [GB] | |||||
| a LNO-CCSD(T)/def2-TZVP is also feasible in 57 hours and with 17 GB memory.48 b Runtime of DLPNO-CCSD(T0) without the iterative (T1) correction. | |||||||||
| Halocyclization TS | 6 | 63 | aug-cc-pV(T+d)Z | 2203 | 16 | 7.7 (ref. 149) | 16 | 3.4 (ref. 149) | 9.4 |
| Michael-addition TS | 7 | 90 | aug-cc-pVTZ | 3155 | 6 | 470.7 (ref. 29) | 6 | 46.4 (ref. 29) | 26 |
| Vancomycin glycopeptide | 11 of ref. 185 | 176 | def2-QZVP | 8033 | 8 | 163.7 (ref. 26) | 6 | 70.2 | 39.7 |
| Bicarbonate protein | 11 | 565 | def2-SVPa | 5420 | 4 | 40.0b (ref. 180) | 10 | 16.2 (ref. 48) | 13.2 |
| Crambin protein | 9 of ref. 178 | 644 | def2-TZVP | 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 075 075 |
4 | 324.8b (ref. 33) | 8 | 52.1 (ref. 46) | 23.5 |
| Lipid transfer protein | 11 | 1023 | def2-QZVP | 44![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 712 712 |
— | — | 6 | 434.4 (ref. 29) | 98 |
Both the DLPNO and LNO methods can be pushed further with triple-ζ basis sets, where even the 644-atom crambin protein computations are feasible.33,46 At this point, the uniquely small data requirement of the LNO-CCSD(T) method becomes advantageous, enabling LNO-CCSD(T)/quadruple-ζ computations even for the 1023-atom lipid transfer protein29 and 500–600-atom LNO-CCSD(T)/triple-ζ computations for open-shell systems.48 To our knowledge, these are the largest CCSD(T) computations ever presented with any local correlation approach. Although not all published yet, we were able to obtain Tight LNO-CCSD(T)/quadruple-ζ results for all systems in Table 5, including the 565-atom open-shell and the 1023-atom closed-shell protein, illustrating the accessible system size for the ECBS(T,Q),TN–T LNO-CCSD(T) composite approach of eqn (7).
The memory (and comparable disk space) requirements of the LNO-CCSD(T) implementation in Table 5 are also remarkable. The optimal memory consumption values of Table 5 are reported in the LNO-CCSD(T) output files, while about 2–3 times more memory economic LNO-CCSD(T) algorithms are also implemented in the MRCC package58,59 (at the cost of somewhat higher disk use). Still, the few 10 s of GB memory need for the large molecules of Table 5, in combination with the affordable runtimes and frequent checkpointing, makes such large-scale LNO-CCSD(T) computations widely accessible even with a modest computer. Moreover, the small memory, disk, and network use of LNO-CCSD(T) enables its uniquely efficient, high-throughput (low competition) execution for many simultaneous computations on computer clusters. These properties are especially useful for popular compute node configurations with many-core CPUs, relatively small memory per core values, and without node-specific local hard drives.
6 Benchmark applications with local CCSD(T) methods
In the context of benchmarking applications, local CCSD(T) methods help to extend current data sets in terms of system size, relevance for practical applications, and inclusion of error-sensitive moieties. The local CCSD(T) benchmark data is then used to assess or train improved lower cost [e.g., DFT, semi-empirical, MM force field (FF), or machine-learning (ML)] approaches. For example, data sets used to benchmark (or parametrize) DFT methods186,187 usually contain a few thousand references partly from experiments but mostly from CCSD(T) computations. However, only a few percent of these reference systems reach ca. 25 atoms [due to the cost of conventional CCSD(T)], which cannot thoroughly probe the size dependence and the combined effect of more shortcomings in lower cost models. The appearance of DLPNO-158,168,175,188–192 and LNO-151,152,167,171,173,176,193,194 based local CCSD(T) benchmarks has already started to overcome these limitations, reaching extended and representative molecules up to the 100 atom range. Representative benchmark applications are reviewed in Sections 6.1 and 6.2 and most of them are summarized in Table 4.6.1 Inter- and intramolecular interactions
The S66 compilation154 and its S66x8 (ref. 169) dimer dissociation extension of Řezáč et al., containing representative dimers with H-bonding, dispersion, and other mixed interactions in dimers of up to 36 atoms, are among the most explored at the (local) CCSD(T) level.29,151,170,195 Recently, we pushed the basis set convergence of both conventional and local approximated CCSD(T)/CBS to one cardinal number higher than available before, with about 0.01 (0.05) kcal mol−1 average (maximum) basis set error estimate in the conventional CCSD(T)/CBS reference.151 Compared to that, the local error in Normal–Tight LNO-CCSD(T) is about 3–4 times higher (0.06 kcal mol−1 average, 0.15 kcal mol−1 maximum), and can be converged to match this few hundredths of a kcal mol−1 range with tighter LNO settings.151 The TightPNO DLPNO-CCSD(T1) results were slightly better than Normal LNO-CCSD(T), being in the range of 0.1 (0.4) kcal mol−1 average (maximum) errors. Reassuringly, using tight settings and large basis sets, it was possible to approach the conventional CCSD(T)/CBS results within about 0.1 kcal mol−1 uncertainty with LNO-CCSD(T), as well as with the PNO-L-37 and PNO-based39 local CCSD(T) methods.151Similarly detailed investigations were reported for the alkene conformation set (ACONFL) of Ehlert et al. containing CnH2n+2 conformers for n = 12, 16, and 20.172 The first, VeryTightPNO DLPNO-CCSD(T1)/aug-cc-pVTZ conformation energies were extended with CBS corrections using MP2/aug-cc-pV(T,Q)Z, which were revisited by Santra and Martin using larger basis sets in a veryTight LNO-CCSD(T)/aug-cc-pV(Q,5)Z-based approach.173 Most recently, Werner and Hansen reported tight PNO-LCCSD(T)-F12b/haug-cc-pVQZ results within at least 0.1 kcal mol−1 agreement with veryTight LNO-CCSD(T)/aug-cc-pV(Q,5)Z, providing an independent verification for the ACONFL conformation energies.196 Thus, these ACONFL studies represent an additional example, that systematic convergence with respect to the local and basis set approximations can lead to 0.1 kcal mol−1 level agreement between different local CCSD(T) methods.
This accuracy expectation has to be somewhat relaxed above this 30–60 atom range, especially if the interaction strength or surface also increases with the system size. An extensively studied example in the 48–101 atom range is the L7 compilation of Hobza and co-workers containing biochemical [e.g., guanine trimer, phenylalanine residue trimer, guanine–cytosine (GC) tetramer] and extended π–π complexes [e.g., (coronene)2 or dimers of circumcoronene (C3) with adenine (A) and GC (C3A and C3GC)].156 Recently, we significantly improved the convergence level of local CCSD(T) results for the L7 set using Tight–veryTight LAF- and aug-cc-pV(Q,5)Z CBS-extrapolated LNO-CCSD(T).152 We also made comparisons with state-of-the-art fixed-node diffusion Monte Carlo (FN-DMC) results in collaboration with Al-Hamdani, Zen, Tkatchenko, and co-workers.152 As expected from such high-level models, most LNO-CCSD(T) and FN-DMC results are found to be in agreement; that is, they match within their error estimates. Additionally, the notable scatter in some of the previous DLPNO-CCSD(T)34,158–161,197,198 results could also be understood considering the employed (T0) approximation, NormalPNO settings, non-augmented basis sets, or double-ζ level CCSD(T) energy components. However, in the subset posing more challenges152,157,158 (large π-systems of L7 and a Buckyball in a cycloparaphenyleneacetylene ring supramolecular complex), the size-extensive and long-range interactions involve practically all (72 to 132) atoms leading to a ca. 25 to 100 kcal mol−1 correlation energy contribution to the interaction energies. Here, the sum of the LNO and basis set incompleteness error estimates were found to be 1 kcal mol−1 or higher even at the Tight–veryTight LNO-CCSD(T)/aug-cc-pV(Q,5)Z level, which indicates the difficulty of reaching CCSD(T)/CBS. The deviation of the best LNO-CCSD(T) and FN-DMC results can reach up to 2.5 ± 1.4 and 4.5 ± 2.3 kcal mol−1 for the (coronene)2 and C3GC complexes, respectively, with about half of the difference covered by the combined LNO-CCSD(T) and FN-DMC error estimates.152 The yet unresolved deviation of 10.6 ± 3.1 kcal mol−1 for the Buckyball-in-ring complex shows that one has to be very cautious with such practically size-extensive properties and large π-systems even with state-of-the-art DMC and CC methods.152
Well-converged LNO-CCSD(T) results with robust and small error estimates for the S66, ACONFL, L7, and other compilations were also utilized to benchmark or improve DFT, MM FF, or ML approaches. For instance, the accuracy of lower-cost wave function and dispersion corrected DFT methods was extensively assessed on the L7 set compared to the LNO-CCSD(T) or the average of the LNO-CCSD(T) and FN-DMC interaction energies.193,199–208
In another important type of molecular interaction application, the description of strong polarization effects and the interaction of the polarized ligands near ionic species can be particularly complicated for empirical methods. In cooperation with Varma, Wineman-Fisher, Delgado, and co-workers, we developed a set of reference ion–ligand complexation energies representative of ionic interactions in solvent and protein environments close to the CCSD(T)/CBS level.209–212 These reference results were also employed to considerably improve the performance of polarizable MM FFs for the description of ions and their environments in strong electric fields.209–212 The ion–ligand complexes investigated were of Mm+–Ln type: Na+ and K+ complexed with L = H2O, CH3OH, NH2CHO for n = 1, 4;210 Mg2+ complexed with (H2O)n=1,6, HCOO−, N-methyl-alanine, and (dimethyl-phosphate)n=1,2;209,212 as well as methylated ammonium NH(4−n)Men+ for n = 1, 4, modeling N-methylated lysine interactions with amino acid side chain models: L = H2O, CH3OH, NH2CHO, HCOO−, C6H6, C6H5OH, C8H7N.211 Due to the moderate system size of at most 39 atoms, the Tight–veryTight LAF extrapolated LNO-CCSD(T)/aug-cc-pV(Q,5)Z level was routinely affordable in all four studies. Therefore, it was not necessary to test or employ lower-level local and basis set approximations, but usually the Normal–Tight and aug-cc-pV(T,Q)Z level is similarly suitable. The benefit of the higher level treatment is that it provides robust and very low error estimates of a few tenths of a kcal mol−1, which is excellent, considering that these ion–ligand interaction energies reach hundreds of kcal mol−1.209–212
6.2 Main group and transition metal chemistry
The accuracy of local CCSD(T) methods is thoroughly characterized for small main group species of up to a few dozen atoms (Section 4). As established by the benchmarks against canonical CCSD(T) in Table 4 (cf. rows 1–4 and 6), on average 0.1–0.2 (at least ca. 0.5–1.0) kcal mol−1 accuracy can be expected from (Normal) LNO-CCSD(T) with respect to conventional CCSD(T). These benchmarks already include various properties (reaction, radical formation, atomization, isomerization, ionization, spin-states, etc.) focusing on small main group species of up to a few dozen atoms. Specifically, Paulechka and Kazakov reported about 0.4 kcal mol−1 average LNO errors for the atomization energies of 31 important organic species (e.g., butane, ethanol, benzene, urea).164 The NWH set composed for the assessment of (D)LPNO methods30 also contains fairly complicated organic species (47) and their 23 reactions and isomerizations, including 2,3-dimethylbut-2-ene dimerization to octamethylcyclobutane, p-xylene dimerization to [2,2]paracyclophane as well as drastic reisomerization of C12H12 and C9O3 species covering a ca. 100 kcal mol−1 reaction energy range. As shown in Fig. S3† of the ESI and discussed in ref. 29, the LNO-CCSD(T) reaction energies show a rapid convergence with MAEs of 0.4, 0.14, and 0.08 kcal mol−1 with the Loose, Normal, and Tight settings, respectively. Turning to the more involved case of open-shell species, 30 radical stabilization energies (RSE30),165 21 vertical ionization potentials (IP21),47,165 and 12 aryl carbene (AC21) singlet-triplet gaps168 of relatively small, 10–23 atom organic species were also benchmarked against conventional CCSD(T) references.48,166 These are again properties, where moderate local error compensation can occur, while the energy differences, especially for the 184–323 kcal mol−1 IPs are substantial. Nevertheless, it is informative to study these more complicated benchmark sets too, especially since the LNO-CCSD(T) MAEs are in the 0.1–0.2 kcal mol−1 range already with the Normal settings.48 One should note that this good performance could be partly attributed to the relatively small system size and the community should keep pushing the limits of the accessible system size for quality reference computations.Compared to the above cases, the difficulties noted in Section 4 regarding the increasing molecule size, large π-systems, size-extensive properties, etc. could increase the uncertainty of the local approximations and could necessitate tighter settings (or convergence studies depending on the target accuracy). Two specific compilations were benchmarked in this complicated category. The isomerization and corresponding kinetics of Höckel, Mobius, and twisted [24]penta-, [28]hexa-, and [32]heptaphyrins by Martin and co-workers177 as well as of C40 fullerenes by Karton and Chan174 containing 24–40 delocalized π-electrons. Here, the systems size of 40–67 atoms become representative and the electronic structures are probably more involved than in usual practical applications (as shown by the large (T) contributions reaching the 10 kcal mol−1 range). Thus the outstanding performance of LNO-CCSD(T) with respect to the tested PNO-based methods and to the canonical CCSD(T) reference is reassuring (cf. 0.5–0.9 kcal mol−1 MAE and the ca. 1.8 kcal mol−1 maximum errors in Tables 4 and S1†).
Taking into account these challenges, a number of studies already provided valuable benchmarks for biomolecules or their fragments up to even the 100–200 atom range, representing typical structural, interaction, or reaction motifs. Here, of course, the role of local CCSD(T) is reversed, i.e., not tested against conventional CCSD(T), but serves as a reference, for example, for lower-level approximations. Such DLPNO- and LNO-CCSD(T) benchmarks, e.g., for biomolecule–drug,213,214 as well as amino acid, nucleobase and ion152,211,212 interactions, peptide192 and RNA backbone fragment215 conformations, and enzyme reaction models,216,217 are useful to assess the accuracy and contribute to the improvement of lower-cost models for biochemical simulations.
Compared to that, recent benchmarking efforts illustrated the higher level of difficulty in obtaining converged local CCSD(T) results on various real-life transition metal (TM) reactions.171,175,176,188,190,218,219 Such active testing and discussion between the user and developer communities27,48,220–223 are important and helpful to identify and overcome the limitations and improve the capabilities of current local CCSD(T) methods. Here, even the composition of representative and practical test sets is a significant challenge. Namely, the larger number of d-block elements and their more easily varied oxidation states represent a broader chemical space. Additionally, such TM systems more often exhibit technical complications including multi-reference electronic structure, real or artificial symmetry breaking, multiple HF/KS solutions, convergence of local and basis set errors for CCSD(T), and so on. Thus, the preparation of a high quality, representative compilation free of the noted technical difficulties is alone a formidable task. The few noted compilations in this category mostly employed some earlier versions of the (D)LPNO method and are getting increasing attention from the perspective of the development and assessment of novel DFT methods. The 10 item set of Weymuth, Couzijn, Chen, and Reiher (WCCR10) reported also gas-phase experimental ligand dissociation energies for large TM complexes of 42–174 atoms.218,224 More recently, Grimme, Hansen, and co-workers started to systematically cover closed-190 and open-shell188 d-block chemistry by reporting TightPNO and CBS(T,Q) quality references and corresponding DFT accuracy analysis for 41 and 61 representative TM reactions of up to 120 and 93 atoms, respectively.
Compared to the above case, detailed benchmarks of various local CCSD(T) results against conventional CCSD(T) are even more scarce, cf. the two sets noted in Table 4 (rows 9 and 13). Specifically, the reactions with Ru-complexes cover hydroarylation and oxidative coupling routes, intermediates, and TSs of reactions catalyzed by various Ru(II/III)-chloride-carbonyl species containing 180 reaction energies and barriers with molecules of 25 (41) atoms on average (at maximum).171 The Metal–Organic Barrier Heights (MOBH35) compilation was introduced by Iron and Janes175 and then revisited by Semidalas and Martin.176 The revised set collects 27 (out of the original 35, small enough and single-reference) reactions and corresponding barriers formed from molecules of 42 (65) atoms on average (at maximum). Normal LNO-CCSD(T) performs well for both the Ru-complex and MOBH sets with MAEs of 0.36 and 0.13 kcal mol−1, respectively, while the same MAE values for NormalPNO DLPNO-CCSD(T1) are 5–6 times larger, partly due to the considerable connected triple excitation contributions.171,176 Compared to the performance of their respective default settings, the mean absolute errors are halved by using both Tight LNO-CCSD(T) and TightPNO DLPNO-CCSD(T1) for the reactions of Ru-complexes.171 The much slower improvement with the tighter settings of both methods for the MOBH set can be partly attributed to the small, double-ζ basis used and should also be considered an indicator of the increasing wave function complexity. Nevertheless, using tighter settings and CBS(T,Q) level basis corrections, the LNO-CCSD(T)-based revised MOBH reference values of Semidalas and Martin176 already contributed to the assessment of advanced DFT methods.208,225–228
7 Local CCSD(T) applications for (bio)chemistry
Local CCSD(T) methods can also be employed directly in computational protocols modeling chemical processes. Such applications often require high accuracy and involve systems that are sensitive to the sources of errors in lower-cost approaches, such as self-interaction, functional, or dispersion errors in DFT methods. Despite impressive and continuous progress in DFT approaches, certain ionic, aromatic, polarized, or σ–hole interactions, as well as systems with open-shells or (transition) metal atoms, bond breaking, transition state structures, electron delocalization, etc. can still pose challenges. For instance, modeling catalytic processes can involve large systems with multiple difficulties. In such cases, especially in lack of experimental references, well-converged local CCSD(T) results can guide the selection of DFT methods or can provide reliable electronic energies. We review representative local CCSD(T) applications in Sections 7.1–7.4 (summarized in Table 6).| Computed property | Molecule/system description |
|---|---|
| Inter- and intramolecular interactions (Sections 7.1 and 6.1, additional examples in Table 4) | |
| Cation–amino acid side chain interaction | N-Methylated lysine with L = H2O, CH3OH, NH2CHO, HCOO−, C6H6, C6H5OH, C8H7N211 |
| Mm+–Ln metal cation–ligand interaction | Mm+ = Na+, K+, or Mg2+, L = H2O, CH3OH, NH2CHO, HCOO−, N-methyl-alanine, dimethyl-phosphate209,210,212 |
| Anion–receptor binding | Anions (F−, Cl−, Br−, CH3COO−, H2PO−4, NO3−) & 14 receptor motifs167 |
| Conformation energy | DrugBank-T dataset: 168 drug-like molecules of up to 30 heavy atoms194 |
| Conformation energy | Linked cellulose and lignin components (60–70 atoms),229 thermodynamic properties of menthol isomers230 |
| Dimer or cluster formation | 42 drug–protein dimers (54–64 atoms),214 water cluster formation of up to 30 molecules (90 atoms)231 |
| Supramolecular (host–guest) complexes) | (Bio)chemical complexes (L7 set, max 101 atom),152 fluorescent probe & dye complexes (max 200 atom)232–234 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|
| Main group chemistry (Sections 7.2 and 6.2, additional examples in Table 4) | |
| Enthalpy of formation & atomization | C, N, O, H, F, Cl, S, & Br atom containing organic compounds up to 34 atoms164,235–240 |
| Reaction enthalpy | Hydroformylation reaction including chain elongation, branching, & substituent effects241 |
| Radical stability & dimerization | Phosphinyl & phosphonyl radicals: ring size, delocalization & steric effects (81–162 atoms)242,243 |
| Deprotonation or aromatic stabilization | pKa of medium-sized sulfonamide derivatives,244 carborane-fused heterocycles245 |
| Reaction mechanism | Phosphane catalyzed ynone reduction,246 CO2 capture and release,247 curing of epoxy resins by oligoamides248 |
| Reaction mechanism | Arsinidene & stibinidene reactions with quinones,249 pericyclic reaction forming a triphosphatricyclo compound250 |
| Mechanism & stereoselectivity | Organocatalytic Michael-addition,155 asymmetric hydrogenation via frustrated Lewis pairs (90 atoms)251 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|
| Transition metal chemistry (Sections 7.3 and 6.2, additional examples in Table 4) | |
| Reaction energy | Stability of carbenes & silylenes in forming ferrocenophanes,252 Fe3(CO)12 with unsaturated aromatic thioketones253 |
| Reaction energy | Rh & Ir complexes with pyridine di-imine ligands,254,255 Co–C bond breaking in coenzyme B12 (209 atoms)48 |
| Spin state energies | 5A & 3A spin states of a single-molecule magnet Fe(II) complex (175 atoms)48 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|
| Crystal systems and surface chemistry (Section 7.4) | |
| Surface adsorption | CO binding on MgO ionic crystal,144 20-atom gold nanoclusters adsorbed on the MgO surface256 |
| Vacancy formation in metal oxides | O vacancies in rutile TiO2 & rock salt MgO257 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|
| Biochemical systems (Section 7.5) | |
| Enzyme reaction | Catechol-O-methyltransferase,129D-alanine oxidation by D-amino-acid oxidase48 (571–601 QM atoms) |
| Spin state and single point energies | Fe(II) spin states in photosystem II bicarbonate (565 QM atom),48 HIV-1 integrase model (2380 QM atoms)46 |
| Protein–ligand binding | 79-Atom ligand in lipid transfer protein (1023 QM atoms)29 |
7.1 Inter- and intramolecular interactions
Despite their ubiquity, modeling certain non-covalent interaction patterns, such as ion–ligand, σ–hole, or extended π–π interactions, remains notoriously challenging.258,259 The corresponding polarization, charge transfer, dispersion, etc. and especially their coupling require high-order treatment motivating the use of (local) CCSD(T) for such inter- and intramolecular interactions.Besides the benchmark studies for molecular interactions in Section 6.1, including cation–ligand interactions, local CCSD(T) applications for anionic complexes were also reported. Ho and co-workers studied anion (F−, Cl−, Br−, CH3COO−, H2PO−4, NO3−) binding with 14 common anion receptor motifs represented by various urea, thiourea, deltamide, squareamide, etc. derivatives.167 On a subset of 40 complexes, the DLPNO and LNO approximations were also assessed with respect to conventional CCSD(T) (cf. row 5 of Table 4). The average 0.35 kcal mol−1TightPNO DLPNO-CCSD(T1) and 0.1 kcal mol−1Tight LNO-CCSD(T) errors were both excellent, verifying the choice of the Tight LNO-CCSD(T)/haug-cc-pV(T,Q)Z-level reference used for the broad binding affinity study of ref. 167.
Recently, Zho and co-workers reported large-scale conformation energy benchmarks and the assessment of their deep learning-based DFT methods against Tight LNO-CCSD(T) for the DrugBank-T dataset (containing 7 conformers for all 168 molecules of up to 30 heavy atoms).194 In a wide conformer search for lignocellulose variants (linked cellulose and lignin components of 60–70 atoms), Chan et al. utilized accurate LNO-CCSD(T)/haug-cc-pVTZ+ΔMP2/CBS(T,Q) (ECBS(T,Q),TLNO-CCSD(T),MP2) results for ca. 130 conformers.229 In cooperation with Puleva, Sandonas, Tkatchenko, and co-workers, we studied the complexation energy and dissociation curves of 42 extended dimers (54–64 atoms) representative of drug–protein interactions using a wide range of theoretical methods.214 Counterpoise corrected ECBS(D,T),DN–T LNO-CCSD(T) showed a 0.2–0.5 kcal mol−1 uncertainty against ECBS(T,Q),TT-vTLNO-CCSD(T), and were available routinely for 90 dimer structures (in 10–30 hour wall time on 8–16 cores per composite dimer energy).214 In ref. 230, aiming at the thermodynamic properties of menthol isomers, an LNO-CCSD(T)/aug-cc-pVQZ level conformer exploration was employed. Bakó, Hamza, and co-workers computed LNO-CCSD(T)/aug-cc-pV(T,Q)Z-level cluster formation and many-body interaction energy components for 31 water clusters with up to 30 water molecules (90 atoms).231 Accurate LNO-CCSD(T) complexation energies were also utilized for supramolecular dimers of up to 200 atoms, including challenging π–π and ionic interactions, in combined experimental and computational studies.232–234 In particular, LNO-CCSD(T) complexation energies contributed to the characterization of uracil and hydroxyflavone fluorophore containing fluorescent probes with ATP.232 Host–guest binding modes between an extended fluorescent dye with a cucurbituril host233 as well as an anionic carboxylato-pillar-arene macrocycle with cationic guests (oxazine dye and vitamin B1)234 were also obtained at the LNO-CCSD(T)/aug-cc-pVTZ level.
7.2 Main group chemistry
When exploring chemical reactions, especially with large catalysts, in addition to the challenges with intermolecular interactions, difficulties in modeling covalent bond breaking, non-equilibrium structures, and issues caused by self-interaction DFT errors can also appear. For example, the transition state DFT computations are often more challenging than for (local) minimum structures,191 which can warrant the use of (local) CCSD(T) also for main group chemistry (see Table 6).Motivated by the outstanding performance of LNO-CCSD(T) for atomization energies of organic species, Paulechka, Kazakov and co-workers developed a protocol164,235,236 for computing thermodynamic properties (including enthalpies of formation, atomization energies, and partly torsion barriers and rotational constants) utilizing LNO-CCSD(T)/aug-cc-pVXZ (X = Q or 5) level results. The enthalpies of formation reported with this protocol have uncertainties close to that of the measurements and thus exhibit excellent (ca. 0.5–0.7 kcal mol−1) agreement with experimental results.164,235–240 The efficiency of this protocol and LNO-CCSD(T) enabled such accurate thermodynamic property computations for hundreds of (C, N, O, H, F, Cl, S, and Br containing) organic compounds up to 34 atoms.164,235–240 Similarly, in collaboration with Kégl and Papp, we obtained N–T LNO-CCSD(T)/aug-cc-pV(T,Q)Z hydroformylation reaction enthalpies with an about 0.1 kcal mol−1 uncertainty, verified in comparison to T–vT and aug-cc-pV(Q,5)Z level LNO-CCSD(T) computations.241 These LNO-CCSD(T) results perfectly match the available experimental hydroformylation enthalpies within the error bars. Moreover, the efficiency of LNO-CCSD(T) enabled the study of about 50 variants, including aliphatic and vinyl aromatic substrates as well as the chain elongation, branching, and substituent effects.241
Well-converged LNO-CCSD(T) results also contributed to various studies exploring reaction mechanisms, catalysis, selectivity, etc. in main group chemistry for large systems up to ca. 100–200 atoms. In collaboration with Benkő and Ott, our Normal–Tight LNO-CCSD(T)/aug-cc-pV(T,Q)Z results contributed to the search for stable carbocyclic phosphinyl radicals against dimerization.242 The reliable computational exploration of ring size, delocalization, and steric effects on the radical stability,242 as well as an extension to phosphonyl species243 were assisted by multiple LNO-CCSD(T) computations for open-shell radicals up to 81 atoms and dimers up to 162 atoms. Ho et al. utilized Tight LNO-CCSD(T)/haug-cc-pV(T,Q)Z reference gas-phase deprotonation energies for a set of medium-sized sulfonamide derivatives to select reliable DFT methods for corresponding pKa computations.244 In additional studies using LNO-CCSD(T) benchmarks in p-block chemistry, the reactivity of arsinidene and stibinidene with quinones,249 the reaction mechanism of the phosphane catalyzed ynone reduction with pinacolborane,246 the level of aromaticity in carborane-fused heterocycles,245 the catalytic effect of isophorondiamine-based oligoamides on the curing of epoxy resins,248 and the mechanism of four consecutive pericyclic reactions forming a novel triphosphatricyclo compound250 were investigated. In a collaboration with Pápai, Földes, Hamza, and co-workers,155veryTight LNO-CCSD(T)/aug-cc-pV(T,Q)Z results29 provided reliable benchmarks to assess competing mechanisms of an organocatalytic Michael-addition reaction (Fig. 7 and S7†) determining the stereocontrol. Similar sized, 90-atom transition state computations at the LNO-CCSD(T)/aug-cc-pV(T,Q)Z level contributed to another stereoselectivity study for the asymmetric hydrogenation of imines via frustrated Lewis pair catalysts.251 Most recently, Pápai, Laczkó and co-workers studied the capture and release of CO2via superbases using ECBS(T,Q),TN–T LNO-CCSD(T) corrected free-energies.247
7.3 Transition metal chemistry
Transition metal (TM) systems often pose additional modeling challenges compared to main group molecules. These include the more complicated wave function around the metal atoms, higher probability for more than one relevant electronic state, for the appearance of open-shell species, and/or for the decreased dominance of the HF determinant. For these reasons, on the one hand, DFT predictions for open-shell and organometallic species more frequently lay outside chemical accuracy than for main group molecules, and sometimes, it could be challenging to find a functional that is accurate for the right reasons.175,188,190,218,260,261 On the other hand, single reference (local) CCSD(T) requires about 3–4× operations and data for open-shell species, and it remains reliable only for wave functions with at least ca. 80–90% contribution from the mean-field reference determinant. Moreover, due to the more complicated, delocalized, and/or possibly open-shell electronic structure around the metal atoms, the correlation energy contribution and, thus, potential local approximation errors can also increase. Thus, both DFT and local CCSD(T) computations require care to avoid these pitfalls.Taking these into consideration, the cautious use of local CCSD(T) methods can provide valuable contributions to computational TM chemistry studies.252–255,260–262 For example, Kelemen and co-workers studied the stability of a number of carbenes, silylenes, and their analogues in forming ferrocenophanes using also DFT- and LNO-CCSD(T)-based isodesmic reaction energies for ca. 50 variants.252 Seeber and co-workers investigated reactions of α–β-unsaturated aromatic thioketones with Fe3(CO)12 at the Tight LNO-CCSD(T)/cc-pVQZ level.253 Burger and co-workers computed Gibbs free energies using LNO-CCSD(T) energies to study the reactivity254 as well as the electronic structure and stability of Rh and Ir complexes with square-planar pyridine di-imine ligands (up to 112 atoms).255 Our recent computations demonstrate the reach of LNO-CCSD(T) for even larger open-shell TM systems including the triplet and quintet spin states of a single-molecule magnet candidate Fe(II) complex (175 atoms), the homolytic bond breaking of the coenzyme B12 forming a 179-atom CobIIalamin radical, and spin-states of a 565-atom photosystem II (PSII) bicarbonate model containing an Fe(II) ion.48
7.4 Condensed phase systems: surfaces and solvent or solid environments
The applications above employed gas-phase local CCSD(T) electronic energies, which were in some of the studies also combined with DFT-based free energy corrections and/or a continuum solvent environment. As well-converged local CCSD(T) energies are available for ever larger and often flexible molecules, the sampling of conformations as well as the modeling of environment effects will also become more important. Since efficient gradient implementations are far from available for the local CCSD(T) methods, the DFT-based free energy treatment will probably remain frequently employed in this context in the near future. One alternative could be using system specific ML-FFs to describe the motion of the nuclei on CCSD(T)-level potential energy surfaces. Pioneering studies already reported conventional or accelerated CCSD(T)-based ML-FF training and applications up to molecules of mostly 10–15 atoms.263–273The possibilities for extending local CC methods with models for the environment are considerably broader. Most local CCSD(T) implementations can be combined with MM models in a QM/MM framework, as shown below for biochemical or crystal environments.128,129,142–144 Currently, the polarizable continuum model (PCM) for solute–solvent interactions can mostly be included at the HF level, for example, for LNO-CCSD(T), with a notable recent exception for the coupling of DLPNO methods and PCM at the “perturbation theory energy singles” level.274 Besides these classical models, environment effects can also be taken into account via quantum chemical treatments, such as quantum embedding into DFT environment40,128,129,132,133 or multi-layer local correlation approaches128,129,134–140 (as introduced in Section 2.4).
Additional environment modeling approaches are also emerging in the local CC context for periodic systems, including processes on crystal surfaces or in periodic solids, lower-dimension systems, or liquids.51,275–277 The combination of periodic symmetry and efficient local approximations is still challenging for coupled (direct) methods at the CCSD(T) level, while lower-order electron correlation models and fragmentation schemes have become available recently.278–281 For example, Usvyat, Maschio, Schütz, and co-workers extensively developed periodic local methods up to MP2 and direct ring-CC,275,280,282 while Schäfer, Grüneis, and co-workers presented a periodic CCSD-in-RPA embedding approach.283 Yang, Chan, and co-workers combined many-body expansion and local CCSD(T) ideas to compute the lattice energy of crystal benzene with an accuracy challenging the experiments at the time.284 Recently, Daru, Behler, and Marx constructed a high dimensional local CCSD(T)-level ML potential for liquid water, providing accurate condensed phase properties.273
Alternatively, the highly optimized local CCSD(T) implementations can be readily employed via cluster approaches, that is, for a finite part of a periodic system. The potentially slow convergence of the cluster computations to the bulk limit can be accelerated using various (e.g., mechanical,276 electrostatic,143,144,285etc.) embedding approaches. In particular, an electrostatic embedded cluster approach achieved successes also in combination with local CCSD(T) methods, where increasingly larger quantum mechanically treated clusters of the bulk crystal (or surface) are surrounded by a (hemi)sphere of effective core potentials and formal MM point charges.143,144,257,285 Recently, Shi, Michaelides, and co-workers introduced the SKZCAM approach to optimize the size, shape, and charge of the embedded clusters to further decrease the cost of the local CCSD(T) embedded cluster calculations.144,256,257
The potential of combining LNO-CCSD(T) with the embedded clusters approach was demonstrated for vacancy formation in metal oxides,257 metal nanocluster adsorption on metal-oxides,256 and the extensively studied CO binding on MgO surface.144,286–288 In collaboration with Shi, Zen, Kapil, Grüneis, and Michaelides, the agreement between periodic CCSD(T), periodic DMC, and embedded cluster LNO-CCSD(T) results was demonstrated. The three high level methods are consistent not only with each other but also with experimental CO on MgO adsorption energies within their ca. 0.25–0.6 kcal mol−1 uncertainty estimates (see Fig. 12).144 This agreement was made possible by extensive recent developments in all three benchmark computational methods, enabling robust error estimates and converged results with respect to both the wave function approximations and basis set as well as the bulk and dilute CO coverage limits. These methods were thus able to utilize the power of systematic convergence in the key computational aspects as discussed in Fig. 4 and Section 3.1.144 Remarkably, the combination of optimized cluster sizes and the efficiency of LNO-CCSD(T) enables an uncertainty estimate of only 0.25 kcal mol−1. This accuracy and the widely affordable requirements (few 10 GB memory and few-days-long, 10–20 CPU core jobs) of such computations open the door to routinely accessible benchmark accuracy for processes involving ionic crystals.144
 | ||
| Fig. 12 Adsorption energy of CO on MgO from previous experimental (1999–) and theoretical (2002–) investigations taken from the literature compared to the recent cluster model based LNO-CCSD(T), periodic CCSD(T), and FN-DMC theoretical results, as detailed in ref. 144. The latter 3 high-level computational results match reinterpreted experimental adsorption energies with consistent error bars. The inset illustrates the first few, increasingly larger cluster models used for the embedded cluster computations.144 | ||
7.5 Biochemical systems
The combined complexities occurring in enzyme reactions along the reaction path and surrounded by the protein environment can call for the accuracy provided by high-level wave function methods. While canonical CCSD(T) embedded in DFT and/or MM environments can deal with small active sites of up to 10–20 atoms,289,290 more and more studies point out the need for larger QM regions containing at least a few 100 atoms.291–293 This embedded site size can now be reached with local CCSD(T) methods. While multiple proof of concept studies were presented by the local correlation method developers,128,129,136–138,142 the first independent applications are just starting to appear.294–297 Cerqueira and co-workers reported a reaction mechanistic study for the 3C-like protease of SARS-CoV-2 using ca. 70 QM-atom, DLPNO-CCSD(T0)/CBS(D,T)/MM energy corrected DFT/MM profiles with good agreement with kinetic measurements.296 Using a similar methodology, they also reported an eight-step catalytic mechanism and a ca. 2 kcal mol−1 agreement between the rate determining barrier and experimental rates for serine hydroxymethyltransferase, which is a drug target relevant to malaria.295 Some of the same authors adopted this level of theory to study the catalytic transfer of acyl moieties between domains of the human fatty acid synthase.297 Medina and Jaña used ca. 50 atoms for the high-level DLPNO-CCSD(T)/CBS(D,T) in their ONIOM setup to study the catalytic mechanism of meropenem drug hydrolysis by a metallo-β-lactamase with relevance to antibiotic resistance.294 Sparta, Bistoni, Riplinger, Neese, and co-workers reported DLPNO-CCSD(T0)/triple-ζ computations (i) without embedding for the 644-atom crambin protein,33 (ii) using multi-level DLPNO for an ellipticine-DNA complex,136 and (iii) QM/MM for two enzyme reaction barrier heights142 with embedded regions ranging up to 307 atoms. The latter study also benchmarked DFT methods against the local CCSD(T) reference barriers for selected steps of a hydroxylation reaction catalyzed by p-hydroxybenzoate hydroxylase and a Baeyer–Villiger reaction catalyzed by cyclohexanone monooxygenase.142Our large-scale LNO-CCSD(T)/triple-ζ level biochemical computations include an HIV-1 integrase model with 2380 atoms,46 and a methylation reaction catalyzed by catechol-O-methyltransferase.129 The latter study also includes a detailed multi-layer embedding benchmark using a 571 QM-atom LNO-CCSD(T)/MM reference. There we show that chemically accurate embedding of LNO-CCSD(T) is feasible for the noted reaction energy already with 50 embedded atoms if we use local MP2 for the environment. Compared to that, LNO-CCSD(T)/MM and LNO-CCSD(T)-in-DFT embedding approaches converge slower with the system size, reaching chemical accuracy at around 150–200 atoms.129
Regarding open-shell biomolecules, we reported at the LNO-CCSD(T)/triple-ζ level spin state splitting energies for the 565 QM-atom PSII bicarbonate protein fragment.48 The gap of the quintet and triplet states with spin densities, localized mostly on an Fe(II) center, can exhibit slow basis set convergence and manageable SCF convergence issues for the low-spin state. At the same LNO-CCSD(T)/triple-ζ level, we also reported reaction energies for the oxidation of D-alanine by a 601-atom D-amino-acid oxidase (DAAO) model.48 Here, open-shell species occur as O2− oxidizes the flavin adenine dinucleotide moiety.48,298 These DAAO computations again represent challenges which can be managed only with state-of-the-art methods. Namely, for the triplet states only one of the unpaired electrons localizes well on the oxygen molecule or its derivatives, while the other singly occupied LMO is delocalized over the entire flavin moiety. Consequently, the latter singly occupied LMO has almost twice as many strongly interacting pairs causing significantly increased computational demand.
Reaching basis set convergence via LNO-CCSD(T)/quadruple-ζ was also possible166 for these 565-atom PSII and 601-atom DAAO systems, and was already reported for the 644-atom crambin protein46 and the ligand binding energy of the 1023 QM-atom lipid transfer protein complex of Fig. 11.29 The 79-atom ligand in the latter is representative of the size of many substrates or drugs. At the same time, the ca. 1000 QM atoms mark the current limits of local CCSD(T) in biochemistry. While the high-level many-body contribution to molecular interactions is relatively well-understood for large systems, the domain of large ligand–protein interactions at the scale of 100 kcal mol−1 correlation energy contributions remains practically unexplored. This should improve in the near future, as all of the 500+ QM-atom LNO-CCSD(T) computations were completed using a single node with 6–8 cores for the closed-shell and 20–40 cores for the open-shell systems. While such large computations take days to weeks of runtime (which should decrease further via improved parallelization), the restartability and the only 20–100 GB memory requirement of LNO-CCSD(T) already make them feasible with widely accessible hardware. This recent progress enables high-quality LNO-CCSD(T) energy corrections or benchmarks for biomolecules involving 100s of QM atoms for dozens of conformations or snapshots along a reaction profile. This advancement should elevate best practice electronic energy computations for biomolecules to the level accessible only for the smaller molecules in homogeneous catalysis.
8 Conclusions and perspectives
Here, we showed that the CBS limit of CCSD(T) can now be affordably and reliably approached using the local natural orbital (LNO) and other advanced local correlation methods (such as DLPNO) up to hundreds of atoms. The systematically improvable property of wave function methods can be retained for local approaches, using a series of local correlation settings (e.g., Loose, Normal, Tight), as well as the conventional AO basis set and CC excitation level hierarchies. Unlike for alternative models, e.g., with empirical parameters, such a systematic approach also enables extrapolation, composite method definitions, and an estimate for the remaining model error.On the basis of such system-specific convergence tests, benchmark publications, and/or experience in the literature, it is straightforward to select local and basis set settings for a computational project applicable in a black box manner. To that end, the following general observations and recommendations can be helpful:
(1) The level of accuracy for the local approximations, e.g., with default (normal) or tight settings, can depend on the molecule, computed property, or threshold definitions in different implementations. On average, the default (Normal) LNO-CCSD(T) settings are designed to recover CCSD(T) well within chemical accuracy, while complicated cases (e.g., in point (3)) may require tighter settings.
(2) Rapid convergence and shorter compute times can be expected for the more straightforward cases. (i) Energy differences or differences of reaction energies, barrier heights, etc. among chemically similar compounds, especially if their structural difference is limited to a small number of atoms. Such size-independent properties occur in most elementary reaction steps affecting only a few functional groups, certain conformational changes, or molecular interactions across a small surface. (ii) Well-localized wave functions, e.g., in many main group compounds or when the volumetric density of electrons and AOs is relatively small. This occurs, e.g., in large biomolecules, (clusters from) molecular liquids or crystals, or in systems of reduced dimensions (e.g., quasi-linear, quasi-planar, or porous systems).
(3) Especially for the more complicated cases, e.g., when the targeted property also increases with size, local approximation errors and BSSE may grow considerably with the number of atoms. Potential challenging cases include (i) significant electron delocalization (e.g., extended π-systems or around transition metal atoms), (ii) lack of error compensation (e.g., atomization, cluster formation from smaller molecules, multiple small reactants forming a large product, spin-state energetics), (iii) cumulative effect from many contributions (e.g., interaction between large surfaces or energy of net reaction with many elementary steps), or the combination thereof. The high volumetric density of electrons and AOs, such as in densely packed ionic crystals, as well as the potentially more complicated electronic structure of open-shell species may also increase the computational cost.
(4) Unlike for most DFT approaches, the basis set convergence of wave function methods is substantially slower, and corresponding BSSE can be very high. Especially for larger systems, even triple-ζ CCSD(T) results can be far from chemically accurate. The performance of MP2-based basis set corrections commonly added to triple- or even double-ζ CCSD(T) also deteriorates with increasing system size. These approaches should and now can be affordably replaced for high accuracy by, e.g., CBS(T,Q) level basis corrections at the Normal LNO-CCSD(T) level (see Section 3.4).
(5) Our efficient LNO implementation, CBS and LAF extrapolations, as well as composite basis set corrections (or embedding approaches) can further decrease the cost of well-converged LNO-CCSD(T) computations and robust error estimates. Compared to exact CCSD(T), on average (at maximum) Normal LNO-CCSD(T) errors of a few tenths (∼0.5) of kcal mol−1 can be expected for the simpler properties (point 2) of smaller molecules (ca. <30 atoms). These error measures increase 2–3 times for the challenging and/or larger test sets in Table 4. Nevertheless, Tight or Normal–Tight LAF extrapolated LNO-CCSD(T) is mostly within chemical accuracy even for the more complicated applications.
(6) Multiple local correlation methods, including DLPNO-CCSD(T1) and LNO-CCSD(T), also converge systematically to conventional CCSD(T), and one finds, e.g., TightPNO DLPNO-CCSD(T1) and Normal LNO-CCSD(T) error statistics to be comparable. In terms of the wall-time and even more so the data requirements, Normal LNO-CCSD(T) outperforms NormalPNO DLPNO-CCSD(T1) [and thus it is substantially more efficient than the similarly accurate TightPNO DLPNO-CCSD(T1)].
Owing to almost a decade of extensive optimization by the author and his co-workers,29,44–48 highly accurate Tight LNO-CCSD(T)/CBS(T,Q) electronic energies can be computed routinely for real-life molecules of 50–100 atoms using widely accessible computers (ca. 10 cores and a few 10s of GB memory). Uniquely, quadruple-ζ level LNO-CCSD(T) computations scale up to 1000-atom proteins, taking a few 1000 CPU core hours and ca. 100 GB memory with the Normal settings. These results demonstrate the outstanding accuracy/cost performance and (asymptotically constant) data storage demand of our LNO-CCSD(T), and consequently also of our local MP2 and double-hybrid DFT codes. Since well-converged LNO-CCSD(T)/CBS energies can be computed in about 1–2 order of magnitude higher cost than efficient DF-based Hartree–Fock or hybrid DFT, a large number of LNO-CCSD(T) computations are accessible to test or, if needed, to even replace rung-4 DFT electronic energies in current computational protocols.
Thus, affordable and well-converged energies and uncertainty estimates provided by LNO-CCSD(T), alongside its user-friendly and open-source implementation in the MRCC package58,59 open many possibilities for its utilization. Here, we reviewed more than 50 LNO-CCSD(T) applications from the literature including: (i) accurate LNO-CCSD(T) benchmarks for representative and large systems in order to assess the accuracy and improve the performance of lower-cost, mostly empirically parametrized (e.g., DFT, semi-empirical, MM, or ML) methods, and (ii) LNO-CCSD(T) applications across molecular interactions as well as main group, transition metal, bio-, and surface chemistry.
In the near future, one can anticipate a shift in local CC development toward a more intensive expansion of their functionality (e.g., for measurable molecular properties, excited states, environment models, and stronger correlation). Active developments are also targeting the improvement of accuracy and efficiency of local CC methods, but some slowdown can be expected on this front due to the high complexity of these methods, both from the theoretical and computer science perspectives. In contrast, the availability of local CCSD(T)/CBS estimates with affordable resources should now enable relatively routine access to gold standard energies for a much broader audience, well beyond the few percent of early adopters equipped with extensive computational resources.
The wider access to accurate references at the hundred-atom range will add to our understanding of complex quantum mechanical effects in large systems, contribute to the future development of lower-cost approximations, and should also increase the ability of modeling to assist and cooperate with experiments. With more experience in large systems, the categorization of applications will become more clear where, e.g., DFT methods can be benchmarked and trusted with high confidence and where local CCSD(T) will remain more reliable. Areas involving complex processes, e.g., with large open-shell species, on surfaces, and in solvent or biochemical environments, are currently practically uncharted by high-order wave function methods. We believe that efficient local CCSD(T) methods, such as LNO-CCSD(T), can significantly contribute to the modeling and understanding of such hardly accessible systems.
Author contributions
All work in this feature review article was performed by its single author, Péter R. Nagy.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The author is grateful for the contributions of collaborators and group members: Prof. Mihály Kállay (LNO methods), László Gyevi-Nagy [DF-CCSD(T) code], Bernát Szabó (open-shell LNO methods), Gyula Samu (efficient ERI evaluation), József Csóka (efficient SCF methods), Bence Hégely (DFT embedding), and Balázs Lőrincz (benchmark computations). The author is thankful for useful discussions about the manuscript to Prof. Imre Pápai, János Daru, Dénes Berta, Benjamin Shi, and Gergő Laczkó. The financial support from the ERC Starting Grant No. 101076972, “accuracy”, the National Research, Development, and Innovation Office (NKFIH, Grant No. FK142489), the János Bolyai Research Scholarship of the Hungarian Academy of Sciences, ÚNKP-23-5-BME-408 New National Excellence Program of the Ministry for Culture and Innovation sourced from the NKFIH fund, and the computing time granted by the Hungarian Governmental Information-Technology Development Agency on the Komondor HPC are gratefully acknowledged.Notes and references
- I. Shavitt and R. J. Bartlett, Many-Body Methods in Chemistry and Physics: MBPT and Coupled-Cluster Theory, Cambridge University Press, 2009 Search PubMed.
- R. J. Bartlett and M. Musiał, Rev. Mod. Phys., 2007, 79, 291 CrossRef.
- A. L. L. East and W. D. Allen, J. Chem. Phys., 1993, 99, 4638 CrossRef.
- A. Császár, W. D. Allen and H. F. Schaefer III, J. Chem. Phys., 1998, 108, 9751 CrossRef.
- A. Ganyecz, M. Kállay and J. Csontos, J. Chem. Theory Comput., 2017, 13, 4193 CrossRef PubMed.
- A. Karton, N. Sylvetsky and J. M. L. Martin, J. Comput. Chem., 2017, 38, 2063 CrossRef PubMed.
- D. A. Dixon, D. Feller and K. A. Peterson, Annual Reports in Computational Chemistry, Elsevier, 2012, vol. 8, p. 1 Search PubMed.
- A. Mahler and A. K. Wilson, J. Chem. Theory Comput., 2013, 9, 1402 CrossRef CAS PubMed.
- S. Di Grande, M. Kállay and V. Barone, J. Comput. Chem., 2023, 44, 2149 CrossRef CAS.
- B. J. Esselman, M. A. Zdanovskaia, A. N. Owen, J. F. Stanton, R. C. Woods and R. J. McMahon, J. Am. Chem. Soc., 2023, 145, 21785 CrossRef CAS PubMed.
- K. Raghavachari, G. W. Trucks, J. A. Pople and M. Head-Gordon, Chem. Phys. Lett., 1989, 157, 479 CrossRef CAS.
- M. J. O. Deegan and P. J. Knowles, Chem. Phys. Lett., 1994, 227, 321 CrossRef CAS.
- V. M. Anisimov, G. H. Bauer, K. Chadalavada, R. M. Olson, J. W. Glenski, W. T. C. Kramer, E. Aprà and K. Kowalski, J. Chem. Theory Comput., 2014, 10, 4307 CrossRef CAS PubMed.
- A. E. DePrince and C. D. Sherrill, J. Chem. Theory Comput., 2013, 9, 2687 CrossRef CAS.
- E. Epifanovsky, D. Zuev, X. Feng, K. Khistyaev, Y. Shao and A. I. Krylov, J. Chem. Phys., 2013, 139, 134105 CrossRef PubMed.
- T. Janowski and P. Pulay, J. Chem. Theory Comput., 2008, 4, 1585 CrossRef CAS.
- M. Pitoňák, F. Aquilante, P. Hobza, P. Neogrády, J. Noga and M. Urban, Collect. Czech. Chem. Commun., 2011, 76, 713 CrossRef.
- E. Deumens, V. F. Lotrich, A. Perera, M. J. Ponton, B. A. Sanders and R. J. Bartlett, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2011, 1, 895 Search PubMed.
- C. Peng, J. A. Calvin and E. F. Valeev, Int. J. Quantum Chem., 2019, 119, e25894 CrossRef.
- D. Datta and M. S. Gordon, J. Chem. Theory Comput., 2021, 17, 4799 CrossRef.
- J. J. Eriksen, Mol. Phys., 2017, 115, 2086 CrossRef.
- L. Gyevi-Nagy, M. Kállay and P. R. Nagy, J. Chem. Theory Comput., 2020, 16, 366 CrossRef PubMed.
- L. Gyevi-Nagy, M. Kállay and P. R. Nagy, J. Chem. Theory Comput., 2021, 17, 860 CrossRef.
- P. R. Nagy, L. Gyevi-Nagy and M. Kállay, Mol. Phys., 2021, 119, e1963495 CrossRef.
- M. Kállay, R. A. Horváth, L. Gyevi-Nagy and P. R. Nagy, J. Chem. Theory Comput., 2023, 19, 174 CrossRef.
- Y. Guo, C. Riplinger, U. Becker, D. G. Liakos, Y. Minenkov, L. Cavallo and F. Neese, J. Chem. Phys., 2018, 148, 011101 CrossRef PubMed.
- Q. Ma and H.-J. Werner, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8, e1371 Search PubMed.
- G. Schmitz and C. Hättig, J. Chem. Phys., 2016, 145, 234107 CrossRef PubMed.
- P. R. Nagy and M. Kállay, J. Chem. Theory Comput., 2019, 15, 5275 CrossRef CAS PubMed.
- F. Neese, F. Wennmohs and A. Hansen, J. Chem. Phys., 2009, 130, 114108 CrossRef PubMed.
- D. G. Liakos, M. Sparta, M. K. Kesharwani, J. M. L. Martin and F. Neese, J. Chem. Theory Comput., 2015, 11, 1525 CrossRef CAS.
- D. G. Liakos and F. Neese, J. Chem. Theory Comput., 2015, 11, 4054 CrossRef CAS PubMed.
- C. Riplinger, P. Pinski, U. Becker, E. F. Valeev and F. Neese, J. Chem. Phys., 2016, 144, 024109 CrossRef.
- F. Pavošević, C. Peng, P. Pinski, C. Riplinger, F. Neese and E. F. Valeev, J. Chem. Phys., 2017, 146, 174108 CrossRef.
- Y. Guo, C. Riplinger, D. G. Liakos, U. Becker, M. Saitow and F. Neese, J. Chem. Phys., 2020, 152, 024116 CrossRef CAS PubMed.
- Q. Ma and H.-J. Werner, J. Chem. Theory Comput., 2018, 14, 198 CrossRef CAS PubMed.
- Q. Ma and H.-J. Werner, J. Chem. Theory Comput., 2019, 15, 1044 CrossRef CAS PubMed.
- Q. Ma and H.-J. Werner, J. Chem. Theory Comput., 2021, 17, 902 CrossRef CAS PubMed.
- G. Schmitz, C. Hättig and D. P. Tew, Phys. Chem. Chem. Phys., 2014, 16, 22167 RSC.
- M. Bensberg and J. Neugebauer, J. Chem. Theory Comput., 2020, 16, 3607 CrossRef CAS.
- R. D'Cunha and T. D. Crawford, J. Chem. Theory Comput., 2021, 17, 290 CrossRef.
- Z. Rolik and M. Kállay, J. Chem. Phys., 2011, 135, 104111 CrossRef.
- Z. Rolik, L. Szegedy, I. Ladjánszki, B. Ladóczki and M. Kállay, J. Chem. Phys., 2013, 139, 094105 CrossRef.
- P. R. Nagy, G. Samu and M. Kállay, J. Chem. Theory Comput., 2016, 12, 4897 CrossRef CAS PubMed.
- P. R. Nagy and M. Kállay, J. Chem. Phys., 2017, 146, 214106 CrossRef.
- P. R. Nagy, G. Samu and M. Kállay, J. Chem. Theory Comput., 2018, 14, 4193 CrossRef CAS.
- P. B. Szabó, J. Csóka, M. Kállay and P. R. Nagy, J. Chem. Theory Comput., 2021, 17, 2886 CrossRef.
- P. B. Szabó, J. Csóka, M. Kállay and P. R. Nagy, J. Chem. Theory Comput., 2023, 19, 8166 CrossRef.
- D. Mester, P. R. Nagy and M. Kállay, J. Chem. Theory Comput., 2019, 15, 6111 CrossRef CAS.
- M. Gordon, Fragmentation: Toward Accurate Calculations on Complex Molecular Systems, Wiley, 2017 Search PubMed.
- J. M. Herbert, J. Chem. Phys., 2019, 151, 170901 CrossRef.
- F. Neese, M. Atanasov, G. Bistoni, D. Maganas and S. Ye, J. Am. Chem. Soc., 2019, 141, 2814 CrossRef CAS.
- R. Izsák, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2020, 10, e1445 Search PubMed.
- R. M. Richard, K. U. Lao and J. M. Herbert, Acc. Chem. Res., 2014, 47, 2828 CrossRef CAS.
- D. G. Fedorov, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2017, 7, e1322 Search PubMed.
- N. Sahu and S. R. Gadre, Acc. Chem. Res., 2014, 47, 2739 CrossRef CAS.
- W. Li, Z. Ni and S. Li, Mol. Phys., 2016, 114, 1447 CrossRef CAS.
- M. Kállay, P. R. Nagy, D. Mester, Z. Rolik, G. Samu, J. Csontos, J. Csóka, P. B. Szabó, L. Gyevi-Nagy, B. Hégely, I. Ladjánszki, L. Szegedy, B. Ladóczki, K. Petrov, M. Farkas, P. D. Mezei and Á. Ganyecz, J. Chem. Phys., 2020, 152, 074107 CrossRef.
- M. Kállay, P. R. Nagy, D. Mester, L. Gyevi-Nagy, J. Csóka, P. B. Szabó, Z. Rolik, G. Samu, J. Csontos, B. Hégely, Á. Ganyecz, I. Ladjánszki, L. Szegedy, B. Ladóczki, K. Petrov, M. Farkas, P. D. Mezei and R. A. Horváth, MRCC, a quantum chemical program suite, See https://www.mrcc.hu/, Accessed August 28, 2023.
- F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2017, 8, e1327 Search PubMed.
- T. Korona and H.-J. Werner, J. Chem. Phys., 2003, 118, 3006 CrossRef CAS.
- D. Kats, T. Korona and M. Schütz, J. Chem. Phys., 2006, 125, 104106 CrossRef PubMed.
- K. Ledermüller and M. Schütz, J. Chem. Phys., 2014, 140, 164113 CrossRef PubMed.
- M. S. Frank and C. Hättig, J. Chem. Phys., 2018, 148, 134102 CrossRef PubMed.
- T. D. Crawford and R. A. King, Chem. Phys. Lett., 2002, 366, 611 CrossRef CAS.
- C. Peng, M. C. Clement and E. F. Valeev, J. Chem. Theory Comput., 2018, 14, 5597 CrossRef CAS.
- A. K. Dutta, M. Nooijen, F. Neese and R. Izsák, J. Chem. Theory Comput., 2018, 14, 72 CrossRef CAS.
- P. Baudin, D. Bykov, D. Liakh, P. Ettenhuber and K. Kristensen, Mol. Phys., 2017, 115, 2135 CrossRef CAS.
- P. Pinski and F. Neese, J. Chem. Phys., 2019, 150, 164102 CrossRef.
- M. Dornbach and H.-J. Werner, Mol. Phys., 2019, 117, 1252 CrossRef CAS.
- Z. Ni, Y. Wang, W. Li, P. Pulay and S. Li, J. Chem. Theory Comput., 2019, 15, 3623 CrossRef CAS.
- M. S. Frank, G. Schmitz and C. Hättig, Mol. Phys., 2017, 115, 343 CrossRef CAS.
- S. Schweizer, B. Doser and C. Ochsenfeld, J. Chem. Phys., 2008, 128, 154101 CrossRef.
- D. Bykov, K. Kristensen and T. Kjærgaard, J. Chem. Phys., 2016, 145, 024106 CrossRef PubMed.
- R. Zhou, Q. Liang and J. Yang, J. Chem. Theory Comput., 2020, 16, 196 CrossRef PubMed.
- A. El Azhary, G. Rauhut, P. Pulay and H.-J. Werner, J. Chem. Phys., 1998, 108, 5185 CrossRef CAS.
- C. Naim, P. Besalú-Sala, R. Zaleśny, J. M. Luis, F. Castet and E. Matito, J. Chem. Theory Comput., 2023, 19, 1753 CrossRef CAS PubMed.
- T. D. Crawford, A. Kumar, A. P. Bazanté and R. Di Remigio, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2019, 9, e1406 Search PubMed.
- D. Datta, S. Kossmann and F. Neese, J. Chem. Phys., 2016, 145, 114101 CrossRef.
- T. Korona, K. Pflüger and H.-J. Werner, Phys. Chem. Chem. Phys., 2004, 6, 2059 RSC.
- J. Kozłowska, M. Schwilk, A. Roztoczyńska and W. Bartkowiak, Phys. Chem. Chem. Phys., 2018, 20, 29374 RSC.
- D. B. Krisiloff, C. M. Krauter, F. J. Ricci and E. A. Carter, J. Chem. Theory Comput., 2015, 11, 5242 CrossRef CAS.
- O. Demel, J. Pittner and F. Neese, J. Chem. Theory Comput., 2015, 11, 3104 CrossRef CAS PubMed.
- Y. Guo, K. Sivalingam, E. F. Valeev and F. Neese, J. Chem. Phys., 2016, 144, 094111 CrossRef PubMed.
- F. Menezes, D. Kats and H.-J. Werner, J. Chem. Phys., 2016, 145, 124115 CrossRef PubMed.
- K. Uemura, M. Saitow, T. Ishimaru and T. Yanai, J. Chem. Phys., 2023, 158, 154110 CrossRef CAS.
- J. S. Kurian, H.-Z. Ye, A. Mahajan, T. C. Berkelbach and S. Sharma, J. Chem. Theory Comput., 2024, 20, 134 CrossRef CAS PubMed.
- N. J. Mayhall and K. Raghavachari, J. Chem. Theory Comput., 2011, 7, 1336 CrossRef CAS.
- W. Li, H. Dong, J. Ma and S. Li, Acc. Chem. Res., 2020, 54, 169 CrossRef PubMed.
- H. Nakai, M. Kobayashi, T. Yoshikawa, J. Seino, Y. Ikabata and Y. Nishimura, J. Phys. Chem. A, 2023, 127, 589 CrossRef CAS.
- J. J. Eriksen, P. Baudin, P. Ettenhuber, K. Kristensen, T. Kjærgaard and P. Jørgensen, J. Chem. Theory Comput., 2015, 11, 2984 CrossRef CAS PubMed.
- P. Pulay, Chem. Phys. Lett., 1983, 100, 151 CrossRef CAS.
- P. Pulay and S. Saebø, Theor. Chem. Acc., 1986, 69, 357 Search PubMed.
- S. Saebø and P. Pulay, J. Chem. Phys., 1987, 86, 914 CrossRef.
- S. Saebø and P. Pulay, Chem. Phys. Lett., 1985, 113, 13 CrossRef.
- W. Förner, J. Ladik, P. Otto and J. Čížek, Chem. Phys., 1985, 97, 251 CrossRef.
- N. Flocke and R. J. Bartlett, J. Chem. Phys., 2004, 121, 10935 CrossRef CAS.
- J. Friedrich and M. Dolg, J. Chem. Theory Comput., 2009, 5, 287 CrossRef CAS PubMed.
- B. Fiedler, G. Schmitz, C. Hättig and J. Friedrich, J. Chem. Theory Comput., 2017, 13, 6023 CrossRef CAS.
- Y. Mochizuki, K. Yamashita, T. Nakano, Y. Okiyama, K. Fukuzawa, N. Taguchi and S. Tanaka, Theor. Chem. Acc., 2011, 130, 515 Search PubMed.
- D. Yuan, Y. Li, Z. Ni, P. Pulay, W. Li and S. Li, J. Chem. Theory Comput., 2017, 13, 2696 CrossRef CAS PubMed.
- W. Li, P. Piecuch, J. R. Gour and S. Li, J. Chem. Phys., 2009, 131, 114109 CrossRef PubMed.
- Y. Guo, U. Becker and F. Neese, J. Chem. Phys., 2018, 148, 124117 CrossRef PubMed.
- Z. Ni, W. Li and S. Li, J. Comput. Chem., 2019, 40, 1130 CrossRef CAS PubMed.
- W. Li and S. Li, J. Chem. Phys., 2004, 121, 6649 CrossRef CAS.
- M. Kobayashi and H. Nakai, J. Chem. Phys., 2009, 131, 114108 CrossRef PubMed.
- M. Nakano, T. Yoshikawa, S. Hirata, J. Seino and H. Nakai, J. Comput. Chem., 2017, 38, 2520 CrossRef CAS PubMed.
- M. Schütz, J. Yang, G. K.-L. Chan, F. R. Manby and H.-J. Werner, J. Chem. Phys., 2013, 138, 054109 CrossRef.
- P. E. Maslen, A. D. Dutoi, M. S. Lee, Y. Shao and M. Head-Gordon, Mol. Phys., 2005, 103, 425 CrossRef CAS.
- Y. Jin and R. J. Bartlett, J. Phys. Chem. A, 2018, 123, 371 CrossRef.
- O. Demel, M. J. Lecours, R. Habrovský and M. Nooijen, J. Chem. Phys., 2021, 155, 154104 CrossRef CAS PubMed.
- A. D. Findlater, F. Zahariev and M. S. Gordon, J. Phys. Chem. A, 2015, 119, 3587 CrossRef CAS PubMed.
- P. R. Surján and Á. Szabados, J. Chem. Theory Comput., 2022, 18, 2955 CrossRef PubMed.
- M. Kállay, J. Chem. Phys., 2015, 142, 204105 CrossRef.
- P. Y. Ayala and G. E. Scuseria, J. Chem. Phys., 1999, 110, 3660 CrossRef CAS.
- G. E. Scuseria and P. Y. Ayala, J. Chem. Phys., 1999, 111, 8330 CrossRef CAS.
- S. A. Maurer, D. S. Lambrecht, J. Kussmann and C. Ochsenfeld, J. Chem. Phys., 2013, 138, 014101 CrossRef.
- S. Saebø, J. Baker, K. Wolinski and P. Pulay, J. Chem. Phys., 2004, 120, 11423 CrossRef PubMed.
- P. R. Surján, Chem. Phys. Lett., 2005, 406, 318 CrossRef.
- A. Förster, M. Franchini, E. van Lenthe and L. Visscher, J. Chem. Theory Comput., 2020, 16, 875 CrossRef.
- C. Song and T. J. Martínez, J. Chem. Phys., 2016, 144, 174111 CrossRef PubMed.
- B. Helmich-Paris and S. Knecht, J. Chem. Phys., 2017, 146, 224101 CrossRef.
- R. Zaleśny, M. Papadopoulos, P. Mezey and J. Leszczynski, Linear-Scaling Techniques in Computational Chemistry and Physics: Methods and Applications, Springer, Netherlands, 2011 Search PubMed.
- M. A. Collins and R. P. A. Bettens, Chem. Rev., 2015, 115, 5607 CrossRef CAS.
- K. Raghavachari and A. Saha, Chem. Rev., 2015, 115, 5643 CrossRef CAS.
- M. Kállay, J. Chem. Phys., 2014, 141, 244113 CrossRef PubMed.
- J. Almlöf, Chem. Phys. Lett., 1991, 181, 319 CrossRef.
- B. Hégely, P. R. Nagy, G. G. Ferenczy and M. Kállay, J. Chem. Phys., 2016, 145, 064107 CrossRef.
- B. Hégely, P. R. Nagy and M. Kállay, J. Chem. Theory Comput., 2018, 14, 4600 CrossRef.
- T. Anacker, D. P. Tew and J. Friedrich, J. Chem. Theory Comput., 2016, 12, 65 CrossRef CAS PubMed.
- J. Zhang and M. Dolg, J. Chem. Theory Comput., 2015, 11, 962 CrossRef CAS.
- F. R. Manby, M. Stella, J. D. Goodpaster and T. F. Miller III, J. Chem. Theory Comput., 2012, 8, 2564 CrossRef CAS PubMed.
- J. D. Goodpaster, T. A. Barnes, F. R. Manby and T. F. Miller III, J. Chem. Phys., 2014, 140, 18A507 CrossRef.
- M. Bensberg and J. Neugebauer, J. Chem. Phys., 2021, 155, 224102 CrossRef CAS PubMed.
- Z. Amanollahi, L. Lampe, M. Bensberg, J. Neugebauer and M. Feldt, Phys. Chem. Chem. Phys., 2023, 25, 4635 RSC.
- M. Sparta, M. Retegan, P. Pinski, C. Riplinger, U. Becker and F. Neese, J. Chem. Theory Comput., 2017, 13, 3198 CrossRef CAS PubMed.
- R. A. Mata, H.-J. Werner and M. Schütz, J. Chem. Phys., 2008, 128, 144106 CrossRef PubMed.
- M. Feldt and R. A. Mata, J. Chem. Theory Comput., 2018, 14, 5192 CrossRef CAS.
- W. Li and P. Piecuch, J. Phys. Chem. A, 2010, 114, 6721 CrossRef CAS PubMed.
- S. Li, J. Shen, W. Li and Y. Jiang, J. Chem. Phys., 2006, 125, 074109 CrossRef.
- J. Csóka, B. Hégely, P. R. Nagy and M. Kállay, J. Chem. Phys., 2024, 160, 124113 CrossRef.
- G. Bistoni, I. Polyak, M. Sparta, W. Thiel and F. Neese, J. Chem. Theory Comput., 2018, 14, 3524 CrossRef CAS PubMed.
- A. Kubas, D. Berger, H. Oberhofer, D. Maganas, K. Reuter and F. Neese, J. Phys. Chem. Lett., 2016, 7, 4207 CrossRef CAS PubMed.
- B. Shi, A. Zen, V. Kapil, P. R. Nagy, A. Grüneis and A. Michaelides, J. Am. Chem. Soc., 2023, 145, 25372 CrossRef CAS PubMed.
- A. Karton and J. M. L. Martin, Theor. Chem. Acc., 2006, 115, 330 Search PubMed.
- T. Helgaker, W. Klopper, H. Koch and J. Noga, J. Chem. Phys., 1997, 106, 9639 CrossRef CAS.
- A. Altun, F. Neese and G. Bistoni, J. Chem. Theory Comput., 2020, 16, 6142 CrossRef CAS.
- K. Sorathia and D. P. Tew, J. Chem. Phys., 2020, 153, 174112 CrossRef CAS PubMed.
- G. Laczkó, I. Pápai and P. R. Nagy, 2024, In preparation.
- R. Yousefi, A. Sarkar, K. D. Ashtekar, D. C. Whitehead, T. Kakeshpour, D. Holmes, P. Reed, J. E. Jackson and B. Borhan, J. Am. Chem. Soc., 2020, 142, 7179 CrossRef CAS.
- P. R. Nagy, L. Gyevi-Nagy, B. D. Lőrincz and M. Kállay, Mol. Phys., 2023, 121, e2109526 CrossRef.
- Y. S. Al-Hamdani, P. R. Nagy, D. Barton, M. Kállay, J. G. Brandenburg and A. Tkatchenko, Nat. Commun., 2021, 12, 3927 CrossRef CAS PubMed.
- S. F. Boys and F. Bernardi, Mol. Phys., 1970, 19, 553 CrossRef CAS.
- J. Řezáč, K. E. Riley and P. Hobza, J. Chem. Theory Comput., 2011, 7, 2427 CrossRef.
- T. Földes, Á. Madarász, Á. Révész, Z. Dobi, S. Varga, A. Hamza, P. R. Nagy, P. M. Pihko and I. Pápai, J. Am. Chem. Soc., 2017, 139, 17052 CrossRef.
- R. Sedlak, T. Janowski, M. Pitoňák, J. Řezáč, P. Pulay and P. Hobza, J. Chem. Theory Comput., 2013, 9, 3364 CrossRef CAS PubMed.
- A. Benali, H. Shin and O. Heinonen, J. Chem. Phys., 2020, 153, 194113 CrossRef CAS.
- F. Ballesteros, S. Dunivan and K. U. Lao, J. Chem. Phys., 2021, 154, 154104 CrossRef CAS PubMed.
- A. S. Christensen, M. Elstner and Q. Cui, J. Chem. Phys., 2015, 143, 084123 CrossRef PubMed.
- K. Carter-Fenk, K. U. Lao, K.-Y. Liu and J. M. Herbert, J. Phys. Chem. Lett., 2019, 10, 2706 CrossRef CAS.
- J. Calbo, E. Ortí, J. C. Sancho-García and J. Aragó, J. Chem. Theory Comput., 2015, 11, 932 CrossRef CAS PubMed.
- R. Huenerbein, B. Schirmer, J. Moellmann and S. Grimme, Phys. Chem. Chem. Phys., 2010, 12, 6940 RSC.
- D. G. Liakos and F. Neese, J. Phys. Chem. A, 2012, 116, 4801 CrossRef CAS.
- E. Paulechka and A. Kazakov, J. Chem. Theory Comput., 2018, 14, 5920 CrossRef CAS PubMed.
- Q. Ma and H.-J. Werner, J. Chem. Theory Comput., 2020, 16, 3135 CrossRef CAS.
- P. B. Szabó, J. Csóka, M. Kállay and P. R. Nagy, 2024, in preparation.
- I. Sandler, S. Sharma, B. Chan and J. Ho, J. Phys. Chem. A, 2021, 125, 9838 CrossRef CAS PubMed.
- R. Ghafarian Shirazi, F. Neese and D. A. Pantazis, J. Chem. Theory Comput., 2018, 14, 4733 CrossRef CAS.
- J. Řezáč, K. E. Riley and P. Hobza, J. Chem. Theory Comput., 2011, 7, 3466 CrossRef.
- G. Santra, E. Semidalas, N. Mehta, A. Karton and J. M. L. Martin, Phys. Chem. Chem. Phys., 2022, 24, 25555 RSC.
- I. Efremenko and J. M. L. Martin, J. Phys. Chem. A, 2021, 125, 8987 CrossRef CAS PubMed.
- S. Ehlert, S. Grimme and A. Hansen, J. Phys. Chem. A, 2022, 126, 3521 CrossRef CAS PubMed.
- G. Santra and J. M. Martin, J. Phys. Chem. A, 2022, 126, 9375 CrossRef CAS PubMed.
- A. Karton and B. Chan, Comput. Theor. Chem., 2022, 1217, 113874 CrossRef CAS.
- M. A. Iron and T. Janes, J. Phys. Chem. A, 2019, 123, 3761 CrossRef CAS PubMed.
- E. Semidalas and J. M. L. Martin, J. Chem. Theory Comput., 2022, 18, 883 CrossRef CAS PubMed.
- N. Sylvetsky, A. Banerjee, M. Alonso and J. M. L. Martin, J. Chem. Theory Comput., 2020, 16, 3641 CrossRef CAS.
- C. Riplinger, B. Sandhoefer, A. Hansen and F. Neese, J. Chem. Phys., 2013, 139, 134101 CrossRef PubMed.
- H. Neugebauer, P. Pinski, S. Grimme, F. Neese and M. Bursch, J. Chem. Theory Comput., 2023, 19, 7695 CrossRef CAS.
- A. Kumar, F. Neese and E. F. Valeev, J. Chem. Phys., 2020, 153, 094105 CrossRef CAS PubMed.
- R. Polly, H.-J. Werner, F. R. Manby and P. J. Knowles, Mol. Phys., 2004, 102, 2311 CrossRef CAS.
- J. Csóka and M. Kállay, Mol. Phys., 2020, 118, e1769213 CrossRef.
- C. Köppl and H.-J. Werner, J. Chem. Theory Comput., 2016, 12, 3122 CrossRef PubMed.
- F. Neese, F. Wennmohs, A. Hansen and U. Becker, Chem. Phys., 2009, 356, 98 CrossRef CAS.
- C. Riplinger and F. Neese, J. Chem. Phys., 2013, 138, 034106 CrossRef PubMed.
- L. Goerigk, A. Hansen, C. Bauer, S. Ehrlich, A. Najibi and S. Grimme, Phys. Chem. Chem. Phys., 2017, 19, 32184 RSC.
- N. Mardirossian and M. Head-Gordon, Mol. Phys., 2017, 115, 2315 CrossRef CAS.
- L. R. Maurer, M. Bursch, S. Grimme and A. Hansen, J. Chem. Theory Comput., 2021, 17, 6134 CrossRef CAS PubMed.
- G. Bistoni, A. A. Auer and F. Neese, Chem. - Eur. J., 2017, 23, 865 CrossRef CAS.
- S. Dohm, A. Hansen, M. Steinmetz, S. Grimme and M. P. Checinski, J. Chem. Theory Comput., 2018, 14, 2596 CrossRef CAS PubMed.
- V. K. Prasad, Z. Pei, S. Edelmann, A. Otero-de-la-Roza and G. A. DiLabio, J. Chem. Theory Comput., 2022, 18, 151 CrossRef CAS.
- J. Řezáč, D. Bí, O. Gutten and L. Rulíšek, J. Chem. Theory Comput., 2018, 14, 1254 CrossRef PubMed.
- S. Grimme, A. Hansen, S. Ehlert and J.-M. Mewes, J. Chem. Phys., 2021, 154, 064103 CrossRef CAS PubMed.
- J. Xiao, Y. Chen, L. Zhang, H. Wang and T. Zhu, Artif. Intell. Chem., 2024, 2, 100037 CrossRef.
- E. Semidalas, G. Santra, N. Mehta and J. M. L. Martin, AIP Conf. Proc., 2022, 2611, 020016 CrossRef.
- H.-J. Werner and A. Hansen, J. Chem. Theory Comput., 2023, 19, 7007 CrossRef CAS.
- J. G. Brandenburg, C. Bannwarth, A. Hansen and S. Grimme, J. Chem. Phys., 2018, 148, 064104 CrossRef.
- J.-L. Chen, T. Sun, Y.-B. Wang and W. Wang, J. Comput. Chem., 2020, 41, 1252 CrossRef CAS PubMed.
- T. J. Daas, E. Fabiano, F. Della Sala, P. Gori-Giorgi and S. Vuckovic, J. Phys. Chem. Lett., 2021, 12, 4867 CrossRef PubMed.
- S. Ehlert, U. Huniar, J. Ning, J. W. Furness, J. Sun, A. D. Kaplan, J. P. Perdew and J. G. Brandenburg, J. Chem. Phys., 2021, 154, 061101 CrossRef CAS.
- J. Shee, M. Loipersberger, A. Rettig, J. Lee and M. Head-Gordon, J. Phys. Chem. Lett., 2022, 12, 12084 CrossRef.
- P. Kraus, J. Chem. Theory Comput., 2021, 17, 5651 CrossRef CAS.
- J. Czernek, J. Brus and V. Czerneková, Int. J. Mol. Sci., 2022, 23, 15773 CrossRef CAS PubMed.
- J. Gorges, B. Bädorf, S. Grimme and A. Hansen, Synlett, 2022, 34, 1135 CrossRef.
- G. Montgomery, H. John, 2023, preprint, DOI:10.1016/bs.arcc.2024.03.001.
- M. Thürlemann and S. Riniker, Chem. Sci., 2023, 14, 12661 RSC.
- C. W. Kee, Molecules, 2023, 28, 1715 CrossRef CAS PubMed.
- M. Müller, A. Hansen and S. Grimme, J. Chem. Phys., 2023, 158, 014103 CrossRef PubMed.
- V. Wineman-Fisher, J. M. Delgado, P. R. Nagy, E. Jakobsson, S. A. Pandit and S. Varma, J. Chem. Phys., 2020, 153, 104113 CrossRef CAS PubMed.
- V. Wineman-Fisher, Y. Al-Hamdani, P. R. Nagy, A. Tkatchenko and S. Varma, J. Chem. Phys., 2020, 153, 094115 CrossRef CAS PubMed.
- S. Rahman, V. Wineman-Fisher, P. R. Nagy, Y. Al-Hamdani, A. Tkatchenko and S. Varma, Chem. - Eur. J., 2021, 27, 11005 CrossRef CAS PubMed.
- J. M. Delgado, P. R. Nagy and S. Varma, J. Chem. Inf. Model., 2023, 63, 378 Search PubMed.
- K. Kříž and J. Řezáč, J. Chem. Inf. Model., 2020, 60, 1453 CrossRef PubMed.
- M. Puleva, L. M. Sandonas, B. D. Lőrincz, J. A. C. Martinez, D. M. Rogers, P. R. Nagy and A. Tkatchenko, 2024, in preparation.
- H. Kruse, A. Mladek, K. Gkionis, A. Hansen, S. Grimme and J. Sponer, J. Chem. Theory Comput., 2015, 11, 4972 CrossRef CAS PubMed.
- D. A. Wappett and L. Goerigk, J. Phys. Chem. A, 2024, 128, 62 CrossRef CAS.
- D. A. Wappett and L. Goerigk, J. Chem. Theory Comput., 2023, 19, 8365 CrossRef CAS.
- T. Husch, L. Freitag and M. Reiher, J. Chem. Theory Comput., 2018, 14, 2456 CrossRef CAS.
- M. Radoń, Phys. Chem. Chem. Phys., 2019, 21, 4854–4870 RSC.
- M. Drosou, C. A. Mitsopoulou and D. A. Pantazis, J. Chem. Theory Comput., 2022, 18, 3538 CrossRef CAS.
- A. Altun, C. Riplinger, F. Neese and G. Bistoni, J. Chem. Theory Comput., 2023, 19, 2039 CrossRef CAS PubMed.
- M. Feldt, C. Martín-Fernández and J. N. Harvey, Phys. Chem. Chem. Phys., 2020, 22, 23908 RSC.
- M. Feldt, Q. M. Phung, K. Pierloot, R. A. Mata and J. N. Harvey, J. Chem. Theory Comput., 2019, 15, 922 CrossRef CAS.
- T. Weymuth, E. P. A. Couzijn, P. Chen and M. Reiher, J. Chem. Theory Comput., 2014, 10, 3092 CrossRef CAS PubMed.
- S. Fürst, M. Haasler, R. Grotjahn and M. Kaupp, J. Chem. Theory Comput., 2023, 19, 488 CrossRef.
- A. D. Becke, J. Chem. Phys., 2023, 159, 241101 CrossRef CAS.
- R. Grotjahn and M. Kaupp, Isr. J. Chem., 2023, 63, e202200021 CrossRef CAS.
- T. Gasevic, J. B. Stückrath, S. Grimme and M. Bursch, J. Phys. Chem. A, 2022, 126, 3826 CrossRef CAS.
- B. Chan, W. Dawson and T. Nakajima, J. Phys. Chem. A, 2022, 126, 2119 CrossRef CAS.
- V. Štejfa, A. Bazyleva, M. Fulem, J. Rohlíček, E. Skořepová, K. Růžička and A. V. Blokhin, J. Chem. Thermodyn., 2019, 131, 524 CrossRef.
- I. Bakó, I. Mayer, A. Hamza and L. Pusztai, J. Mol. Liq., 2019, 285, 171 CrossRef.
- M. Bojtár, P. Z. Janzsó-Berend, D. Mester, D. Hessz, M. Kállay, M. Kubinyi and I. Bitter, Beilstein J. Org. Chem., 2018, 14, 747 CrossRef.
- A. Paudics, D. Hessz, M. Bojtár, B. Gyarmati, A. Szilágyi, M. Kállay, I. Bitter and M. Kubinyi, Molecules, 2020, 25, 5111 CrossRef CAS PubMed.
- A. Paudics, D. Hessz, M. Bojtár, I. Bitter, V. Horváth, M. Kállay and M. Kubinyi, Sens. Actuators, B, 2022, 369, 132364 CrossRef CAS.
- E. Paulechka and A. Kazakov, J. Chem. Eng. Data, 2019, 64, 4863 CrossRef CAS.
- E. Paulechka and A. Kazakov, J. Phys. Chem. A, 2021, 125, 8116 CrossRef CAS.
- A. Bazyleva, E. Paulechka, D. H. Zaitsau, A. V. Blokhin and G. J. Kabo, Thermochim. Acta, 2020, 686, 178538 CrossRef CAS PubMed.
- A. Kazakov, E. Paulechka and R. D. Chirico, J. Chem. Eng. Data, 2022, 67, 1834 CrossRef CAS.
- A. Bazyleva, D. H. Zaitsau and G. J. Kabo, J. Chem. Thermodyn., 2023, 186, 107134 CrossRef CAS.
- E. Paulechka and A. Kazakov, J. Phys. Chem. A, 2024, 128, 1339 CrossRef CAS.
- T. Papp, P. R. Nagy and T. Kégl, 2024, in preparation.
- A. Ott, P. R. Nagy and Z. Benkő, Inorg. Chem., 2022, 61, 16266 CrossRef CAS.
- P. Kaymak, M. Yang and Z. Benkő, Dalton Trans., 2023, 52, 13930 RSC.
- Y. Jiang, C. T. Supuran and J. Ho, J. Phys. Chem. A, 2022, 126, 9207 CrossRef CAS PubMed.
- D. Buzskái, M. B. Kovács, E. Hümpfner, Z. Harcsa-Pintér and Z. Kelemen, Chem. Sci., 2022, 13, 11388 RSC.
- E. Hümpfner, D. Buzsáki and Z. Kelemen, ChemistrySelect, 2022, 7, e202201768 CrossRef.
- T. Elliott, L. Charbonneau, E. Gazagnaire, I. Kilpeläinen, B. Kótai, G. Laczkó, I. Pápai and T. Repo, RSC Sustainability, 2024, 2, 1753 RSC.
- L. Kárpáti, Á. Ganyecz, T. Nagy, G. Hamar, E. Banka, M. Kállay and V. Vargha, Polym. Bull., 2019, 77, 4655 CrossRef.
- J. Zechovský, E. Kertész, M. Erben, R. Jambor, A. Růižkča, Z. Benkő and L. Dostál, ChemPlusChem, 2023, 88, e202300018 CrossRef.
- S. Giese, D. Buzsáki, L. Nyulászi and C. Müller, Chem. Commun., 2019, 55, 13812 RSC.
- A. Hamza, K. Sorochkina, B. Kótai, K. Chernichenko, D. Berta, M. Bolte, M. Nieger, T. Repo and I. Pápai, ACS Catal., 2020, 10, 14290 CrossRef CAS.
- D. Buzsáki, L. Nyulászi, R. Pietschnig, D. Gudat and Z. Kelemen, Organometallics, 2022, 41, 2551 CrossRef.
- P. Buday, P. Seeber, C. Zens, H. Abul-Futouh, H. Görls, S. Gräfe, P. Matczak, S. Kupfer, W. Weigand and G. Mloston, Chem. - Eur. J., 2020, 26, 11412 CrossRef CAS.
- M. Stephan, W. Dammann and P. Burger, Dalton Trans., 2022, 51, 13396 RSC.
- M. Stephan, M. Völker, M. Schreyer and P. Burger, Chemistry, 2023, 5, 1961 CrossRef CAS.
- B. X. Shi, A. Michaelides and C. W. Myung, 2023, preprint, 2311.01426, DOI:10.1021/acs.jctc.4c00379.
- B. X. Shi, V. Kapil, A. Zen, J. Chen, A. Alavi and A. Michaelides, J. Chem. Phys., 2022, 156, 124704 CrossRef CAS.
- J. Řezáč and P. Hobza, Chem. Rev., 2016, 116, 5038 CrossRef PubMed.
- Y. S. Al-Hamdani and A. Tkatchenko, J. Chem. Phys., 2019, 150, 010901 CrossRef PubMed.
- Z. Benedek, M. Papp, J. Oláh and T. Szilvási, ACS Catal., 2020, 10, 12555 CrossRef CAS.
- B. Mondal, F. Neese and S. Ye, Inorg. Chem., 2015, 54, 7192 CrossRef CAS.
- C. R. Wick and D. M. Smith, J. Phys. Chem. A, 2018, 122, 1747 CrossRef CAS.
- G. Laude, D. Calderini, D. P. Tew and J. O. Richardson, Faraday Discuss., 2018, 212, 237 RSC.
- C. Schran, J. Behler and D. Marx, J. Chem. Theory Comput., 2020, 16, 88 CrossRef.
- S. Chmiela, H. E. Sauceda, K.-R. Müller and A. Tkatchenko, Nat. Commun., 2018, 9, 3887 CrossRef.
- S. Käser, O. T. Unke and M. Meuwly, New J. Phys., 2020, 22, 055002 CrossRef.
- C. Qu, P. L. Houston, R. Conte, A. Nandi and J. M. Bowman, J. Phys. Chem. Lett., 2021, 12, 4902 CrossRef CAS.
- G. F. von Rudorff and O. A. von Lilienfeld, Sci. Adv., 2021, 7, eabf1173 CrossRef CAS PubMed.
- M. Gacesa, 2023, preprint, 2308.05439, DOI:10.1093/mnras/stae219.
- J. S. Smith, B. T. Nebgen, R. Zubatyuk, N. Lubbers, C. Devereux, K. Barros, S. Tretiak, O. Isayev and A. E. Roitberg, Nat. Commun., 2019, 10, 2903 CrossRef.
- T. A. Young, T. Johnston-Wood, V. L. Deringer and F. Duarte, Chem. Sci., 2021, 12, 10944 RSC.
- B. Gruber, V. Tajti and G. Czakó, J. Chem. Phys., 2022, 157, 074307 CrossRef CAS.
- J. Daru, H. Forbert, J. Behler and D. Marx, Phys. Rev. Lett., 2022, 129, 226001 CrossRef CAS.
- M. Garcia-Ratés, U. Becker and F. Neese, J. Comput. Chem., 2021, 42, 1959 CrossRef PubMed.
- D. Usvyat, L. Maschio and M. Schütz, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8, e1357 Search PubMed.
- J. Sauer, Acc. Chem. Res., 2019, 52, 3502 CrossRef CAS.
- I. Y. Zhang and A. Grüneis, Front. Mater., 2019, 6, 123 CrossRef.
- E. Rebolini, G. Baardsen, A. S. Hansen, K. R. Leikanger and T. B. Pedersen, J. Chem. Theory Comput., 2018, 14, 2427 CrossRef CAS PubMed.
- Y. Wang, Z. Ni, W. Li and S. Li, J. Chem. Theory Comput., 2019, 15, 2933 CrossRef CAS PubMed.
- O. Masur, M. Schütz, L. Maschio and D. Usvyat, J. Chem. Theory Comput., 2016, 12, 5145 CrossRef CAS.
- H.-Z. Ye and T. C. Berkelbach, 2023, preprint 2309, 14640, DOI:10.48550/arXiv.2309.14640.
- M. Schütz, L. Maschio, A. J. Karttunen and D. Usvyat, J. Phys. Chem. Lett., 2017, 8, 1290 CrossRef.
- T. Schäfer, F. Libisch, G. Kresse and A. Grüneis, J. Chem. Phys., 2021, 154, 011101 CrossRef.
- J. Yang, W. Hu, D. Usvyat, D. Matthews, M. Schütz and G. K.-L. Chan, Science, 2014, 345, 640 CrossRef CAS PubMed.
- D. O. Scanlon, C. W. Dunnill, J. Buckeridge, S. A. Shevlin, A. J. Logsdail, S. M. Woodley, C. R. A. Catlow, M. J. Powell, R. G. Palgrave, I. P. Parkin, G. W. Watson, T. W. Keal, P. Sherwood, A. Walsh and A. A. Sokol, Nat. Mater., 2013, 12, 798 CrossRef CAS PubMed.
- A. D. Boese and J. Sauer, Phys. Chem. Chem. Phys., 2013, 15, 16481 RSC.
- M. Alessio, D. Usvyat and J. Sauer, J. Chem. Theory Comput., 2018, 15, 1329 CrossRef PubMed.
- H.-Z. Ye and T. C. Berkelbach, 2023, preprint, 2309.14651, 10.1039/D4FD00041B.
- S. J. Bennie, M. W. van der Kamp, R. C. R. Pennifold, M. Stella, F. R. Manby and A. J. Mulholland, J. Chem. Theory Comput., 2016, 12, 2689 CrossRef CAS PubMed.
- K. E. Ranaghan, D. Shchepanovska, S. J. Bennie, N. Lawan, S. J. Macrae, J. Zurek, F. R. Manby and A. J. Mulholland, J. Chem. Inf. Model., 2019, 59, 2063 CrossRef CAS PubMed.
- H. J. Kulik, J. Zhang, J. P. Klinman and T. J. Martínez, J. Phys. Chem. B, 2016, 120, 11381 CrossRef CAS.
- V. Vennelakanti, A. Nazemi, R. Mehmood, A. H. Steeves and H. J. Kulik, Curr. Opin. Struct. Biol., 2022, 72, 9 CrossRef CAS PubMed.
- R. Mehmood and H. J. Kulik, J. Chem. Theory Comput., 2020, 16, 3121 CrossRef CAS.
- F. E. Medina and G. A. Jaña, ACS Catal., 2022, 12, 36 CrossRef CAS.
- H. S. Fernandes, M. J. Ramos and N. M. F. S. A. Cerqueira, ACS Catal., 2018, 8, 10096 CrossRef CAS.
- H. S. Fernandes, S. F. Sousa and N. M. F. S. A. Cerqueira, Mol. Diversity, 2022, 26, 1373 CrossRef CAS.
- P. Paiva, S. F. Sousa, P. A. Fernandes and M. J. Ramos, ChemCatChem, 2019, 11, 3853 CrossRef CAS.
- D. J. Kiss and G. G. Ferenczy, Org. Biomol. Chem., 2019, 17, 7973 RSC.
Footnotes |
| † Electronic supplementary information (ESI) available: Further theoretical details, DLPNO- and LNO-CCSD(T) reaction and correlation energy benchmarks and analysis, computational requirement measurement and computational details, and example input files. See DOI: https://doi.org/10.1039/d4sc04755a |
| ‡ The contribution of single excitations, if relevant, is considered here to be included in CM1ij,ab to simplify the discussion. |
| § For this reason, sometimes this group of methods is also considered to be fragmentation-based, even though fragmentation of the molecule into subsystems (i.e., smaller molecule parts or atom groups) is not employed. Moreover, the mean-field (HF) step of the computation is done for the entire molecule without any local or, at least, without any fragmentation-based approximation. For this reason, the literature on fragmentation-based methods does not characterize this third, uncoupled group as a fragmentation method51,123–125 and, therefore, it belongs to a third category. |
| ¶ We note that the dashed horizontal line type in Fig. 5 indicates that the conventional CCSD(T) reference is available without the density-fitting (DF) approach, while the local correlation methods converge to the slightly different DF-CCSD(T) result at their LAF limits. Partly this and some cancellation of the reactant and product LNO errors, as shown in Table S3 of the ESI, are also responsible for the almost perfect agreement with the CCSD(T) reference. |
| This journal is © The Royal Society of Chemistry 2024 |