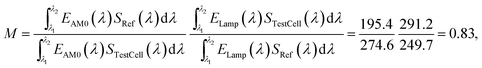Open Access Article
Open Access ArticleLow-intensity low-temperature analysis of perovskite solar cells for deep space applications†
Tyler
Colenbrander
 a,
Jun
Peng
b,
Yiliang
Wu
a,
Jun
Peng
b,
Yiliang
Wu
 b,
Michael
Kelzenberg
c,
Jing-Shun
Huang
d,
Clara
MacFarland
b,
Michael
Kelzenberg
c,
Jing-Shun
Huang
d,
Clara
MacFarland
 a,
Dennis
Thorbourn
a,
Robert
Kowalczyk
a,
Wousik
Kim
a,
Dennis
Thorbourn
a,
Robert
Kowalczyk
a,
Wousik
Kim
 a,
John
Brophy
a,
Anh Dinh
Bui
a,
John
Brophy
a,
Anh Dinh
Bui
 b,
Dang-Thuan
Nguyen
b,
Dang-Thuan
Nguyen
 b,
Hieu T.
Nguyen
b,
Hieu T.
Nguyen
 b,
Harry A.
Atwater
b,
Harry A.
Atwater
 c,
Thomas P.
White
c,
Thomas P.
White
 b and
Jonathan
Grandidier
b and
Jonathan
Grandidier
 *a
*a
aJet Propulsion Laboratory, California Institute of Technology, Pasadena, CA 91109, USA. E-mail: jgrandid@gmail.com
bSchool of Engineering, The Australian National University, Canberra, Australian Capital Territory 2601, Australia
cThomas J. Watson Laboratories of Applied Physics, California Institute of Technology, Pasadena, CA 91125, USA
dCaelux Corporation, 404 N Halstead Street, Pasadena, CA 91107, USA
First published on 5th December 2022
Abstract
High specific power (power per mass) ultralight solar arrays made of perovskite solar cells (PSCs) are being considered to power spacecraft in deep space conditions as far as Neptune (30 AU). To understand how PSCs perform and respond in deep space, we characterize PSCs under low-intensity low-temperature (LILT) conditions before and after low-energy proton irradiation. PSCs show promising performance characteristics under most LILT conditions even after exposure to low-energy protons. However, the measured cell efficiency tends to decrease at extreme lower temperatures, suggesting that further research into cell architectures and materials could improve PSCs for deep space applications.
Introduction
Solar cells are an important power source for enabling non-nuclear exploration of the solar system. Solar cells supply constant, renewable power to a space mission vehicle and its payload when in sight of the sun, allowing for sustained travel to the outer reaches of the solar system. State-of-the-art (SOA) space solar arrays use triple-junction solar cells based on III–V compounds and germanium. However, these cells significantly degrade with radiation exposure, requiring heavy coverglass for shielding. Since perovskites were first identified as a viable photovoltaic material, considerable research efforts have been made regarding perovskite solar cells (PSCs) for space applications.1–12 Preliminary studies suggest that emerging ultrathin, flexible, and lightweight perovskite solar cells are naturally radiation hardened,11–17 potentially enabling high specific power18 solar arrays to be designed for power generation in high radiation and deep space environments. Additionally, the low cost of required materials means that PSCs are cost-effective.19Here, we present two different PSC structures and demonstrate experimental current density–voltage (J–V) and external quantum efficiency measurements (EQE) of PSCs operating in low-intensity low-temperature (LILT) conditions mimicking a deep space environment. The temperatures are as low as −170 °C and light intensities as low as 1.52 W m−2, which corresponds to solar irradiance at Neptune, 30 astronomical units (AU) from the Sun. In this study, we label the light intensity of a given measurement based on distance from the Sun in AU, since solar intensity drops off as the square of distance. 1.0 AU is the distance between the Earth and the Sun and thus corresponds to the Air Mass Zero (AM0) spectrum.
Previous LILT studies1,2 looking at different PSC device structures have observed similar performance trends with respect to temperature and light intensity as we report here. Brown et al. demonstrated temperature-dependent EQE and LILT J–V measurements in Mars, Jupiter, and Saturn environments for a triple-cation PSC device fabricated using an n–i–p architecture, meaning that the cell is illuminated from the electron transport layer (ETL) side.1 They reported temperature-dependent EQE and photoluminescence (PL) measurements that show an increase in bandgap energy with increasing temperature for perovskites and the absence of low-temperature phase transitions in the triple-cation PSC.1 In our study, we observe these same effects in a double-cation PSC device fabricated using a p–i–n architecture, meaning that the cell is illuminated from the hole transport layer (HTL) side. Furthermore, Brown et al. presented J–V curves for PSCs operating in Earth, Mars, Jupiter, and Saturn conditions, which demonstrate that the low-temperature device performance improves at lower light intensities, ideal for deep space applications.1 Our study confirms these trends for two different PSC device architectures, while extending the LILT condition range to light intensities matching Uranus (19.2 AU) and Neptune (30.0 AU). Sun et al. performed a LILT study on a triple-cation PSC device fabricated using a p–i–n architecture, which looked at simulated Martian surface conditions.2 Their work showed long-term stability of PSCs operating in Martian surface conditions and noted that device performance was actually improved slightly after a simulated Martian day.2 Sun et al. also confirmed that low-temperature induced phase transitions could contribute to the self-elimination of intrinsic defect states, improving the device efficiency.2,7
Both studies by Brown et al. and Sun et al. state the promise of PSCs for space applications, but continued research is required before PSCs become a viable technology. To the best of our knowledge, our study presents the most comprehensive LILT condition study thus far, testing two different PSC architectures under a combination of five different light intensities and six different temperatures. Due to the large size of our data set, we can present cell efficiency charts that demonstrate clear trends with respect to light intensity and temperature, which highlight areas for future improvement of PSCs for deep space applications.
Furthermore, we complement our LILT study by considering the effect of low-energy proton radiation. While the radiation hardness of PSCs has been heavily documented,11–17 recent studies have emphasized that low-energy protons are the most appropriate radiation source for creating atomic vacancies and probing radiation effects in perovskites representative of space conditions.4,16 Higher energy particles, which many previous PSC tests have used due to their use in radiation tests for III–V and silicon cells,20 could actually create localized healing and make tests less reliable.4 Thus, Kirmani et al. call for new low-energy proton radiation tests, such as the ones performed in this study. We do observe some degradation in device performance after radiation, but analysis of a champion cell shows that it is possible for a PSC to retain a substantial portion of its pre-radiation efficiency compared to SOA space solar cells.
PSCs have the potential to outperform SOA space solar cells in two key metrics that are important for space applications: radiation resistance and specific power. However, it remains unclear whether this would be true in extreme LILT conditions because very low temperatures at distances like Uranus (19.2 AU) are difficult to measure experimentally due to temperatures lower than what can be achieved using liquid nitrogen. Thus, while initial measurements of PSC performance in less severe LILT conditions look promising, our measurements also suggest that performance would decrease at very low temperatures, and improvements to cell architectures and materials would likely be needed to improve PSC performance.
Results and discussion
Specific power of a perovskite solar array
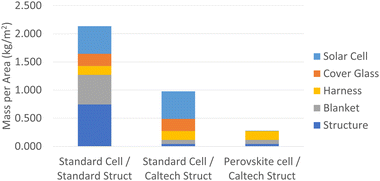
The specific power of a solar cell is especially important for space applications where the weight of payloads is a serious consideration. Gdoutos et al.21 from Caltech have developed a lightweight 1.7 m × 1.7 m prototype solar array structure with areal density of 150 g m−2. This array structure is designed to be scalable up to 60 m × 60 m. At this size, it is estimated to have an areal density of 50 g m−2 because areal density decreases for larger structures.21 Because perovskite solar cells are a thin-film technology that can be deposited via low-temperature processes, they can be fabricated on a range of thin, lightweight, and flexible substrates or foils. At the cell level (i.e., not encapsulated or integrated into a module), flexible perovskite solar cells have been demonstrated with specific power values as high as 26 kW kg−1, compared to values of <2.4 kW kg−1 for current high-efficiency multi-junction cells used in most space applications.22,23Fig. 1 presents the mass of different solar array combinations using either SOA space solar cells or perovskite solar cells. We calculate the areal density if these cells were to be mounted on a standard structure24 or on an ultralight structure currently being developed at Caltech.21 Standard SOA solar cells on a standard structure have an areal density of 2.13 kg m−2, whereas PSCs on the ultralight Caltech structure would have an areal density of 0.25 kg m−2.21,22 The drastic reduction in areal density enables a high specific power for the PSCs mounted on the Caltech structure. Large ultralight and high specific power solar arrays could enable a new class of deep space mission and a non-nuclear exploration of the solar system.Perovskite solar cell structure
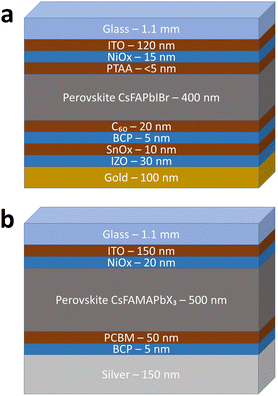
Perovskites are a group of compounds that have the same ABX3 crystal structure as the mineral perovskite (calcium titanate – CaTiO3). In a typical perovskite solar cell, the A site has a large cation such as methylammonium (MA), formamidinium (FA), cesium (Cs), rubidium (Rb), or a combination of these. The B site is a smaller cation such as lead (Pb) or tin (Sn). The X site balances the charge with one or more of the halides iodine (I), bromine (Br), or chlorine (Cl).19 Since 2012, when the first solid state heterojunction methylammonium lead iodide (MAPbI3) perovskite cell was introduced,25 perovskite solar cell technology has been one of the fastest growing solar technologies, with efficiencies now reaching 25%.26Fig. 2(a) and (b) show the perovskite solar cell structure for cells from The Australian National University (ANU) and Caelux Corporation, respectively. The ANU PSCs had an active area of 1 cm2 and utilized a double-cation, mixed halide perovskite with composition Cs0.22FA0.78PbI2.55Br0.45 for the active layer. The Caelux PSCs had an active area of 0.13 cm2 and utilized a similar triple-cation perovskite with composition Cs0.09FA0.8MA0.11PbI2.85Br0.15 for the active layer. In both cells, the top layer of glass serves as a rigid superstrate during the fabrication process and provides some physical and environmental protection. However, preliminary studies on perovskite solar cells show radiation tolerance surpassing other known photovoltaic materials, even when radiated from the rear (non-glass) side.11–17 While further studies are required to fully understand and verify these results, they suggest that perovskite cells may not require a heavy coverglass for radiation protection, further reducing mass and volume, assuming that perovskite solar cells have sufficient mechanical stability without glass encapsulation, which is an active research topic.27 Thus, in our specific power calculations, we omit the structural glass layer and assume that the same cell structure could be deposited on an ultra-lightweight polyimide film or foil.23
Low-intensity low-temperature (LILT) measurement conditions
To simulate the solar cell operation in deep space, we tested PSCs at various mission-relevant temperatures ranging from 28 °C to −170 °C and light intensities based on the solar irradiance from 1.0 AU to 30.0 AU. Table 1 details the solar light intensities, temperatures, and radiation dose rates at the distances of Earth and the outer planets. Solar light intensity is inversely proportional to the square of distance and is calculated by dividing the value of the solar constant, 1367 W m−2, by the square of the distance (in AU). Approximate solar array operating temperatures at these distances in space are calculated by balancing heat flow through a solar array in thermal equilibrium using the Stefan–Boltzmann law. In determining heat flow, we assume the same solar absorptivity and emissivity for SOA cells and PSCs,28 yielding a close approximation to commonly used values.1,29,30 In actual space missions, these temperature values could vary slightly if the cell absorptivity, emissivity, or efficiency differs or if the solar intensity changes due to a particular mission path or distance from the sun. Therefore, we use the values in Table 1 as an approximate flight envelope. Lastly, the radiation dose rates are calculated at L = 7 of each planet under 100 mil aluminum shielding.31L = 7 means 7 times a planet's radius from the planet's center on the equatorial plane and line with the same magnetic field at different magnetic latitudes.| Planet | Distance (AU) | Solar intensity (W m−2) | Temperature (°C) | Radiation dose rate (rad s−1) |
|---|---|---|---|---|
| Earth | 1.0 | 1367 | 60 | 3 × 10−4 |
| Jupiter | 5.5 | 45.2 | −140 | 8 × 10−1 |
| Saturn | 9.5 | 15.2 | −165 | 6 × 10−5 |
| Uranus | 19.2 | 3.71 | −200 | 8 × 10−4 |
| Neptune | 30.0 | 1.52 | −230 | 3 × 10−4 |
Low-intensity low-temperature (LILT) current density–voltage (J–V) measurements
We first analyze LILT J–V measurements taken on PSCs from ANU and Caelux. These measurements were taken using an X-25 solar simulator at temperatures and light intensities determined by Table 1. The solar simulator was calibrated using InGaP and GaAs calibration standards. To properly measure the PSC test cells, a spectral mismatch correction factor32 was calculated for our experimental setup as:and applied to the PSC experimental data by dividing the measured PSC test cell current by M.
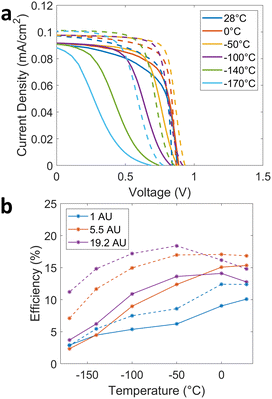
Fig. 3 shows the J–V curves of a selected ANU PSC labeled ANU9 and a selected Caelux PSC labeled CA3 at 1.0 AU and 19.2 AU. As intensity decreases from 1.0 AU to 19.2 AU, the measured current decreases, which follows from the decrease in the number of incident photons. The J–V curves of better performing cells have a higher fill factor, the ratio of the maximum power to the product of the open-circuit voltage and short-circuit current. In Fig. 3, we visually observe that fill factor tends to decrease as temperature decreases, although this trend is not necessarily monotonic at temperatures >−100 °C. For the ANU cell at 1.0 AU in Fig. 3(a), the highest fill factor is achieved at 28 °C with a value of 0.50. As temperature decreases to −170 °C, the fill factor decreases monotonically to 0.164. However, for the ANU cell at 19.2 AU in Fig. 3(b), the highest fill factor is achieved in the middle of the temperature range at −50 °C with a value of 0.75. As temperature increases to 28 °C or decreases to −170 °C, we observe a decrease in fill factors to values of 0.67 and 0.53, respectively. For the Caelux cell at 1.0 AU in Fig. 3(c), the highest fill factor is achieved at 0 °C with a value of 0.69, while at temperatures of −100 °C and −140 °C, we observe decreasing fill factors of 0.38 and 0.14, respectively. For the Caelux cell at 19.2 AU in Fig. 3(d), the highest fill factor is achieved at −50 °C with a value of 0.68, and again we see a decrease in fill factor at −100 °C and −140 °C with values of 0.65 and 0.34, respectively.
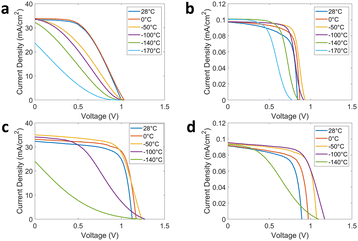 | ||
| Fig. 3 Pre-radiation LILT J–V curves for (a) ANU9 cell at 1.0 AU, (b) ANU9 cell at 19.2 AU, (c) Caelux CA3 cell at 1.0 AU, and (d) Caelux CA3 cell at 19.2 AU. | ||
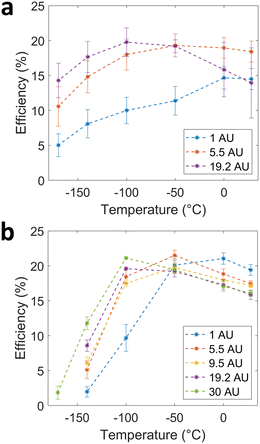
To further explore the effects of temperature and incident light intensity, we look at the average cell efficiency for the PSCs as a function of temperature at each intensity, shown in Fig. 4. We observe a non-monotonic temperature dependence, which has also been observed for a NiOx/triple-cation PSC device in a recent study of the temperature coefficients of PSCs.33 Notably, Moot et al. found that these temperature-dependent trends were different for four different PSC device structures,33 suggesting that the ideal PSC device architecture may differ depending on the specific LILT conditions. Importantly, Moot et al. also highlight reversible changes in device efficiency with respect to temperature, ruling out degradation as a mechanism for performance change.33 To consider the effects of temperature-induced or light-induced degradation in our study, we performed the same 28 °C room temperature measurement before and after subjecting the PSCs to LILT conditions. As shown in Fig. S6–S8 (ESI†), no signs of degradation are present, suggesting that the observed trends are indeed reversible. Furthermore, we observe that as light intensity decreases, the temperature at which maximum efficiency is measured decreases. This leads to a trend at lower temperatures, where the device efficiency improves as light intensity decreases. This is attributed to a more efficient extraction rate for the minority electrons under illumination, as shown previously for a different PSC structure by Brown et al.1 We confirm these previous results from Brown et al. and Moot et al. and further explain the trends by considering the effects of non-radiative recombination, series resistance, and material conductivity.
Non-radiative recombination is an unwanted process in solar cells because it reduces the charge carrier density in the solar cell, impacting the voltage, and to a lesser extent, the current.34 Typically, the effects of non-radiative recombination are lessened as temperature decreases35 which could explain the increase in efficiency as temperature drops from 28 °C to −50 °C. The initial increase in open-circuit voltage with a decrease in temperature (which is particularly obvious for the Caelux cells in Fig. 3(c) and (d)) is the result of a reduction in non-radiative recombination via thermally activated traps, and thus an increase in charge carrier density in the active layer of the cell. This is also observed in steady-state PL measurements of perovskite films of the type used in the ANU cells (Fig. S1, ESI†), which show a monotonic increase in emission intensity with decreasing temperature. We also observe a small red-shift in the PL emission peak. Similar temperature-dependent trends in emission intensity and wavelength have also been reported by others.1,7,36
Fig. 4 also demonstrates increased efficiencies at lower light intensities, which can likely be attributed to the effect of series resistance. Series resistance losses can come from anywhere in the cell and they cause a voltage loss proportional to the current. Thus, power losses due to series resistance increase as light intensity increases because of the higher maximum power point current. Fig. 3(a) shows a J–V curve indicative of the presence of series resistance, leading to a significant voltage loss in the cell at the maximum power point, which explains the poor fill factor at higher intensities. But, towards 19.2 AU, the effects of series resistance are lessened, and the fill factor improves.
We also consider series resistance, in conjunction with the material conductivity of individual layers in the cell, with respect to temperature. Series resistance can be extracted from the measured J–V curves37 by approximating the slope of the curve at the open-circuit voltage point (Fig. S2, ESI†). This method is a rough approximation and does not work well at lower light intensities, but it demonstrates that the overall device series resistance increases as temperature decreases, which is also reported by others.36
To locate the effects of series resistance in the PSC architecture, we refer to the material conductivity of layers in the devices. As shown for C60,38 tin oxide,39 and phenyl-C61-butyric acid methyl ester (PCBM)36 layers, the conductivities of these layers drop significantly as temperature decreases. C60 and tin oxide layers are used as electron transport layers in the ANU PSC and PCBM is used as an electron transport layer in the Caelux PSC. A loss in conductivity contributes to an increase in series resistance with decreasing temperature, thus limiting the device efficiency. Furthermore, the effects of reduced conductivity have been reported by other groups that also observed similar S-shaped J–V curves to those we observe in Fig. 3 at lower temperatures. These were attributed to a pile-up of electrons and holes at the perovskite and charge transport layer interface.36 Thus, it is clear that the effects of series resistance and material conductivity play a large role in the PSC device efficiency. The overall increase in the device series resistance at lower temperatures explains the large loss in efficiency that comes at the low-temperature side of Fig. 4 for both the ANU and Caelux PSCs.
Furthermore, it has been shown that carrier mobility and carrier diffusion lengths in perovskite layers using the canonical CH3NH3PbI3 composition tend to increase at lower temperatures.40,41 Thus, combined with the increased carrier lifetime implied by the increase in PL emission we observed in Fig. S1 (ESI†), this indicates that the optoelectronic quality of the perovskite layers improve with decreasing temperature. So, while overall device efficiency drops at low temperatures, this drop is likely due to factors like series resistance of the charge transport layers or the interfaces between the charge transport layers and the perovskite. This suggests that further device optimization for LILT conditions should target these areas of the cell architecture to improve upon.
The effects of non-radiative recombination and series resistance together create an optimal temperature at which the device efficiency is a maximum. At 1.0 AU in Fig. 4(b), series resistance at lower temperatures plays a large role, so the maximum efficiency occurs at a relatively high temperature. At 9.5 AU, resistive losses are proportionally smaller, so cell performance initially benefits from reduced non-radiative recombination at lower temperature; hence, cell performance peaks at a lower temperature compared to 1.0 AU. As the light intensity is further reduced to 19.2 AU and 30 AU, series resistance losses become very low, so the optimum efficiency temperature drops further. However, we still observe a drop in efficiency at the extreme lower temperatures, suggesting that conductivity losses and/or other temperature-dependent contributions cannot be ignored.
Thus, we observe that the maximum efficiency point shifts towards lower temperatures as the light intensity decreases. In Fig. 4(a), the maximum average efficiency at 1.0 AU is 14.7%, which occurs at a temperature of 0 °C. When the intensity decreases to 19.2 AU, the maximum average efficiency increases to 19.8% and is attained at a lower temperature of −100 °C. This trend is demonstrated further in Fig. 4(b), where the maximum efficiency at 1.0 AU is 21.0% at 0 °C, then shifts to −50 °C at 5.5 AU and 9.5 AU with maximum efficiencies of 21.5% and 19.8%, respectively, and then shifts to −100 °C at 19.2 AU and 30 AU with maximum efficiencies of 19.6% and 21.1%, respectively. This trend is well-matched to space applications where both operating temperatures and light intensity decrease with distance from the Sun. However, it is important to note that with our current results, the temperatures and light intensities listed in Table 1 do not match the optimal conditions. Thus, while the trend looks promising for deep space applications, optimization of cell materials and architectures could further improve the performance under LILT conditions.
Temperature-dependent external quantum efficiency (EQE) measurements
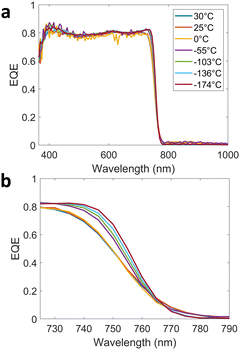
We look at temperature-dependent EQE measurements of the PSCs. One ANU PSC was tested at various temperatures ranging from 30 °C down to approximately −170 °C, and the resulting EQE curves are shown in Fig. 5(a). The EQE plateaus around 0.8 and the bandgap is shown to be around 760 nm or 1.63 eV. We observe little change due to temperature, which is unlike the temperature-dependent EQE measurements taken on other solar cells42 that demonstrate a much larger bandgap shift with temperature. With the photoluminescence data shown in Fig. S1 (ESI†), we observe that bandgap energy increases with increasing temperature. This trend is opposite that of traditional semiconductors,43 and it has been documented previously for PSCs.1,33Fig. 5(b) zooms into the wavelength region near the bandgap, and we observe a small but clear temperature trend as the EQE curve steepens as the temperature is decreased, and there is slight red-shift of <5 nm, indicating bandgap narrowing. Furthermore, existing measurements in the literature1 demonstrate a similar weak dependence of bandgap on temperature in PSCs. This suggests that perovskites are unusual compared to other common semiconductors used in space-based solar cells such as III–V materials, where a pronounced temperature dependence is expected.42Low-energy proton radiation measurements
Due to the low thickness of perovskite solar cells, low-energy particles can have a strong interaction with the active material and potentially inhibit the solar cell performance. This is in contrast to high energy particles, which are more likely to pass straight through with minimal damage. Recent studies have highlighted the need for further analysis of PSCs under low-energy proton radiation,4,16 so considering the energy deposition efficiency of a particle's energy and the energy range of available accelerator laboratories, the 75 keV proton was selected as the low-energy proton test condition.The expected total ionizing dose (TID) and the displacement damage dose (DDD) of the perovskite solar cell under Europa Clipper mission fluence in space configuration (isotropic velocity distribution) was calculated using a Monte Carlo high-energy particle transport tool, MCNP6.44 The TID was estimated from the direct (total energy deposition) output of the MCNP6. The DDD of protons or electrons was calculated by an energy integration of the product of (1) differential flux of given particles in the perovskite solar cell (MCNP6 output) and (2) the published Nonionizing Energy Loss (NIEL) of corresponding energies.45,46 The NIEL of the tested perovskite solar cell material is not known, therefore the NIEL value of HgCdTe was used because among the materials with known NIEL values, it is the most similar to the perovskite material based on the atomic numbers of the constituents and relative compositions. For the laboratory test carried out at the Boeing Radiation Effects Laboratory (BREL), the TID and the DDD were simulated at various energies of protons by a similar method described above, but in a lab configuration (directional beam).
We evaluated the impact of low-energy protons at 75 keV with a flux of 2 × 109 p+cm−2 s−1 for up to 24 hours in 6 hours increments at room temperature. These exposures correspond to doses of 4.32 × 1013 p+cm−2, 8.64 × 1013 p+cm−2, 1.30 × 1014 p+cm−2, and 1.73 × 1014 p+cm−2. The highest fluence of 75 keV proton corresponds to about one third of the TID and twice of the DDD of the Europa Clipper mission.
After low-energy proton radiation was conducted, the same LILT J–V measurements as the pre-radiation measurements were taken again. The presentation of the data set can be found in the ESI† (Fig. S4 and S5), which demonstrates cell parameters with respect to radiation fluence. As expected, cell efficiency decreases with respect to radiation fluence and becomes severely limited at the highest fluence. However, the chosen radiation fluences are relatively high compared to typical proton radiation testing conditions for space solar cells.11–15 This was chosen to study the proton radiation response of unshielded PSCs in harsh radiation conditions for long missions such as Europa Clipper.
Thus, we focus our analysis here on the lowest radiation fluence of 4.35 × 1013 p+cm−2, which is still a higher fluence than many of the previous experiments cited above. The analysis here demonstrates that when measured under LILT conditions, it is possible for PSCs to be relatively robust to moderate low-energy proton radiation exposure. The cell ANU9 was radiated with 75 keV low-energy protons with a fluence of 4.35 × 1013 p+cm−2. Fig. 6(a) shows the J–V curves of the ANU9 cell at 19.2 AU and Fig. 6(b) shows the post-radiation efficiency with respect to temperature for the ANU9 cell. Compared to the pre-radiation J–V curves (dotted lines), we observe some degradation in the cell performance, but it still retains much of its efficiency. Compared to current SOA cells that have been tested without coverglass,47,48 the PSC retains a much higher fraction of its pre-radiation efficiency.
Discussion of PSC performance
Our study confirms temperature-dependent and intensity-dependent trends from previous studies2,33,44 utilizing two distinct cell architectures from ANU and Caelux, while also performing radiation tests on the same cells to contribute to the limited literature on low-energy proton radiation tests for PSCs.4,16 With the resulting large data set of measured PSC efficiencies, we predict how the ANU PSCs would perform relative to SOA cells in the context of a space mission to Jupiter (5.5 AU, −140 °C from Table 1). Measured without the effects of radiation, SOA cells have demonstrated efficiencies exceeding 35% at 5.5 AU and −140 °C.49 With this efficiency, a standard24 SOA space solar array has an estimated specific power of 6.5 W kg−1. This value could be increased using the ultralight Caltech structure,21 yielding a projected specific power of 12 W kg−1. We compare these values to the projected specific power of ANU PSCs mounted without coverglass on an ultralight Caltech structure,21 using both pre-radiation and post-radiation efficiencies. Pre-radiation efficiencies are an average of 3 measured cells, as shown in Fig. 4(a), and post-radiation efficiencies are from the champion cell as shown in Fig. 6(b). Then, at 5.5 AU and −140 °C, the projected ultralight PSC array specific power is around 24 W kg−1 before radiation and 7.3 W kg−1 after radiation. The projected ultralight PSC array specific power clearly exceeds estimated standard SOA space solar array values. However, if the SOA cells were to be similarly mounted on an ultralight Caltech structure, then the PSC array does not have a clear advantage, particularly when comparing with the post-radiation PSC value. Although the SOA values are assuming no radiation, the SOA cells typically employ a protective coverglass layer to prevent severe radiation degradation. Thus, because the SOA values assume coverglass and the PSC values do not assume coverglass, we compare the beginning-of-life SOA value (6.5 W kg−1, 12 W kg−1 with ultralight structure) and the post-radiation PSC value (7.3 W kg−1). From this comparison, PSCs show promise to enable higher specific power arrays than currently available. However, if improvements were made to SOA cell arrays that would likewise enable the SOA cells to be mounted on ultralight structures, the PSCs tested here would not offer a conclusive advantage over SOA cells, especially if we consider more extreme LILT conditions where the PSC performance degraded.We cannot make a direct comparison at more extreme LILT conditions such as Uranus (19.2 AU, −200 °C) because this requires a temperature of −200 °C, and the lowest temperature that can be tested in the LN2-cooled photovoltaic setup at JPL is −170 °C. However, both Fig. 4 and 6(b) suggest that efficiencies would likely decrease at lower temperatures like −200 °C, and thus PSCs may not outperform SOA cells. Because these low temperatures are not currently achievable, further research must be done to make the comparison between PSCs and SOA cells at these extreme conditions. Regardless, the measured PSCs suffer significant reduction in cell efficiency at extreme low temperatures, suggesting that cell architectures and materials may have to be optimized for LILT conditions.
A comparison of the temperature and illumination dependent performance of the ANU and Caelux cells in Fig. 3 and 4 reveals significant differences between the two cell types which may provide guidance on future optimization for LILT conditions. Apart from the active areas (1 cm2versus 0.13 cm2), which could explain the relatively high series resistance, and hence low fill factor of the ANU cells under 1.0 AU illumination, other notable differences between the cells are the perovskite composition and the rear electron transport layer stack. It is likely that both may contribute to the differences in LILT performance, but further LILT studies that compare different types of PSC architectures and material choices are required to identify the specific contributions of each layer and the optimal material combinations. In this context, we propose that future studies and optimization for LILT performance should focus on three distinct aspects of the cell design: (i) tuning of the perovskite composition to take advantage of low-temperature phase transitions that can improve material quality;7 (ii) selecting charge transport materials with a high carrier concentration and/or intentionally increasing the doping level so a reasonable conductivity can be maintained at low temperatures, and (iii) optimizing the device structure and fabrication to maximize shunt resistance, as low-light performance is severely impacted by low shunt resistance.50 To support this, detailed characterization of the fundamental semiconducting properties (e.g. bandgap, energy levels, mobility, carrier density, etc.) of different perovskite compositions and charge transport layers at deep-space temperatures below −170 °C is required, as much of this information is currently unavailable. Then, on the device level, along with light J–V measurements and EQE measurements such as the ones in this study, other solar cell characterization techniques such as dark J–V measurements or power-dependent measurements could be employed to further investigate device performance in LILT and radiation conditions. Lastly, in situ characterization of PSCs in radiation and LILT conditions simultaneously would help to eliminate uncertainty introduced by the handling of devices and delay between irradiation and characterization of devices. While much work has gone into researching PSCs for space applications, continued research that compares specific materials and device structures33 in full LILT and radiation conditions is vital to enabling viable PSCs for deep space missions.
Experimental
ANU cell fabrication
The indium tin oxide (ITO) substrates were sequentially cleaned in detergent, acetone, isopropyl alcohol and ethyl alcohol for 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) min in an ultrasonic bath, and then dried with nitrogen. Cleaned ITO substrates were exposed to approximately 30
min in an ultrasonic bath, and then dried with nitrogen. Cleaned ITO substrates were exposed to approximately 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) min of UV–O3 treatment before the subsequent deposition step. ∼15 nm nickel oxide thin films were deposited on the pre-cleaned ITO substrates by radiofrequency magnetron sputtering at 150 W and 18
min of UV–O3 treatment before the subsequent deposition step. ∼15 nm nickel oxide thin films were deposited on the pre-cleaned ITO substrates by radiofrequency magnetron sputtering at 150 W and 18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sccm Ar and 2 sccm O2 gas using a nickel oxide target under a pressure of 1.5
sccm Ar and 2 sccm O2 gas using a nickel oxide target under a pressure of 1.5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) mTorr. The pre-fabricated nickel oxide thin films were then transferred to a furnace, and annealed 30
mTorr. The pre-fabricated nickel oxide thin films were then transferred to a furnace, and annealed 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) min under a controlled oxygen atmosphere. For the ∼5 nm PTAA (a poly(triaryl amine) semiconductor) thin film deposition, ∼50 uL PTAA solution (2 mg ml−1 in chlorobenzene) was dropped onto the ITO/NiOx substrates and deposited by spin-coating at 4000 rpm for 20 s. The perovskite film (Cs0.22FA0.78Pb(Cl0.03Br0.15I0.85)3, 1.2 mmol (68.6 mg CsI, 99.1 mg PbBr2, 161 mg FAI, 429 mg PbI2) in 0.8 ml dimethylformamide (DMF) and 0.2 ml dimethyl sulfoxide (DMSO) with 5 mol% MACl and 3 mol% PbCl2 additive) was deposited by one-step spin-coating at 3000 rpm with a ramp of 100 rpm s−1 for 12 s. After spinning, the substrate was transferred immediately into a vacuum chamber and pumped down to 120 mTorr for 20 s, then 1.5 torr for 15 s before releasing the pressure to ambient, followed by annealing on the hot plate at 120 °C for 15 min. After the substrate had cooled down, GuBr solution (2.5 mg ml−1 in 2-propanol) was spun on at 4000 rpm with a ramp of 1000 rpm for 15 s, followed by annealing on the hot plate at 120 °C for 15 min. The C60 (20 nm) and bathocuproine (BCP) (∼5 nm) electron transport layers were sequentially deposited via thermal evaporation at 0.1 A s−1. Next, a thin sputter-protection layer of SnOx (∼10 nm) was deposited by atomic layer deposition at 83 °C (Beneq TFS200). The hot source vessel (55 °C) was charged with N2 for 200 ms before a 100 ms pulse of the TDMASn, followed by 12 s purge with N2 at 300 sccm, water pulse for 200 ms and 12 s purge with N2 at 300 sccm. Then a 30 nm indium zinc oxide (IZO) layer was deposited by sputtering. Finally, the ∼100
min under a controlled oxygen atmosphere. For the ∼5 nm PTAA (a poly(triaryl amine) semiconductor) thin film deposition, ∼50 uL PTAA solution (2 mg ml−1 in chlorobenzene) was dropped onto the ITO/NiOx substrates and deposited by spin-coating at 4000 rpm for 20 s. The perovskite film (Cs0.22FA0.78Pb(Cl0.03Br0.15I0.85)3, 1.2 mmol (68.6 mg CsI, 99.1 mg PbBr2, 161 mg FAI, 429 mg PbI2) in 0.8 ml dimethylformamide (DMF) and 0.2 ml dimethyl sulfoxide (DMSO) with 5 mol% MACl and 3 mol% PbCl2 additive) was deposited by one-step spin-coating at 3000 rpm with a ramp of 100 rpm s−1 for 12 s. After spinning, the substrate was transferred immediately into a vacuum chamber and pumped down to 120 mTorr for 20 s, then 1.5 torr for 15 s before releasing the pressure to ambient, followed by annealing on the hot plate at 120 °C for 15 min. After the substrate had cooled down, GuBr solution (2.5 mg ml−1 in 2-propanol) was spun on at 4000 rpm with a ramp of 1000 rpm for 15 s, followed by annealing on the hot plate at 120 °C for 15 min. The C60 (20 nm) and bathocuproine (BCP) (∼5 nm) electron transport layers were sequentially deposited via thermal evaporation at 0.1 A s−1. Next, a thin sputter-protection layer of SnOx (∼10 nm) was deposited by atomic layer deposition at 83 °C (Beneq TFS200). The hot source vessel (55 °C) was charged with N2 for 200 ms before a 100 ms pulse of the TDMASn, followed by 12 s purge with N2 at 300 sccm, water pulse for 200 ms and 12 s purge with N2 at 300 sccm. Then a 30 nm indium zinc oxide (IZO) layer was deposited by sputtering. Finally, the ∼100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) nm gold electrode was deposited through a shadow mask (cell area 1.0
nm gold electrode was deposited through a shadow mask (cell area 1.0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cm2).
cm2).
Caelux cell fabrication
Patterned ITO glass substrates with sheet resistance of 15 Ohm sq−1 were cleaned in soap water, DI water, Acetone and then isopropyl alcohol for 15 min respectively, followed by 15 min treatment in UV ozone. NiO of 20 nm were deposited by a RF sputter at 120 W and then annealed in N2/H2 (95/5) at 350 °C for 10 min. After cooling down to room temperature, NiO-coated substrates were transferred into N2-filled glovebox. Perovskite precursor of 1.3 M Cs0.09FA0.8MA0.11Pb(I0.95Br0.05)3 was dissolved in DMF/DMSO (v/v 4/1). 50 μl precursor was deposited on NiO and spun at 4500 rpm for 40 s, and antisolvent DEE of 200 μl was dripped at 7 s before the end of spinning. Then samples were annealed at 110 °C for 10 min. The thickness of perovskite is around 500 nm. PCBM (20 mg ml−1 in chlorobenzene) was deposited on perovskite layer at 1000 rpm for 60 s and followed by BCP (0.5 mg ml−1 in isopropyl alcohol) at 4000 rpm for 20 s. Silver of 120 nm was thermally evaporated under vacuum at 1 × 10−6 Torr. The active area is 0.13 cm2.Light current density–voltage measurements
Light J–V measurements were taken at JPL using the Spectrolab X-25 Mk II Solar Simulator. The measured cells were held in vacuum and light J–V measurements were taken while varying light intensity and temperature. To record the operating temperature of each individual cell tested, a thermocouple was attached to the back of each cell. The bulb light intensity was adjusted for different measurements to correspond to the solar intensity at distances from the sun of 1.0 AU, 5.5 AU, 9.5 AU, 19.2 AU, and 30 AU. These solar intensities were calibrated using InGaP and GaAs standard calibration cells. The cell temperature was lowered using LN2, and the lowest achievable cell temperature in the lab is −170 °C. Starting at 1.0 AU and then going to lower intensities, light J–V measurements were taken at 28 °C, 0 °C, −50 °C, −100 °C, −140 °C, −170 °C with a tolerance of ±5 °C. For each light intensity and temperature condition, the voltage of each cell is swept three times in each the forward and reverse direction, and the resulting current is measured. The standard deviation between the three sweeps was typically <1%, so our results present each cell as the average of the three forward sweeps for consistency and brevity. Additionally, in the presentation of J–V curves, the figures depicting J–V curves show the first forward sweep of each case. After measuring at −170 °C, the system was brought back up to 28 °C and a new measurement was taken and compared to the initial 28 °C measurement to verify the reversibility of trends and lamp and cell stability in LILT conditions. In all our experiments, we found that the measurements taken at 28 °C both before and after cooling and heating were consistent, indicating cell and lamp stability. The same exact procedure, equipment, and cells were used for both the pre-radiation and post-radiation measurements.External quantum efficiency measurements
EQE measurements were taken with JPL's test setup. A Spectral Products DK240 high resolution ¼ meter monochromator was used to generate a narrow-spectrum beam, which was directed through a vacuum chamber's optical window and onto the cell mounted within. The beam was calibrated with a bare silicon standard. Vacuum was drawn in the chamber, and EQE was measured at 28 °C, 0 °C, −50 °C, −100 °C, −140 °C, −170 °C, and then again at 28 °C, all with a tolerance of ±5 °C. Calibration and measurements were completed with room lights turned off to reduce error.Proton radiation
Proton radiation was conducted at the Boeing Radiation Effects Laboratory (BREL). The cells were exposed to 75 keV protons with a flux of 2 × 109 p+cm2 s−1 for up to 24 hours in 6 hours increments. These exposures correspond to doses of 4.32 × 1013 p+cm−2, 8.64 × 1013 p+cm−2, 1.30 × 1014 p+cm−2, and 1.73 × 1014 p+cm−2. The glass layer used to grow the perovskite solar cells acts as an unwanted radiation protection layer for the purpose of this study. Therefore, to evaluate the true impact of proton radiation on perovskites, the solar cells were exposed with the back layer facing the proton beam. To perform the tests, the cells were placed in the radiation chamber at room temperature. The test plate had four columns of cells, with each column corresponding to the amount of time that the cells were irradiated. Each column had one ANU cell, but we could not test the Caelux cells similarly because the Caelux cells are part of a single footprint made up of many cells. Thus, they could not be separated for the radiation test. Additionally, one ANU control cell was shipped and handled like the other cells but not subject to proton radiation. Because proton radiation was conducted at a different facility than the LILT J–V measurements, shipping and handling time between the irradiation and characterization could introduce the potential for performance recovery or other changes in device performance. While some performance change is unavoidable, all cells, including the control cells, were shipped and handled with the same protocol to preserve the validity of comparisons between cells at difference radiation fluences.Photoluminescence characterization
Further experimental details on the low-temperature photoluminescence measurements can be found in the ESI.†Conclusions
We have conducted a study of two different types of PSCs in lab-controlled deep space conditions across a wide temperature and light intensity range. The PSCs have different structural compositions, and thus respond differently to light intensity and temperature. The Caelux PSCs start off with a higher efficiency of 19.4% at 1.0 AU and 28 °C compared the ANU PSC efficiency of 14.5%. However, at the most extreme LILT conditions tested (19.2 AU, −170 °C), the ANU PSCs retain a relatively high efficiency of around 14.3% while the Caelux PSCs suffer a larger loss in efficiency, down to 8.6% (19.2 AU, −140 °C). While the rate at which efficiency changes as a function of light intensity and temperature differs between the cells, both PSCs demonstrate a trend where the optimum efficiency temperature decreases as intensity decreases. While this trend is promising for deep space applications, the measured optimal conditions do not correspond with actual mission-relevant conditions, and the PSCs demonstrate reduced performance at very low temperatures. We also show post-radiation LILT data for a champion ANU cell that demonstrates that PSCs can retain a substantial portion of their pre-radiation efficiency even without protective coverglass. However, as with the pre-radiation measurements, we observe reduced performance at very low temperatures. These observations prompt research looking at the cell architecture and material composition to determine if PSCs can be better optimized for LILT conditions, particularly by looking at the charge transport layers and material interfaces as mentioned in our discussion section. With further development, PSCs could potentially enable ultralight photovoltaic structures for deep space applications.Author contributions
T. C. contributed to conceptualization, data curation and analysis, experimental procedures, and writing. J. P., Y. W., J. H., A. D. B., D. N., and H. T. N. contributed to cell fabrication and material characterization. M. K., C. M., and R. K. contributed to cell characterization and experimental measurements. D. T., W. K., and J. B. contributed to conceptualization and planning of the experimental test conditions. H. A. A., T. P. W., and J. G. contributed to conceptualization, analysis, reviewing, and supervising the work. All authors have discussed the results and commented on the manuscript.Conflicts of interest
The authors declare no conflicts of interest.Acknowledgements
The author would like to thank Joel Schwartz for helpful discussions. This research was carried out at The Australian National University, Caelux Corporation, the California Institute of Technology, and the Jet Propulsion Laboratory, California Institute of Technology, under contract with the National Aeronautics and Space Administration (80NM0018D0004). This work was supported by the Australian Government through the Australian Renewable Energy Agency (ARENA) and the Australian Research Council. J. P., H. T. N., and Y. W. are recipients of postdoctoral fellowships from the Australian Centre for Advanced Photovoltaics (ACAP). T. P. W. is the recipient of an Australian Research Council Future Fellowship (project number FT180100302) funded by the Australian Government. Responsibility for the views, information, or advice expressed herein is not accepted by the Australian Government. Work performed at Caltech was supported by the Space Solar Power Project. We acknowledge the assistance of Arthur Rugtvedt and Nathaniel Williams at BREL.Notes and references
- C. R. Brown, G. E. Eperon, V. R. Whiteside and I. R. Sellers, ACS Appl. Energy Mater., 2019, 2, 814–821 CrossRef CAS.
- M. Sun, Y. Zheng, Y. Shi, G. Zhang and Y. Shao, Phys. Chem. Chem. Phys., 2022, 24, 17716–17722 RSC.
- C. R. Brown, G. E. Eperon, V. R. Whiteside and I. R. Sellers, in 2019 IEEE 46th Photovoltaic Specialists Conference (PVSC), 2019, pp. 2374–2376.
- A. R. Kirmani, B. K. Durant, J. Grandidier, N. M. Haegel, M. D. Kelzenberg, Y. M. Lao, M. D. McGehee, L. McMillon-Brown, D. P. Ostrowski, T. J. Peshek, B. Rout, I. R. Sellers, M. Steger, D. Walker, D. M. Wilt, K. T. VanSant and J. M. Luther, Joule, 2022, 6, 1015–1031 CrossRef CAS.
- V. Romano, A. Agresti, R. Verduci and G. D’Angelo, ACS Energy Lett., 2022, 7, 2490–2514 CrossRef CAS PubMed.
- I. Cardinaletti, T. Vangerven, S. Nagels, R. Cornelissen, D. Schreurs, J. Hruby, J. Vodnik, D. Devisscher, J. Kesters, J. D’Haen, A. Franquet, V. Spampinato, T. Conard, W. Maes, W. Deferme and J. V. Manca, Sol. Energy Mater. Sol. Cells, 2018, 182, 121–127 CrossRef CAS.
- Y. Chen, S. Tan, N. Li, B. Huang, X. Niu, L. Li, M. Sun, Y. Zhang, X. Zhang, C. Zhu, N. Yang, H. Zai, Y. Wu, S. Ma, Y. Bai, Q. Chen, F. Xiao, K. Sun and H. Zhou, Joule, 2020, 4, 1961–1976 CrossRef CAS.
- A. W. Y. Ho-Baillie, H. G. J. Sullivan, T. A. Bannerman, H. P. Talathi, J. Bing, S. Tang, A. Xu, D. Bhattacharyya, I. H. Cairns and D. R. McKenzie, Adv. Mater. Technol., 2022, 7, 2101059 CrossRef CAS.
- L. McMillon-Brown, K. M. Crowley, K. T. VanSant and T. J. Peshek, in 2021 IEEE 48th Photovoltaic Specialists Conference (PVSC), 2021, pp. 0222–0225.
- Y. Tu, J. Wu, G. Xu, X. Yang, R. Cai, Q. Gong, R. Zhu and W. Huang, Adv. Mater., 2021, 33, 2006545 CrossRef CAS PubMed.
- J.-S. Huang, M. D. Kelzenberg, P. Espinet-Gonzalez, C. Mann, D. Walker, A. Naqavi, N. Vaidya, E. Warmann and H. A. Atwater, in 2017 IEEE 44th Photovoltaic Specialist Conference (PVSC), IEEE, Washington, DC, 2017, pp. 1248–1252.
- Y. Miyazawa, M. Ikegami, H.-W. Chen, T. Ohshima, M. Imaizumi, K. Hirose and T. Miyasaka, iScience, 2018, 2, 148–155 CrossRef CAS PubMed.
- F. Lang, M. Jošt, K. Frohna, E. Köhnen, A. Al-Ashouri, A. R. Bowman, T. Bertram, A. B. Morales-Vilches, D. Koushik, E. M. Tennyson, K. Galkowski, G. Landi, M. Creatore, B. Stannowski, C. A. Kaufmann, J. Bundesmann, J. Rappich, B. Rech, A. Denker, S. Albrecht, H.-C. Neitzert, N. H. Nickel and S. D. Stranks, Joule, 2020, 4, 1054–1069 Search PubMed.
- F. Lang, G. E. Eperon, K. Frohna, E. M. Tennyson, A. Al-Ashouri, G. Kourkafas, J. Bundesmann, A. Denker, K. G. West, L. C. Hirst, H.-C. Neitzert and S. D. Stranks, Adv. Energy Mater., 2021, 11, 2102246 CrossRef CAS.
- F. Lang, N. H. Nickel, J. Bundesmann, S. Seidel, A. Denker, S. Albrecht, V. V. Brus, J. Rappich, B. Rech, G. Landi and H. C. Neitzert, Adv. Mater., 2016, 28, 8726–8731 CrossRef CAS PubMed.
- B. K. Durant, H. Afshari, S. Singh, B. Rout, G. E. Eperon and I. R. Sellers, ACS Energy Lett., 2021, 6, 2362–2368 Search PubMed.
- B. K. Durant, H. Afshari, S. Sourabh, V. Yeddu, M. T. Bamidele, S. Singh, B. Rout, G. E. Eperon, D. Young Kim and I. R. Sellers, in 2021 IEEE 48th Photovoltaic Specialists Conference (PVSC), 2021, pp. 1111–1114.
- L. Li, S. Zhang, Z. Yang, E. E. S. Berthold and W. Chen, J. Energy Chem., 2018, 27, 673–689 CrossRef.
- J.-P. Correa-Baena, M. Saliba, T. Buonassisi, M. Grätzel, A. Abate, W. Tress and A. Hagfeldt, Science, 2017, 358, 739–744 CrossRef CAS PubMed.
- S. R. Messenger, G. P. Summers, E. A. Burke, R. J. Walters and M. A. Xapsos, Prog. Photovolt. Res. Appl., 2021, 9, 103–121 CrossRef.
- E. Gdoutos, C. Leclerc, F. Royer, D. A. Türk and S. Pellegrino, AIAA Scitech 2019 Forum DOI:10.2514/6.2019-1749.
- M. Kaltenbrunner, G. Adam, E. D. Głowacki, M. Drack, R. Schwödiauer, L. Leonat, D. H. Apaydin, H. Groiss, M. C. Scharber, M. S. White, N. S. Sariciftci and S. Bauer, Nat. Mater., 2015, 14, 1032–1039 Search PubMed.
- G. Lee, M. Kim, Y. W. Choi, N. Ahn, J. Jang, J. Yoon, S. M. Kim, J.-G. Lee, D. Kang, H. S. Jung and M. Choi, Energy Environ. Sci., 2019, 12, 3182–3191 RSC.
- M. K. Chamberlain, S. H. Kiefer and J. Banik, AIAA Scitech 2019 Forum, American Institute of Aeronautics and Astronautics, 2019.
- H.-S. Kim, C.-R. Lee, J.-H. Im, K.-B. Lee, T. Moehl, A. Marchioro, S.-J. Moon, R. Humphry-Baker, J.-H. Yum, J. E. Moser, M. Grätzel and N.-G. Park, Sci. Rep., 2012, 2, 591 Search PubMed.
- M. Jeong, I. W. Choi, E. M. Go, Y. Cho, M. Kim, B. Lee, S. Jeong, Y. Jo, H. W. Choi, J. Lee, J.-H. Bae, S. K. Kwak, D. S. Kim and C. Yang, Science, 2020, 7 Search PubMed.
- I. K. Popoola, M. A. Gondal and T. F. Qahtan, Renewable Sustainable Energy, 2018, 82, 3127–3151 Search PubMed.
- L. Yue, B. Yan, M. Attridge and Z. Wang, Sol. Energy, 2016, 124, 143–152 CrossRef CAS.
- A. Boca, J. Grandidier, P. Stella, P. Chiu, X.-Q. Liu, J. Ermer, C. McPheeters, C. Kerestes and P. Sharps, in 2018 IEEE 7th World Conference on Photovoltaic Energy Conversion (WCPEC) (A Joint Conference of 45th IEEE PVSC, 28th PVSEC 34th EU PVSEC), 2018, pp. 3324–3328.
- G. A. Landis and J. Fincannon, in 2015 IEEE 42nd Photovoltaic Specialist Conference (PVSC), IEEE, New Orleans, LA, 2015, pp. 1–5.
- I. Jun, H. B. Garrett and R. W. Evans, IEEE Trans. Plasma Sci., 2019, 47, 3923–3930 Search PubMed.
- M. O. Reese, A. R. Marshall and G. Rumbles, Nanostructured Materials for Type III Photovoltaics, 2017, pp. 1–32 Search PubMed.
- T. Moot, J. B. Patel, G. McAndrews, E. J. Wolf, D. Morales, I. E. Gould, B. A. Rosales, C. C. Boyd, L. M. Wheeler, P. A. Parilla, S. W. Johnston, L. T. Schelhas, M. D. McGehee and J. M. Luther, ACS Energy Lett., 2021, 6, 2038–2047 CrossRef CAS.
- D. Luo, R. Su, W. Zhang, Q. Gong and R. Zhu, Nat. Rev. Mater., 2020, 5, 44–60 CrossRef CAS.
- M. Gerhard, B. Louis, R. Camacho, A. Merdasa, J. Li, A. Kiligaridis, A. Dobrovolsky, J. Hofkens and I. G. Scheblykin, Nat. Commun., 2019, 10, 1698 CrossRef PubMed.
- S. Shao and M. A. Loi, Adv. Mater. Interfaces, 2020, 7, 1901469 CrossRef CAS.
- C. Chibbaro, M. Zimbone, G. Litrico, P. Baeri, M. L. Lo Trovato and F. Aleo, J. Appl. Phys., 2011, 110, 044505 CrossRef.
- B. Mishori, E. A. Katz, D. Faiman, A. Belu-Marian and Y. Shapira, Fullerene Sci. Technol., 1998, 6, 113–124 CrossRef CAS.
- M. P. Rajeeva, C. S. Naveen, A. R. Lamani, V. P. Bothla and H. S. Jayanna, AIP Conf. Proc., 2015, 1665, 050091 Search PubMed.
- R. L. Milot, G. E. Eperon, H. J. Snaith, M. B. Johnston and L. M. Herz, Adv. Funct. Mater., 2015, 25, 6218–6227 CrossRef CAS.
- C. Q. Xia, J. Peng, S. Poncé, J. B. Patel, A. D. Wright, T. W. Crothers, M. Uller Rothmann, J. Borchert, R. L. Milot, H. Kraus, Q. Lin, F. Giustino, L. M. Herz and M. B. Johnston, J. Phys. Chem. Lett., 2021, 12, 3607–3617 Search PubMed.
- A. W. Walker, J. F. Wheeldon, O. Thériault, M. D. Yandt and K. Hinzer, in 2011 37th IEEE Photovoltaic Specialists Conference, 2011, pp. 000564–000569.
- Y. P. Varshni, Physica, 1967, 34, 149–154 Search PubMed.
- F. B. Brown, B. C. Kiedrowski, J. S. Bull, J. T. Goorley, H. G. Hughes and M. R. James, International Conference on Nuclear Criticality, Edinburgh, Scotland, 2011 Search PubMed.
- B. C. Fodness, P. W. Marshall, R. A. Reed, T. M. Jordan, J. C. Pickel, I. Jun, M. A. Xapsos, E. A. Burke and R. Ladbury, in Proceedings of the 7th European Conference on Radiation and Its Effects on Components and Systems, 2003, RADECS 2003, 2003, pp. 479–485.
- I. Jun, W. Kim and R. Evans, IEEE Trans. Nucl. Sci., 2009, 56, 3229–3235 CAS.
- N. Chandrasekaran, T. Soga, Y. Inuzuka, H. Taguchi, M. Imaizumi, T. Ohshima and T. Jimbo, Jpn. J. Appl. Phys., 2004, 43, L1302–L1304 CrossRef.
- R. Wang, Z. Guo and G. Wang, Sol. Energy Mater. Sol. Cells, 2006, 90, 1052–1057 Search PubMed.
- A. Boca, in 2019 IEEE 46th Photovoltaic Specialists Conference (PVSC), 2019, pp. 2787–2791.
- S. Zhu and Y. Li, Solid-State Electron., 2020, 173, 107903 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2ya00218c |
| This journal is © The Royal Society of Chemistry 2023 |