Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Do electron distributions with orbital degree of freedom exhibit anisotropy?†
Taishun
Manjo
 a,
Shunsuke
Kitou
b,
Naoyuki
Katayama
a,
Shin
Nakamura
c,
Takuro
Katsufuji
d,
Yoichi
Nii
ef,
Taka-hisa
Arima
a,
Shunsuke
Kitou
b,
Naoyuki
Katayama
a,
Shin
Nakamura
c,
Takuro
Katsufuji
d,
Yoichi
Nii
ef,
Taka-hisa
Arima
 bg,
Joji
Nasu
fh,
Takumi
Hasegawa
i,
Kunihisa
Sugimoto
bg,
Joji
Nasu
fh,
Takumi
Hasegawa
i,
Kunihisa
Sugimoto
 j,
Daisuke
Ishikawa
kl,
Alfred Q. R.
Baron
kl and
Hiroshi
Sawa
*a
j,
Daisuke
Ishikawa
kl,
Alfred Q. R.
Baron
kl and
Hiroshi
Sawa
*a
aDepartment of Applied Physics, Nagoya University, Nagoya 464-8603, Japan. E-mail: z47827a@cc.nagoya-u.ac.jp
bRIKEN Center for Emergent Matter Science, Wako 351-0198, Japan
cDepartment of Science and Engineering, Teikyo University, Utsunomiya 320-8551, Japan
dDepartment of Physics, Waseda University, Shinjuku 169-8555, Japan
eInstitute for Materials Research, Tohoku University, Sendai 980-8577, Japan
fPRESTO, Japan Science and Technology Agency (JST), Kawaguchi 332-0012, Japan
gDepartment of Advanced Materials Science, The University of Tokyo, Kashiwa 277-8561, Japan
hDepartment of Physics, Tohoku University, Sendai 980-8578, Japan
iGraduate School of Advanced Science and Engineering, Hiroshima University, Higashi-Hiroshima 739-8521, Japan
jJapan Synchrotron Radiation Research Institute (JASRI), SPring-8, Hyogo 679-5198, Japan
kPrecision Spectroscopy Division, CSRR, SPring-8/JASRI, Hyogo 679-5198, Japan
lMaterials Dynamics Laboratory, RIKEN SPring-8 Center, Hyogo 679-5198, Japan
First published on 24th February 2022
Abstract
Orbital degrees of freedom appear in partially filled degenerate orbitals and are responsible for a variety of physical properties. Although many methods for directly observing orbital states in ordered states have been proposed, it is difficult to determine degenerate orbital states directly. We found that high-precision diffraction data obtained by synchrotron radiation X-rays can be used to observe only the valence electron density distribution with minimal analytical bias. The results obtained using this method clearly showed the anisotropy of the partially filled degenerate 3d orbital states in spinel vanadium oxide FeV2O4. The 3d orbital quantum state was successfully determined from this anisotropy.
Introduction
The interplay of charge, spin, orbital, and lattice degrees of freedom driven by electron correlation is a unifying principle across a wide range of transition metal systems.1–5 Such a picture provides a framework for determining whether one-electron physics is inadequate in a particular situation. The orbital degree of freedom in partially filled d-electron orbitals and related aspects such as orbital order, orbital waves, specific magnetic properties, and insulator–metal transitions has aroused considerable interest. Therefore, several methods have been proposed to observe orbital states, such as high harmonics generated from femtosecond laser pulses,6 ultraviolet angle-resolved photoelectron spectroscopy,7 resonant X-ray scattering,8 and non-resonant inelastic synchrotron X-ray scattering.9 Despite the need to observe the orbital degrees of freedom, these experimental methods only allow for determining the orbital ordered or stable state. Even first-principles calculations cannot easily determine metastable states at finite temperatures. Orbital degrees of freedom are realized when degenerate orbitals are partially filled, but since there are few reports of their observation, the electron distribution in degenerate orbitals is only vaguely understood. In the high-temperature region, the anisotropy of degenerate orbitals is expected to be suppressed due to thermal fluctuations caused by the surrounding atoms and crystal field. The anisotropy of two or more degenerate orbitals would still not be uniquely determined, since orbitals with different symmetries are hybridized by quantum mechanical interference. Therefore, it has been widely believed that the degeneracy of localized orbitals blurs anisotropic electronic distributions. However, this physical prediction is yet to be confirmed.We aimed to observe the valence electron density (VED) distribution to determine the orbital state. Our proposed core differential Fourier synthesis (CDFS) method10,11 allows us to directly observe the 3D distribution of the VED by synchrotron X-ray diffraction (XRD). This method calculates the VED; ρν(r) in the unit cell by subtracting the structure factor calculated using only the core–shell electrons from the experimental structure factor by the XRD, and then inverse Fourier transforming this difference structure factor as shown in eqn (1). The CDFS is an innovative method that exploits a blind spot in the analysis of diffraction data by minimizing the effect of censoring of the inverse Fourier transform with finite coefficients, which is usually a problem (Fig. S1, ESI†). In eqn (1), K is the scattering vector. Fobs|(K)| is the absolute value of the experimentally observed crystal structure factor. fcorej is the jth atomic scattering factor with only the core electrons contribution. There are several publicly available databases of atomic scattering factors fcore for these core–shell electrons. Tj is the jth atomic displacement parameter. P and Pcore represent the phase factor. Pcore is with only the core electrons contribution calculated as Pcore = Fcorecal (K)/|Fcorecal (K)|. nν is the total number of valence electrons contained in the unit cell. Since |F(000)| is not experimentally observable, we add the nν/V term to correct the VED distribution data.
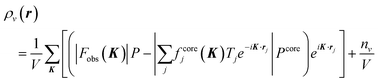 | (1) |
The configuration of the partially occupied d orbitals leads to peculiar magnetic and electronic transitions, such as the Verwey transition of Fe3O4.14 In this study, we focus on the orbital state of vanadium spinel oxide FeV2O4, which has an isomorphous structure as magnetite, in the high-temperature phase. In this system, despite the lack of charge degrees of freedom due to the Mott insulator, both electronic correlations and geometric frustration are present, resulting in an interplay between the different degrees of freedom, such as spin, orbital, and lattice, which leads to three successive phase transitions with decreasing temperature.15–24 FeV2O4 has been widely studied from both experimental and theoretical perspectives; however, owing to the intertwining of the multiple degrees of freedom, it is difficult to understand the orbital state completely. AV2O4 with other cations at the Fe site has been studied to avoid multiple degrees of freedom. For example, nonmagnetic A-site (A = Mg,25 Zn,26 Cd27) and magnetic but orbitally inactive A-site (A = Mn,28 Co29) have been studied. The role of Fe was also studied in the isomorphic material FeCr2O4.30 By integrating these studies, the crystal structure of FeV2O4 is predicted to change from cubic to tetragonal (a > c) at 140 K due to Fe orbital ordering, to orthorhombic at 110 K due to Fe-spin-orbital interaction, and to tetragonal (a < c) at 65 K due to V orbital ordering. Although there has been considerable discussion on the origin of the phase transition, mainly focusing on the orbital ordered state of V, there are few reports that have definitively determined the electronic state of the high-symmetry cubic phase.
In FeV2O4, because the formal charges of Fe and V are +2 and +3, the electron configurations are 3d6 and 3d2, respectively. The S = 2 spin at the Fe site and the S = 1 spin at the V site is determined by the magnetization experiment.16 The unit cell consists of a 3D structure of 8 FeO4 tetrahedra and 16 VO6 octahedra (Fig. 1A). This system has three structural phase transitions with decreasing temperature, but there is only one crystallographically independent site each for Fe, V, and O in all phases. In the cubic phase of the space group Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m, because FeO4 is a regular tetrahedron, the 3d orbitals of Fe2+ split into lower doubly degenerate e orbitals and higher triply degenerate t2 orbitals. Owing to the high-spin configuration, five electrons with an up-spin form the half-closed shell configuration, and one “down-spin electron” on the e orbital is responsible for the orbital degree of freedom (Fig. 1B). Therefore, Fe2+ has both spin and orbital degrees of freedom. In contrast, the octahedral site of VO6 has inversion symmetry, and the 3d orbitals of V3+ are divided into lower triply degenerate t2g orbitals and higher doubly degenerate eg orbitals. If VO6 forms a regular octahedron (Oh), then 3d2 electrons occupy triple degenerate t2g orbitals in a high-spin configuration (Fig. 1B), and V3+ has spin and orbital degrees of freedom. However, the 3d state is complicated because of a slight D3d distortion in the VO6 octahedron. Therefore, the FeV2O4 system has spin and orbital degrees of freedom at both the Fe2+ and V3+ sites.
m, because FeO4 is a regular tetrahedron, the 3d orbitals of Fe2+ split into lower doubly degenerate e orbitals and higher triply degenerate t2 orbitals. Owing to the high-spin configuration, five electrons with an up-spin form the half-closed shell configuration, and one “down-spin electron” on the e orbital is responsible for the orbital degree of freedom (Fig. 1B). Therefore, Fe2+ has both spin and orbital degrees of freedom. In contrast, the octahedral site of VO6 has inversion symmetry, and the 3d orbitals of V3+ are divided into lower triply degenerate t2g orbitals and higher doubly degenerate eg orbitals. If VO6 forms a regular octahedron (Oh), then 3d2 electrons occupy triple degenerate t2g orbitals in a high-spin configuration (Fig. 1B), and V3+ has spin and orbital degrees of freedom. However, the 3d state is complicated because of a slight D3d distortion in the VO6 octahedron. Therefore, the FeV2O4 system has spin and orbital degrees of freedom at both the Fe2+ and V3+ sites.
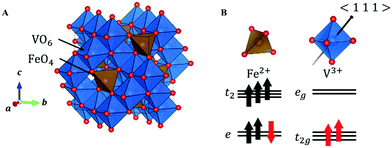 | ||
| Fig. 1 (A) Crystal structure of FeV2O4 in the cubic phase. (B) The orbital states of V and Fe in the cubic phase. The black arrow in VO6 indicates the 〈1 1 1〉 direction. | ||
The VO6 octahedron has a D3d-type distortion that satisfies the .![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m site symmetry at the V site. The triply degenerate t2g orbitals are further split into one orbital and two degenerate orbitals by the crystal field formed by the surrounding anions. One orbital wave function is uniquely described by the following formula because the 〈1 1 1〉 direction is the quantum axis.
m site symmetry at the V site. The triply degenerate t2g orbitals are further split into one orbital and two degenerate orbitals by the crystal field formed by the surrounding anions. One orbital wave function is uniquely described by the following formula because the 〈1 1 1〉 direction is the quantum axis.
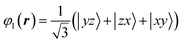 | (2) |
In this formula, x, y, and z are determined to be parallel to lattice vectors a, b, and c, respectively. In contrast, the two wavefunctions of doubly degenerate orbitals of t2g are not uniquely described. When these two orbital wavefunctions are denoted by φ2 and φ3, three wave functions, φ1, φ2 and φ3, in t2g have to be orthogonal to each other. Determining the energy level of the post-split orbital is difficult because of the small D3d-type distortion. There are no charge degrees of freedom and the volume of the VO6 octahedron is conserved. In the case of FeV2O4 in the cubic phase, the octahedron of VO6 extends in the 〈1 1 1〉 direction, and the area of the oxygen triangular surface perpendicular to the quantum axis is smaller than that of the regular octahedron. When calculating the V3+-3d2 orbital state using the Q-mode analysis,31 the t2g orbitals split into lower doubly degenerate orbitals and higher φ1 orbital. In contrast, when calculating the V3+-3d2 orbital state using a point-charge model with the Ewald method32 (for details of the calculation method, see ref. (10)), the t2g orbitals split into the lower φ1 orbital and higher doubly degenerate orbitals. It is important to note that the triple degeneracy of the t2g orbitals is maintained when the effect of the D3d-type strain is considerably weaker than that of the thermal fluctuation. Therefore, we attempted to determine the correct orbital state from the 3D distribution of VED obtained by the CDFS method.
Crystal structure and results of CDFS method
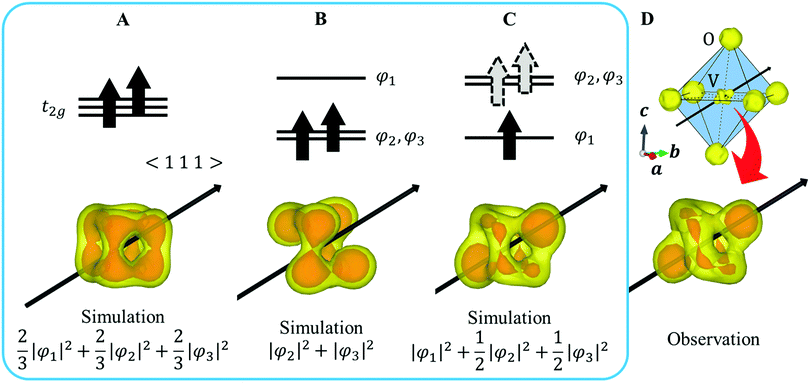
XRD experiments were performed using single crystals on the BL02B1 beamline at the synchrotron facility SPring-8 in Japan [see ESI† Section 1]. Fig. 2D and 4B show the observed VED around the V (1/2 1/2 1/2) and the Fe (1/8, 1/8, 1/8) sites at 160 K. The VED around the V site is more clearly anisotropic than the Fe site. The reason is that only 1/6 of the 3d electrons contribute to the anisotropy in the Fe site, whereas the V site directly reflects the anisotropy of the 3d2 electrons. The anisotropy of the VED at the V site was considered as follows:We defined φ2 and φ3 such that that the three wavefunctions, including φ1, are orthogonal to simulate the 3D VED distribution.
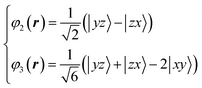 | (3) |
When a valence electron occupies the φi orbital, |φi|2 corresponds to VED. Because the CDFS method extracts only the VED, information on the phase of the orbital wave function is not obtained. Here, we expected the effect of the orbital angular moment l to be negligible and focused mainly on the Jahn–Teller effect.
First, we assume an orbital state where the energy gap of the t2g orbital is smaller than the thermal excitation energy. In this case, the t2g orbital can be regarded as triple degenerate, and φ1, φ2, and φ3 orbitals are occupied by the two 3d electrons with equal probability. The VED was simulated as 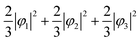 (Fig. 2A). Next, we assumed the orbital state calculated using Q-mode analysis, in which the degenerate orbitals are stabilized. Because the two 3d electrons occupy the degenerated φ2 and φ3, the VED is described as |φ2|2 + |φ3|2, as shown in Fig. 2B. The simulated VEDs do not reproduce the observed electron density (Fig. 2D). Next, we focused on the orbital state calculated by the point-charge model. In simple consideration, the two 3d electrons form a spin singlet on stabilized φ1, but it does not satisfy S = 1 at the V site. In general, the energy gap of the t2g orbitals due to the D3d distortion is small, and Hund's rules are considered. In this case, one electron occupies the lower φ1, and the other one is lifted to the degenerate orbitals and occupies either φ2 or φ3. This electron configuration satisfies S = 1. In addition, the simulated VEDs such that the lifted electrons occupy only φ2 or φ3 orbital states also did not reproduce the observed VED (Fig. S2) [see ESI† Section 2 for details]. Therefore, we assumed that the electrons on the double degenerate orbitals occupied both orbitals with equal probability. The simulation as
(Fig. 2A). Next, we assumed the orbital state calculated using Q-mode analysis, in which the degenerate orbitals are stabilized. Because the two 3d electrons occupy the degenerated φ2 and φ3, the VED is described as |φ2|2 + |φ3|2, as shown in Fig. 2B. The simulated VEDs do not reproduce the observed electron density (Fig. 2D). Next, we focused on the orbital state calculated by the point-charge model. In simple consideration, the two 3d electrons form a spin singlet on stabilized φ1, but it does not satisfy S = 1 at the V site. In general, the energy gap of the t2g orbitals due to the D3d distortion is small, and Hund's rules are considered. In this case, one electron occupies the lower φ1, and the other one is lifted to the degenerate orbitals and occupies either φ2 or φ3. This electron configuration satisfies S = 1. In addition, the simulated VEDs such that the lifted electrons occupy only φ2 or φ3 orbital states also did not reproduce the observed VED (Fig. S2) [see ESI† Section 2 for details]. Therefore, we assumed that the electrons on the double degenerate orbitals occupied both orbitals with equal probability. The simulation as 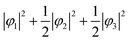 resulted in the VED distribution shown in Fig. 2C, which perfectly reproduced the experimental result. This result clearly means one electron occupies the lowest φ1, and another electron is on the degenerate orbitals composed of φ2 and φ3. VED analysis by the CDFS method found that the degenerate orbitals reflect the anisotropy of their constituent orbitals in the cubic phase.
resulted in the VED distribution shown in Fig. 2C, which perfectly reproduced the experimental result. This result clearly means one electron occupies the lowest φ1, and another electron is on the degenerate orbitals composed of φ2 and φ3. VED analysis by the CDFS method found that the degenerate orbitals reflect the anisotropy of their constituent orbitals in the cubic phase.
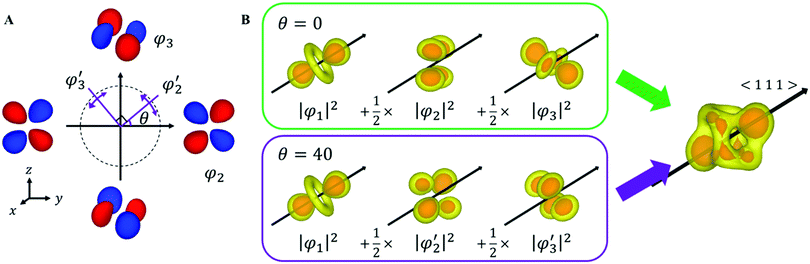
Here, we reconsider the degenerate orbital. As described above, the double degenerate orbital wavefunctions of t2g are not uniquely described. The wavefunctions can also be represented as follows with an arbitrary phase value θ:
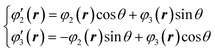 | (4) |
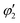 , and
, and 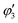 are orthogonal to each other. The orbital degrees of freedom mean that θ fluctuates in time and site j as θj(t). Fig. 3 shows the schematic image of the fluctuating orbital. However, the VED obtained by XRD measurements was space- and time-averaged. The image in which the electron on the degenerate orbital occupies both orbitals with equal probability is a simplified representation. The observed electron density ρν with the fluctuated orbital states within the Born–Oppenheimer approximation is
are orthogonal to each other. The orbital degrees of freedom mean that θ fluctuates in time and site j as θj(t). Fig. 3 shows the schematic image of the fluctuating orbital. However, the VED obtained by XRD measurements was space- and time-averaged. The image in which the electron on the degenerate orbital occupies both orbitals with equal probability is a simplified representation. The observed electron density ρν with the fluctuated orbital states within the Born–Oppenheimer approximation is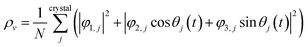 | (5) |
Here, N is the number of V sites in the crystal, j is the label of the V sites in the entire crystal, and t is the time. The linear combination wavefunction of the degenerate orbitals is realized at each V site. However, the simulated VEDs at each V site do not suffice the site symmetry at the V site (.![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m) (Fig. S3, ESI†). The average of the sum over the entire crystal is observed as the electron density. The average is equivalent to:
m) (Fig. S3, ESI†). The average of the sum over the entire crystal is observed as the electron density. The average is equivalent to:
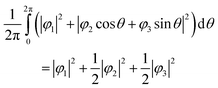 | (6) |
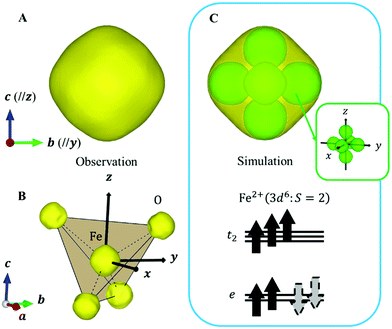
Next, we focused on the Fe sites. When the VED of the CDFS analysis is viewed from the a-axis, the VED has a slight anisotropy extending in the direction of lattice axes a, b, and c at 160 K (Fig. 4A). Applying the same analogy as that applied to the V site, the Fe2+-3d6 orbital state should be understood from the VED. The anisotropy of the VED is responsible for “down-spin electron” on the e orbitals. In cubic phase, FeO4 is a regular tetrahedron that satisfies the ![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) 3m site symmetry at the Fe site, and the e orbitals remain degenerate. The two wave functions of the e orbital of Fe can be expressed as:
3m site symmetry at the Fe site, and the e orbitals remain degenerate. The two wave functions of the e orbital of Fe can be expressed as:
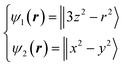 | (7) |
Similar to that for the V site, the wavefunction of “down-spin electron” can also be described as follows using an arbitrary phase value θ′.
ψ′(r) = ψ1(r) cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ′ + ψ2(r) sin θ′ + ψ2(r) sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ′ θ′ | (8) |
Because this electron exists on degenerate e orbitals, the averaged orbital state, which is 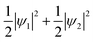 , is realized (Fig. 4C). Although the anisotropy of the VED around Fe is smaller than that around V, the electron configuration of Fe2+-3d6 is well reproduced in real space.
, is realized (Fig. 4C). Although the anisotropy of the VED around Fe is smaller than that around V, the electron configuration of Fe2+-3d6 is well reproduced in real space.
Since cubic-tetragonal structural transition in FeV2O4 occurs at 140 K, it is obvious that the electron orbitals have temporal fluctuations in cubic phase. Depending on the orbital fluctuations, a lattice fluctuation occurs due to the electron–lattice interaction. This phase transition is predicted to be mainly due to Fe orbital order.18 To confirm the orbital states below the phase transition temperature, direct observation is necessary. In the high-temperature tetragonal phase, a precise structural analysis of single crystals was performed, paying attention to the domain formation and site symmetry reduction [see ESI† Section 3]. The structural analysis at 120 K shows that the VO6 octahedron and FeO4 tetrahedron are slightly deformed, particularly FeO4 is compressed along the c-axis. This means a “down-spin electron” of Fe occupies the ψ1 orbital due to Fe orbital order. In fact, when VED was extracted by using CDFS method, the anisotropy of Fe2+-3d6 including ψ1 orbital asymmetry was observed (Fig. S4, ESI†), but the anisotropy of the V-site orbital was maintained (Fig. S5, ESI†). When the orbital degeneracy of Fe is resolved, the symmetry of FeO4 is lowered due to JT strain, but it is interesting to see how the phonons behave when the orbital degrees of freedom at the V site is preserved.
Analysis result of inelastic X-ray scattering (IXS)
The distortion in the form of compression/elongation of the FeO4 tetrahedron coupled with the wave function in eqn (7) corresponds to the E-symmetry. The 8 FeO4 tetrahedra existing in the unit cell can be divided into two types based on the reversed quantization axis (Fig. S6, ESI†). When these two types of FeO4 are distorted in the in-phase, this phonon mode is called the Eg mode, and when they are in the anti-phase, this phonon mode is called the Eu mode. The IXS experiments were performed on the RIKEN BL43LXU beamline at SPring-8 [see ESI† Section 4, 5]. As a result, the slight softening of the transverse acoustic (TA) mode dispersing along the [1 1 0] and polarized along [−1 1 0], as shown in Fig. 5, indicates that the lattice distorts toward the transition point. This TA mode corresponds to the Eg mode. In contrast, the longitudinal optical (LO) mode dispersing and polarization along [0 0 l], corresponding to the Eg mode, was not observed due to weak intensity. Another LO mode corresponding to the Eu mode showed no temperature dependence in the range of T = 150–300 K (Fig. S9, ESI†).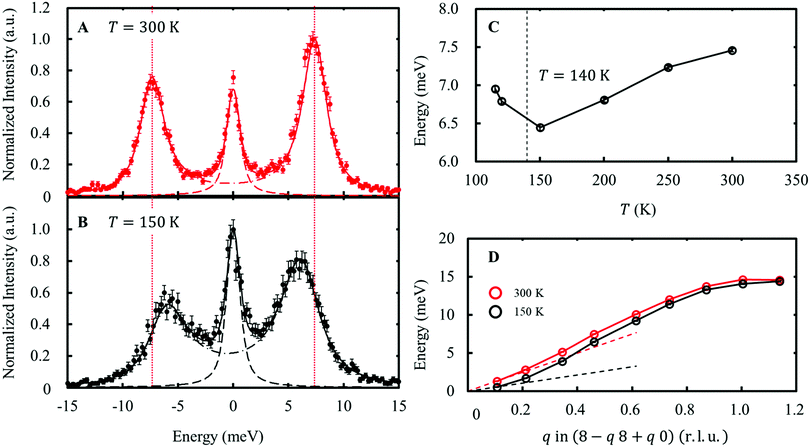 | ||
| Fig. 5 Energy scan data at Q = (7.54 8.45 –0.03) at 300 K (A) and 150 K (B). The phonon peaks correspond to the Eg TA mode. The solid lines indicate fitting results using two lines, corresponding to an elastic peak (dashed line) and a pair of phonon peaks (dash-dotted line). The vertical dotted line indicates the phonon energy at 300 K. (C) The temperature dependence of the phonon energy at Q = (7.54 8.45 –0.03). (D) Phonon dispersions of the Eg TA mode at 300 K and 150 K. The dashed lines indicate the linear dispersions expected from the elastic stiffness constants at each temperature [see ESI† Section 2.3]. | ||
As shown in the dispersion diagram of the Eg TA mode in Fig. 5C, softening of the Eg TA mode is observed up to q ∼0.7 r.l.u. (approximately 8.5 Å in real space). This softening is different from the usual precursor phenomenon of structural phase transitions. This is because the deformation mode, which should be coupled to orbital fluctuations, preserves the orbital degrees of freedom at the V site. This observed dispersion closely resembles the nematic state of iron-based superconductors, in which orbital degrees of freedom play an important role33 This result may be related to the distribution of the electron–lattice interaction when the orbital degrees of freedom are mixed at several different sites. To address this issue, we plan to conduct research on the same in the future. [see ESI† Section 6].
Conclusions
It was found that the VED with orbital degrees of freedom in FeV2O4 maintained a state reflecting orbital anisotropy even at relatively high temperatures. By directly observing the VED of the cubic phase, the orbital state can be directly determined without the need to estimate the crystal field or Hund's coupling constant due to the distortion of the VO6 octahedron. We showed that such orbital states are likely to be universal in the high-symmetry phase and that the quantum parameters can be determined directly by simply combining them with the CDFS method, provided that the accuracy of the diffraction measurements is ensured. Understanding the electronic states with orbital degrees of freedom will provide new prospects to reveal physical properties.Author contributions
T. M., S. K., and H. S. designed and coordinated this study. S. N., and T. K. synthesized the samples. T. M., S. K., and H. S. performed the XRD and the IXS experiments. K. H., and D. I. supported the XRD and the IXS experiments the as the beamline scientist. T. H. performed the first-principles calculations of phonon. T. H., and A. B. discussed the IXS experimental results. N. K., Y. N., T. A., and J. N. advised this study. T. M., and H. S. wrote the manuscript. All authors discussed the experimental results and contributed to the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank K. Kojima, T. Hara, and Y. Hosogi for supporting the IXS experiments, Y. Wakabayashi, H. Fukui, and K. Siratori, for their fruitful discussions. The synchrotron radiation experiments were performed at SPring-8 with the approval of the Japan Synchrotron Radiation Research Institute (JASRI) (Proposal No. 2019A0070–2021A0070/BL02B1, 2020A0835/BL43LXU, and 2021A1575/BL43LXU). The work leading to these results has received funding from Yamada Science Foundation.References
- Y. Tokura and N. Nagaosa, Orbital physics in transition-metal oxides, Science, 2000, 288, 462–468 CrossRef CAS PubMed.
- K. I. Kugel’ and D. I. Khomskiĭ, The Jahn-Teller effect and magnetism: transition metal compounds, Sov. Phys. Usp., 1982, 25, 231–256 CrossRef.
- A. J. Millis, Lattice effects in magnetoresistive manganese perovskites, Nature, 1998, 392, 147–150 CrossRef CAS.
- E. Dagotto, Complexity in strongly correlated electronic systems, Science, 2005, 309, 257–262 CrossRef CAS PubMed.
- A. Georges, L. d e’Medici and J. Mravlje, Strong Correlations from Hund's Coupling, Annu. Rev. Condens. Matter Phys., 2013, 4, 137–178 CrossRef CAS.
- J. Itatani, J. Levesque, D. Zeidler, H. Niikura, H. Pépin, J. C. Kieffer, P. B. Corkum and C. M. Villeneuve, Tomographic imaging of molecular orbitals, Nature, 2004, 432, 867–871 CrossRef CAS PubMed.
- P. Puschnig, S. Berkebile, A. J. Fleming, G. Koller, K. Emtsev, T. Seyller, J. D. Riley, C. Ambrosch-Draxl, F. P. Netzer and M. G. Ramsey, Reconstruction of molecular orbital densities from photoemission data, Science, 2009, 326, 702–706 CrossRef CAS PubMed.
- Y. Murakami, J. P. Hill, D. Gibbs, M. Blume, I. Koyama, M. Tanaka, H. Kawata, T. Arima, Y. Tokura, K. Hirota and Y. Endoh, Resonant X-Ray Scattering from Orbital Ordering in LaMnO3, Phys. Rev. Lett., 1998, 81, 582–585 CrossRef CAS.
- H. Yavas, M. Sundermann, K. Chen, A. Amorese, A. Severing, H. Gretarsson, M. W. Haverkort and L. H. Tjeng, Direct imaging of orbitals in quantum materials, Nat. Phys., 2019, 15, 599 Search PubMed.
- S. Kitou, T. Manjo, N. Katayama, T. Shishidou, T. Arima, Y. Taguchi, Y. Tokura, T. Nakamura, T. Yokoyama, K. Sugimoto and H. Sawa, Collapse of the simple localized 3d1 orbital picture in Mott insulator, Phys. Rev. Res., 2020, 2, 033503 Search PubMed.
- S. Kitou, Y. Hosogi, R. Kitaura, T. Naito, T. Nakamura and H. Sawa, Direct Observation of Molecular Orbitals Using Synchrotron X-ray Diffraction, Crystals, 2020, 10, 998 Search PubMed.
- H. Sawa, Y. Wakabayashi, Y. Murata, M. Murata and K. Komatsu, Floating Single Hydrogen Molecule in an Open-Cage Fullerene, Angew. Chem., 2005, 117, 2017–2019 CrossRef.
- S. Aoyagi, E. Nishibori, H. Sawa, K. Sugimoto, M. Tanaka, Y. Miyata, R. Kitaura, H. Shinohara, H. Okada, T. Sakai, Y. Ono, K. Kawachi, S. Yokoo, S. Ono, K. Omote, Y. Kasama, S. Ishikawa, T. Komuro and H. Tobita, layered ionic crystal of polar Li@C60 superatoms, Nat. Chem., 2010, 2, 678 CrossRef CAS PubMed.
- E. J. W. Verway, Electronic Conduction of Magnetite (Fe3O4) and its Transition Point at Low Temperature, Nature, 1939, 144, 327–328 CrossRef.
- S. H. Lee, H. Takagi, D. Louca, M. Matsuda, S. Ji, H. Ueda, Y. Ueda, T. Katsufuji, J. H. Chung, S. Park, S. W. Cheong and C. Broholm, Frustrated Magnetism and Cooperative Phase Transition in Spinels, J. Phys. Soc. Jpn., 2010, 79, 011004 CrossRef.
- T. Katsufuji, T. Suzuki, H. Takei, M. Shingu, K. Kato, K. Osaka, M. Tanaka, H. Sagayama and T. Arima, Structural and Magnetic Properties of Spinel FeV2O4 with Two Ions Having Orbital Degrees of Freedom, J. Phys. Soc. Jpn., 2008, 77, 053708 CrossRef.
- G. J. MacDougall, V. O. Garlea, A. A. Aczel, H. D. Zhou and E. Nagler, Magnetic order and ice rules in the multiferroic spinel FeV2O4, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 060414(R) CrossRef.
- Y. Nii, H. Sagayama, A. Aoyagi, R. Sakai, S. Maki, E. Nishibori, H. Sawa, K. Sugimoto, H. Ohsumi and M. Takata, Orbital structures in spinel vanadates AV2O4 (A = Fe, Mn), Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 125142 CrossRef.
- A. Kismarahardja, J. S. Brooks, H. D. Zhou, E. S. Choi, K. Matsubayashi and Y. Uwatoko, Dielectric properties of single crystal spinels in the series FeV2O4, MnV2O4, and CoV2O4 in high magnetic fields, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 054432 CrossRef.
- S. Nakamura and A. Fuwa, Distinct Evidence of Orbital Order in Spinel Oxide FeV2O4 by 57Fe Mössbauer Spectroscopy, J. Phys. Soc. Jpn., 2016, 85, 014702 CrossRef.
- B. R. Myoung, S. J. Kim, J. T. Lim, T. Kouh and C. S. Kim, Microscopic evidence of magnetic and structure phase transition in multiferroic spinel FeV2O4, AIP Adv., 2017, 7, 055828 CrossRef.
- Q. Zhang, M. Ramazanoglu, S. Chi, Y. Liu, T. A. Lograsso and D. Vaknin, Magnetic excitations and anomalous spin–wave broadening in mutiferroic FeV2O4, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 224416 CrossRef.
- K. Matsuura, H. Sagayama, Y. Nii, N. D. Khanh, N. Abe and T. Arima, X-ray magnetic circular dichroism of an orbital ordered state in the spinel–type vanadium oxide AV2O4 (A = Mn, Fe), Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92, 035133 CrossRef.
- D. Dey, T. Maitra and A. Taraphder, Orbital ordering in Fe1-xMnxV2O4: A first-principles study, Phys. Rev. B, 2016, 93, 195133 CrossRef.
- H. Mamiya, M. Onoda, T. Furubayashi, J. Tang and I. Nakatani, Structural and magnetic studies on vanadium spinel MgV2O4, J. Appl. Phys., 1997, 81, 5289–5291 CrossRef CAS.
- Y. Ueda, N. Fujiwara and H. Yasuoka, Magnetic and Structural Transitions in (LixZn1-x)V2O4 with the Spinel Structure, J. Phys. Soc. Jpn., 1997, 66, 778–783 CrossRef CAS.
- M. Onoda and J. Hasegawa, A distortion of pseudotetramers coupled with the Jahn–Teller effect in the geometrically frustrated spinel system CdV2O4, J. Phys.: Condens. Matter, 2003, 15, L95–L102 CrossRef CAS.
- R. Plumier and M. Sougi, Observation of a first order transition in the ferrimagnetic spinel MnV2O4, Solid State Commun., 1987, 64, 53–55 CrossRef CAS.
- A. Kismarahardja, J. S. Brooks, A. Kiswandhi, K. Matsubayashi, R. Yamanaka, Y. Uwatoko, J. Whalen, T. Siegrist and H. D. Zhou, Co[V2]O4: A Spinel Approaching the Itinerant Electron Limit, Phys. Rev. Lett., 2011, 106, 056602 CrossRef CAS PubMed.
- S. Ohtani, Y. Watanabe, M. Saito, N. Abe, K. Taniguchi, H. Sagayama, T. Arima, M. Watanabe and Y. Noda, Orbital dilution effect in ferrimagnetic Fe1-xMnxCr2O4: competition between anharmonic lattice potential and spin–orbit coupling, J. Phys.: Condens. Matter, 2010, 22, 176003 CrossRef CAS PubMed.
- K. Siratori and K. Kohn, Ground State of a dε Electron in an Elastic Octahedron of Ligands, J. Phys. Soc. Jpn., 2010, 79, 114720 CrossRef.
- P. P. Ewald, Die Berechnung optischer und elektrostatischer Gitterpotentiale, Ann. Phys., 1921, 369, 253–287 CrossRef.
- A. M. Merritt, F. Weber and J. P. Castellan, Th. Wolf, D. Ishikawa, A. H. Said, A. Alatas, R. M. Fernandes, A. R. R. Baron, D. Reznik, Nematic Correlation Length in Iron–Based Superconductors Probed by Inelastic X-Ray Scattering, Phys. Rev. Lett., 2020, 124, 157001 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1ma01113h |
| This journal is © The Royal Society of Chemistry 2022 |