Fragmentation of interstellar methanol by collisions with He˙+: an experimental and computational study†
Vincent
Richardson
 a,
Emília
Valença Ferreira de Aragão
a,
Emília
Valença Ferreira de Aragão
 bc,
Xiao
He
a,
Fernando
Pirani
bc,
Xiao
He
a,
Fernando
Pirani
 bd,
Luca
Mancini
bd,
Luca
Mancini
 b,
Noelia
Faginas-Lago
b,
Noelia
Faginas-Lago
 bc,
Marzio
Rosi
bc,
Marzio
Rosi
 d,
Luca Matteo
Martini
d,
Luca Matteo
Martini
 a and
Daniela
Ascenzi
a and
Daniela
Ascenzi
 *a
*a
aDepartment of Physics, University of Trento, Trento, Italy. E-mail: daniela.ascenzi@unitn.it
bDepartment of Chemistry, Biology and Biotechnology, Università degli studi di Perugia, Perugia, Italy
cMaster-Tec s.r.l., Via Sicilia 41, Perugia, Italy
dDepartment of Civil and Environmental Engineering, Università degli studi di Perugia, Perugia, Italy
First published on 8th September 2022
Abstract
Methanol is a key species in astrochemistry as its presence and reactivity provides a primary route to the synthesis of more complex interstellar organic molecules (iCOMs) that may eventually be incorporated in newly formed planetary systems. In the interstellar medium, methanol is formed by hydrogenation of CO ices on grains, and its fate upon collisions with interstellar ions should be accounted for to correctly model iCOM abundances in objects at various stages of stellar evolution. The absolute cross sections (CSs) and branching ratios (BRs) for the collisions of He˙+ ions with CH3OH are measured, as a function of the collision energy, using a Guided Ion Beam Mass Spectrometer (GIB-MS). Insights into the dissociative electron (charge) exchange mechanism have been obtained by computing the entrance and exit multidimensional Potential Energy Surfaces (PESs) and by modelling the non-adiabatic transitions using an improved Landau–Zener–Stückelberg approach. Notably, the dynamical treatment reproducing the experimental findings includes a strong orientation effect of the system formed by the small He˙+ ion and the highly polar CH3OH molecule, in the electric field gradient associated to the strongly anisotropic intermolecular interaction. This is a stereodynamical effect that plays a fundamental role in collision events occurring under a variety of conditions, with kinetic energy confined within intervals ranging from the sub-thermal to the hyper-thermal regime.
1 Introduction
Methanol (CH3OH) is one of the most abundant and ubiquitous interstellar Complex Organic Molecules (iCOMs)1 with countless detections in various environments, from molecular clouds to comets. Methanol is a key astrochemical molecule because its reactivity represents a major route to the synthesis of more complex organic species such as esters, ketones and aldehydes, that are the prebiotic precursors of sugars, amino acids and other biomolecules.2–4Since its first interstellar detection in 1970,5 methanol has been regularly detected at various stages of stellar evolution, from the cold and dark pre-stellar core phase (see ref. 6 and refs therein) to the protostar phase, where it has been widely observed towards hot cores and hot corinos, the gas phase envelopes surrounding young stellar objects of high or low masses, under either warm or cold conditions (see for instance7–11 for the most recent surveys of iCOMs detections in Class 0 and Class I Solar-like protostars). At the protostellar stage, methanol is also detected in shocked gases associated with low-mass protostellar outflows.12 Although with more difficulty, CH3OH has been detected in protoplanetary disks, the next stage of stellar evolution which directly precedes the formation of a planetary system, thereby demonstrating that methanol, and consequently larger iCOMs, are present at the planet formation stage.13–17 CH3OH has been detected as a volatile species in several comets, including 67P/Churyumov-Gerasimenko by the recently concluded Rosetta mission,18–20 as ice on the surface of a Kuiper Belt Object (KBO)21 and it is among the few iCOMs detected in other galaxies.22
Chemical modelling, experimental determinations and astronomical observations23–25 have clearly established that methanol observed in regions of star formation is synthesized by successive hydrogenation of CO-rich ice mantles.3,4 Following formation, it can be released into the gas phase via thermal desorption under warm conditions or via non-thermal desorption processes (i.e. by gaining desorption energy via interactions with photons, electrons, cosmic rays, grain–grain collisions or exothermic chemical reactions in the solid phase) in cold environments. Once in the gas phase, methanol can contribute to synthesize more complex species via neutral–neutral or ion–neutral reactions. For instance, it can be protonated by reactions with H3+ or HCO+ ions and further react with either CH3OH or HCOOH to eventually lead to the formation of dimethyl ether and methylformate, respectively.26,27 Additionally, H abstraction by the hydroxyl (OH) radical can lead to formation of H2O plus CH2OH/CH3O.28
To explain the abundance of methanol, that in some astronomical environments can be as high as 3 × 10−5 with respect to H2,1 accurate measurements of the rate constants for formation and destruction routes are required. In addition to interactions with photons and electrons, reactions with ions are among the main destruction routes for methanol. The most relevant ions in this respect are H+, He˙+ and H2+, which are formed by the interaction of cosmic rays with H or He, as well as H2. From H+ and H2+, H3+ and HCO+ can be produced by ion-molecule reactions with H2 and CO, two of the most abundant neutrals in the ISM. Reactions with He˙+, H3+ and HCO+ are therefore expected to be the dominant destruction mechanisms for the vast majority of iCOMs, including methanol. However, while H3+ and HCO+ reactions involve proton transfer processes which can be, but are not necessarily, dissociative, the large recombination energy of He˙+, is expected to lead to a greater degree of methanol dissociation.
While the reactions of H3+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 29,30 and HCO+
29,30 and HCO+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 30–32 with CH3OH have been amply studied, to the best of our knowledge, no previous experimental or theoretical studies have been performed on the reaction of He˙+ and the rate constant and branching ratios (BRs) reported in the astrochemical databases KIDA (KInetic Database for Astrochemistry33 available at https://kida.astrochem-tools.org/) and UDfA (UMIST Database for Astrochemistry34 available at https://udfa.ajmarkwick.net/) are estimates based on chemical analogies and simple modelling of ion–neutral reactivity. Though such estimates can be useful when experimental/computational values are not available, they can sometimes differ significantly from the true values, as demonstrated by previous work on the reactivity of He˙+ with dimethyl ether (CH3OCH3) and methyl formate (HCOOCH3),35–37 for which the rate coefficients, BRs and their temperature dependences have been found to differ substantially from the estimates reported in the databases, as a consequence of stereodynamical effects present at low collision energies.
30–32 with CH3OH have been amply studied, to the best of our knowledge, no previous experimental or theoretical studies have been performed on the reaction of He˙+ and the rate constant and branching ratios (BRs) reported in the astrochemical databases KIDA (KInetic Database for Astrochemistry33 available at https://kida.astrochem-tools.org/) and UDfA (UMIST Database for Astrochemistry34 available at https://udfa.ajmarkwick.net/) are estimates based on chemical analogies and simple modelling of ion–neutral reactivity. Though such estimates can be useful when experimental/computational values are not available, they can sometimes differ significantly from the true values, as demonstrated by previous work on the reactivity of He˙+ with dimethyl ether (CH3OCH3) and methyl formate (HCOOCH3),35–37 for which the rate coefficients, BRs and their temperature dependences have been found to differ substantially from the estimates reported in the databases, as a consequence of stereodynamical effects present at low collision energies.
In this paper we report the first experimental determination of the partial and total ionization cross sections (CSs) of CH3OH upon collisions with He˙+ ions as a function of the collision energy (in the range from ∼0.04 to ∼10 eV) using guided ion beam mass spectrometry. Experimental results are interpreted by an improved Landau–Zener approach based on an analytical expression of the Potential Energy (hyper)Surfaces (PESs) for the entrance and exit channels leading to the formation of the CH3OH˙+ radical cation in highly excited electronic states. The PESs have been obtained by a semi-empirical method, where involved parameters, defined on phenomenological ground, have a proper physical meaning, thus guaranteeing an internally consistent representation of the interaction in the full space of the relative configuration of reagents. This is a key prerequisite to carry out molecular dynamics simulations over a range of collision energies that extends from sub-thermal up to hyper-thermal values. Moreover, the internal energy content of the resultant molecular ion is such that several fragmentation channels are energetically accessible.
In the entrance channel a natural orientation of a polar reagent, such as CH3OH, occurs because of the large electric field gradients probed by the rotating molecule within the strongly anisotropic PES, arising from the intermolecular interaction with the very small He˙+ cation. This polarization effect leads to the preferential formation of the non covalent adduct (the precursor state of reaction) in specific configurations confined within a narrow angular cone, giving rise to the so called pendular states.38,39 In other words, the most stable configurations of the precursors are rather different with respect to the transition state promoting direct electron transfer, and this generates a pronounced steric effect on the dynamical evolution of reactive events. Such stereodynamical effects become increasingly significant at low collision energies.
Comparison of the experimental results with the model outcomes indicates that the preferential geometries assumed by the reagents at low collision energies inhibit charge exchange, thus giving rate coefficients at low temperatures (most relevant for the interstellar medium) that differ substantially from those reported in astrochemical databases. Note that, for the title reaction, the routinely used capture theory methods overestimate the experimental absolute cross section values and are unable to reproduce their energy dependence in the probed energy range, providing divergent results at low collision energies (see also ref. 35–37). Ab initio calculations are used to define the shape of the molecular orbitals of the methanol molecule from which the electron is captured and to evaluate the energetics of the various fragmentation channels of the CH3OH˙+ radical cation.
2 Experimental
2.1 Experimental methodology
The experimental data presented as part of this work have been collected using the Trento Guided Ion Beam Mass Spectrometer (GIB-MS), which has been described in detail previously40,41 and so it is only covered briefly here. The Trento GIB-MS is a tandem mass spectrometer composed of two octopoles (O) and two quadrupole mass filters (Q) in a O–Q–O–Q configuration that allows for the investigation of bimolecular reactions of mass-selected ions. Absolute CSs and BRs as a function of the collision energy (ECM) are derived by measuring the yields of both parent and product ions.He˙+ ions are produced by electron ionization at electron energies in the range 55–65 eV. Electrons are emitted by a thoriated tungsten filament with the emission current stabilized by an electronic feedback mechanism. He is introduced into the ion source by a variable leak valve (Agilent Technologies/Varian model 951-5106) at pressures in the range 10−7–10−8 mbar.
Following ionization, ions pass through the first octopole, which acts as a ion guide, before being mass selected by the first quadrupole. Reactions occur in the second octopole, which is surrounded by a 10 cm long scattering cell. The pressure of the neutral gas in the scattering cell surrounding the second octopole is monitored by a spinning rotor gauge (SRG2 MKS Instruments, MA, USA). In order to be able to convert experimental CSs to absolute CSs, calibration experiments have been performed on the He˙+ + SiCl4 system, which is the subject of previous study using a similar set-up,42 details of which are given in the ESI.† In this way, an effective cell length value equal to 8.3 ± 4.0 cm has been obtained, with the magnitude of the uncertainty resulting from the literature CSs used in the calibration.42
The collision energy in the laboratory frame is dependent on both the reagent ion charge (+1 in the case of this work) and the difference between the ion source and reaction cell potentials. The retarding potential method was applied to the reagent ion beam43 to determine the maximum of the first derivative of the reagent ion yield, which defines the zero of the kinetic energy. In this way, we have estimated an average reagent ion beam FWHM of ∼1 eV in the laboratory frame, equivalent to ∼0.9 eV in the center-of-mass (CM) frame. By varying the potentials of the second octopole and all subsequent optics, we are able to scan a collision energy range from ∼0.05 to ∼10 eV in the CM frame (ECM).
The reaction cell is filled with a ∼10% mixture of CH3OH in Ar at variable pressures in the range of 1.0 × 10−8 to 1.3 × 10−4 mbar. The dilution of CH3OH in Ar is performed in order both to stabilise the vapour pressure of CH3OH and to keep any secondary reaction at a reduced level. The chosen pressure interval further aids to limit the impact of secondary reactions, while still providing an accurate pressure measurement and a dynamic range from 10−1 to 102 Å2 for the absolute CSs.
In order to limit the effects of potential drifts in source pressure, reaction cell pressure and electron emission current, data are collected in the so-called multi-scan mode, where signals are recorded for parent (He˙+) and product ions at a single point (e.g. at a specific ECM or CH3OH pressure in the collision cell) before moving to the next one. To account for potential differences in the collection efficiency of He˙+ ions when the collection optics are optimized for product ions, parent ion intensities have been recorded at the product ion optimisation with gas (CH3OH/Ar mixture in the present case) in the scattering cell (IProd(CM)). Subsequently, the IProd(CM) is re-scaled to give the real He˙+ intensity (IPar(CM)) by optimizing the collection optics at the parent ion with no gas in the cell and using eqn (1):
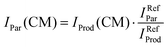 | (1) |
2.2 Experimental results
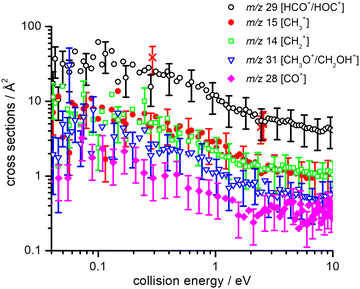
By recording mass spectra at different neutral gas pressures charged products from the reaction of He˙+ with CH3OH have been identified at m/z 14, 15, 28, 29 and 31. Additional peaks observed at m/z 33, 41 and 47 have been identified as deriving from secondary reaction of the m/z 29 product with both Ar and CH3OH (see the ESI† for a typical mass spectrum). Notably, as we do not observe a product at m/z 32, corresponding to the formation of CH3OH˙+, we are able to conclude that the electron transfer process is completely dissociative.The limited resolution of our quadrupole mass spectrometer at m/z = 1 and 2 makes it infeasible to obtain results at these masses. Hence, potential products at such m/z values are not considered in the analysis. On the basis of previous results on the dissociative ionization of methanol via electrons and photons,44,45 we can expect that the contribution of the neglected ions to total yield should not exceed a few percent. In particular, in the case of photons,45 the BR for H+ is 1% at 24.5 eV photon energy and 3% at 30 eV, with even smaller values for H2+ (0% and 0.3% at 24.5 and 30 eV photon energy respectively). Additionally, the AE of H2+ is measured to be 26.5 eV, which is higher than the recombination energy carried by He˙+. Similarly, in the case of electrons44 the BR for H+ is 1.2% at 30 eV electron energy and 5.5% at 65 eV, with smaller values for H2+ (0.07% and 0.3% at 30 and 65 eV electron energy respectively). Therefore, in our case, an upper limit for BR(H+) of ∼0.05 (a value that is within the experimental uncertainty for some products) can be assumed, while the formation of H2+ can be neglected.
The corresponding reaction pathways for the products are given in eqn (2)–(6) with the thermochemistries shown in Table 1, while the secondary reactions are described by eqn (7)–(9).
| He˙+ + CH3OH → CH2˙+ + H2O/(OH˙ + H˙) + He | (2) |
| → CH3+ + OH˙ + He | (3) |
| → CO˙+ + 2H2/(H2 + 2H˙)/4H˙ + He | (4) |
| → HCO+/HOC+ + H˙ + H2 + He | (5) |
| → CH2OH+/CH3O+ + H˙ + He | (6) |
| HCO+ + Ar → ArH+ + CO | (7) |
| HCO+ + CH3OH → CH3OH2+ + CO | (8) |
| CH3OH2+ + CH3OH → (CH3)2OH+ + H2O | (9) |
| Reaction products | Eqn | Reaction enthalpya (eV) | Reaction enthalpyb (eV) |
|---|---|---|---|
| a Calculated using formation enthalpies ΔfH° (298 K) of CH3OH and of He˙+ taken from Active Thermochemical Database49 and NIST48 respectively. Formation enthalpies ΔfH° (298 K) for the reaction products as indicated in notes c–g. b This work, at 298 K. c ΔfH° (298 K) of CH2˙+ from ref. 49, of H2O and H˙ from ref. 48 and of OH˙ from ref. 51. d ΔfH° (298 K) of CH3+ from ref. 49. e ΔfH° (298 K) and IE of CO from ref. 48. f ΔfH° (298 K) of HCO+ and HOC+ from ref. 49. g ΔfH° (298 K) of CH2OH+ and CH3O+ from ref. 49. | |||
| CH2˙+ + H2O + He | (2a) | −10.56 ± 0.10c | −10.66 |
| CH2˙+ + OH˙ + H˙ + He | (2b) | −5.41 ± 0.10c | −5.60 |
| CH3+ + OH˙ + He | (3) | −10.77 ± 0.10d | −10.86 |
| CO˙+ + 2H2 + He | (4a) | −9.64 ± 0.10e | −9.61 |
| CO˙+ + H2 + 2H˙ + He | (4b) | −5.12 ± 0.10e | −5.14 |
| CO˙+ + 4H˙ + He | (4c) | −0.60 ± 0.10e | −0.67 |
| HCO+ + H˙ + H2 + He | (5a) | −11.67 ± 0.10f | −11.66 |
| HOC+ + H˙ + H2 + He | (5b) | −10.01 ± 0.10f | −10.03 |
| CH2OH+ + H˙ + He | (6a) | −12.89 ± 0.10g | −12.89 |
| CH3O+ + H˙ + He | (6b) | −9.31 ± 0.10g | −9.41 |
Reaction (8) has been studied extensively in literature, and its rate constant is reported to be in the range of 1.4 × 10−9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 30,32 to 2.7 × 10−9 cm3 s−1,30,46 while rate constants for reaction (9) have been reported in the range of 3 × 10−11
30,32 to 2.7 × 10−9 cm3 s−1,30,46 while rate constants for reaction (9) have been reported in the range of 3 × 10−11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 30,32 to 4.6 × 10−10 cm3 s−1.30,47 As the proton transfer from HCO+/HOC+ to Ar is endothermic by ∼2.3 and ∼0.65 eV respectively,48,49 and no reaction was observed in previous studies of the process,50 the observation of a minor m/z 41 product also indicates that a small proportion of the [HCO]+ product ions are internally excited. We are therefore able to correct for the secondary reactions by summing the m/z 41, 33 and 47 products to the m/z 29 one, with the BRs calculated following this correction being given in Table 2, along with those currently available in literature.
30,32 to 4.6 × 10−10 cm3 s−1.30,47 As the proton transfer from HCO+/HOC+ to Ar is endothermic by ∼2.3 and ∼0.65 eV respectively,48,49 and no reaction was observed in previous studies of the process,50 the observation of a minor m/z 41 product also indicates that a small proportion of the [HCO]+ product ions are internally excited. We are therefore able to correct for the secondary reactions by summing the m/z 41, 33 and 47 products to the m/z 29 one, with the BRs calculated following this correction being given in Table 2, along with those currently available in literature.
| Reaction products | Eqn | BRa | BRb | BRc |
|---|---|---|---|---|
| a This work. b From KIDA database.33,52 c From UDfA (UMIST Database for Astrochemistry).34,53 | ||||
| CH2˙+ + H2O/(OH˙ + H˙) + He | (2a and b) | 0.08 ± 0.02 | — | — |
| CH3+ + OH˙ + He | (3) | 0.10 ± 0.03 | 0.50 | 0.50 |
| OH+ + CH3˙ + He | — | — | 0.50 | 0.50 |
| CO˙+ + 2H2/(H2 + 2H˙)/(4H˙) + He | (4a–c) | 0.03 ± 0.02 | — | — |
| HCO+/HOC+ + H˙ + H2 + He | (5a and b) | 0.74 ± 0.18 | — | — |
| CH2OH+/CH3O+ + H˙ + He | (6a and b) | 0.05 ± 0.04 | — | — |
Absolute CSs for the various channels have been recorded as a function of ECM and results are shown in Fig. 1, where the data for m/z 29 [HCO+/HOC+] include the correction for the contribution from secondary reaction products. For all products, we observe a decrease in CS with increasing ECM, with no significant difference in trend being observed between the different channels. The total CSs (obtained by summing over all the channels) as a function of ECM are reported in Fig. 2.
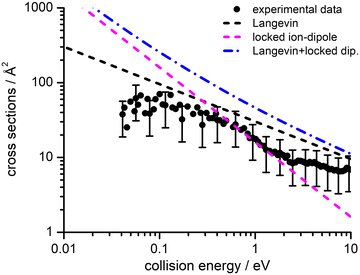 | ||
| Fig. 2 Experimental total CSs for the electron exchange reaction of He˙+ with CH3OH as a function of the collision energy (ECM). The black filled circles represent the measured total CSs, with error bars representing a 50% uncertainty on the absolute values of the cross-section. The lines represent total CSs as estimated from the following simple capture models: Langevin (black dashed line), locked-dipole (magenta dashed line) and the sum of the latter two models (blue dashed-dotted line). For the sake of clarity some of the error bars in the data points have been omitted, but for all data points the uncertainty on the absolute cross section value is approximately ±50% arising from the error propagation on the calibration of the effective cell length (see details in the ESI†). | ||
As our experimental set-up can only discriminate between product channels of different mass-to-charge (m/z) ratios, it is not possible to differentiate between different isomers of the ionic products (namely HCO+/HOC+ and CH3O+/CH2OH+) and between different combinations of the neutral co-products. Hence in Tables 1 and 2 all the thermochemically accessible combinations of products have been indicated.
It is interesting to compare the experimental BRs observed here, upon dissociative ionization of methanol by collisions with He˙+, with other experimental investigations using electrons or photons as the ionizing agents. Regarding electron ionization, numerous measurements have been reported on relative partial ionization CSs of methanol for ionizing electron energies from 20 to 500 eV (see ref. 44, 54–57 and references therein). In all cases and at all ionizing electron energies, the primary product is CH3O+/CH2OH+ (with a BR equal to 0.37 at an electron energy of 30 eV that decreases to 0.30 at 100 eV, according to ref. 44). Conversely, the HCO+/HOC+ fragment, that is the major product in this work, has a BR of 0.18 that only marginally increases (to 0.20) at 100 eV.
The photodissociation of methanol upon single photon absorption in the gas phase has been amply studied both experimentally45,58–62 and theoretically.63 Relative or absolute photoionization CSs for the production of both the molecular and fragment ions have been measured in the VUV region, from the ionization threshold58,59 up to 80 eV,45 as well as in the X ray region,64 using Photoelectron Photoion Coincidence (PEPICO) spectroscopy60,61,64 and dipole (e, e + ion) spectroscopy.45 The most relevant study to compare with present results is from Burton et al.,45 where photoionization efficiencies and ionic photofragmentation BRs have been measured/calculated up to 80 eV. The explored energy range includes photoionization from the inner valence orbitals of CH3OH that are involved in the charge exchange with He˙+, as detailed in Section 3. Experimental values at a photon energy of 24.5 eV (close to the ionization energy of He) give CH3O+/CH2OH+ as the most abundant fragment (BR = 0.306), followed by the HCO+/HOC+ fragment (BR = 0.244). When the photon energy is increased to 80 eV the amount of CH3O+/CH2OH+ fragment decreases (BR = 0.169) and the HCO+/HOC+ ion becomes the dominant one (BR = 0.215). This is in line with the results from a PEPICO study on the dissociative photoionization of energy selected methanol radical cations (with an internal energy up to ∼7 eV)61 where, at the highest internal energy of ∼7 eV, the fractional abundance of HCO+/HOC+ dominates the breakdown diagram for CH3OH with a BR value of 0.72.
It should be also noted that even at very large electron or photon energies, there is a fraction (about 16–20%) of methanol molecules that are ionized but survive fragmentation, leading to non zero CH3OH˙+ product detection at m/z = 32. For collisions with electrons from ∼60 up to 100 eV the BR for CH3OH˙+ remains constant at ∼0.20,44 with a similar BR of 0.16 obtained for the dissociative photo-ionization at both 8045 and 10064 eV photon energies. This is different from the present study, where the methanol radical cation is never detected, thus indicating that collisions with He˙+ lead to a greater degree of dissociation than those with either electrons or photons.
Another interesting comparison is with Li et al.,65 who performed RRKM calculations to simulate relative product yields for fragmentation at different internal energies of the CH3OH˙+ radical cations. Calculations were reported at internal energies of 1.55, 3.10 and 4.64 eV and, at the highest energy, the HCO+/HOC+ channel is observed as the major one, with a BR = 0.68, a value that is not dissimilar to our findings.
3 Theoretical methodologies
We have performed a preliminary comparison between the experimental total CSs, measured as a function of the collision energy, with the predictions from traditional capture models. Such a comparison, given in Fig. 2, shows important inconsistencies between predictions and experimental findings. It is therefore necessary to develop a more detailed treatment of the interaction potential and of the collision dynamics. To this purpose, we provide, in analytical form, the multidimensional PES both in entrance and exit channels and adopt a treatment of the electron exchange process based on the Landau–Zener–Stückelberg approach. The relevant details of the theoretical methodologies exploited in this study are given in the following subsections.3.1 Representation of the [He–CH3OH]˙+ interacting system
The geometry of the [He–CH3OH]˙+ complex is defined using a reference frame centered on the center of mass (CM) of the methanol molecule. The latter is subdivided into three constituent parts: the “effective atom” Ceff, which has the mass and the polarizability of a methyl group, the O atom and the H atom of the hydroxyl group. In particular, the polarizability of methanol, assumed equal to 3.21 Å3,66,67 is partitioned in three components, with 2.20 Å3 assigned to Ceff, 0.76 Å3 assigned to O and 0.25 Å3 assigned to the hydroxyl H atom. The polarizability components obtained in this way are transferable values, i.e. they allow an evaluation of the polarizability of other molecules (for instance the dimethyl ether, previously investigated in ref. 37) in which methyl groups, H and/or O atoms are involved.The geometrical parameters for methanol are derived through ab initio calculations, resulting in a value of 1.42 Å for the C–O bond length and 109.0° for the Ceff–O–H bond angle. In the adopted reference frame (see Fig. 3), the Cartesian coordinates (x, y, z) of the atoms in the methanol molecule are (in units of Å): O (−0.687, 0.096, 0), Ceff (0.729, −0.047, 0), H (−1.090, −0.777, 0). To simplify the mathematical description of the interaction potential, the geometries of reagents are expressed using spherical coordinates (R,θ,φ), where R is the distance connecting the center of mass of the methanol molecule with the position of the He˙+ ion and θ defines the direction of the incoming ion. In particular, θ = 0° and 90° correspond to He˙+ approaching perpendicularly and along the xy plane, defined by the position of the O, H and Ceff groups. The angle φ specifies the projection of the R vector on the xy plane. An illustration of the coordinates used for the representation of the potential is reported in Fig. 3.
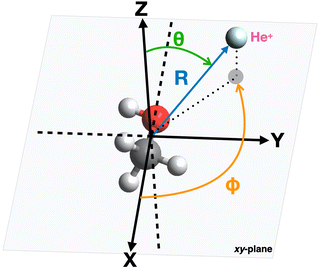 | ||
| Fig. 3 Illustration of the coordinates and reference system used for the representation of the interaction potential between He˙+ and CH3OH. | ||
3.2 Entrance channel: He˙+ + CH3OH
The PES for the interaction of He˙+ with CH3OH is given as the sum of two different contributions: an electrostatic component, Velec, and a non electrostatic component, Vnelec. Velec is calculated considering the Coulomb interaction between He˙+ and the effective charges residing on Ceff, O and H atoms. For CH3OH, ElectroStatic Potential (ESP) derived atomic charges are obtained from ab initio calculations, using the B3LYP functional68,69 in conjunction with the correlation consistent basis set aug-cc-pVTZ.70,71 Using this formalism the total dipole moment for the methanol molecule is determined to be 1.700 Debye66 and the resulting effective atomic charges are 0.2301e for Ceff, −0.6064e for O and 0.3762e for H atom, leading to an electrostatic term that can be expressed (in meV) as: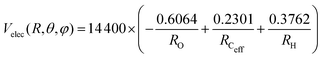 | (10) |
The Vnelec component is determined considering the combination between size repulsion contributions, operating at short distance, and induction and dispersion attraction contributions, operating at large intermolecular distances. Such contributions are expressed as a sum of three terms that account for the interaction of He˙+ with the three effective atoms of the methanol molecule (Ceff, O and H). For each interaction pair the non electrostatic component is formulated by the Improved Lennard-Jones (ILJ) model,72 which effectively describes both long-range and short-range interactions. The ILJ potential for a given interaction pair is given by the following equation:
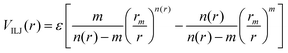 | (11) |
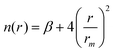 | (12) |
| Vnelec(R,θ,φ) = VILJ(RCeff) + VILJ(RO) + VILJ(RH) | (13) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 36,37 and the value of ε and rm parameters are obtained by correlation formulas representing the leading components of the intermolecular interaction in terms of polarizability components and charge of involved partners (see ref. 73 and references therein)
36,37 and the value of ε and rm parameters are obtained by correlation formulas representing the leading components of the intermolecular interaction in terms of polarizability components and charge of involved partners (see ref. 73 and references therein)
| Interacting pair | ε (meV) | r m (Å) | m | |
|---|---|---|---|---|
| Entrance | He˙+–Ceff | 312 | 2.58 | 4 |
| He˙+–O | 125 | 2.39 | 4 | |
| He˙+–H | 76 | 2.05 | 4 | |
| Exit | He–Ceff | 2.3 | 3.69 | 6 |
| He–O | 1.7 | 3.38 | 6 | |
| He–H | 0.9 | 2.97 | 6 | |
3.3 Exit channel: He + CH3OH˙+
The PES of the exit channel is comprised of a short range size repulsion and a long range attraction, with this latter term depending on the non-electrostatic contributions, i.e. induction (Vind) and dispersion, with these two terms being similar in magnitude. The sum of the dispersion attraction and size repulsion effects is described as a van der Waals interaction, VvdW, which is expressed, similarly to what already done for the entrance channel, in terms of three improved Lennard-Jones (ILJ) functions, one for each interaction pair: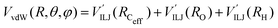 | (14) |
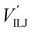 contributions, together with the same VILJ terms for the entrance potentials are reported in Table 3.
contributions, together with the same VILJ terms for the entrance potentials are reported in Table 3.
The molecular ion is formed in an excited state, by ejection of one electron from an inner valence molecular orbital (MO) and its polarizability is assumed to be the same as that of the neutral methanol and is therefore partitioned in the same way.
An additional induction term represents the ion-induced dipole contribution, describing the interaction between the CH3OH˙+ radical cation and the He atom. The induction term Vind (in meV) is expressed as a function of the polarizability of He (αHe = 0.2 Å3) and the distance (R, in Å) between the two interacting partners, via the following expression:
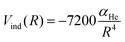 | (15) |
3.4 Crossing points between entrance and exit channels
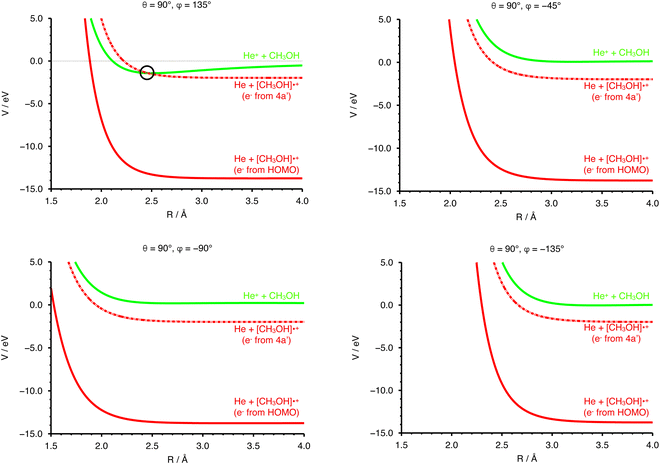
The collisional energy of the present experiment, spanning a range from ∼0.04 to 10 eV, allows for a non-adiabatic transition located at the crossing between the entrance and the exit PESs. Nevertheless, the difference in the ionization energy (IE) of the two species (24.59 eV for He and 10.84 eV for CH3OH74) does not allow a crossing between entrance and exit channel in the case of an electron ejected by the HOMO of the methanol molecule.In order to have a crossing between the entrance and the exit potentials, the electron must be removed from an inner valence molecular orbital, with a high ionization potential. The calculated electronic configuration for methanol is (1a′)2 (2a′)2 (3a′)2 (4a′)2 (5a′)2 (1a′′)2 (6a′)2 (7a′)2 (2a′′)2. According to previous investigations the experimental ionization energy of the inner valence orbital 4a′ (representing the HOMO−5 orbital) is 22.65 eV,75 in good agreement with a recent re-evaluation which gave a value of 22.623 eV,76 enough to promote the electron transfer process. Note that the other molecular orbitals of CH3OH have ionization energies that are too low with respect to the recombination energy of He˙+, thus giving either no crossings between the entrance and exit PES or crossings that are not accessible within the collision energy range probed in the present experiments. The PES for the exit channel can be rescaled considering the value of IE of the 4a′ orbital, allowing for the identification of a crossing point between the entrance and the scaled exit potentials.
In Fig. 4 the curves obtained by PES cuts at four different configurations are shown. For each configuration three curves are reported, representing the entrance (green), exit (red) and scaled exit potentials (red-dashed) resulting from the removal of an electron from the inner 4a orbital. The zero of the energy scale is taken to coincide with the value at R → ∞ of the PES of the entrance channel. For one of the most attractive configurations (e.g. θ = 90° and φ = 135°, see left upper panel of Fig. 4), one relevant crossing point between the entrance and the exit curves is located at R = 2.464 Å. For unfavourable configurations (e.g. θ = 90° and φ = −45°, −90° and −135°, see the other three panels in Fig. 4) the crossing points are either not present or inaccessible since they are too high in energy.
In order to properly evaluate the occurrence probability of the electron transfer process, the electron density distribution of methanol must be taken into account. For this reason, electronic structure calculations were performed at the B3LYP/aug-cc-pVTZ level of theory in order to obtain the electron density map of the 4a′ (HOMO−5) molecular orbital, shown in Fig. 5, directly involved in the electron transfer to He˙+.
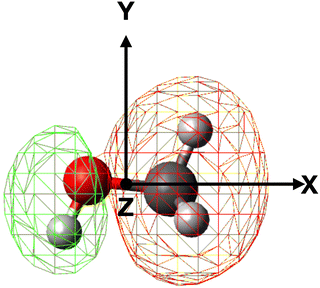 | ||
| Fig. 5 Electron density map of the 4a′ (HOMO−5) inner valence molecular orbital of neutral methanol. | ||
3.5 The Landau–Zener–Stückelberg treatment extended to dissociative electron exchange reactions
The transition probability at the crossing point between the two curves is treated by adopting the same strategy successfully used in previous investigations.37,77,78 More specifically, the Landau–Zener–Stückelberg approach79–81 is used for the implementation of a one-dimensional model, that considers specific slices of the multidimensional PES at fixed values of θ and φ as a function of the reaction coordinate R. The CS for the electron exchange process is calculated considering a cone of configurations with θ and φ values around 90° and 120°, respectively. The probability of passage through a crossing between the two curves is given by: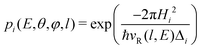 | (16) |
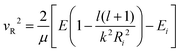 | (17) |
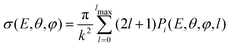 | (18) |
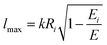 | (19) |
According to the guidelines discussed in ref. 37, for low collision energies the lmax value should be reduced to avoid the non-physical condition of a centrifugal barrier in the entrance channel higher than the available collision energy. Such a limitation in the lmax leads to smaller CSs for collision energies smaller than ∼100 meV.
Applying the same criteria as discussed in ref. 36 and 37, Pi can be here represented as:
| Pi = (1 − pi)(1 + pi) | (20) |
It should be noted that any orientation dependence of Pi appears indirectly in the evaluation of the crossing position and of the radial velocity.
3.6 Potential energy surface for the dissociation process
The energetics and fragmentation pathways of CH3OH˙+ radical cation are investigated through ab initio calculations. The analysis of the Potential Energy diagram for the dissociation of CH3OH˙+, starting from its ground electronic state, is performed adopting a computational strategy successfully used in the past for the investigation of several processes.82–84 Calculations start with optimization of the geometry of all identified stationary points in the PES by means of Density functional theory (DFT). In the present work, geometry optimization has been performed using two different functionals: B3LYP and ωB97X-D,85 both in in conjunction with the correlation consistent basis set aug-cc-pVTZ.Harmonic vibrational frequencies are evaluated, at the same level of theory, in order to identify the nature of each stationary point, i.e. minimum if all the frequencies are real and transition state if there is one, and only one, imaginary frequency. Subsequently, the energies of all the stationary points are evaluated at an higher level of theory, i.e. CCSD(T)86–88/aug-cc-pVTZ. The zero-point energy corrections, evaluated at the B3LYP/aug-cc-pVTZ level or at the ωB97X-D/aug-cc-pVTZ level, are then added to the CCSD(T) energies to obtain values at 0 K. All calculations are performed using Gaussian09,89 while the frequencies analysis is performed using AVOGADRO.90 Results of the calculations employing the ωB97X-D functional are reported in the next Section, where they are also compared with existing literature values. Complementary data extracted from the B3LYP calculations are listed in the ESI.†
4 Results and discussion
4.1 Potential energy surface for the dissociation process
The CH3OH˙+ cation, formed directly after the electron transfer to He˙+, possesses a high degree of internal energy. As a consequence, a fast electronic rearrangement is expected, leading to instantaneous dissociation. The PES for the dissociation of the CH3OH˙+ cation from its ground electronic state is reported in Fig. 6. The calculated energies (at the CCSD(T)/aug-cc-pVTZ//ωB97X-D/aug-cc-pVTZ level) are reported considering the CH3OH˙+ cation as reference (with energy of 0.0 eV).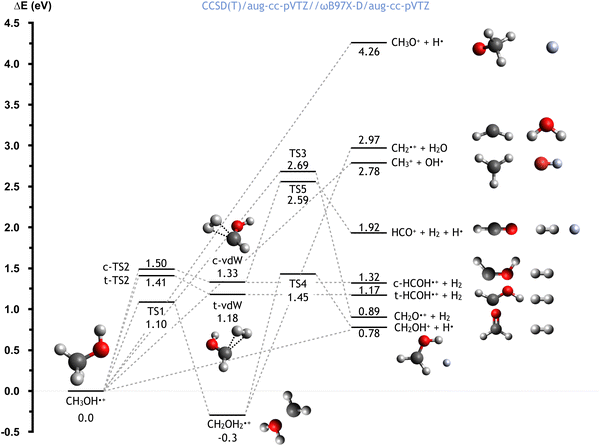 | ||
| Fig. 6 Schematic representation of the PES for the dissociation of the CH3OH˙+ cation, with the energies (reported in eV) evaluated at the CCSD(T)/aug-cc-pVTZ//ωB97X-D/aug-cc-pVTZ level of theory. A similar figure with the energies computed at the CCSD(T)/aug-cc-pVTZ//B3LYP/aug-ccpVTZ level is reported in the ESI.† | ||
Once formed, the aforementioned cation can directly dissociate leading to the formation of six different combinations of products. The breaking of the C–O bond leads to the formation of the OH radical plus the CH3+ cation, with a relative energy of 2.78 eV, in a barrierless process. Another process with no energy barrier is H atom elimination, leading to the concominant formation of the CH3O+ cation, with an endothermicity of 4.26 eV. Four different processes lead to the formation of molecular hydrogen. Firstly, the co-ejection of the H atom of the hydroxyl group with one of the three methyl hydrogens leads to the formation of CH2O+ + H2, with an overall energy of 0.89 eV, and a barrier, TS3, of 2.69 eV. Alternatively, the elimination of two methyl hydrogens first leads to the formation of cis/trans van der Waals complexes (indicated as c-vdW and t-vdW in Fig. 6), which are higher in energy by 1.33 and 1.18 eV respectively. In the case of c-vdW, the subsequent breaking of the O–H bond can lead to the formation of HCO+ + H2 + H. This has an overall endothermicity of 1.92 eV with a barrier of 2.59 eV (via TS5). Without cleavage of the O–H bond, c-vdW and t-vdW lead to cis- and trans-HCOH+ + H2, with reaction energies of 1.32 and 1.17 eV respectively.
An alternative reaction mechanism is the isomerization of CH3OH˙+via an 1,2 H-shift, leading to the formation of CH2OH2+, with a reaction energy of −0.30 eV and a barrier of 1.10 eV (via TS1). The resultant cation can dissociate, via a barrier located 1.45 eV above the zero energy (TS4), to give H + CH2OH+, with a reaction energy of 0.78 eV (relative to CH3OH˙+). Alternatively, the cleavage of the C–O bond leads to the formation of water, together with the CH2+ cation, in a barrierless process with a reaction energy of 2.97 eV (relative to CH3OH˙+).
Importantly, this PES describes the fragmentation of ground state CH3OH˙+ whereas, as can be the case in the reaction studied in this work, the removal of an electron from an inner molecular orbital leads to the formation of CH3OH˙+ in an excited state. This therefore means that, though some of these channels are endothermic in the case of the ground state, all are accessible for the excited state.
Several theoretical investigations have been performed in the recent years in order to properly understand the fragmentation pathways of the CH3OH˙+ cation.91–93 To the best of our knowledge, the first theoretical investigation goes back to 1991, when Ma et al.93 analyzed the main isomerization and fragmentation pathways of ionized methanol, leading to two main product channels: HOC+ + H2 + H and HCO+ + H2 + H. These authors identified different long range interacting complexes, relevant to the formation of H2, which interacts with the remaining co-fragment prior to its elimination. More accurate CCSD(T)/cc-pVTZ//B3LYP/6-311++G(d,p) calculations have been performed by Wu et al.,92 revealing the possible formation of other important species, including H3/H3+ and CH2+ + H2O. Finally, Li et al.91 reported a complete investigation of the global PES for the fragmentation of CH3OH˙+ using both DFT theory (B3LYP/6-311G(d,p)) and more accurate G3(MP2,CCSD) methods for energy evaluations. Different product channels have been identified, leading to the formation of H, OH, H2O and H2 as neutral co-fragments. In the present work we performed a new evaluation of the stationary points on the fragmentation PES in order to provide a global picture of all the possible product channels to assist the interpretation of experimental results.
4.2 Potential energy surface and dynamics of the electron transfer process
The initial approach of He˙+ towards methanol has been simulated from multiple directions by varying the cation's spherical coordinates θ and φ. From here on, we refer to each θ and φ pair as a “configuration” of the system. In order to fully understand the effect of the orientation of the two interacting partners on the entrance potential, the PES has been calculated at a set of fixed distances for different values of θ. At R values corresponding to 3, 5, 10, 15 and 20 Å the entrance potential has been evaluated at φ = −90° and 90° over a range of θ angles between 0° and 90°. A slice of the entrance channel PES is reported in Fig. 7, where a strong repulsive potential is present at φ = −90°, corresponding to He˙+ approaching the H atom of the OH group. The potential appears to be attractive when the He˙+ approaches the region of OH group (φ = 90°), due to a strong effect of the electrostatic component of the interaction. A minimum in the potential is observed at θ ≈ 90°, a configuration in which the ion is located in the same plane as the Ceff–O–H atoms of the molecule.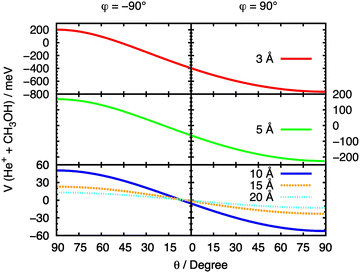 | ||
| Fig. 7 Cuts of the PES for the entrance channel of the He˙+ + CH3OH system for φ = 90° and φ = −90° considering the variation of θ at fixed values of R. | ||
In Fig. 8, a similar procedure has been applied, with the same set of fixed R values, to the θ = 90° case, in order to evaluate the effect of the variation of the angle φ on the entrance potential. In this case, a minimum in the potential is observed at 90° ≤ φ ≤ 150°, which corresponds to a configuration in which the ion approaches the O atom.
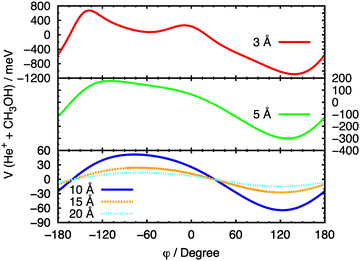 | ||
| Fig. 8 Cuts of the PES for the entrance channel of the He˙+ + CH3OH system for θ = 90° considering the variation of φ at fixed values of R. | ||
This is further illustrated in Fig. 9, where the PES for the approach of the ion in the xy plane (i.e. with θ = 90° and −180° ≤ φ ≤ 180°) has been presented in a three-dimensional plot, with the attractive and repulsive contributions being represented by blue and yellow, respectively. The figure shows that, due to the polarity of the methanol molecule, the entrance channel PES is strongly anisotropic. For this reason, it is expected that the reagents, during their approach, tend to assume spontaneously the most attractive configuration, especially under sufficiently long collision times.
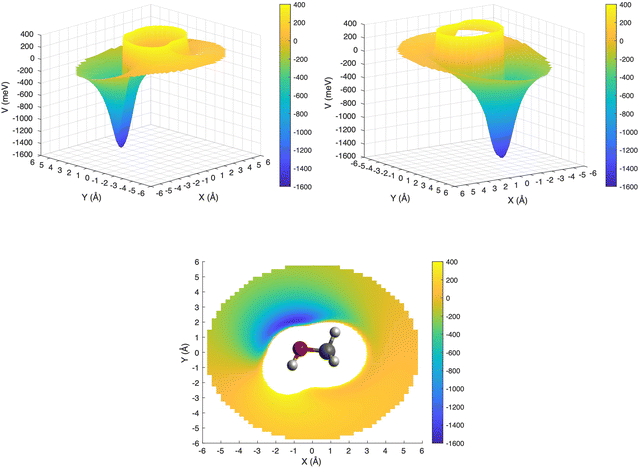 | ||
| Fig. 9 3D PES for the entrance channel with the attractive and repulsive contributions reported in blue and yellow, respectively. | ||
In addition to the relative orientation in the entrance channel, the position and energy of crossing(s) between the entrance and exit channels also needs to be investigated. In Fig. 4 (left upper panel) we have selected the configuration (θ = 90°, φ = 135°) for which the entrance PES as a function of R shows a deep potential well. In the same panel of Fig. 4 the exit PES has been reported for the same configuration, rescaled by the IE value of the 4a molecular orbital of CH3OH, to represent the removal of the electron from this inner molecular orbital. The resulting crossing point is located at a distance between He˙+ and the center of mass of the methanol molecule of 2.462 Å, with V = −1.419 eV. Hence, for this configuration, an exothermic crossing can occur, and similar behaviours is expected for other configurations. The strong anisotropy of the PES is expected to have an effect on the electron transfer process. In particular, assuming that the most attractive configurations lead to a significant contribution to the CS, only select configurations drive the charge exchange process, namely those corresponding to the approach of He˙+ towards the oxygen side. As a consequence the reaction probability is only non-zero for a select set of configurations.
4.3 Electron transfer cross sections
The calculation of the electron transfer CSs have been performed using two different approaches to account for the two different dynamical collision regimes.This disagreement represents a robust indication that the adopted assumption is unsatisfactory and that the dynamical treatment must take into account the role played by the strong anisotropy of the PES on the reagents side, which tends to channel the approaching particles in specific relative configurations. In particular, as observed in similar systems previously investigated with the same technique,36,37 in the strong electric field generated by the very small He˙+ ions, the anisotropic molecule will seek to orient its dipole moment around the configuration of minimum energy.
As can be observed in Fig. 8, the energy barriers arising from the interaction anisotropy become comparable to the mean rotational energy of CH3OH at R ∼ 15 Å. However, at shorter distances, the barrier that inhibits the rotation becomes insurmountable and the molecule librates like a pendulum around the position of minimum energy. In this case, the collision system is confined in a so-called pendular state, in which molecular rotations are transformed into bending vibrations of the collision complex (for further details see Fig. 6 of ref. 36). As the distance decreases, so does the amplitude of the oscillation, and eventually the molecule is locked in its preferential orientation.
Orientation effects of this type become increasingly efficient at low collision energies, as the collision time becomes sufficiently long with respect to the rotational period of the molecule. They can influence the dynamics of the electron exchange process by channelling most of the trajectories in narrow angular cones confined around the most attractive configurations of the intermolecular interaction (see Fig. 7–9). Considering that the most attractive geometries are the least efficient for the electron transfer process, when the extension and symmetry of the molecular orbitals involved in the electron exchange are taken into account, the reaction can essentially be promoted by the coupling between the rotational angular momentum of nuclei in the complex and the orbital angular momentum of the electrons (Coriolis coupling).
To evaluate the magnitude of the coupling and to account for its orientation dependence, the modelling was properly extended to include the change with E of the original orientation in the collision complex. In particular, the coupling is expected to be less efficient when reagent molecules are strongly oriented. Following the guidelines given in ref. 37, the Landau expression for the coupling has been adopted:
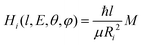 | (21) |
In the above equation the M term has been extended as:
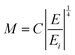 | (22) |
At the higher collision energies (E ≥ 4 eV) the collision time decreases and so the reorientation of CH3OH towards the most attractive configurations is expected to be infeasible. To account for this we have assumed that, in the collision energy range 2 ≤ E ≤ 4 eV, a dynamic regime that encompasses both effects is required to reproduce the experimental data. Accordingly, the collision energy dependence of the total ionization CS σt(E) has been calculated as a weighted sum of σcone(E) and of σsphere(E):
| σt(E) = σcone(E)f0(E) + σsphere(E)(1 − f0(E)) | (23) |
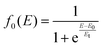 | (24) |
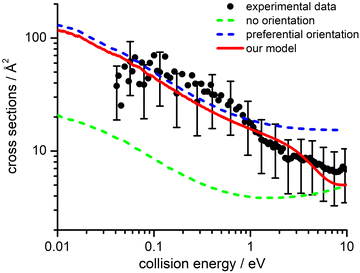
The values of E0 and Et factors define, respectively, the E values at which the two limiting regimes of the collision dynamics exhibit the same weight and how fast the passage between the two calculation methods occurs. In the present study E0 and Et have been selected, respectively, in the range of 3.0 and 1.5 eV and the so calculated CS are reported as red line in Fig. 10. From this it can be seen that at low collision energies (when ECM < ∼1.5 eV) the preferential orientations model effectively fits the experimental results, while at higher energies (ECM > 5 eV) the isotropic model better reproduces the absolute value of CS. As a result, at higher collision energies the strong stereodynamical effect tends to vanish.
Observed stereo-dynamical effects indicate that for several configurations, defined in a statistical way by the isotropic model, the crossing points are either not present or energetically inaccessible since they are too high in energy. In addition, for some configurations, the turning points (the distance of closest approach of reagents) are too external with respect to the crossing points opening the charge exchange channel. Such crossing points become accessible only at very high collision energies, probing shorter intermolecular distances.
4.4 Cross sections and rate coefficients: comparison with previous models
CSs and rate coefficients for ion–molecule reactions, with their dependence on energies/temperature, are usually evaluated using various types of capture models (see ref. 94 for a very recent review). For the system here presented such models are unable to correctly describe the absolute values and the collision energy dependence of CSs, measured under thermal and hyper-thermal conditions. In particular, at a collision energy of 60 meV (confined in the thermal range) the CS predicted by classical capture models is a factor 5–7 larger respected to the measured value (see Fig. 2).The present treatment, adopted to correctly reproduce the experimental findings, suggests that observed deviations from predictions of capture models are representative of stereo-dynamical effects, ascribed to the strong interaction anisotropy in the entrance channel of the reaction. Such anisotropic interactions lead to the formation of a precursor state, localized at short intermolecular distances, in specific configurations. Moreover, the symmetry of molecular orbital, of relevance for the chemical forces involved in the electron exchange, at the PE curves crossings, further controls the selectivity of the process. Such stereo-dynamical effects are expected to play an increased role also under sub-thermal conditions, because the increase of the collision time favours the formation of the precursor state in its most stable configurations.
From the CSs obtained using the improved Landau–Zener–Stückelberg method described in the previous section (namely the red line from Fig. 10), it is possible to evaluate the reaction rate coefficient as a function of temperature (k(T)) in the thermal and hyper-thermal range and to attempt an extrapolation under sub-thermal conditions. The k(T) can be calculated by averaging the computed total integral cross section over a Maxwell-Boltzmann distribution of collision energies, following the definition of rate constant in collision theory in chemical kinetics (see for instance Section 1.2.5 of ref. 95 and 35).
At 300 K our model gives an estimated rate coefficient of 1.0 × 10−9 cm3 s−1, which is smaller than the values from KIDA33 (k = 4.8 × 10−9 cm3 s−1 from classical trajectory scaling method of Su and Chesnavich52,96,97) and UDfA34 (k = 2.2 × 10−9 cm3 s−1). When we attempt an extrapolation at the low temperatures relevant for interstellar conditions (∼10 K) our estimated rate is about a factor 10–30 lower respect to KIDA value (k = 2.0 × 10−8 cm3 s−1 at 10 K![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 33) and to the long range transition state theory model of Georgievskii and Klippenstein98 that estimates a k = 2.3 × 10−8 cm3 s−1 at 10 K. Present and previous results,35 obtained with the same methodology, raise the important question that capture models, extensively used to describe ion-molecule reactions, can exhibit a different degree of reliability, depending on the specific features of the reagents. This represents a crucial problem to collect reliable/accurate rate coefficients for plasmas and astrochemical databases. In our opinion this open question can be properly addressed by performing, under the same conditions, additional experiments extended at low collision energies (i.e. below 0.05 eV, that are unfortunately unfeasible using our experimental set-up), in order to provide internally consistent data for different ion-molecule reactions.
33) and to the long range transition state theory model of Georgievskii and Klippenstein98 that estimates a k = 2.3 × 10−8 cm3 s−1 at 10 K. Present and previous results,35 obtained with the same methodology, raise the important question that capture models, extensively used to describe ion-molecule reactions, can exhibit a different degree of reliability, depending on the specific features of the reagents. This represents a crucial problem to collect reliable/accurate rate coefficients for plasmas and astrochemical databases. In our opinion this open question can be properly addressed by performing, under the same conditions, additional experiments extended at low collision energies (i.e. below 0.05 eV, that are unfortunately unfeasible using our experimental set-up), in order to provide internally consistent data for different ion-molecule reactions.
5 Conclusions/summary
• We have reported measurements of the absolute cross sections (CSs) and branching ratios (BRs) for the collisions of He˙+ ions with CH3OH as a function of the collision energy, in the range from ∼0.04 to ∼10 eV.• A striking difference is observed between our experimental BRs and the estimates reported in astrochemical databases. In both cases the electron exchange process is completely dissociative; but while databases indicate a BR of 0.50 for the two channels CH3+ plus OH and OH+ plus CH3, our results, summarized in Table 2, show that the most abundant fragment is HCO+/HOC+ with a BR equal to 0.74 ± 0.18, the CH3+ fragment is the second most abundant (with BR = 0.10 ± 0.03) and the OH+ fragment is not detected.
• A theoretical interpretation in support of experimental results is proposed, based on analytical expressions for the entrance and exit multidimensional PESs, and on the modelling of non-adiabatic transitions via a Landau–Zener–Stückelberg approach, to estimate transition probabilities at crossings between diabatic curves.
• In addition to all constraints of traditional capture methods, the present treatment encloses: (i) the definition of a separation distance range where charge transfer coupling manifests. This information, together with the role of centrifugal barrier in the entrance channels, selects the l values effectively triggering the reaction; (ii) the indication of the molecular orbitals involved in the electron transfer process; (iii) the structure and stability of the precursor state more efficiently formed by collisions at each l value.
• The collision dynamics is treated within a semiclassical method, expected to be quantitative for collision energies larger than 1 meV (∼10 K) and semi-quantitative for lower energies, where quantum effects may become prominent.
• It is shown that the (diabatic) reactant surface does not cross the product surface that correlates asymptotically with the ground state of CH3OH˙+. Crossing is possible only assuming that the electron is removed by an inner valence orbital (namely the 4a′ having a vertical ionization energy ∼11.67 eV higher than the HOMO), thus the nascent radical cation is formed in a highly excited state that quickly dissociates.
• To reproduce experimental findings a strong orientation effect of the polar CH3OH molecule in the electric field generated by He˙+ should be assumed. This is a general result and points to the fact that stereo-chemical effects should not be disregarded when seeking to obtain reasonable estimates of dynamical processes. For recent examples of the influence of stereochemical effects on the reactivity of other ion–molecule systems at low and ultra low collision energies see for instance.99–105
• The experimental CSs and product BRs here reported should be used when modelling the abundance of the ubiquitous methanol molecule in the interstellar medium, with special reference to those regions where collisions with He˙+ are expected to be among the main destruction routes.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This project has received funding from the European Unions Horizon 2020 research and innovation programme under the Marie Sklodowska Curie grant agreement no. 811312 for the project “Astro-Chemical Origins” (ACO) and from MUR PRIN 2020 project n. 2020AFB3FX “Astrochemistry beyond the second period elements”. The authors thank the Herla Project (http://www.hpc.unipg.it/hosting/vherla/vherla.html) – Universit’a degli Studi di Perugia for allocated computing time. The authors thank the Dipartimento di Ingegneria Civile ed Ambientale of the University of Perugia for allocated computing time within the project “Dipartimenti di Eccellenza 2018–2022”. N. F.-L. thanks MUR and the University of Perugia for the financial support of the AMIS project through the “Dipartimenti di Eccellenza” programme. N.F.-L. also acknowledges the Fondo Ricerca di Base 2021 (RICBASE2021FAGINAS) del Dipartimento di Chimica, Biologia e Biotecnologie della Universit’a di Perugia for financial support. We are grateful to Prof. Paolo Tosi (Depart. Physics, University of Trento) for useful discussions and to Mr Damiano Avi for technical assistance during the experiments.Notes and references
- E. Herbst and E. F. van Dishoeck, Annu. Rev. Astron. Astrophys., 2009, 47, 427–480 CrossRef CAS
.
- S. A. Sandford, M. Nuevo, P. P. Bera and T. J. Lee, Chem. Rev., 2020, 120, 4616–4659 CrossRef CAS PubMed
.
-
J. K. Jorgensen, A. Belloche and R. T. Garrod, Annual Review of Astronomy and Astrophysics, ed. E. VanDishoeck and R. Kennicutt, 2020, vol. 58, pp. 727–778, DOI:10.1146/annurev-astro-032620-021927
.
- K. I. Oberg and E. A. Bergin, Phys. Rep., 2021, 893, 1–48 CrossRef CAS
.
- J. A. Ball, C. A. Gottlieb, A. E. Lilley and H. E. Radford, Astrophys. J., 1970, 162, L203 CrossRef CAS
.
- S. Spezzano, A. Fuente, P. Caselli, A. Vasyunin, D. Navarro-Almaida, M. Rodriguez-Baras, A. Punanova, C. Vastel and V. Wakelam, Astron. Astrophys., 2021, 657, A10 CrossRef
.
- C.-F. Lee, Z.-Y. Li, P. T. P. Ho, N. Hirano, Q. Zhang and H. Shang, Astrophys. J., 2017, 843, 27 CrossRef
.
- A. Belloche, A. J. Maury, S. Maret, S. Anderl, A. Bacmann, P. Andre, S. Bontemps, S. Cabrit, C. Codella, M. Gaudel, F. Gueth, C. Lefevre, B. Lefloch, L. Podio and L. Testi, Astron. Astrophys., 2020, 635, A198 CrossRef CAS
.
- Y.-L. Yang, N. Sakai, Y. Zhang, N. M. Murillo, Z. E. Zhang, A. E. Higuchi, S. Zeng, A. Lopez-Sepulcre, S. Yamamoto, B. Lefloch, M. Bouvier, C. Ceccarelli, T. Hirota, M. Imai, Y. Oya, T. Sakai and Y. Watanabe, Astrophys. J., 2021, 910, 20 CrossRef CAS
.
- L. Chahine, A. Lopez-Sepulcre, R. Neri, C. Ceccarelli, S. Mercimek, C. Codella, M. Bouvier, E. Bianchi, C. Favre, L. Podio, F. O. Alves, N. Sakai and S. Yamamoto, Astron. Astrophys., 2022, 657, A78 CrossRef CAS
.
- S. Mercimek, C. Codella, L. Podio, E. Bianchi, L. Chahine, M. Bouvier, A. Lopez-Sepulcre, R. Neri and C. Ceccarelli, Astron. Astrophys., 2022, 659, A67 CrossRef CAS
.
- M. De Simone, C. Codella, C. Ceccarelli, A. Lopez-Sepulcre, A. Witzel, R. Neri, N. Balucani, P. Caselli, C. Favre, F. Fontani, B. Lefloch, J. Ospina-Zamudio, J. E. Pineda and V. Taquet, Astron. Astrophys., 2020, 640, A75 CrossRef CAS
.
- C. Walsh, R. A. Loomis, K. I. Oberg, M. Kama, M. L. R. van't Hoff, T. J. Millar, Y. Aikawa, E. Herbst, S. L. W. Weaver and H. Nomura, Astrophys. J. Lett., 2016, 823, L10 CrossRef
.
- M. L. R. van’t Hoff, J. J. Tobin, L. Trapman, D. Harsono, P. D. Sheehan, W. J. Fischer, S. T. Megeath and E. F. van Dishoeck, Astrophys. J. Lett., 2018, 864, 23 CrossRef
.
- L. Podio, A. Garufi, C. Codella, D. Fedele, E. Bianchi, F. Bacciotti, C. Ceccarelli, C. Favre, S. Mercimek, K. Rygl and L. Testi, Astron. Astrophys., 2020, 642, L7 CrossRef CAS
.
- N. van Der Marel, A. S. Booth, M. Leemker, E. F. van Dishoeck and S. Ohashi, Astron. Astrophys., 2021, 651, L5 CrossRef CAS
.
- A. S. Booth, C. Walsh, J. Terwisscha van Scheltinga, E. F. van Dishoeck, J. D. Ilee, M. R. Hogerheijde, M. Kama and H. Nomura, Nat. Astronomy, 2021, 5, 684–690 CrossRef
.
- L. Le Roy, K. Altwegg, H. Balsiger, J.-J. Berthelier, A. Bieler, C. Briois, U. Calmonte, M. R. Combi, J. De Keyser, F. Dhooghe, B. Fiethe, S. A. Fuselier, S. Gasc, T. I. Gombosi, M. Haessig, A. Jaeckel, M. Rubin and C.-Y. Tzou, Astron. Astrophys., 2015, 583, A1 CrossRef
.
- M. Rubin, D. Bekaert, V. M. W. Broadley, M. N. Drozdovskaya and S. F. Wampfler, ACS Earth Space Chem., 2019, 3, 1792–1811 CrossRef CAS
.
-
K. Altwegg, H. Balsiger and S. A. Fuselier, in Annual Review of Astronomy And Astrophysics, ed. S. Faber, E. VanDishoeck and R. Kennicutt, 2019, vol. 57, pp. 113–155 Search PubMed
.
- W. M. Grundy, M. K. Bird, D. T. Britt, J. C. Cook, D. P. Cruikshank, C. J. A. Howett, S. Krijt, I. R. Linscott, C. B. Olkin, A. H. Parker, S. Protopapa, M. Ruaud, O. M. Umurhan, L. A. Young, C. M. D. Ore, J. Kavelaars, J. T. Keane, Y. J. Pendleton, S. B. Porter, F. Scipioni, J. R. Spencer, S. A. Stern, A. J. Verbiscer, H. A. Weaver, R. P. Binzel, M. W. Buie, B. J. Buratti, A. Cheng, A. M. Earle, H. A. Elliott, L. Gabasova, G. R. Gladstone, M. E. Hill, M. Horanyi, D. E. Jennings, A. W. Lunsford, D. J. McComas, W. B. McKinnon, R. L. McNutt, Jr., J. M. Moore, J. W. Parker, E. Quirico, D. C. Reuter, P. M. Schenk, B. Schmitt, M. R. Showalter, K. N. Singer, G. E. Weigle, II and A. M. Zangari, Science, 2020, 367(6481), eaay3705, DOI:10.1126/science.aay3705
.
- M. Sewilo, S. B. Charnley, P. Schilke, V. Taquet, J. M. Oliveira, T. Shimonishi, E. Wirstrom, R. Indebetouw, J. L. Ward, J. T. van Loon, J. Wiseman, S. Zahorecz, T. Onishi, A. Kawamura, C.-H. R. Chen, Y. Fukui and R. H. Golshan, ACS Earth Space Chem., 2019, 3, 2088–2109 CrossRef CAS
.
- B. Mueller, B. M. Giuliano, M. Goto and P. Caselli, Astron. Astrophys., 2021, 652, A126 CrossRef CAS
.
- A. C. A. Boogert, P. A. Gerakines and D. C. B. Whittet, Annu. Rev. Astron. Astrophys., 2015, 53, 541–581, DOI:10.1146/annurev-astro-082214-122348
.
- G. W. Fuchs, H. M. Cuppen, S. Ioppolo, C. Romanzin, S. E. Bisschop, S. Andersson, E. F. van Dishoeck and H. Linnartz, Astron. Astrophys., 2009, 505, 629–639 CrossRef CAS
.
- I. Jimenez-Serra, A. I. Vasyunin, P. Caselli, N. Marcelino, N. Billot, S. Viti, L. Testi, C. Vastel, B. Lefloch and R. Bachiller, Astrophys. J. Lett., 2016, 830, L6 CrossRef PubMed
.
- D. Skouteris, N. Balucani, C. Ceccarelli, N. F. Lago, C. Codella, S. Falcinelli and M. Rosi, Mon. Not. R. Astron. Soc., 2019, 482, 3567–3575 CrossRef CAS
.
- A. J. Ocana, S. Blazquez, A. Potapov, B. Ballesteros, A. Canosa, M. Antinolo, L. Vereecken, J. Albaladejo and E. Jimenez, Phys. Chem. Chem. Phys., 2019, 21, 6942–6957 RSC
.
- H. Lee, M. Drucker and N. Adams, Int. J. Mass Spectrom. Ion Processes, 1992, 117, 101–114 CrossRef CAS
.
- V. Anicich, An Index of the Literature for Bimolecular Gas Phase Cation-Molecule Reaction Kinetics, 2003, Available at: http://hdl.handle.net/2014/7981.
- J. Moryl and J. Farrar, J. Phys. Chem., 1982, 86, 2020–2027 CrossRef CAS
.
- T. Schindler, C. Berg, G. Niedner-Schatteburg, V. Bondybey, C. Lugez, A. Schriver and L. Schriver, J. Phys. Chem., 1994, 98, 4316–4319 CrossRef CAS
.
- V. Wakelam, J.-C. Loison, E. Herbst, B. Pavone, A. Bergeat, K. Béroff, M. Chabot, A. Faure, D. Galli, W. D. Geppert, D. Gerlich, P. Gratier, N. Harada, K. M. Hickson, P. Honvault, S. J. Klippenstein, S. D. L. Picard, G. Nyman, M. Ruaud, S. Schlemmer, I. R. Sims, D. Talbi, J. Tennyson and R. Wester, Astrophys. J., Suppl. Ser., 2015, 217, 20 CrossRef
.
- D. McElroy, C. Walsh, A. J. Markwick, M. A. Cordiner, K. Smith and T. J. Millar, Astron. Astrophys., 2013, 550, A36 CrossRef
.
- D. Ascenzi, A. Cernuto, N. Balucani, P. Tosi, C. Ceccarelli, L. M. Martini and F. Pirani, Astron. Astrophys., 2019, 625, A72 CrossRef CAS
.
- A. Cernuto, F. Pirani, L. M. Martini, P. Tosi and D. Ascenzi, ChemPhysChem, 2018, 19, 51–59 CrossRef CAS
.
- A. Cernuto, P. Tosi, L. M. Martini, F. Pirani and D. Ascenzi, Phys. Chem. Chem. Phys., 2017, 19, 19554–19565 RSC
.
- B. Friedrich, D. Pullman and D. Herschbach, J. Phys. Chem., 1991, 95, 8118–8129 CrossRef CAS
.
- B. Friedrich and D. Herschbach, Nature, 1991, 353, 412–414 CrossRef CAS
.
- D. Ascenzi, N. Cont, G. Guella, P. Franceschi and P. Tosi, J. Phys. Chem. A, 2007, 111, 12513–12523 CrossRef CAS PubMed
.
- P. Franceschi, L. Penasa, D. Ascenzi, D. Bassi, M. Scotoni and P. Tosi, Int. J. Mass Spectrom., 2007, 265, 224–229 CrossRef CAS
.
- E. R. Fisher and P. Armentrout, J. Phys. Chem., 1991, 95, 4765–4772 CrossRef CAS
.
- E. Teloy and D. Gerlich, Chem. Phys., 1974, 4, 417–427 CrossRef CAS
.
- K. M. Douglas and S. D. Price, J. Chem. Phys., 2009, 131, 224305 CrossRef
.
- G. Burton, W. Chan, G. Cooper and C. Brion, Chem. Phys., 1992, 167, 349–367 CrossRef CAS
.
- S. Tanner, G. Mackay and D. Bohme, Can. J. Chem., 1979, 57, 2350–2354 CrossRef CAS
.
- T. Dang and V. Bierbaum, Int. J. Mass Spectrom. Ion Proc., 1992, 117, 65–82 CrossRef
.
-
A. Kramida, Y. Ralchenko and J. Reader, NIST Atomic Spectra Database (version 5.8), [Online], 2020 Search PubMed
.
-
B. Ruscic and D. Bross, Active Thermochemical Tables (ATcT) values based on ver. 1.122p of the Thermochemical Network, [Online], 2020 Search PubMed
.
- W. Wagner-Redeker, P. Kemper, M. Jarrod and M. Bowers, J. Chem. Phys., 1985, 83, 1121–1131 CrossRef CAS
.
- J. Herbon, R. Hanson, D. Golden and C. Bowman, Proc. Combust. Inst., 2002, 29, 1201–1208 CrossRef CAS
.
- D. E. Woon and E. Herbst, Astrophys. J., Suppl. Ser., 2009, 185, 273 CrossRef CAS
.
- S. Prasad and W. Huntress, Astrophys. J., Suppl. Ser., 1980, 43, 1–35 CrossRef CAS
.
- K. Goswami, A. Arora, A. Bharadvaja and K. Baluja, Eur. Phys. J. D, 2021, 75, 228 CrossRef CAS
.
- K. L. Nixon, W. A. D. Pires, R. F. C. Neves, H. V. Duque, D. B. Jones, M. J. Brunger and M. C. A. Lopes, Int. J. Mass Spectrom., 2016, 404, 48–59, DOI:10.1016/j.ijms.2016.05.006
.
- A. Zavilopulo, F. Chipev and L. Kokhtych, Nucl. Instrum. Methods Phys. Res., Sect. A, 2005, 233, 302–306 CrossRef CAS
.
- S. Srivastava, E. Krishnakumar, A. F. Fucaloro and T. van Note, J. Geophys. Res., 1996, 101, 26155–26160 CrossRef CAS
.
- K. Refaey and W. Chupka, J. Chem. Phys., 1968, 48, 5205–5219 CrossRef CAS
.
- J. Berkowitz, J. Chem. Phys., 1978, 69, 3044–3054 CrossRef CAS
.
- T. Nishimura, Y. Niwa, T. Tsuchiya and H. Nozoye, J. Chem. Phys., 1980, 72, 2222–2225 CrossRef CAS
.
- S. Borkar, B. Sztaray and A. Bodi, Phys. Chem. Chem. Phys., 2011, 13, 13009–13020 RSC
.
- D. Catone, M. Satta, M. C. Castrovilli, P. Bolognesi, L. Avaldi and A. Cartoni, Chem. Phys. Lett., 2021, 771, 138467 CrossRef CAS
.
- C. Lavin, M. V. Vega and A. M. Velasco, J. Phys. Chem. A, 2012, 116, 11913–11919 CrossRef CAS PubMed
.
- S. Pilling, R. Neves, A. C. F. Santos and H. M. Boechat-Roberty, Astron. Astrophys., 2007, 464, 393–398 CrossRef CAS
.
- C. Li, C.-H. Chin, T. Zhu and J. Z. H. Zhang, J. Mol. Struct., 2020, 1217, 128410 CrossRef CAS
.
- NIST Computational Chemistry Comparison and Benchmark Database, NIST Standard Reference Database Number 101, ed. R. D. Johnson III, https://cccbdb.nist.gov/, Release 21, August 2020.
- M. Gussoni, R. Rui and G. Zerbi, J. Mol. Struct., 1998, 447, 163–215 CrossRef CAS
.
- A. D. Becke, J. Chem. Phys., 1993, 98, 1372–1377 CrossRef CAS
.
- P. J. Stephens, F. J. Devlin, C. F. Chabalowski and M. J. Frisch, J. Phys. Chem., 1994, 98, 11623–11627 CrossRef CAS
.
- T. H. Dunning Jr, J. Chem. Phys., 1989, 90, 1007–1023 CrossRef
.
- D. E. Woon and T. H. Dunning Jr, J. Chem. Phys., 1993, 98, 1358–1371 CrossRef CAS
.
- F. Pirani, S. Brizi, L. F. Roncaratti, P. Casavecchia, D. Cappelletti and F. Vecchiocattivi, Phys. Chem. Chem. Phys., 2008, 10, 5489–5503 RSC
.
- F. Pirani, G. Maciel, D. Cappelletti and V. Aquilanti, Int. Rev. Phys. Chem., 2006, 25, 169 Search PubMed
.
- P. Linstorm, J. Phys. Chem. Ref. Data, Monogr., 1998, 9, 1–1951 Search PubMed
.
- M. B. Robin and N. A. Kuebler, J. Electron Spectrosc. Relat. Phenom., 1972/73, 1, 13–28 Search PubMed
.
- S. Thurmer, T. Shinno and T. Suzuki, J. Phys. Chem. A, 2021, 125, 2492–2503 CrossRef CAS PubMed
.
- R. Candori, S. Cavalli, F. Pirani, A. Volpi, D. Cappelletti, P. Tosi and D. Bassi, J. Chem. Phys., 2001, 115, 8888–8898 CrossRef CAS
.
- R. Candori, F. Pirani, D. Cappelletti, P. Tosi and D. Bassi, Int. J. Mass Spectrom., 2003, 223, 499–506 CrossRef
.
- C. Zener, Proc. R. Soc. London, Ser. A, 1932, 137, 696–702 Search PubMed
.
-
E. Nikitin and S. Umanskii, Theory of Slow Atomic Collisions, aus: Springer Series in Chemical Physics, 1984, vol. 30 Search PubMed
.
- E. Nikitin, Annu. Rev. Phys. Chem., 1999, 50, 1–21 CrossRef CAS PubMed
.
- M. Rosi, L. Mancini, D. Skouteris, C. Ceccarelli, N. F. Lago, L. Podio, C. Codella, B. Lefloch and N. Balucani, Chem. Phys. Lett., 2018, 695, 87–93 CrossRef CAS
.
- N. Balucani, D. Skouteris, C. Ceccarelli, C. Codella, S. Falcinelli and M. Rosi, Mol. Astrophys., 2018, 13, 30–37 CrossRef
.
- C. Berteloite, S. D. Le Picard, I. R. Sims, M. Rosi, F. Leonori, R. Petrucci, N. Balucani, X. Wang and P. Casavecchia, Phys. Chem. Chem. Phys., 2011, 13, 8485–8501 RSC
.
- J.-D. Chai and M. Head-Gordon, Phys. Chem. Chem. Phys., 2008, 10, 6615–6620 RSC
.
- R. J. Bartlett, Annu. Rev. Phys. Chem., 1981, 32, 359–401 CrossRef CAS
.
- K. Raghavachari, G. W. Trucks, J. A. Pople and M. Head-Gordon, Chem. Phys. Lett., 1989, 157, 479–483 CrossRef CAS
.
- J. Olsen, P. Jørgensen, H. Koch, A. Balkova and R. J. Bartlett, J. Chem. Phys., 1996, 104, 8007–8015 CrossRef CAS
.
-
M. Frisch, G. Trucks, H. Schlegel, G. Scuseria, M. Robb, J. Cheeseman, G. Scalmani, V. Barone, B. Mennucci and G. Petersson, et al., Gaussian 09, rev. A. 02, Gaussian, 2009 Search PubMed
.
- M. D. Hanwell, D. E. Curtis, D. C. Lonie, T. Vandermeersch, E. Zurek and G. R. Hutchison, J. Cheminf., 2012, 4, 1–17 Search PubMed
.
- C. Li, C.-H. Chin, T. Zhu and J. Z. H. Zhang, J. Mol. Struct., 2020, 1217, 128410 CrossRef CAS
.
- H. Wu, Y. Xue, J. Wen, H. Wang, Q. Fan, G. Chen, J. Zhu, F. Qu and J. Guo, RSC Adv., 2019, 9, 16683–16689 RSC
.
- N. L. Ma, B. J. Smith, J. A. Pople and L. Radom, J. Am. Chem. Soc., 1991, 113, 7903–7912 CrossRef CAS
.
- A. Tsikritea, J. A. Diprose, T. P. Softley and B. R. Heazlewood, Phys. Chem. Chem. Phys., 2022, 157, 060901 CAS
.
-
Tutorials in Molecular Reaction Dynamics, ed. M. Brouard and C. Vallance, RCS Publishing, Cambridge UK, 2010 Search PubMed
.
- W. J. Chesnavich, T. Su and M. T. Bowers, J. Chem. Phys., 1980, 72, 2641–2655 CrossRef CAS
.
- T. Su and W. J. Chesnavich, J. Chem. Phys., 1982, 76, 5183–5185 CrossRef CAS
.
- Y. Georgievskii and S. J. Klippenstein, J. Chem. Phys., 2005, 122, 194103 CrossRef
.
- A. Kilaj, J. Wang, P. Stranak, M. Schwilk, U. Rivero, L. Xu, O. A. von Lilienfeld, J. Kupper and S. Willitsch, Nat. Commun., 2021, 12, 6047 CrossRef CAS PubMed
.
- A. D. Doerfler, P. Eberle, D. Koner, M. Tomza, M. Meuwly and S. Willitsch, Nat. Commun., 2019, 10, 5429 CrossRef
.
- A. Kilaj, H. Gao, D. Rosch, U. Rivero, J. Kuepper and S. Willitsch, Nat. Commun., 2018, 9, 2096 CrossRef
.
- V. Zhelyazkova, F. B. Martins, V. M. Zesko and F. Merkt, Phys. Chem. Chem. Phys., 2022, 24, 2843–2858 RSC
.
- V. Zhelyazkova, F. B. Martins, V. J. A. Agner, H. Schmutz and F. Merkt, Phys. Chem. Chem. Phys., 2021, 23, 21606–21622 RSC
.
- V. Zhelyazkova, F. B. Martins, V. J. A. Agner, H. Schmutz and F. Merkt, Phys. Rev. Lett., 2020, 125, 263401 CrossRef CAS
.
- K. Hoveler, J. Deiglmayr and F. Merkt, Mol. Phys., 2021, 119, 17–18 CrossRef
, SI.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2cp02458f |
| This journal is © the Owner Societies 2022 |