Open Access Article
Open Access ArticleArray based real-time measurement of fluid viscosities and mass-densities to monitor biological filament formation†
Paolo
Oliva
 *a,
Benjamin Andreas
Bircher‡
a,
Cora-Ann
Schoenenberger
b and
Thomas
Braun
a
*a,
Benjamin Andreas
Bircher‡
a,
Cora-Ann
Schoenenberger
b and
Thomas
Braun
a
aCenter for Cellular Imaging and Nanoanalytics (C-CINA), University of Basel, Mattenstrasse 26, Basel, Switzerland. E-mail: paolo.oliva@unibas.ch; thomas.braun@unibas.ch
bDepartment of Chemistry, University of Basel, Mattenstrasse 24a, Basel, Switzerland. E-mail: cora-ann.schoenenberger@unibas.ch
First published on 4th March 2019
Abstract
Liquid mass density and viscosity are fundamental characteristics of fluids. Their quantification by means of classical viscosity and density meters has several drawbacks: (i) the liquid-density and the viscosity cannot be measured simultaneously, (ii) sample volumes in the mL-range are consumed, (iii) the measurements cannot be multiplexed, and, (iv) the quantifications are time-consuming (minutes). Nano-mechanical transducers promise to overcome these limitations. We use fully clamped, gold coated silicon-nitride membranes with a thickness of 200 nm to measure liquid viscosity and density of samples of 1 μL volumes residing above the membrane in a miniature well. Photo-thermal actuation is used to excite the membrane, and an optical deflection system measures the response. From the response spectra, the eigenfrequency (f) and the quality (Q) factor are extracted and used to determine liquid density and viscosity by applying a three-point calibrated, simplified lumped model. We tested the system using calibrated solutions with viscosities in the range of 1–219 mPa s and mass densities between 998 kg m−3 and 1235 kg m−3. Real-time measurements were performed that characterize the polymerization of G-actin to F-actin filaments. The method presented promises to overcome the aforementioned limitations and thereby enables the real-time characterization of sub-μL sample volumes in a multiplexed manner.
1 Introduction
Viscosity and mass density are fundamental liquid properties. They can be measured using classical methods, e.g., by employing Ostwald viscometers to measure the fluid viscosity or by the application of volume-measuring containers in combination with mass balances to determine the liquid density. However, these conventional methods need milliliter sample volumes, and the measurement takes a significant amount of time.Over the past few years, several methods have been proposed to minimize sample volumes and reduce measurement times. These can be classified as miniaturized Ostwald viscometers employing microfluidics technology,1 droplet-based microfluidics methods,2 thermal noise detection,3 and thickness-shear resonators (QCM or SH-SAW sensors).4,5 A broad research domain is based on the development of micro-rheology assays, which are used to measure rheological properties of a medium, such as the viscoelasticity and the loss and shear modulus of biological filaments, at small scales. These new techniques include dynamic light scattering (DLS),6 diffuse wave spectroscopy (DWS),7,8 video-particle tracking,9 microfluidic stagnation flow,10–12 and microfluidic capillary viscometry.13–18
Cantilever-based nano-mechanical sensors allow the real-time measurement of liquid mass-density and viscosity of μL-sized volumes.19,20 These sensors characterize the cantilever vibrational response to external driving forces. Excitation can be achieved in different ways: photo-thermally,21–23 by inducing Lorentz forces,24,25 and piezo-electrically.26,27 For example, cantilevers were used as sensors to measure the coagulation of blood plasma.28,29
However, these cantilever-based sensors have limitations: First, the strong damping of fully-immersed cantilevers leads to low-quality factors (Q) and, thus, limits measurement precision and prevents the characterization of liquids with high viscosities. Second, non-transparent liquids disturb the optical readout system that measures the deflection of the cantilever. Third, multiplexed real-time measurements are difficult because either an array of cantilevers measures geometrically-separated liquid droplets, or a stream of sequential liquid droplets passes the cantilever transducer. The latter allows high-throughput screening, but individual samples are exposed only for a short period of approximately 1 s20 which is usually too short to allow rheokinetic measurements of chemical reactions.19
In this report, we use fully clamped silicon-nitride membranes, that are photo-thermally excited, in combination with an optical read-out system that enables the recording of spurious-free response-spectra of the membrane. From the response spectra the eigenfrequency (f) and the quality factor (Q) were extracted by using the driven damped harmonic oscillator model (DDHO) (ch. 2†). The extracted values were subsequently used to determine the liquid density and viscosity by applying the reduced order model (ROM),30 which is based on a three-point calibration. This system has several advantages: (i) the membrane and the silicon base form a tiny well, and only sub-microliter sample volumes are needed, (ii) higher viscosity and mass density resolution is achieved due to higher Q-factors,31 (iii) the membranes can be arrayed for multiplexed measurements, and, (iv) broad measurable liquid density and viscosity range.
2 Materials and methods
2.1 Reference solutions
Reference solutions were prepared by mixing liquid glycerine (Cat-nr. 131339.1211, PanRec AppliChem, ITW Reagents) with water for molecular biology (Cat-nr. H20MB0501, Millipore). The reference viscosities and mass densities were measured with an automated viscosity (Anton Paar, AMVn Viscometer, Switzerland) and density meter (Anton Paar, DMA 4500, Switzerland). For details see ESI,† ch. 1.2.2 Protein solutions
Lyophilized G-actin (globular actin) from rabbit skeletal muscle (Cat-nr. 8101-01), G-actin buffer at pH 8.2, containing adenosintriphosphate (ATP), CaCl2 and dithiothreitol (DTT) (MonoMix, Cat-nr. 5100-01) and polymerization inducing buffer PolyMix (Cat-nr. 5000-01) were purchased from Hypermol (Bielefeld, Germany). Before the experiments the G-actin lyophilized powder was reconstituted with water to a final concentration of 1 mg mL−1, centrifuged for 10 min (15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 × g) and stored on ice.
000 × g) and stored on ice.
2.3 Sensor setup
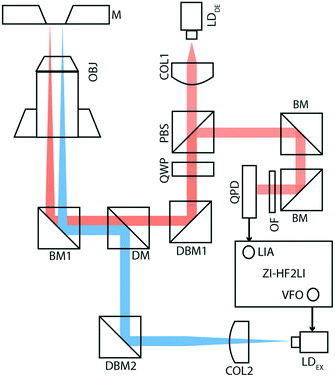
Fig. 1 shows the membrane transducer, the liquid handling system, and its integration in the set-up. Fig. 2 depicts a schematic representation of the photo-thermal excitation, the optical beam deflection system (OBD), and the electronic components adapted from a previous setup.20 These components enable the use of silicon-nitride membranes as nano-mechanical resonators.The set-up consists of a detection- and an excitation part, which are mechanically separated from the measurement chamber. The detection part is composed of a laser beam (LDDE, λ = 785.4 nm, PDE = 4.9 mW; 51nanoFCM-H06, Schäfer + Kirchhoff GmbH, Hamburg, Germany) with a wavelength of 785.4 nm which sequentially passes through a collimator (COL1; TC12APC-780, Thorlabs, Germany) and an optical isolator (ISO; IO-3D-780-VLP, Thorlabs, Germany). For monitoring the intensity of the detection laser, a beam-splitter (8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 92; CM1-BP108, Thorlabs, Germany) with a photo-diode (PD1; PDA100A-EC, Thorlabs, Germany) has been mounted after the optical isolator. To obtain circularly polarized light, a polarizing beam-splitter (PBS; CM1-PBS252, Thorlabs, Germany) and a quarter wave-plate (QWP; AQWP05M-600, Thorlabs, Germany) have been inserted in the optical pathway. The laser beam finally reflects at a broadband mirror (BM1; BB1-EO2, Thorlabs, Germany) and is focused using a microscope objective (OBJ; RMS4X, Thorlabs, Germany). The beam reflects off the gold-coated surface of the silicon nitride membrane and follows the same optical pathway ending on a quadrant photodiode (QPD; S5980, Hamamatsu, Japan), which is placed after the PBS. The newly designed QPD has a bandwidth of 3.5 MHz.
92; CM1-BP108, Thorlabs, Germany) with a photo-diode (PD1; PDA100A-EC, Thorlabs, Germany) has been mounted after the optical isolator. To obtain circularly polarized light, a polarizing beam-splitter (PBS; CM1-PBS252, Thorlabs, Germany) and a quarter wave-plate (QWP; AQWP05M-600, Thorlabs, Germany) have been inserted in the optical pathway. The laser beam finally reflects at a broadband mirror (BM1; BB1-EO2, Thorlabs, Germany) and is focused using a microscope objective (OBJ; RMS4X, Thorlabs, Germany). The beam reflects off the gold-coated surface of the silicon nitride membrane and follows the same optical pathway ending on a quadrant photodiode (QPD; S5980, Hamamatsu, Japan), which is placed after the PBS. The newly designed QPD has a bandwidth of 3.5 MHz.
The excitation part of the setup is composed of a laser beam (LDEX, λ = 405 nm, PEX = 8.7 mW; DLM-405/70F, Elovis) with a wavelength of 405 nm, which passes through a collimator (COL2; TC12FC-405, Thorlabs, Germany), a beam-splitter (8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 92; CM1-BP108, Thorlabs, Germany), a dichroic mirror (DM; DMLP567, Thorlabs, Germany), and a broadband mirror (BM1), and is finally focused on the gold-coated membrane using the same objective (OBJ).
92; CM1-BP108, Thorlabs, Germany), a dichroic mirror (DM; DMLP567, Thorlabs, Germany), and a broadband mirror (BM1), and is finally focused on the gold-coated membrane using the same objective (OBJ).
Using the internal variable frequency oscillator (VFO) and lock-in amplifier (LIA) integrated with Zurich Instruments HF2LI (ZI-HF2LI), the amplitude and phase spectra of different modes were recorded. The reference signal is fed into the excitation laser which drives the oscillation of the membrane. To monitor the dynamic deflection detected by the QPD, the input signal was split into two components: the first line was used as an input signal to the Zurich Instruments lock-in amplifier. The QPD used was designed to reach a 10-fold amplification. The second line was first low-pass filtered (fc,DC = 80 Hz) and then amplified ten times, to avoid noise amplification. This component was then fed into an analog input of a National Instruments card (NI-9215) and read out.
The new control software was developed as an openBEB module32 in LabVIEW. To collect and save the amplitude and phase data, a separate module was programmed, which enables the user to perform either a single sweep or a sequential acquisition of a specific frequency range.
2.4 Data analysis collection
Fig. 3 shows a schematic representation of a typical measurement. To measure the liquid density and the viscosity, the quality factor and the eigenfrequency were tracked by sweeping the modulation frequency of the excitation laser and recording the frequency-dependent response of the membrane using the read-out laser. From a series of response-spectra, the eigenfrequency and the quality factor were determined. The reduced order model30 enables the determination of the liquid viscosity and density after a three-point calibration30 (ch. 2†). By measuring the eigenfrequencies (fexp) and the quality factors (Qexp) of three known liquids which cover a broad density and viscosity range, the calibration coefficients, m0k, mρk,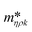 , c0k, cηk,
, c0k, cηk, 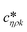 , of the reduced order model can be determined. The resulting values are inserted into the following equations and solved for the liquid density, ρ, and the viscosity η:
, of the reduced order model can be determined. The resulting values are inserted into the following equations and solved for the liquid density, ρ, and the viscosity η: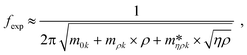 | (1) |
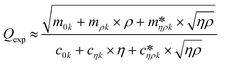 | (2) |
 | ||
| Fig. 3 Schematic overview of the measurement workflow: the membrane resonator is actuated by a modulated laser diode (blue) driven by the variable frequency oscillator (VFO). The membrane response is optically read out (red laser) and quantified by a digital lock-in amplifier (LIA). Note that the gold layer on the membrane absorbs 67% of the incoming blue light leading to a photo-thermal actuation of the membrane, and reflects 97% of the red light for the read-out of the membrane response.19 Spectra are recorded continuously by sweeping the frequency space, resulting in a time series of amplitude and phase spectra. From the series of amplitude and phase response spectra, the time-dependent eigenfrequency fn(t) and the time-dependent quality factors Qn(t) can be determined by fitting a driven damped harmonic oscillator model (DDHO) to each spectrum. After the determination of these parameters the liquid density ρn(t) and the viscosity ηn(t) can be calculated by applying the reduced order model (ROM).30 | ||
Before starting with the measurements, the detection and excitation laser were aligned. The laser positioning on the silicon-nitride membrane is simplified by calculating the Jacobi- and Hess matrix of the respective mode shape function. It is essential to determine the correct placement of the excitation and detection otherwise the vibrational amplitudes are strongly reduced.23
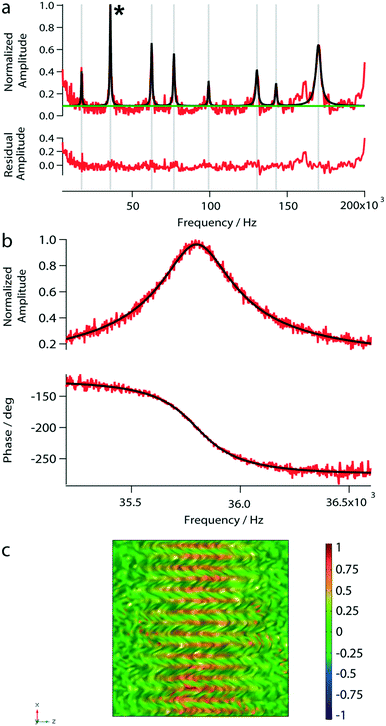
After having placed the laser spots on a distinct area, the spectrum of a reference fluid was determined by a sweep over a frequency range (from 5 kHz to 200 kHz). Next, the vibrational mode was chosen. By choosing modes with higher eigenfrequencies, the sensitivity to viscosity and mass density changes is increased.33 Because of the higher amplitude and the highest signal-to-noise ratio, we typically chose the second peak around 35.8 kHz for our experiments (see Fig. 4). The mode shapes represent the superposition of lower modes.34
After having selected the mode, the respective frequency range was chosen and again swept repeatedly. The resulting amplitude and phase curves were analyzed in the following ways: (i) Lorentzian fit to the amplitude, (ii) peak frequency and quality factor were extracted, and, (iii) the phase curve was fitted by a driven damped harmonic oscillator model (DDHO) using the derived parameters from the Lorentzian as starting points (ch. 5†).
2.5 Humidity chamber, sample stage, and sample priming
To avoid thermal and ambient-induced deflection drifts,35 viscosity changes, and evaporation of the sample the environment was controlled by placing the membrane transducer in a specially designed climate chamber made of plexiglass (Fig. 1c). The humidity of the chamber was regulated at 73% for a dew-point temperature of 20 °C, and all experiments were performed at this temperature.To regulate the humidity set-point, a humidity sensor (HIH-4000-002, Honeywell, Distrelec, Switzerland) was installed. The humid air is introduced from an MH-Series humidifier (MH-110-12S-2, Perma Pure, New Jersey, USA) which contains a selectively permeable Nafion membrane surrounded by water. After passing the walls of this membrane the water evaporates due to the pressure difference between the incoming dry gas and the water supply. This humidifying tube allows the transfer of heat and water vapor pressure between a gas stream and a water supply. The flow rate is controlled using a calibrated flow meter (Q140E13G, Vögtlin Instruments, Aesch, Switzerland). Typically a flow rate of 1.667 L min−1 is used. To avoid cooling of the tube and therefore decreasing the humidification efficiency, a resistor wire (Block, FA-Nr. 708951, Distrelec, Switzerland) was wrapped around it. Using a PID-Controller the current through the wire can be regulated. The resistor wire has a total resistance of 100.8 Ω and with this heating system a maximum relative humidity of 90.4% at 24 °C (Ttube = 27 °C) can be achieved. The temperature of the copper plate was regulated with an accuracy of ±0.05% using two Peltier-elements and a PID-controller.
Sample volumes were typically 1 μL, which requires a precise pumping system with a minimal dead volume. A syringe pump (KDS900, KD Scientific, Holliston, MA, U.S.A.) and a 500 μL syringe were used to aspirate a few microliters of the test sample. Using a fused silica capillary (TSP-180350, ID = 180 μm, OD = 350 μm) that is connected to the syringe and mounted on a movable XYZ-stage, the sample droplet can be precisely placed on the silicon-nitride membrane. A surveillance camera (Prosilica GC750C, Basler, Germany) with a mounted 12× zoom body tube (1-50330, Navitar, USA) facilitates the alignment of the capillary (Fig. 1b).
2.6 Membrane preparation
Stochiometric silicon-nitride membranes (NSX5100D, Norcada, Edmonton, Canada) with a window size of 1 × 1 mm2 and a thickness of 200 nm spanned over a 5 × 5 mm2 silicon support were used.Before each experiment, the membranes were washed with acetone, rinsed with nanopure water, and then plasma cleaned (O2, gas flow 0.003379 Pa m3 s−1, 13.32 Pa, power 30 W; Solarus, Model 950, Gatan) for 40 s. Subsequently, 0.4 μL of a PLL(20)-g[3.5]-PEG(2) solution at a concentration of 1 mg mL−1 (SuSoS AG, Dübendorf, Switzerland) was deposited in the well and incubated for 1 h at room temperature. After this step, the membrane was rinsed with nanopure water. The membrane passivation was done to avoid protein sticking to the silicon-nitride surface, which would cause errors in the measured fluid properties.
2.7 Finite element simulations of membrane behaviours
To analyze the eigenfrequency of a fully clamped membrane the solid mechanics and heat transfer modules were used and combined with a thermal expansion multiphysics module. Due to the laser heating up the gold layer, a material-dependent expansion causes the oscillation of the membrane. The tensile stress of the silicon-nitride layer and the mass added to the well damped the oscillation. In the simulation the added mass corresponds to 1 μL of water. The physics modules were integrated in a pre-stressed eigenfrequency analysis. For the meshing the entire geometry was divided into two parts. A free triangular node with an extremely fine element size was added to the upper and lower surface of the blocks. The mesh of the remaining geometry was divided into 400 equally distributed rectangulars per domain.
2.8 Electron microscopy specimen preparation
We used transmission electron microscopy (TEM) of negatively stained samples to observe the presence (or absence) of actin filaments. After the liquid viscosity measurement, the sample was removed from the silicon-nitride well and applied to a glow-discharged carbon-coated EM-grid. The sample was adsorbed to the grid for 75 s at room temperature. Excess liquid was blotted with filter-paper, and subsequently the grid was washed for three times with 5 μL of nanopure water. After washing, the sample was negatively stained twice for 20 s with 5 μL of 2% uranyl acetate.3 Results
3.1 Photo-thermal excitation of silicon-nitride membranes
To test the photo-thermal actuation and beam-deflection read-out system, we measured the amplitude response spectrum of the nanomechanical membrane loaded with 1 μL of water. Eight eigenfrequency peaks were observed in the amplitude spectrum (Fig. 4a). However, below 5 kHz the peak-amplitudes are close to the noise level. The found eigenfrequencies are in excellent agreement with our simulations (Table 1). Furthermore, we characterized the second peak at 35.8 kHz by sweeping over a frequency range of 5 kHz to 200 kHz as shown in Fig. 4b. The bandwidth of the variable frequency oscillator was adapted to minimize the noise; usually, a bandwidth of 15.1 Hz was used. Note, that for the subsequent measurements we used the eigenfrequency around 35.8 kHz.| f exp [Hz] | f sim [Hz] |
|---|---|
17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 247 ± 64.22 247 ± 64.22 |
17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 218 218 |
35![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 862 ± 23.66 862 ± 23.66 |
35![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 866 866 |
62![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 488 ± 41.73 488 ± 41.73 |
62![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 494 494 |
76![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 894 ± 52.28 894 ± 52.28 |
76![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 895 895 |
3.2 Viscosity and mass density measurements of Newtonian liquids
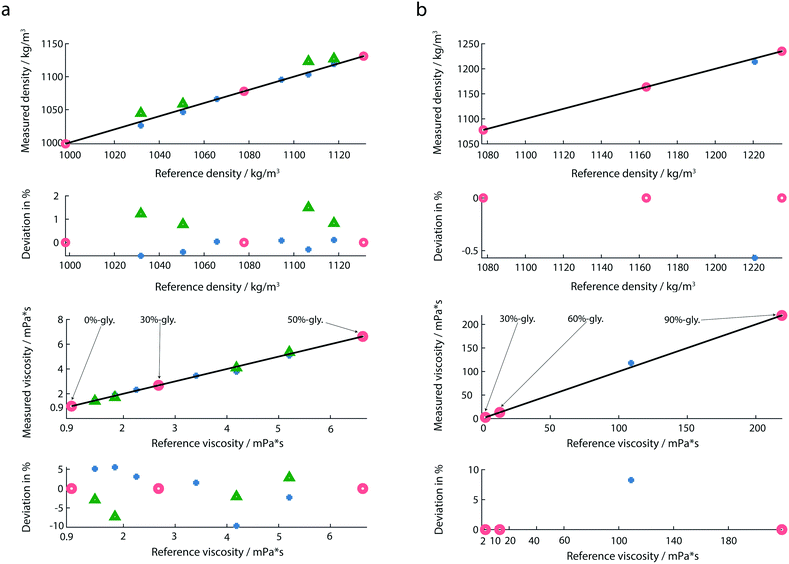
The response of the membrane resonator depends on the properties of the deposited fluid. For the liquid viscosity and density measurements, the sensor was first calibrated using at least three reference solutions as described before.20,30 The eigenfrequencies and quality factors of the calibration liquids were used to determine the coefficients required in the linear system of equations of the reduced order model.30 Calculated coefficients of the calibration model for all measurements are provided in the ESI† (ch. 2). After calibration, the liquid-samples were placed on the membrane, and the amplitude and the phase spectra were recorded. From these spectra, the eigenfrequencies and Q-factors were extracted, and the calibrated reduced order model allowed the determination of mass density (ρ), and viscosity (η) of the test-fluids loaded on the membrane. For all experiments droplet volumes of 1 μL were used. To avoid sample contamination, the wells were rinsed with 3 μL of water after every measurement.We noticed, that the calibration fluids chosen need to cover the expected viscosity range of the test-fluids. An extrapolation of the model to viscosity measurements that were far away from the calibration liquids led to significant errors. In order to cover the large range of viscosities, we used two calibration sets: for lowly viscous fluids (from 0 mPa s to 6.63 mPa s), the chosen calibration fluids were 0%-, 30%- and 50%-glycerol (Fig. 5a). For highly viscous fluids (from 13.2 mPa s to 219 mPa s) 30%-, 60%- and 90%-glycerol were chosen as reference fluids (Fig. 5b). In both calibration sets 30%-glycerol was chosen as the calibration point in order to avoid large deviations in the calculation of the liquid properties of the test sample. For highly viscous fluids, the test sample was 85%-glycerol.
3.3 Real-time characterization of G-actin polymerization
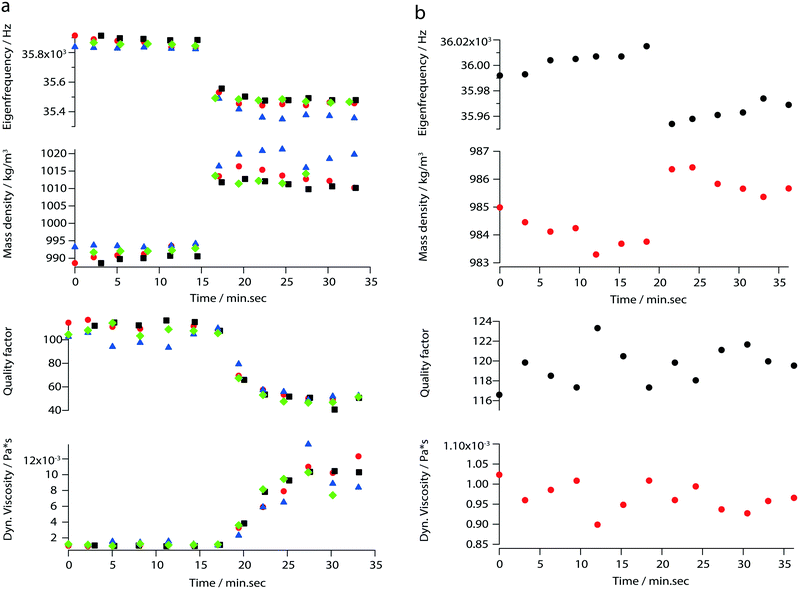
In addition to the viscosity and mass density measurements, the formation of actin filaments in real-time was tracked as follows: 0.9 μL of monomeric G-actin was placed on the silicon-nitride membrane. The excitation and detection of the membrane oscillations were started, and an equilibrium state of the eigenfrequency was obtained after 20 min. Subsequently, 0.1 μL of PolyMix at pH 7.4, containing KCl, ATP and MgCl2, was added to trigger actin polymerization. Immediately, the sequential acquisition of the amplitude and phase curve with a digital lock-in amplifier was started and run for 50 min (Fig. 6a). After the addition of 0.1 μL PolyMix, a slowly decreasing quality factor was observed. The eigenfrequency rapidly changed and achieved a steady-state after a few minutes (Fig. 6a). As a negative control, the same experiment was performed by adding 0.1 μL MonoMix buffer at pH 8.2 containing ATP, CaCl2 and DTT that does not promote F-actin formation (Fig. 6b). Some fluctuations of the eigenfrequencies and quality factors were observed with the MonoMix buffer, but compared to using PolyMix, no significant decrease of the quality factor was observed (Fig. 6b): the eigenfrequency drop of approximately 0.2% is due to the addition of 0.1 μL MonoMix buffer. To confirm that the polymerization of G-actin was not dependent on the specific membrane, the entire measurement was repeated several times using different membranes (ch. 4†).After the measurement, the droplet was collected from the membrane, negatively stained and visualized in the electron microscope. As illustrated in Fig. 7 the sample contained long actin filaments.
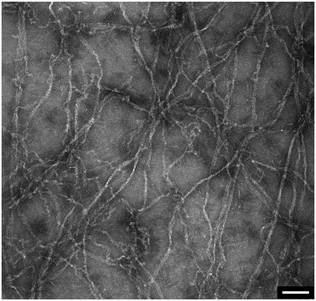 | ||
| Fig. 7 Post-measurement sample analysis by transmission electron microscopy. Long actin filaments are detected in G-actin samples that were incubated with polymerization buffer. Scale bar: 100 nm. | ||
4 Discussion
4.1 Photo-thermal excitation of silicon-nitride membranes
We used photo-thermal excitation of fully clamped silicon-nitride membranes that form a small well with the silicon base. Membranes with a frame size of 1 × 1 mm2 were used to perform measurements of volumes between 0.5 μL and 1 μL. Compared to fully immersed resonators, a particular advantage of these transducers is the higher quality factor that results in a higher viscosity and mass density resolution. By analyzing the second vibrational mode, we were able to achieve a quality factor of Q = 135 using water loaded membranes with this set-up. In comparison cantilever-based sensors20 reach a quality factor of Q = 10 for the third vibrational mode. However, at frequencies lower than 5 kHz the peak amplitudes were close to the noise level. The lower limit corresponds to the bandwidth of the read-out electronics. We observed an upper limit (around 60 kHz) which could be due to (i) inefficient heat transfer needed to relax the tension introduced in the membrane bilayer after the photon pulse, or (ii) the clamping loss.Heat transfer simulations show that the cooling time of the stressed bilayer after a laser pulse is enough to induce oscillation. The so-called phonon-tunneling, which is an external loss, is one of the significant damping effects of membrane resonators. To avoid the propagation of acoustic waves into the silicon frame, the vibrational mode has to be placed within a phononic bandgap. For blocking acoustic waves a phononic crystal and the membrane frame should form a defect.
Commercially available membrane do not fulfill the above criterion. Simulation show a bandgap between 600–800 kHz indicating that the missing phononic bandgap could be responsible for the high damping effect in the low-frequency regime (ch. 6†). To achieve a higher signal-to-noise ratio (higher quality factor) and increase the bandwidth, a new silicon base could be designed. The dimensions of the new silicon base have to be determined in such a way that a phononic bandgap is present within the wanted frequency range.
4.2 Viscosity and mass density measurements of Newtonian liquids
As indicated by maximal deviations of 1.5% for the mass density and 9.6% for the viscosity (Fig. 5a), the determination of the mass density is more accurate than that of the viscosity. Compared to previous studies,20 we observed a larger deviation in the determination of the viscosity. A possible reason is the use of a different environment controlling system. A slight change in the temperature and humidity could affect the liquid properties. Another measure which could further minimize the measured deviation is the integration of an interferometer instead of an optical beam deflection read-out system.By performing multiplexed measurements, we could further minimize the measurement time and realize a high-throughput at the same accuracy.
An additional advantage of our set-up is the broad range of viscosity and mass density that can be measured (Fig. 5b). Experiments with highly viscous glycerol solutions were performed. In the case of highly viscous glycerol solutions the determination of the reference viscosities by the classical Anton Paar viscometer was not possible due to the high rolling time. Instead, the theoretical values for the viscosities of 85%- and 90%-glycerol were used.
The use of the reduced order model leads to an accurate density and viscosity determination only if the calibration fluids have the same viscosity–density behavior and range as the sample liquids. An extrapolation of the liquid properties should be avoided. Further information can be found in the ESI† (ch. 2).
4.3 Real-time characterization of G-actin polymerization
By measuring mass density and viscosity, we were able to follow G-actin polymerization in real-time in a label-free manner. In previous studies, the filament formation and bundling were analyzed using microfluidic devices by observing the polymerization of fluorescently labeled actin monomers in KCl and MgCl2 gradients.36During the data acquisition, a decreasing amplitude and a slight frequency shift (ch. 3†) were observed. These two behaviors are related to the formation of actin filaments (F-actin) where the increasing viscosity leads to higher damping which implicate decreasing quality factors. At the same time, filament growth results in a denser liquid. Corresponding to the three steps of actin polymerization, i.e., a nucleation, an elongation and a steady-state phase, three states are revealed by the curves presented in Fig. 6a.
The ability to follow filament formation in real-time was also confirmed by the negative control (Fig. 6b). In the absence of polymerization inducing buffer, fluctuating eigenfrequencies and quality factors were visible, but no significant decrease or increase of the quality factor and eigenfrequency were observed over time.
5 Conclusions
We present a method based on fully clamped silicon-nitride membranes to characterize the viscosity and mass density of Newtonian and non-Newtonian fluids that requires only minute amounts of sample (V = 1 μL). A three-point calibration approach is applied to calculate the viscosity and liquid density values from the eigenfrequency and the quality factor. The measurements show a maximal deviation of 1.5% for the mass density, and a maximal difference of 9.6% for the viscosity when compared to calibrated liquids. The sensor format enables multiplexed measurements, and in contrast to conventional methods, the measurement time is independent of the fluid viscosity. Once the system is correctly calibrated, the platform can be used to characterize various liquids in a short time period. For a single sample, it only takes around three minutes to measure the amplitude and phase curve and calculate the liquid properties. The measurement time can further be reduced by automating the sample priming. Moreover, by combining the multiplexed membrane measurements with a fast read-out system, e.g., a dual PLL frequency tracking system,20,37 the time resolution of rheokinetic measurements can be increased to the millisecond regime.With the method presented it is also possible to measure the viscosity and mass densities of biological samples. In our particular case, the changes of the liquid properties were related to the formation of actin filaments from monomeric actin.
We envisage that the improved measurement platform is suitable to characterize interactions of biomolecules in a label and functionalization-free manner.
Author contributions
T. B. conceived the research project. B. A. B. helped with the manuscript preparation and previously developed the device to measure the viscosity and mass density by using photo-thermally excited cantilevers. P. O. modified the existing device to measure liquid properties using photo-thermally excited silicon-nitride membranes and performed all the experiments and data analysis. C-A. S. helped with the data analysis of the actin measurements and manuscript preparation.Conflicts of interest
The authors confirm that there are no conflicts of interest to declare.Acknowledgements
The authors acknowledge Henning Stahlberg (C-CINA, Biozentrum, University of Basel) for providing facilities. Sascha Martin (Mechanical Workshop, Swiss Nanoscience Institute, University of Basel) for the construction of several mechanical parts. Andreas Tonin (Electronics lab, Swiss Nanoscience Institute, University of Basel) for the development of the QPD. François Huber (Department of Physics, University of Basel) for coating the silicon-nitride membranes. Carola Alampi (BioEM Lab, Biozentrum, University of Basel) for taking several pictures with the SEM. Andrej Bieri, Andri Fränkl, Amanda Lewis and Luca Rima for reviewing the manuscript. Claudio Schmidli and Cedric Leu (C-CINA, Biozentrum, University of Basel) for expert discussions. Financial support is acknowledged from the Swiss Nanoscience Institute (SNI Ph.D. Project 1501).References
- M. Zou, S. Cai, Z. Zhao, L. Chen, Y. Zhao, X. Fan and S. Chen, Rev. Sci. Instrum., 2015, 86, 104302 CrossRef PubMed.
- Y. Li, K. R. Ward and M. A. Burns, Anal. Chem., 2017, 89, 3996–4006 CrossRef CAS PubMed.
- F. A. Sandoval, M. Sepúlveda, L. Bellon and F. Melo, Sensors, 2015, 15, 27905–27916 CrossRef PubMed.
- G. L. Hayward and G. Z. Chu, Anal. Chim. Acta, 1994, 288, 179–185 CrossRef CAS.
- T. Morita, M. Sugimoto and J. Kondoh, Jpn. J. Appl. Phys., 2009, 48, 07GG15 Search PubMed.
- F. He, G. W. Becker, J. R. Litowski, L. O. Narhi, D. N. Brems and V. I. Razinkov, Anal. Biochem., 2010, 399, 141–143 CrossRef CAS PubMed.
- D. Weitz, J. Zhu, D. J. Durian, H. Gang and D. J. Pine, Phys. Scr., 1993, T49, 610–621 CrossRef.
- T. Mason, H. Gang and D. A. Woltz, J. Opt. Soc. Am. A, 1997, 14, 139–149 CrossRef CAS.
- F. Ortega, H. Ritacco and R. G. Rubio, Curr. Opin. Colloid Interface Sci., 2010, 15, 237–245 CrossRef CAS.
- G. G. Fuller and L. G. Leal, Rheol. Acta, 1980, 19, 580–600 CrossRef CAS.
- J. F. Schoonen, F. H. Swartjes, G. W. Peters, F. Baaijens and H. E. Meijer, J. Non-Newtonian Fluid Mech., 1998, 79, 529–561 CrossRef CAS.
- S. D. Hudson, F. R. Phelan, M. D. Handler, J. T. Cabral, K. B. Migler and E. J. Amis, Appl. Phys. Lett., 2004, 85, 335–337 CrossRef CAS.
- K. Kang, L. J. Lee and K. W. Koelling, Exp. Fluids, 2005, 38, 222–232 CrossRef CAS.
- C. J. Pipe, T. S. Majmudar and G. H. McKinley, Rheol. Acta, 2008, 47, 621–642 CrossRef CAS.
- N. Srivastava, R. D. Davenport and M. A. Burns, Anal. Chem., 2005, 77, 383–392 CrossRef CAS PubMed.
- G. Degré, P. Joseph, P. Tabeling, S. Lerouge, M. Cloitre and A. Ajdari, Appl. Phys. Lett., 2006, 89, 24104 CrossRef.
- Z. Han, X. Tang and B. Zheng, J. Micromech. Microeng., 2007, 17, 1828–1834 CrossRef CAS.
- Y.-Y. Lin, C.-W. Lin, L.-J. Yang and A.-B. Wang, Electrochim. Acta, 2007, 52, 2876–2883 CrossRef CAS.
- B. A. Bircher, L. Duempelmann, K. Renggli, H. P. Lang, C. Gerber, N. Bruns and T. Braun, Anal. Chem., 2013, 85, 8676–8683 CrossRef CAS PubMed.
- B. A. Bircher, R. Krenger and T. Braun, Sens. Actuators, B, 2016, 223, 784–790 CrossRef CAS.
- D. Ramos, J. Tamayo, J. Mertens and M. Calleja, J. Appl. Phys., 2006, 99, 124904 CrossRef.
- D. Ramos, J. Mertens, M. Calleja and J. Tamayo, Appl. Phys. Lett., 2008, 92, 173108 CrossRef.
- B. A. Bircher, H. P. Lang, L. Duempelmann, C. Gerber and T. Braun, Micro Nano Lett., 2013, 8, 770–774 CrossRef.
- O. Enders, F. Korte and H.-A. Kolb, Surf. Interface Anal., 2004, 36, 119–123 CrossRef CAS.
- S. Somnath, J. O. Liu, M. Bakir, C. B. Prater and W. P. King, Nanotechnology, 2014, 25, 395501 CrossRef PubMed.
- H. Asakawa and T. Fukuma, Rev. Sci. Instrum., 2009, 80, 103703 CrossRef PubMed.
- S. S. Lee and R. M. White, Sens. Actuators, A, 1996, 52, 41–45 CrossRef CAS.
- O. Cakmak, C. Elbuken, E. Ermek, A. Mostafazadeh, I. Baris, B. E. Alaca, I. H. Kavakli and H. Urey, Methods, 2013, 63, 225–232 CrossRef CAS PubMed.
- F. Padovani, J. Duffy and M. Hegner, Anal. Chem., 2017, 89, 751–758 CrossRef CAS PubMed.
- M. Heinisch, E. K. Reichel, I. Dufour and B. Jakoby, Procedia Eng., 2014, 87, 472–475 CrossRef.
- Z. Wu and X. Ma, Proc. R. Soc. A, 2016, 472, 20150728 CrossRef PubMed.
- C. Ramakrishan, A. Bieri, N. Sauter, S. Roizard, P. Ringler, S. A. Mueller, K. N. Goldie, K. Enimanev, H. Stahlberg, B. Rinn and T. Braun, BMC Bioinf., 2014, 15, 84 CrossRef PubMed.
- M. K. Ghatkesar, V. Barwich, T. Braun, J.-P. Ramseyer, C. Gerber, M. Hegner, H. P. Lang, U. Drechsler and M. Despont, Nanotechnology, 2007, 18, 445502 CrossRef.
- F. Duvigneau, S. Koch, R. Orszulik, E. Woschke and U. Gabbert, Technische Mechanik, 2016, 36, 180–189 Search PubMed.
- T. Thundat, R. J. Warmack, G. Y. Chen and D. P. Allison, Appl. Phys. Lett., 1994, 64, 2894–2896 CrossRef CAS.
- N. Strelnikova, F. Herren, C.-A. Schoenenberger and T. Pfohl, Front. Mater., 2016, 3, 2707 Search PubMed.
- P. Rust, I. Leibacher and J. Dual, Procedia Eng., 2011, 25, 587–590 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c8lc01343h |
| ‡ Current address: Federal Institute of Metrology, Lindenweg 50, Bern-Wabern, Switzerland E-mail: benjamin.bircher@metas.ch. |
| This journal is © The Royal Society of Chemistry 2019 |