 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Intramolecular multi-bond strain: the unrecognized side of the dichotomy of conjugated systems
Yirong
Mo
*ab,
Huaiyu
Zhang
ab,
Peifeng
Su
a,
Peter D.
Jarowski
*c and
Wei
Wu
*ad
aThe State Key Laboratory of Physical Chemistry of Solid Surfaces, Fujian Provincial Key Laboratory of Theoretical and Computational Chemistry and College of Chemistry and Chemical Engineering, Xiamen University, Xiamen, Fujian 361005, China
bDepartment of Chemistry, Western Michigan University, Kalamazoo, Michigan 49008, USA. E-mail: ymo@wmich.edu
cUniversity of Surrey, Advanced Technology Institute, Guildford, GU2 7XH, UK. E-mail: peterjarowski@gmail.com
diChEM, Xiamen University, Xiamen, Fujian 361005, China. E-mail: weiwu@xmu.edu.cn
First published on 20th May 2016
Abstract
Electron conjugation stabilizes unsaturated systems and diminishes the differences among bond distances. Experimentally, Kistiakowsky and coworkers first measured and noticed the difference between the hydrogenation heats of carbon–carbon double bonds in conjugated systems. For instance, the hydrogenation heat of butadiene is 57.1 kcal mol−1, which is less than two times that of the hydrogenation heat of 1-butene (30.3 kcal mol−1), and the difference (3.5 kcal mol−1) is the extra stabilization due to the resonance between two double bonds in the former, and is referred to as the experimental resonance energy. Following Kistiakowsky's definition, Rogers et al. studied the stepwise hydrogenation of 1,3-butadiyne and concluded that there is no conjugation stabilization in this molecule. This claim received objections instantly, but Rogers and coworkers further showed the destabilizing conjugation in 2,3-butanedione and cyanogen. Within resonance theory, the conjugation energy is derived “by subtracting the actual energy of the molecule in question from that of the most stable contributing structure.” The notable difference between the experimental and theoretical resonance energies lies in that the former needs other real reference molecules while the latter does not. Here we propose and validate a new concept, intramolecular multi-bond strain, which refers to the repulsion among π bonds. The π–π repulsion, which is contributed to by both Pauli exchange and electrostatic interaction, is quantified with the B4H2 model system (16.9 kcal mol−1), and is compared with the σ–σ repulsion in B2H4 (7.7 kcal mol−1). The significance of the π–π repulsion can be demonstrated by the much longer carbon–nitrogen bond in nitrobenzene (1.486 Å) than in aniline (1.407 Å), the very long and weak nitrogen–nitrogen bond (1.756 Å) in dinitrogen tetroxide, and the instability of long polyynes. This new concept successfully reconciles the discrepancy between experimental and theoretical conjugation energies. However, we maintain that by definition, electron conjugation must be stabilizing.
1. Introduction
Ever since the proposal of strain theory by Baeyer in 1885,1 the concept of molecular strain has been well accepted as one of the key factors influencing the preference of molecular conformations and reactivity.2–10 Strain energy is often derived as the difference between the experimental heat of formation for a strained molecule and the expected heat of formation for a hypothetical strain-free molecule with the same number of atoms which is derived from group contributions of additivity methods11,12 or ab initio computations.13,14 Strain is also addressed in terms of bond length, bond angle, torsional angle and noncovalent interactions. In general, molecular strain can be classified as either ring strain, such as in cyclopropane,14–19 or steric strain, such as in eclipsed ethane.20–25Different from destabilizing molecular strains, electron delocalization refers to the electron transfer from one moiety to another, and includes hyperconjugation and conjugation based on the symmetry of the orbitals involved. A notable example in this regard is conjugated linear molecules.26 By definition, electron delocalization must be a stabilizing factor, otherwise nature would choose an electron localized structure. This effect has been well recognized in conjugated systems such as graphene and conductive polymers and many organic pigments which are widely used in organo-luminescent devices and dye-sensitized solar cells. A conjugated system cannot be well described with a single Lewis structure where each bonding pair of electrons is localized on no more than two atoms and thus a resonance theory is needed.27,28 Theoretically, conjugation (resonance) energy can be derived “by subtracting the actual energy of the molecule in question from that of the most stable contributing structure”28 using ab initio valence bond (VB) theory.29–32 The popular molecular orbital (MO) theory, however, has difficulties in defining electron-localized states for references in the way VB theory does,33 though approximate approaches have been developed particularly in the study of electron transfer processes.34–38 Alternatively, other reference molecules have to be chosen and various isodesmic and homodesmotic model reactions need to be designed to estimate resonance energies,39 but the intrusion of other effects in the reference systems, such as strain, hyperconjugation, Coulomb repulsion imbalance, and uncompensated van der Waals (dispersion) attractions, has been recognized.40,41 Experimentally, Kistiakowsky and coworkers first measured and noticed the differences between the hydrogenation heats of the carbon–carbon double bonds in substituted and/or conjugated systems.42,43 For instance, the hydrogenation heat of butadiene is 57.1 kcal mol−1, which is less than two times the hydrogenation heat of 1-butene (30.3 kcal mol−1), and the difference (3.5 kcal mol−1) is the extra stabilization due to the resonance between two double bonds in the former, and is referred to as the Kistiakowsky resonance energy. The process can be expressed as the sequential hydrogenation in the following steps (in kcal mol−1)43
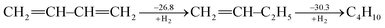 | (1) |
If we take ethylene instead of 1-butene as the reference, however, the difference would be 8.5 kcal mol−1.
Following Kistiakowsky's definition,42 Rogers et al. computationally studied the stepwise hydrogenation of 1,3-butadiyne as
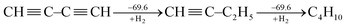 | (2) |
Rogers' claim that the conjugation stabilization in 1,3-butadiyne is zero received objections instantly.47–49 Jarowski et al. pointed out that there is significant hyperconjugation from the ethyl group to the triple bond (i.e., σ → π*) in 1-butyne.48 This stabilizing force leads to an underestimation of the conjugation with Kistiakowsky's definition. Jarowski et al. predicted conjugation energies of 9.3 kcal mol−1 for diynes and 8.2 kcal mol−1 for dienes. Based on the energy decomposition analysis between two fragments (˙C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CH and ˙CH
CH and ˙CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH2), Cappel et al. estimated the conjugative stabilization in 1,3-butadiyne (45.0 kcal mol−1) to be about twice the value of that in 1,3-butadiene (19.5 kcal mol−1).47 Nevertheless, Rogers et al. continued their work and showed the cases of 2,3-butanedione and cyanogen where the conjugation is even destabilizing, e.g.
CH2), Cappel et al. estimated the conjugative stabilization in 1,3-butadiyne (45.0 kcal mol−1) to be about twice the value of that in 1,3-butadiene (19.5 kcal mol−1).47 Nevertheless, Rogers et al. continued their work and showed the cases of 2,3-butanedione and cyanogen where the conjugation is even destabilizing, e.g.
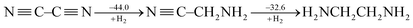 | (3) |
Rogers surmised that the lack of overall thermodynamic stabilization in polyynes is due to the repulsions among the six electrons of each triple bond.50 But this kind of interaction exists in ethyne as well and the extra stabilization in 1,3-butadiyne with reference to ethyne is still only 10.0 kcal mol−1.
A molecular structure results from a balance of repulsive and attractive forces. Electron delocalization is an electronic effect and concerns charge transfer from an occupied bond orbital to vicinal unoccupied anti-bond orbitals, while a steric effect reflects the interaction between neighbouring occupied bond orbitals, and generally comprises the classical electrostatic (e.g., local dipole–dipole interaction) term and quantum mechanical Pauli exchange repulsion. Thus, by definition, conjugation must be stabilizing. The seeming lack of stabilization or even destabilization found by Rogers et al. must result from a certain unrecognized repulsion. Here we propose and demonstrate a new concept, intramolecular multi-bond strain, as the source of significant repulsion among π bonds, which has not been well appreciated.
2. Synopsis
Multi-bond strain refers to the repulsion among conjugated π bonds or hyperconjugated σ–π bonds that, up until now, has not been identified with only the stabilizing conjugative or hyperconjugative interactions being generally recognized. The coexistence of the stabilizing and destabilizing forces can be better described by the following orbital interaction diagrams (Fig. 1). We consider two neighbouring π bonds on fragments A and B. The conjugation occurs between an occupied orbital (πA or πB) and the other moiety's virtual orbital (π*B or π*A) as shown in Fig. 1a. This has been the focal point for π conjugation, and ab initio valence bond (VB) methods,29–32,51 including our block-localized wavefunction (BLW)52–54 can evaluate the magnitude of this stabilizing effect. However, the interaction between occupied orbitals πA and πB cannot be neglected; this interaction is obviously repulsive and is usually termed steric repulsion (Fig. 1b). We emphasize that the steric effect is generally composed of both Pauli exchange repulsion and local dipole–dipole electrostatic interactions, and multi-bond strain exactly reflects this destabilizing factor. The overall π–π interaction results from both the stabilizing and destabilizing components, as shown in Fig. 1c. The relative stability of 1π versus the destability of 2π reflects Kistiakowsky's experimental resonance energy, whereas Fig. 1a highlights the Pauling–Wheland definition of theoretical resonance energy. Thus, the discrepancy between the experimental and theoretical definitions of resonance is the repulsion shown in Fig. 1b.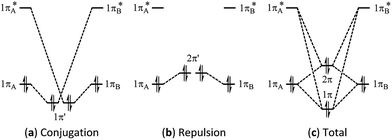 | ||
| Fig. 1 Orbital interaction diagrams showing (a) conjugation, (b) repulsion and (c) the sum of conjugation and repulsion in two symmetrical conjugated π bonds. | ||
3. Estimation of the repulsive interaction
Here we compare the relative σ–σ and π–π repulsions with model systems of linear B2H4 (ref. 55–57) and B4H2 at the B3LYP/6-311+G(d,p) level using the BLW method52–54 which is the simplest variant of ab initio valence bond (VB) theory. The reason that we chose boron systems here is that the boron atom is electron-deficient and thus we can strictly keep its certain p orbitals unoccupied and examine the evolution of repulsive interactions with little interference, while importantly, the neutrality of these systems is maintained, e.g., in planar B2H4, there is no π electron in the pπ orbitals. By keeping these pπ orbitals vacant,57 we rotate one BH2 group to the perpendicular conformation. The energy lowering in this process can be solely ascribed to the relief of the σ–σ repulsion between BH bonds (ΔEs in Fig. 2a). Computations show that the energy reduction is 7.7 kcal mol−1, accompanied by a boron–boron bond shortening of 0.057 Å. This energetics is considerably higher than the rotation barrier in ethane (2.7 kcal mol−1 at the same theoretical level) as there is still significant repulsion even in the latter's staggered conformation. We note that ΔEs is contributed to by both the Pauli repulsion and electrostatic repulsion as the BH bond is slightly polar. The introduction of the σ–π* hyperconjugative interaction would further shorten the BB bond and stabilize the perpendicular conformation by 7.5 kcal mol−1. In total the rotation barrier in B2H4 is 15.2 kcal mol−1.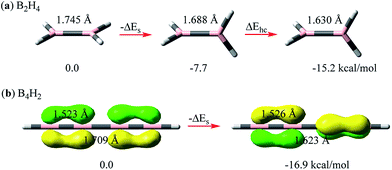 | ||
| Fig. 2 Energetic and structural changes along the rotation of interacting moieties (either σ or π bonds) from a parallel to perpendicular orientation for (a) B2H4 and (b) B4H2. | ||
Linear B4H2 (HB![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) B–B
B–B![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) BH) offers an interesting opportunity to directly probe the π–π repulsion with two localized π pairs that are either parallel or perpendicularly arranged. The ground state of linear B4H2 has two 4-center-2-electron (Π24) bonds, and if we strictly localize each pair on two terminal B–B bonds with the BLW method,52–54 we derive the localized state with two perpendicular π bonds (shown on the right side of Fig. 2b). The double bond and central single bond distances are 1.526 and 1.623 Å, respectively. Differently, we can also arrange the two π bonds in the same direction. This results in an enhanced repulsion between them and the strictly localized system is destabilized by 16.9 kcal mol−1. The comparison of B2H4 and B4H2 reveals that the π–π repulsion is possibly stronger than the σ–σ repulsion. Accordingly, the central B–B single bond stretches by 0.086 Å to 1.709 Å. This surprisingly high repulsion signifies the strain in all conjugated systems. The delocalization between the π bonds, much like in butadiene, stabilizes the system by 10.8 kcal mol−1 and shortens the central bond by 0.066 Å. Notably, since the π–π resonance stabilization in the Π44 state of B4H2 is less than the π–π repulsion, this molecule would exhibit destabilizing conjugation following eqn (3).
BH) offers an interesting opportunity to directly probe the π–π repulsion with two localized π pairs that are either parallel or perpendicularly arranged. The ground state of linear B4H2 has two 4-center-2-electron (Π24) bonds, and if we strictly localize each pair on two terminal B–B bonds with the BLW method,52–54 we derive the localized state with two perpendicular π bonds (shown on the right side of Fig. 2b). The double bond and central single bond distances are 1.526 and 1.623 Å, respectively. Differently, we can also arrange the two π bonds in the same direction. This results in an enhanced repulsion between them and the strictly localized system is destabilized by 16.9 kcal mol−1. The comparison of B2H4 and B4H2 reveals that the π–π repulsion is possibly stronger than the σ–σ repulsion. Accordingly, the central B–B single bond stretches by 0.086 Å to 1.709 Å. This surprisingly high repulsion signifies the strain in all conjugated systems. The delocalization between the π bonds, much like in butadiene, stabilizes the system by 10.8 kcal mol−1 and shortens the central bond by 0.066 Å. Notably, since the π–π resonance stabilization in the Π44 state of B4H2 is less than the π–π repulsion, this molecule would exhibit destabilizing conjugation following eqn (3).
It should also be pointed out that the π–π repulsion has been long implicated in the discussion of π-distortivity in benzene,58–63 the seminal example of aromaticity, notably by Shaik and Hiberty,64–67 who concluded that the π-electronic component of benzene prefers a localizing distortion with alternating bond lengths and the symmetrical structure with equal bonds is actually imposed by the σ electrons, though the π-electronic resonance necessarily stabilizes the system. Their concept of the dual character of conjugated systems is generally reflected in Fig. 1. In other words, the nature of the distortive tendency of the π-component in benzene results from the π–π repulsion among the three π bonds in the Kekulé structure.
4. Indicators of the π–π repulsion
The magnitude of the stabilizing conjugation effect can be evaluated with the reference of the most stable resonance structure which can be well defined using VB theory. The estimation of the intramolecular repulsion, however, seems challenging as there is no obvious reference. This is unlike the study of intermolecular interactions where we take the separated monomers as the reference state, but at least for the model molecule B4H2, we can retain the molecular structure but change its electronic structure, and derive the localized orbital energies. When the two localized orbitals are perpendicular to each other (shown on the right side of Fig. 2b), we assign their orbital energies to 1πA (or 1πB), as shown in Fig. 1. When the two localized orbitals are parallel to each other, their energies will be pushed up as 2π′ due to repulsion, as shown in the middle of Fig. 1. The energy difference ΔEorb between 1πA and 2π′ thus measures the strength of repulsion, and so is the overall energy difference ΔEs between the two electronic states. Fig. 3 shows the correlations of ΔEorb and ΔEs with the variation of the central BB bond distance.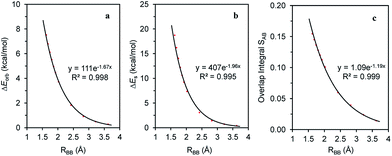 | ||
| Fig. 3 Correlations of (a) ΔEorb; (b) ΔEs and (c) overlap integral S12 with the central BB bond distance in the B4H2 model system. | ||
Fig. 3 shows the excellent exponential correlation of the energy terms with the bond distance. Considering that the energy terms are implicated by both the Pauli exchange and electrostatic interaction and the consensus that the Pauli repulsion increases exponentially as atomic wavefunctions decay exponentially,68 we speculate that in B4H2 the π–π repulsion is largely contributed to by the Pauli exchange repulsion. In addition, Fig. 3 indicates a linear relationship between the orbital energy difference (ΔEorb) and the steric energy (ΔEs). As expected, the overlap integral between the two π orbitals in the parallel orientation (1πA and 1πB in Fig. 1) is a good indicator of the steric repulsion in this case as a similar exponential correlation with the distance can be found (Fig. 3c).
5. Conjugation and repulsion in butadiene (1), butadiyne (2), cyanogen (3) and α-dicarbonyl (4)
We first compare the resonance in the two most typical conjugated systems, butadiene and butadiyne. A comparison of the DFT and BLW optimizations shows that the localization of π electrons on their respective multiple bonds considerably stretches the central CC bonds by 0.071 and 0.101 Å, respectively for 1 and 2, and the optimal distances reflect the intrinsically shorter Csp–Csp (1.465 Å) versus Csp2–Csp2 (1.528 Å) single σ bonds. In the meantime, the deactivation of resonance modestly shortens the double and triple bond lengths which are essentially the same as the bond distances in ethylene (1.329 Å) and acetylene (1.199 Å) at the same B3LYP/6-311+G(d,p) level. Theoretically, there are two types of resonance energies, namely vertical resonance energy (VRE) and adiabatic resonance energy (ARE). The former is the energy difference between DFT and BLW computations of the same structure, while the latter is the energy difference between the optimal delocalized state (i.e., DFT optimization) and the optimal localized state (i.e., BLW optimization). Fig. 4 shows the change in VRE along the central CC bond distance in the conjugated systems studied in this work. Much like in Fig. 3, there is an excellent exponential correlation between VRE and the central bond distance in each molecule.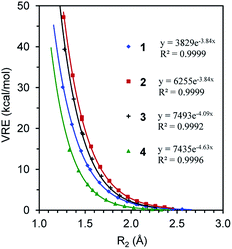 | ||
| Fig. 4 The exponential correlation of vertical resonance energy (VRE) with the central CC bond distance (R2) in butadiene (1), butadiyne (2), cyanogen (3) and α-dicarbonyl (4). | ||
In the DFT optimized geometries, the VRE of butadiyne (32.9 kcal mol−1) is a little more than two times that of the value in butadiene (14.5 kcal mol−1). This is in agreement with the studies by Kollmar,46 and Cappel et al.,47 and consistent with the facts that the central bond in butadiyne is shorter than in butadiene and there are two Π44 bonds in the former but only one in the latter. The ARE is supposed to be comparable to experimental resonance energies with reference to individual multiple bonds such as ethylene and acetylene. However, isodesmic reactions show that the experimental resonance energies (EREs) for butadiene (8.5 kcal mol−1) and butadiyne (10.0 kcal mol−1) are not only similar but also considerably lower than the theoretical AREs (12.6 and 27.0 kcal mol−1 for 1 and 2, respectively). If we take the difference between ARE and ERE as the steric contribution, the steric repulsion in butadiene and butadiyne are 4.1 and 18.8 kcal mol−1 respectively. The latter is much more than two times the former, due to the much shortened central CC bond distance, and the repulsive force increases exponentially along the distance (Fig. 3). It should be noted that our AREs are very close to the evaluations of conjugation stabilization (14.8 and 27.1 kcal mol−1) in butadiene and butadiyne by Wodrich et al. who reinterpreted the differences in the hydrogenations of the first and second multi-bond in eqn (1) and (2) after introducing the “protobranching” concept.69
One way to estimate the intramolecular steric repulsion ΔEs is the compression energy,28 which is the difference between the VRE of the optimal DFT structure and the ARE and reflects the energy cost for the structural change (dominated by the central CC single bond variation ΔR2) when conjugation is deactivated. Here we propose a force constant k to evaluate and compare the magnitude of the intramolecular steric repulsion
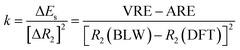 | (4) |
Table 1 shows that butadiyne has a much higher k value than butadiene. Of course, k measures the change of repulsion with the distance, i.e., the repulsive force, rather than the absolute energetic value of the steric repulsion. While the π–π repulsion considerably offsets the theoretical resonance energy (ARE) and leads to the experimental resonance energy (ERE), the repulsion in butadiyne is much stronger than in butadiene. In the end, both molecules exhibit comparable EREs, and interestingly, as found by Rogers et al.,44,45 there is zero thermodynamic conjugation stabilization in butadiyne.
| Molecule | State | R 1 | R 2 | VRE | ARE | ERE | k |
|---|---|---|---|---|---|---|---|
| a Reaction enthalpy at 298 K. | |||||||
| Butadiene | DFT | 1.338 | 1.457 | 14.5 | 12.6 | 8.5 | 382 |
| BLW | 1.326 | 1.528 | 10.9 | ||||
| Butadiyne | DFT | 1.207 | 1.364 | 32.9 | 27.0 | 10.0 | 589 |
| BLW | 1.194 | 1.465 | 22.2 | ||||
| Cyanogen | DFT | 1.155 | 1.376 | 27.2 | 22.7 | −4.3a | 576 |
| BLW | 1.145 | 1.467 | 18.9 | ||||
| α-Dicarbonyl | DFT | 1.203 | 1.529 | 6.3 | 5.6 | 4.3a | 380 |
| BLW | 1.196 | 1.583 | 4.9 | ||||
We further look at the cases of cyanogen (3) and α-dicarbonyl (4) where Rogers et al. showed even thermodynamic destabilization.70 Indeed, we confirmed a reduced conjugation stabilization in both systems, compared with butadiyne and butadiene, respectively. The central CC bond in cyanogen is 0.012 Å longer than that in butadiyne. But when π electrons are localized, the optimal central bond lengths are quite similar (1.465 versus 1.467 Å) and correspond to the Csp–Csp single σ bond. This suggests a stronger repulsion between the triple bonds in cyanogen than in butadiyne, most likely due to the polarity of the CO π bonds which lead to dipole–dipole electrostatic repulsion. In fact, if we use the isodesmic reaction eqn (5) to measure the experimental resonance energy, we find that the ERE is even negative at the G3 theoretical level. This is consistent with eqn (3) where the hydrogenation of the first cyano group is more exothermic than the hydrogenation of the second cyano group. The stretched central C–C bond in α-dicarbonyl is an example where the π–π electrostatic repulsion plays a big role.
 | (5) |
 | (6) |
Electron density difference (EDD) maps can be used to directly visualize the resonance, as the electron density difference between the electron-localized state (BLW) and the electron-delocalized state (DFT) reflects the movement of electron density. Fig. 5 plots the EDD maps of the four conjugated systems studied here. The orange color means a gain of electron density while the cyan color shows a loss of electron density. Following the conventional view, resonance moves the π electron density from multiple bonds to the linking single bonds, leading to the significant shortening of the central bonds.
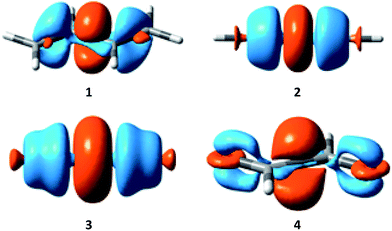 | ||
| Fig. 5 Electron density difference (EDD) maps showing the resonance in butadiene (1), butadiyne (2), cyanogen (3) and α-dicarbonyl (4). | ||
6. Conclusion
Conjugation has been associated with high stability, planarity, small bond length alternation and many other physicochemical properties such as the bathochromic shift and lifetime of excited states. However, this is only one side of the story and concomitantly there is significant repulsion between π bonds which has not been well-recognized. In other words, while conjugation results in the stabilization of a conjugated system, the stability of the system is not solely determined by the conjugation, and there is intramolecular π–π repulsion which counteracts the stabilizing forces. This unrecognized repulsion is the culprit for the findings that conjugation has no stability or even is destabilizing. Considering that “strain, in a general sense, represents a cornerstone of the 150 year old field of conformational analysis”,71 here we propose the concept of intramolecular multi-bond strain to recognize the π–π repulsion. The magnitude of the π–π repulsion can be quantitatively assessed with the linear B4H2 (16.9 kcal mol−1), in comparison with the σ–σ repulsion in B2H4 (7.7 kcal mol−1). This new concept thus elucidates the difference between experimental and theoretical conjugation energies, although by definition, conjugation or resonance must be stabilizing.Although quantum Pauli exchange repulsion is the primary cause for the π–π repulsion when the π bonds are nonpolar, local dipole–dipole repulsion can contribute and sometimes even dominate the π–π repulsion in cases with polarized π electron densities. The strong π–π repulsion is also implicated in numerous experimental findings. One notable example is the much longer carbon–nitrogen bond in nitrobenzene (1.486 Å) than in aniline (1.407 Å). Due to the resonance of the lone nitrogen pair to more electronegative oxygen atoms in the nitro group, there is a significant π dipole, which repels the π electron density in the benzene ring via both Pauli exchange and electrostatic interactions, leading to a long carbon–nitrogen bond in nitrobenzene.72 In fact, the strong π–π electrostatic repulsion, as shown by the much longer central C–C bond distance in α-dicarbonyl than in butadiene when conjugation is quenched (Table 1), is the major culprit for the remarkably stretched nitrogen–nitrogen bond in the weakly bound dinitrogen tetroxide (1.756 Å) compared with the single bond in hydrazine (1.47 Å).73 With both the electrostatic and Pauli repulsion deactivated, the nitrogen–nitrogen bond in dinitrogen tetroxide can be dramatically shortened to 1.471 Å as optimized by the BLW method at the B3LYP/6-311+G(d,p) level.72 The well-recognized instability of long polyynes should be contributed to by the strong intramolecular multi-bond strain as well.74–77
7. Methodology
The block-localized wavefunction (BLW) method originates from ab initio valence bond (VB) theory as it simplifies the original Heitler–London–Slater–Pauling (HLSP) function to a BLW of only one Slater determinant form with block-localized MOs. Orbitals in the same subspace are subject to the orthogonality constraint, but orbitals belonging to different subspaces are nonorthogonal. Thus, the BLW method combines the advantages or features of both MO and VB theories. In general, for an electron-localized state which is usually the most stable resonance structure, we partition the system to k blocks and define its wavefunction with a BLW (here we assume that the number of electrons in each block is even (equal to 2ni) and thus orbitals are doubly occupied) as| ΨBLW = det|φ112φ122…φ1n12…φi12…φini2…φknk2| = Â[Φ1…Φi…Φk] | (7) |
| Φi = Â[φi12φi22…φini2] | (8) |
| RE = E(ΨBLW) − E(ΨDFT) | (9) |
Geometry optimizations and calculations for adiabatic states with the regular DFT and diabatic states with the BLW method were performed with our in-house version of the quantum mechanical software GAMESS.78
Acknowledgements
This work was supported by the US National Science Foundation under the grant CNS-1126438 and a grant from the Faculty Research and Creative Activities Award (FRACAA), Western Michigan University (WMU). HZ acknowledges the financial support from the China Scholarship Council (CSC). WW is grateful for the funding from the National Science Foundation of China (20873106) and the Ministry of Science and Technology of China (2011CB808504). PDJ would like to thank the EPSRC National Service for Computational Chemistry Software (NSCCS) at Imperial College London for the use of their computing facility.Notes and references
- A. Baeyer, Ber. Dtsch. Chem. Ges., 1885, 18, 2269–2281 CrossRef.
- P. v. R. Schleyer, J. E. Williams and K. R. Blanchard, J. Am. Chem. Soc., 1970, 92, 2377–2386 CrossRef CAS.
- J. F. Liebman and A. Greenberg, Strained Organic Compounds, Academic Press, New York, 1978 Search PubMed.
- K. Wiberg, Angew. Chem., Int. Ed., 1986, 25, 312–322 CrossRef.
- A. de Meijere, Angew. Chem., Int. Ed., 1979, 18, 809–826 CrossRef.
- J. Michl and J. Gladysz, Chem. Rev., 1989, 89, 973 CrossRef.
- K. B. Wiberg, in Reactive Intermediate Chemistry, ed. R. A. Moss, M. S. Platz and M. Jones, John Wiley & Sons, Inc, Hoboken, NJ, USA, 2003 Search PubMed.
- B. M. Gimarc and M. Zhao, Coord. Chem. Rev., 1997, 158, 385–412 CrossRef CAS.
- M. D. Newton, in Applications of Electronic Structure Theory, ed. H. F. Schaefer III, Springer, US, New York, 1977, pp. 223–275 Search PubMed.
- B. Pinter, T. Fievez, F. M. Bickelhaupt, P. Geerlings and F. De Proft, Phys. Chem. Chem. Phys., 2012, 14, 9846–9854 RSC.
- J. L. Franklin, Ind. Eng. Chem., 1949, 41, 1070–1076 CrossRef CAS.
- E. M. Engler, J. D. Andose and P. v. R. Schleyer, J. Am. Chem. Soc., 1973, 95, 8005–8025 CrossRef CAS.
- T. Dudev and C. Lim, J. Am. Chem. Soc., 1998, 120, 4450–4458 CrossRef CAS.
- D. Barić and Z. B. Maksić, Theor. Chem. Acc., 2005, 114, 222–228 CrossRef.
- A. Greenberg and J. Liebman, Strained Organic Molecules, Academic Press, New York, 1978 Search PubMed.
- D. Cremer and E. Kraka, in Molecular Structure and Energetics, Structure and Reactivity, ed. J. F. Liebman and A. Greenberg, VCH Publishers, Deerfield Beach, USA, 1988, vol. 7, p. 65 Search PubMed.
- A. Meijere, Angew. Chem., Int. Ed., 1979, 18, 809–826 CrossRef.
- P. v. R. Schleyer, in Substituent Effects in Radical Chemistry, ed. H. G. Viehe, Z. Janousek and R. Merenyi, Nato ASI Series C-189, Reidel, Dordrecht, 1986, pp. 69–81 Search PubMed.
- W. Wu, B. Ma, J. Wu, P. v. R. Schleyer and Y. Mo, Chem.–Eur. J., 2009, 15, 9730–9736 CrossRef CAS PubMed.
- F. M. Bickelhaupt and E. J. Baerends, Angew. Chem., Int. Ed., 2003, 42, 4183–4188 CrossRef CAS PubMed.
- Y. Mo and J. Gao, Acc. Chem. Res., 2007, 40, 113–119 CrossRef CAS PubMed.
- Y. Mo, W. Wu, L. Song, M. Lin, Q. Zhang and J. Gao, Angew. Chem., Int. Ed., 2004, 43, 1986–1990 CrossRef CAS PubMed.
- V. Pophristic and L. Goodman, Nature, 2001, 411, 565–568 CrossRef CAS PubMed.
- F. Weinhold, Angew. Chem., Int. Ed., 2003, 42, 4188–4194 CrossRef CAS.
- S. Liu, J. Chem. Phys., 2007, 126, 244103 CrossRef PubMed.
- C. H. Hendon, D. Tiana, A. T. Murray, D. R. Carbery and A. Walsh, Chem. Sci., 2013, 4, 4278–4284 RSC.
- L. C. Pauling, The Nature of the Chemical Bond, Cornell University Press, Ithaca, NY, 1960 Search PubMed.
- G. W. Wheland, The Theory of Resonance, John Wiley & Sons, New York, 1944 Search PubMed.
- Valence Bond Theory, ed. D. L. Cooper, Elsevier, Amsterdam, 2002 Search PubMed.
- G. A. Gallup, Valence Bond Methods: Theory and Applications, Cambridge University Press, New York, 2002 Search PubMed.
- S. S. Shaik and P. C. Hiberty, A Chemist's Guide to Valence Bond Theory, Wiley, Hoboken, New Jersey, 2008 Search PubMed.
- W. Wu, P. Su, S. Shaik and P. C. Hiberty, Chem. Rev., 2011, 111, 7557–7593 CrossRef CAS PubMed.
- M. J. S. Dewar and H. N. Schmeising, Tetrahedron, 1959, 5, 166–178 CrossRef CAS.
- T. Ziegler and A. Rauk, Theor. Chem. Acc., 1977, 46, 1–10 CrossRef CAS.
- T. Pacher, L. S. Cederbaum and H. Köppel, J. Chem. Phys., 1988, 89, 7367–7381 CrossRef CAS.
- M. D. Newton, Int. J. Quantum Chem., 2000, 77, 255–263 CrossRef CAS.
- A. A. Voityuk and N. Rösch, J. Chem. Phys., 2002, 117, 5607–5616 CrossRef CAS.
- Q. Wu and T. Van Voorhis, J. Chem. Theory Comput., 2009, 2, 765–774 CrossRef PubMed.
- W. J. Hehre, L. Radom, P. v. R. Schleyer and J. A. Pople, Ab Initio Molecular Orbital Theory, Wiley, New York, 1986 Search PubMed.
- M. K. Cyranski, P. v. R. Schleyer, T. M. Krygowski, H. Jiao and G. Hohlneicher, Tetrahedron, 2003, 59, 1657–1665 CrossRef CAS.
- S. W. Slayden and J. F. Liebman, Chem. Rev., 2001, 101, 1541–1566 CrossRef CAS PubMed.
- G. B. Kistiakowsky, J. R. Ruhoff, H. A. Smith and W. E. Vaughan, J. Am. Chem. Soc., 1936, 58, 146–153 CrossRef CAS.
- J. B. Conant and G. B. Kistiakowsky, Chem. Rev., 1937, 20, 181–194 CrossRef CAS.
- D. W. Rogers, N. Matsunaga, A. A. Zavitsas, F. J. McLafferty and J. F. Liebman, Org. Lett., 2003, 5, 2373–2375 CrossRef CAS PubMed.
- D. W. Rogers, N. Matsunaga, F. J. McLafferty, A. A. Zavitsas and J. F. Liebman, J. Org. Chem., 2004, 69, 7143–7147 CrossRef CAS PubMed.
- H. Kollmar, J. Am. Chem. Soc., 1979, 101, 4832–4840 CrossRef CAS.
- D. Cappel, S. Tüllmann, A. Krapp and G. Frenking, Angew. Chem., Int. Ed., 2005, 44, 3617–3620 CrossRef CAS PubMed.
- P. D. Jarowski, M. D. Wodrich, C. S. Wannere, P. v. R. Schleyer and K. N. Houk, J. Am. Chem. Soc., 2004, 126, 15036–15037 CrossRef CAS PubMed.
- F. Feixas, E. Matito, J. Poater and M. Solà, J. Phys. Chem. A, 2011, 115, 13104–13113 CrossRef CAS PubMed.
- D. W. Rogers, A. Z. Zavitsas and N. Matsunaga, J. Chem. Educ., 2010, 87, 1357–1359 CrossRef CAS.
- D. L. Cooper, J. Gerratt and M. Raimondi, Nature, 1986, 323, 699–701 CrossRef CAS.
- Y. Mo, in The Chemical Bond: Fundamental Aspects of Chemical Bonding, ed. G. Frenking and S. Shaik, Wiley-VCH, Weinheim, Germany, 2014 Search PubMed.
- Y. Mo and S. D. Peyerimhoff, J. Chem. Phys., 1998, 109, 1687–1697 CrossRef CAS.
- Y. Mo, L. Song and Y. Lin, J. Phys. Chem. A, 2007, 111, 8291–8301 CrossRef CAS PubMed.
- M. A. Vincent and H. F. Schaefer III, J. Am. Chem. Soc., 1981, 103, 5677–5680 CrossRef CAS.
- I. Demachy and F. Volatron, J. Phys. Chem., 1994, 98, 10728–10734 CrossRef CAS.
- Y. Mo and Z. Lin, J. Chem. Phys., 1996, 105, 1046–1050 CrossRef CAS.
- H. C. Longuet-Higgins and L. Salem, Proc. R. Soc. London, Ser. A, 1959, 251, 172–185 CrossRef CAS.
- R. S. Berry, J. Chem. Phys., 1961, 35, 2253–2254 CrossRef CAS.
- C. A. Coulson and W. T. Dixon, Tetrahedron, 1962, 17, 215–228 CrossRef CAS.
- G. Binsch, E. Heilbronner and J. N. Murrell, Mol. Phys., 1966, 11, 305–320 CrossRef CAS.
- S. S. Shaik and R. Bar, Nouv. J. Chim., 1984, 8, 411–420 CAS.
- K. Jug and A. M. Köster, J. Am. Chem. Soc., 1990, 112, 6772–6777 CrossRef CAS.
- S. S. Shaik and P. C. Hiberty, J. Am. Chem. Soc., 1985, 107, 3089–3095 CrossRef CAS.
- P. C. Hiberty, D. Danovich, A. Shurki and S. Shaik, J. Am. Chem. Soc., 1995, 117, 7760–7768 CrossRef CAS.
- S. S. Shaik, P. C. Hiberty, J. M. Lefour and G. Ohanessian, J. Am. Chem. Soc., 1987, 109, 363–374 CrossRef CAS.
- S. Shaik, A. Shurki, D. Danovich and P. C. Hiberty, Chem. Rev., 2001, 101, 1501–1539 CrossRef CAS PubMed.
- R. A. Buckingham, Proc. R. Soc. London, Ser. A, 1938, 168, 264–283 CrossRef CAS.
- M. D. Wodrich, C. S. Wannere, Y. Mo, P. D. Jarowski, K. N. Houk and P. v. R. Schleyer, Chem. Eur. J., 2007, 13, 7731–7744 CrossRef CAS PubMed.
- A. Z. Zavitsas, D. W. Rogers and N. Matsunaga, Aust. J. Chem., 2011, 64, 390–393 CrossRef CAS.
- J. F. Gonthier, S. N. Steinmann, M. D. Wodrich and C. Corminboeuf, Chem. Soc. Rev., 2012, 41, 4671–4687 RSC.
- H. Zhang, X. Jian, W. Wu and Y. Mo, Phys. Chem. Chem. Phys., 2016, 18, 11821–11828 RSC.
- S. S. Wesolowski, J. T. Fermann, T. D. Crawford and H. F. Schaefer III, J. Chem. Phys., 1997, 106, 7178–7184 CrossRef CAS.
- F. Cataldo, Fullerenes, Nanotubes, Carbon Nanostruct., 2004, 12, 633–646 CrossRef CAS.
- F. Cataldo, Polym. Degrad. Stab., 2006, 91, 317–323 CrossRef CAS.
- D. Heymann, Carbon, 2005, 43, 2235–2242 CrossRef CAS.
- S. Szafert and J. A. Gladysz, Chem. Rev., 2003, 103, 4175–4205 CrossRef CAS PubMed.
- M. W. Schmidt, K. K. Baldridge, J. A. Boatz, S. T. Elbert, M. S. Gordon, J. J. Jensen, S. Koseki, N. Matsunaga, K. A. Nguyen, S. Su, T. L. Windus, M. Dupuis and J. A. J. Montgomery, J. Comput. Chem., 1993, 14, 1347–1363 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2016 |
