Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Metal carbonyl complexes of phosphaamidines. Coordinative integrity detected in C-amino(λ3,σ2)-phosphaalkene isomers coordinated through n(P) HOMO−1 donor orbitals†
Jason D.
Masuda
a and
René T.
Boeré
*b
aDepartment of Chemistry, Saint Mary's University, Halifax, Nova Scotia, Canada B3H 3C2
bDepartment of Chemistry and Biochemistry, University of Lethbridge, Lethbridge, Alberta, Canada T1K 3M4. E-mail: boere@uleth.ca; Fax: +403-329-2057; Tel: +403-329-2045
First published on 5th October 2015
Abstract
Metal(0) complexes L(Cr,Mo,W)(CO)5 have been prepared from 1,3-bis(2,6-diisopropylphenyl)-2-(4-methylphenyl)-3-aza-1(λ3,σ2)-phosphapropene and 1,3-bis(2,6-diisopropylphenyl)-2-(4-methoxyphenyl)-3-aza-1(λ3,σ2)-phosphapropene using standard methods. Full characterization of four products and crystal structures of these complexes as well as the methoxyphenyl-phosphapropene are reported. The ligands coordinate κP, common for simple phosphaalkenes, despite the strongly-perturbing amino substitution at the double bond C atoms. Analyses of the NMR and vibrational spectroscopic data reveal that the complexes have very similar character to similarly-coordinated phosphaalkenes, with strong σ-donor character. The presence of some net π-interactions (acceptor or donor) is indicated by structures in which the ligands coordinate fully eclipsed with the M–CO groups. The synthetic and structural results have been augmented by B3PW91/LANL2DZ calculations that reproduce the structures of the Cr complexes accurately. The calculated vibrational spectra are used to confirm the assignment of the ν(C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) O) vibrational data. Detailed orbital interaction diagrams based on DFT calculations are reported for the title complexes as well as for the Cr(CO)5 complex of Mes–P
O) vibrational data. Detailed orbital interaction diagrams based on DFT calculations are reported for the title complexes as well as for the Cr(CO)5 complex of Mes–P![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CPh2. The electronic absorption spectra of the title complexes have intense low-energy absorptions ranging from 24
CPh2. The electronic absorption spectra of the title complexes have intense low-energy absorptions ranging from 24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 to 25
500 to 25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 300 cm−1, which can be interpreted qualitatively using the DFT results.
300 cm−1, which can be interpreted qualitatively using the DFT results.
Introduction
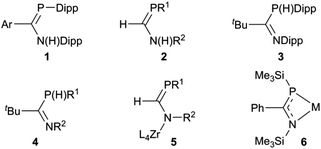
Interest in P(III) monophosphaamidine‡ chemistry has increased greatly in recent years after languishing for a long time since the initial discoveries by Issleib et al. at the dawn of phosphorus–carbon multiple bond chemistry.1,2 In 2004 we published the first modern results on an N,P-disubstituted aryl phosphaamidine 1 (Chart 1) and demonstrated that it could be deprotonated with lithium and potassium reagents; crystal structures of the neutral phosphaamidine and the two metal derivatives were reported.3 Song et al. reported the first phosphorus derivative of formamidine 2 (H on the C backbone) including a lithium complex with a structure similar to ours (and also provided a nice survey of much of the older literature).4 Thereafter, Li et al. reported the synthesis of a new exemplar 3 with tBu on the backbone with crystal structures of Li, K and Tl derivatives.5 Most recently, van Dijk et al. have reported several additional examples of such phosphaamidines 4, all with backbone tBu and various aromatic groups on N and P, as well as some lithium and rhodium complexes.6 In parallel with these reports using conventional synthesis followed by complexation of deprotonated anions, Waterman has reported the elegant assembly of phosphaformamidinate complexes 5 from precursors coordinated to a zirconium scorpionate framework.7–9 His group also recently reported the first example of a coordinated arsaformamidinate.10 Several examples of the NCP unit 6, i.e. 1,3-azaphosphaallyls of Mg, Ca, Sr, Ba, Li and Sn have been prepared by silyl migration (the N and P substituents are thereby always a TMS group).11,12 This recent work follows on a more extensive exploration by many workers on metal complexes of tri-substituted analogues which lack an ionisable H atom and hence tend to be prepared exclusively in one tautomeric form,13–18 including conventional phosphaalkenes,19–31 phosphacumulenes,32–40 alkoxy- (“Becker”) phosphaalkenes R′PC(R)OR′′,41–44 aminophosphaalkenes R′PC(R)NR′′2 (ref. 45–48) and diaminophosphaalkenes R′PC(NR′′2)2.49 The latter three types are sometimes referred to as ‘polarized phosphaalkenes’ or as having ‘reverse electron demand’ compared to R′P![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CR2 and R′P
CR2 and R′P![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CRR′′.50,51
CRR′′.50,51
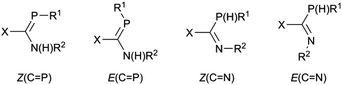
Our entry into this field of research was from organic amidinates which can be tuned with a wide variety of substituents R, R′ and R′′ in the R′NC(R)NR′′ positions, and can be synthesised by many routes, of which the deprotonation of R′NC(R)NHR′′ is the most common and the most versatile.52 Thus after preparing a series of amidines 7 using the bulky 2,6-diisopropylphenyl (Dipp) group for R′ and R′′ with R = aryl, methyl or trifluoromethyl on the carbon backbone (see Scheme 1),53–55 our aim is to prepare and investigate phosphaamidines that are exact molecular copies exchanging only N for P.
We also reported (Scheme 1) that amidines 7 react with Mo(CO)6 under thermal conditions to give the η6-aryl coordinated Mo(CO)3 complexes 8 as the only stable metal derivatives (that is, zero-valent Mo prefers the electron-rich aromatic ring to N atom coordination).53,54 By contrast, less-bulky amidines react under similar conditions to afford L4M2 “lantern” amidinate complexes via a redox reaction.56 Once the corresponding phosphaamidines 1 were in hand, we wanted to know how these would react with M(CO)6. Unlike common R3P ligands, 1 have a choice between side-on (κ2P,C) coordination of the P![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C double bond and the n(P) orbital (κP).
C double bond and the n(P) orbital (κP).
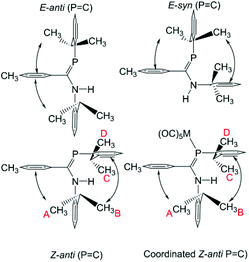
A second motivation for this study relates to the propensity of 1 to isomerize in solution. This issue will be the subject of a separate publication,57 but briefly it is found that for some combinations of substituents X, R1 and R2, pure samples dissolve to give up to four different interchanging solution species, and there is evidence that these include the expected E/Z isomers at the double bonds as well as C-amino-(λ3,σ2)-aminophosphaalkene/C-(λ3,σ3)-phosphinoimine tautomers (Scheme 2). It was thus of interest to see what effect coordination to metals will have on species prone to such an isomerization; LM(CO)5 complexes of Cr, Mo and W have an extensive history for the stabilization of reactive low-coordinated main group compounds.19–49
Synthesis of LM(CO)5 complexes
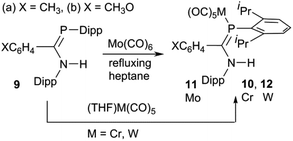
The phosphaamidines 9 were synthesized as reported in the literature.3,57 The molybdenum complexes 11 were prepared by a thermal reaction of 9 with Mo(CO)6 in refluxing n-heptane (Scheme 3), conditions previously shown to be suitable for the reactions of 7 (Scheme 1).53 Over the course of 4–8 h, the solution IR bands of aliquots taken from the reaction mixture slowly lost bands from Mo(CO)6 and were replaced by a new pattern diagnostic of LMo(CO)5. The reaction was stopped when the hexacarbonyl peak no longer decreased; meanwhile the solution turned from colourless to bright yellow-green. Direct cooling of these yellow solutions produced a reasonable yield of crystalline solids that could be recrystallized from the same solvent to afford analytically pure materials that were also suitable for crystallography. Similar direct thermal reactions of Cr(CO)6 and W(CO)6 do not go to completion and on prolonged heating lead to decomposition rather than the desired products. LM(CO)5 complexes 10 and 12 were instead obtained by a reaction with photochemically produced (THF)M(CO)5 at room temperature in THF as the solvent.58 The ligands readily displace THF to form the products. After the reaction was judged complete based on solution FTIR aliquots, the THF was removed and the products recrystallized from THF or diethyl ether.Crystal structures
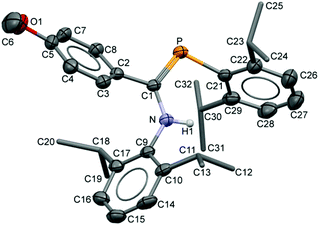
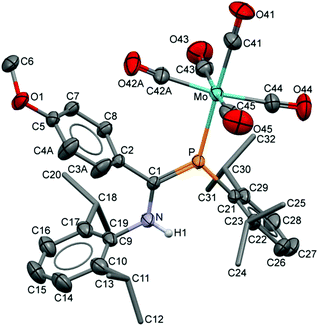
The compositions of the ligands 9 and their M(CO)5 complexes 10–12 have been confirmed by using single-crystal X-ray structures, all determined on an area-detector diffractometer at RT. The structure of 9a was previously published.3 The molecular structure with the atom numbering scheme of 9b is presented in Fig. 1. As the Cr, Mo and W complexes of 9a are isostructural, only the molecular structure of 10 is presented in Fig. 2 with the common atom numbering scheme (for 11a and 12, see Fig. S1 and S2 in the ESI†). The major component of the disorder model for the molecular structure of 11b is presented in Fig. 3. Selected interatomic distances and angles are shown in Table 1 whilst the crystal and parameter data are found in Table S3.† None of the structures have significant inter-molecular contacts and in particular neither the ligands nor the metal complex display conventional hydrogen bonding involving the NH group.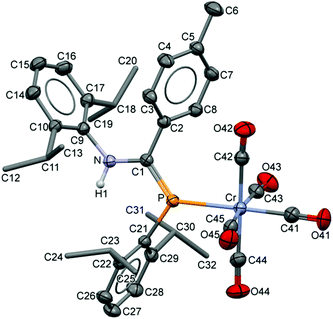 | ||
| Fig. 2 Displacement ellipsoid plot (30% probability) of the molecular structure of 10 as found in the crystal structure (295 K). The atom numbering scheme is provided; H atoms on C are omitted and the iPr C are rendered as tubes for clarity. The isostructural Mo and W complexes use the same numbering scheme (Fig. S1 and S2†). | ||
| Parameter | 9a | 9b | 10 | 10 (DFT)b | 11a | 11b | 12 |
|---|---|---|---|---|---|---|---|
| a Ref. 3. b Geometry optimized B3PW91/LANL2DZ hybrid DFT calculations, confirmed to have zero imaginary frequencies (Fig. S4). c Plane 1: C21,P,C1,N,C9; plane 2: C2,C3,C4,C5,C7,C8. d Plane 3: C9,C10,C14,C15,C16,C17. e Plane 4: C21,C22,C26,C27,C28,C29. f C1–P–Mo–C42A; for C1–P–Mo–C42B, 18.9(5)°. | |||||||
| P–C1 | 1.709(2) | 1.716(2) | 1.701(2) | 1.771 | 1.7031(19) | 1.697(2) | 1.706(5) |
| N–C1 | 1.367(3) | 1.365(3) | 1.361(3) | 1.372 | 1.365(3) | 1.362(4) | 1.346(8) |
| C1–C2 | 1.488(3) | 1.480(3) | 1.484(3) | 1.486 | 1.488(3) | 1.485(3) | 1.477(8) |
| P–C21 | 1.847(2) | 1.849(2) | 1.834(2) | 1.896 | 1.839(2) | 1.837(3) | 1.834(6) |
| N–C9 | 1.430(3) | 1.434(3) | 1.447(3) | 1.452 | 1.442(2) | 1.446(3) | 1.441(7) |
| N–H1 | 0.860 | 0.87(2) | 0.86(3) | 1.018 | 0.83(2) | 0.856(18) | 0.88(2) |
| P–M | — | — | 2.4259(7) | 2.507 | 2.5612(6) | 2.5559(8) | 2.5378(16) |
| M–C41 | — | — | 1.845(3) | 1.824 | 1.984(3) | 1.967(4) | 1.982(7) |
| M–C42 | — | — | 1.905(3) | 1.872 | 2.059(3) | 2.056(9) | 2.034(7) |
| M–C43 | — | — | 1.905(3) | 1.871 | 2.064(3) | 2.033(4) | 2.063(8) |
| M–C44 | — | — | 1.884(3) | 1.866 | 2.036(3) | 2.016(3) | 2.015(7) |
| M–C45 | — | — | 1.881(3) | 1.867 | 2.025(3) | 2.028(4) | 2.036(7) |
| C41–O41 | — | — | 1.143(3) | 1.183 | 1.141(3) | 1.144(4) | 1.141(9) |
| C42–O42 | — | — | 1.133(3) | 1.177 | 1.130(3) | 1.134(9) | 1.144(9) |
| C43–O43 | — | — | 1.135(3) | 1.178 | 1.127(3) | 1.140(4) | 1.121(10) |
| C44–O44 | — | — | 1.138(3) | 1.179 | 1.128(3) | 1.137(4) | 1.145(9) |
| C45–O45 | — | — | 1.145(3) | 1.179 | 1.147(3) | 1.143(4) | 1.138(9) |
| P–C1–N | 123.4(2) | 123.11(18) | 122.98(16) | 123.7 | 123.28(15) | 124.53(19) | 123.3(4) |
| P–C1–C2 | 116.4(2) | 115.80(18) | 119.41(16) | 117.8 | 118.80(15) | 118.33(18) | 118.8(4) |
| N–C1–C2 | 120.0(2) | 120.9(2) | 117.61(17) | 118.4 | 117.92(17) | 117.1(2) | 117.9(5) |
| C1–N–C9 | 131.7(2) | 130.9(2) | 125.0(2) | 126.5 | 125.2(5) | 124.8(2) | 125.9(5) |
| C1–P–C21 | 101.9(1) | 103.54(11) | 106.73(10) | 105.1 | 107.11(9) | 106.23(12) | 107.1(3) |
| C1–P–M | — | — | 130.38(8) | 127.4 | 130.41(7) | 130.05(9) | 130.3(2) |
| C21–P–M | — | — | 121.09(6) | 124.8 | 121.25(6) | 123.66(8) | 121.09(18) |
| C1–P–C21 | 101.9(1) | 103.54(11) | 106.73(10) | 105.1 | 107.11(9) | 106.23(12) | 107.1(3) |
| C1–N–H | — | — | 113.7(16) | 116.1 | 115.5(16) | 116(2) | 124(5) |
| C1–N–C9 | — | — | 125.02(18) | 126.5 | 125.25(17) | 124.8(2) | 125.9(5) |
| P–M–C41 | — | — | 177.63(9) | 175.8 | 177.48(8) | 177.13(12) | 177.3(2) |
| P–M–C42 | — | — | 91.81(7) | 96.1 | 92.16(7) | 98.0(3) | 91.8(2) |
| P–M–C43 | — | — | 90.99(8) | 87.1 | 91.53(7) | 91.78(10) | 91.0(2) |
| P–M–C44 | — | — | 88.90(8) | 88.3 | 88.86(8) | 88.54(10) | 88.6(2) |
| P–M–C45 | — | — | 95.58(8) | 90.6 | 95.72(7) | 93.37(10) | 96.2(2) |
| C1–P–M–C42 | 26.1(1) | 7.9 | 23.6(1) | 4.1(3) f | 24.9(3) | ||
| ∠Pl1–Pl2c | 42.57 | 45.17(6) | 61.89(09) | 59.8 | 60.36(8) | 74.3(2) | 60.8(2) |
| ∠Pl1–Pl3d | 59.55 | 57.88(8) | 75.83(8) | 83.6 | 75.56(7) | 79.3(1) | 75.5(2) |
| ∠Pl1–Pl4e | 77.66 | 61.9(1) | 79.66(9) | 84.0 | 83.41(8) | 88.2(1) | 84.0(2) |
All four metal complexes share the same gross features: the ligand is connected via the n(P) HOMO−1 orbital (see below) in the common κP coordination mode.13,18 In each case, the phosphaamidine backbone composed of C1, C2, P, N, C9 and C21 is found to be planar and M lies in or close to this plane (defined as “plane 1”, see Table 1). All three aryl rings (planes 2–4 in Table 1) approach a perpendicular orientation (∠60°–∠88°) to this plane; the rotation of the backbone tolyl or mesityl rings, ∠Pl1–Pl2, is 15–20° larger than in 9. In all cases, the solid state structures contain the ligands in the Z-anti(P![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C) C-amino-(λ3,σ2)-aminophosphaalkene geometry (as is also found in the crystal structures of 9) with the M(CO)5 groups in the exo position. In these conformations, the iPr groups of the phosphino Dipp rings provide “side shields” for the phosphorus nucleus as well as the P
C) C-amino-(λ3,σ2)-aminophosphaalkene geometry (as is also found in the crystal structures of 9) with the M(CO)5 groups in the exo position. In these conformations, the iPr groups of the phosphino Dipp rings provide “side shields” for the phosphorus nucleus as well as the P![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C π bond. Within the molecular structures, 11b has a planar phosphino Dipp ring from which the P atom deviates by only 0.0693(4) Å. The isostructural series 10, 11a and 12 have deviations of 0.29–0.30 Å. Consideration of Table 1 also confirms that the metric parameters of the coordinated phosphaamidines 10–12 are very similar to those of the free molecules 9. The average P
C π bond. Within the molecular structures, 11b has a planar phosphino Dipp ring from which the P atom deviates by only 0.0693(4) Å. The isostructural series 10, 11a and 12 have deviations of 0.29–0.30 Å. Consideration of Table 1 also confirms that the metric parameters of the coordinated phosphaamidines 10–12 are very similar to those of the free molecules 9. The average P![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bond length among all four metal complexes is 1.702(3) Å and the N–C bond length is 1.359(7) Å (errors here are std. dev.), statistically indistinguishable from the values in 9. In 11a the P–C1–C2 angle has opened up to 118.80(15)° compared to 116.4(2)° in 9a, whilst the sums of angles around C1 remain very close to 360°: 359.9(3)° and 360.0 (3)°, respectively. It is the N–C1–C2 angle that closes to make up the difference, perhaps indicative of steric crowding of the tolyl ring by the equatorial CO groups of the metal. The same effect is observed for the structures of 10, 11a and 12.
C bond length among all four metal complexes is 1.702(3) Å and the N–C bond length is 1.359(7) Å (errors here are std. dev.), statistically indistinguishable from the values in 9. In 11a the P–C1–C2 angle has opened up to 118.80(15)° compared to 116.4(2)° in 9a, whilst the sums of angles around C1 remain very close to 360°: 359.9(3)° and 360.0 (3)°, respectively. It is the N–C1–C2 angle that closes to make up the difference, perhaps indicative of steric crowding of the tolyl ring by the equatorial CO groups of the metal. The same effect is observed for the structures of 10, 11a and 12.
There has been extensive discussion in the literature on the structural consequences of amine substitution on phosphaalkenes, which can have a dramatic effect on geometry. In order to fit 10–12 into a suitable context, a survey was undertaken of all non-cyclic phosphaalkene complexes of Group 6 M(CO)5 reported in the Cambridge Structural Database (CSD). The results are compiled in Table S1† along with the CSD refcodes and literature citations (for readers without access to the CSD, diagrams of all cited structures are provided in Fig. S3†). There is in fact wide diversity amongst these structures and there are relatively few “conventional” phosphaalkenes where the C is substituted only with hydrocarbon groups, so that to make sense of the data the types of substituents R1,2 at C and R at P are also listed along with a descriptive phrase of the compound type. The results have been compiled into a histogram shown in Fig. 4.
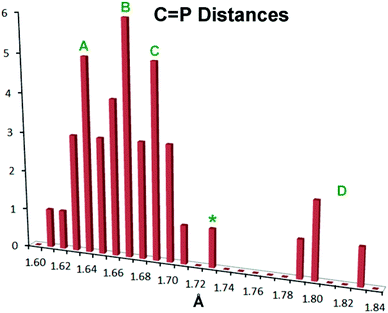 | ||
Fig. 4 Histogram showing P![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bond distances in known metal Group 6 M(CO)5 complexes of acyclic phosphaalkenes and related complexes (CSD Release 5.36, May 2015).59 See the text for details. C bond distances in known metal Group 6 M(CO)5 complexes of acyclic phosphaalkenes and related complexes (CSD Release 5.36, May 2015).59 See the text for details. | ||
Within this histogram there are two distinct regions, the majority of exemplars centred on 1.67 Å (labelled “A”–“C” in Fig. 4) which are structurally uniform and display “end-on” coordination from the in-plane n(P) orbital, despite the wide diversity of substituents. There is also an outlying group “D” nearer 1.80 Å, which are molecules with one or two dimethylamino groups at the P![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C carbon, and are all coordinated “side-on” to the metal, albeit through the P atom only.47–49 Within the major distribution, it is possible to distinguish two distinct groups: group “A”, ranging from d(P
C carbon, and are all coordinated “side-on” to the metal, albeit through the P atom only.47–49 Within the major distribution, it is possible to distinguish two distinct groups: group “A”, ranging from d(P![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C) 1.61 Å–1.68 Å, which can be attributed to phosphaalkenes bearing only H or organic moieties (including cumulenes) at carbon; and Group “C”, extending from 1.67 Å to 1.71 Å, which are phosphaalkenes where one of the substituents at C is an alkoxy group (so-called Becker phosphaalkenes),60 or are very strained organic groups such as cyclopropane. This group includes 10–12. The overall distribution maximum “B” at 1.67 Å borrows intensity from these neighbouring distributions. Thus, substitution at the P
C) 1.61 Å–1.68 Å, which can be attributed to phosphaalkenes bearing only H or organic moieties (including cumulenes) at carbon; and Group “C”, extending from 1.67 Å to 1.71 Å, which are phosphaalkenes where one of the substituents at C is an alkoxy group (so-called Becker phosphaalkenes),60 or are very strained organic groups such as cyclopropane. This group includes 10–12. The overall distribution maximum “B” at 1.67 Å borrows intensity from these neighbouring distributions. Thus, substitution at the P![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C carbon by a single aromatic amine such as the DippN groups does not lead to distinctly longer P
C carbon by a single aromatic amine such as the DippN groups does not lead to distinctly longer P![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bonds, although 10–12 certainly flank the long-end slope of the distribution.
C bonds, although 10–12 certainly flank the long-end slope of the distribution.
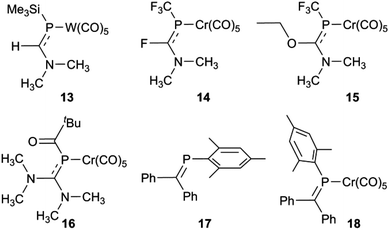
So what is going on with the outlier aminophosphaalkenes in Table S1† and Fig. 4? The peak marked * belongs to 13 (Chart 2; refcode ENEBUU).46 The structures in group “D” are, in order of increasing d(P![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C), 14 (GEJYUP),4915 (VOJMUC)48 and 16 (CODNUE).49 All of these have one or two NMe2 substituents at C and most also have strongly electron-withdrawing groups on P (14–16). It is instructive to compare these with 10–12 using two additional criteria: (i) the deviation of P out-of-plane (oop) of its attachment points (M, C1 and C21 in our numbering scheme); (ii) the dihedral angle between the planes defined by M, P plus the three carbonyl C atoms within the M,P plane (C41, C42 and C44 in our numbering scheme) and the plane containing the P
C), 14 (GEJYUP),4915 (VOJMUC)48 and 16 (CODNUE).49 All of these have one or two NMe2 substituents at C and most also have strongly electron-withdrawing groups on P (14–16). It is instructive to compare these with 10–12 using two additional criteria: (i) the deviation of P out-of-plane (oop) of its attachment points (M, C1 and C21 in our numbering scheme); (ii) the dihedral angle between the planes defined by M, P plus the three carbonyl C atoms within the M,P plane (C41, C42 and C44 in our numbering scheme) and the plane containing the P![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bond (P, N, C1, C2, C21 and C9 in our numbering scheme). The P oop distances (Å) are: 11b, 0.03; 10, 0.15; 11a, 0.13; 12, 0.14; 13, 0.38; 14, 0.87 and 0.90; 15, 0.82; 16, 0.61 (listed in the order of P
C bond (P, N, C1, C2, C21 and C9 in our numbering scheme). The P oop distances (Å) are: 11b, 0.03; 10, 0.15; 11a, 0.13; 12, 0.14; 13, 0.38; 14, 0.87 and 0.90; 15, 0.82; 16, 0.61 (listed in the order of P![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C distances in Table S1†). The specified dihedral angles (°) are: 11b, 12.2; 10, 15.3; 11a, 14.7; 12, 14.7; 13, 42.3; 14, 64 and 64.0; 15, 62.6; 16, 49.8. Both series correlate strongly with d(P
C distances in Table S1†). The specified dihedral angles (°) are: 11b, 12.2; 10, 15.3; 11a, 14.7; 12, 14.7; 13, 42.3; 14, 64 and 64.0; 15, 62.6; 16, 49.8. Both series correlate strongly with d(P![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C) (R2 = 0.85 and 0.84, respectively, see Fig. S5†). Evidently, strong hybridization towards pyramidal phosphorus is associated with M(CO)5-coordinated phosphaalkenes bearing very strong electronic donors at C, especially when accompanied by electron withdrawing groups at P. This re-hybridization has the consequence of greatly lengthening the P–C bond. Such distortions do not occur in 10–12 which fit in sequence with other κP-coordinated phosphaalkenes.
C) (R2 = 0.85 and 0.84, respectively, see Fig. S5†). Evidently, strong hybridization towards pyramidal phosphorus is associated with M(CO)5-coordinated phosphaalkenes bearing very strong electronic donors at C, especially when accompanied by electron withdrawing groups at P. This re-hybridization has the consequence of greatly lengthening the P–C bond. Such distortions do not occur in 10–12 which fit in sequence with other κP-coordinated phosphaalkenes.
Solution structure: NMR evidence
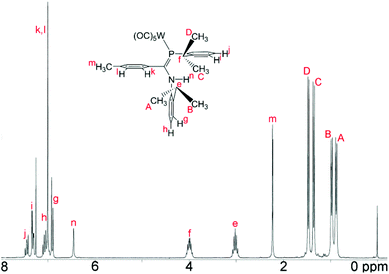
The 1H NMR data for, in particular, the iPr methyl groups are diagnostic of the solution-phase behaviour of phosphaamidines 9 and complexes 10–12. These data are compiled in Table 2 along with those for the methine signals; 2-D NMR has been used to confirm the assignments, starting from the methine signals for the Dipp group attached to phosphorus, which are unambiguously identifiable as doublets of septets from coupling to 31P (f in Fig. 5). From this it can be easily established that the signals labelled as A and B are for methyl groups attached to the amino Dipp ring. Scheme 4 shows the relative orientation for the three most likely isomeric forms for 9a in its phosphaalkene isomer. In the Z-anti(P![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C) conformation alone, methyl groups on this ring experience significant anisotropic ring-shielding from the (the more proximate) backbone aryl group at A and from the (somewhat more distant) phosphine Dipp ring at B. These effects induce the unusual high-frequency chemical shifts for methyls A and B. By contrast, the methyl groups of the phosphino Dipp ring are at normal chemical shifts; the differentiation whereby C is mildly shifted to higher frequency can possibly be attributed to a weak anisotropic shielding from the P
C) conformation alone, methyl groups on this ring experience significant anisotropic ring-shielding from the (the more proximate) backbone aryl group at A and from the (somewhat more distant) phosphine Dipp ring at B. These effects induce the unusual high-frequency chemical shifts for methyls A and B. By contrast, the methyl groups of the phosphino Dipp ring are at normal chemical shifts; the differentiation whereby C is mildly shifted to higher frequency can possibly be attributed to a weak anisotropic shielding from the P![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C π system. Note with reference to Scheme 4 that neither the E-anti nor E-syn geometries are able to induce such a pattern of anisotropic shielding distributed to these specific methyl groups. E-anti would affect one methyl group on each of the Dipp rings, whereas E-syn is expected to have the anisotropic shielding effect on the phosphino Dipp ring.
C π system. Note with reference to Scheme 4 that neither the E-anti nor E-syn geometries are able to induce such a pattern of anisotropic shielding distributed to these specific methyl groups. E-anti would affect one methyl group on each of the Dipp rings, whereas E-syn is expected to have the anisotropic shielding effect on the phosphino Dipp ring.
| Atom/Grp | Parameter | 9a | 9b | 10 | 11a | 11b | 12 |
|---|---|---|---|---|---|---|---|
| a NMR data recorded in CDCl3. b The major one amongst four solution species. c Somewhat line broadened. | |||||||
| iPr–CH3A (amino) | δ (1H) | 0.81 | 0.83 | 0.86c | 0.79c | 0.88c | 0.88c |
| 3 J HH, Hz | 6.7 | 6.9 | 6.6 | 6.7 | 6.7 | 6.7 | |
| iPr–CH3B (amino) | δ (1H) | 0.89 | 0.92 | 0.99c | 0.92c | 0.98c | 0.97c |
| 3 J HH, Hz | 6.7 | 6.9 | 6.7 | 6.7 | 6.9 | 6.7 | |
| iPr–CH3C (phosphino) | δ (1H) | 1.27 | 1.27 | 1.36 | 1.29 | 1.35 | 1.36 |
| 3 J HH, Hz | 6.9 | 6.7 | 6.7 | 6.7 | 6.7 | 6.7 | |
| iPr–CH3D (phosphino) | δ (1H) | 1.35 | 1.36 | 1.47 | 1.40 | 1.45 | 1.47 |
| 3 J HH, Hz | 6.9 | 6.9 | 6.7 | 6.7 | 6.7 | 6.7 | |
| R = 4-CH3or 4-CH3O | δ (1H) | 2.22 | 3.70 | 2.22 | 2.15 | 3.71 | 2.23 |
| 7 J PH, Hz | — | — | 1.8 | 1.8 | — | 1.8 | |
| iPr–H (amino) | δ (1H) | 3.00 | 3.00 | 2.96 | 2.96 | 3.01 | 3.02 |
| 3 J HH, Hz | 6.7 | 6.8 | 6.7 | 6.6 | 6.6 | 6.8 | |
| iPr–H (phosphino) | δ (1H) | 3.84 | 3.85 | 4.00 | 3.91 | 4.00 | 3.99 |
| 3 J HH, Hz | 6.9 | 6.7 | 6.7 | 6.7 | 6.7 | 6.7 | |
| 4 J PH, Hz | 3.4 | 3.4 | 4.6 | 4.6 | 4.7 | 4.6 | |
| N–H | δ (1H) | 6.24 | 6.24 | 6.50* | 6.43* | 6.45* | 6.45* |
| 3 J PH, Hz | 1.0 | 2.4 | — | — | — | — | |
| 31P NMR | δ (31P) | 53.6 | 51.4 | 45.0 | 30.2 | 29.6 | 6.0 |
| 1 J WP, Hz | 255 | ||||||
| Δδ(31P) | −8.4 | −23.2 | −21.8 | −47.4 | |||
An interesting feature of the spectra of the complexes is that the high-frequency methyl signals A and B are somewhat line-broadened compared to C and D (an effect absent in free 9). This implies somewhat slow rotation of the iPr groups on the amino Dipp ring, consistent with stronger steric congestion with the backbone aryl group (the smaller C–N–C angle in the complexes has already been noted). Table 2 also reports the NMR data for the major isomers observed for 9 in CDCl3 (the isomer distributions are strongly solvent-dependent). The remarkable similarity of the data between 9a and complexes 10, 11a and 12 as well as between 9b and 11b provides strong evidence that the geometry of this majority solution-phase isomer is also Z-anti(P![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C), as also occurs in their crystal structures (ref. 3 and Fig. 1).
C), as also occurs in their crystal structures (ref. 3 and Fig. 1).
The 31P chemical shifts of the complexes are all at higher frequencies compared to 9, with the magnitude of Δδ(31P) increasing in the order Cr < Mo < W. A similar trend has been reported for other λ3,σ2 compounds61 and is also well-known for triorganophosphine LM(CO)5 complexes.62 In 12 the value of 1J(183W–31P) = 255 Hz. Mathey and co-workers prepared a number of reactive Ph–P![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CR2 as the W(CO)5 complexes, which have 1JWP ranging from 251 to 259 Hz; for similar tBu–P
CR2 as the W(CO)5 complexes, which have 1JWP ranging from 251 to 259 Hz; for similar tBu–P![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CR2 the values are 244–245 Hz. Yoshifuji et al. reported for a series of W(CO)5 complexes of Mes*–P
CR2 the values are 244–245 Hz. Yoshifuji et al. reported for a series of W(CO)5 complexes of Mes*–P![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CR2 that 1JWP ranges from 269 to 273 Hz. The “Becker” phosphaalkene (Me3Si)2CH–P
CR2 that 1JWP ranges from 269 to 273 Hz. The “Becker” phosphaalkene (Me3Si)2CH–P![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C(Ph)OC(
C(Ph)OC(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O)Ph W(CO)5 complex is reported to have 1JWP = 267 Hz.41 This small sampling suggests that only substituents on phosphorus have a distinct influence on the size of the one-bond metal–phosphorus coupling; indeed it has been demonstrated that the size of 1JWP in LM(CO)5 complexes depends primarily on the electronegativity of the substituents directly attached to phosphorus.62,63 The only other amino-substituted compound available for comparison is Me3Si–P
O)Ph W(CO)5 complex is reported to have 1JWP = 267 Hz.41 This small sampling suggests that only substituents on phosphorus have a distinct influence on the size of the one-bond metal–phosphorus coupling; indeed it has been demonstrated that the size of 1JWP in LM(CO)5 complexes depends primarily on the electronegativity of the substituents directly attached to phosphorus.62,63 The only other amino-substituted compound available for comparison is Me3Si–P![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C(H)–NMe2 for which 1JWP = 186 Hz;46 since the trimethylsilyl group is so much more electropositive than a Dipp group, no meaningful conclusion can be drawn from this comparison.
C(H)–NMe2 for which 1JWP = 186 Hz;46 since the trimethylsilyl group is so much more electropositive than a Dipp group, no meaningful conclusion can be drawn from this comparison.
Only limited 13C data were obtained, since 10 is the only complex to resist decomposition long enough for the accumulation of a good spectrum. The 13CO data for 10 (δ(COeq) 216.0, 2JPC = 15.1 Hz; δ(COax) 229.9, 2JPC = 4.9 Hz) are very similar to those in 18 (δ(COeq) 214.8, 2JPC = 16 Hz; (δ(COax) 221.4, 2JPC = 3 Hz). All these resonances are deshielded compared to Cr(CO)6, δ(CO) = −211.2,64 but the greater deshielding of the axial 13CO indicates lower π acceptor and higher σ donor ability of the trans ligand compared to carbon monoxide.65 By this criterion, a Δδ from the hexacarbonyl shift, there is little difference in the πacc/σdon ratios between 10, Δδ = 6.9, and 18, Δδ = 6.6 ppm.
Infrared spectra
The infrared spectra in the ν(NH) and ν(C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) O) regions for 9–12 are presented in Table 3. It is well-known that the A1(2) vibration in LM(CO)5 complexes reflects the stretching frequency of the axial CO group that is trans to L.66 This mode should have considerable intensity, though generally it is found to be less intense than E. It is also the case that the E mode can split under conditions of lowered symmetry, either due to a very asymmetrical ligand L or due to symmetry lowering from lattice effects. Unlike many of the classic ligands in coordination chemistry including R3P, the data for LM(CO)5 phosphaalkenes are rather scattered and incomplete. We have therefore taken great care to collect data in several solvents – for ease of comparison with the literature data – and at various concentrations. We consider the data collected in n-heptane to be the most similar to gas-phase values, and assign the weak band at around 2070 cm−1 to A1(1), a non-controversial assignment. The B2 band is always extremely weak. For the remaining carbonyl stretching bands, based on the variability of the low-energy bands to conditions and literature precedents, we tentatively assign those at ∼1950 cm−1 to the A1(2) vibration, and the remaining bands to a split in the E band induced by the large, asymmetric ligands. In chloroform solution, the E vibration is found to be even more intense and is sufficiently broad to overlap the A1(2) vibration almost completely. The bands at ∼1930 cm−1 (heptane), ∼1915 cm−1 (CHCl3) and ∼1907 cm−1 (KBr) are assigned to the other branch of the E vibration. These assignments are confirmed by the results of the B3PW91/LANL2DZ frequency calculation on the optimized geometry of 10 (Table 3 and Fig. 6).
O) regions for 9–12 are presented in Table 3. It is well-known that the A1(2) vibration in LM(CO)5 complexes reflects the stretching frequency of the axial CO group that is trans to L.66 This mode should have considerable intensity, though generally it is found to be less intense than E. It is also the case that the E mode can split under conditions of lowered symmetry, either due to a very asymmetrical ligand L or due to symmetry lowering from lattice effects. Unlike many of the classic ligands in coordination chemistry including R3P, the data for LM(CO)5 phosphaalkenes are rather scattered and incomplete. We have therefore taken great care to collect data in several solvents – for ease of comparison with the literature data – and at various concentrations. We consider the data collected in n-heptane to be the most similar to gas-phase values, and assign the weak band at around 2070 cm−1 to A1(1), a non-controversial assignment. The B2 band is always extremely weak. For the remaining carbonyl stretching bands, based on the variability of the low-energy bands to conditions and literature precedents, we tentatively assign those at ∼1950 cm−1 to the A1(2) vibration, and the remaining bands to a split in the E band induced by the large, asymmetric ligands. In chloroform solution, the E vibration is found to be even more intense and is sufficiently broad to overlap the A1(2) vibration almost completely. The bands at ∼1930 cm−1 (heptane), ∼1915 cm−1 (CHCl3) and ∼1907 cm−1 (KBr) are assigned to the other branch of the E vibration. These assignments are confirmed by the results of the B3PW91/LANL2DZ frequency calculation on the optimized geometry of 10 (Table 3 and Fig. 6).
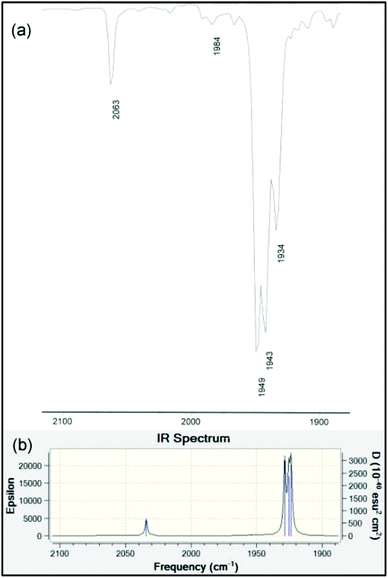 | ||
| Fig. 6 (a) Experimental solution IR spectrum in the carbonyl stretching region of 10 measured dilute in hexane. (b) Computed gas-phase IR spectrum at the B3PW91/LANDL2DZ level of theory (data in Table 3). | ||
| n-Heptane | NH | CO A1(1) | CO B2 | CO A1(2) | CO Ea | CO Eb |
|---|---|---|---|---|---|---|
| a FTIR data in solution (cm−1); for additional solvent and KBr pressed-pellets, see Table S2. b From a frequency calculation on the optimized geometry using B3PW91/LANL2DZ, uncorrected. | ||||||
| 9a | 3354 m | |||||
| 9b | 3354 m | |||||
| 10 | — | 2063 w | 1984 w | 1949 vs | 1943 vs | 1934 s |
| 10 (DFT calc.)b | 3561 w | 2034 m | 1954 w | 1929 vs | 1926 s | 1924 vs |
| 11a | — | 2072 w | 1989 w | 1955 vs | 1947 vs | 1933 s |
| 11b | — | 2071 w | 1989 w | 1955 vs | 1947 vs | 1933 s |
| 12 | — | 2070 w | 1989 w | 1948 vs | 1939 vs | 1929 s |
There are very few solution-phase IR data available for the many M(CO)5 complexes in the literature; most reports are from solids in KBr or from Nujol™ mulls, data that are more susceptible to lattice effects. The spectrum of the Cr(CO)5 complex 18 of phosphaalkene 17 was reported in cyclohexane with ν(C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) O) of 1955 and 1901 cm−1, with the former taken as A1(2).31 More complete data are available for the Cr(CO)5 complex of Cp*(CO)2Fe–C(H)
O) of 1955 and 1901 cm−1, with the former taken as A1(2).31 More complete data are available for the Cr(CO)5 complex of Cp*(CO)2Fe–C(H)![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) P–CH(SiCH3)2 which has a short P
P–CH(SiCH3)2 which has a short P![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bond similar to conventional phosphaalkenes (refcode TACKOX in Table S1†): cyclopentane solution, 2067(m), 1980(w), 1945(vs), 1935(vs), 1931(vs) cm−1.28 These data are almost indistinguishable from those of 10 in n-heptane. The Cr(CO)5 complex of κP-2,4,6-triphenylphosphorine by contrast has an A1(2) vibration at 1968 cm−1, indicative of a higher πacc/σdon ratio.67 Furthermore, the A1(2) data for 10–12 are very close to those of M(CO)5 complexes of R3P (at Cr, R = Ph: 1944 cm−1; R = tBu: 1937 cm−1).67 Taken together, these data suggest that 9 are weak π-acceptors and good σ-donors and not significantly different, in this regard, from conventional phosphaalkenes.
C bond similar to conventional phosphaalkenes (refcode TACKOX in Table S1†): cyclopentane solution, 2067(m), 1980(w), 1945(vs), 1935(vs), 1931(vs) cm−1.28 These data are almost indistinguishable from those of 10 in n-heptane. The Cr(CO)5 complex of κP-2,4,6-triphenylphosphorine by contrast has an A1(2) vibration at 1968 cm−1, indicative of a higher πacc/σdon ratio.67 Furthermore, the A1(2) data for 10–12 are very close to those of M(CO)5 complexes of R3P (at Cr, R = Ph: 1944 cm−1; R = tBu: 1937 cm−1).67 Taken together, these data suggest that 9 are weak π-acceptors and good σ-donors and not significantly different, in this regard, from conventional phosphaalkenes.
Bonding in metal complexes
Surprisingly little investigation has been undertaken on the electronic structures of M(CO)5 complexes of phosphaalkenes despite the many examples of such compounds that have been prepared over the past forty years. An early observation of facile E/Z isomerism of a coordinated conventional phosphaalkene68 elicited an investigation using EHMO methods.69 These authors concluded that phosphaalkenes coordinate to Cr(CO)5via σ bonds and that any π bonding is negligible. This conclusion is in error at least insofar as they predicted that the C1–P–M–C42 dihedral angle minimizes to 45° and that rotation of the P–M bond is facile. A consideration of all the structures in the main distribution in Fig. 6 consistently shows that this dihedral is close to zero. In the crystal structures of 10–12, this dihedral (Table 1) ranges from 8.3(2)° to 26.1(1)°; in the B3PW91/LANL2DZ optimized geometry it is only 7.9°. This suggests that the phosphaamidine geometry adopts an eclipsed orientation to the metal CO ligands against the opposing steric forces.More recently, DFT calculations using modified SBK effective core potential basis sets were reported in which two model ligands, namely HP![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH2 and HP
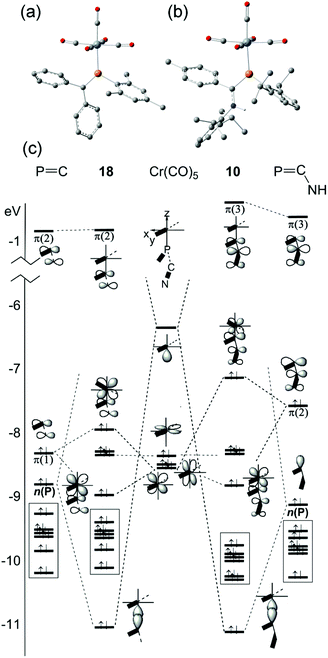
CH2 and HP![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C(H)–NH2, are coordinated to M(CO)5 (M = Cr, Mo, W).51 This paper seems primarily devoted to explaining the highly-distorted coordination mode exhibited in 14 and 15, including the discovery that complex 14 is capable of attaching to a second Cr(CO)5 group at P.70 These studies demonstrate that such bis metal coordination is likely induced by the strongly electron-withdrawing CF3 groups at P. The calculations also show that the geometry of the model phosphaalkene and aminophosphaalkene do not change much in the singly-coordinated, κP mode. This report is scarce in other details of the calculations and does not address the electronic structures of these complexes in detail. We have therefore undertaken DFT studies using the B3PW91 functional on the full molecular structure of 10 (Fig. 7b), a method which has previously shown good results in our hands for low-valent chromium complexes. In this study, the effective core potential basis set LANL2DZ was employed which has been shown to give good results for early transition metals. To gain further perspective, a similar set of calculations was performed on 18 (Fig. 7a), one of the best-known conventional phosphaalkene Cr(CO)5 complexes. The computed geometry of 10 included in Table 1 is in good agreement with the experimentally-determined results (see also Fig. S4† for pictures of the structure and an overlay with the X-ray geometry). A fragment orbital analysis was then developed using the LANL2DZ results (on the X-ray geometries) in conjunction with PM3 semi-empirical calculations for the fragments (Fig. 7c).
C(H)–NH2, are coordinated to M(CO)5 (M = Cr, Mo, W).51 This paper seems primarily devoted to explaining the highly-distorted coordination mode exhibited in 14 and 15, including the discovery that complex 14 is capable of attaching to a second Cr(CO)5 group at P.70 These studies demonstrate that such bis metal coordination is likely induced by the strongly electron-withdrawing CF3 groups at P. The calculations also show that the geometry of the model phosphaalkene and aminophosphaalkene do not change much in the singly-coordinated, κP mode. This report is scarce in other details of the calculations and does not address the electronic structures of these complexes in detail. We have therefore undertaken DFT studies using the B3PW91 functional on the full molecular structure of 10 (Fig. 7b), a method which has previously shown good results in our hands for low-valent chromium complexes. In this study, the effective core potential basis set LANL2DZ was employed which has been shown to give good results for early transition metals. To gain further perspective, a similar set of calculations was performed on 18 (Fig. 7a), one of the best-known conventional phosphaalkene Cr(CO)5 complexes. The computed geometry of 10 included in Table 1 is in good agreement with the experimentally-determined results (see also Fig. S4† for pictures of the structure and an overlay with the X-ray geometry). A fragment orbital analysis was then developed using the LANL2DZ results (on the X-ray geometries) in conjunction with PM3 semi-empirical calculations for the fragments (Fig. 7c).
The frontier molecular orbitals (FMO) of the Cr(CO)5 fragment in the centre of the diagram are well known, consisting of an empty Cr dz2 orbital and three filled dxz, dyz and dxz orbitals (in this orientation, dx2−y2 is bonding to the equatorial carbonyl ligands).69 The FMOs of Mes–P![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CPh2, 17, are shown on the right, consisting of the π(2) LUMO, the π(1) HOMO and just below this the n(P) orbital. This is in full agreement with the earlier DFT study except that Fig. 7c also shows the filled aromatic π orbitals from the Mes and Ph rings that are not present in the simple model ligands.51 The interaction of these fragments to form 18 is dominated by σ-bonding between the metal LUMO (dz2) and the HOMO−1 of the phosphaalkene. The bonding interaction stabilizes well below the filled aromatic π orbitals (shown as boxes in the diagram). Metal dxz and dyz orbitals are non-interacting with the incoming ligand; the net π interaction is between the metal dxz and ligand π(1) orbitals, resulting in two new filled π-type orbitals. The net effect raises the HOMO energy in the complex (for which, see below). These calculations also confirm that there is very little interaction with the high-lying π(2) MO which transforms almost unchanged into the complex and remains the LUMO. The “net π bonding/antibonding” in 18 therefore depends on the relative strengths of the interactions in the HOMO and HOMO−3 of the complex.
CPh2, 17, are shown on the right, consisting of the π(2) LUMO, the π(1) HOMO and just below this the n(P) orbital. This is in full agreement with the earlier DFT study except that Fig. 7c also shows the filled aromatic π orbitals from the Mes and Ph rings that are not present in the simple model ligands.51 The interaction of these fragments to form 18 is dominated by σ-bonding between the metal LUMO (dz2) and the HOMO−1 of the phosphaalkene. The bonding interaction stabilizes well below the filled aromatic π orbitals (shown as boxes in the diagram). Metal dxz and dyz orbitals are non-interacting with the incoming ligand; the net π interaction is between the metal dxz and ligand π(1) orbitals, resulting in two new filled π-type orbitals. The net effect raises the HOMO energy in the complex (for which, see below). These calculations also confirm that there is very little interaction with the high-lying π(2) MO which transforms almost unchanged into the complex and remains the LUMO. The “net π bonding/antibonding” in 18 therefore depends on the relative strengths of the interactions in the HOMO and HOMO−3 of the complex.
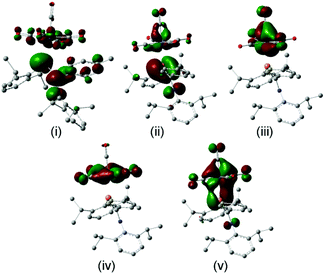
The FMOs of the aminophosphaalkene isomer of 9a are shown on the far right of the diagram. These differ from 17 by the presence of the strongly donating nitrogen px orbital (not shown), resulting in a new π(1) that has strong C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N π bonding character.51 As a consequence, the HOMO is now π(2) and is raised considerably in energy compared to the HOMO of 17. The electronegativity of the nitrogen also serves to lower the energy of HOMO−1 which still has predominantly n(P) character and still forms the dominant bonding interaction with the metal LUMO, which again stabilizes below the filled aromatic π ligands (boxed). The bonding (HOMO−3) and anti-bonding (HOMO) interactions again determine the net π-bonding character. Unlike in 18, in 10 the π(3) LUMO is weakly destabilized. The key FMOs in 10 are shown more accurately in Fig. 8 than in the cartoons within Fig. 7c. These pictures help to emphasize: (i) the out-of-phase interaction between π(3) and the d orbitals in the LUMO; (ii) the destabilizing d–p π interaction in the HOMO that is evidently dominated by the ligand in 10 and the non-interacting HOMO−1 and HOMO−2 dominated by metal dyz and dxy in (iii) and (iv). Finally, in (v) the in-phase d–p π interaction has more metal than ligand character in 10 than is the case for the equivalent orbital in 18. This difference in the characters of HOMO and HOMO−3 is a direct consequence of the higher-lying ligand π HOMO in 9 compared to 17. These calculations also corroborate the spectroscopic evidence that there is no obvious π-back-bonding in either 10 or 18. The π interactions more or less cancel out each other for these zero-valent complexes with these electron-rich ligands. The bonding is therefore predominantly, but not exclusively, of σ character.
N π bonding character.51 As a consequence, the HOMO is now π(2) and is raised considerably in energy compared to the HOMO of 17. The electronegativity of the nitrogen also serves to lower the energy of HOMO−1 which still has predominantly n(P) character and still forms the dominant bonding interaction with the metal LUMO, which again stabilizes below the filled aromatic π ligands (boxed). The bonding (HOMO−3) and anti-bonding (HOMO) interactions again determine the net π-bonding character. Unlike in 18, in 10 the π(3) LUMO is weakly destabilized. The key FMOs in 10 are shown more accurately in Fig. 8 than in the cartoons within Fig. 7c. These pictures help to emphasize: (i) the out-of-phase interaction between π(3) and the d orbitals in the LUMO; (ii) the destabilizing d–p π interaction in the HOMO that is evidently dominated by the ligand in 10 and the non-interacting HOMO−1 and HOMO−2 dominated by metal dyz and dxy in (iii) and (iv). Finally, in (v) the in-phase d–p π interaction has more metal than ligand character in 10 than is the case for the equivalent orbital in 18. This difference in the characters of HOMO and HOMO−3 is a direct consequence of the higher-lying ligand π HOMO in 9 compared to 17. These calculations also corroborate the spectroscopic evidence that there is no obvious π-back-bonding in either 10 or 18. The π interactions more or less cancel out each other for these zero-valent complexes with these electron-rich ligands. The bonding is therefore predominantly, but not exclusively, of σ character.
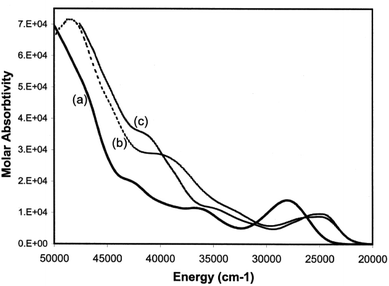
Electronic spectra
Having developed a pictorial representation for the orbital manifolds in 10 and 18, it is now fruitful to consider the electronic absorption spectra. The data for the complexes are shown in Table 4, and representative spectra obtained in hexanes solution are provided in Fig. 9. The colours of the ligands 9 and the metal complexes 10–12 are all yellow. The ligands have a low-energy, rather intense, absorption in the visible responsible for their yellow colours with maxima around 28![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1 which can be confidently assigned to allowed π* ← π transitions.
000 cm−1 which can be confidently assigned to allowed π* ← π transitions.
| Compound | λ 1 | λ 2 | λ 3 | λ 4 |
|---|---|---|---|---|
a Measured in hexanes in 10 mm quartz cuvettes. Data in cm−1 with log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ε in parentheses.
b
Ref. 31 – both measured in THF.
c 49 ε in parentheses.
b
Ref. 31 – both measured in THF.
c 49![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 300 (4.87) in CH3OH solution. 300 (4.87) in CH3OH solution.
|
||||
| 9a | 28![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 (4.15) 000 (4.15) |
36![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 (4.04) 000 (4.04) |
43![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 300 (4.30) 300 (4.30) |
>50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000c 000c |
| 10 | 24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 (3.93) 500 (3.93) |
∼34![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 sh {∼4.1} 000 sh {∼4.1} |
40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 800 (4.46) 800 (4.46) |
48![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 300 (4.85) 300 (4.85) |
| 11b | 25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 300 (4.01) 300 (4.01) |
35![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 700 sh (∼4.14) 700 sh (∼4.14) |
40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 (4.51) 500 (4.51) |
>47![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 600 600 |
| 12 | 24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 600 (3.98) 600 (3.98) |
35![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 700 (4.08) 700 (4.08) |
41![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 800 (4.56) 800 (4.56) |
41![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 800 (4.56) 800 (4.56) |
| 17 | 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 900 (2.84) 900 (2.84) |
37![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 300 (3.01) 300 (3.01) |
39![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 400 (4.20) 400 (4.20) |
— |
| 18 | 24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 900 (4.28) 900 (4.28) |
— | 39![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 (4.73) 500 (4.73) |
— |
For each of the metal complexes, there is a distinct bathochromic shift in λ1, while retaining considerable intensity (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ε ≈ 4), which we therefore also ascribe to an allowed π* ← π transition. More detailed assignments will require sophisticated calculations that are beyond the scope of this paper. Qualitatively, the data show that in 10–12, the HOMO–LUMO gap is lowered by some 3400 to 3500 cm−1 in the complexes compared to the free phosphaamidines, which amounts to 13% reduction in the energy gap. By contrast, in the conventional phosphaalkene 17, complexation to Cr(CO)5 lowers the HOMO–LUMO gap by some 6000 cm−1, a reduction in the energy gap of 20%.31 These data can be understood in the context of the changes in energy levels shown in Fig. 7c. Whilst the HOMO of 18 is considerably increased in energy due to the repulsive π interaction with the ligand, the LUMO is predicted to remain unchanged, and hence ΔE is significantly reduced in the complex. In the case of 10, while the HOMO is also increased in energy, so is the LUMO and hence ΔE is reduced by a smaller amount. Finally, it is worth mentioning that the typical yellow colours of phosphine-substituted LM(CO)5 complexes of Group 6 metals are usually attributed to an MLCT process.58 Insofar as the HOMOs of both 10 and 18 are calculated to have more metal d character than their LUMOs, this generalization is also valid for phosphaalkene and phosphaamidine complexes.
ε ≈ 4), which we therefore also ascribe to an allowed π* ← π transition. More detailed assignments will require sophisticated calculations that are beyond the scope of this paper. Qualitatively, the data show that in 10–12, the HOMO–LUMO gap is lowered by some 3400 to 3500 cm−1 in the complexes compared to the free phosphaamidines, which amounts to 13% reduction in the energy gap. By contrast, in the conventional phosphaalkene 17, complexation to Cr(CO)5 lowers the HOMO–LUMO gap by some 6000 cm−1, a reduction in the energy gap of 20%.31 These data can be understood in the context of the changes in energy levels shown in Fig. 7c. Whilst the HOMO of 18 is considerably increased in energy due to the repulsive π interaction with the ligand, the LUMO is predicted to remain unchanged, and hence ΔE is significantly reduced in the complex. In the case of 10, while the HOMO is also increased in energy, so is the LUMO and hence ΔE is reduced by a smaller amount. Finally, it is worth mentioning that the typical yellow colours of phosphine-substituted LM(CO)5 complexes of Group 6 metals are usually attributed to an MLCT process.58 Insofar as the HOMOs of both 10 and 18 are calculated to have more metal d character than their LUMOs, this generalization is also valid for phosphaalkene and phosphaamidine complexes.
Conclusions
Replacement of one nitrogen atom in bulky aryl N,N′-disubstituted amidines by phosphorus produces the atom-equivalent N,P-monophosphaamidines. This element-exchange has a profound effect on the coordination of these ligands as neutral molecules in LM(CO)5 complexes of Cr, Mo and W. Whereas the all-nitrogen bulky amidines can coordinate weakly through the imino nitrogen atom, such species are unstable with respect to η6–π coordination from the very electron-rich Dipp rings. By contrast, the monophosphaamidines form robust LM(CO)5 complexes that are coordinated in the classical κP coordination mode of phosphaalkenes, with an essentially planar ligand core oriented in-plane to the metal atoms and eclipsed with the CO ligands. Complexes 10–12 greatly expand on metal carbonyl complexes of “aminophosphaalkenes” of which there were previously only four structurally characterized in the literature (if 16 is included despite the double-substitution at C).46–49 The P![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bond lengths of these coordinated species show the expected trends for electron-donating substituents delocalized into the highly polarizable heavy-element π bond. Coordination induces a significant bathochromic shift in the lowest absorption maxima. Semi-empirical and DFT calculations indicate that the destabilization of the HOMO is greater than that of the LUMO, resulting in a 3400 to 3500 cm−1 reduction in the energy of the allowed π* ← π transition upon coordination.
C bond lengths of these coordinated species show the expected trends for electron-donating substituents delocalized into the highly polarizable heavy-element π bond. Coordination induces a significant bathochromic shift in the lowest absorption maxima. Semi-empirical and DFT calculations indicate that the destabilization of the HOMO is greater than that of the LUMO, resulting in a 3400 to 3500 cm−1 reduction in the energy of the allowed π* ← π transition upon coordination.
Group 6 carbonyl complexes have proven once again to be very useful “test-beds” for examining the properties of unsaturated main group compounds; in the work reported here, complexation is not essential for the preparation of the phosphaamidines which are electronically stabilized by nitrogen π donation,27,29 but instead is necessary to select one of several solution-phase isomers and suppress the isomerization processes. Most importantly from the perspective of developing new phosphaamidinate coordination complexes,6 the preparation of 10–12 provides assurances that the properties of “aminophosphaalkenes” bearing DippN groups – a moiety that has seen extensive use in chelating pincer ligand designs (such as NACNAC) – do not show the extreme changes in character as occurs with single or double substitution at C by the very powerful electron-donating NMe2 groups as in 13 and 16, especially when combined with strongly electron-withdrawing substituents as in 14 and 15. Behaviour similar to amidinates can therefore be expected for anions derived from 9.
Experimental
General
All experimental procedures were performed under a nitrogen atmosphere using modified Schlenk techniques. Metal carbonyls (Strem) were used as received. Solvents were reagent grade or better and used as received (methanol, ethanol, hexanes) or distilled over LiAlH4 (n-heptane). Infrared spectra were recorded on a Bomem MB-100 or a Nicolet Avatar 360 spectrometer as KBr pellets or in a 0.1 mm NaCl solution cavity cell. 1H, 31P (without decoupling) and 13C-{1H} NMR spectra were recorded on a Bruker AC250/Tecmag Macspect spectrometer operating at 250.13, 101.26 and 62.90 MHz, respectively, or a Varian INOVA 500 operating at 499.3, 202.1 and 125.6 MHz. 1H NMR signals were referenced to tetramethylsilane, 13P to external H3PO4, 13C to CDCl3. Electronic absorption spectra were obtained in 1 cm path-length Teflon-stoppered cuvettes on a Cary 1E spectrophotometer. Mass spectra analyses were undertaken in the Department of Chemistry, University of Alberta. Elemental analyses were performed by MHW Laboratories, Phoenix, Az. Phosphaamidines 9a,b were produced as described elsewhere.3,57 Solutions of (THF)Cr,W(CO)5 were prepared by photolysis in THF solution and the reaction progress monitored by solution FTIR of aliquots.![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C (d, JCP = 5.4 Hz), 216.0 COeq (d, JCP = 15.1 Hz), 222.9 COax (d, JCP = 4.9 Hz). 31P NMR (CDCl3): δ 45.03 ppm (s). IR (KBr pellet) cm−1: 3358(w), 3054(w), 2966(w), 2927(w), 2870(w), 2069(s), 1955(vs), 1929(vs), 1907(vs), 1607(w), 1480(w), 1465(m), 1383(w), 1361(w), 1323(m), 1264(w), 1202(w), 1178(w), 815(w), 804(w), 759(w), 748(w) 607(m), 587(m).
C (d, JCP = 5.4 Hz), 216.0 COeq (d, JCP = 15.1 Hz), 222.9 COax (d, JCP = 4.9 Hz). 31P NMR (CDCl3): δ 45.03 ppm (s). IR (KBr pellet) cm−1: 3358(w), 3054(w), 2966(w), 2927(w), 2870(w), 2069(s), 1955(vs), 1929(vs), 1907(vs), 1607(w), 1480(w), 1465(m), 1383(w), 1361(w), 1323(m), 1264(w), 1202(w), 1178(w), 815(w), 804(w), 759(w), 748(w) 607(m), 587(m).
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C (d, JCP = 5.4 Hz), 204.9 COeq (d, JCP = 10.7 Hz), 211.7 COax (d, JCP = 30.8 Hz); some decomposition during data collection. 31P NMR (CDCl3): δ 30.17 ppm (s). IR (KBr pellet) cm−1: 3362(w), 2963(w), 2927(w), 2869(w), 2061(s), 1994(m), 1986(m), 1946(vs), 1926(vs), 1913(vs), 1906(vs), 1461(w), 1384(w), 1363(w), 1321(w), 1204(w), 1108(w), 1056(w), 804(w)759(w), 748(w), 670(m), 656(m), 455(w).
C (d, JCP = 5.4 Hz), 204.9 COeq (d, JCP = 10.7 Hz), 211.7 COax (d, JCP = 30.8 Hz); some decomposition during data collection. 31P NMR (CDCl3): δ 30.17 ppm (s). IR (KBr pellet) cm−1: 3362(w), 2963(w), 2927(w), 2869(w), 2061(s), 1994(m), 1986(m), 1946(vs), 1926(vs), 1913(vs), 1906(vs), 1461(w), 1384(w), 1363(w), 1321(w), 1204(w), 1108(w), 1056(w), 804(w)759(w), 748(w), 670(m), 656(m), 455(w).
X-ray crystallography
Suitable crystals were selected and glued to a fine glass-fibre using epoxy resin. Data were collected on a Stoe IPDS image-plate diffractometer system using Mo Kα radiation and a graphite monochromator. A ϕ-oscillation technique was employed to measure data at ambient temperature (the diffractometer was not equipped for low-temperature data collection). Data were corrected for Lorentz-polarization and either analytical or numerical (face-indexed) absorption corrections were applied. Data collection and post processing made use of the Stoe IPDS v2.36 software.71 Structures were solved using direct methods within the SHELXTL suite of software; model refinement was undertaken in SHELX-2014.72 In the case of 11b and 12, it was necessary to use a bond-distance constraint to obtain geometrically reasonable N–H distances. Displacement ellipsoids were high as expected for data collected at RT, particularly for pendant groups such as the ortho-iPr, and thus the enhanced rigid-bond restraints (RIGU) recommended for such cases were used.73 The shape and size of the displacement ellipsoids for C42/O42 in 11b were indicative of disorder; coupled to this was the apparent disorder in the backbone phenyl ring atoms C3/C4. A two-part disorder model was successfully refined with 65![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 35 occupancy ratios (see Fig. S6†). Attempts at refining iPr group rotational disorder in all of these structures were judged to be unhelpful and a simple anisotropic refinement was adopted instead. Structures were visualized and illustrations were prepared using Mercury 3.5.74 Crystal and experimental data are collected in Table S3 in the ESI.† Representations of the molecular structures are provided in Fig. 1–3 and S1, 2,† while selected interatomic distances and angles are provided in Table 1. Structure depositions: 9b, CCDC 1421316; 101421317; 11a, 1421318; 11b, 1421319; 101421320 contain the supplementary crystallographic data for this paper.
35 occupancy ratios (see Fig. S6†). Attempts at refining iPr group rotational disorder in all of these structures were judged to be unhelpful and a simple anisotropic refinement was adopted instead. Structures were visualized and illustrations were prepared using Mercury 3.5.74 Crystal and experimental data are collected in Table S3 in the ESI.† Representations of the molecular structures are provided in Fig. 1–3 and S1, 2,† while selected interatomic distances and angles are provided in Table 1. Structure depositions: 9b, CCDC 1421316; 101421317; 11a, 1421318; 11b, 1421319; 101421320 contain the supplementary crystallographic data for this paper.
Computation
Geometries for the computational studies were taken initially from the X-ray crystal structures. Calculations were performed using DFT at the B3PW91/LANL2DZ level of theory using Gaussian 03W.75 The orbital energy interaction diagram was constructed using a combination of DFT and PM3 semi-empirical methods (the latter employing HyperChem release 8.0.10).76 Calculations were deliberately restricted to the chromium examples to avoid having to deal with relativistic effects beyond the scope of this study. The geometry of 18 is taken from the deposited structure (CDC refcode MESTCR). Subsequently, full geometry optimizations were undertaken on 10 and 18 and the results were compared to those from the frozen geometries; the agreement was excellent. The geometries were confirmed to be at least local minima from the absence of imaginary frequencies in the full vibrational spectra calculations of the optimized structures. The Cartesian coordinates from these geometry-optimized calculations are provided in Tables S4 and S5,† and 3D structural pictures are shown in Fig. S4 and S7.†Acknowledgements
We are indebted to Dr Gotthelf Wolmershäuser (Fachbereich Chemie der Universität Kaiserslautern, Erwin-Schrödinger-Straße, D-67663 Kaiserslautern, Germany) for collecting all the X-ray diffraction data. Financial support of this work by the Natural Sciences and Engineering Research Council of Canada and the University of Lethbridge is gratefully acknowledged. We thank a referee for the suggestion of refining a disorder model for 11b.Notes and references
- K. Issleib and O. Löw, Z. Anorg. Allg. Chem., 1966, 346, 241–254 CrossRef CAS . The title of this paper “P-substituted acid phosphides RCO-PR′2 and phosphamidines RC(NR)-PR′2” indicates a deliberate effort to replace a nitrogen with a phosphorus in amides and amidines.
- K. Issleib, H. Schmidt and H. Meyer, J. Organomet. Chem., 1978, 160, 47–57 CrossRef CAS . In this, the first study reporting on N,P-disubstituted (and hence potentially ionisable) derivatives, their terminology shifts to “phosphaamidine”.
- R. T. Boeré, M. L. Cole, P. C. Junk, J. D. Masuda and G. Wolmershäuser, Chem. Commun., 2004, 2564–2565 RSC.
- M. Song, B. Donnadieu, M. Soleilhavoup and G. Bertrand, Chem. – Asian J., 2007, 2, 904–908 CrossRef CAS PubMed . See references therein for a reasonably comprehensive survey of the background.
- X. Li, H. Song and C. Cui, Dalton Trans., 2009, 9728–9730 RSC.
- T. van Dijk, S. Burck, M. K. Rong, A. J. Rosenthal, M. Nieger, J. C. Slootweg and K. Lammertsma, Angew. Chem., Int. Ed., 2014, 53, 9068–9071 CrossRef CAS PubMed.
- S. N. MacMillan, J. M. Tanski and R. Waterman, Chem. Commun., 2007, 4172–4174 RSC.
- A. J. Roering, S. E. Leshinski, S. M. Chan, T. Shalumova, S. N. MacMillan, J. M. Tanski and R. Waterman, Organometallics, 2010, 29, 2557–2565 CrossRef CAS.
- A. J. Roering, L. T. Elrod, J. K. Pagano, S. L. Guillot, S. M. Chan, J. M. Tanskib and R. Waterman, Dalton Trans., 2013, 42, 1159–1167 RSC.
- A. F. Maddox, J. J. Davidson, T. Shalumova, J. M. Tanski and R. Waterman, Inorg. Chem., 2013, 52, 7811–7816 CrossRef CAS PubMed.
- M. Westerhausen and M. H. Digeser, Inorg. Chem., 1997, 36, 521–527 CrossRef CAS.
- M. Westerhausen and M. H. Digeser, Z. Anorg. Allg. Chem., 1997, 623, 1237–1242 CrossRef CAS.
- P. Le Floch, Coord. Chem. Rev., 2006, 250, 627–681 CrossRef CAS.
- J. D. Protasiewicz, Multiply bonded compounds of Group 15 elements, in Comprehensive Inorganic Chemistry II, Elsevier, 2013, pp. 325–348 Search PubMed.
- R. C. Fischer and P. P. Power, Chem. Rev., 2010, 110, 3877–3923 CrossRef CAS PubMed.
- N. C. Norman, Polyhedron, 1993, 12, 2431–2466 CrossRef CAS.
- A. N. Chernega, M. Yu. Antipin and Yu. T. Struchkov, J. Struct. Chem., 1988, 29, 265–303 CrossRef.
- J. F. Nixon, Chem. Rev., 1988, 88, 1327–1362 CrossRef CAS.
- M. Klein, C. Albrecht, G. Schnakenburg and R. Streubel, Organometallics, 2013, 32, 4938–4943 CrossRef CAS.
- C. Albrecht, L. Shi, J. M. Pérez, M. van Gastel, S. Schwieger, F. Neese and R. Streubel, Chem. – Eur. J., 2012, 18, 9780–9783 CrossRef CAS PubMed.
- S. Ito, S. Kimura and M. Yoshifuji, Chem. Lett., 2002, 708–709 CrossRef CAS.
- T. W. Mackewitz, D. Ullrich, U. Bergsträsser, S. Leininger and M. Regitz, Liebigs Ann., 1997, 1827–1839 CrossRef CAS.
- M. Hobbold, R. Streubel, M. H. A. Benvenutti, P. B. Hitchcock and J. F. Nixon, Organometallics, 1997, 16, 3726–3728 CrossRef CAS.
- R. Streubel, M. Hobbold, J. Jeske and P. G. Jones, Angew. Chem., Int. Ed. Engl., 1997, 36, 1095–1097 CrossRef CAS.
- L. Weber, I. Schumann, H.-G. Stammler and B. Neumann, Chem. Ber., 1994, 127, 1349–1353 CrossRef CAS.
- E. Fuchs, B. Breit, H. Heydt, W. Schoeller, T. Busch, C. Kruger, P. Betz and M. Regitz, Chem. Ber., 1991, 124, 2843–2855 CrossRef CAS.
- A. Marinetti, S. Bauer, L. Ricard and F. Mathey, J. Chem. Soc., Dalton Trans., 1991, 597–602 RSC.
- L. Weber, E. Lücke, A. Müller and H. Bögge, Z. Anorg. Allg. Chem., 1990, 583, 91–101 CrossRef CAS.
- A. Marinetti, S. Bauer, L. Ricard and F. Mathey, Organometallics, 1990, 9, 793–798 CrossRef CAS.
- B. A. Boyd, R. J. Thoma, W. H. Watson and R. H. Neilson, Organometallics, 1988, 7, 572–574 CrossRef CAS.
- T. C. Klebach, R. Lourens, F. Bickelhaupt, C. H. Stam and A. van Herk, J. Organomet. Chem., 1981, 210, 211–221 CrossRef CAS.
- A. Özbolat-Schön, M. Bode, G. Schnakenburg, A. Anoop, M. van Gastel, F. Neese and R. Streubel, Angew. Chem., Int. Ed., 2010, 49, 6894–6898 CrossRef PubMed.
- J. Escudié and H. Ranaivonjatovo, Organometallics, 2007, 26, 1542–1559 CrossRef.
- S. Ito, S. Kimura and M. Yoshifuji, Org. Lett., 2003, 5, 1111–1114 CrossRef CAS PubMed.
- K. Toyota, S. Kawasaki and M. Yoshifuji, Tetrahedron Lett., 2002, 43, 7953–7959 CrossRef CAS.
- S. Ito, K. Toyota and M. Yoshifuji, J. Organomet. Chem., 1998, 553, 135–140 CrossRef CAS.
- M. Yoshifuji, K. Toyota, T. Uesugi, I. Miyahara and K. Hirotsu, J. Organomet. Chem., 1993, 461, 81–84 CrossRef CAS.
- M. Nieger, N. Siabalis and R. Appel, Z. Kristallogr., 1993, 206, 295–297 CAS.
- M. Yoshifuji, K. Toyota, T. Niitsu, N. Inamoto and K. Hirotsu, J. Organomet. Chem., 1990, 389, C12–C15 CrossRef CAS.
- M. Yoshifuji, K. Toyota, T. Sato, N. Inamoto and K. Hirotsu, Heteroat. Chem., 1990, 1, 339–342 CAS.
- V. Nesterov, L. Duan, G. Schnakenburg and R. Streubel, Eur. J. Inorg. Chem., 2011, 567–572 CrossRef CAS.
- S. Ito, S. Kimura and M. Yoshifuji, Bull. Chem. Soc. Jpn., 2003, 76, 405–412 CrossRef CAS.
- L. Weber, M. Meyer, H.-G. Stammler and B. Neumann, Chem. – Eur. J., 2001, 7, 5401–5408 CrossRef CAS.
- L. Weber, B. Quasdorff, H.-G. Stammler and B. Neumann, Chem. – Eur. J., 1998, 4, 469–475 CrossRef CAS.
- L. Boubekeur, L. Ricard, P. Le Floch and N. Mézailles, Organometallics, 2005, 24, 3856–3863 CrossRef CAS.
- L. Weber, M. Meyer, H.-G. Stammler and B. Neumann, Organometallics, 2003, 22, 5063–5068 CrossRef CAS.
- J. Grobe, D. Le Van, U. Althoff, B. Krebs, M. Dartmann and R. Gleiter, Heteroat. Chem., 1991, 2, 385–394 CrossRef CAS.
- J. Grobe, D. Le Van, J. Nientiedt, B. Krebs and M. Dartmann, Chem. Ber., 1988, 121, 655–664 CrossRef CAS.
- L. Weber, S. Uthmann, H.-G. Stammler, B. Neumann, W. W. Schoeller, R. Boese and D. Blaser, Eur. J. Inorg. Chem., 1999, 2369–2381 CrossRef CAS.
- L. Weber, Eur. J. Inorg. Chem., 2005, 4590–4597 CrossRef CAS.
- W. W. Schoeller, A. B. Rozhenko and S. Grigoleit, Eur. J. Inorg. Chem., 2001, 2891–2898 CrossRef CAS.
- J. B. Barker and M. Kilner, Coord. Chem. Rev., 1994, 133, 219–300 CrossRef CAS.
- R. T. Boeré, V. Klassen and G. Wolmershäuser, J. Chem. Soc., Dalton Trans., 1998, 4147–4154 RSC.
- R. T. Boeré, V. Klassen and G. Wolmershäuser, Can. J. Chem., 2000, 78, 583–589 CrossRef.
- M. P. Coles, Dalton Trans., 2006, 985–1001 RSC.
- F. A. Cotton, T. Inglis, M. Kilner and T. R. Webb, Inorg. Chem., 1975, 14, 2023–2026 CrossRef CAS.
- J. D. Masuda, L. Mokhtabad Amrei and R. T. Boeré, in preparation.
- G. Wilkinson, R. D. Gillard and J. A. McCleverty, Comprehensive Coordination Chemistry, Pergamon Press, New York, 1st edn, 1987 Search PubMed.
- F. H. Allen, Acta Crystallogr., Sect. B: Struct. Sci., 2002, 58, 380–388 CrossRef.
- J. Dugal-Tessier, E. D. Conrad, G. R. Dake and D. P. Gates, Phosphaalkenes, in Phosphorus(III) Ligands in Homogeneous catalysis: design and synthesis, ed. P. C. J. Kamer and P. W. N. N. van Leeuwen, Wiley, 2012, p. 239 Search PubMed.
- M. Yoshifuji, K. Shibayama, T. Hashida, K. Toyota, T. Niitsu, I. Matsuda, T. Sato and N. Inamoto, J. Organomet. Chem., 1986, 311, C63–C67 CrossRef CAS.
- P. S. Pregosin and R. W. Kunz, 31P and 13C NMR of transition metal phosphine complexes, Springer-Verlag, Berlin, 1979 Search PubMed.
- R. L. Keiter and J. G. Verkade, Inorg. Chem., 1969, 8, 2115–2120 CrossRef CAS.
- G. M. Bodner, Inorg. Chem., 1975, 14, 2694–2699 CrossRef CAS.
- İ. A. Mour, S. Ozkar and C. G. Kreiter, Z. Naturforsch., 1994, 49b, 1059–1062 Search PubMed.
- D. S. Braterman, Metal Carbonyl Spectra, Academic Press, New York, 1975 Search PubMed.
- J. Deberitz and H. Nöth, J. Organomet. Chem., 1973, 49, 453–467 CrossRef CAS.
- M. Yoshifuji, K. Toyota and N. Inamato, Tetrahedron Lett., 1985, 26, 1727–1730 CrossRef CAS.
- M. T. Nguyen, M. A. McGinn and A. F. Hegarty, Polyhedron, 1986, 5, 1223–1226 CrossRef.
- J. Grobe, D. Le Van, B. Krebs, R. Fröhlich and A. Schiemann, J. Organomet. Chem., 1990, 389, C29–C33 CrossRef CAS.
- STOE & Cie GmbH, Darmstadt 64295 Germany.
- G. M. Sheldrick, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 2015, 71, 3–8 CrossRef PubMed.
- A. Thorn, B. Dittrich and G. M. Sheldrick, Acta Crystallogr., Sect. A: Fundam. Crystallogr., 2012, 68, 448–451 CrossRef CAS.
- C. F. Macrae, I. J. Bruno, J. A. Chisholm, P. R. Edgington, P. McCabe, E. Pidcock, L. Rodriguez-Monge, R. Taylor, J. van de Streek and P. A. Wood, J. Appl. Crystallogr., 2008, 41, 466–470 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, J. A. Montgomery Jr., T. Vreven, K. N. Kudin, J. C. Burant, J. M. Millam, S. S. Iyengar, J. Tomasi, V. Barone, B. Mennucci, M. Cossi, G. Scalmani, N. Rega, G. A. Petersson, H. Nakatsuji, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, M. Klene, X. Li, J. E. Knox, H. P. Hratchian, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, P. Y. Ayala, K. Morokuma, G. A. Voth, P. Salvador, J. J. Dannenberg, V. G. Zakrzewski, S. Dapprich, A. D. Daniels, M. C. Strain, O. Farkas, D. K. Malick, A. D. Rabuck, K. Raghavachari, J. B. Foresman, J. V. Ortiz, Q. Cui, A. G. Baboul, S. Clifford, J. Cioslowski, B. B. Stefanov, G. Liu, A. Liashenko, P. Piskorz, I. Komaromi, R. L. Martin, D. J. Fox, T. Keith, M. A. Al-Laham, C. Y. Peng, A. Nanayakkara, M. Challacombe, P. M. W. Gill, B. Johnson, W. Chen, M. W. Wong, C. Gonzalez and J. A. Pople, Gaussian 03, Revision C.02, Gaussian, Inc., Wallingford CT, 2004 Search PubMed.
- HyperChem™ Release 8.0.10 for Windows, Hypercube Inc., 1995–2011 Search PubMed.
- N. Nebra, C. Lescot, P. Dauban, S. Mallet-Ladeira, B. Martin-Vaca and D. Bourissou, Eur. J. Org. Chem., 2013, 984–990 CrossRef CAS.
Footnotes |
† Electronic supplementary information (ESI) available: Thermal ellipsoid plots of isostructural 11a, 12; table of P![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bond distances from the CSD, with structure diagrams; DFT structure of 10 and overlay with X-ray geometry; graphs of correlations between out-of-plane distances and dihedral angles with P C bond distances from the CSD, with structure diagrams; DFT structure of 10 and overlay with X-ray geometry; graphs of correlations between out-of-plane distances and dihedral angles with P![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C distances; additional FTIR data; refined disorder model of 11b, crystal and refinement parameters; Cartesian coordinates of DFT structures. CCDC 1421316–1421320. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c5dt03393d C distances; additional FTIR data; refined disorder model of 11b, crystal and refinement parameters; Cartesian coordinates of DFT structures. CCDC 1421316–1421320. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c5dt03393d |
| ‡ Phosphorus can substitute for one or both nitrogen atoms in the organic amidine functional group where the pnictogens are normally in the +3 oxidation state, resulting in 1(λ3,σ2)-monophosphaamidines or 1,3(λ3,σ2)-diphosphaamidines, which can then form the corresponding phosphaamidinates if there is at least one ionisable hydrogen atom. Alternatively, phosphorus in the +5 oxidation state can replace the backbone carbon atom, resulting in inorganic 2(λ5,σ2)-phosphaamidines and amidinates;77 the latter modality has previously been named “fosfam”. |
| This journal is © The Royal Society of Chemistry 2016 |