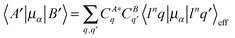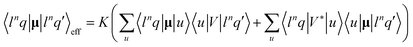Chiral sensing of amino acids and proteins chelating with Eu^III complexes by Raman optical activity spectroscopy

Abstract

Chiroptical spectroscopy of lanthanides sensitively reflects their environment and finds various applications including probing protein structures. However, the measurement is often hampered by instrumental detection limits. In the present study circularly polarized luminescence (CPL) of a europium complex induced by amino acids is monitored by Raman optical activity (ROA) spectroscopy, which enables us to detect weak CPL bands invisible to conventional CPL spectrometers. In detail, the spectroscopic response to the protonation state could be studied, e.g. histidine at pH = 2 showed an opposite sign of the strongest CPL band in contrast to that at pH = 7. The spectra were interpreted qualitatively on the basis of the ligand-field theory and related to CPL induced by an external magnetic field. Free energy profiles obtained by molecular dynamic simulations for differently charged alanine and histidine forms are in qualitative agreement with the spectroscopic data. The sensitivity and specificity of the detection promise future applications in probing peptide and protein side chains, chemical imaging and medical diagnosis. This potential is observed for human milk and hen egg-white lysozymes; these proteins have a similar structure, but very different induced CPL spectra.

---

Introduction

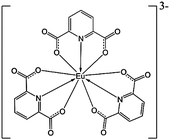
Lanthanide complexes are popular probes used in analytical and medicinal chemistry.^1,2 They exhibit unique spectroscopic properties due to their electronic structure, such as the relatively isolated 4f-shell electrons and a wealth of spectroscopically active electronic transitions.³ Their luminescence is particularly sensitive to the environment of the lanthanide metal; circularly polarized luminescence (CPL), difference in the emission of left- and right-circularly polarized light, provides additional information about molecular chirality, and is thus commonly employed in biologically oriented applications.^4–7

However, the development of molecular biologically relevant probes based on lanthanides is not straightforward. For example, many europium(III) complexes decompose in the aqueous environment⁸ or the luminescence in water solutions is strongly affected by interaction with the O–H groups. The Na₃[Eu(DPA)₃] complex (Scheme 1) used here and similar tris-dipicolinate (DPA) complexes of lanthanides appear to be more universal because they are stable also in water. Such complexes can also be prepared relatively easily and their chiral spectroscopic response sensitively reflects their chemical neighborhood.

Scheme 1 The [Eu(DPA)₃]³⁻ ion.

The sensitivity comes from the unperturbed geometry of the complex that possesses the D₃ symmetry and forms enantiomers of opposite helicity. They can be imagined as left- and right-propellers and in a standard notation they are referred to as “Δ” and “Λ”. In achiral samples they are present in equal amounts. However, the Δ ↔ Λ equilibrium can be perturbed by interactions with chiral ligands, as revealed by previous CPL experiments.^9–14 In general, such chirality transfer is referred to as the Pfeiffer effect.¹⁵

So far, CPL experiments on induced chirality in metal complexes used weak excitation sources and were mostly oriented to detect strong CPL bands in crystals exhibiting high CPL to total luminescence ratios.¹⁶ Only recently, solution complexes providing a strong signal were targeted by this technique as well.^14,17 In the Raman optical activity (ROA) instrument the luminescence is excited by more intense laser radiation; in addition the circularly polarized components are detected using a sensitive artifact-resistant detection scheme.¹⁸ Thus very weak fluorescence bands can be detected as well. In a recent study, we discussed how the fluorescence can be distinguished from the “true” vibrational Raman bands.¹⁹ A disadvantage of the ROA–CPL approach lies in a limited spectral range of the detected fluorescence (approximately 535–610 nm), i.e. the transitions need to be close to the laser 532 nm excitation radiation. For europium(III) this is a minor drawback only because the metal has a large number of luminescence bands, including about sixty ⁵D → ⁷F transitions in the measurable region. For the systems investigated in the present study, only the strongest bands would be detectable on traditional CPL instruments.

The ROA technique has been developed to measure tiny differences in scattering of the right- and left-circularly polarized light caused by vibrational transitions in chiral molecules.^20,21 It has been applied to a wide range of systems including small organic compounds, complex proteins, saccharides and nucleic acids.^22–26 The difference is difficult to measure; for a typical molecule the ratio of the ROA and Raman signal (“CID”, circular intensity difference) is about 10⁻⁴. Therefore, a strong and easily detectable signal in the presence of lanthanide metal attracted attention for both the plain Raman^27,28 and the ROA^29–31 spectra. As pointed out above, the strongest “ROA” bands correspond neither to Raman scattering nor to vibrational transitions, but they originate from circularly polarized luminescence initiated by the laser radiation.¹⁹

Before, we could detect a record-high CPL activity of a Cs–Eu^III complex by ROA.¹⁹ The dissymmetry factor (“g”, CPL analogue of the CID) of this complex was 1.4, corresponding to a CID of 1.4/2 = 0.7.^32,33 The aqueous complexes studied here provide much smaller g; however, they exhibit remarkable sensitivity to the type and the protonation state of amino acid chain.

At present, a priori theoretical tools providing the link between the spectra and the structure are not available. The principle problems lie in the complicated lanthanide electronic structure, so far fairly inaccessible by contemporary quantum chemistry. Nevertheless, we use the empirical crystal field theory^34–36 enabling us to assign the observed transitions, and on a semi-quantitative basis model the induced chirality.

To document that the structural sensitivity remains even when the europium compound reacts with proteins and thus indicate a more wide range of potential applications of this technique, we also report induced CPL spectra of two structurally very close proteins, human milk and hen egg-white lysozymes. They provide opposite spectral patterns; in fact, we are not aware of any other spectroscopy that would provide signals so different as CPL.

Results and discussion

Eu^III CPL induced by alanine

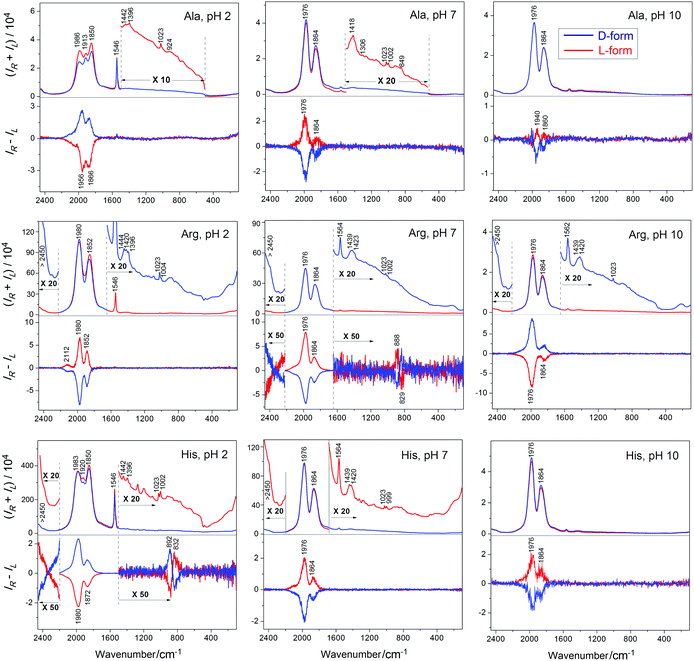
CPL spectra of complex Na₃[Eu(DPA)₃] induced by alanine provide rather weak signals. The Raman (luminescence) and ROA (CPL) spectra are plotted in Fig. 1 (top). At pH 7 and 10, the (total) luminescence is dominated by two strong 1864 and 1976 cm⁻¹ bands, both corresponding to ⁵D₀ → ⁷F₁ transitions of Eu³⁺.³ These are accompanied by corresponding circularly polarized luminescence bands. At pH 2, the fluorescence splits into more bands, and a band at 1546 cm⁻¹ significantly gains in intensity. The highest CID ratio of the polarized and total luminescence components is about 1 × 10⁻⁴ and corresponds to the weak interaction between alanine and the complex (selected CID ratios are listed in Table S1, ESI†). Still, the spectral intensities are much higher than Raman and vibrational ROA of alanine. In the zoomed insets, a few Raman bands may be recognized while ROA is invisible at this scale. True vibrational ROA of alanine is also impossible to measure at such low concentrations. At high concentrations of alanine, observed ROA CID ratios of ∼3 × 10⁻⁴ (Fig. S1, ESI†) are larger than those corresponding to Eu(III) CPL.

Fig. 1 [Eu(DPA)₃]³⁻ (2 mM) Raman and ROA spectra in the presence of L- and D-alanine (20 mM), L- and D-arginine (12 mM) and L- and D-histidine (24 mM) at pH 2, 7 and 10 (experimental details are listed in the Experimental section).

Eu^III CPL induced by histidine and arginine

As discussed before amino acids with the polar side chains interact much more strongly with Na₃[Eu(DPA)₃] and similar complexes than alanine.^16,37 The luminescence, and in particular CPL, is also very sensitive to pH and the protonation state. One can see (Fig. 1), for example, that the low pH of 2 supports a high luminescence intensity of the 1546 cm⁻¹ (⁵D₀ → ⁷F₀) band. Neutral (7) and basic (10) pH provide very similar Raman spectra. In the magnified “Raman” spectra the true vibrational Raman scattering signal specific for each amino acid and the complex is apparent as well: dipicolinate centers around 1420 and 1023 cm⁻¹, and Raman bands of histidine and arginine can be recognized, for example, as CH₂ wagging around 1439 cm⁻¹, C–N valence, ring vibration at 999 cm⁻¹, etc.^38,39 Vibrational Raman and ROA spectra of pure histidine and arginine can be found in Fig. S2 and S3 (ESI†).

The ROA intensities in Fig. 1 comprise CPL only; vibrational ROA at these low concentrations is invisible as for alanine. But the CID ratios are much higher for the charged amino acids, with a maximum of ∼0.007 for the protonated (pH = 2) form of histidine (which can be gradually increased to ∼0.014 with higher concentration of histidine, Fig. S5, ESI†), indicating a much stronger interaction with the europium complex than for alanine. The weakest interaction, at least as judged from the low CID of 4 × 10⁻⁵, is indicated between [Eu(DPA)₃]³⁻ and histidine at pH = 10 (Table S1, ESI†). For the protonated form of histidine and the neutral form of arginine ⁵D₁ → ⁷F₂ transition gives rise to a weak but measurable CPL. This signal appears in a form of couplets (close positive and negative band), different from the one-sign pattern of the strongest bands, which suggests a different mechanism of chirality induction, most probably associated with a perturbation of the D₃ symmetry of the Λ and Δ forms of the complex. Above 2400 cm⁻¹, the signal of a ⁵D₀ → ⁷F₂ band is partially observable as a shoulder, which is at the limit of the operational instrumental range and the intensity might not be reliable.

The complex chirality control achieved by the environmental pH value appears to be very interesting. Let us arbitrarily associate the Λ-configuration of the complex with the positive signal at 1970 cm⁻¹. Then for arginine we observe the following possibility of chirality changes by pH:

Λ (pH = 2) ↔ Λ (pH = 7) ↔ Δ (pH = 10)

For alanine and histidine, we get:

Δ (pH = 2) ↔ Λ (pH = 7) ↔ Λ (pH = 10)

Spectral changes beyond this scheme, such as slight intensity redistribution, band shifts and the occasional appearance of the weaker bands, can be considered as second-order effects.

Eu^III CPL induced by tartaric acid and an external magnet

The spectrum induced by tartaric acid (Fig. 2) is similar to that of alanine, but the two strongest luminescence bands are broader and shifted (to 1978 and 1858 cm⁻¹) and a narrow band appears at 1546 cm⁻¹ (⁵D₀ → ⁷F₀ transition). CPL bands are broader as well, and the CID of the strongest bands increases to 1.7 × 10⁻⁴.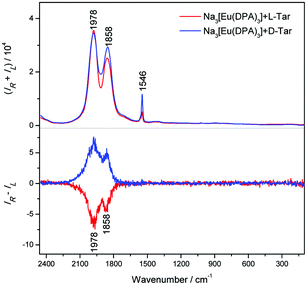

Fig. 2 Raman (upper) and ROA (lower) spectra of complexes with [Eu(DPA)₃]³⁻ (2 mM) with L- and D-forms of tartaric acid (20 mM); the accumulation time was 2 hours.

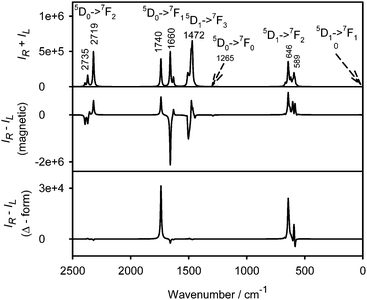
Raman and magnetic ROA spectra⁴⁰ of aqueous solution of plain Na₃[Eu(DPA)₃] (Fig. 3) confirm that the bands observed in the complexes with amino acids originate in europium electronic transitions and facilitate their assignment. Although pure electronic magnetic Raman optical activity has been reported for heavy metal complexes as well,^21,41 control measurements with a 404 nm excitation laser and the degree of circularity confirm¹⁹ that at least the strongest bands are almost exclusively formed by the luminescence and correspond to those observed in the chiral complexes. Only few bands corresponding to the “true” vibrational Raman scattering of the tris(pyridine-2,6-dicarboxylate) ligand can be recognized, such as the CC ring stretch at ∼1423 cm⁻¹ and symmetric breathing mode of the pyridine ring at ∼1023 cm⁻¹.^42,43

Fig. 3 Raman (upper) and magnetic ROA (lower) of Na₃[Eu(DPA)₃] (2 mM) water solution; the accumulation time was 20 minutes.

The magnetic ROA spectra (Fig. 3, lower) are again mostly formed by circularly polarized luminescence. Band positions correspond to those in the complexes with amino acids, but the sign pattern and relative intensities are different, which reflects the different mechanisms of optical activity induced by the magnetic field and by the complexations with chiral ligands. This is best documented on the strongest signal within 1800–2100 cm⁻¹ providing a multiple sign pattern in magnetic ROA/CPL, where the amino acids induced one sign pattern only. In the magnetic field, additional weaker magnetic ROA/CPL bands below 250 cm⁻¹ can be observed, assignable to ⁵D₁ → ⁷F₁ transitions within the Eu³⁺ f-shell electronic system.^3,13,19,44 The strongest observed transitions of Na₃[Eu(DPA)₃] and its complexes with histidine and arginine are summarized in Table 1. The transition assignment is based on the crystal field theory^3,45 and the electronic structure of free Eu³⁺ ions, which is not much perturbed in the complexes.

Table 1 Assignment of the observed Na₃[Eu(DPA)₃] transition in the magnetic and induced CPL experiments, the Raman shift (δ) from the 532 nm laser excitation and the corresponding wavelength (λ) of the emitted light

Transition	Magnetic CPL		Induced CPL-His		Induced CPL-Arg
	δ/cm^−1	λ/nm	δ/cm^−1	λ/nm	δ/cm^−1	λ/nm
^5D0 → ^7F2	>2450	615	>2450	615	>2450	615
	2362	608
	2300	606
^5D0 → ^7F1	2001	595	1983	595	1976	595
	1976	594	1980	595
	1954	594	1920	592
^5D0 → ^7F1	1868	591	1872	591	1864	591
	1864	591	1850	590
^5D0 → ^7F0	1655	583	1546	580	1546	580
^5D1 → ^7F2	909	550	892	558	888	558
	854	557	832	557	829	557
	835	557
	808	556
^5D1 → ^7F1	243	539

---

Theoretical analysis

The crystal field theory also provides a handy tool to qualitatively model the Eu³⁺ spectral intensities and assign observed transition. The calculated luminescence, magnetic and ordinary CPL of the [Eu(DPA)₃]³⁻ ion are plotted in Fig. 4. As expected for an empirical model, the calculated transition energies differ from the observed ones by 200–300 cm⁻¹ and relative spectral intensities are not always matching the experiment, otherwise the simulated spectra well correspond to the observation. For example, the highest-wavenumber transition observed at ∼2000 cm⁻¹ is reproduced at 1740 cm⁻¹, although its relative intensity is significantly underestimated, the lowest one observed at ∼240 cm⁻¹ is reproduced at ∼0 cm⁻¹ (= 532 nm), etc. As in experiment, CPL induced by the magnetic field is different from that exhibited by an enantiomeric (Δ) form, magnetic CPL above 2300 cm⁻¹ is relatively strong compared to (ordinary) CPL, and the strongest ⁵D₀ → ⁷F₁ region exhibits both positive and negative magnetic CPL, while for CPL rather one-sign pattern is simulated. Note that the y-scale has no meaning for magnetic CPL because absolute magnitudes of transition matrix elements are not known.

Fig. 4 Raman, magnetic and ROA/CPL Δ-Na₃[Eu(DPA)₃] spectra and state assignment simulated using the crystal field theory. The y-scale is arbitrary, but the (I_R − I_L (Δ))/(I_R + I_L) ratio is meaningful.

Chiral recognition mechanism

In spite of the large chiroptical effect, the complexes of [Eu(DPA)₃]³⁻ with the amino acids do not appear particularly stable. For example, Raman and ROA spectra of the L-His/Na₃[Eu(DPA)₃] complex measured at different temperatures (Fig. S4, ESI†) reveal that the induced CPL almost vanishes at 90 °C. Also, the dependence of CID on the amino acid/Na₃[Eu(DPA)₃] molar ratio (Fig. S5, ESI†) exhibits a slow convergence and indicates a small stability constant of the resultant “super-complex”.

At present, we do not know the accurate structure of the amino acid associated with the [Eu(DPA)₃]³⁻ ion. Clearly, the positively charged histidine and arginine forms are most attracted to the negatively charged complex, cf. Fig. S6 (ESI†) with its electrostatic potential. The ion pairing, however, can produce high CID and strong CPL only for an interaction additionally sensitive to [Eu(DPA)₃]³⁻ chirality.⁴⁶ This can be provided by hydrogen bonding and electrostatic attractions between the COO⁻ groups of [Eu(DPA)₃]³⁻ and polar amino acid parts, as well as by π–π interactions and van der Waals attraction.

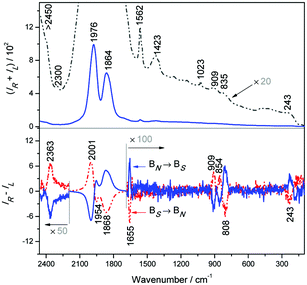
For selected systems we ran molecular dynamics simulations and obtained free energy profiles using the weighted histogram analysis method (WHAM).^35,36 For alanine (Fig. 5) we can see that the protonated (Ala⁺) form is predicted to interact most strongly with the [Eu(DPA)₃]³⁻ ion, with two minima of the energy at approximately 5 and 7 Å. For the Δ-form, the minima have about the same value (−0.8 kcal mol⁻¹), whereas for the Λ-form the distance of 7 Å is more favoured. Note also the energy maximum at ∼9.5 Å, which corresponds to disruption of the hydration spheres of [Eu(DPA)₃]³⁻ and Ala⁺ when they are coming closer.

Fig. 5 Calculated free energy profiles for different L-alanine forms interacting with Δ and Λ enantiomers of [Eu(DPA)₃]³⁻.

For alanine in the zwitterionic form (Ala_zw, middle in Fig. 5) only a very shallow (−0.2 kcal mol⁻¹) minimum appears at ∼7.5 Å for the Λ-enantiomer of [Eu(DPA)₃]³⁻. For Ala_zw and the Δ-enantiomer, as well as for the deprotonated amino acid (Ala⁻, bottom of the figure), no significant minima of the energy are apparent. This behavior qualitatively well corresponds to the spectroscopic results (Fig. 1), where Ala⁺ provided the largest chiral response while the other forms gave much weaker CPL intensities.

Similar behaviour of the free energy was obtained also for histidine (Fig. 6). However, its energy profiles for the Δ and Λ enantiomers are more different than those for alanine, and the energy scale suggests that the interaction with [Eu(DPA)₃]³⁻ is in general stronger. For example, the double-protonated form (His²⁺) provides only a weak (∼−0.7 kcal mol⁻¹) energy minimum with the Λ-enantiomer, but its associate with the Δ-enantiomer of [Eu(DPA)₃]³⁻ is stabilized by 3.1 kcal mol⁻¹ around 8 Å. This is in agreement with both the spectroscopic results described above (Fig. 1) and the different histidine structure providing more binding sites than alanine.

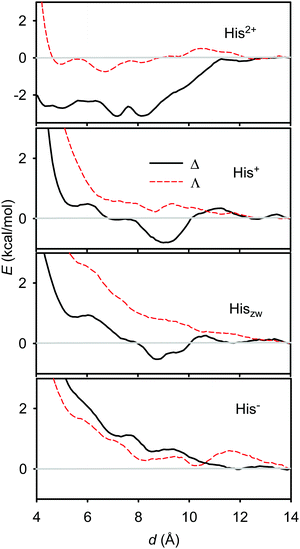Fig. 6 Calculated free energy profiles for different L-histidine forms interacting with Δ and Λ enantiomers of [Eu(DPA)₃]³⁻.

Geometries of His²⁺ associates with Δ- and Λ-[Eu(DPA)₃]³⁻ obtained by the molecular dynamic simulations are shown in Fig. 7. As also shown in Fig. 6, the formation of the first system is associated with the stabilization energy of 3.1 kcal mol⁻¹, while the second is stabilized by 0.7 kcal only. At this point, however, we wish to warn the reader that although the simulations provide a plausible explanation of the experiment, they may be hampered by limited configurational sampling, restriction to one protonation state, a 1 : 1 complex : amino acid ratio, and force field accuracy. Nevertheless, the results document the possibility of chiral discrimination and the energetics and stereochemistry involved. For the first structure in Fig. 7, for example, a π–π stacking between the histidine five-membered ring and the DPA ligand is possible, while the Δ configuration does not enable it. More realistic energy and geometry estimates are intended for future studies as the perturbation of the Δ ↔ Λ equilibrium is associated with rather small energy differences, which are especially difficult to reproduce for the weak chirality sensitive interactions.⁴⁷ For the ⁵D₀ → ⁷F₁ transition in [Eu(DPA)₃]³⁻ a maximal g-factor of ∼0.1 was reported,⁴⁸ which again indicates a partial stereoselection in our experiments only.

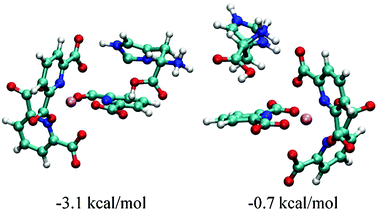Fig. 7 Geometries and formation free energies of L-histidine complexes with the Δ (left) and Λ (right) form of [Eu(DPA)₃]³⁻.

[Eu(DPA)₃]³⁻ complexes with human milk and hen egg-white lysozymes

Luminescence and induced CPL spectra of the lysozyme mixtures with [Eu(DPA)₃]³⁻, together with the vibrational Raman and ROA spectra of pure proteins as obtained in ref. 49, are shown in Fig. 8. The two proteins are fairly similar, and the vibrational ROA/Raman spectra (upper part of the figure) differ in minor features only. Also the luminescence spectra are almost the same. However, the [Eu(DPA)₃]³⁻ complex in the presence of the lysozymes provides induced CPL spectra of different chiralities. The strong ⁵D₀ → ⁷F₁ 1976 and 1875 cm⁻¹ bands of human milk lysozyme provide CID ratios of 1.46 × 10⁻² and 7.14 × 10⁻³, respectively, and the signal remains detectable at a much lower concentration (0.5 mg ml⁻¹) of the protein than needed for classical vibrational ROA measurements (>100 mg ml⁻¹). The hen egg-white lysozyme inverses the CPL sign of the strongest bands and provides in absolute magnitude bigger CIDs of −4.65 × 10⁻² and −2.24 × 10⁻². A similar change occurs for the weaker bisignate ⁵D₁ → ⁷F₂ CPL signal at 838 and 887 cm⁻¹. Note that such an induced CPL signal takes full advantage of the ROA laser resource (1000 mW) which is not accessible by traditional CPL spectrometers. The observation is consistent with the sensitive response of the Δ ↔ Λ equilibrium to the individual amino acid chains, and indicates the potential of the method in biochemical analyses.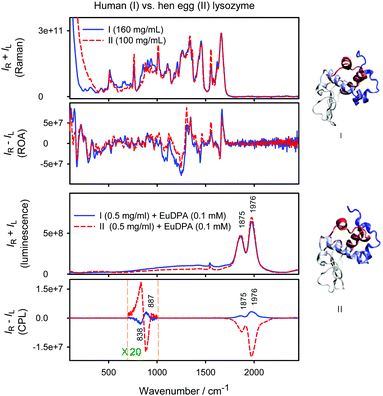

Fig. 8 Normalized Raman and ROA spectra of human milk and hen-egg lysozyme (from ref. 49) and luminescence and CPL spectra of the complexes with [Eu(DPA)₃]³⁻ (this work).

Experimental

Synthesis of the Eu^III complex

The Na₃[Eu(DPA)₃] (DPA = dipicolinate = 2,6-pyridinedicarboxylate) complex was obtained by a reaction of europium carbonate and pyridine-2,6-dicarboxylic acid in the 1 : 3 molar ratio in water, and pH was adjusted to 7 by adding 1 M sodium carbonate solution.

ROA and magnetic ROA experiments

Backscattering Raman and scattered circular polarization (SCP) ROA spectra were acquired on a BioTools ROA spectrometer operating with laser excitation at 532 nm at a resolution of 7 cm⁻¹, and the laser power at the sample was 200–1000 mW. Accumulation times were 1 hour for the ROA spectra of histidine–Eu^III complexes at pH = 2 and arginine at pH = 7; 4 hours for spectral panels of histidine–Eu^III at pH = 7 and Arginine–Eu^III at pH = 2, 10; and 20 hours for spectral panels of histidine–Eu^III at pH = 10 and alanine–Eu^III at pH = 2, 7 and 10, respectively. Magnetic ROA (MROA) spectra^41,50 were acquired under similar conditions, using a magnetic cell providing a field of about 1.5 tesla.⁴⁰ The collection time was 20 min for the MROA spectrum of Na₃[Eu(DPA)₃] with a concentration of 2 mM in water. For ROA spectral measurements of pure amino acids, the collection times were 10 h with a concentration of 0.5 M for L/D-alanine, 0.24 M for L/D-histidine and 0.34 M for L/D-arginine. The pH value was adjusted using 0.1 M HCl or NaOH aqueous solutions. Human milk and hen egg-white lysozymes (Sigma-Aldrich) were dissolved in water. For Raman, ROA and degree of circularity spectral measurements the protein concentration was 0.5 mg ml⁻¹ and the EuDPA complex concentration was 0.1 mM; the measurement took 1 hour. All experiments were performed at room temperature (20 °C). Raman spectra are presented after subtraction of the water background signal. Note that Raman spectra also comprise the total luminescence and the ROA spectra comprise circularly polarized luminescence.

Theoretical calculations

[Eu(DPA)₃]³⁻ geometry was optimized by energy minimization using the Gaussian 09⁵¹ program, the B3LYP functional, the MWB28 pseudopotential and basis set for Eu, and the 6-31G(d,p) basis set for the other atoms. The solvent was modelled by a conductor-like polarizable continuum solvent model (CPCM).⁵²

To assign spectral peaks and approximately simulate spectral intensities, the semi-empirical crystal theory was used.^3,53 The crystal (ligand) potential in Na₃[Eu(DPA)₃] was calculated from ligand electronic density obtained using Gaussian at the B3LYP/6-31G(d,p)/PCM approximation level. The europium wavefunctions and energies were obtained using the Lanthanide program.³⁴ Then spectral intensities were generated using our AnalCFP program interfaced to Lanthanide, using the perturbational approach^54–56 where the Eu³⁺ free-ion wavefunction was perturbed by the same DPA ligand electrostatic potential. For example, the electric dipole moment matrix element for a transition between states A and B (α = x, y, or z) was calculated as

where C^X_q are the expansion coefficients to individual electronic configurations lⁿq′ (n = 6 electrons in l = f-shell). Effective dipole moments among the configurations were obtained as
where K is a constant, V is the ligand electrostatic potential, and u denote configurations where one electron is transferred to the g or d-shell. Note that the plain dipole moments within the f-shell configurations 〈f⁶q|μ_α|f⁶q′〉 are zero; thus the spectrum is very sensitive to the lanthanide environment entering through the potential V. For magnetic CPL, the sum over states formula was used as developed previously for magnetic circular dichroism.⁵⁷ The potential was calculated from nuclear charges and electron density obtained by the Gaussian calculation.

Interaction of L-histidine with the Λ and Δ [Eu(DPA)₃]³⁻ forms was also studied using molecular dynamics and the Amber14⁵⁸ software. Variously protonated histidine and alanine amino acids with the [Eu(DPA)₃]³⁻ ion were placed inside a cubic box (30 Å a side) filled with water molecules. For a large distance of the two components, the energy of the system was minimized, and the geometry was equilibrated during a 1 ns NVT dynamics, using an integration step of 1 fs, temperature of 300 K, and the GAFF⁵⁹ (DPA ligands), Amber14SB⁶⁰ (alanine and histidine) and TIP3P⁶¹ (water) force fields. Europium parameters were taken from ref. 62. Then the distance between carbonyl oxygen of histidine/alanine and europium was decreasing (14–4 Å) in 1 Å steps using 1 ns long constrained dynamics runs and a harmonic potential force constant of 2 kcal Å⁻² mol⁻¹. From resultant histograms the potential of mean force was obtained via the weighted histogram analysis method (WHAM).^35,36

Conclusions

We synthesized the water-soluble Na₃[Eu(DPA)₃] complex and explored its chirality induced by model amino acids. Due to the sensitive ROA instrumentation very weak CPL bands could be detected, invisible to conventional CPL experiments. The results confirm a tight link between measured CPL spectra patterns and the structure; in particular, the circularly polarized component was found to be extremely sensitive to the nature of the interacting ligand. Magnetic ROA spectra were measured as well, comprising mostly magnetically induced CPL, which enabled us to better discriminate and assign observed transitions. On a semi-quantitative basis, the relation of spectral intensities to fine structural changes could be modelled by the crystal field theory, which also confirmed the assignment of the transitions. For various alanine and histidine forms the molecular dynamics modelling confirmed the possibility of chiral discrimination, e.g. it indicated that the π–π stacking involving histidine side chain and electrostatic interactions may be equally important for the complex stabilization. Significant differences in induced CPL in the presence of human milk and hen egg-white lysozymes suggest that the sensitivity of the [Eu(DPA)₃]³⁻ complex may facilitate its applications for sensitive protein detection in analytical chemistry and chemical imaging.

Acknowledgements

This work was supported by the Czech Science Foundation (16-08764Y, 16-05935 and S15-09072S).

Notes and references

1. M. C. Heffern, L. M. Matosziuk and T. J. Meade, Chem. Rev., 2014, 114, 4496–4539.
2. J. C. G. Bunzli and S. V. Eliseeva, Chem. Sci., 2013, 4, 1939–1949.
3. K. Binnemans, Coord. Chem. Rev., 2015, 295, 1–45.
4. F. Zinna and L. Di Bari, Chirality, 2015, 27, 1–13.
5. L. Benda, J. Štěpánek, J. Kaminský and P. Bouř, in Comprehensive Chirality, ed. E. M. Carreira and H. Yamamoto, Elsevier, Amsterdam, 2012, vol. 8, pp. 520–544.
6. L. Benda, P. Bouř, N. Müller and V. Sychrovský, J. Phys. Chem. B, 2009, 113, 5273–5281.
7. E. M. Sanchez-Carnerero, A. R. Agarrabeitia, F. Moreno, B. L. Maroto, G. Muller, M. J. Ortiz and S. de la Moya, Chem. – Eur. J., 2015, 21, 13488–13500.
8. V. Andrushchenko, D. Padula, E. Zhivotova, S. Yamamoto and P. Bouř, Chirality, 2014, 26, 655–662.
9. H. G. Brittain, Inorg. Chem., 1981, 20, 3007–3013.
10. H. G. Brittain, J. Coord. Chem., 1989, 20, 331–347.
11. E. Huskowska and J. P. Riehl, Inorg. Chem., 1995, 34, 5615–5621.
12. G. Muller and J. P. Riehl, J. Fluoresc., 2005, 15, 553–558.
13. P. Gawryszewska, J. Legendziewicz, Z. Ciunik, N. Esfandiari, G. Muller, C. Piguet, M. Cantuel and J. P. Riehl, Chirality, 2006, 18, 406–412.
14. A. Moussa, C. Pham, S. Bommireddy and G. Muller, Chirality, 2009, 497–506.
15. S. Kirschner, N. Ahmad, C. Munir and R. J. Pollock, Pure Appl. Chem., 1979, 51, 913–923.
16. J. P. Riehl and G. Muller, in Comprehensive chiroptical spectroscopy, volume 1: Instrumentation, methodologies, and theoretical simulations, ed. N. Berova, P. L. Polavarapu, K. Nakanishi and R. W. Woody, John Wiley & Sons, New Jersey, 2012, vol. 1, pp. 65–90.
17. B. T. Nguyen, A. J. Ingram and G. Muller, Chirality, 2016, 28, 325–331.
18. W. Hug, Appl. Spectrosc., 2003, 57, 1–13.
19. T. Wu, J. Kapitán, V. Mašek and P. Bouř, Angew. Chem., Int. Ed., 2015, 54, 14933–14936.
20. L. Nafie, Vibrational optical activity: Principles and applications, Wiley, Chichester, 2011.
21. L. D. Barron, Molecular Light Scattering and Optical Activity, Cambridge University Press, Cambridge, 2004.
22. J. Haesler, I. Schindelholz, E. Riguet, C. G. Bochet and W. Hug, Nature, 2007, 446, 526–529.
23. S. Luber and M. Reiher, ChemPhysChem, 2010, 11, 1876–1887.
24. E. W. Blanch, L. Hecht, C. D. Syme, V. Volpetti, G. P. Lomonossoff, K. Nielsen and L. D. Barron, J. Gen. Virol., 2002, 83, 2593–2600.
25. E. W. Blanch, I. H. McColl, L. Hecht, K. Nielsen and L. D. Barron, Vib. Spectrosc., 2004, 35, 87–92.
26. Z. Q. Wen, L. D. Barron and L. Hecht, J. Am. Chem. Soc., 1993, 115, 285–292.
27. M. Vargek, T. B. Freedman, E. Lee and L. A. Nafie, Chem. Phys. Lett., 1998, 287, 359–364.
28. J. A. Koningstein, Russ. Chem. Rev., 1973, 42, 834–850.
29. S. Yamamoto and P. Bouř, Angew. Chem., Int. Ed., 2012, 51, 11058–11061.
30. C. Merten, H. Li, X. Lu, A. Hartwiga and L. A. Nafie, J. Raman Spectrosc., 2010, 41, 1563–1565.
31. T. Wu, J. Hudecová, X. Z. You, M. Urbanová and P. Bouř, Chem. – Eur. J., 2015, 21, 5807–5813.
32. J. L. Lunkley, D. Shirotani, K. Yamanari, S. Kaizaki and G. Muller, J. Am. Chem. Soc., 2008, 130, 13814–13815.
33. J. L. Lunkley, D. Shirotani, K. Yamanari, S. Kaizaki and G. Muller, Inorg. Chem., 2011, 50, 12724–12732.
34. S. Edvardsson and D. Åberg, Comput. Phys. Commun., 2001, 133, 396–406.
35. S. Kumar, D. Bouzida, R. H. Swendsen, P. A. Kollman and J. M. Rosenberg, J. Comput. Chem., 1992, 13, 1011–1021.
36. B. Roux, Comput. Phys. Commun., 1995, 91, 275–282.
37. K. Okutani, K. Nozaki and M. Iwamura, Inorg. Chem., 2014, 53, 5527–5537.
38. E. Deplazes, W. van Bronswijk, F. Zhu, L. D. Barron, S. Ma, L. A. Nafie and K. J. Jalkanen, Theor. Chem. Acc., 2008, 119, 155–176.
39. X. Li, K. H. Hopmann, J. Hudecová, W. Stensen, J. Novotná, M. Urbanová, J. S. Svendsen, P. Bouř and K. Ruud, J. Phys. Chem. A, 2012, 116, 2554–2563.
40. J. Šebestik and P. Bouř, Angew. Chem., Int. Ed., 2014, 53, 9236–9239.
41. L. D. Barron and J. Vrbancich, J. Raman Spectrosc., 1983, 14, 118–125.
42. A. A. Kolomenskii and H. A. Schuessler, Spectrochim. Acta, Part A, 2005, 61, 647–651.
43. L. B. Kong, P. Setlow and Y. Q. Li, Analyst, 2012, 137, 3683–3689.
44. D. R. Foster and F. S. Richardson, Inorg. Chem., 1983, 22, 3996–4002.
45. J. R. G. Thorne, M. Jones, C. S. McCaw, K. M. Murdoch, R. G. Denning and N. M. Khaidukov, J. Phys.: Condens. Matter, 1999, 11, 7851–7866.
46. A. Berthod, Anal. Chem., 2006, 78, 2093–2099.
47. J. Kessler, M. Dračínský and P. Bouř, J. Phys. Chem. A, 2015, 119, 5260–5268.
48. P. Gawryszenska, J. Legendziewicz, Z. Ciunik, N. Esfandiari, G. Muller, C. Piguuet, M. Cantuel and J. P. Riehl, Chirality, 2006, 18, 406–412.
49. J. Kessler, J. Kapitán and P. Bouř, J. Phys. Chem. Lett., 2015, 6, 3314–3319.
50. L. D. Barron and J. Vrbancich, J. Raman Spectrosc., 1984, 15, 47–50.
51. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Revision D.01., 2013.
52. A. Klamt, J. Phys. Chem., 1995, 99, 2224–2235.
53. W. T. Carnall, G. L. Goodman, K. Rajnak and R. S. Rana, J. Chem. Phys., 1989, 90, 3443–3457.
54. G. S. Ofelt, J. Chem. Phys., 1962, 37, 511–520.
55. B. R. Judd, Phys. Rev., 1962, 127, 750–761.
56. F. S. Richardson and T. R. Faulkner, J. Chem. Phys., 1982, 76, 1595–1606.
57. P. Štěpánek and P. Bouř, J. Comput. Chem., 2015, 36, 723–730.
58. D. A. Pearlman, D. A. Case, J. W. Caldwell, W. S. Ross, T. E. Cheatham, S. Debolt, D. M. Ferguson, G. Seibel and P. A. Kollman, Comput. Phys. Commun., 1995, 91, 1–41.
59. J. Wang, R. M. Wolf, J. W. Caldwell, P. A. Kollman and D. A. Case, J. Comput. Chem., 2005, 25, 1157–1174.
60. K. Lindorff-Larsen, S. Piana, K. Palmo, P. Maragakis, J. L. Klepeis, R. O. Dror and D. E. Shaw, Proteins, 2010, 78, 1950–1958.
61. W. L. Jorgensen, J. Chandrasekhar and J. D. Madura, J. Chem. Phys., 1983, 79, 926–935.
62. P. Li, L. F. Song and K. M. Merz, J. Phys. Chem. B, 2015, 119, 883–895.

---

Footnote

† Electronic supplementary information (ESI) available: Raman and ROA spectra of alanine, histidine and arginine, Raman and ROA spectra of the L-His/[Eu(DPA)₃]³⁻ complex at different temperatures, CID dependence on molar ratios of L-Arg/[Eu(DPA)₃]³⁻ at pH 7 and L-His/[Eu(DPA)₃]³⁻ at pH 2, calculated [Eu(DPA)₃]³⁻ electrostatic potential, Raman and degree of circularity spectra of [Eu(DPA)₃]³⁻ chelated with human milk lysozyme, and CID ratios for ⁵D₀ → ⁷F₁ transition of the [Eu(DPA)₃]³⁻ complex induced by amino acids. See DOI: 10.1039/c6cp03968e

---