Open Access Article
Open Access ArticleVisualizing partial solvation at the air–water interface†
Kenneth D.
Judd
 ,
Sean W.
Parsons
,
Dmitry B.
Eremin
,
Sean W.
Parsons
,
Dmitry B.
Eremin
 ,
Valery V.
Fokin
and
Jahan M.
Dawlaty
,
Valery V.
Fokin
and
Jahan M.
Dawlaty
 *
*
Department of Chemistry, The University of Southern California, Los Angeles, CA 90089, USA. E-mail: dawlaty@usc.edu
First published on 24th April 2024
Abstract
Despite significant research, the mechanistic nuances of unusual reactivity at the air–water interface, especially in microdroplets, remain elusive. The likely contributors include electric fields and partial solvation at the interface. To reveal these intricacies, we measure the frequency shift of a well-defined azide vibrational probe at the air–water interface, while independently controlling the surface charge density by introducing surfactants. First, we establish the response of the probe in the bulk and demonstrate that it is sensitive to both electrostatics and hydrogen bonding. From interfacial spectroscopy we infer that the azide is neither fully hydrated nor in a completely aprotic dielectric environment; instead, it experiences an intermediate environment. In the presence of hydrogen bond-accepting sulphate surfactants, competition arises for interfacial water with the azide. However, the dominant influence stems from the electrostatic effect of their negative heads, resulting in a significant blue-shift. Conversely, for the positive ammonium surfactants, our data indicate a balanced interplay between electrostatics and hydrogen bonding, leading to a minimal shift in the probe. Our results demonstrate partial solvation at the interface and highlights that both hydrogen bonding and electrostatics may assist or oppose each other in polarizing a reactant, intermediate, or product at the interface, which is important for understanding and tuning interfacial reactivity.
Introduction
The reaction rate of many important chemical reactions is accelerated when the reaction occurs in systems with a large amount of “excess interface” between water and air or oil, in some cases by multiple orders of magnitude. This reaction enhancement has been observed in hydrophobic-water emulsions,1–4 small water droplets (<100 μm),5–7 and thin aqueous films.8,9 Reaction acceleration in these systems is often accompanied by improved product selectivity,6,10–14 and some reactions which do not proceed in bulk water such as spontaneous hydrogen peroxide generation have been found to occur in these aqueous droplets.7 These interface-rich systems have been proposed as the ideal environments for the origin of biogenic molecules15–17 and reactions relevant to the origin of life have recently been reported in microdroplets.18–22 In addition, it is believed that aqueous interfaces may have untapped potential for chemical synthesis at large scale.9,23–27 A question that remains unanswered, however, is whether these enhanced reaction rates and the related phenomena translate to the planar air/water interface. Otherwise stated, are these observations at micro-level exclusively a product of the complexity of processes occurring during nebulization, which is often used in electrospray ionization mass spectrometry?28–30 Or are these phenomena translatable at scale to preparative production of added-value chemicals using properties of aqueous interfaces, similar to phase transfer catalysis?25,31,32Currently, there is no unified theory that explains the interesting behaviour of chemical reactions at the aqueous interface. The most commonly invoked hypotheses are the presence of strong interfacial electric fields5,7,33–38 and the reaction energetics associated with partial hydration at the aqueous/hydrophobic interface.5,39–42 Electrostatics and hydration are two centrally important quantities that dictate solvation. To better understand solvation, or more specifically, electrostatics and hydrogen bonding at the air–water interface, here we report a tailored surfactant bearing an azide group that is sensitive to these effects. Azides have been extensively studied as vibrational probes in complex environments and their behaviour is well-known.43–57 Our azide surfactant forms a well-defined monolayer at the interface and its density is precisely controlled in a Langmuir trough. The electrostatics of the interface is controlled by surfactants with charged headgroups that are mixed within the azide monolayer in well-defined proportions verified by interfacial spectroscopy. Neutral alcohol-bearing surfactants are used to change the effective hydration of the probe at the interface without altering the surface electrostatics. Finally, the influence of ions in the bulk subphase is independently controlled by varying the salt concentration. With control over the above variables, the azide vibrational spectra are collected by IR Reflection Absorption Spectroscopy (IRRAS). The shift of the azide antisymmetric stretching frequency which reports on its local electrostatic and hydration environment over a few angstroms scale is analysed.
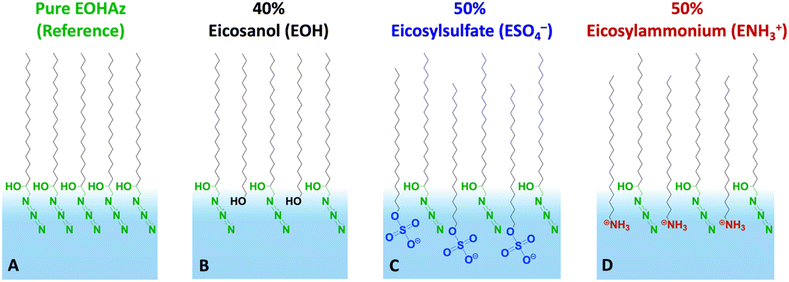
Our results reveal several new insights, including an intermediate or partially solvating interfacial environment, a balance between the electrostatics and hydrogen bonding, and the relative insensitivity of the probe to the bulk salt concentration. The cartoon in Fig. 1 depicts the various mixed monolayers in this study, along with the names of the molecules and their corresponding acronyms used in this paper.
Results and discussion
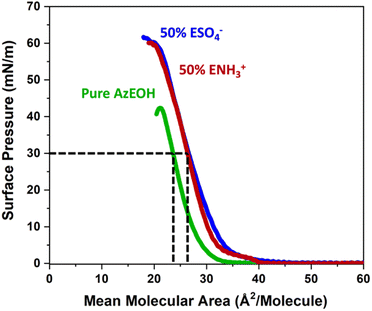
First, we present results on control over surface density of the molecules using the Langmuir trough and its verification by IRRAS. Then we will discuss the spectral shifts of the azide peak when the various tuning parameters of the experiment such as azide density, surface charge, and subphase ionic strength are varied. This will be followed by the interpretation of the shifts as a competition between electrostatics and hydration of the azide probe.The pure azide surfactant (AzEOH) produced a well-defined surface pressure–area (Π–A) isotherm shown in Fig. 2 (green line), with collapse occurring at a mean molecular area (MMA) consistent with other single-tailed saturated surfactants.58–62 Isotherms of the highest charge density mixed monolayers of sulphate and ammonium are also shown in Fig. 2. These isotherms are similar to the pure azide aside isotherm aside from a small expansion in the MMA and an increase in surface pressure at monolayer collapse, both of which are common with charged monolayers.60,63 Note that for all spectroscopic measurements, the surface pressure was held at a constant value of 30 mN m−1.
The corresponding change in the MMA for each surfactant was accounted for in calculating the net surface density of each species as:
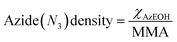 | (1) |
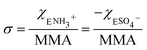 | (2) |
The MMA for each combination of species at every surface density was retrieved from multiple Π–A isotherm measurements to acquire error bars (Section S2†). With the accurately determined MMA, the surface charge density linearly increased as a function of the charged species contribution to the monolayer. It could be tuned between −1.9 e nm−2 and +1.9 e nm−2 using the two charged surfactants, with the two extremes corresponding to 50% of the molecules on the surface carrying a charge.
Mixed monolayers of ammonium were prepared over a 10 mM HCl subphase (Section S3†) to ensure its full protonation and stability as shown in previous work.64 For consistency, the same ionic strength was maintained for the mixed sulphate monolayers with 10 mM NaOH in the subphase. For further consistency, the pure azide monolayers were separately prepared over both 10 mM HCl and 10 mM NaOH, which produced identical IRRAS spectra (Section S2†) confirming the choice of ions in solution at this concentration did not affect the azide peak. The data from both acidic and basic subphases were included in the data analysis for the pure azide monolayer.
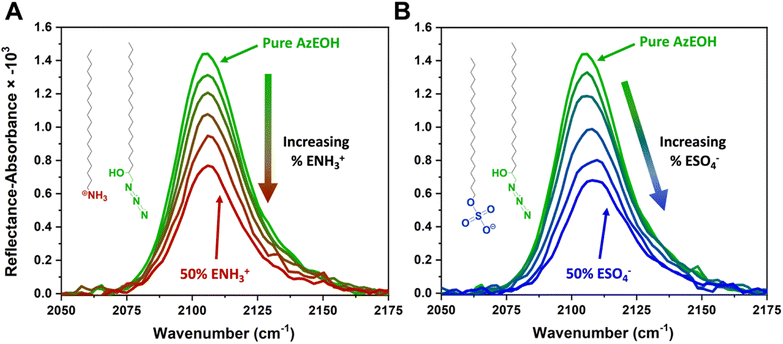
Fig. 3 shows the evolution of the spectra of the azide peak as the monolayer is diluted by the ammonium or sulphate surfactants. As expected, the net azide peak area decreases as azide is replaced by the charged surfactants. The peak area as a function of azide density is shown in Fig. 4. The points fit very well to a straight line, and this linear behavior confirms the correct assignment of the surface densities for various surface species. It also confirms that the charged surfactants are not lost to the subphase and contribute to the monolayers by diluting the azide at the correct proportion. Note that the figure does have error bars on the horizontal axis for each data point, which is retrieved from multiple Π–A isotherms for each species (Section S2†). However, these error bars are nearly imperceptible in comparison to the larger error bars for the IRRAS peak areas.
 | ||
| Fig. 3 IRRAS spectra of azide stretch at the surface as it is diluted by the (A) ammonium and (B) sulphate surfactants at 30 mN m−1 surface pressure. | ||
 | ||
| Fig. 4 Linear correlation between the spectral area of the azide peak from Fig. 3 as a function of azide surface density, confirming the successful dilution of azides at the interface by the charged surfactants. The dashed line is a linear fit to all data points with a slope of 0.1191. | ||
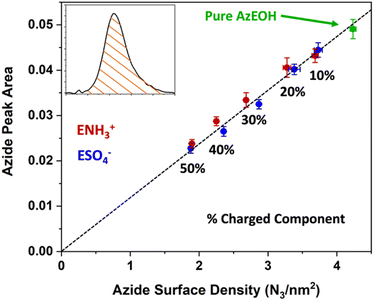
With the above description establishing confidence in dialing the correct azide and surface charge density, now we consider the spectral shifts as a function of various parameters. The frequency of the azide peak as a function of charge density is plotted in Fig. 5. In a previous study, both the peak frequency (mode) and the frequency that splits the spectral area in half (median) were considered to analyse the shift of the azide peak.54
 | ||
| Fig. 5 Frequency of the azide peak as a function of surface charge density. Additional details and peak properties can be found in Section S5.† | ||
We also retrieved both metrics for our spectra, but since peak frequency (mode) is most commonly used, we report it in the main text. The trend for the median frequency is shown in Section S5† and follows a qualitatively similar behaviour. The data shows a nearly linear blue-shift of about 3 cm−1 relative to pure azide with increasing negative surface charge. However, increasing the positive surface charge produces only a modest initial blue-shift that tapers off towards higher charge density. This behaviour is more evident in the median frequency trend shown in the ESI,† and even suggests a red-shift of the azide at higher positive charge densities.
To understand the trend, it is important to note that two major factors influence the solvation of the azide probe and consequently its frequency – electrostatics and hydrogen bonding. While the charged heads change the interfacial electric fields, they also alter the hydrogen bond network and hydration of species at the interface. Prior to further discussing the trend, it is necessary to understand the behaviour of azide towards hydration and local dielectric solvation in the bulk.
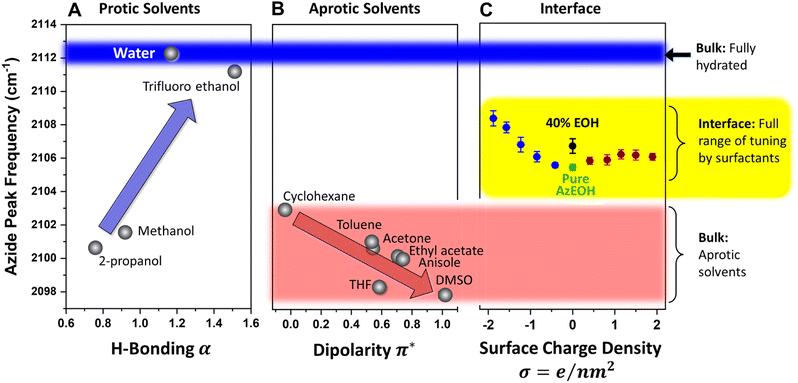
Since our azide has a long hydrophobic tail, it is not suitable for bulk solvatochromic studies in many solvents. Furthermore, since our azide is slightly modified for surface activity by an additional alcohol group, we cannot use the published azide solvatochromic data. Therefore, to understand the behaviour of azide in the bulk, we synthesized a shorter surfactant with six carbons and the same headgroup structure as AzEOH. This change in chain length is not expected to change the response of the azide head to its local environment significantly. The frequency of this azide in bulk solvents is shown in Fig. 6. Note that we have classified the solvents into two groups, protic (Fig. 6A) and aprotic (Fig. 6B), as is customary in solvatochromic studies.54,56,65,66 Furthermore, we plot the frequency with respect to the commonly accepted Kamlet–Taft (KT) parameters of the solvents.67–74 The KT parameter α represents the strength of hydrogen bond donation of a solvent. As shown in Fig. 6A, our azide frequency in protic solvents blue-shifts with increasing hydrogen bond donation consistent with prior work.54,56
A similar trend is observed with respect to the pKa of the solvent (Section S6†), with the more acidic solvents causing a larger blue-shift. Azide is particularly sensitive to hydrogen bond donation from water54 and its frequency within bulk water serves a reference point for the state of maximum hydration, which we will compare to the interfacial hydration later. Since the bulk hydrogen bond network of water hydrates the azide maximally, any reduction in that network by interfacial constraints is expected to redshift the azide. We will shortly use this lesson from the KT α plot for analyzing our surface data.
For the aprotic solvents, the azide frequency in bulk solution is plotted versus the KT-π∗ parameter, an empirical parameter indicating the solvent dipolarity.69 Note that some aprotic solvents may also have a non-zero KT α. To avoid convoluting the two effects, we have only considered aprotic solvents whose reported KT α = 0, as is customary with this type of analysis.66,69,75 The azide frequency, as shown in Fig. 6B, shows an expected red-shift with increasing solvent dipolarity. Taking cyclohexane as a reference, note that DMSO induces a red-shift of about 5 cm−1. This contrasts with hydrogen bonding due to water which induces a 9 cm−1 blue-shift relative to cyclohexane. This observation highlights the importance of hydrogen bonding in dictating the azide frequency. The KT π∗ plot indicates that our azide does respond to the solvent dipolarity, and therefore likely to the local electrostatics of the interface. Even though varying values of Stark tuning rates have been reported for various azides in the literature,43,44 it is agreed that azides do respond to electrostatic fields and our data is consistent with that view. Our data indicates the direction of the electrostatic shift is the same as the more studied nitrile group.56,66,76,77
Armed with the knowledge of the behaviour of our azide in the bulk, we return to the interpretation of the azide at the interface. The data from Fig. 5 is shown again in Fig. 6C, this time in the context of the values obtained in bulk solvents. In addition, the azide peak of 40% eicosanol (EOH) was determined and included in this plot. First, the pure azide frequency 2105.4 cm−1 (green point in Fig. 6C) is significantly red-shifted from the azide immersed in bulk water (2112.3 cm−1, Fig. 6A). Azide in the typical extremes of aprotic solvents, DMSO and cyclohexane, exhibits a shift to 2098 cm−1 and 2103 cm−1 respectively (Fig. 6B). Therefore, the frequency of azide at the interface corresponds to neither a fully hydrated azide nor to an azide in a low dipolarity solvent. This is a clear indication of partially solvating interfacial environment. Parsing this partial solvation to electrostatic and hydrogen bonding contributions is more involved and will be discussed shortly.
The above observation has relevance for reactivity at the air–water interface because the azide can be imagined as a reactant that is influenced by electrostatics and hydration environment of the interface. Our data suggests that the interface may induce a net effect on such a reactant that may not be achievable in either water or any dielectric solvent.
In all the above, an important piece of the surface electrostatics is missing, which is the ionic strength of the subphase. Ions within the solution affect the surface electrostatics both through non-specific screening of the surface potential and specific binding to charged groups at the interface. Therefore, it is imperative to study the influence of salt in the subphase on the frequency shifts. Since this influence is expected to be the largest for highly charged surfaces, we performed our IRRAS experiments for the highest charge density mixed monolayers discussed earlier, but with a total ionic strength of 100 mM and 1 M through addition of NaCl. Our first observation from the Π–A isotherms were that the monolayers were considerably expanded at 30 mN m−1 surface pressure, thereby resulting in a smaller surface density.
After accounting for this density change, the IRRAS data were acquired and analysed. For comparison, the peak frequencies are added to the previous data and shown in Fig. 7.
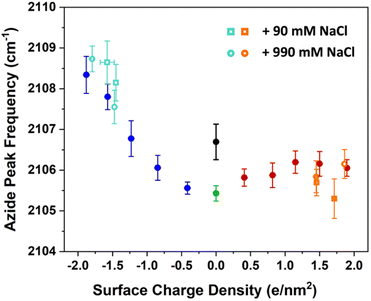 | ||
| Fig. 7 The azide peak frequency as the monolayers are diluted by charged surfactants. The figures here include the data from previous low ionic strength experiments in Fig. 3 in addition to experiments with higher salt concentration of 100 mM (open circles) and 1 M (open squares). The orange and aqua colours represent data with ammonium and sulphate surfactants respectively. The comparison shows that salt concentration affects the frequency shifts only minimally relative to low ionic strength experiments, with a mild blue-shift for the sulphate and a mild red-shift for the ammonium surfactants. Spectra and additional details can be found in Section S7.† | ||
The figure shows that the influence of salts on the frequency shifts is quite minimal. Ten-fold and 100-fold increase in ionic strength has shifted the frequency only marginally by about 1 cm−1 to higher values for the sulphate mixed monolayers and to lower values for the ammonium mixed monolayers. For all lower surface charge densities, no considerable shift was observed between high salt and low salt experiments. One may be tempted to explain this insensitivity as a partial success of continuum surface electrostatic theories.78–80 These theories predict that for a fixed charge density at the surface, the bulk salt concentration reduces the surface potential ϕ(0) due to attraction of counter ions to the interface. But at the same time, the salt ions screen the penetration of the potential into the bulk ϕ(z), thereby increasing its gradient which is proportional to the electric field 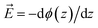 . As shown in the Section S3,† the attenuation of ϕ(0) and increase of the potential gradient counteract each other resulting into the lack of sensitivity of interfacial fields to salt concentration. However, we discourage the reader from interpreting our results as a success of the continuum theory. Importantly, the continuum theory ignores specific ion pairing, ion size, and solvation shell of ions.
. As shown in the Section S3,† the attenuation of ϕ(0) and increase of the potential gradient counteract each other resulting into the lack of sensitivity of interfacial fields to salt concentration. However, we discourage the reader from interpreting our results as a success of the continuum theory. Importantly, the continuum theory ignores specific ion pairing, ion size, and solvation shell of ions.
It is quite likely that the relative geometry of the screening ion, the charged head group, the azide surfactant, and any intervening water molecule is quite complex and variable. Our observation of the expansion of monolayers due to addition of salts may arise due to such complexities. Therefore, while the measured azide frequencies are valuable, they are inadequate for uniquely resolving such structures. The main message from the salt concentration dependence is that the influence of salts on azide frequency is relatively small and only perceived at larger surface charge densities. This observation has consequences for continuum theories of electrostatics at the interface, where large electric fields at the surface are hypothesized to polarize or dissociate molecules as proposed steps for accelerated reactivity.7
Finally, we present a hypothesized picture in Fig. 8 that summarizes all the results consistently and provides some insight into the combined effects of electrostatics and hydration at the interface. Note that knowing the molecular-scale structural details of monolayers are quite complicated to determine. Structural fluctuations over several time scales have been reported for monolayers at the air–water interface.61,81 Furthermore, a clear definition of the water boundary can be debated, since water molecules have been reported to penetrate beyond the surfactant heads.82–85
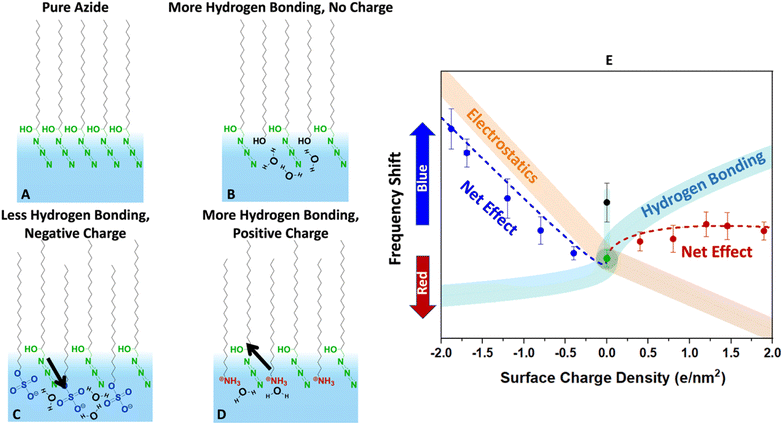 | ||
| Fig. 8 Conjectured effects of hydration and electrostatics on the azide frequency depicted in the cartoons (A–D). The diagram (E) describes the expected change in the vibrational frequency of the azide due to each factor along with their net effect. (A) The pure azide monolayer is likely densely packed (based on the collapse point in isotherms) and laterally hydrogen bonded to itself. While there may be hydrogen bonding to water molecules, the monolayer is far from fully hydrated based on its low frequency compared to bulk water in Fig. 6. (B) Inserting alcohol-bearing surfactants increases the distance between the azides and help it hydrate better. The extra hydrogen bonding causes a blue-shift (black data point in E). (C) Sulphates are solvated very well and dip deep into the surface. However, they are strong hydrogen bond acceptors and compete with the azide for hydrogen bonding. This by itself would cause a red-shift (aqua trace in E). However, the negative heads produce an electric field that induces a blue-shift (orange trace in E). The data suggests that the electrostatics effect is larger. (D) The ammonium surfactants are hydrogen bond donors. They do not compete with the azides for hydrogen bonds and help hydrate the azide better. This would produce a blue-shift (aqua trace in E). However, their positive charge causes a shift in the opposite direction (orange trace in E). The net effect due to this competition is a small frequency shift. | ||
Despite these complexities it is beneficial to put the measured data in the more general context of partial hydration and electrostatics so that insight can be gained for tuning surface reactions with the choice of surfactants. In other words, even though our data clearly indicates partial solvation of the azide probe, parsing that to the electrostatic and hydrogen bonding contributions is difficult, and Fig. 8 is our most self-consistent and likely useful approach towards that goal.
The pure azide surfactants (Fig. 8A) are well packed for IRRAS experiments, with an MMA of 24 Å2. At such density, the azide heads are close to each other and are likely significantly deprived from interacting with water. This is evident in Fig. 6, which shows that the azide frequency in a pure azide monolayer (2105 cm−1) is closer to its frequency in purely dielectric bulk cyclohexane (2103 cm−1) than in bulk water (2112 cm−1). Therefore, the pure azide surfactant in our packed monolayers should be viewed as quite dehydrated relative to when fully hydrated in bulk water.
When some of the azide heads are replaced by alcohols at similar MMA (Fig. 8B) the smaller head of the alcohol surfactant increases water exposure for the remaining azide groups. The alcohol groups act as both a hydrogen bond donor and an acceptor, therefore are likely to attract water near itself and around the azide. This causes the azide to experience a better hydrated environment resulting in a blue-shift of the azide peak frequency for 40% EOH (Fig. 8E).
When some azide heads are replaced with sulphate (Fig. 8C) the remaining azides may experience a frequency shift due to changes in hydration. However, the sulphate head is large, and it is unlikely the remaining azides gain exposure to water in mixed sulphate monolayers. In addition, sulphate is a very good hydrogen bond acceptor and likely to steal water hydrogen bonds from the remaining azides. Thus, we expect adding sulphate should further deprive the azide of hydrogen bonds and cause a red-shift (light blue line in Fig. 8E).
However, the sulphate carries a charge and therefore may change the electrostatics of the interface unlike the neutral alcohol or azide surfactants. We note hydrating the charged sulphate headgroup is highly free energy favourable and we expect the sulphate heads to probe deeper into solution than the hydrophobic azide heads.
The positioning of sulphate relative to azide in Fig. 8C is shown to reflect that, and in this orientation our dipolarity-frequency bulk data in Fig. 6B indicate the field would cause a blue-shift in the frequency. Therefore, the electrostatic influence of the sulphate group is shown by the orange stripe in Fig. 8E. Our data suggests that the electrostatic influence of the sulphate head overwhelms its capability to reduce hydrogen bonding for the azide and therefore a nearly linear blue-shift is observed.
The ammonium surfactant heads are smaller than sulphate and provide more solvent exposure to the remaining azides. More significantly, the ammonium group is a hydrogen bond donor and does not compete with azide for hydrogen bonds when replacing some azides (Fig. 8D). In fact, the same water molecule that is accepting a hydrogen bond from ammonium may serve as an excellent hydrogen bond donor to the azide. Ammonium itself may even donate hydrogen bonds to the remaining azides. All of these factors suggest adding ammonium to the azide monolayer would increase hydrogen bonding to the azide and produce a blue-shift as indicated by the aqua stripe in Fig. 8E. However, the field from charged ammonium is oriented antiparallel to that of sulphate, and thus would produce a red-shift in the azide frequency (orange stripe in Fig. 8E). Therefore, because hydrogen bonding and electrostatics operate in opposite directions with similar influence, the net effect is a small blue-shift for the azide at low ammonium density which becomes a red-shift as the ammonium density increases.
The frequency shift of the azide arises from the change in its electronic structure corresponding to its polarization by the fields or hydrogen bonding. Thinking more broadly, one may imagine a reactant, intermediate, transition state, or product of a reaction at the interface that is sensitive to either hydrogen bonding, field, or both. While many reactions may already benefit from the partial solvation at interfaces, optimizing and tuning of their thermodynamics or kinetics requires tailored surfactants that can bring about the needed change. Further experimental and computational work is needed to create a systematic understanding built upon this study.
Conclusions
Unusual reactivities at the air–water interface inspired us to study the interface from the perspective of the azide vibrational probe that is sensitive to both electrostatics and hydration. Our main finding is that the azide probe feels a partially solvated environment at the interface. The frequency of the pure azide monolayer is smaller than fully hydrated azide in bulk water and is larger than the frequency of azide in low dielectric and low dipolarity solvents. This shows that the electronic structure of azide is polarized in a way that is neither possible in bulk water nor in an organic solvent. We conjecture that if azide was a reactant, this unique polarization would translate to unique reactivity.Furthermore, we observed that adding charged surfactants to the monolayer changes both hydration and the electrostatics of the azide probe. We propose that there is ample room for creating designer surfactants to bring about the appropriate balance of electrostatics and hydration to an interfacial reaction.
We also noted that addition of salts to the subphase only minimally affected the frequency of azide. This is important for scenarios where salts are implicated in creating large electrostatic fields at the interface due to screening of the surface potential over small distances.
Azide is a useful IR probe that can be measured at sub-monolayer density in a relatively simple IRRAS experiment. It has potential to serve as the air–water interface probe to understand phenomena, such as reactive geometries, reaction rates, probing depths, and specific ion interactions. We hope that it is used as one of the many tools to understand the reactivity of air–water interfaces.
Data availability
We have provided all relevant data in the ESI† of the paper.Author contributions
K. D. J. conceptualized the study, conducted spectroscopy and Langmuir trough experiments, analysed the data, and wrote the original draft of the manuscript. S. W. P. conducted spectroscopy and Langmuir trough experiments and analysed the data. D. B. E. conceptualized and supervised the study, conducted synthetic experiments, and analysed the data. V. V. F. supervised the study. J. M. D. conceptualized and supervised the study, analysed the data. All authors discussed the results and contributed to the manuscript writing and approved the final version.Conflicts of interest
There are no conflicts to declare.Acknowledgements
K. D. J., S. W. P. and J. M. D. were supported by the Multi-University Research Initiative (MURI) of the Air Force Office of Scientific Research AFOSR (FA9550-21-1-0170). J. M. D. was also supported by the grant CHE 2154493 from the National Science Foundation (NSF). D. B. E. thanks Agilent Technologies for Agilent Postdoctoral Fellowship. All mass spectra were recorded at the Agilent Center for Excellence in Biomolecular Characterization at USC. The authors thank Dr Sasha Sundstrom for the artwork of the Table of Contents graphic.Notes and references
- D. C. Rideout and R. Breslow, J. Am. Chem. Soc., 1980, 102, 7816–7817 CrossRef CAS
.
- P. A. Grieco, K. Yoshida and P. Garner, J. Org. Chem., 1983, 48, 3137–3139 CrossRef CAS
.
- R. Breslow, Acc. Chem. Res., 1991, 24, 159–164 CrossRef CAS
.
- S. Narayan, J. Muldoon, M. G. Finn, V. V. Fokin, H. C. Kolb and K. B. Sharpless, Angew. Chem., Int. Ed., 2005, 44, 3275–3279 CrossRef CAS PubMed
.
- X. Yan, R. M. Bain and R. G. Cooks, Angew. Chem., Int. Ed., 2016, 55, 12960–12972 CrossRef CAS PubMed
.
- L. Qiu, M. D. Psimos and R. G. Cooks, J. Am. Soc. Mass Spectrom., 2022, 33, 1362–1367 CrossRef CAS PubMed
.
- J. K. Lee, K. L. Walker, H. S. Han, J. Kang, F. B. Prinz, R. M. Waymouth, H. G. Nam and R. N. Zare, Proc. Natl. Acad. Sci. U.S.A., 2019, 116, 19294–19298 CrossRef CAS PubMed
.
- A. K. Badu-Tawiah, D. I. Campbell and R. G. Cooks, J. Am. Soc. Mass Spectrom., 2012, 23, 1461–1468 CrossRef CAS PubMed
.
- H. Nie, Z. Wei, L. Qiu, X. Chen, D. T. Holden and R. G. Cooks, Chem. Sci., 2020, 11, 2356–2361 RSC
.
- F. Yang, R. D. Urban, J. Lorenz, J. Griebel, N. Koohbor, M. Rohdenburg, H. Knorke, D. Fuhrmann, A. Charvat, B. Abel, V. A. Azov and J. Warneke, Angew. Chem., Int. Ed., 2024, 63, e202314784 CrossRef CAS PubMed
.
- D. González-Cruz, D. Tejedor, P. de Armas, E. Q. Morales and F. García-Tellado, Chem. Commun., 2006, 26, 2798–2800 RSC
.
- N. Mase, Y. Nakai, N. Ohara, H. Yoda, K. Takabe, F. Tanaka and C. F. Barbas, J. Am. Chem. Soc., 2006, 128, 734–735 CrossRef CAS PubMed
.
- E. Gnanamani, X. Yan and R. N. Zare, Angew. Chem., Int. Ed., 2020, 59, 3069–3072 CrossRef CAS PubMed
.
- D. B. Eremin and V. V. Fokin, J. Am. Chem. Soc., 2021, 143, 18374–18379 CrossRef CAS PubMed
.
- P. A. Bachmann, P. L. Luisi and J. Lang, Nature, 1992, 357, 57–59 CrossRef CAS
.
- A. Tuck, Surv. Geophys., 2002, 23, 379–409 CrossRef
.
- D. J. Donaldson, H. Tervahattu, A. F. Tuck and V. Vaida, Origins Life Evol. Biospheres, 2004, 34, 57–67 CrossRef CAS PubMed
.
- I. Nam, J. K. Lee, H. G. Nam and R. N. Zare, Proc. Natl. Acad. Sci. U.S.A., 2017, 114, 12396–12400 CrossRef CAS PubMed
.
- V. Vaida, Proc. Natl. Acad. Sci. U.S.A., 2017, 114, 12359–12361 CrossRef CAS PubMed
.
- I. Nam, H. G. Nam and R. N. Zare, Proc. Natl. Acad. Sci. U.S.A., 2018, 115, 36–40 CrossRef CAS PubMed
.
- A. D. Castañeda, Z. Li, T. Joo, K. Benham, B. T. Burcar, R. Krishnamurthy, C. L. Liotta, N. L. Ng and T. M. Orlando, Sci. Rep., 2019, 9, 13527 CrossRef PubMed
.
- D. T. Holden, N. M. Morato and R. G. Cooks, Proc. Natl. Acad. Sci. U.S.A., 2022, 119, e2212642119 CrossRef CAS PubMed
.
- K. R. Wilson, A. M. Prophet, G. Rovelli, M. D. Willis, R. J. Rapf and M. I. Jacobs, Chem. Sci., 2020, 11, 8533–8545 RSC
.
- F. Zhou, Z. Hearne, C.-J. Li and C. Opin, Green Sustainability, 2019, 18, 118–123 Search PubMed
.
- X. Zhu, W. Zhang, Q. Lin, M. Ye, L. Xue, J. Liu, Y. Wang and H. Cheng, ACS Sustainable Chem. Eng., 2019, 7, 6486–6491 CrossRef CAS
.
- P. Zhao, H. P. Gunawardena, X. Zhong, R. N. Zare and H. Chen, Anal. Chem., 2021, 93, 3997–4005 CrossRef CAS PubMed
.
- C. F. Chamberlayne and R. N. Zare, J. Chem. Phys., 2022, 156, 054705 CrossRef CAS PubMed
.
- A. Gallo, A. S. F. Farinha, M. Dinis, A.-H. Emwas, A. Santana, R. J. Nielsen, W. A. Goddard and H. Mishra, Chem. Sci., 2019, 10, 2566–2577 RSC
.
- G. Rovelli, M. I. Jacobs, M. D. Willis, R. J. Rapf, A. M. Prophet and K. R. Wilson, Chem. Sci., 2020, 11, 13026–13043 RSC
.
- J. N. Smith, R. C. Flagan and J. L. Beauchamp, J. Phys. Chem. A, 2002, 106, 9957–9967 CrossRef CAS
.
- M. Makosza, Pure Appl. Chem., 2000, 72, 1399–1403 CrossRef CAS
.
- K. Maruoka, Org. Process Res. Dev., 2008, 12, 679–697 CrossRef CAS
.
- M. F. Ruiz-Lopez, X. Assfeld, J. I. Garcia, J. A. Mayoral and L. Salvatella, J. Am. Chem. Soc., 1993, 115, 8780–8787 CrossRef CAS
.
- C. F. Chamberlayne and R. N. Zare, J. Chem. Phys., 2020, 152, 184702 CrossRef CAS PubMed
.
- H. Xiong, J. K. Lee, R. N. Zare and W. Min, J. Phys. Chem. Lett., 2020, 11, 7423–7428 CrossRef CAS PubMed
.
- H. Hao, I. Leven and T. Head-Gordon, Nat. Commun., 2022, 13, 280 CrossRef CAS PubMed
.
- M. T. C. Martins-Costa and M. F. Ruiz-López, J. Am. Chem. Soc., 2023, 145, 1400–1406 CrossRef CAS PubMed
.
- C. Zhu, L. N. Pham, X. Yuan, H. Ouyang, M. L. Coote and X. Zhang, J. Am. Chem. Soc., 2023, 145, 21207–21212 CrossRef CAS PubMed
.
- Y. Jung and R. A. Marcus, J. Am. Chem. Soc., 2007, 129, 5492–5502 CrossRef CAS PubMed
.
- Y. Jung and R. A. Marcus, J. Phys.: Condens. Matter, 2010, 22, 284117 CrossRef PubMed
.
- N. Narendra, X. Chen, J. Wang, J. Charles, R. G. Cooks and T. Kubis, J. Phys. Chem. A, 2020, 124, 4984–4989 CrossRef CAS
.
- L. Qiu, Z. Wei, H. Nie and R. G. Cooks, ChemPlusChem, 2021, 86, 1362–1365 CrossRef CAS
.
- I. T. Suydam and S. G. Boxer, Biochemistry, 2003, 42, 12050–12055 CrossRef CAS PubMed
.
- L. N. Silverman, M. E. Pitzer, P. O. Ankomah, S. G. Boxer and E. E. Fenlon, J. Phys. Chem. B, 2007, 111, 11611–11613 CrossRef CAS PubMed
.
- J.-H. Choi, K.-I. Oh and M. Cho, J. Chem. Phys., 2008, 129, 174512 CrossRef PubMed
.
- K.-I. Oh, J.-H. Lee, C. Joo, H. Han and M. Cho, J. Phys. Chem. B, 2008, 112, 10352–10357 CrossRef CAS PubMed
.
- X. S. Gai, E. E. Fenlon and S. H. Brewer, J. Phys. Chem. B, 2010, 114, 7958–7966 CrossRef CAS PubMed
.
- M. W. Nydegger, S. Dutta and C. M. Cheatum, J. Chem. Phys., 2010, 133, 134506 CrossRef PubMed
.
- H. Taskent-Sezgin, J. Chung, P. S. Banerjee, S. Nagarajan, R. B. Dyer, I. Carrico and D. P. Raleigh, Angew. Chem., Int. Ed., 2010, 49, 7473–7475 CrossRef CAS PubMed
.
- J.-H. Choi, D. Raleigh and M. Cho, J. Phys. Chem. Lett., 2011, 2, 2158–2162 CrossRef CAS PubMed
.
- S. Dutta, W. Rock, R. J. Cook, A. Kohen and C. M. Cheatum, J. Chem. Phys., 2011, 135, 055106 CrossRef PubMed
.
- X. S. Gai, B. A. Coutifaris, S. H. Brewer and E. E. Fenlon, Phys. Chem. Chem. Phys., 2011, 13, 5926–5930 RSC
.
- H. Lee, J.-H. Choi and M. Cho, J. Chem. Phys., 2012, 137, 114307 CrossRef PubMed
.
- M. P. Wolfshorndl, R. Baskin, I. Dhawan and C. H. Londergan, J. Phys. Chem. B, 2012, 116, 1172–1179 CrossRef CAS PubMed
.
- M. Maj, C. Ahn, D. Kossowska, K. Park, K. Kwak, H. Han and M. Cho, Phys. Chem. Chem. Phys., 2015, 17, 11770–11778 RSC
.
- M. Maj, C. Ahn, B. Błasiak, K. Kwak, H. Han and M. Cho, J. Phys. Chem. B, 2016, 120, 10167–10180 CrossRef CAS PubMed
.
- B. Błasiak, C. H. Londergan, L. J. Webb and M. Cho, Acc. Chem. Res., 2017, 50, 968–976 CrossRef PubMed
.
- I. Langmuir, J. Am. Chem. Soc., 1917, 39, 1848–1906 CrossRef CAS
.
- N. K. Adam and W. B. Hardy, Proc.: Math., Phys. Eng. Sci., 1921, 99, 336–351 CAS
.
- E. D. Goddard, O. Kao and H. C. Kung, J. Colloid Interface Sci., 1968, 27, 616–624 CrossRef CAS
.
- E. Pezron, P. M. Claesson, J. M. Berg and D. Vollhardt, J. Colloid Interface Sci., 1990, 138, 245–254 CrossRef CAS
.
- E. Tyrode and R. Corkery, J. Phys. Chem. C, 2018, 122, 28775–28786 CrossRef CAS
.
- J. Davies, Proc.: Math., Phys. Eng. Sci., 1951, 208, 224–247 CAS
.
- Z. Avazbaeva, W. Sung, J. Lee, M. D. Phan, K. Shin, D. Vaknin and D. Kim, Langmuir, 2015, 31, 13753–13758 CrossRef CAS PubMed
.
- O. W. Kolling, Appl. Spectrosc., 2000, 54, 890–893 CrossRef CAS
.
- D. J. Aschaffenburg and R. S. Moog, J. Phys. Chem. B, 2009, 113, 12736–12743 CrossRef CAS PubMed
.
- R. W. Taft and M. J. Kamlet, J. Am. Chem. Soc., 1976, 98, 2886–2894 CrossRef CAS
.
- M. J. Kamlet and R. W. Taft, J. Am. Chem. Soc., 1976, 98, 377–383 CrossRef CAS
.
- M. J. Kamlet, J. L. Abboud and R. W. Taft, J. Am. Chem. Soc., 1977, 99, 6027–6038 CrossRef CAS
.
- M. J. Kamlet, J. L. M. Abboud, M. H. Abraham and R. W. Taft, J. Org. Chem., 1983, 48, 2877–2887 CrossRef CAS
.
- E. Buncel and S. Rajagopal, Acc. Chem. Res., 1990, 23, 226–231 CrossRef CAS
.
- Y. Marcus, Chem. Soc. Rev., 1993, 22, 409–416 RSC
.
- C. Reichardt, Chem. Rev., 1994, 94, 2319–2358 CrossRef CAS
.
- R. Cabot and C. A. Hunter, Chem. Soc. Rev., 2012, 41, 3485–3492 RSC
.
- M. V. Garcia and M. I. Redondo, Spectrochim. Acta, 1987, 43A, 879–885 CrossRef CAS
.
- S. Bagchi, S. D. Fried and S. G. Boxer, J. Am. Chem. Soc., 2012, 134, 10373–10376 CrossRef CAS PubMed
.
- S. A. Sorenson, J. G. Patrow and J. M. Dawlaty, J. Am. Chem. Soc., 2017, 139, 2369–2378 CrossRef CAS
.
- M. Gouy, J. Phys. Theor. Appl., 1910, 9, 457–468 CrossRef
.
- D. L. Chapman, Philos. Mag., 1913, 25, 475–481 Search PubMed
.
- D. C. Grahame, Chem. Rev., 1947, 41, 441–501 CrossRef CAS PubMed
.
- C. Yan, J. E. Thomaz, Y.-L. Wang, J. Nishida, R. Yuan, J. P. Breen and M. D. Fayer, J. Am. Chem. Soc., 2017, 139, 16518–16527 CrossRef CAS PubMed
.
- E. Tyrode, C. M. Johnson, A. Kumpulainen, M. W. Rutland and P. M. Claesson, J. Am. Chem. Soc., 2005, 127, 16848–16859 CrossRef CAS PubMed
.
- X. Chen, W. Hua, Z. Huang and H. C. Allen, J. Am. Chem. Soc., 2010, 132, 11336–11342 CrossRef CAS PubMed
.
- Y. Nojima, Y. Suzuki and S. Yamaguchi, J. Phys. Chem. C, 2017, 121, 2173–2180 CrossRef CAS
.
- M. M. Sartin, W. Sung, S. Nihonyanagi and T. Tahara, J. Chem. Phys., 2018, 149, 024703 CrossRef PubMed
.
Footnote |
| † Electronic supplementary information (ESI) available: Synthetic methods and characterization, additional isotherms, addi-tional IR spectra, experimentally determined averages and error of isotherm and IRRAS peak properties, surface electrostatics of the interface, and additional peak property plots. See DOI: https://doi.org/10.1039/d4sc01311e |
| This journal is © The Royal Society of Chemistry 2024 |