Structural stability and thermoelectric properties of cation- and anion-doped Mg₂Si_0.4Sn_0.6

Abstract

Undoped, anion-doped (Sb, Bi), and cation-doped (Ca, Zn) solid solutions of Mg₂Si_0.4Sn_0.6 have been prepared by a commercially feasible large-scale solid state synthesis method. The compositional and structural stability of the prepared samples are investigated by high resolution synchrotron powder X-ray diffraction (PXRD) in the potential application temperature range of 300–750 K. Quantitative compositional and structural information are extracted from the multi-temperature PXRD data by the Rietveld method. Detailed analysis of the PXRD data reveals an irreversible thermally induced partial conversion of Mg₂Si_0.4Sn_0.6 into a discrete Sn-rich Mg₂Si_1−xSn_x-phase in the undoped and anion-doped samples. On the other hand, the cation-doped samples only undergo very minor compositional and structural changes with increasing temperature, indicating a stabilizing effect of Ca and Zn on the Mg₂Si_0.4Sn_0.6 solid solution. The structural instability of the undoped and anion-doped samples is corroborated by the measured electrical resistivity as function of temperature in the same temperature range, in which a clear difference is observed between values during initial heating and subsequent cooling. In contrast, the resistivity data of the cation-doped samples exhibit good repeatability for two thermal cycles, confirming that cation doping greatly improves the thermal stability. This work highlights the importance of conducting multiple temperature cycles in the measurement of physical properties combined with a thorough structural characterization in studies of thermoelectric materials.

---

Introduction

The physical properties of functional materials, including thermoelectric materials, are directly determined by material characteristics such as phase composition, structure, microstructure, etc.^1,2 Consequently, the first step in any materials science study should always be establishing which material is being investigated. However, in the field of thermoelectricity less emphasis is often given to the structural characterization of the materials in question. Diffraction data are typically used only for conducting a quick initial assessment of the phase composition by indexing of a few of the main Bragg peaks, often overlooking the more subtle features in the diffraction pattern which may contain crucial information.³ The importance given to the structural characterization is generally in contrast to the scrutinizing of subtle and potentially less significant features in the measured physical properties. In addition, the temperature dependence of the thermoelectric properties necessitates physical characterization to be carried out over an extended temperature range,⁴ which may induce compositional and structural changes.^5–7 In some studies, the characterization of physical properties as a function of temperature is carried out by several different measurements on the same sample, neglecting the influence of thermal history. Consequently, any structural and compositional changes induced by the repeated thermal cycling of the material may be overlooked and erroneous conclusions may be drawn.

In recent years, Mg₂Si_1−xSn_x-based compounds have attracted substantial interest as potential materials for thermoelectric energy conversion in the medium temperature range ∼500–900 K.^6,8–13 Relatively large thermoelectric figure-of-merit, zT, values above 1 are often reported.^14–24 In addition, the chemical constituents are abundant, low-cost and environmentally benign, which makes Mg₂Si_1−xSn_x a suitable candidate for large-scale commercial applications. Mg₂Si and Mg₂Sn are known to form solid solutions of Mg₂Si_1−xSn_x, but the presence and extent of a miscibility gap in the phase diagram remains a controversial topic.^25,26 Thermodynamic modeling based on experimental data predicts a splitting into discrete Sn- and Si-rich phases in the 0.1 ≲ x ≲ 0.7 region below ∼1150 K.²⁷ The miscibility gap narrows with increasing temperature, making the composition Mg₂Si_0.4Sn_0.6 thermodynamically unstable at 300 K but stable above ∼700 K. However, there have been several reports of seemingly stable solid solutions (undoped and doped) being synthesized within the miscibility gap.^{11,12,15,28–32} The explanation may be slow kinetics related to the phase separation at ambient conditions. Despite the well-known structural instability and formation Mg₂Si_1−xSn_x solid solutions in the system, repeated thermal cycling in the measurement of physical properties combined with meticulous structural characterization before and after thermal cycling, employing sufficiently resolved powder X-ray diffraction (PXRD) and Rietveld analysis, is rarely seen in the literature.

In this work, the influence of various anion (Sb, Bi) and cation (Ca, Zn) dopants on the structural stability and thermoelectric properties of Mg₂Si_0.4Sn_0.6 is investigated. The samples have been prepared by relatively large-scale solid state syntheses which makes it a feasible route for commercialization. In addition, the study is focused on the thermal stability of the compound, which is another key aspect in real-life applications of functional materials. Characterization by multiple temperature high resolution synchrotron powder X-ray diffraction has been carried out, and the structural evolution with temperature is followed. Quantitative information is extracted from the PXRD patterns through in-depth analysis by the Rietveld method. The ability of the various dopants to stabilize the compound within the miscibility gap is investigated. In order to simultaneously eliminate and accentuate the influence of the thermal history of the samples, characterization of the various physical properties is carried out on fresh and identically sintered pellets from the same synthesis batch.

Experimental

Sample preparation

Relatively large-scale solid state syntheses of five different nominal compositions, Mg_2.15Si_0.4Sn_0.6 (MGS_undoped), Mg_2.15(Si_0.4Sn_0.6)_0.98Sb_0.02 (MGS_Sb), Mg_2.15(Si_0.4Sn_0.6)_0.98Bi_0.02 (MGS_Bi), Mg_2.11Ca_0.04Si_0.4Sn_0.6 (MGS_Ca) and Mg_2.11Zn_0.04Si_0.4Sn_0.6 (MGS_Zn), were carried out by the direct reaction of the constituent elements. A total of 100 g of the given stoichiometric quantities of Mg (Chempur, 99+%), Si (Chempur, 98.5+%), Sn (Alfa Aesar, 99.8+%), Sb (Sigma-Aldrich, 99.5+%), Bi (Sigma-Aldrich, 99.999%), Ca (Alfa Aesar, 99.5+%) and Zn (Sigma-Aldrich, analytical grade) powders were weighed and thoroughly mixed for 30 minutes in a mechanical mixer. In all cases, an excess molar amount of 7.5% Mg was added to compensate for evaporation at the elevated synthesis temperatures.³³ The mixtures were loaded into alumina crucibles and reacted in a furnace at 1075 K for >20 hours in a 5% H₂ in Ar atmosphere. The final ingots were crushed and ground into powders (<45 μm) before being compacted by spark plasma sintering (SPS) at 975 K and 60 MPa to obtain dense pellets with a thickness of ∼2.5 mm. For all samples, a density, d, of 2.9(2) g cm⁻³ was calculated from the mass and dimensions of the compacted pellets, which is within 95(6)% of the theoretical density, 3.04 g cm⁻³, of Mg₂Si_0.4Sn_0.6. Diffraction patterns measured on a number of different pellets illustrating the reproducibility of the employed SPS procedure are given in the ESI.†

Structural characterization

The crystal structure at room temperature and the structural evolution with temperature were investigated by high resolution synchrotron PXRD. The diffraction experiments were conducted at the BL44B2 beamline, SPring-8, Japan, using an image plate detector and a beam size of 0.5 × 1 mm.³⁴ The exact X-ray wavelength was determined to be 0.500443(4) Å from Rietveld refinement of a CeO₂ standard (a = 5.411651 Å) at room temperature. Diffraction patterns were collected on powders which were filed off the entire thickness of the pellets and packed under Ar in Ø = 0.3 mm (inner diameter) quartz capillaries. In the temperature study an initial diffraction pattern was collected at 300 K before the sample was heated to 450 K and data was measured at 50 K intervals up to 750 K and again after cooling back to 315 K. Subsequently, two more heating cycles were carried out with the data being measured only at 750 and 315 K. During all experiments the heating rate was 50 K min⁻¹ and the cooling rate 100 K min⁻¹.

Data analysis

The PXRD patterns were analyzed by Rietveld refinement using the Fullprof Suite software package.³⁵ The refinements were carried out based on the structure of Mg₂Si_1−xSn_x (neglecting the influence of the minute amounts of dopant on the structure) in the cubic Fm3̄m space group illustrated in Fig. 1 using the VESTA software.³⁶ Small amounts of Sn and MgO impurities were identified in certain samples and these were modeled in space groups I4₁/amd and Fm3̄m, respectively.^37,38 The instrumental contribution to the peak profiles was determined by Rietveld refinement of data obtained from a CeO₂ standard, and it was corrected for in the refinements. The Thompson–Cox–Hastings formulation of the pseudo-Voigt function was applied to describe the peak profiles. The residual peak broadening after instrumental correction was described by refinement of profile parameters related to isotropic microstrain [Gaussian (U) and Lorentzian (X) contribution].³⁹ The background was modeled using a linear interpolation between a set of background points of refinable intensity. Atomic displacement parameters (ADPs) and atomic positions were held fixed while the scale factor, unit cell parameters, peak profile and background parameters were refined. Simultaneous refinement of the ADPs and atomic occupancies lead to unphysical results due to the broad and often irregular peak profiles. The ADPs were therefore fixed at values estimated by stoichiometrically weighted extrapolation from Rietveld refinements of multi-temperature high resolution PXRD data of the pure Mg₂Si and Mg₂Sn end members.⁴⁰ The ADPs of the impurities were held fixed at 0.5 for Sn and typical room temperature literature values for MgO in the refinements at all temperatures.³⁸ Fixing the ADPs facilitated constrained refinement of Sn and Si occupancies in the Mg₂Si_1−xSn_x structure. From the refined parameters, the weight fraction W of phase i was calculated by the formula, W_i = [S_iZ_iM_iV_i/t_i]/sum(j)[S_jZ_jM_jV_j/t_j], where S is the scale factor, Z is the formula units in the unit cell, M is formula unit mass, V is the unit cell volume and t is the Brindley particle absorption contrast factor defined as, 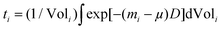, where m is the linear absorption coefficient, μ is the average linear absorption coefficient of the entire sample, D is the crystallite diameter and Vol is the crystallite volume.⁴¹

Fig. 1 The cubic Mg₂Si_1−xSn_x crystal structure with green spheres representing Mg and blue spheres representing Si and Sn.

Physical characterization

Transport properties were measured for all samples from room temperature to 725 K. Electrical resistivity, ρ, and Hall coefficient, R_H, were measured on an in-house system employing the Van der Pauw method in a magnetic field of 1.25 T.^42,43 The Hall carrier concentration, n_H, was calculated by 1/eR_H, where e is the elementary charge and the Hall carrier mobility, μ_H, was then calculated using the relation μ_H = 1/n_Heρ. The resistivity was measured during both heating and cooling for 2 cycles. The thermal diffusivity, D, was determined by the flash diffusivity method^44,45 using a Netzsch LFA 457 laser flash apparatus. A standard pyroceram 9606 sample was measured and employed as the reference for the calculation of the specific heat capacity, C_p. The density, d, was calculated from the mass and dimensions of the pellet. The total thermal conductivity was then calculated by κ = dDC_p. The Seebeck coefficient was measured from the slope of the thermopower versus temperature gradient using chromel-niobium thermocouples on an in-house system,⁴⁶ similar to the one reported by Iwanaga et al.⁴⁷ The various characterizations were always performed over at least one full thermal cycle using a freshly prepared pellet to avoid differences in thermal history from affecting results. The estimated measurement uncertainties are listed as follows: 5% for electrical resistivity, 5% for Seebeck coefficient, 6% for thermal diffusivity, and the combined uncertainty for zT is about 20%.

Results and discussion

Room temperature PXRD

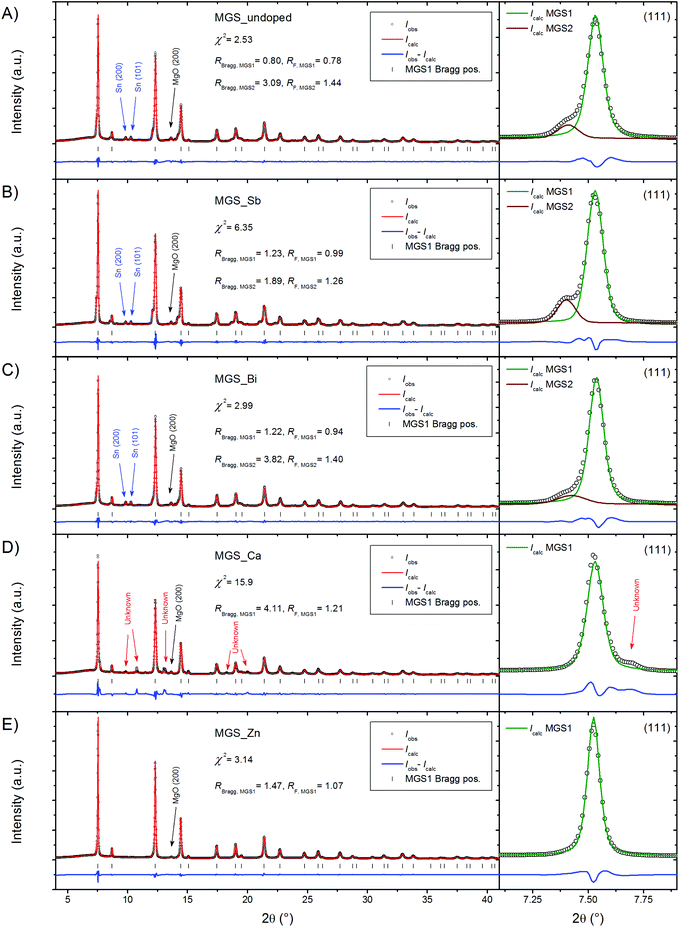
High resolution PXRD patterns measured at 300 K on powder filed off the SPS pressed pellets are shown in Fig. 2. Structural features were discernable up to a 2θ of 60° and the Rietveld refinements were thus performed with this as the upper boundary; however for clarity the upper limit of the shown region has been reduced to 40° in the figure. The diffraction data were modeled using the Rietveld method revealing the presence of a dominant Mg₂Si_1−xSn_x (MGS1) phase in all of the samples. A small amount of MgO, most evident from the peak at 2θ = 13.63°, was found to be present in all diffraction patterns. For the undoped, Sb-doped and Bi-doped samples the presence of a small amount of Sn impurity is also seen from two closely spaced and equally intense peaks at 2θ = 9.84° and 10.28°. In the Ca-doped sample the Sn impurity is absent; however, a different impurity phase has appeared instead. The impurity peak positions and relative intensities resemble those of the perovskite structure CaSnO₃ in the Pbnm space group. It seems plausible that the presence of Ca could induce the formation of an impurity phase incorporating surplus Sn. However, a satisfactory refinement employing the perovskite type structure was not achieved. The relatively weak and overlapping peaks in addition to the vast amount of possible phases containing combinations of Mg, Si, Sn, Ca and O, which are some of the most common elements in the earth's crust, complicate reliable identification of the impurity and the attempt was abandoned. Contrary to Ca, the doping by Zn seems to favor the Mg₂Si_1−xSn_x phase and no other impurities except a small amount of MgO are observed in the diffraction pattern.

Fig. 2 (A–E) PXRD patterns of the five synthesized samples including Rietveld refined models. The enlarged figures on the right show the Mg₂Si_1−xSn_x (111) peak of the corresponding pattern and the contributions of the different Mg₂Si_1−xSn_x phases incorporated in the modeling.

Considering the diffraction patterns in their entirety may lead to the conclusion that the samples consist of a single Mg₂Si_1−xSn_x phase (apart from the aforementioned impurities). However, a closer examination of the individual peaks, as illustrated in the magnification of the (111) peaks in Fig. 2, reveals that this is not the case. In the diffraction patterns of MGS_undoped, MGS_Sb, and MGS_Bi, a shoulder is visible on the left side of the (111) peak and the shoulder is consistently present on all the diffraction peaks of the main Mg₂Si_1−xSn_x phase (MGS1), indicating the presence of a bimodal distribution of solid solutions between MGS1 and another discrete Mg₂Si_1−xSn_x phase (MGS2). These structural subtleties may significantly influence the material properties.

Quantitative phase analysis

Rietveld refinements of the room temperature PXRD patterns were carried out in order to extract structural and compositional information. The phase compositions of the five samples, calculated from the refined parameters as described in the data analysis section, are illustrated in Fig. 3.

Fig. 3 Phase compositions of the samples obtained from Rietveld refinement of high resolution synchrotron PXRD data measured at room temperature. *The actual MGS1 and MgO weight percentages in MGS_Ca are slightly lower than indicated due to the presence of an unidentified impurity phase.

The two Mg₂Si_1−xSn_x phases make up the bulk (∼78–97%) of all the samples. In MGS_undoped, MGS_Sb, and MGS_Bi, the secondary MGS2 phase accounts for 6.2(1)%, 10.5(2)% and 5.3(1)% of the Mg₂Si_1−xSn_x, while MGS_Ca and MGS_Zn only contain the main phase at room temperature. Considerable amounts of MgO impurity (4–15%) are present in all the samples and for MGS_undoped, MGS_Sb, and MGS_Ca, small amounts of Sn (∼1–2%) are found as well. Notably, the actual MGS1 and MgO contents in the MGS_Ca sample are slightly lower than indicated as the unknown impurity phase was not accounted for in the refinement. The accuracy of quantitative phase analysis from PXRD experiments is influenced by microabsorption.⁴⁸ The effect arises when the sample contains phases with different absorption coefficients and/or crystallite size distributions. This causes reflections from heavily absorbing phases to be suppressed while those of lighter absorbers are effectively enhanced. The coarseness of the samples makes it difficult to determine the crystallite size which again makes it hard to determine an appropriate Brindley particle absorption contrast.⁴⁹ The Brindley factor t was therefore set to 1 for all phases in the refinements. Since MgO has a relatively low linear absorption coefficient (1.70 cm⁻¹) compared to Mg₂Si_0.4Sn_0.6 (28.37 cm⁻¹), Mg₂Sn (44.70 cm⁻¹) and Sn (128.23 cm⁻¹) at the given X-ray energy, the weight fraction of MgO will be overestimated. On the other hand, the amount of Sn in the sample is underestimated. Consequently, the values presented here should only be used as an indication of the composition, and for relative comparison among samples.

Stoichiometry

In addition to the phase composition, the refinements also yield structural information about the samples. The stoichiometric parameter x has been calculated from the mutually constrained refinement of atomic Si and Sn occupancies on the 4a Wyckoff site in the structure. The obtained stoichiometries of MGS1 in the samples are all close to but slightly higher than the target value of x = 0.6. The unit cell length and x values can be used as indicators of the stoichiometry and they are in very good agreement considering that the composition Mg₂Si_0.4Sn_0.6 (x = 0.6) is expected to have a unit cell length of ∼6.62 Å at room temperature.³¹ The secondary MGS2 phase present in MGS_undoped, MGS_Sb, and MGS_Bi is generally very Sn-rich. The refinements occasionally resulted in Sn occupancies above the limit of the atomic site, making it necessary to constrain it to full occupancy. Fig. 4 shows the refined unit cell parameters as a function of the obtained stoichiometries. The results agree with values obtained in a compositional study by Søndergaard et al.³¹ and with the unit cell parameters obtained from Rietveld refinement of the pure Mg₂Si and Mg₂Sn.⁴⁰

Fig. 4 Refined unit cell parameters as a function of x in Mg₂Si_1−xSn_x calculated from the refined atomic occupancies and plotted together with values reported by Søndergaard et al.³¹ The estimated standard deviations are smaller than the symbols. A linear fit to the data reported by Søndergaard et al. has been added to illustrate the validity of Vegard's law for this system. The target stoichiometry is indicated by the dashed black vertical line.

In conclusion, it has been found that the stoichiometry of the main MGS1 phase, which makes up the bulk of the samples (>78%), is very close to the targeted value. At room temperature, the secondary Sn-rich MGS2 phase, which was observed in smaller amounts (<11%) in certain samples, seems to be the phase pure Mg₂Sn (x = 1) in MGS_undoped and MGS_Bi, and Mg₂Sn_0.95(1)Si_0.05(1) for MGS_Sb. Considering that the only impurities visible from the PXRD data are Sn and MgO, this leads to the question of where the remaining Si has gone since it is not observable in the crystalline part of the sample.

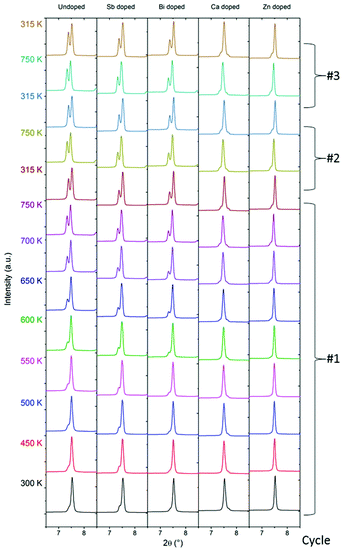
Multi-temperature PXRD

The thermoelectric performance of a material is highly dependent on its structure and composition, which both may change with temperature. The advantage of the Mg₂Si_1−xSn_x compounds is their ability to perform in the medium temperature range, 500–900 K. Consequently, the structural stability of the compound in this temperature region is of great interest. After the initial measurement of room temperature synchrotron PXRD data, the samples were thermally cycled from 300 to 750 K three times in Ar-filled capillaries, with diffraction patterns being collected at selected temperatures. Fig. 5 shows the evolution of the Mg₂Si_1−xSn_x (111) Bragg peak with temperature for the five samples. Diffraction data of the entire 2θ range are provided in the ESI.†

Fig. 5 Mg₂Si_1−xSn_x (111) Bragg peak for the different samples measured during thermal cycling.

For MGS_undoped, MGS_Sb and MGS_Bi, the amount of Sn-rich MGS2 phase increases when the temperature increases. This is apparent from the initially subtle shoulder on the left of the peak which develops into a separate and easily distinguishable Bragg peak. However, for the cation-doped samples MGS_Ca and MGS_Zn, only slight changes are observed when heating. A hint of a shoulder indicating the formation of a Sn-rich MGS2 phase is observed when the temperature is increased above 600 K. It seems that the doping by Ca or Zn dramatically improves the thermal stability of the MGS1 phase. Subsequent cycling of the temperature down to 315 K and back to 750 K only introduces a minor change in these samples.

The data shown in Fig. 5 were collected on powder samples in an Argon atmosphere, whereas physical property data are collected on pressed pellets. It is possible that decomposition processes may not be as significant in pressed pellets e.g. due to the pressed material having much less exposed surfaces. However, this is not the case as shown in the ESI Fig. S8–S12,† which plots conventional PXRD data measured in reflection geometry on the top and bottom sides of the pressed pellets before and after thermal cycling (300–725 K). Indeed, the PXRD data of the pellets agree very well with the multi-temperature synchrontron PXRD data with significant peak splitting occurring both on the top and bottom sides in the MGS_undoped, MGS_Sb and MGS_Bi samples. For the MGS_Ca and MGS_Zn samples only subtle changes are observed in the PXRD patterns following thermal cycling confirming the stabilizing effect of Ca and Zn doping also on the pellets.

Structural and compositional evolution

Rietveld refinements were carried out on the PXRD patterns in order to extract quantitative information. In Fig. 6, the evolution of weight fraction (A), stoichiometry (B), unit cell length (C) and microstrain (D) of MGS1 and MGS2 during the first heating to 750 K is shown on the left while the subsequent cycles are presented on the right.

Fig. 6 (A) Evolution of MGS1 and MGS2 weight percentages with temperature. (B) MGS1 and MGS2 stoichiometry as a function of temperature. (C) Refined unit cell lengths of MGS1 and MGS2 as a function of temperature. (D) Stokes-Wilson upper limit isotropic microstrain for MGS1 and MGS2 normalized by the final value as a function of temperature.

The refined weight fractions of MGS1 and MGS2 shown in Fig. 6(A) confirm the initial assessment from the (111) Bragg peaks in Fig. 5 showing a simultaneous decrease in MGS1 and increase of MGS2. The highest degree of phase separation takes place in MGS_undoped where MGS2 goes from initially accounting for 6.9% of the total Mg₂Si_1−xSn_x content at 300 K to 28.6% at 750 K. A less dramatic, however still significant, evolution in phase composition occurs in MGS_Sb and MGS_Bi where MGS2 go from 11.3% to 22.7% and 6.3% to 20.0% of the total Mg₂Si_1−xSn_x content respectively. In MGS_Ca and MGS_Zn no MGS2 phase was observed at 300 K, however a slight amount forms when heating the samples above 550 K. Consequently, MGS2 accounts for 3.1% of the Mg₂Si_1−xSn_x content in the Ca-doped and 8.7% in the Zn-doped at 750 K. The phase compositions of all samples remain relatively stable during the subsequent heating cycles. As mentioned earlier, the lack of microabsorption correction in the weight fraction calculation causes the relative amount of MGS2 to be underestimated and the given percentages should thus only be used as estimates.

The compositional stability of the individual MGS1 and MGS2 phases in the bimodal solid solution systems was also determined. Fig. 6(B) shows the stoichiometry parameter, x, for the Mg₂Si_1−xSn_x phases as a function of temperature. The parameter has been calculated from the refined Si and Sn occupancies on the atomic Wyckoff 4a site in the structure and represents the mean stoichiometry of the given group of solid solutions, i.e. MGS1 or MGS2-phase. The stoichiometries of the main MGS1 phases remain stable at their initial values slightly above the targeted x = 0.6 throughout the temperature scans for all five samples. For MGS_undoped the x of MGS2 decreases gradually in a somewhat linear fashion with temperature, starting at x = 1 at 300 K and reaching x = 0.88(1) at 750 K. For the Sb-doped sample a slight decrease from x = 0.95(1) to 0.91(1) is observed. The MGS2 stoichiometry in MGS_Bi and MGS_Ca remain stable at the maximum x = 1 value. For MGS_Zn the MGS2 stoichiometry drops relatively fast from 1 to 0.92(1) after the secondary phase appears at 550 K.

The evolution of the crystallographic unit cell lengths of MGS1 and MGS2 with temperature is shown in Fig. 6(C). For all the samples the unit cell length increases linearly with temperature due to the thermal expansion of the material. Slight variations are seen which are likely related to the changes in stoichiometry for the MGS2 phases.

Fig. 6(D) shows the evolution of the Stokes-Wilson upper-limit isotropic microstrain, found from the modeling of peak profiles in the refinements.³⁹ The strain has been normalized by the final value attained after the three thermal cycles. Within the Stokes-Wilson approximation, the strain varies from crystallite to crystallite but takes on a constant value within each crystallite. This effectively means that the calculated strain can be used as a measure of the distribution of Mg₂Si_1−xSn_x phases around the mean stoichiometry. For all samples, the peaks sharpen and the strain decreases indicating a phase separation towards specific discrete stoichiometries. Most dramatic is the sharpening of the MGS2 distributions. The abnormal behavior of MGS2 in the Ca-doped sample is caused by the presence of the unknown impurity which is not included in the refined model. Additional thermal cycling induces no further changes in the refined Stokes-Wilson upper-limit isotropic microstrain.

The results illustrate the importance of investigating the structural and compositional changes that take place when subjecting the material to elevated temperatures. The phase composition of the material changes dramatically with temperature for certain samples during the first heating while remaining relatively stable during additional cycling of the samples in the same temperature range. Performing structural and compositional characterization solely prior to thermal cycling thus may lead to false conclusions. In the case of the investigated undoped, Sb-doped, Bi-doped, Ca-doped and Zn-doped Mg₂Si_1−xSn_x samples it is clearly more meaningful performing the characterization after thermal cycling. Furthermore, the results show the importance of performing several thermal cycles in the characterization of the thermoelectric properties.

Thermoelectric properties

Thermal stability of electrical resistivity

Electrical resistivity is an intrinsic and fundamental physical property for a thermoelectric material. The thermal stability of electrical resistivity thus could be adopted as an effective indicator for the stability of a thermoelectric material. Temperature dependent electrical resistivities of all samples during two thermal cycles are shown in Fig. 7. Freshly prepared pellets were used for the resistivity measurements to avoid the influence of thermal history on the results. This makes it possible to link the thermal stability of the electrical properties to the structural evolution with temperature. It is obvious that the behaviors of the temperature dependent resistivity data of the MGS_undoped, MGS_Sb, and MGS_Bi samples are distinct from those of MGS_Ca and MGS_Zn samples.

Fig. 7 Temperature dependence of electrical resistivity during heating and cooling of the first and second thermal cycles.

For MGS_undoped, MGS_Sb, and MGS_Bi, the resistivity undergoes a considerable decrease in the first heating curve but only a minor increase during the subsequent first cooling curve. The difference between the first heating and cooling curves is substantial, indicating an irreversible process for the first thermal cycle. The rapid decrease of the first heating curve can be well explained by the temperature-dependent structural evolution, i.e., the increasing amount of the secondary MGS2 phase with increasing temperature (see Fig. 6(A)). For the MGS_undoped sample, the resistivity data of the second thermal cycle are consistent with the first cooling curve; however, for the anion-doped samples MGS_Sb and MGS_Bi, the second cooling curve still cannot repeat the first cooling curve. The above results reveal that Sb-doped and Bi-doped samples are not thermally stable, highlighting the importance of conducting structural characterization after the property measurement.

For MGS_Ca, in spite of the slight difference of the first heating curve for the resistivity data in the temperature range of 300–400 K, the first cooling curve and second heating/cooling curve of the two thermal cycles show excellent consistency between each other. In addition, the resistivity data of the MGS_Zn sample is reproduced upon repeated heating and cooling for two thermal cycles. The good repeatability of the resistivity curves in MGS_Ca and MGS_Zn is consistent with the very slight change of structures with increasing temperature (see Fig. 6(A)). Thus, the cation doping by Ca or Zn greatly improves the thermal stability of MGS1 phase.

Electronic transport properties

In Fig. 8, the temperature dependences of the measured Hall transport data of the cooling curve from the first cycle are plotted along with polynomial fits to the raw data points. The initial heating curves were discarded due to the abnormal behavior related to the phase separation seen in the structural characterization (Fig. 5 and 6). An increase in Hall carrier concentration, n_H, with increasing temperature (Fig. 8(A)) is observed for all samples within the entire measured temperature range. Compared with the undoped sample, MGS_Sb, MGS_Bi, and MGS_Ca show slightly enhanced carrier concentrations in the low temperature range of 300–600 K and comparable values at high temperatures, while MGS_Zn displays almost the same n_H curve. The magnitudes of the Hall carrier concentration values of the anion- and cation-doped samples are relatively low compared to previously reported values.^6,22 The negligible impact of the cation doping may be explained by the isoelectronic valence of Mg and the dopants, Ca and Zn. Successful anion doping by Sb or Bi is known to cause a significant increase in carrier concentration.^24,31 However, our samples doped by Sb or Bi depict only a small enhancement of carrier concentration, which is probably due to the difficulty of optimizing thermoelectric performance in the employed large-scale synthesis method.

Fig. 8 Electronic transport properties of all samples from room temperature to 725 K during first cooling. (A) Hall carrier concentration. (B) Hall carrier mobility. (C) Electrical conductivity.

The Hall carrier mobility μ_H was calculated from the resistivity, ρ, and carrier concentration, n_H, as follows, μ_H = 1/(n_Heρ), and is shown in Fig. 8(B). The dashed lines illustrate μ_H ∝ T⁻¹ and μ_H ∝ T^−3/2 temperature dependences emphasizing the boundaries for the applicability of acoustic phonon scattering theory.⁵⁰ For the anion-doped samples, it seems that acoustic phonon scattering dominates the transport behavior at elevated temperature while alloy scattering (μ_H ∝ T^−1/2) contributes more significantly around ambient conditions. The Ca- and Zn-doped samples demonstrate acoustic phonon dominated scattering behavior throughout almost the entire temperature interval. Notably, the phase stability of the Zn-doped sample gives it a significantly higher mobility below 550 K due to the absence of impurity scattering.

Fig. 8(C) shows the measured electrical conductivity as a function of temperature. Compared with the undoped sample, the electrical conductivity values of cation-doped samples are enhanced by a factor of ∼2.4 at 350 K and a factor of ∼1.47 at 725 K. However, for the anion-doped samples, the conductivity at 350 K is similar to that of MGS_undoped and exhibits about 33% enhancement. Heavy doping of Mg₂Si_0.4Sn_0.6 usually results in a more metallic-like behavior i.e. larger absolute values which decrease somewhat linearly with temperature.^22,30,31 However, the doped samples prepared by the present large-scale synthesis method, exhibit typical semiconductor-like behavior, where the electrical conductivity increases with increasing temperature.

Fig. 9(A) shows the measured Seebeck coefficient data of the cooling curve of the first thermal cycle and a curve generated from polynomial fits to the raw data points. The absolute value of the Seebeck coefficient decreases with increasing temperature for all samples, which is consistent with the trend of the temperature-dependent resistivity data. At lower temperatures MGS_Zn has the largest Seebeck coefficient of ∼400 μV K⁻¹ at 375 K but it drops relatively fast with temperature and is overtaken by MGS_Sb and MGS_Bi above 500 K which both decrease in a slow linear fashion. The curves of MGS_undoped and MGS_Ca nearly coincide and follow a trend similar to MGS_Zn but with lower values.

Fig. 9 (A) Seebeck coefficient as a function of temperature. (B) Power factor as a function of temperature.

Fig. 9(B) shows the power factor of all samples as a function of temperature. The power factor of the undoped sample exhibits a nearly temperature-independent behavior from 350 to 475 K and then a gentle decreasing trend in the higher temperature range of 475–725 K. The power factor values of MGS_Zn and MGS_Ca decrease as the temperature increases. However, the power factors of anion-doped samples MGS_Sb and MGS_Bi increase with increasing temperature and then decrease, attaining maximum values of 5.8 and 5.6 μW cm⁻¹ K⁻² at 650 K and 675 K, respectively.

Thermal transport properties

The thermal conductivities of the samples are shown in Fig. 10(A) along with a linear interpolation between the raw data points of the cooling curve of the first thermal cycle. The curves all have a minimum at around 500 K and the values are generally lower than previously reported thermal conductivities in the literature.^6,11,22 The anion-doped samples attain the lowest thermal conductivities while both the cation-doped samples have higher thermal conductivities than the undoped throughout the entire temperature range. Notably, the Zn-doped sample has a significantly higher thermal conductivity than the rest. This is likely related to the low amount of impurity in the MGS_Zn sample which limits the elastic scattering of phonons at lattice defects.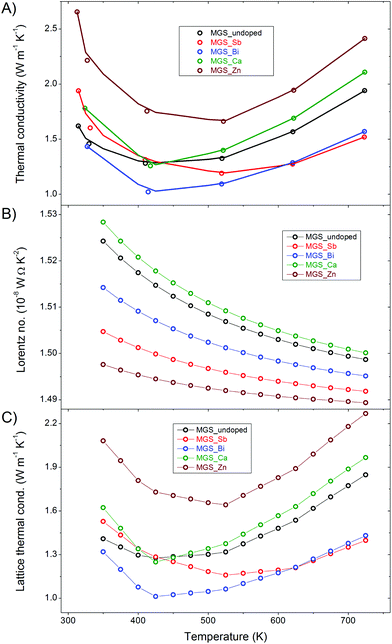

Fig. 10 Thermal transport properties as a function of temperature (A) Total thermal conductivity. (B) Lorentz number. (C) Lattice thermal conductivity.

The total thermal conductivity, κ, shown in Fig. 10(A), is the sum of a lattice component, κ_L, and an electronic component, κ_e, i.e. κ = κ_L + κ_e. The electronic contribution can be estimated based on the Wiedemann–Franz law, κ_e = LσT, where L is the Lorentz number, σ is the electrical conductivity and T is the temperature. The Lorentz number (Fig. 10(B)) has been calculated using the single parabolic band model and assuming an acoustic phonon scattering mechanism for the entire temperature range.⁵¹ Detailed information about the calculation of the Lorenz number can be found in the ESI.† The very low Hall carrier concentration means that the electronic contribution to the thermal conductivity becomes minor. This is clearly illustrated by the similarity of the lattice (Fig. 10(C)) and the total thermal conductivity curves, where only a slight difference at high temperature is observed. The total and lattice thermal conductivity values all show increasing trends at high temperatures, which may be attributed to the bipolar conduction effect.

Thermoelectric figure of merit

The temperature dependent dimensionless figure of merit, zT, was calculated and is shown in Fig. 11. Doping by Sb and Bi significantly improves the thermoelectric performance of the material at high temperatures attaining a maximum zT at ∼650 K of 0.28 and 0.26, respectively. The cation doping by Ca and Zn only improves the performance slightly compared with the undoped sample. The advantage of the anion-doped samples seems to stem from their superior Seebeck coefficients along with the higher thermal conductivity of the cation-doped samples.

Fig. 11 Dimensionless figure of merit as a function of temperature.

The highest zT values attained in this study are significantly lower than the zT values reported in a number of similar investigations in the literature, where zT values above 1 are routinely obtained.^14–24 This may be attributed to the challenges associated with optimizing thermoelectric performance in large-scale, commercially viable synthesis methods.

Importance of detailed structural analysis

Fig. 12 illustrates an alternate way of presenting the room temperature high-resolution synchrotron PXRD data from Fig. 2. Here, the same data has been formatted to fit the style which is currently the norm and considered acceptable in the thermoelectric literature. This serves to illustrate, how improper formatting of even the best, high-resolution synchrotron PXRD data, can result in impurities and structural subtleties becoming indistinguishable from the dominant peaks and background. If the measured high resolution synchrotron data in this study were presented like this, the structural differences and changes described in detail above could have been completely neglected. In the bulk of the literature on Mg₂Si_1−xSn_x based thermoelectric materials, stacking/overlapping of PXRD patterns, formatting using thick lines or symbols, heavy compression of intensities (Y-axes) in the PXRD data plots, which are scaled to fit in a single article column and/or in many cases relocated to ESI,† makes it a difficult task even for an expert reader to critically evaluate the reported results. In addition, the assessment of phase purity is often based on the ‘successful’ crude indexing of the main Bragg reflections, which is as demonstrated above far from conclusive evidence. For a robust structural analysis it is necessary to employ modeling methods, such as Rietveld refinement, to extract reliable and quantitative information from the PXRD data.

Fig. 12 High resolution synchrotron PXRD data presented in the size and style currently the norm in the thermoelectric literature.

If one uses the plotting procedure in Fig. 12, one could conclude that all samples are phase pure. In fact, as shown in Fig. 3, the investigated samples contain up to around 20% impurity phases. In the ESI Fig. S1 and S2† PXRD data measured for less than 30 minutes on an in-house Rigaku SmartLab diffractometer using Cu radiation are shown. The data clearly show that even standard laboratory diffractometers can provide sufficient resolution to discern the important structural subtleties of the present samples. As discussed above interpretation of the thermoelectric transport data would be of very limited value if not coupled with a robust structural analysis. The lack of data quality and limited importance given to structural analysis in the thermoelectric literature may be a serious limitation for making real progress the field, since interpretation of the transport properties possibly is based on wrong assumptions. Relating physical properties to structural features by meticulous characterization and analysis is the key to truly designing and tailoring functional materials with specific properties.

Conclusions

Multi-temperature high resolution synchrotron PXRD measurements combined with Rietveld analysis reveals a partial conversion of the main Mg₂Si_0.4Sn_0.6 into a separate Sn-rich Mg₂Si_1−xSn_x-phase for undoped and anion-doped (Sb, Bi) samples when heated from room temperature to 750 K. On the other hand, cation (Ca, Zn) doping is found to have a stabilizing effect on the solid solutions. The thermally induced structural and compositional changes are reflected in the electric resistivity measured over the same temperature range, where large discrepancies between values obtained during the initial heating and the subsequent cycles are observed for the undoped and anion-doped samples. Consequently, the characterization of the thermoelectric transport properties is based on values measured during cooling after initially heating the samples to 725 K. The present work serves to illustrate the importance of conducting a meticulous structural characterization in studies of thermoelectric materials.

Acknowledgements

This study was supported by Det Energiteknologiske Udviklings- og Demonstrationsprogram and Innovation Fund Denmark (Center for Thermoelectric Energy Conversion), the Danish National Research Foundation (Center for Materials Crystallography, DNRF93), and the Danish Center for Synchrotron and Neutron Reseach (Danscatt). The authors would like to thank the RIKEN-Harima institute for the allocated synchrotron beamtime at beamline BL44B2, SPring-8, Japan.

Notes and references

1. G. J. Snyder and E. S. Toberer, Nat. Mater., 2008, 7, 105.
2. G. S. Nolas, J. Poon and M. Kanatzidis, MRS Bull., 2006, 31, 199.
3. T. L. Christiansen, E. D. Bojesen, M. Søndergaard, S. Birgisson, J. Becker and B. B. Iversen, CrystEngComm, 2016, 18, 1996.
4. K. A. Borup, J. de Boor, H. Wang, F. Drymiotis, F. Gascoin, X. Shi, L. D. Chen, M. I. Fedorov, E. Muller, B. B. Iversen and G. J. Snyder, Energy Environ. Sci., 2015, 8, 423.
5. A. B. Blichfeld and B. B. Iversen, J. Mater. Chem. C, 2015, 3, 10543.
6. M. Søndergaard, M. Christensen, K. A. Borup, H. Yin and B. B. Iversen, J. Mater. Sci., 2013, 48, 2002.
7. T. Barbier, P. Lemoine, S. Gascoin, O. I. Lebedev, A. Kaltzoglou, P. Vaqueiro, A. V. Powell, R. I. Smith and E. Guilmeau, J. Alloys Compd., 2015, 634, 253.
8. M. B. A. Bashir, S. M. Said, M. F. M. Sabri, D. A. Shnawah and M. H. Elsheikh, Renewable Sustainable Energy Rev., 2014, 37, 569.
9. H. L. Gao, X. X. Liu, T. J. Zhu, S. H. Yang and X. B. Zhao, J. Electron. Mater., 2011, 40, 830.
10. M. Ioannou, G. Polymeris, E. Hatzikraniotis, A. U. Khan, K. M. Paraskevopoulos and T. Kyratsi, J. Electron. Mater., 2013, 42, 1827.
11. V. K. Zaitsev, M. I. Fedorov, E. A. Gurieva, I. S. Eremin, P. P. Konstantinov, A. Y. Samunin and M. V. Vedernikov, Phys. Rev. B: Condens. Matter, 2006, 74, 045207.
12. Q. Zhang, T. J. Zhu, A. J. Zhou, H. Yin and X. B. Zhao, Phys. Scr., 2007, 2007, 123.
13. D. Cederkrantz, N. Farahi, K. A. Borup, B. B. Iversen, M. Nygren and A. E. C. Palmqvist, J. Appl. Phys., 2012, 111, 023701.
14. Q. Zhang, J. He, T. J. Zhu, S. N. Zhang, X. B. Zhao and T. M. Tritt, Appl. Phys. Lett., 2008, 93, 102109.
15. X. H. Liu, T. J. Zhu, H. Wang, L. P. Hu, H. H. Xie, G. Y. Jiang, G. J. Snyder and X. B. Zhao, Adv. Energy Mater., 2013, 3, 1238.
16. W. Liu, Q. Zhang, X. Tang, H. Li and J. Sharp, J. Electron. Mater., 2011, 40, 1062.
17. L. Wei, T. Xinfeng and S. Jeff, J. Phys. D: Appl. Phys., 2010, 43, 085406.
18. W. Liu, X. Tang, H. Li, J. Sharp, X. Zhou and C. Uher, Chem. Mater., 2011, 23, 5256.
19. A. U. Khan, N. V. Vlachos, E. Hatzikraniotis, G. S. Polymeris, C. B. Lioutas, E. C. Stefanaki, K. M. Paraskevopoulos, I. Giapintzakis and T. Kyratsi, Acta Mater., 2014, 77, 43.
20. H. L. Gao, T. J. Zhu, X. B. Zhao and Y. Deng, J. Solid State Chem., 2014, 220, 157.
21. A. U. Khan, N. Vlachos and T. Kyratsi, Scr. Mater., 2013, 69, 606.
22. W. Liu, X. F. Tang, H. Li, K. Yin, J. Sharp, X. Y. Zhou and C. Uher, J. Mater. Chem., 2012, 22, 13653.
23. M. Søndergaard, M. Christensen, K. A. Borup, H. Yin and B. B. Iversen, Acta Mater., 2012, 60, 5745.
24. W. Liu, H. Chi, H. Sun, Q. Zhang, K. Yin, X. F. Tang, Q. J. Zhang and C. Uher, Phys. Chem. Chem. Phys., 2014, 16, 6893.
25. L. Chen, G. Jiang, Y. Chen, Z. Du, X. Zhao, T. Zhu, J. He and T. M. Tritt, J. Mater. Res., 2011, 26, 3038.
26. Q. Zhang, J. He, X. B. Zhao, S. N. Zhang, T. J. Zhu, H. Yin and T. M. Tritt, J. Phys. D: Appl. Phys., 2008, 41, 185103.
27. I. H. Jung, D. H. Kang, W. J. Park, N. J. Kim and S. Ahn, CALPHAD: Comput. Coupling Phase Diagrams Thermochem., 2007, 31, 192.
28. Z. L. Du, G. Y. Jiang, Y. Chen, H. L. Gao, T. J. Zhu and X. B. Zhao, J. Electron. Mater., 2012, 41, 1222.
29. H. Gao, T. Zhu, X. Liu, L. Chen and X. Zhao, J. Mater. Chem., 2011, 21, 5933.
30. H. L. Gao, T. J. Zhu, X. B. Zhao and Y. Deng, Dalton Trans., 2014, 43, 14072.
31. M. Søndergaard, M. Christensen, K. A. Borup, H. Yin and B. B. Iversen, J. Electron. Mater., 2013, 42, 1417.
32. A. Y. Samunin, V. K. Zaitsev, P. P. Konstantinov, M. I. Fedorov, G. N. Isachenko, A. T. Burkov, S. V. Novikov and E. A. Gurieva, J. Electron. Mater., 2013, 42, 1676.
33. W. Liu, X. F. Tang, H. Li, J. Sharp, X. Y. Zhou and C. Uher, Chem. Mater., 2011, 23, 5256.
34. S. Adachi, T. Oguchi, H. Tanida, S. Y. Park, H. Shimizu, H. Miyatake, N. Kamiya, Y. Shiro, Y. Inoue, T. Ueki and T. Iizuka, Nucl. Instrum. Methods Phys. Res., 2001, 467–468(Part 1), 711.
35. J. Rodriguez-Carvajal, Physica B, 1993, 192, 55.
36. K. Momma and F. Izumi, J. Appl. Crystallogr., 2011, 44, 1272.
37. H. E. Swanson, Standard x-ray diffraction powder patterns, U.S. Dept. of Commerce, National Bureau of Standards, Washington, DC, 1953.
38. S. Sasaki, K. Fujino and Y. Takeuchi, Proc. Jpn. Acad., Ser. B, 1979, 55, 43.
39. A. Leineweber and E. J. Mittemeijer, J. Appl. Crystallogr., 2010, 43, 981.
40. H. L. Andersen, J. Zhang, H. Yin, K. Kato and B. B. Iversen, in preparation.
41. J. C. Taylor and C. E. Matulis, J. Appl. Crystallogr., 1991, 24, 14.
42. K. A. Borup, E. S. Toberer, L. D. Zoltan, G. Nakatsukasa, M. Errico, J. P. Fleurial, B. B. Iversen and G. J. Snyder, Rev. Sci. Instrum., 2012, 83, 123902.
43. L. J. van der Pauw, Philips Res. Rep., 1958, 13, 1.
44. J. W. Vandersande, A. Zoltan and C. Wood, Int. J. Thermophys., 1989, 10, 251.
45. C. B. Vining, A. Zoltan and J. W. Vandersande, Int. J. Thermophys., 1989, 10, 259.
46. K. A. Borup, PhD thesis, Aarhus University, 2014.
47. S. Iwanaga, E. S. Toberer, A. LaLonde and G. J. Snyder, Rev. Sci. Instrum., 2011, 82, 063905.
48. S. J. L. Billinge and R. E. Dinnebier, Powder Diffraction: Theory and Practice, RSC Publishing, Cambridge, 2008.
49. R. J. Hill and C. J. Howard, J. Appl. Crystallogr., 1987, 20, 467.
50. K. Koumoto and T. Mori, Thermoelectric Nanomaterials: Materials Design and Applications, Springer-Verlag, Berlin, Heidelberg, 2013.
51. H. J. Goldsmid, Thermoelectric refrigeration, Plenum Press, New York, 1964.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c6qi00520a

---