Femtosecond to nanosecond excited state dynamics of vapor deposited copper phthalocyanine thin films

Abstract

Vapor deposited thin films of copper phthalocyanine (CuPc) were investigated using transient absorption spectroscopy. Exciton–exciton annihilation dominated the kinetics at high exciton densities. When annihilation was minimized, the observed lifetime was measured to be 8.6 ± 0.6 ns, which is over an order of magnitude longer than previous reports. In comparison with metal free phthalocyanine (H₂Pc), the data show evidence that the presence of copper induces an ultrafast relaxation process taking place on the ca. 500 fs timescale. By comparison to recent time-resolved photoemission studies, this is assigned as ultrafast intersystem crossing. As the intersystem crossing occurs ca. 10⁴ times faster than lifetime decay, it is likely that triplets are the dominant excitons in vapor deposited CuPc films. The exciton lifetime of CuPc thin films is ca. 35 times longer than H₂Pc thin films, while the diffusion lengths reported in the literature are typically quite similar for the two materials. These findings suggest that despite appearing to be similar materials at first glance, CuPc and H₂Pc may transport energy in dramatically different ways. This has important implications on the design and mechanistic understanding of devices where phthalocyanines are used as an excitonic material.

---

1 Introduction

Copper phthalocyanine has been one of the most widely studied materials in organic electronics for several decades. For photovoltaic applications it was used in the first modern two-layer structure by Tang in 1986.¹ Given its historical significance and the continual interest in CuPc as a low cost active material in organic electronic devices it is somewhat surprising that the electronic excited states of the material have not been thoroughly characterized with time-resolved techniques. Two of the simplest and most obvious questions are: what is the character of the electronic excited states in these films? and, what are the lifetimes? These two pieces of information are critical to developing a mechanistic understanding of the transport of energy in materials.^2–4

In neat films, there are two commonly invoked energy transfer mechanisms, Dexter⁵ and Förster,⁶ which have different physics that govern their efficiency.^2–4 The relative rates of these mechanisms can be sensitive to the spin multiplicity of the exciton. As the motion of energy in organic materials is typically understood to take place via a diffusive process, the lifetime is a critical component to determining the exciton diffusion length – i.e. the average distance that an exciton can travel before decaying. Though fabricating and optimizing devices does not directly require this knowledge, doing so with a rational design strategy does. Herein we utilize transient absorption spectroscopy to characterize the excited states of CuPc thin films. Experiments on H₂Pc are also presented to help understand the role of the copper atom in the excited state dynamics (Fig. 1).

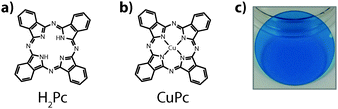Fig. 1 The structure of (a) metal-free phthalocyanine (H₂Pc) and (b) copper phthalocyanine (CuPc). (c) An example thin film of phthalocyanine, vapor-deposited on a quartz substrate.

2 Experimental

2.1 Transient absorption spectroscopy

The femtosecond–picosecond pump–probe measurements were performed using a home-built Ti:sapphire laser system described elsewhere in more detail.⁷ For some experiments the sample was excited with a small portion of the fundamental of the regenerative amplifier (λ = 820 nm, Δλ_fwhm = 26 nm, Δt_fwhm = 75 fs measured by autocorrelation) or the second harmonic (λ = 410 nm, Δλ_fwhm = 10 nm, Δt_fwhm estimated to be 250 fs from signal rise time). Experiments with visible excitation used the output of a nonlinear optical parametric amplifier tunable throughout the visible (Δλ_fwhm = 10–20 nm, Δt_fwhm typically ca. 50 fs measured by cross correlation). In both cases the pump beam was chopped at the second subharmonic (500 Hz) of the amplifier. The pump power was measured with a silicon power meter and adjusted with a waveplate followed by a polarizer. The probe consisted of a white light continuum generated by focusing 820 nm pulses into a 2 mm sapphire window. The residual fundamental light was removed prior to the sample with a Calflex X optical filter (Optics Balzers).

The pump and probe beams were focused with a lens and parabolic mirror respectively and intersected at the sample with a crossing angle of ca. 7°. The polarization of the pump was set to the magic angle (54.7°) with respect to the probe. The width of the pump beam was determined via measuring the energy transmitted through a pinhole rastered across the sample plane, and varied from 100 μm to 1 mm depending on the requirements of the experiments. The probe diameter was <100 μm. Excitation densities were calculated according to ρ_exciton = α(λ_pump) × I₀(λ_pump) which is a valid approximation for low optical densities at the pump wavelength. Here α is the absorption coefficient (units of 1 cm⁻¹) as obtained with ellipsometry of the neat films, and I₀ is the incident photon flux (units of photons per cm² per pulse) calculated using the fwhm of the pump beam at the sample plane. As the focus of this work is not the annihilation itself, no great effort was made to quantify the excitation density more precisely, and we estimate a potential systematic error on the order of 50% could be present due to uncertainties in the spatial profile of the beams, uncertainties in the absorption coefficient, the unknown amount of scattered pump light, the excitation profile in the propagation direction of the beam, the calibration of the power meter, and the pump probe overlap. This systematic uncertainty does not affect the results or conclusions.

The probe beam transmitted the sample, was collimated with a lens and directed towards a detector. For full frequency data the probe was focused into a spectrograph/silicon diode array (Princeton Scientific 2150i/256 pixel Hamamatsu Si array). For single color probe experiments where a higher signal to noise was required the light was directed through a 10 nm bandpass filter at the specified wavelength and was focused onto a ThorLabs Det110 detector operating at zero bias (battery terminals shorted). This signal was amplified and low pass filtered via a current amplifier (SRS 570) and the peak of this signal was sampled by a DAQ card (National Instruments) at 1 kHz. This detection scheme is based off of the one employed by Werley et al. and allowed for greater flexibility than using a lock-in amplifier.⁸ For example it is easy to remove catastrophically noisy samples from the averaging and thus improve the convergence of long time averaging.

For the nanosecond pump–probe measurements the same femtosecond pump source was used, however, the probe source was an electronically delayed (SRS DG535) 470 nm pulsed diode laser (Picoquant PDL 800-B, LDH-P-C-470) in the manner described by Schmidhammer et al.⁹ The instrument response function of the system was approximated by measuring the transient absorption of a methanol solution of 1,1′-diethyl-4,4′-dicyanine iodide excited at 820 nm and probed at 470 nm; this yielded a fwhm of ca. 300 ps. The timing accuracy of the system was confirmed by measuring the transient decay at 470 nm of a methanol solution of Rhodamine 101 excited at 545 nm; the measured value was within error of the of the literature value of the fluorescence decay (4.6 ± 0.1 ns).¹⁰

For the high time resolution data in Fig. 6 the data was corrected for the chirp in the probe continuum via measuring the cross phase modulation from a bare quartz substrate. The data in Fig. 3 was corrected via inspecting the rise of the transient absorption signal; as this method of chirp correction is less accurate, the data before 400 fs is not shown. Time-domain fitting was performed using an iterative least-squares approach with the following functional form: f(t;a,τ) = a × exp(−t/τ). Uncertainties are reported at the 95% confidence interval level.

2.2 Sample preparation

Thin films of neat H₂Pc and CuPc were deposited by vacuum thermal sublimation. The H₂Pc was purchased from Sigma-Aldrich, and the CuPc was obtained from Acros Organics. Both materials were used as purchased without further purification. Prior to deposition, the quartz substrates (GM Associates) were cleaned by sonicating in tergitol and acetone before being boiled in isopropyl alcohol. All organic materials were deposited at pressures below 10⁻⁶ Torr with a total deposition rate (as measured by a calibrated quartz crystal monitor) of 0.2 nm s⁻¹. For the experiments conducted with 610 nm, 820 nm, and 410 nm excitation using a white light probe the films were between 42 nm and 78 nm. For the nanosecond single color experiments conducted using off-resonant excitation (531 nm and 820 nm) the films were between 255 nm and 318 nm thick (as measured by spectroscopic ellipsometry).

All data presented in the manuscript (except Fig. 5) was collected on a spinning sample which had a linear velocity such that the sample volume was replaced between each laser shot. For the nanosecond resolved pump–probe experiments in Fig. 5 the samples were stationary and housed in vacuum (ca. <10 Torr) during measurements; this was done to minimize the noise. In the present systems we observed no significant difference in the kinetics of the vacuum-housed stationary and air-exposed rotating films. Experiments were performed at room temperature and all samples were transported to the spectrometer in air.

3 Results and discussion

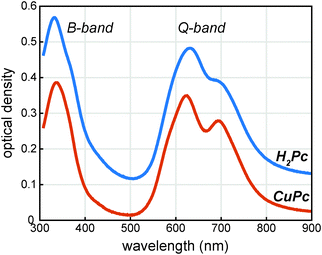
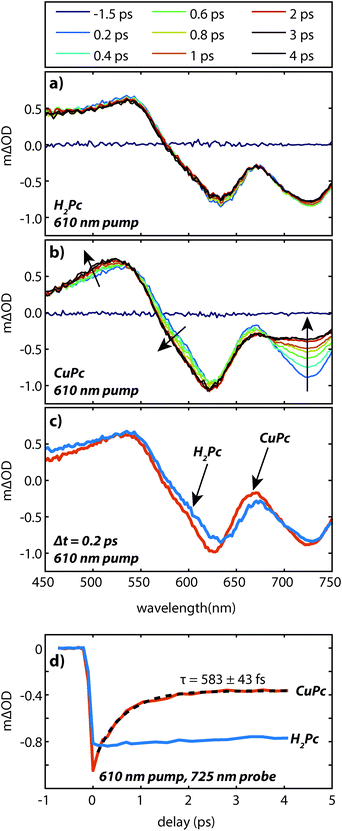
The UV/visible absorption spectrum of a CuPc sample is shown in Fig. 2 and for comparison the UV/visible absorption spectrum of a H₂Pc sample is also shown. Vapor deposited thin films of CuPc are polycrystalline with the α-phase structure similar to vapor deposited thin films of H₂Pc films.¹¹ As the electronic transitions in the visible dominantly originate from the phthalocyanine π system, the similar molecular packing of both the H₂Pc and CuPc vapor deposited films yields similar absorption spectra.¹² The reduced symmetry of the H₂Pc molecule does not appear to dramatically effect the UV/visible spectrum; the symmetry reduction at most appears to broaden and shift the absorption features of the Q-band only slightly.

Fig. 2 UV/visible absorption spectra of phthalocyanine thin films vapor deposited on quartz. The H₂Pc and CuPc films are 58 nm and 53 nm thick respectively. The H₂Pc spectrum is offset vertically by 0.1 units for viewing.

Fig. 3 Transient absorption spectra of vapor deposited CuPc (ca. 60 nm) on quartz excited at (a) 410 nm and (b) 820 nm. Arrows indicate the spectral evolution, and the inverted ground state absorption spectrum (arbitrarily scaled for viewing) is shown as a thick black line for comparison.

In order to probe the excited states, a thin film of CuPc was initially excited using a 410 nm pulse and probed with a white light continuum (Fig. 3a). The transient spectra show a broad positive excited state absorption feature centered around 520 nm, and a negative signal assigned as the ground state bleach that extends from about 560 nm to 750 nm. The shape of the bleaching signal does not match the ground state absorption spectrum and thus it can be surmised that a positive excited state absorption signal overlaps with the negative ground state bleach in this region. No stimulated emission is expected in this system as it has no measurable fluorescence in this region.¹³

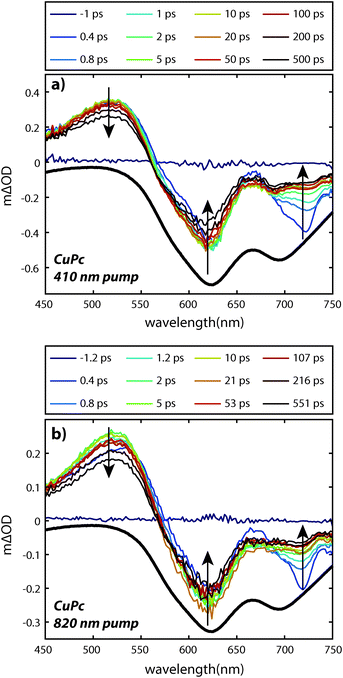
The transient spectra decay on two distinct timescales and in different regions. A fast decay is observed over the first picosecond at 725 nm, while the entire transient appears to decay on the nanosecond timescale. The 410 nm pump pulse excites the system into the low energy tail of the B-band and Kasha's rule would predict that rapid interband and intraband relaxation should occur. In order to understand the relative importance of these processes in the data we also excited the system with an 820 nm pump pulse which excites the system into the low energy tail of the Q-band for comparison (Fig. 3b). Within experimental error the transients are qualitatively identical; the same holds true when using a pump pulse at 610 nm (see Fig. 6 below). This suggests that either the interband and intraband relaxation occur substantially faster than 400 fs or that transient absorption spectroscopy is insensitive to these relaxation processes. Regardless, neither the fast nor slow dynamics are dramatically affected by the 1.5 eV of excess pump energy from the 410 nm excitation as compared to the 820 nm excitation. Small differences in the spectral shapes can be attributed to thermal effects^14–16 due to heating of the film (ΔT < 1 K for Fig. 3). (For a discussion of the effects of heating see the ESI.†)

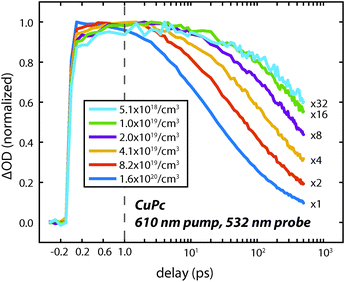
To understand the nature of the fast and slow dynamics we consider them separately. By varying the photon fluence it was observed that the long time decay is highly dependent on the initial exciton density; higher exciton densities resulted in faster decays. This behavior is consistent with a bimolecular exciton–exciton annihilation process with a decay dependent on the exciton density.^14,17 For small exciton densities this annihilation process will be negligible and the monomolecular lifetime decay will be observed. In Fig. 4 the excited state absorption is probed for varying pump fluences. Similar to our previous work on H₂Pc the decay appears to stop changing at exciton densities of about 5 × 10¹⁸ cm⁻³.¹⁸ However, at this exciton density the lifetime is too long to measure accurately with an optical delay.

Fig. 4 Decay dynamics of the CuPc excited state absorption feature at 532 nm measured using a 610 nm pump pulse with several different photon fluences on a ca. 60 nm thick film. The estimated exciton density is indicated in the legend. The scale factors for the data are shown on the right.

Fig. 5 Decay dynamics of the CuPc excited state absorption feature at 470 nm measured using either a 510 nm or 820 nm pump pulse on a 255 nm thick film. The instrument response function is shown and is ca. 300 ps. The data are fit to a single exponential starting at 1 ns. For 531 nm excitation τ = 8.4 ± 0.8 and for 820 nm excitation τ = 8.8 ± 0.8. The excitation density is estimated to be 2 × 10¹⁸ cm⁻³ and 1 × 10¹⁸ cm⁻³ for the 820 nm and 531 nm excitation respectively.

Fig. 6 Transient absorption data of vapor deposited (a) H₂Pc and (b) CuPc (ca. 60 nm) excited at 610 nm under the same pump conditions. Arrows indicate the spectral evolution. (c) A comparison of the transient spectra of H₂Pc and CuPc films at Δt = 200 fs. (d) Kinetics at a probe wavelength of 725 nm for H₂Pc and CuPc films.

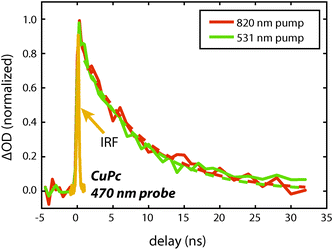
To measure the lifetime decay out into the nanosecond time range we switched from using a femtosecond continuum probe to using an electronically timed 470 nm pulsed diode laser to probe the excited state population. Because the diode laser gives lower signal-to-noise on these measurements, it required us to use thicker films in order to increase the magnitude of the excited state absorption signal. Due to the high absorption coefficient of the material, exciting near the peak of the visible portion of the absorption spectrum (610 nm) created an excitation profile strongly peaked at the front of the sample. In order to create a more uniform exciton profile and make better use of the probe volume the sample was excited off peak resonance. To verify that spectral inhomogeneity was not strongly perturbing the measurements, the sample was excited at both 531 nm and 820 nm. Fig. 5 shows data collected at these two wavelengths at an excitation density of ca. 10¹⁸ cm⁻³. At this density the decays are reasonably approximated as a single exponential (without a vertical offset) and the two data sets acquired at different pump wavelengths are within error of one another yielding an averaged lifetime of 8.6 ± 0.6 ns. This value should be regarded as a lower bound on the lifetime as the currently available signal-to-noise does not permit decreasing the power further, however, we note that increasing the photon fluence by a factor of 5 yielded only a small increase in the decay rate during the first few nanoseconds that is assigned as arising from annihilation. As the presented fits start at 1 ns they were not sensitive to this change, i.e. there was no statistical significant change in the single exponential lifetime between these two excitation densities. The fact that the single exponential decay is a reasonable fit also suggests that this lifetime is likely close to the limiting value.

The faster (sub-picosecond) decay process was found to be independent on the pump fluence over a wide range. In order to understand this fast process in more detail we compare the early time spectra of CuPc to those of H₂Pc performed under identical conditions using resonant 610 nm excitation (Fig. 6a and b). In the case of H₂Pc the spectra from 200 fs to 4 ps were nearly static, however, the CuPc data shows a clear evolution over this same timescale. Most notably, the negative feature at 725 nm decays to under half of its initial value. The negative feature at ca. 610 nm and the positive feature at 520 nm redshift slightly. A transient taken at 725 nm for both data sets is shown in Fig. 6d. The CuPc sample undergoes an ultrafast relaxation process with a single exponential time constant of 583 ± 43 fs that is not present in the H₂Pc sample. In order to compare the H₂Pc and CuPc spectra more closely the spectra taken at 200 fs for both films are plotted in Fig. 6c. At 200 fs, the spectra are nearly identical.

These data suggest the following scenario. The UV/visible and transient absorption spectra recorded for H₂Pc and CuPc are evidence that the initially generated excited state in both films is quite similar. As the H₂Pc system has no heavy atoms and has not been implicated as a singlet fission chromophore, this excited state can be assigned as a singlet exciton which is likely spread over at least two molecules. For H₂Pc, previous work in our lab showed the singlet exciton to decay with a lifetime of 239 ps.¹⁸ The sub-picosecond spectral evolution in CuPc then implies that the singlet exciton in CuPc rapidly evolves into something different. Recent two-photon photoemission measurements have observed a sub-picosecond process on a similar timescale (τ₁ = 200 fs and τ₂ = 800 fs) and assigned it to be intersystem crossing.¹⁹ This assignment was based on the energetic location of the observed peaks with respect to the molecular HOMO and the S₀–T₁ gap, which was estimated via the phosphorescence and absorption spectra. Thus the sub-picosecond evolution in the transient absorption data is assigned to intersystem crossing. This assignment is consistent with previous work on CuPc molecules in solution^20,21 and with the lack of fluorescence from CuPc.¹³ The ultrafast intersystem crossing has been rationalized by noting that the paramagnetic Cu atom may couple to the ligand based exciton and facilitate the intersystem crossing despite not having a large heavy atom induced spin orbit coupling.²² Given that the internal conversion in H₂Pc thin films occurs at least two orders of magnitude slower¹⁸ than the assigned intersystem crossing in CuPc thin films it is likely that the triplet yield is on the order of unity.

The triplet state has a lifetime of at least 8.6 ns. This lifetime is on the same order of magnitude to that of a synthetic CuPc dimer in ethanol, which lived for 5.7 ns.²¹ To contrast the results here, there have been several reports that indicate a CuPc exciton lifetime on the order of 200 ps. In some cases the excitation densities were quite high necessitating a modeling of the annihilation process which is prone to systematic error.²³ In another case only delays times out to 150 ps were accessible and despite being described as being α-phase, the nanowire morphology of that sample may not be identical to the vapor deposited films here.²⁴ In the photoemission measurements the samples were only a few monolayers thick.²⁵ Therefore due to the limitations of these previous measurements, we believe that the 8.6 ns lifetime given here is the most accurate given to date, and is more than one order of magnitude longer than previous measurements.

Interestingly, we note that the dynamics and spectral shapes are remarkably insensitive to the pump wavelength. As stated earlier, this implies either the interband and intraband relaxation occur faster than our time resolution, or alternatively, that transient absorption spectroscopy is relatively insensitive to these processes. Recent experiments using higher time resolution techniques suggest found ca. 10 fs interband relaxation occurs for methylene blue H-aggregates,²⁶ suggesting that it is possible that the rates of these relaxation processes may be responsible for the observed lack of sensitivity of pump wavelength observed in the present study. Future work will be required to understand this point in more detail.

We can now turn to the potential implications that these measurements have for devices. The lack of fluorescence and triplet nature of the CuPc excited state imply that when CuPc is used as an excitonic material that Förster energy transfer will not dominate the energy transport in the film. Instead, a Dexter mechanism will be operative, which is a shorter range interaction. Furthermore, because of the short length scale on which Dexter transfer operates, it is unlikely, though not impossible, that dilution of the chromophore in a wide band gap material will improve its energy transport as it did for subphthalocyanine chloride thin films.²⁷

The observed CuPc lifetime can also be related to the transport of energy in H₂Pc films. In these films we recently measured the singlet lifetime to be 239 ps.¹⁸ This is about 35 times shorter than the CuPc triplet exciton lifetime measured here. If it is assumed that the triplet exciton is responsible for energy transfer in CuPc and that the singlet exciton is responsible for energy transfer in H₂Pc, we can use the expression for the exciton diffusion length, 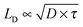to determine the diffusion constant if the diffusion lengths are known. Although the literature values for the diffusion lengths are somewhat scattered⁴ the most recent reports give values in the range of 4–8 nm,^28,29 and thus it would appear that the diffusion constant for the CuPc triplets is an order of magnitude smaller than the diffusion constant for the H₂Pc singlets. The most obvious explanation would be that the transport in H₂Pc is dominated by a Förster mechanism, though a low spectral overlap and H-aggregate character (small radiative rate from the relaxed exciton) make this explanation questionable.^21,30,31 Alternatively, if a Dexter mechanism dominated the transport in both materials then since the α-phase structure is very similar between the two materials¹¹ it would seem that a notable difference in the spatial distribution of the CuPc triplet wavefunction must be important. Another possible explanation could be that the transport in these materials might be limited by the nanoscale morphology and thus not well described by a simple diffusion model; this might be plausible given that published crystallite sizes in α-phase phthalocyanines grown at room temperature are on the order of 30 nm in diameter.^32,33

A great deal of effort is currently being expended trying to understand and engineer the motion of energy in organic materials, however, there are relatively few examples of a system where excitations of different spin multiplicity can be prepared and studied. We believe that the CuPc and H₂Pc systems provide a unique opportunity to analyze the motion of singlets and triplets within a nearly identical lattice. Understanding the difference between the apparent diffusion coefficients of CuPc and H₂Pc will be an important step towards understanding how energy moves through organic photovoltaic materials. The spectral changes associated with intersystem crossing in the phthalocyanine lattice will be helpful in future studies aimed at watching the motion of energy in real time.

4 Conclusions

In conclusion, we have monitored the excited states of a vapor deposited CuPc thin film using transient absorption spectroscopy. Evolution of the transient spectrum on the sub-picosecond timescale is assigned to ultrafast intersystem crossing to the triplet state. Measurements of the lifetime collected at an excitation density of ca. 10¹⁸ cm⁻³ yield an observed lifetime of 8.6 ± 0.6 ns. While the reported diffusion lengths of CuPc and H₂Pc are identical within error, the observed lifetimes differ by a factor of ×35. This suggests that the effective diffusivity of the singlet and triplet excitons in the α-phase of these two phthalocyanines are quite different.

Acknowledgements

The authors are grateful to Philip Goff for technical assistance in setting up the experiments. This work was supported primarily by the National Science Foundation (NSF) Program in Solid State and Materials Chemistry (DMR-1307066).

References

1. C. W. Tang, Appl. Phys. Lett., 1986, 48, 183.
2. G. D. Scholes, Annu. Rev. Phys. Chem., 2003, 54, 57–87.
3. S. M. Menke and R. J. Holmes, Energy Environ. Sci., 2014, 7, 499–512.
4. O. V. Mikhnenko, P. W. M. Blom and T.-Q. Nguyen, Energy Environ. Sci., 2015, 8, 1867–1888.
5. D. L. Dexter, J. Chem. Phys., 1953, 21, 836.
6. T. Forster, Discuss. Faraday Soc., 1959, 27, 7.
7. A. S. Huss, T. Pappenfus, J. Bohnsack, M. Burand, K. R. Mann and D. A. Blank, J. Phys. Chem. A, 2009, 113, 10202–10210.
8. C. A. Werley, S. M. Teo and K. A. Nelson, Rev. Sci. Instrum., 2011, 82, 123108.
9. U. Schmidhammer, S. Roth, E. Riedle, A. A. Tishkov and H. Mayr, Rev. Sci. Instrum., 2005, 76, 093111.
10. D. Magde, G. E. Rojas and P. G. Seybold, Photochem. Photobiol., 1999, 70, 737–744.
11. M. Ashida, N. Uyeda and E. Suito, Bull. Chem. Soc. Jpn., 1966, 39, 2616–2624.
12. E. A. Lucia and F. D. Verderame, J. Chem. Phys., 1968, 48, 2674–2681.
13. K. Yoshino, M. Hikida, K. Tatsuno, K. Kaneto and Y. Inuishi, J. Phys. Soc. Jpn., 1973, 34, 441–445.
14. V. Gulbinas, M. Chachisvilis, L. Valkunas and V. Sundström, J. Phys. Chem., 1996, 100, 2213–2219.
15. S. Albert-Seifried and R. H. Friend, Appl. Phys. Lett., 2011, 98, 223304.
16. V. M. Nichols, K. Broch, F. Schreiber and C. J. Bardeen, J. Phys. Chem. C, 2015, 119, 12856–12864.
17. B. I. Greene and R. R. Millard, Phys. Rev. Lett., 1985, 55, 1331–1334.
18. B. W. Caplins, T. K. Mullenbach, R. J. Holmes and D. A. Blank, J. Phys. Chem. C, 2015, 119, 27340–27347.
19. G. J. Dutton, W. Jin, J. E. Reutt-Robey and S. W. Robey, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 073407.
20. J. McVie, R. S. Sinclair and T. G. Truscott, J. Chem. Soc., Faraday Trans. 2, 1978, 74, 1870–1879.
21. A. V. Nikolaitchik, O. Korth and M. A. J. Rodgers, J. Phys. Chem. A, 1999, 103, 7587–7596.
22. M.-H. Ha-Thi, N. Shafizadeh, L. Poisson and B. Soep, J. Phys. Chem. A, 2013, 117, 8111–8118.
23. Y. Hosokawa, K. Watanabe, T. Asahi, H. Fukumura and H. Masuhara, Bull. Chem. Soc. Jpn., 1999, 72, 909–914.
24. Y. Z. Ma, K. Xiao and R. W. Shaw, J. Phys. Chem. C, 2012, 116, 21588–21593.
25. G. Dutton and S. Robey, J. Phys. Chem. C, 2012, 116, 19173–19181.
26. J. C. Dean, D. G. Oblinsky, S. Rafiq and G. D. Scholes, J. Phys. Chem. B, 2016, 120, 440–454.
27. S. M. Menke, W. A. Luhman and R. J. Holmes, Nat. Mater., 2013, 12, 152–157.
28. F. Piersimoni, D. Cheyns, K. Vandewal, J. V. Manca and B. P. Rand, J. Phys. Chem. Lett., 2012, 3, 2064–2068.
29. M. Ichikawa, Thin Solid Films, 2013, 527, 239–243.
30. Y. Sakakibara, R. N. Bera, T. Mizutani, K. Ishida, M. Tokumoto and T. Tani, J. Phys. Chem. B, 2001, 105, 1547–1553.
31. W. Freyer, C. C. Neacsu and M. B. Raschke, J. Lumin., 2008, 128, 661–672.
32. K. P. Gentry, T. Gredig and I. K. Schuller, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 174118.
33. I. Kim, H. M. Haverinen, Z. Wang, S. Madakuni, Y. Kim, J. Li and G. E. Jabbour, Chem. Mater., 2009, 21, 4256–4260.

---

Footnote

† Electronic supplementary information (ESI) available: Temperature dependent UV/visible absorption spectrum. See DOI: 10.1039/c6cp00958a

---