Open Access Article
Open Access ArticleElectrocapillarity and zero-frequency differential capacitance at the interface between mercury and ionic liquids measured using the pendant drop method
Naoya
Nishi
*,
Atsunori
Hashimoto
,
Eiji
Minami
and
Tetsuo
Sakka
Department of Energy and Hydrocarbon Chemistry, Graduate School of Engineering, Kyoto University, Kyoto 615-8510, Japan. E-mail: nishi.naoya.7e@kyoto-u.ac.jp; Tel: +81-75-383-2491
First published on 12th January 2015
Abstract
The structure of ionic liquids (ILs) at the electrochemical IL|Hg interface has been studied using the pendant drop method. From the electrocapillarity (potential dependence of interfacial tension) differential capacitance (Cd) at zero frequency (in other words, static differential capacitance or differential capacitance in equilibrium) has been evaluated. The potential dependence of zero-frequency Cd at the IL|Hg interface exhibits one or two local maxima near the potential of zero charge (Epzc), depending on the cation of the ILs. For 1-ethyl-3-methylimidazolium tetrafluoroborate, an IL with the cation having a short alkyl chain, the Cdvs. potential curve has one local maximum whereas another IL, 1-octyl-3-methylimidazolium tetrafluoroborate, with the cation having a long alkyl chain, shows two maxima. These behaviors of zero-frequency Cd agree with prediction by recent theoretical and simulation studies for the electrical double layer in ILs. At negative and positive potentials far from Epzc, the zero-frequency Cd increases for both the ILs studied. The increase in zero-frequency Cd is attributable to the densification of ionic layers in the electrical double layer.
1 Introduction
Ionic liquids (ILs), which are salts composed of entirely ions and are liquid at ambient temperature, have potential applications in electrochemical devices, because of their unique properties such as negligible volatility, low flammability, electrochemical stability, and peculiar solvation toward solutes.1–3 For the electrochemical applications of ILs, it is of crucial importance to clarify and to control the interfacial structure and its dependence on the electrode potential. The differential capacitance (Cd), which is the derivative of surface charge density on the electrode with respect to potential, is a measure of how the structure in the electrical double layer (EDL) responds to the potential change and has been intensively measured and reported at the electrochemical interface of ILs by using electrochemical impedance spectroscopy (EIS).4–13 In EIS, a.c. voltage is applied to the electrochemical cell with a frequency, e.g., 1 kHz, to evaluate Cd. The Cd measured by EIS was confirmed to be equal to the zero-frequency (static) Cd for the Hg|aqueous solution interface,14 where the zero-frequency Cd can be evaluated from electrocapillarity, i.e., potential dependence of interfacial tension. For the electrochemical interface of ILs, unlike aqueous solutions, however, this seems not to be the case, because the structure in EDL of ILs shows ultraslow relaxation in response to the potential change, typically on the order of seconds or minutes,15–21 which is slower than the time scale of EIS. The ultraslow relaxation leads to deviation of the Cd values obtained by EIS from the zero-frequency Cd. In fact, several groups reported frequency dependence of Cd18,22–28 and hysteresis in potential dependence of Cd22,29–31 measured using EIS at the electrochemical interface of ILs. Due to such complications, limitation of EIS to unambiguously measure Cd at the electrochemical interface of ILs has also been discussed.25,32 To avoid the confusion caused by frequency dependence of Cd, experimental evaluation of zero-frequency Cd for EDL of ILs would be desirable. Theoretical and simulation studies such as mean field theory3,33–35 and molecular dynamics (MD) simulations36–44 always predict zero-frequency Cd (capacitance in equilibrium) and the predicted and experimental zero-frequency Cd could directly be compared and discussed if the latter is available. One of the interesting predictions from the theory is behavior of zero-frequency Cd as a function of electrode potential: bell-shape (one-hump) or camel-shape (two-hump) zero-frequency Cdvs. potential curves depending on the compacity of ILs,3,33 both of which are totally different from the U-shape curve derived from the Gouy–Chapman theory45,46 for conventional electrolyte solutions. This behavior stems from the fact that ions have finite size. Excluded volume not only between an ion at the first ionic layer and the electrode surface but also between two neighboring ions has to be considered for EDL of ILs. Furthermore, for the application of ILs to energy storage devices, the zero-frequency Cd reflects the total capacity for energy storage, whereas the high-frequency Cd reflects the power of the devices. Both characteristics are important for such an application, however, experimental data of zero-frequency Cd for the electrochemical IL interface have been unavailable so far.Here, we will present experimental zero-frequency Cd data at the IL|Hg interface from electrocapillarity (potential dependence of interfacial tension, γ) measured using the pendant drop method. We used Hg as an electrode material because the liquid|liquid interface is indispensable to measure γ by using the pendant drop method. A good advantage in using Hg is that we do not have to consider the dependence of Cd on the crystal surfaces and the effective area of the electrode, because an atomically flat interface is spontaneously formed even with capillary waves present at soft interfaces. Electrocapillarity at the IL|Hg interface has already been reported by several researchers. However, the studies used the drop time method5,6,47–54 and the drop weight method,55 both of which are “dynamic” methods and have a time scale of several seconds that is much faster than the ultraslow relaxation of the structure in EDL of ILs. Possibly being aware of the time-scale problem, they did not thermodynamically analyze their electrocapillarity data to obtain zero-frequency Cd, except two studies53,55 where the authors formally fitted polynomial to electrocapillarity data and differentiated it twice to obtain the polynomial function of Cd. In the present study, long-time measurements of γ by the pendant drop method enabled us to track the ultraslow relaxation of the structure at the IL|Hg interface to the potential change and to evaluate γ in equilibrium, which was used in thermodynamic analysis to obtain the zero-frequency Cd. In this paper, we will discuss the IL-specific shape of the zero-frequency Cdvs. potential curve and the dependence of the curve on IL-constituting ions.
2 Experimental
Two ILs, [C2mim+]BF4− and [C8mim+]BF4−, were used in the present study, where Cnmim+ denotes 1-alkyl-3-methylimidazolium and n is the number of carbon atoms in the alkyl chain. [C8mim+]Cl− and [C2mim+]Br− were synthesized by mixing 1-methylimidazole (Tokyo Chemical Industry) with 1-chlorooctane (Tokyo Chemical Industry) and 1-bromoethane (Tokyo Chemical Industry), respectively.56 [C8mim+]BF4− was prepared57 and purified15,58 in the same way as literature methods. For the preparation of [C2mim+]BF4−, aqueous solutions of equimolar amounts of [C2mim+]Br− and Na+BF4− were mixed, followed by removing water using an evaporator. The mixed salts were dissolved in dichloromethane and the precipitated NaBr was filtered off. [C2mim+]BF4− dissolved in dichloromethane was purified as in the case of [C8mim+]BF4−. Before measurements, volatile impurities were removed from ILs by using a rotary oil pump for more than 6 h at 50 °C. Hg was purchased (Aldrich, 99.9999%), and purified physically by passing it through a PTFE filter twice and then chemically by passing it in 7 wt% nitric acid in a separating funnel, in which the purified Hg was kept until the measurements.A pendant drop method59–61 was employed to measure γ. The details of the apparatus were described in a paper by Kitazumi and Kakiuchi.62 The optical cell (width, height, and optical length are 20, 40, and 20 mm, respectively) filled with an IL was set in a jacketed holder at 25.0 ± 0.1 °C. A pendant drop of Hg hanging from the glass tube with an inner diameter of 2 mm in the IL was illuminated with paralleled light. An image of the drop was taken using a CCD camera equipped with a telecentric zoom lens. The contour of the drop was extracted from the image by using a homemade program. A theoretical curve calculated using the Bashforth–Adams differential equation63 was fitted to the contour of the drop using SALS, a software for the nonlinear least-squares fitting.64 Three fitting parameters R0, Δz, and β are the radius of curvature at the origin of the contour of the drop, an error of origin of z axis (vertical direction), and 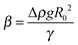 , respectively, where Δρ and g are the density difference of Hg and IL and the acceleration of gravity. The ρ values for [C2mim+]BF4− and [C8mim+]BF4− were measured to be 1.2802 and 1.1009 g cm−3, respectively, at 25.0 °C using a density meter (DA-505, KEM), which agree with those in the literature for [C2mim+]BF4−
, respectively, where Δρ and g are the density difference of Hg and IL and the acceleration of gravity. The ρ values for [C2mim+]BF4− and [C8mim+]BF4− were measured to be 1.2802 and 1.1009 g cm−3, respectively, at 25.0 °C using a density meter (DA-505, KEM), which agree with those in the literature for [C2mim+]BF4−![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 65–67 and [C8mim+]BF4−.68,69 The ρ value for Hg was adopted to be 13.5336 g cm−3 at 25.0 °C from the literature.70 The γ values were evaluated from the two fitted parameters, β and R0, and the fixed parameter, Δρ.
65–67 and [C8mim+]BF4−.68,69 The ρ value for Hg was adopted to be 13.5336 g cm−3 at 25.0 °C from the literature.70 The γ values were evaluated from the two fitted parameters, β and R0, and the fixed parameter, Δρ.
The potential at the IL|Hg interface was controlled using a three-electrode electrochemical system. Pt wire was immersed in Hg, which acts as a working electrode (WE), inside the glass tube to externally control the potential. A Ag wire coated with AgCl was directly immersed in the IL as a quasi-reference electrode (QRE), and a Pt coiled wire as a counter electrode (CE). The potential of the Hg WE with respect to the Ag/AgCl QRE, denoted as E, was controlled using a PC-controlled potentiostat (HA1010mM1A, Hokuto Denko). At each potential, measurements were continued for sufficiently long time, typically more than 5 min to equilibrate the interfacial structure at the IL|Hg interface.
The γ value that became independent of time was adopted as γ in equilibrium at the potential. The number of measurements was 3–20 for each potential.
3 Results and discussion
The electrocapillary curve obtained at the [C2mim+]BF4−|Hg interface is shown in Fig. 1a as solid circles. The γ values were successfully measured within the potential window of the [C2mim+]BF4−|Hg shown in the cyclic voltammogram in Fig. 1b. The shape of γ as a function of E is parabolic, which means that the interfacial excess energy decreases with increase of the absolute value of the interfacial charge density on Hg, |qM|. The potential at the apex of the parabola is the potential of zero charge, Epzc, where the interface is not charged (qM = 0). Also shown in Fig. 1a as open circles are data from a previous study by Alam et al. using the drop time method51 which is a “dynamic” method. The present data using the pendant drop method agree with those using the drop time method at E ≥ 0.3 V, positive side of the parabola. On the other hand, discrepancy is discernible for data from the two methods at E < 0.3 V; the γ values using the pendant drop method are greater than those using the drop time method, for more negative potentials.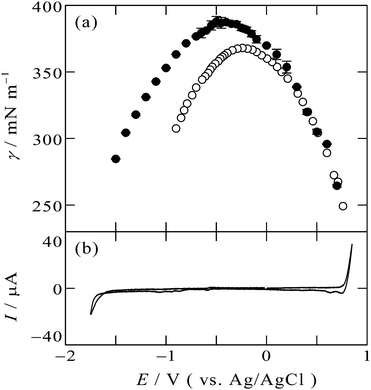 | ||
| Fig. 1 (a) Electrocapillarity at the [C2mim+]BF4−|Hg interface measured by the pendant drop method (solid circles) in the present study and by the drop time method (open circles),51 with error bars of one standard deviation. (b) Cyclic voltammogram at the [C2mim+]BF4−|Hg interface with a scan rate of 20 mV s−1. | ||
This discrepancy is ascribable to the ultraslow relaxation of the structure at the IL|Hg interface. The open circuit potential EOCP was measured to be around +0.3 V. When we apply potential around EOCP, the potential difference is small and the EDL structure relatively easily reaches the equilibrium state at the potential, therefore, γ from the dynamic method and the static method agree with each other. On the other hand, at negative potentials far from EOCP, the time scale of the drop time method, several seconds,6,48 is not long enough for the completion of the ultraslow relaxation, leading to the larger discrepancy at more negative potentials. Another factor we may have to consider for the ultraslow relaxation is asymmetry of the relaxation time to the potential step direction, which we recently found by using surface plasmon resonance at the interface between gold and an IL, trioctylmethylammonium bis(nonafluorobutanesulfonyl)amide.20 For the case of the Au|IL interface, the time constant against the positive step is much slower than that against the negative step, and specific interaction between the ammonium cation and gold surface was considered as a possible reason for the asymmetry.20 However, the present case seems to be explained by the opposite tendency: slower time constant for the negative step. The opposite tendency may be caused by another specific interaction between different metal (Hg) surface and different ions (C2mim+ or BF4−) for the present case.
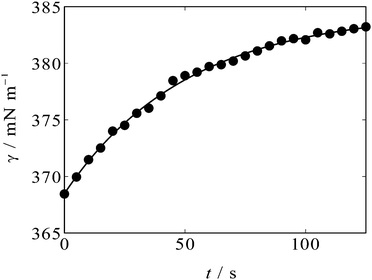
An example of the time variation of γ after the potential step is shown in Fig. 2. One can see that γ rises after t = 0 s when the potential is stepped from OCP (+0.3 V, positive side of the parabola) to −0.3 V, near the apex of the parabola. The solid curve in Fig. 2 is an exponential decay curve fitted to the data. The time constant of the decay was found to be 50 s. Such ultraslow relaxation was reported for the electrochemical interfaces of ILs15–21 and the data indicate that the interfacial structure at the [C2mim+]BF4−|Hg interface also varies in response to the potential perturbation at this time scale.
Another IL, [C8mim+]BF4−, with C8mim+ having a longer alkyl chain than C2mim+, exhibits similar tendency to [C2mim+]BF4−. Fig. 3a and b show the electrocapillary curve and the cyclic voltammogram at the [C8mim+]BF4−|Hg interface, respectively. This interface also exhibit EOCP at +0.3 V, and γ around EOCP determined by the pendant drop method (solid squares) and the drop time method (open squares) is similar, whereas at more negative potentials than EOCPγ obtained by the pendant drop method is greater than that obtained by the drop time method.
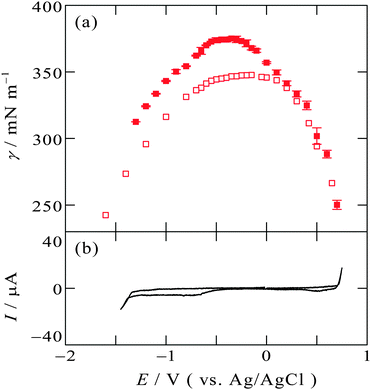 | ||
| Fig. 3 (a) Electrocapillarity at the [C8mim+]BF4−|Hg interface measured by the pendant drop method (solid squares) in the present study and by the drop time method (open squares),51 with error bars of one standard deviation. (b) Cyclic voltammogram at the [C8mim+]BF4−|Hg interface with a scan rate of 20 mV s−1. | ||
The γ values in equilibrium obtained using the pendant drop method enable us for the thermodynamic analysis. The differentiation of γ with E gives qM, as follows
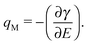 | (1) |
The zero-frequency Cd may be written as
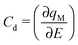 | (2) |
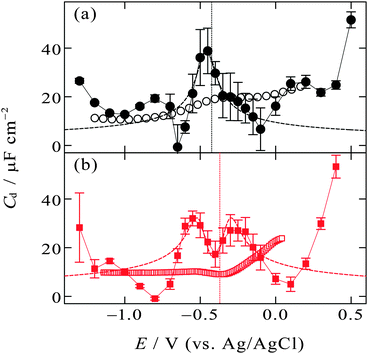 | ||
| Fig. 5 Zero-frequency differential capacitance (solid circles and solid squares) as a function of the electrode potential (a) at the [C2mim+]BF4−|Hg interface and (b) at the [C8mim+]BF4−|Hg interface with error bars of one standard deviation. Vertical dotted lines are at the potential of zero charge. The open circles and squares are high-frequency (1 kHz) differential capacitance obtained from the literature.48,49 The dashed lines are fitted curves of eqn (3) to experimental plots within the potential region (a) from −0.15 to −0.55 V, (b) from −0.1 to −0.65 V. | ||
On the other hand, the [C8mim+]BF4−|Hg interface exhibits camel shape dependence, in which two local maxima exist at negative and positive sides of Epzc (Fig. 5b). The camel shape was also predicted by the mean field theory for EDL of ILs when the ILs have “compacity”, η, less than 1/3.3,33 The compacity is a measure of how much the charge on ions can be packed in EDL compared with the bulk condition and defined as 2c0/cmax where c0 and cmax are the bulk concentration and the maximal possible local concentration of the charge, respectively. For ILs having a neutral moiety (long alkyl chain in the present case) and thus having low compacity, ions can gather to the interface replacing not counter ions but the neutral moiety, leading to the increase in the zero-frequency Cd with increasing |E − Epzc| as expected in the GC model. After neutral moieties in the first ionic layer are depleted due to the replacement, the behavior of the zero-frequency Cd goes back to IL-like decrease instead of GC-like increase with increasing |E − Epzc|, resulting in the two local maxima in the Cdvs. E plots. The IL [C8mim+]BF4− is composed of only ions and does not contain molecules, however, the non-charged octyl moiety in C8mim+ can behave as “molecules” that can be replaced by the anions or the charged-moiety of C8mim+ when the interface becomes charged up. Such behavior was also confirmed by Monte Carlo (MC) simulation of the IL|electrode interface.72,73 The study using a coarse-grain model for the ions constituting ILs suggested that ILs without a neutral moiety show bell-shape dependence of Cd whereas ILs having a neutral moiety show camel-shape dependence. A series of theoretical and simulation studies well accord with the present experimental results for zero-frequency Cd where [C2mim+]BF4− without a long alkyl chain shows bell-shape dependence and [C8mim+]BF4− with a long alkyl chain shows camel-shape dependence (Fig. 5). On the other hand, this is not the case for recent MD simulation studies on the dependence of zero-frequency Cd on the alkyl chain length for Cnmim+-based ILs of bis(trifluoromethanesulfonyl)amide (TFSA−)41 or bis(fluorosulfonyl)amide (FSA−)43 at the atomically flat or atomically rough graphite interface. The results did not show the bell-shape to camel-shape transition except for [Cnmim+][FSA−] at the atomically rough graphite interface. No transition for [Cnmim+][TFSA−] and [Cnmim+][FSA−] at the atomically flat graphite interface may be due to larger size and therefore a larger neutral moiety for TFSA− and FSA− than BF4−. A future experimental study on the dependence of the zero-frequency Cd on IL anions using the pendant drop method at the atomically flat Hg interface will enable further discussion. Note that it is zero-frequency Cd that can be predicted by theoretical and simulation studies and that was measured by the pendant drop method in the present study. Cd at a non-zero frequency measured using EIS should be different from zero-frequency Cd when considering ultraslow relaxation at IL interfaces with a time constant slower than the EIS frequency (e.g. 1 kHz). To compare the difference, in Fig. 5, Cd data at 1 kHz using EIS are shown as open symbols, which were measured for the [C2mim+]BF4−|Hg interface48 and the [C8mim+]BF4−|Hg interface49 by Alam et al. One can see less featured shape of the EIS Cd compared with the zero-frequency Cd (solid symbols), which is likely due to the ultraslow relaxation of the structure in EDL of ILs.
The mean field theory33,34 proposed an analytical solution for the potential dependence of the zero-frequency Cd for EDL of ILs as
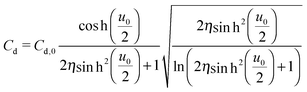 | (3) |
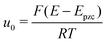 is the normalized potential with the Faraday constant F, the gas constant R, and the absolute temperature T. Note that the mean field theory does not incorporate local electrostatic interaction between ions that leads to the overscreening effect. The overscreening effect was predicted to be non-negligible33 and was found in MD simulation,36,39,44,74,75 some of which suggested that the overscreening effect is remarkable especially for small |u0|.36,74,75 At this stage, we only have the mean field theory to be compared with the present data. Although it was found that MD results qualitatively approved the mean field theory,72,74 a MD (or MC) simulation for the present Hg|IL interface system is required to quantitatively investigate the overscreening effect, and such a simulation study is now in progress in our laboratory. We fitted the theoretical curve of eqn (3) to the experimental data to extract the compacity for these ILs. For the fitting we limited the experimental data only for E ∼ Epzc, −0.15 to −0.55 V for [C2mim+]BF4− and −0.1 to −0.65 V for [C8mim+]BF4−, because of unpredicted behavior in the plots (will be described below) outside the potential region. Although the potential dependence of the compacity that stems from different ionic compacities for the cation and anion in IL was also proposed,33 we did not use it because of the limitation of the potential region. The fitted curves are shown in Fig. 5 as the dashed lines. The fitted η value for [C2mim+]BF4− is 0.5 (Epzc and Cd,0 are −0.46 V and 40 μF cm−2, respectively). The compacity value agrees with MD simulation result, η = 0.43, for a model IL composed of spherical ions without a neutral moiety.3,36 The compacity for [C8mim+]BF4− is 0.05 (Epzc and Cd,0 are −0.41 V and 16 μF cm−2, respectively). As expected, the value is less than 1/3, the demarcation value between bell-shape and camel-shape behaviors.33 Since the compacity is unity minus the sum of void fraction and the fraction of neutral moieties in IL-ions, we can understand the lower compacity for [C8mim+]BF4− having a longer neutral alkyl chain than that for [C2mim+]BF4−. However, the value 0.05 for [C8mim+]BF4− seems too low compared with 0.5 for [C2mim+]BF4− even when considering that the neutral octyl chain lowers the compacity for [C8mim+]BF4−. The lower compacity is probably due to a greater void fraction in [C8mim+]BF4− than [C2mim+]BF4−. The idea is supported by a study on theoretical analysis of the surface tension and the void fraction of ILs, where ILs of cations with a longer alkyl chain tend to have a greater void fraction.76
is the normalized potential with the Faraday constant F, the gas constant R, and the absolute temperature T. Note that the mean field theory does not incorporate local electrostatic interaction between ions that leads to the overscreening effect. The overscreening effect was predicted to be non-negligible33 and was found in MD simulation,36,39,44,74,75 some of which suggested that the overscreening effect is remarkable especially for small |u0|.36,74,75 At this stage, we only have the mean field theory to be compared with the present data. Although it was found that MD results qualitatively approved the mean field theory,72,74 a MD (or MC) simulation for the present Hg|IL interface system is required to quantitatively investigate the overscreening effect, and such a simulation study is now in progress in our laboratory. We fitted the theoretical curve of eqn (3) to the experimental data to extract the compacity for these ILs. For the fitting we limited the experimental data only for E ∼ Epzc, −0.15 to −0.55 V for [C2mim+]BF4− and −0.1 to −0.65 V for [C8mim+]BF4−, because of unpredicted behavior in the plots (will be described below) outside the potential region. Although the potential dependence of the compacity that stems from different ionic compacities for the cation and anion in IL was also proposed,33 we did not use it because of the limitation of the potential region. The fitted curves are shown in Fig. 5 as the dashed lines. The fitted η value for [C2mim+]BF4− is 0.5 (Epzc and Cd,0 are −0.46 V and 40 μF cm−2, respectively). The compacity value agrees with MD simulation result, η = 0.43, for a model IL composed of spherical ions without a neutral moiety.3,36 The compacity for [C8mim+]BF4− is 0.05 (Epzc and Cd,0 are −0.41 V and 16 μF cm−2, respectively). As expected, the value is less than 1/3, the demarcation value between bell-shape and camel-shape behaviors.33 Since the compacity is unity minus the sum of void fraction and the fraction of neutral moieties in IL-ions, we can understand the lower compacity for [C8mim+]BF4− having a longer neutral alkyl chain than that for [C2mim+]BF4−. However, the value 0.05 for [C8mim+]BF4− seems too low compared with 0.5 for [C2mim+]BF4− even when considering that the neutral octyl chain lowers the compacity for [C8mim+]BF4−. The lower compacity is probably due to a greater void fraction in [C8mim+]BF4− than [C2mim+]BF4−. The idea is supported by a study on theoretical analysis of the surface tension and the void fraction of ILs, where ILs of cations with a longer alkyl chain tend to have a greater void fraction.76
After the fitting, features that were not predicted in the mean field theory are clear by comparing the experimental data (solid symbols) and the fitted curves (dashed lines) in Fig. 5. For both [C2mim+]BF4− and [C8mim+]BF4−, when increasing |E − Epzc| from E = Epzc one can see a decrease in experimental zero-frequency Cd after the local maxima to values lower than fitted curves of eqn (3). Although we are not sure the reason for the low zero-frequency Cd, one possibility is stabilization of ionic layers at the potential region due to local ion–ion interaction that are not taken into account in the mean field theory. Solid-like ionic layers of ILs at interfaces have been reported by several groups.77–80 Such stabilization could lead to little ion exchange in EDL for charging up and thus to low capacitance. An existence of the energy barrier for the ion exchange in EDL of ILs was also verified using surface-enhanced IR absorption spectroscopy.81 Another unpredicted feature is the increase in zero-frequency Cd when E goes far from Epzc both in the positive and negative directions. Such increase has been found even for non-zero frequency Cd by EIS at the potential window limit of the Hg interface of [C2mim+]BF4−![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5 and other IL.6 A MD simulation on the graphite interface of [C4mim+]BF4− showed a similar trend in zero-frequency Cd.42 The increase in zero-frequency Cd at the potential regions far from Epzc may remind electrochemists of the zero-frequency Cd behavior at the interface between Hg and aqueous electrolyte solutions (W).82 For the Hg|W interface, the Gouy–Chapman model,45,46 which is also a mean-field theory, well explains the Cd behavior only around Epzc. On the other hand, at potentials far from Epzc, the increase in zero-frequency Cd with increasing |E − Epzc| was confirmed, which cannot be explained by the Gouy–Chapman model. This interesting phenomenon at the Hg|W interface has stimulated theoretical studies of EDL and several possible reasons have been proposed such as electrostriction of EDL,83 interfacial complexation of Hg with an electrolyte anion,83 orientational change of water molecules in the inner layer,84 and densification of the inner layer.85 In spite of considerable theoretical efforts, the reason for the Cd increase has not been fully clarified yet (see a recent review on EDL for details86). One may associate the orientational change of water molecules in the inner layer at the Hg|W interface84 with ion behavior at the Hg|IL interface; the orientational changes of the ions in the inner layer would be one of the possible reasons for the Cd increase. To probe any change in the interfacial structure depending on the potential, we used in situ spectroscopic ellipsometry for the interface between Hg and four ILs including [C8mim+]BF4−. The results showed a potential-dependent structure at the interface and were well reproduced with a model incorporating ionic layers whose density is higher than bulk at E ≫ Epzc.71 Therefore, it is likely that the ionic layers at the interface become densified reacting to the strong electric field at the interface when the interface is highly charged at potentials far from Epzc.
5 and other IL.6 A MD simulation on the graphite interface of [C4mim+]BF4− showed a similar trend in zero-frequency Cd.42 The increase in zero-frequency Cd at the potential regions far from Epzc may remind electrochemists of the zero-frequency Cd behavior at the interface between Hg and aqueous electrolyte solutions (W).82 For the Hg|W interface, the Gouy–Chapman model,45,46 which is also a mean-field theory, well explains the Cd behavior only around Epzc. On the other hand, at potentials far from Epzc, the increase in zero-frequency Cd with increasing |E − Epzc| was confirmed, which cannot be explained by the Gouy–Chapman model. This interesting phenomenon at the Hg|W interface has stimulated theoretical studies of EDL and several possible reasons have been proposed such as electrostriction of EDL,83 interfacial complexation of Hg with an electrolyte anion,83 orientational change of water molecules in the inner layer,84 and densification of the inner layer.85 In spite of considerable theoretical efforts, the reason for the Cd increase has not been fully clarified yet (see a recent review on EDL for details86). One may associate the orientational change of water molecules in the inner layer at the Hg|W interface84 with ion behavior at the Hg|IL interface; the orientational changes of the ions in the inner layer would be one of the possible reasons for the Cd increase. To probe any change in the interfacial structure depending on the potential, we used in situ spectroscopic ellipsometry for the interface between Hg and four ILs including [C8mim+]BF4−. The results showed a potential-dependent structure at the interface and were well reproduced with a model incorporating ionic layers whose density is higher than bulk at E ≫ Epzc.71 Therefore, it is likely that the ionic layers at the interface become densified reacting to the strong electric field at the interface when the interface is highly charged at potentials far from Epzc.
4 Conclusions
In a recent review on EDL in ILs by Fedorov and Kornyshev,3 they described “The fact that impedance measurements cannot reliably assess equilibrium characteristics is not a problem of the EDL theory that operates with equilibrium properties, but rather a problem of experimental techniques available these days.” This paper presented that one experimental technique, the pendant drop method, is available to measure zero-frequency Cd (Cd in equilibrium) for the electrochemical interface of ILs, where it is unlikely to be possible for EIS to assess the quantity. The measured zero-frequency Cd at the Hg|IL interface demonstrates peculiar potential dependences: bell shape or camel shape depending on the cation species of ILs. Such behaviors were predicted in 2007 by mean field theory,33 however, they have not been confirmed with experimental zero-frequency capacitance, although some studies on non-zero frequency capacitance measured by EIS have supported the theory.7,72 It should be noted that the pendant drop method has some drawbacks; it limits the electrode material (should be liquid) and the experiment is neither easy or fast compared with EIS. Nevertheless, the method still provides valuable experimental data that can be compared with and could improve the theory of EDL in ILs.Acknowledgements
This work was partly supported by a Grant-in-Aid for Scientific Research (no. 26410149) and by a grant from the UBE Foundation (N.N.). We appreciate Dr Yuki Kitazumi for building the apparatus of the pendant drop method and for encoding the analysis program.References
- M. Armand, F. Endres, D. R. Macfarlane, H. Ohno and B. Scrosati, Nat. Mater., 2009, 8, 621–629 CrossRef CAS PubMed.
- Electrochemical Aspects of Ionic Liquids, ed. H. Ohno, Wiley, Hoboken, 2nd edn, 2011 Search PubMed.
- M. V. Fedorov and A. A. Kornyshev, Chem. Rev., 2014, 114, 2978–3036 CrossRef CAS PubMed.
- R. J. Gale and R. A. Osteryoung, Electrochim. Acta, 1980, 25, 1527–1529 CrossRef CAS.
- C. Nanjundiah, S. F. McDevitt and V. R. Koch, J. Electrochem. Soc., 1997, 144, 3392–3397 CrossRef CAS PubMed.
- M. T. Alam, M. M. Islam, T. Okajima and T. Ohsaka, Electrochem. Commun., 2007, 9, 2370–2374 CrossRef CAS PubMed.
- M. M. Islam, M. T. Alam and T. Ohsaka, J. Phys. Chem. C, 2008, 112, 16568–16574 CAS.
- M. M. Islam, M. T. Alam, T. Okajima and T. Ohsaka, J. Phys. Chem. C, 2009, 113, 3386–3389 CAS.
- Y. Z. Su, Y. C. Fu, J. W. Yan, Z. B. Chen and B. W. Mao, Angew. Chem., Int. Ed., 2009, 48, 5148–5151 CrossRef CAS PubMed.
- B. Bozzini, A. Bund, B. Busson, C. Humbert, A. Ispas, C. Mele and A. Tadjeddine, Electrochem. Commun., 2010, 12, 56–60 CrossRef CAS PubMed.
- J. P. Zheng, P. C. Goonetilleke, C. M. Pettit and D. Roy, Talanta, 2010, 81, 1045–1055 CrossRef CAS PubMed.
- L. Siinor, K. Lust and E. Lust, J. Electrochem. Soc., 2010, 157, F83–F87 CrossRef CAS PubMed.
- T. F. Esterle, D. Sun, M. R. Roberts, P. N. Bartlett and J. R. Owen, Phys. Chem. Chem. Phys., 2012, 14, 3872–3881 RSC.
- M. Proskurnin and A. Frumkin, Trans. Faraday Soc., 1935, 31, 110–115 RSC.
- Y. Yasui, Y. Kitazumi, R. Ishimatsu, N. Nishi and T. Kakiuchi, J. Phys. Chem. B, 2009, 113, 3273–3276 CrossRef CAS PubMed.
- I. Bou-Malham and L. Bureau, Soft Matter, 2010, 6, 4062–4065 RSC.
- S. Makino, Y. Kitazumi, N. Nishi and T. Kakiuchi, Electrochem. Commun., 2011, 13, 1365–1368 CrossRef CAS PubMed.
- B. Roling, M. Drüschler and B. Huber, Faraday Discuss., 2012, 154, 303–311 RSC.
- M. Drüschler, N. Borisenko, J. Wallauer, C. Winter, B. Huber, F. Endres and B. Roling, Phys. Chem. Chem. Phys., 2012, 14, 5090–5099 RSC.
- N. Nishi, Y. Hirano, T. Motokawa and T. Kakiuchi, Phys. Chem. Chem. Phys., 2013, 15, 11615–11619 RSC.
- A. Uysal, H. Zhou, G. Feng, S. S. Lee, S. Li, P. Fenter, P. T. Cummings, P. F. Fulvio, S. Dai, J. K. McDonough and Y. Gogotsi, J. Phys. Chem. C, 2014, 118, 569–574 CAS.
- V. Lockett, R. Sedev, J. Ralston, M. Horne and T. Rodopoulos, J. Phys. Chem. C, 2008, 112, 7486–7495 CAS.
- M. Gnahm, T. Pajkossy and D. M. Kolb, Electrochim. Acta, 2010, 55, 6212–6217 CrossRef CAS PubMed.
- M. Drüschler, B. Huber and B. Roling, J. Phys. Chem. C, 2011, 115, 6802–6808 Search PubMed.
- T. Pajkossy and D. M. Kolb, Electrochem. Commun., 2011, 13, 284–286 CrossRef CAS PubMed.
- Y. Su, J. Yan, M. Li, M. Zhang and B. Mao, J. Phys. Chem. C, 2013, 117, 205–212 CAS.
- L. Siinor, R. Arendi, K. Lust and E. Lust, J. Electroanal. Chem., 2013, 689, 51–56 CrossRef CAS PubMed.
- J. Wallauer, M. Drüschler, B. Huber and B. Roling, Z. Naturforsch., B: Chem. Sci., 2013, 68, 1143–1153 CrossRef CAS.
- T. R. Gore, T. Bond, W. Zhang, R. W. J. Scott and I. J. Burgess, Electrochem. Commun., 2010, 12, 1340–1343 CrossRef CAS PubMed.
- M. Drüschler, B. Huber, S. Passerini and B. Roling, J. Phys. Chem. C, 2010, 114, 3614–3617 Search PubMed.
- M. T. Alam, J. Masud, M. M. Islam, T. Okajima and T. Ohsaka, J. Phys. Chem. C, 2011, 115, 19797–19804 CAS.
- H. Wang and L. Pilon, Electrochim. Acta, 2012, 63, 55–63 CrossRef CAS PubMed.
- A. A. Kornyshev, J. Phys. Chem. B, 2007, 111, 5545–5557 CrossRef CAS PubMed.
- M. S. Kilic, M. Z. Bazant and A. Ajdari, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2007, 75, 021502 CrossRef.
- K. B. Oldham, J. Electroanal. Chem., 2008, 613, 131–138 CrossRef CAS PubMed.
- M. V. Fedorov and A. A. Kornyshev, Electrochim. Acta, 2008, 53, 6835–6840 CrossRef CAS PubMed.
- G. Feng, J. S. Zhang and R. Qiao, J. Phys. Chem. C, 2009, 113, 4549–4559 CAS.
- J. Vatamanu, O. Borodin and G. D. Smith, J. Am. Chem. Soc., 2010, 132, 14825–14833 CrossRef CAS PubMed.
- G. Feng, J. Huang, B. G. Sumpter, V. Meunier and R. Qiao, Phys. Chem. Chem. Phys., 2011, 13, 14723–14734 RSC.
- X. Si, S. Li, Y. Wang, S. Ye and T. Yan, ChemPhysChem, 2012, 13, 1671–1676 CrossRef CAS PubMed.
- J. Vatamanu, O. Borodin, D. Bedrov and G. D. Smith, J. Phys. Chem. C, 2012, 116, 7940–7951 CAS.
- Z. Hu, J. Vatamanu, O. Borodin and D. Bedrov, Phys. Chem. Chem. Phys., 2013, 15, 14234–14247 RSC.
- Z. Hu, J. Vatamanu, O. Borodin and D. Bedrov, Electrochim. Acta, 2014, 145, 40–52 CrossRef CAS PubMed.
- M. Sha, Q. Dou, F. Luo, G. Zhu and G. Wu, ACS Appl. Mater. Interfaces, 2014, 6, 12556–12565 CAS.
- L. G. Gouy, J. Phys., 1910, 9, 457–468 Search PubMed.
- D. L. Chapman, Philos. Mag., 1913, 25, 475–481 CrossRef.
- M. M. Islam, M. T. Alam, T. Okajima and T. Ohsaka, J. Phys. Chem. B, 2007, 111, 12849–12856 CrossRef CAS PubMed.
- M. T. Alam, M. M. Islam, T. Okajima and T. Ohsaka, J. Phys. Chem. C, 2007, 111, 18326–18333 CAS.
- M. T. Alam, M. Islam, T. Okajima and T. Ohsaka, J. Phys. Chem. C, 2008, 112, 2601–2606 CAS.
- F. Silva, C. Gomes, M. Figueiredo, R. Costa, A. Martins and C. M. Pereira, J. Electroanal. Chem., 2008, 622, 153–160 CrossRef CAS PubMed.
- M. T. Alam, M. M. Islam, T. Okajima and T. Ohsaka, J. Phys. Chem. C, 2009, 113, 6596–6601 CAS.
- R. Costa, C. M. Pereira and F. Silva, Phys. Chem. Chem. Phys., 2010, 12, 11125–11132 RSC.
- M. Ammam, D. Di Caprio and L. Gaillon, Electrochim. Acta, 2012, 61, 207–215 CrossRef CAS PubMed.
- R. Costa, C. M. Pereira and F. Silva, RSC Adv., 2013, 3, 11697–11706 RSC.
- A. Lewandowski, T. Majkowski and M. Galinski, Z. Naturforsch., A: Phys. Sci., 2009, 64, 263–268 CAS.
- C. M. Gordon, J. D. Holbrey, A. R. Kennedy and K. R. Seddon, J. Mater. Chem., 1998, 8, 2627–2636 RSC.
- X. Creary and E. D. Willis, Org. Synth., 2005, 82, 166–169 CrossRef CAS.
- M. J. Earle, C. M. Gordon, N. V. Plechkova, K. R. Seddon and T. Welton, Anal. Chem., 2007, 79, 758–764 CrossRef CAS PubMed.
- J. Andreas, E. Hauser and W. Tucker, J. Phys. Chem., 1938, 42, 1001–1019 CrossRef CAS.
- H. H. Girault, D. J. Schiffrin and B. D. V. Smith, J. Electroanal. Chem., 1982, 137, 207–217 CrossRef CAS.
- T. Kakiuchi, M. Nakanishi and M. Senda, Bull. Chem. Soc. Jpn., 1988, 61, 1845–1851 CrossRef CAS.
- Y. Kitazumi and T. Kakiuchi, Langmuir, 2009, 25, 8062–8068 CrossRef CAS PubMed.
- F. Bashforth and J. C. Adams, An Attempt to Test the Theories of Capillary Action, Cambridge University Press, London, 1883 Search PubMed.
- T. Nakagawa and Y. Oyanagi, in Recent Developments in Statistical Inference and Data Analysis, ed. K. Matusita, North-Holland, Amsterdam, 1980, pp. 221–225 Search PubMed.
- E. Rilo, J. Pico, S. Garcia-Garabal, L. M. Varela and O. Cabeza, Fluid Phase Equilib., 2009, 285, 83–89 CrossRef CAS PubMed.
- J. Vila, P. Ginés, E. Rilo, O. Cabeza and L. M. Varela, Fluid Phase Equilib., 2006, 247, 32–39 CrossRef CAS PubMed.
- A. Stoppa, O. Zech, W. Kunz and R. Buchner, J. Chem. Eng. Data, 2010, 55, 1768–1773 CrossRef CAS.
- T. Singh and A. Kumar, J. Chem. Thermodyn., 2008, 40, 417–423 CrossRef CAS PubMed.
- J. Restolho, A. P. Serro, J. L. Mata and B. Saramago, J. Chem. Eng. Data, 2009, 54, 950–955 CrossRef CAS.
- D. Ambrose, Metrologia, 1990, 27, 245–247 CrossRef.
- N. Nishi, J. Uchiyashiki, R. Oogami and T. Sakka, Thin Solid Films, 2014, 571, 735–738 CrossRef CAS PubMed.
- M. V. Fedorov, N. Georgi and A. A. Kornyshev, Electrochem. Commun., 2010, 12, 296–299 CrossRef CAS PubMed.
- N. Georgi, A. A. Kornyshev and M. V. Fedorov, J. Electroanal. Chem., 2010, 649, 261–267 CrossRef CAS PubMed.
- M. V. Fedorov and A. A. Kornyshev, J. Phys. Chem. B, 2008, 112, 11868–11872 CrossRef CAS PubMed.
- V. Ivaništšev, S. O'Connor and M. V. Fedorov, Electrochem. Commun., 2014, 48, 61–64 CrossRef PubMed.
- C. Larriba, Y. Yoshida and J. F. de la Mora, J. Phys. Chem. B, 2008, 112, 12401–12407 CrossRef CAS PubMed.
- Y. Yokota, T. Harada and K. Fukui, Chem. Commun., 2010, 46, 8627–8629 RSC.
- R. Köhler, J. Restolho, R. Krastev, K. Shimizu, J. N. Canongia Lopes and B. Saramago, J. Phys. Chem. Lett., 2011, 2, 1551–1555 CrossRef.
- X. Zhang, L. Lu and Y. Cai, Langmuir, 2012, 28, 9593–9600 CrossRef CAS PubMed.
- M. Rosa Castillo, J. M. Fraile and J. A. Mayoral, Langmuir, 2012, 28, 11364–11375 CrossRef PubMed.
- K. Motobayashi, K. Minami, N. Nishi, T. Sakka and M. Osawa, J. Phys. Chem. Lett., 2013, 4, 3110–3114 CrossRef CAS.
- D. C. Grahame, Chem. Rev., 1947, 41, 441–501 CrossRef CAS.
- R. Watts-Tobin, Philos. Mag., 1961, 6, 133–153 CrossRef CAS.
- R. Guidelli, in Trends in Interfacial Electrochemistry, ed. A. F. Silva, Reidel, Dordrecht, 1986, vol. 179, pp. 387–452 Search PubMed.
- J. R. MacDonald and C. A. Barlow, Jr., J. Chem. Phys., 1962, 36, 3062–3080 CrossRef PubMed.
- B. B. Damaskin and O. A. Petrii, J. Solid State Electrochem., 2011, 15, 1317–1334 CrossRef CAS.
| This journal is © the Owner Societies 2015 |