 Open Access Article
Open Access ArticleBenchmark thermochemistry of chloramines, bromamines, and bromochloramines: halogen oxidants stabilized by electron correlation†
Daniela
Trogolo
and
J. Samuel
Arey‡
*
Environmental Chemistry Modeling Laboratory, École Polytechnique Fédérale de Lausanne (EPFL), Station 2, 1015 Lausanne, Switzerland. E-mail: samuel.arey@epfl.ch; Fax: +41 (0)21 693 8070; Tel: +41 (0)21 693 8031
First published on 2nd January 2015
Abstract
Chloramines, bromamines, and bromochloramines are halogen-containing oxidants that arise from the reaction of hypohalous acids with ammonia in water. Although relevant to both water disinfection chemistry and biochemistry, these molecules are difficult to study in the laboratory, and their thermochemical properties remain poorly established. We developed a benchmark level ab initio calculation protocol, termed TA14, adapted from the Weizmann theory and Feller–Peterson–Dixon approaches to determine the molecular structures and thermochemical properties of these compounds. We find that the halamine molecules are bound largely, and in some cases entirely, by electron correlation forces. This presumably explains their high reactivity as electrophilic oxidants. We provide computed heats of formation at 0 K (ΔfH00![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K) and at 298 K (ΔfH0298
K) and at 298 K (ΔfH0298![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K) and Gibbs free energies of formation at 298 K (ΔfG0298
K) and Gibbs free energies of formation at 298 K (ΔfG0298![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K) for the 9 inorganic chloramines, bromamines, bromochloramines in gas phase. Based on comparisons to previous theoretical and experimental data for a set of 11 small molecules containing N, O, H, Cl, and Br, we propose uncertainties ranging from 1 to 3 kJ mol−1 for computed thermodynamic properties of the halamines. Reported thermochemical data enable the determination of equilibrium constants for reactions involving halamines, opening possibilities for more quantitative studies of the chemistry of these poorly understood compounds.
K) for the 9 inorganic chloramines, bromamines, bromochloramines in gas phase. Based on comparisons to previous theoretical and experimental data for a set of 11 small molecules containing N, O, H, Cl, and Br, we propose uncertainties ranging from 1 to 3 kJ mol−1 for computed thermodynamic properties of the halamines. Reported thermochemical data enable the determination of equilibrium constants for reactions involving halamines, opening possibilities for more quantitative studies of the chemistry of these poorly understood compounds.
1 Introduction
Halogen-containing oxidants have long received attention, due to their role in processes affecting human health and environmental hygiene.1,2 Chlorination and chloramination are the predominant methods of drinking water disinfection in the United States.3–5 Chlorine is commonly applied either as gaseous Cl2, which dissolves in water at room temperature, or as a salt of hypochlorite, OCl−:| Cl2 + H2O → HOCl + HCl | (1) |
 | (2) |
| NH3 + HOCl ⇌ NH2Cl + H2O | (3) |
| NH2Cl + HOCl ⇌ NHCl2 + H2O | (4) |
| NHCl2 + HOCl ⇌ NCl3 + H2O | (5) |
Bromamines and bromochloramines may arise as well, in bromine-containing waters.14–22 During disinfection treatment, bromide can become oxidized to hypobromous acid/hypobromite, contributing to the formation of bromamines and bromochloramines in water.23 The role of bromide in monochloramine decay was considered in the kinetic model provided by Vikesland et al.13 Lei et al. reported on the formation kinetics of bromamines,24 and Luh and Mariñas recently investigated the formation kinetics of bromochloramines, providing more information on their aqueous chemistry.25
Chloramines and bromamines are implicated in the formation of potentially toxic disinfection byproducts (DBPs) during water treatment.3,4,26–28 Chloramines can undergo substitution and oxidation reactions involving natural organic matter.29 Snyder and Margerum30 and then Isaac and Morris31,32 showed that monochloramine could transfer chlorine to organic nitrogen compounds by general acid catalysis. During water disinfection, monochloramine can play a direct role in the formation of halonitriles, halonitroalkanes and nitrosamines.33 Monochloramine reactions with dissolved organic matter can also lead to production of haloacetic acids.34 The reaction between dichloramines and organic nitrogen precursors such as dimethylamine can explain the observed production of N-nitrosodimethylamine (NDMA) and other nitrosamines,35,36 which are probable human carcinogens according to the US Environmental Protection Agency. Fewer data are available concerning the role of bromamines and bromochloramines in reactions that lead to DBP formation. Le Roux et al. reported an enhancement of the formation of NDMA from reactions between bromine-containing oxidant species and tertiary amines or dimethylamine, suggesting a direct role of bromamines.27 Monobromamine and dibromamine were also found to react with cyanide ion (CN−) leading to the formation of CNBr, a volatile DBP.28 According to Valentine,37 the bromine atom of bromochloramine is highly reactive. Despite their considerable roles in disinfection byproduct formation, the speciation of chloramines, bromamines, and bromochloramines is not fully known, and this impedes mechanistic studies of DBP formation, which can involve many potential reaction pathways.
Due to the volatility of chloramines,38,39 these molecules also have implications in the poor air quality in indoor swimming pools. According to Richardson et al.,40 NH2Cl, NHCl2, NCl3 can escape into the atmosphere of swimming pool environments. They contribute to the typical smell and irritant properties of the air of these facilities.41
Chloramines and bromamines are also released extracellularly by activated mammalian eosinophils and neutrophils (white blood cells).42,43 The haem enzymes eosinophil peroxidase and myeloperoxidase catalyse the production of HOBr and HOCl that can react with extracellular matrix, including proteins, proteoglycans, and other nitrogen organic compounds, generating substituted bromamines and chloramines.43–47 The N-bromination reactions promoted by HOBr, which exhibits higher rate constants than the corresponding reactions by HOCl, may damage tissue, affecting cellular and tissue function, in inflammatory diseases such as asthma.45 Moreover, the so-generated halamines can undergo one-electron reduction processes that cleave the N–X (where X = Cl or Br) bond.48,49 Indeed, redox-active metal ions and superoxide radicals can reduce N-halogenated species, leading to the formation of N-centered radicals and radical bromine atoms.49
Despite these concerns, halamine speciation is not fully understood and thus the reactivities of halamines with components of natural waters and biological fluids are difficult to study. Halamines are unstable at neutral pH and autodecompose by a complex set of reactions only partially known.11,13,29 As a consequence, kinetic experiments on chloramine formation cannot be always successfully conducted under realistic water conditions found in water treatment facilities.11 Additionally, sampling and analysis of the chloramines in the atmosphere is difficult, requiring specific sampling devices and analytical methods.41 Due to these challenges, fundamental thermochemical properties of halamines have not been extensively determined with experiments either in gas phase or in aqueous phase.
Quantum computational methods could offer more tractable estimates of the thermochemistry of chloramines, bromamines, and bromochloramines. However existing work is limited. In 1997, Milburn et al.50 reported theoretical enthalpy of formation values for inorganic chloramines at MP451–54 and QCISD(T)55 levels of theory. More recently, Rayne and Forest56 estimated gas phase standard state enthalpies of formation at 298 K (ΔfH0298![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K) for 398 species that contained the elements hydrogen through bromine at the G457 level, including NH2Cl, NHCl2, NCl3, NH2Br, and NHBr2. This approach produced a MAD (mean absolute deviation) of 2.68 kcal mol−1 with respect to experimental ΔfH0298
K) for 398 species that contained the elements hydrogen through bromine at the G457 level, including NH2Cl, NHCl2, NCl3, NH2Br, and NHBr2. This approach produced a MAD (mean absolute deviation) of 2.68 kcal mol−1 with respect to experimental ΔfH0298![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K values for 144 compounds. More recently, Rayne and Forest58 assessed new ΔfH0298
K values for 144 compounds. More recently, Rayne and Forest58 assessed new ΔfH0298![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K values for NH2Cl, NHCl2, and NCl3 using G4MP2.59 These estimates likely have about 2–3 kcal mol−1 uncertainties. In 2011, monochloramine was included in the W4-11 dataset:60 this is the only halamine whose total atomization energy was determined with benchmark accuracy. Finally, thermochemistry estimates remain absent for NBr3 and for the bromochloramines.
K values for NH2Cl, NHCl2, and NCl3 using G4MP2.59 These estimates likely have about 2–3 kcal mol−1 uncertainties. In 2011, monochloramine was included in the W4-11 dataset:60 this is the only halamine whose total atomization energy was determined with benchmark accuracy. Finally, thermochemistry estimates remain absent for NBr3 and for the bromochloramines.
Calculations of energies for compounds containing halogens are not without their difficulties. Therefore chloramines, bromamines, and bromochloramines require a carefully constructed ab initio computational recipe, with attention to several fine quantum mechanical effects, in order to obtain accurate thermochemistry data. Since these inorganic molecules contain the heavy elements chlorine and bromine, fine quantum mechanical effects must be evaluated properly if sub-kcal mol−1 or sub-kJ mol−1 energies are sought. Indeed, the “gold standard of quantum chemistry”, or CCSD(T) with complete basis-set limit extrapolation, has to be combined with core valence correlation energy calculations and relativistic effects in order to predict accurate thermochemistry for chlorine- and bromine-containing molecules.61–64 For molecules with elements from the first and second rows, relativistic and core-correlation contributions to bond energies are relatively small,61,63,65 but these components increase with the size of the atoms involved. For example, Feller et al. reported scalar relativistic contributions of −0.14 kcal mol−1 and −0.54 kcal mol−1 to the total atomization energies (TAE) of Cl2 and Br2, respectively.63 Core-valence correlation components of the TAEs of these molecules were −0.13 kcal mol−1 and 0.29 kcal mol−1, respectively.63 Post-CCSD(T) energy contributions may also be important. The magnitude of post-CCSD(T) effects is small for systems that are reasonably described by a single reference configuration.61 However, for species affected by severe nondynamical correlation, post-CCSD(T) contributions to the TAE may exceed 1 kcal mol−1.63,66 Halogen-containing molecules often exhibit severe nondynamical correlation effects; examples include F2, FO2, F2O2, FO, F2O, OClO, and ClOO.65 Hence, for chloramines and bromamines, we suspected that an extension of the correlation treatment beyond CCSD(T) may be needed.
Specialized methods, such as the HEAT (high-accurate extrapolated ab initio thermochemistry),67–69 Weizmann-n,61,70,71 and Feller–Peterson–Dixon (FPD)63,64,72 protocols have been designed to estimate accurate thermochemistry even for difficult cases as those described above. W4 provided thermochemical data up to chlorine-containing molecules with a ‘benchmark accuracy’ of 1 kJ mol−1 (0.24 kcal mol−1).61 The HEAT target accuracy was sub-kJ mol−1 for first-row systems, whereas the FPD approach suggested an accuracy of 0.2 to 0.4 kcal mol−1 for small molecules up to the third row. The FPD protocol is more flexible, being developed molecule-by-molecule, and has been applied up to bromine-containing species, including BrO, Br2, HBr, BrF, and BrCl.63 These computational methods (Weizmann-n, FPD) are commonly recognized as benchmarks for small molecules. Although we were inspired by these established methods, we did not apply any of these protocols in their prescribed formulation. The W3 method does not include second order spin–orbit corrections, and W3 treats core–valence correlation energy with only the MTSmall basis set. These choices would not be appropriate for benchmark thermochemistry of molecules containing bromine. On the other hand, the more rigorous W4 and FPD procedures were intractably expensive for the not-so-small halamine species, with available algorithms and hardware. Hence the halamines warranted the development of a tailored computational recipe for the determination of high-accuracy thermochemistry.
In the present study, we calculated high-quality benchmark gas-phase thermochemical data, including total atomization energies, heats of formation at 0 K and at 298 K, and Gibbs free energies of formation at 298 K for chloramines, bromamines, bromochloramines, and other related small halogenated molecules. For this purpose, we developed a computational protocol, termed as TA14 in the remainder of the manuscript, which is adapted from the high-quality Weizmann-n, and Feller–Peterson–Dixon (FDP) procedures. TA14 combines a systematic sequence of coupled cluster methods up to CCSDTQ with large correlation consistent basis sets and includes relativistic effects, core–valence electron correlation, and diagonal Born–Oppenheimer correction, aiming for kJ mol−1 accuracy with affordable computing time. A test set of small compounds containing chlorine and bromine was chosen to briefly evaluate the performance of the protocol, and comparisons with high-quality experimental values and previously published computational benchmarks are made. This leads to the first published set of high accuracy thermochemistry data for chloramines, bromamines, and bromochloramines.
2 Methods
2.1 Selected molecules of study and reference data
Our chemical set comprised 20 neutral inorganic molecules, divided by chemical composition into non-halamines (set A) and halamines (set B). Set A includes H2, N2, O2, Cl2, Br2, HCl, HBr, HOCl, HOBr, H2O, and NH3. Set B contains NH2Cl, NHCl2, NCl3, NH2Br, NHBr2, NBr3, NHBrCl, NBrCl2, and NBr2Cl.Experimental enthalpies of formation and experimental total atomization energies were available in the literature for the entire set A. Experimental total atomization energies at 0 K, TAEExpt0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K, heats of formation at 0 K, ΔfH0,Expt0
K, heats of formation at 0 K, ΔfH0,Expt0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K, and at 298 K, ΔfH0,Expt298
K, and at 298 K, ΔfH0,Expt298![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K, and Gibbs free energies of formation, ΔfG0,Expt298
K, and Gibbs free energies of formation, ΔfG0,Expt298![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K, are taken from several sources: CODATA,73 the Active ThermoChemical Tables,74,75 JANAF thermochemical database,76 and NIST Computational Chemistry Comparison and Benchmark DataBase (CCCBDB).77 In cases where several experimental values were available for the same molecule, the value with the lowest listed uncertainty was selected.
K, are taken from several sources: CODATA,73 the Active ThermoChemical Tables,74,75 JANAF thermochemical database,76 and NIST Computational Chemistry Comparison and Benchmark DataBase (CCCBDB).77 In cases where several experimental values were available for the same molecule, the value with the lowest listed uncertainty was selected.
2.2 Model chemistries and basis sets
Hartree–Fock, CCSD,78 and CCSD(T)78–80 calculations were carried out using the program CFOUR.81 CCSDT,82–84 CCSDT(Q),85 and CCSDTQ86–88 calculations were conducted with the MRCC package89 interfaced to the CFOUR program suite. Scalar relativistic calculations and B2PLYPD90,91 frequency analysis were conducted using Gaussian09.92 Second-order molecular spin–orbit components were computed with NWchem.93The basis sets employed in all calculations belong to the correlation consistent family of Dunning and co-workers94–98 and are abbreviated PVXZ, AVXZ, and AWCVXZ for cc-pVXZ, aug-cc-pVXZ, and aug-cc-pWCVXZ basis set types, respectively, throughout the remainder of the article. The aug-cc-pV(X+d)Z basis sets employed by Wn methods were not available for bromine. Complete basis-set limit results were achieved using different extrapolation formulae, as explained below.
2.3 Geometries and frequencies
With three exceptions, all reference geometries were obtained at the all-electron (AE)-CCSD(T)/AVQZ level. For NBrCl2, NBr2Cl, and NBr3, geometries were optimized at the all-electron (AE)-CCSD(T)/AVTZ level. For open-shell species, single-point energy calculations were based on UHF reference wave functions, whereas the default restricted Hartree–Fock reference was employed for the closed-shell molecules. Due to high spin contamination using an unrestricted reference, O2 was treated as a restricted open-shell species. The Watts–Gauss–Bartlett99 (e.g., CFOUR/ACESII) definition of restricted open-shell CCSD(T) was applied. These reference geometries were used for electronic energy calculations, and they are given in the ESI† for all molecules.Harmonic and anharmonic zero-point vibrational energies were computed at 298 K using analytic second derivatives for the B2PLYPD/AVQZ model chemistry. The VPT2100,101 approach was applied to compute the anharmonic corrections as implemented in Gaussian09. Anharmonic frequencies are reported in the ESI† for all the halamines and the hypohalous acids. Since Gaussian09 does not allow the calculations of anharmonic frequency contributions for linear molecules, we employed B2PLYPD/AVQZ for harmonic frequency calculations and combined these with experimental anharmonic contributions for diatomic molecules.102–104 Molecular rotations were determined assuming rigid geometries, thus rotations were assumed uncoupled to vibrations. Based on these frequency data and corresponding B2PLYPD/AVQZ geometries, zero-point vibrational energies and thermal contributions to the gas phase enthalpy and gas phase Gibbs free energy were computed at 298 K in the NVT ensemble for all studied molecules.105
2.4 Electronic energies
Our methodology for computing the electronic energy was adapted from the recently developed W3, W4, and FPD protocols,61,63,71 and it is aimed to being an appropriate compromise between computing cost and basis set convergence. By including all terms that can contribute to the energy at the sub-kJ mol−1 level, the TA14 protocol allows the determination of high quality electronic energies and thermodynamic properties of halogenated compounds. The protocol applied to compute the electronic energy is purely ab initio: no fitted parameters or empirical terms are included.An overview of the TA14 protocol, together with other highly accurate thermochemistry composite methods, is shown in Table 1. Within the Born–Oppenheimer approximation, the total energy of a compound may be separated into electronic and vibrational contributions. The ground state electronic energy is expressed by the following additivity scheme:
 | (6) |
In eqn (6), the term EHF,Extrap is the Hartree–Fock energy, and ΔECCSD,Extrap, ΔE(T),Extrap and ΔET–(T),Extrap are valence correlation energies, where the label “Extrap” indicates extrapolation to the complete basis-set limit, explained further below. ΔECCSD,Extrap is given by the CCSD energy contribution, and ΔE(T),Extrap describes the energy contribution from the perturbative treatment of triple excitations. ΔET–(T),Extrap describes the energy difference between full triples and the perturbative triples approximation. ΔE(Q) and ΔEQ–(Q) are the perturbative quadruples contribution and the full quadruples contribution, respectively. The resulting frozen core FC-CCSDTQ energy is very close to the frozen-core non-relativistic FullCI limit.106 ΔECORE is the last nonrelativistic component of the total energy and describes core–valence correlation effects. The term ΔEREL represents scalar relativistic effects. First-order and second-order spin–orbit corrections are given as ΔE1st![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) SO and ΔE2nd
SO and ΔE2nd![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) SO, and ΔEDBOC is the diagonal Born–Oppenheimer correction. Each of these terms is explained in detail below.
SO, and ΔEDBOC is the diagonal Born–Oppenheimer correction. Each of these terms is explained in detail below.
| Component | FPD63![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) d d |
W371 | W461 | TA14 |
|---|---|---|---|---|
| a See W2,70 W371 and W461 protocols. b The VPT2 approach was used. c W4.2 also includes this higher core shell contribution. d This Feller–Peterson–Dixon procedure was defined for Br2.63 | ||||
| Reference geometry | FC-CCSD(T)/AV6Z | FC-CCSD(T)/pV(Q+d)Z | FC-CCSD(T)/pV(Q+d)Z | AE-CCSD(T)/AVQZ |
| Anharmonic ZPVE | Expt data | CCSD(T)/VTZ+1a | CCSD(T)/VTZ+1a | B2PLYPD/AVQZb |
| Electronic energy | ||||
| HF extrapolation | AV6Z | AV(Q,5)+dZ | AV(5,6)+dZ | AV(Q,5)Z |
| Valence CCSD extrapolation | AV6Z | AV(Q,5)+dZ | AV(5,6)+dZ | AV(Q,5)Z |
| Valence (T) extrapolation | AV6Z | AV(T,Q)+dZ | AV(Q,5)+dZ | AV(T,Q)Z |
| Valence T–(T) extrapolation | PVQZ | PV(D,T)Z | PV(D,T)Z | PV(T,Q)Z |
| Valence (Q) | 1.25 PVDZ | 1.10 PVTZ | PVTZ | |
| Valence Q–(Q) | 1.25 PVDZ | 1.10 PVDZ | PVDZ | |
| Valence Q | PVTZ | |||
| Valence 5 | PVDZ | PVDZ | ||
| Valence 6 | PVDZ | |||
| CCSD(T) core shell | PWCV5Z | MTSmall | AWCV(T,Q)Z | AWCV(T,Q)Z |
| T–(T) core shell | PWCVTZc | |||
| CCSDTQ core shell | PWCVDZ | |||
| Scalar relativistic CCSD(T) | DK-PVTZ | MTSmall | DK-AV(Q+d)Z | DK-AVQZ |
| First-order atomic spin–orbit correction | Expt data | Expt data | Expt data | Expt data |
| Second-order molecular spin–orbit correction | CAS-CI/AVTZ-PP | SO-B3LYP/ECP | ||
| DBOC | HF/AVTZ | HF/AVTZ | HF/AVQZ, CCSD/AVDZ | |
To obtain high accuracy estimates of HF and electronic correlation energies, extrapolation techniques can be applied, requiring large correlation-consistent basis sets.107 We applied the extrapolation formulae proposed in W4 theory for the Hartree–Fock energies and the extrapolation formulae given in W3 theory for the correlation energies to obtain accurate ab initio thermochemistry properties. Theoretical results obtained using this approach are labeled “Best” in the remainder of the article. The Hartree–Fock energy extrapolation is based on the Karton–Martin modification108 of Jensen's formula:109
 | (7) |
The correlation energy results are extrapolated separately from the Hartree–Fock components. The CCSD energy typically converges more slowly than the Hartree–Fock energy.111–113 The extrapolations to the infinite basis-set limit for several correlation energy contributions were carried out with the two-term A + B/Lα expression used extensively in Wn theories61,65,70,71 and expressed in this form:
 | (8) |
As recommended by Klopper and co-workers,111 the (T) valence correlation energy contribution was evaluated separately from the CCSD contributions, with smaller basis sets. The more expensive (T) contribution converges to the basis set limit more quickly than the CCSD correlation energy.111,112 Our best estimate ΔE(T),Extrap energy contributions were calculated with the AV{T,Q}Z basis set pair and were extrapolated using eqn (8).
Post-CCSD(T) contributions to the electronic energy were determined with smaller basis sets. Higher-order correlated energies converge to the complete basis set limit more efficiently than the energies computed at CCSD(T) level.64,114 In the present work, the ΔET–(T),Extrap term was extrapolated from CCSDT-CCSD(T) energy differences with the PVTZ and PVQZ basis sets. However for NBrCl2, NBr2Cl, NHBr2, NHBrCl and NBr3, we instead used the PV{D,T}Z basis set pair, due to computational limitations.
Separately, we also applied the widely used extrapolation method of Halkier for the Hartree–Fock and CCSD, (T), and T–(T) correlation energies, leading to a second estimate of computed thermodynamic properties. Halkier et al.113,115 proposed applying two-term extrapolation procedures based on calculations with hierarchical correlation-consistent basis sets:
 | (9) |
As explained by Peterson et al.,64 CCSDT(Q) corrections should always be included in order to counterbalance the CCSDT energy contributions, which are typically less close to the FullCI limit than CCSD(T) values. The ΔE(Q) contributions were calculated as the CCSDT(Q)-CCSDT energy difference with the PVTZ basis set. For NBr3 and NBr2Cl, the ΔE(Q) contribution was computed with the PVDZ basis set. ΔEQ–(Q) was computed as the energy difference CCSDTQ-CCSDT(Q) with the PVDZ basis set. We chose to apply the UHF reference wave function on the ROHF oxygen molecule in the calculation of quadruple excitation correlation energy contributions. Due to its high computational cost, the CCSDTQ correlation energy was not computed for NBr3.
For most molecules, ΔECORE was assessed as the energy difference between all-electron CCSD(T)/AWCV{T,Q}Z and frozen-core CCSD(T)/AWCV{T,Q}Z calculations, applying eqn (8) to extrapolate each energy to the complete basis-set limit. For NHBrCl the ΔECORE was computed at the AWCVQZ level, whereas for NBr3 and NBr2Cl, this contribution was obtained at the AWCVTZ level, due to computational cost, and no extrapolation formula was applied.
Relativistic contributions were computed as follows. Scalar relativistic effects (ΔEREL) are quantitatively recovered within the second-order Douglas–Kroll–Hess approximation,117–122 and these were obtained from the energy difference between relativistic CCSD(T)/AVQZ-DK and non-relativistic CCSD(T)/AVQZ calculations. Atomic first-order spin–orbit coupling terms, ΔE1st![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) SO, were taken from the experimental fine structure.123 For heavy elements such as bromine, second-order molecular spin–orbit contributions have non-negligible contributions.63,124 These energy contributions, ΔE2nd
SO, were taken from the experimental fine structure.123 For heavy elements such as bromine, second-order molecular spin–orbit contributions have non-negligible contributions.63,124 These energy contributions, ΔE2nd![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) SO, were carried out with SO-DFT calculations at the B3LYP125,126 level. The CRENBL basis sets and AREPs (averaged relativistic effective potentials) with spin–orbit operators were employed for the non-hydrogen atoms.127–132 Although implemented with HF/AVTZ in the W4 scheme, post-HF contributions to the diagonal Born–Oppenheimer correction have been better reproduced when including the CCSD energy contribution.133 ΔEDBOC calculations thus were conducted at CCSD/AVDZ level, where the HF electronic energy contribution was calculated with the AVQZ basis set:
SO, were carried out with SO-DFT calculations at the B3LYP125,126 level. The CRENBL basis sets and AREPs (averaged relativistic effective potentials) with spin–orbit operators were employed for the non-hydrogen atoms.127–132 Although implemented with HF/AVTZ in the W4 scheme, post-HF contributions to the diagonal Born–Oppenheimer correction have been better reproduced when including the CCSD energy contribution.133 ΔEDBOC calculations thus were conducted at CCSD/AVDZ level, where the HF electronic energy contribution was calculated with the AVQZ basis set:
| ΔEDBOC = ΔEHF/AVQZDBOC + ΔΔECCSD/AVDZDBOC | (10) |
2.5 Thermochemical properties
To construct standard enthalpies of formation at 0 K and 298 K at 1 atm pressure, we determined the electronic energies and the total atomization energies of all species. Total atomization energies at the bottom of the theoretical potential energy well (TAEe(M)) and at 0 K (TAE0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K(M)) were calculated ab initio as:
K(M)) were calculated ab initio as: | (11) |
TAETA140![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K(M) = TAETA14e(M) − ZPVETA14(M) K(M) = TAETA14e(M) − ZPVETA14(M) | (12) |
The method to calculate standard enthalpies of formation has been described previously by Curtiss et al.134 Briefly the procedure was as follows. A theoretical enthalpy of formation of a molecule M at 0 K can be calculated as the difference between the summed experimental enthalpies of formation of the atoms contained in the molecule at 0 K, 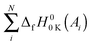 , and the theoretical atomization energy TAE0
, and the theoretical atomization energy TAE0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K(M) of the molecule. The superscript “0” refers to 1 atm standard state. For each molecule:
K(M) of the molecule. The superscript “0” refers to 1 atm standard state. For each molecule:
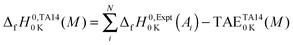 | (13) |
A theoretical enthalpy of formation at 298 K was obtained by applying the following formula:
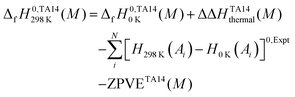 | (14) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K(Ai) − H0
K(Ai) − H0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K(Ai)]0,Expt is the experimental integrated heat capacity for each atom Ai at its standard state. The experimental atomic enthalpy corrections and the integrated heat capacity values for each element are taken from the CODATA thermochemical database (Table 2).73 In eqn (14), computed zero-point vibrational energy contributions (already included in the total atomization energies) were subtracted from enthalpies of formation of the molecule at 0 K to avoid their double-counting.
K(Ai)]0,Expt is the experimental integrated heat capacity for each atom Ai at its standard state. The experimental atomic enthalpy corrections and the integrated heat capacity values for each element are taken from the CODATA thermochemical database (Table 2).73 In eqn (14), computed zero-point vibrational energy contributions (already included in the total atomization energies) were subtracted from enthalpies of formation of the molecule at 0 K to avoid their double-counting.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K(Ai), integrated atomic heat capacities [H298
K(Ai), integrated atomic heat capacities [H298![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K(Ai) − H0
K(Ai) − H0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K(Ai)]0,Expt (kcal mol−1), and entropies (cal mol−1 K−1) for selected diatomic molecules at 298 K at their standard state
K(Ai)]0,Expt (kcal mol−1), and entropies (cal mol−1 K−1) for selected diatomic molecules at 298 K at their standard state
| Element Ai | Reference state | ΔfH0,Expt0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K(Ai) K(Ai) |
[H298![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K(Ai) − H0 K(Ai) − H0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K(Ai)]0,Expt K(Ai)]0,Expt |
S
0,Expt298![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K(Di) K(Di) |
|---|---|---|---|---|
| H | H2,gas | 51.6336 ± 0.0014 | 1.012 ± 0.000 | 31.2333 ± 0.0007 |
| N | N2,gas | 112.5287 ± 0.0956 | 1.036 ± 0.000 | 45.7957 ± 0.0010 |
| O | O2,gas | 58.9842 ± 0.0239 | 1.037 ± 0.000 | 49.0325 ± 0.0012 |
| Cl | Cl2,gas | 28.5901 ± 0.0019 | 1.097 ± 0.000 | 53.3176 ± 0.0024 |
| Br | Br2,liq | 28.1836 ± 0.0287 | 2.930 ± 0.001 | 36.38 |
We computed the Gibbs free energy of formation of each molecule as follows. We combined the computed entropy of formation, ΔfS0,TA14298![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K(M), to the gas phase enthalpy of formation:
K(M), to the gas phase enthalpy of formation:
ΔfG0,TA14298![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K(M) = ΔfH0,TA14298 K(M) = ΔfH0,TA14298![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K(M) − TΔfS0,TA14298 K(M) − TΔfS0,TA14298![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K(M) K(M) | (15) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K(M) was calculated as follows:
K(M) was calculated as follows: | (16) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K(M) comprises computed anharmonic vibrational, rotational, and translational contributions to the molecular entropy at 298 K. For the diatomic molecules, the anharmonic contribution to vibrations was taken from experimental data, as discussed above. S0,Expt298
K(M) comprises computed anharmonic vibrational, rotational, and translational contributions to the molecular entropy at 298 K. For the diatomic molecules, the anharmonic contribution to vibrations was taken from experimental data, as discussed above. S0,Expt298![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K(Di) is the experimental entropy for each diatomic element at its standard state, as taken from the CODATA thermochemical database (Table 2),73 and νi is the appropriate stoichiometric coefficient. For example, the ΔfS0,TA14298
K(Di) is the experimental entropy for each diatomic element at its standard state, as taken from the CODATA thermochemical database (Table 2),73 and νi is the appropriate stoichiometric coefficient. For example, the ΔfS0,TA14298![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K value of HOBr is:
K value of HOBr is: | (17) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K(M) and ΔfG0,TA14298
K(M) and ΔfG0,TA14298![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K(M) values are thus based on a combination of experimental data (e.g., ΔfH0,Expt0
K(M) values are thus based on a combination of experimental data (e.g., ΔfH0,Expt0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K(Ai), [H298
K(Ai), [H298![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K(Ai) − H0
K(Ai) − H0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K(Ai)]0,Expt, and S0,Expt298
K(Ai)]0,Expt, and S0,Expt298![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K(Ai)) and computational results (TAETA140
K(Ai)) and computational results (TAETA140![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K(M), ΔΔHTA14thermal(M), and S0,TA14298
K(M), ΔΔHTA14thermal(M), and S0,TA14298![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K(M)), but they are considered as theoretical values.
K(M)), but they are considered as theoretical values.
2.6 Diagnostics for nondynamical correlation effects
Diagnostics for nondynamical correlation (NDC) effects provide an indication of the importance of post-CCSD(T) electronic contributions for thermochemical applications. Among several proposed diagnostics, the %TAE[HF] is the most affordable a priori energy-based diagnostic, and %TAE[(T)] is a more reliable indicator that also requires no post-CCSD(T) calculations.61 %TAE[post-CCSD(T)] is an a posteriori diagnostic to evaluate the post-CCSD(T) contributions to total atomization energy.61 These diagnostics are calculated as follows: | (18) |
 | (19) |
 | (20) |
3 Results and discussion
We computed total atomization energies at 0 K, standard heats of formation at 0 K and at 298 K, and Gibbs free energies of formation at 298 K for bromamines, chloramines, bromochloramines, and other related molecules. First, we report total atomization energy data and discuss the electronic energy contributions to bond formation in these molecules. This is followed by a discussion of diagnostics for nondynamical correlation. Then, to assess the performance of the TA14 approach, we compare our computed property data to experimental data and other published benchmarks, where available. Finally we briefly discuss the implications of thermochemistry data for halamines.3.1 Total atomization energies
Benchmark-level total atomization energies were obtained with the TA14 method, taking into account our best estimate CCSD(T) and post-CCSD(T) contributions, core–valence electronic correlation, relativistic effects and DBOC contributions. The component breakdown of the total atomization energies at the bottom of the potential energy well, TAEe, and at 0 K, TAE0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K, is displayed in Table 3 for both chemical sets A and B.
K, is displayed in Table 3 for both chemical sets A and B.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K) [kcal mol−1]
K) [kcal mol−1]
| HFa | CCSDb | (T)b | T–(T)b | (Q) | Q–(Q) | Core shellb | Scalar relat. | 1st order spin–orbit | 2nd order spin–orbit | DBOC | TAEe | ZPVE | TAE0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K K |
|
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| a Hartree–Fock energies extrapolated using eqn (7). b Correlation energies extrapolated using eqn (8). c For diatomic molecules, harmonic zero-point vibrational energy values were computed, and experimental anharmonicity contributions were added to these values. d For NBrCl2, NBr2Cl, NHBr2, NHBrCl and NBr3 this contribution is computed with the pV(D,T)Z basis set pair. e For NBr2Cl and NBr3 this contribution is computed with the pVDZ basis set. f Not available. g For NBr2Cl and NBr3 this contribution is computed with the AWCVTZ basis set, and no extrapolation to the complete basis set limit was applied. h For NHBrCl this contribution is computed with the AWCVQZ basis set, and no extrapolation to the complete basis set limit was applied. | ||||||||||||||
| Set A | ||||||||||||||
| H2 | 83.85 | 25.67 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.01 | 0.00 | 0.00 | 0.02 | 109.54 | 6.21c | 103.34 |
| N2 | 115.42 | 102.22 | 9.46 | −0.75 | 1.08 | −0.15 | 1.07 | −0.14 | 0.00 | 0.00 | 0.00 | 228.20 | 3.33c | 224.87 |
| O2 | 18.77 | 91.70 | 9.24 | −0.42 | 1.08 | −0.12 | 0.45 | −0.18 | −0.45 | 0.00 | 0.00 | 120.07 | 2.19c | 117.88 |
| Cl2 | 19.23 | 35.65 | 4.79 | −0.44 | 0.43 | −0.02 | 0.22 | −0.18 | −1.68 | −0.09 | 0.00 | 57.91 | 0.79c | 57.12 |
| Br2 | 16.09 | 32.08 | 4.17 | −0.32 | 0.35 | −0.02 | 0.54 | −0.36 | −7.02 | 0.40 | 0.00 | 45.91 | 0.47c | 45.44 |
| HCl | 77.08 | 28.75 | 1.60 | −0.14 | 0.09 | 0.00 | 0.25 | −0.24 | −0.84 | −0.05 | 0.03 | 106.51 | 4.17c | 102.32 |
| HBr | 65.12 | 26.93 | 1.40 | −0.08 | 0.08 | 0.00 | 0.57 | −0.49 | −3.51 | 0.19 | 0.02 | 90.23 | 3.75c | 86.48 |
| HOCl | 78.82 | 80.11 | 6.93 | −0.50 | 0.59 | 0.05 | 0.40 | −0.31 | −1.06 | −0.05 | 0.03 | 165.01 | 7.92 | 157.09 |
| HOBr | 76.75 | 79.30 | 6.75 | −0.46 | 0.59 | −0.07 | 0.39 | −0.65 | −3.73 | 0.20 | 0.04 | 159.10 | 7.91 | 151.19 |
| H2O | 155.92 | 73.14 | 3.59 | −0.23 | 0.19 | −0.02 | 0.48 | −0.26 | −0.22 | 0.00 | 0.09 | 232.67 | 13.22 | 219.454 |
| NH3 | 201.12 | 92.28 | 3.92 | −0.15 | 0.02 | −0.02 | 0.79 | −0.24 | 0.00 | 0.00 | 0.09 | 297.81 | 21.20 | 276.61 |
| Set B | ||||||||||||||
| NH2Cl | 142.01 | 98.49 | 6.95 | −0.46 | 0.47 | −0.04 | 0.74 | −0.38 | −0.84 | −0.05 | 0.05 | 246.95 | 16.30 | 230.65 |
| NHCl2 | 79.84 | 107.66 | 10.92 | −0.89 | 0.93 | −0.09 | 0.70 | −0.39 | −1.68 | −0.09 | 0.02 | 196.92 | 10.45 | 186.48 |
| NCl3 | 13.78 | 119.64 | 15.92 | −1.46 | 1.58 | −0.20 | 0.62 | −0.29 | −2.52 | −0.14 | 0.01 | 146.45 | 3.84 | 143.11 |
| NH2Br | 135.81 | 97.75 | 6.85 | −0.41 | 0.48 | −0.04 | 0.92 | −0.63 | −3.51 | 0.20 | 0.05 | 237.46 | 15.93 | 221.53 |
| NHBr2 | 66.13 | 106.55 | 10.76 | −0.81d | 0.97 | −0.11 | 1.11 | −0.54 | −7.02 | 0.40 | 0.02 | 177.44 | 9.81 | 167.64 |
| NBr3 | −7.29 | 118.63 | 15.93 | −1.39d | 1.29e | N/Af | 3.24g | −0.14 | −10.54 | 0.61 | 0.01 | 120.34 | 2.98 | 117.36 |
| NHBrCl | 73.51 | 107.14 | 10.87 | −0.83d | 0.95 | −0.10 | 1.22h | −0.45 | −4.35 | 0.15 | 0.02 | 188.12 | 10.13 | 177.99 |
| NBrCl2 | 5.04 | 120.29 | 16.41 | −1.41d | 1.74 | −0.24 | 0.66 | −0.20 | −5.19 | 0.11 | 0.01 | 137.21 | 3.56 | 133.65 |
| NBr2Cl | −0.58 | 119.12 | 16.01 | −1.67d | 1.22e | −0.04 | 2.58g | −0.15 | −7.86 | 0.36 | 0.01 | 129.00 | 3.27 | 125.72 |
Electron correlation is a substantial contributor to the bond formation of chloramines and bromamines. For the monohalogenated species, the ΔECCSD,Extrap and ΔE(T),Extrap energy components together explain >40% of the TAEe. For the dihalogenated and trihalogenated species, the combined ΔECCSD,Extrap and ΔE(T),Extrap contributions dominate over the EHF,Extrap energy component altogether. The EHF,Extrap component dwindles progressively with increasing halogenation. The chloramines and bromamines are thus relatively weakly bound molecules, held together largely by electron correlation forces, and presumably this accounts for their high reactivity.
For both NBr3 and NBr2Cl, the EHF,Extrap component of the TAEe is actually less than zero, indicating that these molecules are not predicted to be stable at the Hartree–Fock level. In other words, electronic correlation effects are entirely responsible for their stable formation. This is an unusual situation; a few other species have been reported to exhibit negative or near-zero Hartree–Fock contributions to the TAEe, and many of them are halogen-containing molecules: O3, MgO, BN(1Σ+), F2, FO2, F2O2, FO, F2O, OClO, and ClOO are characterized by negative or near-zero Hartree–Fock atomization energies, and their stable formation is thus explained entirely by dynamical and nondynamical electron correlation effects.61,135 Dynamical and nondynamical correlation contributions are discussed further in the next section.
Post-CCSD(T) contributions to electronic correlation energies are varied. For example, ΔET–(T),Extrap, ΔE(Q), and ΔEQ–(Q) contributions together account for −0.49 kcal mol−1 of the total atomization energy of NBr2Cl. However for most of the halamines, the ΔET–(T),Extrap, ΔE(Q), and ΔEQ–(Q) components tend to cancel each other. The ΔET–(T),Extrap energy components are destabilizing in all cases (<0), whereas the quadruple excitation contributions are uniformly stabilizing (>0). This is consistent with the trends in post-CCSD(T) components found previously for other small molecules.60,61,114
Core–valence electronic correlation contributions to the total atomization energy are non-negligible for bromamines and chloramines. The ΔECORE values reported for chloramines range from 0.62 kcal mol−1 to 0.74 kcal mol−1. For bromamines and bromochloramines, values range from 0.66 kcal mol−1 (NBrCl2) to 3.24 kcal mol−1 (NBr3). Core–valence electronic correlation contributions thus have critical importance in achieving benchmark accuracy in the TAE.
Relativistic energy components also have an important role for estimating thermochemical properties of these molecules. The ΔEREL and ΔE2nd![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) SO components contribute quantitatively to the total atomization energies of halamines. The scalar relativistic effects, ΔEREL, of halamines are negative with values that range from −0.14 kcal mol−1 (NBr3) to −0.63 kcal mol−1 (NH2Br). ΔE2nd
SO components contribute quantitatively to the total atomization energies of halamines. The scalar relativistic effects, ΔEREL, of halamines are negative with values that range from −0.14 kcal mol−1 (NBr3) to −0.63 kcal mol−1 (NH2Br). ΔE2nd![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) SO values range from −0.14 kcal mol−1 (NCl3) to 0.61 kcal mol−1 (NBr3). These energy contributions, although small, have to be considered to achieve the desired accuracy in TAE calculations. The ΔE1st
SO values range from −0.14 kcal mol−1 (NCl3) to 0.61 kcal mol−1 (NBr3). These energy contributions, although small, have to be considered to achieve the desired accuracy in TAE calculations. The ΔE1st![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) SO contribution is simply an additive function of the elemental composition of the molecule and therefore it is not discussed.
SO contribution is simply an additive function of the elemental composition of the molecule and therefore it is not discussed.
Finally, ΔEDBOC components are the smallest energy contributions considered. Among the halamines, the largest values are 0.05 kcal mol−1 found for NH2Cl and NH2Br.
3.2 Importance of nondynamical correlation for halamines
Nondynamical electron correlation (NDC) contributes substantially to the electronic structure of chloramines and bromamines, and this merits a brief discussion. The nondynamical electronic correlation refers to the interelectronic interactions for those systems where the reference configuration (defined as the HF wavefunction) is affected by quasidegeneracy and is not well-described by a single predominating configuration.136 Chloramines and bromamines all exhibit nondynamical correlation (Table 4). This effect becomes increasingly important with increasing number of halogen atoms in the molecule. The wavefunctions of all four trihalamine species are dominated by multireference character as diagnosed by very low %TAE[HF] values and high %TAE[(T)] values. Monohalamines and dihalamines exhibit mild to moderate levels of nondynamical correlation.| Compound | %TAE[HF] | %TAE[(T)] | %TAE[post-CCSD(T)] | NDC evaluation based on %TAE[(T)]a |
|---|---|---|---|---|
| a Following the qualitative interpretation proposed by Karton et al.,61,65 systems are dominated by dynamic correlation when the %TAE[(T)] value is below 2%, whereas a large nondynamical correlation contribution is indicated by a %TAE[(T)] value greater than 10%. %TAE[(T)] between 2% and 4–5% and between 4–5% and 10% suggest mild and moderate levels of nondynamical correlation, respectively. %TAE[HF] is a more generic and lower-cost predictor for NDC: a %TAE[HF] value above 66.7% indicates a system not affected by NDC, whereas a %TAE[HF] below 20% indicates a molecule dominated by a severe nondynamical correlation. | ||||
| N2 | 50.9 | 4.16 | 0.076 | Mild NDC |
| O2 | 15.7 | 7.72 | 0.443 | Moderate NDC |
| Cl2 | 32.4 | 8.03 | −0.051 | Moderate NDC |
| Br2 | 30.9 | 7.97 | 0.035 | Moderate NDC |
| HCl | 71.8 | 1.49 | 0.048 | Mild NDC |
| HBr | 69.7 | 1.50 | −0.006 | Mild NDC |
| HOCl | 47.6 | 4.18 | 0.084 | Mild NDC |
| HOBr | 47.2 | 4.14 | 0.037 | Mild NDC |
| H2O | 67.1 | 1.54 | −0.029 | Mild NDC |
| NH3 | 67.7 | 1.32 | −0.048 | Mild NDC |
| NH2Cl | 57.4 | 2.81 | −0.012 | Mild NDC |
| NHCl2 | 40.3 | 5.50 | −0.031 | Moderate NDC |
| NCl3 | 9.3 | 10.66 | −0.049 | Severe NDC |
| NH2Br | 56.5 | 2.85 | 0.010 | Mild NDC |
| NHBr2 | 36.1 | 5.86 | 0.022 | Moderate NDC |
| NBr3 | −5.8 | 12.52 | −0.080 | Severe NDC |
| NHBrCl | 38.5 | 5.68 | 0.008 | Moderate NDC |
| NBrCl2 | 3.6 | 11.58 | 0.065 | Severe NDC |
| NBr2Cl | −0.4 | 11.90 | −0.364 | Severe NDC |
These NDC diagnostics provide a rough indication of the reliability of single-reference approaches in the evaluation of the electronic structure. In order to provide a more detailed description of systems dominated by NDC, a multireference electronic structure method is generally required. However, the electronic energies of such systems can be quantitatively recovered with high-order coupled cluster methods based on a single-determinant HF reference.61,66,71
3.3 Comparison of computed TAE0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/h3_char_2009.gif) K values with previous experimental and theoretical data
K values with previous experimental and theoretical data
Our best estimate total atomization energies at 0 K, TAETA140![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K,“Best”, are in excellent agreement with previously published experimental values, where available. For all species in set A there is agreement to within 0.23 kcal mol−1 or less (Table 5). The average absolute deviation from experiments is 0.10 kcal mol−1. The largest disagreement from experiment is for HOCl (0.23 kcal mol−1), followed by HBr with a deviation of −0.14 kcal mol−1. These results indicate that the ab initio protocol employed here has achieved ≤1 kJ mol−1 accuracy for the small molecules of set A. This is consistent with previous high-level ab initio work using comparable methodologies.61,63
K,“Best”, are in excellent agreement with previously published experimental values, where available. For all species in set A there is agreement to within 0.23 kcal mol−1 or less (Table 5). The average absolute deviation from experiments is 0.10 kcal mol−1. The largest disagreement from experiment is for HOCl (0.23 kcal mol−1), followed by HBr with a deviation of −0.14 kcal mol−1. These results indicate that the ab initio protocol employed here has achieved ≤1 kJ mol−1 accuracy for the small molecules of set A. This is consistent with previous high-level ab initio work using comparable methodologies.61,63
| Compound | TAETA140![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K,“Best” K,“Best” |
TAETA140![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K,“Halkier” K,“Halkier” |
TAEW40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K K![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 60,61 60,61 |
TAEFPD0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K K![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 63 63 |
TAEExpt0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K K |
|---|---|---|---|---|---|
a The deviations were calculated considering all available experimental data.
b Only the compounds studied by Karton et al. are considered.
c Reference TAE0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K for HOCl and HOBr are calculated from experimental molecular ΔfH00 K for HOCl and HOBr are calculated from experimental molecular ΔfH00![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K and experimental atomic heat capacities.
d Not available. K and experimental atomic heat capacities.
d Not available.
|
|||||
| Set A | |||||
| H2 | 103.34 | 103.36 | 103.29 | 103.27 ± 0.02 | 103.2777 |
| N2 | 224.87 | 224.93 | 225.01 | 224.88 ± 0.3 | 224.94 ± 0.0161 |
| O2 | 117.88 | 117.88 | 117.88 | 117.92 ± 0.2 | 117.99 ± 0.0061 |
| Cl2 | 57.12 | 57.81 | 57.03 | 57.23 ± 0.3 | 57.18 ± 0.0061 |
| Br2 | 45.44 | 45.50 | N/Ad | 45.39 ± 0.3 | 45.46 ± 0.0777 |
| HCl | 102.32 | 102.59 | 102.23 | 102.15 ± 0.2 | 102.21 ± 0.0061 |
| HBr | 86.48 | 86.48 | N/Ad | 86.47 ± 0.2 | 86.62 ± 0.0577 |
| HOCl | 157.09 | 157.53 | 156.72 | 156.94 ± 0.4 | 156.86 ± 0.03c |
| HOBr | 151.19 | 151.23 | N/Ad | N/Ad | 151.28 ± 0.21c |
| H2O | 219.45 | 219.46 | 219.36 | 219.38 ± 0.2 | 219.36 ± 0.0161 |
| NH3 | 276.61 | 276.66 | 276.60 | 276.48 ± 0.3 | 276.59 ± 0.0161 |
| Average absolute deviation 1 | 0.09 | 0.22 | 0.06 | ||
| Average absolute deviation 2 | 0.10 | 0.28 | 0.06 | 0.06 | |
| Average deviation 1 | 0.00 | 0.18 | −0.03 | ||
| Average deviation 2 | 0.03 | 0.25 | −0.04 | −0.02 | |
| Signed maximum deviation | 0.23 (HOCl) | 0.67 (HOCl) | −0.15 (Cl2) | −0.15 (HBr) | |
| Set B | |||||
| NH2Cl | 230.65 | 231.03 | 230.54 | N/Ad | N/Ad |
| NHCl2 | 186.48 | 187.20 | N/Ad | N/Ad | N/Ad |
| NCl3 | 143.11 | 144.16 | N/Ad | N/Ad | N/Ad |
| NH2Br | 221.53 | 221.58 | N/Ad | N/Ad | N/Ad |
| NHBr2 | 167.64 | 167.70 | N/Ad | N/Ad | N/Ad |
| NBr3 | 117.36 | 117.49 | N/Ad | N/Ad | N/Ad |
| NHBrCl | 177.99 | 178.38 | N/Ad | N/Ad | N/Ad |
| NBrCl2 | 133.65 | 134.34 | N/Ad | N/Ad | N/Ad |
| NBr2Cl | 125.72 | 126.15 | N/Ad | N/Ad | N/Ad |
Our TAETA140![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K,“Best” results are also in very good agreement with previous theoretical values from W4 (TAEW40
K,“Best” results are also in very good agreement with previous theoretical values from W4 (TAEW40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K) and FPD calculations (TAEFPD0
K) and FPD calculations (TAEFPD0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K), where comparisons can be made. TAETA140
K), where comparisons can be made. TAETA140![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K,“Best” and TAEW40
K,“Best” and TAEW40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K agree to within 0.11 kcal mol−1 for monochloramine. For molecule set A, the highest discrepancies between TAETA140
K agree to within 0.11 kcal mol−1 for monochloramine. For molecule set A, the highest discrepancies between TAETA140![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K,“Best” and TAEW40
K,“Best” and TAEW40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K are found for N2 (−0.14 kcal mol−1) and HOCl (0.37 kcal mol−1). These differences can be explained chiefly by a few energy contributions that were computed differently. First, Karton et al. employed a different definition of frozen-core electrons from that implemented in CFOUR, and, as a consequence, the estimates of the core–valence contributions differ by 0.14 kcal mol−1 for HOCl. Second, the W4 estimate of the zero-point vibrational energy of HOCl was 8.18 kcal mol−1, taken from theoretical data137 calculated at the MRCI/AV(D,T,Q)Z level, and this differs from our VPT2-B2PLYPD/AVQZ value (7.92 kcal mol−1) and from the experimental value of 7.97 kcal mol−1.138–140 For N2, discrepancies between the two theoretical methods are likely due to slightly different calculations of post-CCSD(T) contributions. In the W4 protocol, the quadruple excitation energies are calculated as 1.10[(CCSDTQ-CCSDT(Q)) + (CCSDT(Q)-CCSDT)], whereas our estimates are calculated without the empirical scalar factor 1.10. Furthermore, CCSDTQ5 contributions were not included in our protocol. These dissimilarities between our method and W4 produce a discrepancy in the post-CCSD(T) energy value of N2. Finally, for molecule set A, the largest discrepancies between TAETA140
K are found for N2 (−0.14 kcal mol−1) and HOCl (0.37 kcal mol−1). These differences can be explained chiefly by a few energy contributions that were computed differently. First, Karton et al. employed a different definition of frozen-core electrons from that implemented in CFOUR, and, as a consequence, the estimates of the core–valence contributions differ by 0.14 kcal mol−1 for HOCl. Second, the W4 estimate of the zero-point vibrational energy of HOCl was 8.18 kcal mol−1, taken from theoretical data137 calculated at the MRCI/AV(D,T,Q)Z level, and this differs from our VPT2-B2PLYPD/AVQZ value (7.92 kcal mol−1) and from the experimental value of 7.97 kcal mol−1.138–140 For N2, discrepancies between the two theoretical methods are likely due to slightly different calculations of post-CCSD(T) contributions. In the W4 protocol, the quadruple excitation energies are calculated as 1.10[(CCSDTQ-CCSDT(Q)) + (CCSDT(Q)-CCSDT)], whereas our estimates are calculated without the empirical scalar factor 1.10. Furthermore, CCSDTQ5 contributions were not included in our protocol. These dissimilarities between our method and W4 produce a discrepancy in the post-CCSD(T) energy value of N2. Finally, for molecule set A, the largest discrepancies between TAETA140![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K,“Best” and TAEFPD0
K,“Best” and TAEFPD0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K are for HCl and HOCl (0.17 and 0.15 kcal mol−1, respectively). In summary, TA14 exhibits excellent agreement with W4 for monochloramine and excellent agreement with W4 and FPD values for molecules of set A, providing further confirmation that TA14 produces sub-kJ mol−1 accuracy for atomization energies of small molecules containing atoms up to the third row. Based on comparisons between TA14 and these other theoretical methods, we conclude that the predominating sources of uncertainties in our TAE0
K are for HCl and HOCl (0.17 and 0.15 kcal mol−1, respectively). In summary, TA14 exhibits excellent agreement with W4 for monochloramine and excellent agreement with W4 and FPD values for molecules of set A, providing further confirmation that TA14 produces sub-kJ mol−1 accuracy for atomization energies of small molecules containing atoms up to the third row. Based on comparisons between TA14 and these other theoretical methods, we conclude that the predominating sources of uncertainties in our TAE0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K values are in the calculations of the core–valence electron correlation energies and post-CCSD(T) energy treatments.
K values are in the calculations of the core–valence electron correlation energies and post-CCSD(T) energy treatments.
Based on the above comparisons to experimental and previous theoretical data, we conclude that our best TA14 computations have 1 kJ mol−1 (0.24 kcal mol−1) uncertainty in the TAE0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K for the chloramines (NH2Cl, NHCl2, and NCl3) and for monobromamine (NH2Br). We conservatively assign larger uncertainties of 3 kJ mol−1 (0.72 kcal mol−1) for the TAE0
K for the chloramines (NH2Cl, NHCl2, and NCl3) and for monobromamine (NH2Br). We conservatively assign larger uncertainties of 3 kJ mol−1 (0.72 kcal mol−1) for the TAE0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K values of NHBr2, NBr3, NHBrCl, NBrCl2, and NBr2Cl, which exhibit larger core–valence correlation and post-CCSD(T) energy contributions, and for which we were required to apply slightly lower levels of theoretical treatment.
K values of NHBr2, NBr3, NHBrCl, NBrCl2, and NBr2Cl, which exhibit larger core–valence correlation and post-CCSD(T) energy contributions, and for which we were required to apply slightly lower levels of theoretical treatment.
For purposes of further comparisons, we additionally employed the Halkier extrapolation formula (eqn (9)) for the computations of Hartree–Fock and correlation energies. We compared these data with results obtained following our “Best” TA14 approach, which employs W4 extrapolation formulae (eqn (7) and (8)), as shown in Table 5. The TAETA140![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K,“Halkier” values exhibit higher deviations with respect to experiments, with an average absolute deviation of 0.28 kcal mol−1 in the TAE0
K,“Halkier” values exhibit higher deviations with respect to experiments, with an average absolute deviation of 0.28 kcal mol−1 in the TAE0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K. The largest disagreement is found for HOCl, which differs from the experimental data by 0.67 kcal mol−1 using the Halkier extrapolation. Consistent with previous work,61,71 we find that eqn (7) and (8) perform better than the Halkier's extrapolation formula for total atomization energies, with the large basis sets employed here.
K. The largest disagreement is found for HOCl, which differs from the experimental data by 0.67 kcal mol−1 using the Halkier extrapolation. Consistent with previous work,61,71 we find that eqn (7) and (8) perform better than the Halkier's extrapolation formula for total atomization energies, with the large basis sets employed here.
3.4 Gas phase enthalpies of formation at 0 K and at 298 K
Our computed gas phase enthalpies of formation at 0 K, ΔfH0,TA140![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K,“Best”, are in excellent agreement with experimental data for molecule set A. Our best calculated values at 0 K exhibit an average absolute deviation of 0.11 kcal mol−1 from experiment, indicating that the TA14 method achieves confident kJ mol−1 accuracy in the ΔfH00
K,“Best”, are in excellent agreement with experimental data for molecule set A. Our best calculated values at 0 K exhibit an average absolute deviation of 0.11 kcal mol−1 from experiment, indicating that the TA14 method achieves confident kJ mol−1 accuracy in the ΔfH00![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K for these systems. The computed enthalpy of formation at 0 K of HOCl is the most inaccurate, with a deviation of −0.23 kcal mol−1 from experiment and a discrepancy of 0.37 kcal mol−1 with respect to the W4.2 value (−17.51 ± 0.14 kcal mol−1).65 This discrepancy from the W4.2 result arises from electronic and vibration contributions to the TAE0
K for these systems. The computed enthalpy of formation at 0 K of HOCl is the most inaccurate, with a deviation of −0.23 kcal mol−1 from experiment and a discrepancy of 0.37 kcal mol−1 with respect to the W4.2 value (−17.51 ± 0.14 kcal mol−1).65 This discrepancy from the W4.2 result arises from electronic and vibration contributions to the TAE0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K, discussed in the previous section. The computed enthalpies of formation at 0 K for HBr and N2 are overestimated by about 0.20 kcal mol−1 compared to experiment. These discrepancies arise primarily from the uncertainties in the calculations of the electronic contributions to total atomization energies, as discussed in the previous section.
K, discussed in the previous section. The computed enthalpies of formation at 0 K for HBr and N2 are overestimated by about 0.20 kcal mol−1 compared to experiment. These discrepancies arise primarily from the uncertainties in the calculations of the electronic contributions to total atomization energies, as discussed in the previous section.
For molecule set A, computed gas phase enthalpies of formation at 298 K, ΔfH0,TA14298![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K,“Best”, also exhibit sub-kJ mol−1 agreement with available experimental data (Table 7). The largest deviations from experiment were found for HOCl and N2, with differences of −0.20 and 0.18 kcal mol−1, respectively. Errors in the computed gas phase enthalpy of formation are of similar magnitude at 0 K and at 298 K (Tables 6 and 7). It is worth noting that ΔfH0,Expt298
K,“Best”, also exhibit sub-kJ mol−1 agreement with available experimental data (Table 7). The largest deviations from experiment were found for HOCl and N2, with differences of −0.20 and 0.18 kcal mol−1, respectively. Errors in the computed gas phase enthalpy of formation are of similar magnitude at 0 K and at 298 K (Tables 6 and 7). It is worth noting that ΔfH0,Expt298![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K values are probably not independent of reported ΔfH0,Expt0
K values are probably not independent of reported ΔfH0,Expt0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K values. We did not verify whether the experimental data found in different databases, such as JANAF-Thermochemical Tables,76 CODATA,73 ATCT,74,75 and CCCBDB,77 originate from common experimental sources.
K values. We did not verify whether the experimental data found in different databases, such as JANAF-Thermochemical Tables,76 CODATA,73 ATCT,74,75 and CCCBDB,77 originate from common experimental sources.
| Compound | ΔfH0,TA140![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K,“Best” K,“Best” |
ΔfH0,W4.20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K K |
ΔfH0,Expt0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K K |
|---|---|---|---|
| a Not available. | |||
| Set A | |||
| H2 | −0.07 | N/Aa | 0.0073–75 |
| N2 | 0.19 | N/Aa | 0.0073–75 |
| O2 | 0.09 | N/Aa | 0.0073–75 |
| Cl2 | 0.06 | N/Aa | 0.0073–75 |
| Br2 | 10.93 | N/Aa | 10.92 ± 0.0373 |
| HCl | −22.10 | N/Aa | −22.02 ± 0.0273 |
| HBr | −6.66 | N/Aa | −6.80 ± 0.0473 |
| HOCl | −17.88 | −17.51 ± 0.1465 | −17.654 ± 0.00774,75 |
| HOBr | −12.38 | N/Aa | −12.48 ± 0.1674,75 |
| H2O | −57.20 | N/Aa | −57.10 ± 0.01141 |
| NH3 | −9.18 | N/Aa | −9.31 ± 0.0873 |
| Average absolute deviation | 0.11 | ||
| Average deviation | 0.02 | ||
| Signed maximum deviation | −0.23 (HOCl) | ||
| Set B | |||
| NH2Cl | 13.74 | N/Aa | N/Aa |
| NHCl2 | 34.87 | N/Aa | N/Aa |
| NCl3 | 55.19 | N/Aa | N/Aa |
| NH2Br | 22.45 | N/Aa | N/Aa |
| NHBr2 | 52.89 | N/Aa | N/Aa |
| NBr3 | 79.72 | N/Aa | N/Aa |
| NHBrCl | 42.95 | N/Aa | N/Aa |
| NBrCl2 | 64.24 | N/Aa | N/Aa |
| NBr2Cl | 95.21 | N/Aa | N/Aa |
| Compound | ΔfH0,TA14298![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K,“Best” K,“Best” |
ΔfH0,Comp298![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K K |
ΔfH0,Expt298![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K K |
|---|---|---|---|
| a Not available. | |||
| Set A | |||
| H2 | −0.03 | 0.00 ± 0.0263 | 0.0074,75 |
| N2 | 0.18 | 0.2 ± 0.363 | 0.0074,75 |
| O2 | 0.09 | 0.0 ± 0.263 | 0.0074,75 |
| Cl2 | 0.06 | <0.1 ± 0.363 | 0.0074,75 |
| Br2 | 7.38 | 7.4 ± 0.363 | 7.39 ± 0.0374–76 |
| HCl | −22.14 | −22.0 ± 0.263 | −22.030 ± 0.00174,75 |
| HBr | −8.54 | −8.5 ± 0.263 | −8.61 ± 0.0374,75 |
| HOCl | −18.56 | –18.20 ± 0.1465 | −18.357 ± 0.00774,75 |
| −18.1 ± 0.3142 | |||
| −17.9 ± 0.358 | |||
| −18.1 ± 0.463 | |||
| HOBr | −14.90 | –15.3 ± 0.6142 | −15.00 ± 0.1674,75 |
| −14.5756 | |||
| H2O | −57.90 | −57.8 ± 0.263 | −57.80 ± 0.0174–76 |
| −57.6 ± 0.358 | |||
| NH3 | −10.86 | −10.7 ± 0.363 | −10.889 ± 0.00774,75 |
| −10.3 ± 0.358 | |||
| Average absolute deviation | 0.07 | ||
| Average deviation | 0.03 | ||
| Signed maximum deviation | −0.20 (HOCl) | ||
| Set B | |||
| NH2Cl | 12.04 | 13.0256 | N/Aa |
| 12.458 | |||
| NHCl2 | 33.47 | 33.4456 | N/Aa |
| 32.558 | |||
| NCl3 | 54.36 | 53.5656 | N/Aa |
| 52.3758 | |||
| NH2Br | 18.97 | 19.9056 | N/Aa |
| NHBr2 | 48.02 | 47.5656 | N/Aa |
| NBr3 | 73.82 | N/Aa | N/Aa |
| NHBrCl | 39.80 | N/Aa | N/Aa |
| NBrCl2 | 61.72 | N/Aa | N/Aa |
| NBr2Cl | 91.00 | N/Aa | N/Aa |
Chloramines and bromamines are found to be endothermic with respect to the elements in their standard states. ΔfH0,TA14298![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K,“Best” values range from 12.04 kcal mol−1 to 91.00 kcal mol−1 for chloramines, bromamines and bromochloramines (Table 7). No experimental heat of formation data are available for the halamines. Based on comparisons of our dataset with other computed and experimental data for molecule set A, we consider that the major sources of uncertainty in the ΔfH0,TA14298
K,“Best” values range from 12.04 kcal mol−1 to 91.00 kcal mol−1 for chloramines, bromamines and bromochloramines (Table 7). No experimental heat of formation data are available for the halamines. Based on comparisons of our dataset with other computed and experimental data for molecule set A, we consider that the major sources of uncertainty in the ΔfH0,TA14298![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K,“Best” arise from the post-CCSD(T) electron correlation contributions to the TAE0
K,“Best” arise from the post-CCSD(T) electron correlation contributions to the TAE0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K. For the chloramines (NH2Cl, NHCl2, and NCl3) and for monobromamine (NH2Br), we estimate 1 kJ mol−1 (0.24 kcal mol−1) uncertainties in the computed ΔfH00
K. For the chloramines (NH2Cl, NHCl2, and NCl3) and for monobromamine (NH2Br), we estimate 1 kJ mol−1 (0.24 kcal mol−1) uncertainties in the computed ΔfH00![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K and ΔfH0298
K and ΔfH0298![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K estimates. For NHBr2, NBr3, and for the bromochloramines, we assign larger uncertainties of 3 kJ mol−1 (0.72 kcal mol−1) in computed ΔfH00
K estimates. For NHBr2, NBr3, and for the bromochloramines, we assign larger uncertainties of 3 kJ mol−1 (0.72 kcal mol−1) in computed ΔfH00![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K and ΔfH0298
K and ΔfH0298![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K values, for reasons discussed in the section on TAE0
K values, for reasons discussed in the section on TAE0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K data.
K data.
Recently, Rayne and Forest reported standard enthalpies of formation at 298 K for chloramines computed at the G4MP2 and G4 levels and for monobromamine and dibromamine at the G4 level (Table 7).56,58 These protocols represent lower levels of theory than the methods employed here. The G4 and G4MP2 methods do not include any post-CCSD(T) energy calculations and do not employ basis sets larger than 6-31G(2df,p) and 6-31+G(d). Reported G4 estimates of ΔfH0298![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K deviate from our best estimates by 0.03 to 0.98 kcal mol−1 for the chloramines, monobromamine, and dibromamine (Table 7). Reported G4MP2 data exhibit larger deviations from our best estimates, with a difference of 1.99 kcal mol−1 found for the ΔfH0298
K deviate from our best estimates by 0.03 to 0.98 kcal mol−1 for the chloramines, monobromamine, and dibromamine (Table 7). Reported G4MP2 data exhibit larger deviations from our best estimates, with a difference of 1.99 kcal mol−1 found for the ΔfH0298![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K value of trichloramine. Thus our computed enthalpy of formation values substantially improve upon these previously reported estimates.
K value of trichloramine. Thus our computed enthalpy of formation values substantially improve upon these previously reported estimates.
3.5 Gibbs free energies of formation at 298 K
For the molecule set A, our best estimate ΔfG0,TA14298![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K,“Best” values show good agreement with experimental data, with an average absolute deviation of 0.09 kcal mol−1 (Table 8). The ΔfG0,TA14298
K,“Best” values show good agreement with experimental data, with an average absolute deviation of 0.09 kcal mol−1 (Table 8). The ΔfG0,TA14298![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K,“Best” of HOCl exhibits the largest disagreement from experiment, with a deviation of 0.19 kcal mol−1. This is consistent with the accuracy found for the computed enthalpy of formation, ΔfH0,TA14298
K,“Best” of HOCl exhibits the largest disagreement from experiment, with a deviation of 0.19 kcal mol−1. This is consistent with the accuracy found for the computed enthalpy of formation, ΔfH0,TA14298![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K,“Best”. A comparison of computed and experimental ΔfS0298
K,“Best”. A comparison of computed and experimental ΔfS0298![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K values revealed an average absolute error of only 0.08 cal mol−1 K−1 and a maximum unsigned deviation of 0.12 cal mol−1 K−1 (for both H2 and Br2). Errors in the computed entropy thus contribute less than 0.04 kcal mol−1 in the ΔfG0298
K values revealed an average absolute error of only 0.08 cal mol−1 K−1 and a maximum unsigned deviation of 0.12 cal mol−1 K−1 (for both H2 and Br2). Errors in the computed entropy thus contribute less than 0.04 kcal mol−1 in the ΔfG0298![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K, for all molecules of set A.77 Our computed vibrational frequencies are in excellent agreement with experiment, exhibiting an average absolute deviation value of 4 cm−1, and a maximum deviation of −58 cm−1 (for H2), for set A.
K, for all molecules of set A.77 Our computed vibrational frequencies are in excellent agreement with experiment, exhibiting an average absolute deviation value of 4 cm−1, and a maximum deviation of −58 cm−1 (for H2), for set A.
| Compound | ΔfG0,TA14298![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K,“Best” K,“Best” |
ΔfG0,Expt298![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K K |
|---|---|---|
a The ΔfS0,Expt298![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K value for HOBr was calculated using experimental rotational constants143 and experimental vibrational frequencies,144,145 assuming an NVT ensemble, according to statistical mechanic expressions outlined in the Hill textbook.105
b Not available. K value for HOBr was calculated using experimental rotational constants143 and experimental vibrational frequencies,144,145 assuming an NVT ensemble, according to statistical mechanic expressions outlined in the Hill textbook.105
b Not available.
|
||
| Set A | ||
| H2 | −0.03 | 073 |
| N2 | 0.18 | 073 |
| O2 | 0.09 | 073 |
| Cl2 | 0.06 | 073 |
| Br2 | 0.74 | 0.74 ± 0.0373 |
| HCl | −22.85 | −22.744 ± 0.00173 |
| HBr | −12.62 | −12.69 ± 0.0373 |
| HOCl | −15.49 | −15.30 ± 0.0173 |
| HOBr | −15.14 | −15.26a |
| H2O | −54.71 | −54.63 ± 0.0173 |
| NH3 | −3.78 | −3.83 ± 0.0373 |
| Average absolute deviation | 0.09 | |
| Average deviation | −0.02 | |
| Signed maximum deviation | 0.19 (HOCl) | |
| Set B | ||
| NH2Cl | 19.39 | N/Ab |
| NHCl2 | 41.62 | N/Ab |
| NCl3 | 63.38 | N/Ab |
| NH2Br | 22.98 | N/Ab |
| NHBr2 | 49.46 | N/Ab |
| NBr3 | 73.15 | N/Ab |
| NHBrCl | 44.19 | N/Ab |
| NBrCl2 | 67.56 | N/Ab |
| NBr2Cl | 93.46 | N/Ab |
For the computed ΔfG0,TA14298![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K,“Best” values of set A, the most important sources of deviation from experiment were considered to be the uncertainties in the estimation of the core–valence correlation and post-CCSD(T) electronic correlation contributions to total atomization energies. These effects are discussed in previous section.
K,“Best” values of set A, the most important sources of deviation from experiment were considered to be the uncertainties in the estimation of the core–valence correlation and post-CCSD(T) electronic correlation contributions to total atomization energies. These effects are discussed in previous section.
Halamine formation is endergonic with respect to the elemental forms at standard state, with ΔfG0,TA14298![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K,“Best” values ranging from 19.39 kcal mol−1 to 93.46 kcal mol−1. No experimental gas phase thermochemistry data are available for halamines. Based on results for molecule set A, we estimate 1 kJ mol−1 (0.24 kcal mol−1) uncertainties in the computed ΔfG0298
K,“Best” values ranging from 19.39 kcal mol−1 to 93.46 kcal mol−1. No experimental gas phase thermochemistry data are available for halamines. Based on results for molecule set A, we estimate 1 kJ mol−1 (0.24 kcal mol−1) uncertainties in the computed ΔfG0298![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K values of the chloramines (NH2Cl, NHCl2, and NCl3) and of monobromamine (NH2Br). For NHBr2, NBr3, and for the bromochloramines, we assign larger uncertainties of 3 kJ mol−1 (0.72 kcal mol−1) in computed ΔfG0298
K values of the chloramines (NH2Cl, NHCl2, and NCl3) and of monobromamine (NH2Br). For NHBr2, NBr3, and for the bromochloramines, we assign larger uncertainties of 3 kJ mol−1 (0.72 kcal mol−1) in computed ΔfG0298![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K values, for reasons discussed in the section on TAE0
K values, for reasons discussed in the section on TAE0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K data. It is worth noting that, unlike molecules of set A, the di- and tri-halogenated amines contain some low frequencies, with the lowest frequencies ranging from 148 cm−1 (NBr3) to 283 cm−1 (NHCl2) (see ESI†). However, the anharmonic corrections do not account for more than 5 cm−1 of the low-frequency bending modes of any of these species. Accurate gas phase Gibbs free energies of formation at 298 K are key thermodynamic properties for studying reaction chemistry involving halamines. This is illustrated further in the next section.
K data. It is worth noting that, unlike molecules of set A, the di- and tri-halogenated amines contain some low frequencies, with the lowest frequencies ranging from 148 cm−1 (NBr3) to 283 cm−1 (NHCl2) (see ESI†). However, the anharmonic corrections do not account for more than 5 cm−1 of the low-frequency bending modes of any of these species. Accurate gas phase Gibbs free energies of formation at 298 K are key thermodynamic properties for studying reaction chemistry involving halamines. This is illustrated further in the next section.
4 Implications for aqueous chemistry of chloramines and bromamines
The purpose of this study is to provide accurate thermochemistry data describing the formation of chloroamines, bromamines, and bromochloramines. With the W4 and FPD procedures as a guiding basis, we successfully designed a computational method (TA14) that accomplished this goal. It was not our aim to test TA14 against a broad thermochemical database. However, our limited assessment of molecules that are structurally related to the halamines confirms that our approach successfully achieved the targeted level of accuracy in thermochemical properties.The estimation of gas phase free energies of formation of chloramines, bromamines, and bromochloramines allows us to predict the equilibrium constants for the reactions involving these species. By combining gas phase ΔfG0,TA14298![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K,“Best” data reported here together with experimental or computed estimates of solvation free energies for the pertaining species, it is possible to assess the equilibrium constants of the formation of chloramines, bromamines, and bromochloramines in aqueous phase. This can lead to further insights into the thermodynamics and the kinetics of the generation and decomposition processes affecting these reactive species during water treatment. As an illustrative example, we consider the generation of monochloramine from HOCl and NH3 in water, which is an important reaction during water treatment:
K,“Best” data reported here together with experimental or computed estimates of solvation free energies for the pertaining species, it is possible to assess the equilibrium constants of the formation of chloramines, bromamines, and bromochloramines in aqueous phase. This can lead to further insights into the thermodynamics and the kinetics of the generation and decomposition processes affecting these reactive species during water treatment. As an illustrative example, we consider the generation of monochloramine from HOCl and NH3 in water, which is an important reaction during water treatment:
 | (21) |
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Keq,aq = −2.303RT Keq,aq = −2.303RT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ΔrxnGaq, ΔrxnGaq, | (22) |
| ΔrxnGaq = ΔrxnGgas + ΔΔrxnGsolv, | (23) |
Using our theoretical ΔfG0,TA14298![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K,“Best” data to obtain ΔrxnGTA14gas and combining this with experimental ΔΔrxnGExptsolv data, we produce a theoretical estimated equilibrium constant of log
K,“Best” data to obtain ΔrxnGTA14gas and combining this with experimental ΔΔrxnGExptsolv data, we produce a theoretical estimated equilibrium constant of log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KCompeq,aq = 10.5, according to eqn (22) and (23) (Table 9). For comparison, Morris and Isaac9 proposed an experimental value of 11.3 for the equilibrium constant, KExpteq,aq, of monochloramine generation in aqueous phase (eqn (21)), derived from the ratio of the experimental forward rate constant, kf, with the experimental reverse rate constant, kr:
KCompeq,aq = 10.5, according to eqn (22) and (23) (Table 9). For comparison, Morris and Isaac9 proposed an experimental value of 11.3 for the equilibrium constant, KExpteq,aq, of monochloramine generation in aqueous phase (eqn (21)), derived from the ratio of the experimental forward rate constant, kf, with the experimental reverse rate constant, kr:
 | (24) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KCompeq,aq is in reasonable agreement with the experimental estimate (Table 9). We suspect that the discrepancy of 1.3 kcal mol−1 in ΔrxnGCompaq arises mostly from uncertainties in the experimental Henry's law constant data used to estimate ΔΔrxnGsolv or from experimental reaction rate constant data used to estimate ΔrxnGExptaq.
KCompeq,aq is in reasonable agreement with the experimental estimate (Table 9). We suspect that the discrepancy of 1.3 kcal mol−1 in ΔrxnGCompaq arises mostly from uncertainties in the experimental Henry's law constant data used to estimate ΔΔrxnGsolv or from experimental reaction rate constant data used to estimate ΔrxnGExptaq.
Thermodynamic equilibria for hypothetical reactions of halamines with relevant species in natural water, such as inorganic anions and electron-rich organic nucleophiles, can now be determined based on free energies of formation of halamines supplied in the present study. Such reactions are relevant to understanding the chemical sinks of halamines during drinking water treatment as well as the pathways that could lead to the formation of toxic disinfection byproducts.
Acknowledgements
We thank Urs von Gunten (EPFL/EAWAG), Jennifer J. Guerard (UA Fairbanks), Peter R. Tentscher (EPFL), and David Feller (Washington State University) for helpful discussions. We also thank the EPFL centralized HPC facilities for computational resources.References
- C. M. Villanueva and L. Font-Ribera, Ann. Ist. Super. Sanita, 2012, 48, 387–396 CrossRef.
- X. L. Armesto, M. Canle L., M. V. García and J. A. Santaballa, Chem. Rev., 1998, 27, 453–460 RSC.
- National Research Council, Drinking Water and Health, The National Academies Press, Washington, DC, 1980, vol. 2 Search PubMed.
- National Research Council, Drinking Water and Health, Disinfectants and Disinfectants By-Products, The National Academies Press, Washington, DC, 1987, vol. 7 Search PubMed.
- U.S. Environmental Protection Agency, Information about Chloramine in Drinking Water, 2012 Search PubMed.
- J. C. Morris, J. Phys. Chem., 1966, 70, 3798–3805 CrossRef CAS.
- I. Weil and J. C. Morris, J. Am. Chem. Soc., 1949, 71, 1664–1671 CrossRef CAS.
- J. C. Morris, Princ. Appl. Water Chem., 1967, pp. 23–53 Search PubMed.
- J. C. Morris and R. A. Isaac, Water Chlorination Environ. Impact Heal. Eff., Ann Arbor Science, Ann Arbor, MI, 1981, ch. 2, vol. 4, pp. 50–62 Search PubMed.
- D. W. Margerum and E. T. Gray, Organometals Organometalloids, Occur. Fate Environ., 1978, ch. 17, pp. 278–291 Search PubMed.
- C. T. Jafvert and R. L. Valentine, Environ. Sci. Technol., 1992, 26, 577–586 CrossRef CAS.
- R. L. Wolfe, N. R. Ward and B. H. Olson, J. - Am. Water Works Assoc., 1984, 76, 74–88 CAS.
- P. J. Vikesland, K. Ozekin and R. L. Valentine, Water Res., 2001, 35, 1766–1776 CrossRef CAS.
- J. E. Wajon and J. C. Morris, Water Chlorination Environ. Impact Heal. Eff., Ann Arbor Science, Ann Arbor, MI, 1980, ch. 16, vol. 3, pp. 171–181 Search PubMed.
- J. D. Jonhson and R. Overby, J. Sanit. Eng. Div., Am. Soc. Civ. Eng., 1971, 97, 617–628 Search PubMed.
- M. Gazda, L. E. Dejarme, T. K. Choudhury, R. G. Cooks and W. Lafayette, Environ. Sci. Technol., 1993, 27, 557–561 CrossRef CAS.
- M. Gazda and D. W. Margerum, Inorg. Chem., 1994, 33, 118–123 CrossRef CAS.
- G. W. Inman, T. F. LaPointe and J. D. Jonhson, Inorg. Chem., 1976, 15, 3037–3042 CrossRef CAS.
- G. W. Inman and J. D. Johnson, Environ. Sci. Technol., 1984, 4, 219–224 CrossRef PubMed.
- H. Galal-Gorchev and J. C. Morris, Inorg. Chem., 1965, 4, 899–905 CrossRef CAS.
- B. M. Soulard, F. Bloc and A. Hatterer, J. Chem. Soc., Dalton Trans., 1981, 2300–2310 RSC.
- A. Bousher, P. Brimblecombe and D. Midgley, Water Res., 1989, 23, 1049–1058 CrossRef CAS.
- M. B. Heeb, J. Criquet, S. G. Zimmermann-Steffens and U. von Gunten, Water Res., 2014, 48, 15–42 CrossRef CAS PubMed.
- H. Lei, B. J. Mariñas and R. A. Minear, Environ. Sci. Technol., 2004, 38, 2111–2119 CrossRef CAS.
- J. Luh and B. J. Mariñas, Environ. Sci. Technol., 2014, 48, 2843–2852 CrossRef CAS PubMed.
- A. C. Diehl, G. E. Speitel Jr., J. M. Symons, S. W. Krasner, C. J. Hwang and S. E. Barrett, J. - Am. Water Works Assoc., 2000, 92, 76–90 CAS.
- J. Le Roux, H. Gallard and J.-P. Croué, Environ. Sci. Technol., 2012, 46, 1581–1589 CrossRef CAS PubMed.
- H. Lei, R. A. Minear and B. J. Mariñas, Environ. Sci. Technol., 2006, 40, 2559–2564 CrossRef CAS.
- P. J. Vikesland and R. L. Valentine, Environ. Sci. Technol., 1998, 32, 1409–1416 CrossRef CAS.
- M. P. Snyder and D. W. Margerum, Inorg. Chem., 1982, 21, 2545–2550 CrossRef CAS.
- R. A. Isaac and J. C. Morris, Environ. Sci. Technol., 1983, 17, 738–742 CrossRef CAS PubMed.
- R. A. Isaac and J. C. Morris, Environ. Sci. Technol., 1985, 19, 810–814 CrossRef CAS PubMed.
- A. D. Shah and W. A. Mitch, Environ. Sci. Technol., 2012, 46, 119–131 CrossRef CAS PubMed.
- S. E. Duirk and R. L. Valentine, Water Res., 2006, 40, 2667–2674 CrossRef CAS PubMed.
- I. M. Schreiber and W. A. Mitch, Environ. Sci. Technol., 2005, 39, 3811–3818 CrossRef CAS.
- I. M. Schreiber and W. A. Mitch, Environ. Sci. Technol., 2006, 40, 6007–6014 CrossRef CAS.
- R. L. Valentine, Environ. Sci. Technol., 1986, 20, 166–170 CrossRef CAS PubMed.
- G. Holzwarth, R. G. Balmer and L. Soni, Water Res., 1984, 18, 1421–1427 CrossRef CAS.
- N. Cimetiere and J. De Laat, Chemosphere, 2009, 77, 465–470 CrossRef CAS PubMed.
- S. D. Richardson, D. M. DeMarini, M. Kogevinas, P. Fernandez, E. Marco, C. Lourencetti, C. Ballesté, D. Heederik, K. Meliefste, A. B. McKague, R. Marcos, L. Font-Ribera, J. O. Grimalt and C. M. Villanueva, Environ. Health Perspect., 2010, 118, 1523–1530 CrossRef CAS PubMed.
- M. Hery, G. Hecht, J. Gerber, J. Gendre, G. Hubert and J. Rebuffaud, Ann. Occup. Hyg., 1995, 39, 427–439 CrossRef CAS.
- D. I. Pattison and M. J. Davies, Biochemistry, 2004, 43, 4799–4809 CrossRef CAS PubMed.
- E. L. Thomas, P. M. Bozeman, M. M. Jefferson and C. C. King, J. Biol. Chem., 1995, 270, 2906–2913 CrossRef CAS PubMed.
- S. J. Weiss, S. T. Test, C. M. Eckmann, D. Roos and S. Regiani, Science, 1986, 234, 200–203 CAS.
- M. D. Rees, T. N. McNiven and M. J. Davies, Biochem. J., 2007, 401, 587–596 CrossRef CAS PubMed.
- A. L. P. Chapman, O. Skaff, R. Senthilmohan, A. J. Kettle and M. J. Davies, Biochem. J., 2009, 417, 773 CrossRef CAS PubMed.
- Z. Xue, W. H. Lee, K. M. Coburn and Y. Seo, Environ. Sci. Technol., 2014, 48, 3832–3839 CrossRef CAS PubMed.
- D. I. Pattison, R. J. O'Reilly, O. Ska, L. Radom, R. F. Anderson and M. J. Davies, Chem. Res. Toxicol., 2011, 24, 371–382 CrossRef CAS PubMed.
- R. J. O'Reilly, A. Karton and L. Radom, J. Phys. Chem. A, 2013, 117, 460–472 CrossRef PubMed.
- R. K. Milburn, C. F. Rodriquez and A. C. Hopkinson, J. Phys. Chem. B, 1997, 5647, 1837–1844 CrossRef.
- C. Möller and M. Plesset, Phys. Rev., 1934, 46, 618–622 CrossRef.
- R. Krishnan and J. A. Pople, Int. J. Chem. Kinet., 1978, XIV, 91–100 CrossRef.
- R. Krishnan, M. J. Frisch and J. A. Pople, J. Chem. Phys., 1980, 72, 4244 CrossRef CAS PubMed.
- H. B. Schlegel, J. Phys. Chem., 1988, 92, 3075–3078 CrossRef CAS.
- J. A. Pople, M. Head-Gordon and K. Raghavachari, J. Chem. Phys., 1987, 87, 5968 CrossRef CAS PubMed.
- S. Rayne and K. Forest, Comput. Theor. Chem., 2011, 974, 163–179 CrossRef CAS PubMed.
- L. A. Curtiss, P. C. Redfern and K. Raghavachari, J. Chem. Phys., 2007, 126, 084108 CrossRef PubMed.
- S. Rayne and K. Forest, J. Environ. Sci. Health, Part A: Toxic/Hazard. Subst. Environ. Eng., 2014, 49, 753–762 CrossRef CAS PubMed.
- L. A. Curtiss, P. C. Redfern and K. Raghavachari, J. Chem. Phys., 2007, 127, 124105 CrossRef PubMed.
- A. Karton, S. Daon and J. M. L. Martin, Chem. Phys. Lett., 2011, 510, 165–178 CrossRef CAS PubMed.
- A. Karton, E. Rabinovich, J. M. L. Martin and B. Ruscic, J. Chem. Phys., 2006, 125, 144108 CrossRef PubMed.
- A. Karton, P. R. Taylor and J. M. L. Martin, J. Chem. Phys., 2007, 127, 064104 CrossRef PubMed.
- D. Feller, K. A. Peterson and D. A. Dixon, J. Chem. Phys., 2008, 129, 204105 CrossRef PubMed.
- K. A. Peterson, D. Feller and D. A. Dixon, Theor. Chem. Acc., 2012, 131, 1079 CrossRef PubMed.
- A. Karton, S. Parthiban and J. M. L. Martin, J. Phys. Chem. A, 2009, 113, 4802–4816 CrossRef CAS PubMed.
- A. Karton and J. M. L. Martin, J. Chem. Phys., 2011, 135, 144119 CrossRef PubMed.
- A. Tajti, P. G. Szalay, A. G. Császár, M. Kállay, J. Gauss, E. F. Valeev, B. A. Flowers, J. Vázquez and J. F. Stanton, J. Chem. Phys., 2004, 121, 11599–11613 CrossRef CAS PubMed.
- Y. J. Bomble, J. Vázquez, M. Kállay, C. Michauk, P. G. Szalay, A. G. Császár, J. Gauss and J. F. Stanton, J. Chem. Phys., 2006, 125, 64108 CrossRef PubMed.
- M. E. Harding, J. Vázquez, B. Ruscic, A. K. Wilson, J. Gauss and J. F. Stanton, J. Chem. Phys., 2008, 128, 114111 CrossRef PubMed.
- J. M. L. Martin and G. de Oliveira, J. Chem. Phys., 1999, 111, 1843 CrossRef CAS PubMed.
- A. D. Boese, M. Oren, O. Atasoylu, J. M. L. Martin, M. Kallay and J. Gauss, J. Chem. Phys., 2004, 120, 4129–4141 CrossRef CAS PubMed.
- D. Feller, K. A. Peterson and B. Ruscic, Theor. Chem. Acc., 2013, 133, 1407 CrossRef.
- J. D. Cox, D. D. Wagman and V. A. Medvedev, CODATA Key Values for Thermodynamics, Hemisphere Publishing Corp., New York, 1989 Search PubMed.
- B. Ruscic, R. E. Pinzon, M. L. Morton, G. von Laszevski, S. J. Bittner, S. G. Nijsure, K. A. Amin, M. Minkoff and A. F. Wagner, J. Phys. Chem. A, 2004, 108, 9979–9997 CrossRef CAS.
- B. Ruscic, R. E. Pinzon, G. V. Laszewski, D. Kodeboyina, A. Burcat, D. Leahy, D. Montoy and A. F. Wagner, J. Phys.: Conf. Ser., 2005, 16, 561–570 CrossRef CAS.
- M. W. Chase, J. Phys. Chem. Ref. Data, Monogr., 1998, 9, 1–1951 Search PubMed.
- NIST Computational Chemistry Comparison and Benchmark Database, NIST Standard Reference Database Number 101 Release 16a, ed. R. D. Johnson III, 2013 Search PubMed.
- G. D. Purvis, J. Chem. Phys., 1982, 76, 1910 CrossRef CAS PubMed.
- K. Raghavachari, G. W. Trucks, J. A. Pople and M. Head-Gordon, Chem. Phys. Lett., 1989, 157, 479–483 CrossRef CAS.
- J. F. Stanton, Chem. Phys. Lett., 1997, 281, 130–134 CrossRef CAS.
- CFOUR, a quantum chemical program package written by J. F. Stanton, J. Gauss, M. E. Harding, P. G. Szalay with contributions from A. A. Auer, R. J. Bartlett, U. Benedikt, C. Berger, D. E. Bernholdt, Y. J. Bomble, L. Cheng, O. Christiansen, M. Heckert, O. Heun, C. Huber, T.-C. Jagau, D. Jonsson, J. Jusélius, K. Klein, W. J. Lauderdale, D. A. Matthews, T. Metzroth, L. A. Mück, D. P. O'Neill, D. R. Price, E. Prochnow, C. Puzzarini, K. Ruud, F. Schiffmann, W. Schwalbach, C. Simmons, S. Stopkowicz, A. Tajti, J. Vázquez, F. Wang, J. D. Watts and the integral packages MOLECULE (J. Almlöf and P. R. Taylor), PROPS (P. R. Taylor), ABACUS (T. Helgaker, H. J. Aa. Jensen, P. Jørgensen, and J. Olsen), and ECP routines by A. V. Mitin and C. van Wüllen. For the current version, see http://www.cfour.de.
- J. Noga and R. J. Bartlett, J. Chem. Phys., 1987, 86, 7041 CrossRef CAS PubMed.
- G. E. Scuseria and H. F. Schaefer III, Chem. Phys. Lett., 1988, 152, 1–5 CrossRef.
- J. D. Watts and R. J. Bartlett, J. Chem. Phys., 1990, 93, 6104 CrossRef CAS PubMed.
- Y. J. Bomble, J. F. Stanton, M. Kállay and J. Gauss, J. Chem. Phys., 2005, 123, 054101 CrossRef PubMed.
- S. A. Kucharski and R. J. Bartlett, Theor. Chim. Acta, 1991, 80, 387–405 CrossRef CAS.
- N. Oliphant and L. Adamowicz, J. Chem. Phys., 1991, 95, 6645 CrossRef CAS PubMed.
- S. A. Kucharski and R. J. Bartlett, J. Chem. Phys., 1992, 97, 4282 CrossRef CAS PubMed.
- M. Kállay and P. R. Surján, J. Chem. Phys., 2001, 115, 2945 CrossRef PubMed.
- S. Grimme, J. Chem. Phys., 2006, 124, 034108 CrossRef PubMed.
- T. Schwabe and S. Grimme, Phys. Chem. Chem. Phys., 2007, 9, 3397–3406 RSC.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, M. J. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador and E. Al., Gaussian 09 Revision D.01, 2009 Search PubMed.
- M. Valiev, E. J. Bylaska, N. Govind, K. Kowalski, T. P. Straatsma, H. Van Dam, D. Wang, J. Nieplocha, E. Apra, T. L. Windus and W. A. de Jong, Comput. Phys. Commun., 2010, 181, 1477–1489 CrossRef CAS PubMed.
- T. Dunning Jr., J. Chem. Phys., 1989, 90, 1007–1023 CrossRef PubMed.
- R. A. Kendall, T. H. Dunning Jr. and R. J. Harrison, J. Chem. Phys., 1992, 96, 6796–6806 CrossRef CAS PubMed.
- T. H. Dunning Jr, K. A. Peterson and A. K. Wilson, J. Chem. Phys., 2001, 114, 9244 CrossRef PubMed.
- W. A. de Jong, R. J. Harrison and D. A. Dixon, J. Chem. Phys., 2001, 114, 48 CrossRef CAS PubMed.
- K. A. Peterson and T. H. Dunning Jr, J. Chem. Phys., 2002, 117, 10548 CrossRef CAS PubMed.
- J. D. Watts, J. Gauss and R. J. Bartlett, J. Chem. Phys., 1993, 98, 8718 CrossRef CAS PubMed.
- V. Barone, J. Chem. Phys., 2005, 122, 14108 CrossRef PubMed.
- M. Biczysko, P. Panek, G. Scalmani, J. Bloino and V. Barone, J. Chem. Theory Comput., 2010, 6, 2115–2125 CrossRef CAS.
- K. K. Irikura, J. Phys. Chem. Ref. Data, 2007, 36, 389 CrossRef CAS PubMed.
- NIST Chemistry WebBook, NIST Standard Reference Database Number 69, ed. P. J. Linstrom and W. G. Mallard, National Institute of Standards and Technology, Gaithersburg MD, 20899, http://webbook.nist.gov, (accessed September, 2012) Search PubMed.
- G. Herzberg, Molecular Spectra and Molecular Structure. – Spectra of Diatomic Molecules, Krieger Publishing Company, Malabar, Florida, 2nd edn, 1989, vol. 1, p. 660 Search PubMed.
- T. L. Hill, An Introduction to Statistical Thermodynamics, Dover Publications, Inc., New York, 1986, p. 508 Search PubMed.
- S. A. Kucharski and R. J. Bartlett, Chem. Phys. Lett., 1989, 158, 550–555 CrossRef CAS.
- W. Klopper, Mol. Phys., 2001, 99, 481–507 CrossRef CAS.
- A. Karton and J. M. L. Martin, Theor. Chem. Acc., 2005, 115, 330–333 CrossRef PubMed.
- F. Jensen, Theor. Chem. Acc., 2005, 113, 267–273 CrossRef CAS PubMed.
- F. Jensen, Theor. Chem. Acc., 2005, 113, 187–190 CrossRef CAS PubMed.
- W. Klopper, J. Noga, H. Koch and T. Helgaker, Theor. Chem. Acc., 1997, 97, 164–176 CrossRef CAS.
- J. M. L. Martin and P. R. Taylor, J. Chem. Phys., 1997, 106, 8620 CrossRef CAS PubMed.
- A. Halkier, T. Helgaker, P. Jørgensen, W. Klopper, H. Koch, J. Olsen and A. K. Wilson, Chem. Phys. Lett., 1998, 286, 243–252 CrossRef CAS.
- D. Feller, K. A. Peterson and T. D. Crawford, J. Chem. Phys., 2006, 124, 054107 CrossRef PubMed.
- A. Halkier, W. Klopper, T. Helgaker, P. Jørgensen and P. R. Taylor, J. Chem. Phys., 1999, 111, 9157 CrossRef CAS PubMed.
- K. L. Bak, P. Jørgensen, J. Olsen, T. Helgaker and W. Klopper, J. Chem. Phys., 2000, 112, 9229–9242 CrossRef CAS PubMed.
- M. Reiher, Theor. Chem. Acc., 2006, 116, 241–252 CrossRef CAS PubMed.
- M. Douglas and N. M. Kroll, Ann. Phys., 1974, 82, 88–155 Search PubMed.
- B. Hess, Phys. Rev. A: At., Mol., Opt. Phys., 1985, 32, 756–763 CrossRef CAS.
- B. Hess, Phys. Rev. A: At., Mol., Opt. Phys., 1986, 33, 3742–3748 CrossRef CAS.
- G. Jansen and B. Hess, Phys. Rev. A: At., Mol., Opt. Phys., 1989, 39, 6016–6017 CrossRef.
- L. Visscher and K. Dyall, At. Data Nucl. Data Tables, 1997, 67, 207–224 CrossRef CAS.
- C. E. Moore, Atomic Energy Levels, National Bureau of Standards, Washington, D.C., 1971, vol. I and II Search PubMed.
- D. Feller, K. A. Peterson, W. A. de Jong and D. A. Dixon, J. Chem. Phys., 2003, 118, 3510 CrossRef CAS PubMed.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785 CrossRef CAS.
- A. D. Becke, J. Chem. Phys., 1993, 98, 1372–1377 CrossRef CAS PubMed.
- T. H. Dunning Jr. and P. J. Hay, Methods Electron. Struct. Theory, 1977, vol. 3, p. 462 Search PubMed.
- L. R. Kahn, P. Baybutt and D. G. Truhlar, J. Chem. Phys., 1976, 65, 3826 CrossRef CAS PubMed.
- Y. S. Lee, W. C. Ermler and K. S. Pitzer, J. Chem. Phys., 1977, 67, 5861 CrossRef CAS PubMed.
- P. A. Christiansen, Y. S. Lee and K. S. Pitzer, J. Chem. Phys., 1979, 71, 4445 CrossRef CAS PubMed.
- L. F. Pacios and P. A. Christiansen, J. Chem. Phys., 1985, 82, 2664 CrossRef PubMed.
- M. M. Hurley, L. F. Pacios, P. A. Christiansen, R. B. Ross and W. C. Ermler, J. Chem. Phys., 1986, 84, 6840 CrossRef CAS PubMed.
- J. Gauss, A. Tajti, M. Kállay, J. F. Stanton and P. G. Szalay, J. Chem. Phys., 2006, 125, 144111 CrossRef PubMed.
- L. A. Curtiss, K. Raghavachari, P. C. Redfern and J. A. Pople, J. Chem. Phys., 1997, 106, 1063 CrossRef CAS PubMed.
- A. Karton, A. Tarnopolsky, J.-F. Lamère, G. C. Schatz and J. M. L. Martin, J. Phys. Chem. A, 2008, 112, 12868–12886 CrossRef CAS PubMed.
- C. J. Cramer, Essentials of Computational Chemistry Theories and Models, John Wiley & Sons Inc., 2nd edn, 2004, p. 618 Search PubMed.
- K. A. Peterson, S. Skokov and J. M. Bowman, J. Chem. Phys., 1999, 111, 7446 CrossRef CAS PubMed.
- R. Ashby, J. Mol. Spectrosc., 1967, 23, 439–447 CrossRef CAS.
- R. A. Ashby, J. Mol. Spectrosc., 1971, 40, 639–640 CrossRef CAS.
- K. Hedberg and R. M. Badger, J. Chem. Phys., 1951, 19, 508 CrossRef CAS PubMed.
- B. Ruscic, R. E. Pinzon, M. L. Morton, N. K. Srinivasan, M.-C. Su, J. W. Sutherland and J. V. Michael, J. Phys. Chem. A, 2006, 110, 6592–6601 CrossRef CAS PubMed.
- P. A. Denis, J. Phys. Chem. A, 2006, 110, 5887–5892 CrossRef CAS PubMed.
- Y. Koga, H. Takeo, S. Kondo, M. Sugie, C. Matsumura, G. McRae and E. Cohen, J. Mol. Spectrosc., 1989, 138, 467–481 CrossRef CAS.
- G. McRae and E. Cohen, J. Mol. Spectrosc., 1990, 139, 369 CrossRef CAS.
- I. Barnes, V. Bastian, K. Becker, R. Overath and T. Zhu, Int. J. Chem. Kinet., 1989, 21, 499 CrossRef CAS.
- M. D. Liptak and G. C. Shields, Int. J. Quantum Chem., 2001, 85, 727–741 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c4cp03987d |
| ‡ EAWAG, Swiss Federal Institute of Aquatic Science and Technology, Dübendorf, Switzerland. |
| This journal is © the Owner Societies 2015 |
