Baseline correction using adaptive iteratively reweighted penalized least squares
Zhi-Min
Zhang
,
Shan
Chen
and
Yi-Zeng
Liang
*
College of Chemistry and Chemical Engineering, Research Center of Modernization of Chinese Medicines, Central South University, Changsha, 410083, P.R. China. E-mail: yizeng_liang@263.net
First published on 19th February 2010
Abstract
Baseline drift always blurs or even swamps signals and deteriorates analytical results, particularly in multivariate analysis. It is necessary to correct baseline drift to perform further data analysis. Simple or modified polynomial fitting has been found to be effective to some extent. However, this method requires user intervention and is prone to variability especially in low signal-to-noise ratio environments. A novel algorithm named adaptive iteratively reweighted Penalized Least Squares (airPLS) that does not require any user intervention and prior information, such as peak detection etc., is proposed in this work. The method works by iteratively changing weights of sum squares errors (SSE) between the fitted baseline and original signals, and the weights of the SSE are obtained adaptively using the difference between the previously fitted baseline and the original signals. The baseline estimator is fast and flexible. Theory, implementation, and applications in simulated and real datasets are presented. The algorithm is implemented in R language and MATLAB™, which is available as open source software (http://code.google.com/p/airpls).
Introduction
Some signals of analytical instruments, such as chromatography, nuclear magnetic resonance (NMR) and vibrational spectroscopy, basically consist of chemical information, baseline and random noises. However, the existence of the baseline and random noises can negatively affect qualitative or quantitative analytical results, since the baseline always appears as a sample-independent smooth curve. It should be fitted and corrected routinely to mitigate the negative influence. Conventionally, analysts manually point out the two ends of a signal peak, and fit a curve as the baseline using piecewise linear approximation. However, manual piecewise linear approximation is not so effective and its accuracy clearly depends on the user's experience.1 Hence, numerous algorithms have been proposed to make a better estimate of the baseline, and literature on this topic is scattered across many fields, mainly including chromatography,2–6 vibrational spectroscopy7–13 and NMR.14–16In order to improve the signal detection and resolution of chemical components with very low concentrations, Liang et al.2 introduced the roughness penalty method to reduce the influence of this measurement noise. Shao et al.3,4 proposed a novel algorithm which relied on wavelet transform in denoising, baseline correction and determination of component number in overlapping chromatograms. Boelens et al.5 applied asymmetric least squares regression to correct the measured spectra during elution for the background contribution. A method for preprocessing pyrolysis-gas chromatography-differential mobility spectrometry (Py-GC-DMS) data via asymmetric least square (ALS) to remove any unavoidable baseline shifts was also proposed by Cheung et al.6
Using techniques of robust local regression to estimate baselines in spectra, Ruckstuhl et al.7 introduced novel robust baseline estimation. Schechter8 suggested a method to correct for fluctuating nonlinear background in near infrared spectroscopy. Lieber et al.9 described a modification to least-squares polynomial curve fitting to avoid shortcomings of simple curve fitting. By designing and minimizing a non-quadratic cost function, Mazet et al.10 removed Infrared and Raman spectra background fast and simply. Zhao et al.11 developed an improved automated algorithm for fluorescence removal based on modified multi-polynomial fitting with a peak-removal procedure during the first iteration and a statistical method to account for signal noise effects. Morh12 presented sensitive nonlinear iterative peak clipping algorithms to estimate background in various kinds of spectra. Zhang et al.13 suppressed fluorescent background in Raman spectroscopy using a wavelet and penalized least squares algorithm.
Golotvin14 presented a new approach to baseline correction using a smoothed NMR spectrum for both baseline area recognition and modeling. Cobas et al.15 recognized signal-free regions using a continuous wavelet transform (CWT) derivative calculation and fitted baseline based on the Whittaker smoother algorithm. Chang et al.16 designed a robust baseline correction algorithm for signal dense NMR spectra.
In sum, simple or modified polynomial fitting,1,9,11,17–19 penalized or weighted least square,2,5,6,9,10,13,15,20,21 wavelet,3,4,13,22–24 derivatives,13,19,25 and robust local regression7 are frequently used for baseline correction in analytical chemistry. However, each of them has some drawbacks in certain aspects: (1) Simple manual polynomial fitting is not so effective and its accuracy clearly depends on the user's experience;1,13 the modified polynomial fitting methods overcome drawbacks of their predecessor, but their performances are poor in low signal-to-noise and signal-to-background ratio environments.11,13 (2) Penalized least square was initially proposed for smoothing, which relies on peak detection and is prone to produce negative regions in complex signals.13,15,26 (3) Wavelet baseline correction algorithms always suppose that the baseline is well separated in the transformed domain from the signal, but real-world signals do not agree with this hypothesis.24,27 (4) Derivative algorithms change original peak shapes after the correction, which may cause difficulty in the interpretation of the preprocessed spectra.19 (5) Robust local regression requires that the baseline must be smooth and vary slowly, and it also needs to specify the bandwidth and the tuning parameters by the user.7 (6) The baseline Wavelet package13 can't process signals large than 5000 variables in Windows XP®, because there are no appropriate sparse matrix and corresponding linear algebra library in R language.
In this paper, a fast and flexible baseline fitting algorithm is proposed, which relies on adaptive iteratively reweighted penalized least squares (airPLS). An iteratively reweighted procedure is executed to gradually approximate a complex baseline. The weights of iteration are obtained adaptively using SSE between a previously fitted baseline and the original signals. In order to control the smoothness of the fitted baseline, a penalty approach is introduced based on sum squared derivatives of the fitted baseline. The proposed algorithm is intuitional and effective. It can be implemented in less than a 50 lines code in MATLAB® and R language. Since the MATLAB® version is implemented based on sparse matrices and is extremely fast, it is recommended to users.
The paper is organized as follows. Statistical concepts, relevant to the airPLS algorithm, are presented and investigated in the theory section. Then, the airPLS algorithm is applied to simulated data, chromatograms, Raman spectra and NMR signals to demonstrate its performance. Results of the above applications will be presented together with discussions about the proposed algorithm. Finally, some conclusions and perspectives are given in the conclusion section.
Theory
Penalized least squares algorithm
The penalized least squares algorithm is a flexible smoothing method published by Whittaker in 1922.28 Later, Silverman29,30 developed a new smoothing technique in statistics, which was called the roughness penalty method. The penalized least squares algorithm can be regarded as roughness penalty smooth by least squares, which balanced between fidelity to the original data and the roughness of the fitted data. Liang et al.2 introduced it into chemistry as a smoothing technique to improve the signal detection and resolution of chemical components with very low concentrations in hyphenated chromatographic two-way data. Recently, Eilers extended its application scopes to general chemical signal smoothing,26 peak aligning21 and baseline correction.20Assuming x is the vector of the analytical signals, and z is the fitted vector. The lengths of them are both m. The fidelity of z to x can be expressed as the sum square errors between them:
 | (1) |
The roughness of the fitted data z can be written as its squared and summed differences,
 | (2) |
The first differences penalty is adopted to simplify the presentation here. In most cases, the square of the second differences penalties can be a natural way to quantify the roughness.30 The airPLS package offers a parameter for users to choose the orders of the differences.
The balance of fidelity and smoothness can be then measured as the fidelity plus with penalties on the roughness, and it can be given by:
| Q = F + λR = ‖x − z‖2 + λ‖Dz‖2 | (3) |
By finding the vector of partial derivatives and equating it to 0 ( ), we get a linear system of equations that can be easily solved:
), we get a linear system of equations that can be easily solved:
| (I + λD'D)z = x | (4) |
Eqn (4) is a smooth method using the penalized least squares algorithm. In order to correct a baseline using the penalized least squares algorithm, Cobas15 and Zhang13 introduced a weight vector of fidelity, and set zero to the weights vector at a position corresponding to peak segments of x. Fidelity of z to x is changed to
 | (5) |
The eqn (4) changes to
| (W + λD'D)z = Wx | (6) |
Solving the above linear equations, the fitted vector can be obtained easily:
| z = (W + λD'D)−1Wx | (7) |
The baseline correction methods of Cobas15 and Zhang13 both need peak detection before baseline correction, but the existence of a baseline will negatively affect peak detection. Zhang et al. overcame this dilemma by transforming the spectrum into a wavelet space, and finding peaks in the wavelet space. The algorithm proposed by Cobas will produce a negative part when the baseline is complex, and Zhang et al. did some special treatments to some special peak regions, such as peaks with shoulders, overlapping peaks etc., to avoid the appearance of negative parts.13 The algorithm proposed by Zhang et al. is accurate but time consuming, using wavelet transformation and special treatments. One can bear half a minute per spectrum when applied to one-dimension spectra. However, when applied to two-dimensional datasets such as GC-MS and HPLC-DAD, it can't finish correcting one dataset even in an hour. The adaptive iteratively reweighted procedure is proposed to replace peak detection and special treatment steps.
Adaptive iteratively reweighted procedure
Without setting zeros to the weight vector at positions corresponding to peak segments, the penalized least squares algorithm can be certainly categorized as a smoothing algorithm. Eilers20,21 proposed a novel and effective baseline correction algorithm based on asymmetric least squares,31 which means asymmetric weights of least squares. However, it has some drawbacks. Firstly two parameters, namely asymmetry and smoothing parameters, need to be optimized to obtain a satisfactory result. Secondly asymmetry parameters are all the same for all the baseline region points, but we think that the weights of the baseline region should set different values according to the differences between the previously fitted baseline and the original signals.The adaptive iteratively reweighted procedure is similar to the weighted least squares and iteratively reweighted least squares,32–34 but using different ways to calculate the weights and adding a penalty item to control the smoothness of the fitted baseline. Each step of the proposed adaptive iteratively reweighted procedure involves solving a weigthed penalized least squares problem of the following form:
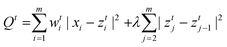 | (8) |
The weight vector w is obtained adaptively using an iterative method. One should give an initial value w0 = 1 at the starting step. After initialization, the w of each iterative step t can be obtained using the following expressions:
 | (9) |
Vector dt consists of negative elements of the differences between x and zt−1 in the t iteration step.
The fitted value zt−1 in the previous (t − 1) iteration is a candidate of baseline. If the value of the ith point is greater than the candidate of baseline, it can be regarded as part of a peak. So its weight is set to zero to ignore it at the next iteration of fitting. In the airPLS algorithm, the iterative and reweight methods are used to automatically and gradually eliminate the points of peaks and preserve the baseline points in the weight vector w.
Iteration will stop either with the maximal iteration times or when the terminative criterion is reached. The termination criterion is defined by:
| |dt| < 0.001 × |x| | (10) |
The flow chart describing the architecture of the proposed algorithm is shown in Fig. 1.
 | ||
| Fig. 1 Flow chart describing the framework of the airPLS algorithm. | ||
Experimental section
Chromatography, Raman and NMR are crucial analytical instruments, whose analytical results are impaired by the appearance of baselines. The airPLS algorithm is applied to them to demonstrate its performance. But the experimental section initially starts with the simulated data with known peak heights.Simulated data
Simulated data consist of linear or curved baselines, analytical signals, and random noise, which can be mathematically described as follows| s(x) = p(x) + b(x) + n(x) | (11) |
Pure signals are three Gaussian peaks with different intensity (listed in Table 1), means and variances. The curved baseline is a sin curve. Random noise n(x) is generated using the random number generator (the rnorm() function of R language), whose intensity is about 1 percent of the simulated signals.
| Ratio of methanol | Added volume of methanol/mL | Added volume of acetonitrile/mL | Added volume of distilled water/mL |
|---|---|---|---|
| a When different volumes of acetonitrile and distilled water were added, the baselines were different. | |||
| 0.01 | 0.5 | 0/10/20 | 49.5/39.5/29.5 |
| 0.04 | 2 | 0/10/20 | 48/38/28 |
| 0.07 | 3.5 | 0/10/20 | 46.5/36.5/26.5 |
| 0.1 | 5 | 0/10/20 | 45/35/25 |
| 0.13 | 6.5 | 0/10/20 | 43.5/33.5/23.5 |
| 0.16 | 8 | 0/10/20 | 42/32/22 |
| 0.2 | 10 | 0/10/20 | 40/30/20 |
| 0.23 | 11.5 | 0/10/20 | 38.5/28.5/18.5 |
| 0.26 | 13 | 0/10/20 | 37/27/17 |
| 0.3 | 15 | 0/10/20 | 35/25/15 |
| 0.33 | 16.5 | 0/5/10 | 33.5/28.5/22.5 |
| 0.36 | 18 | 0/5/10 | 32/27/22 |
| 0.4 | 20 | 0/5/10 | 30/25/20 |
| 0.43 | 21.5 | 0/5/10 | 28.5/23.5/18.5 |
| 0.46 | 23 | 0/5/10 | 27/22/17 |
| 0.5 | 25 | 0/5/10 | 25/20/15 |
| 0.53 | 26.5 | 0/5/10 | 23.5/18.5/13.5 |
| 0.56 | 28 | 0/5/10 | 22/17/12 |
| 0.6 | 30 | 0/5/10 | 20/15/10 |
| 0.63 | 31.5 | 0/5/10 | 18.5/13.5/8.5 |
| 0.66 | 33 | 0/2/5 | 17/15/12 |
| 0.7 | 35 | 0/2/5 | 15/13/10 |
| 0.73 | 36.5 | 0/2/5 | 13.5/11.5/8.5 |
| 0.76 | 38 | 0/2/5 | 12/10/7 |
| 0.8 | 40 | 0/2/5 | 10/8/5 |
| 0.83 | 41.5 | 0/2/5 | 8.5/6.5/3.5 |
| 0.86 | 43 | 0/2/5 | 7/5/2 |
| 0.9 | 45 | 0/2/5 | 5/3/0 |
| 0.93 | 46.5 | 0/1/3.5 | 3.5/2.5/0 |
| 0.96 | 48 | 0/1/2 | 2/1/0 |
| 0.99 | 49.5 | 0/0.25/0.5 | 0.5/0.25/0 |
| 1.00 | 50 | 0 | 0 |
Simulated data are illustrated in Fig. 2. The pure signals can be seen in Fig. 2(a). Fig. 2(b) and Figure 2(c) are pure signals with linear and curved baseline, respectively.
 | ||
| Fig. 2 Simulated data. (a) Pure signal of three Gaussian peaks; (b) pure signal with linear background and random noise; (c) pure signal with curved background and random noise. | ||
Chromatograms
Chromatograms, analyses of the Red Peony Root using HPLC-DAD, were selected to test the proposed algorithm. 8 of Red Peony Root were collected from different producing areas in China, and a standard sample was also bought from the National Institute for control of Pharmaceutical and Biological Products. The experiments were performed at Chromap Co., Ltd Zhuhai, China. 2 UV spectra per second from 200 nm to 600 nm with a bandwidth of 4 nm resulted in 100 data points in each UV spectrum, then the “most peaks rich” wavelength 230 nm was selected. The data were transformed into ASCII format using HP chemstations (version A.09.01) for further analysis. The chromatograms can be seen in Fig. 3. The standard chromatogram is illustrated in Fig. 3(a). 8 chromatograms were plotted in Fig. 3(b), and one can obviously see that the baseline drifts vary from sample to sample. | ||
| Fig. 3 Chromatograms of Red Peony Root to correct. (a) Standard chromatogram. (b) Chromatograms of Red Peony Root were collected from different producing areas. | ||
Raman spectra of medicines tablets for classification
Prednisone Acetate Tablets (PATs) and Glibenclamide Tablets (GTs) were measured using a laser of 785 nm wavelength for excitation by BWTEK i-Raman-785 spectrometer with a 2048 elements thermoelectric cooled linear charge-coupled device (TEC-CCD) arrays. PATs, from 10 different pharmaceutical factories, were recorded using 5000 ms integration times. GTs, from 6 different pharmaceutical factories, were also recorded using 5000 ms integration times to obtain comparable spectra. Since we measured 3 Tablets for each pharmaceutical factory, there are 48 Raman spectra in total.Raman spectra of methanol solutions for regression
Raman spectra for regression were used of ternary mixtures of methanol, acetonitrile and distilled water. Table 1 shows the 94 different combinations of volumes which were measured using a laser of 785 nm wavelength for excitation by BWTEK i-Raman-785 spectrometer too. All the spectra were also recorded using 7500 ms integration times to obtain comparable spectra. A baseline-correction of the 94 spectra was also performed using three different baseline-correction methods. Then, partial least squares (PLS) and cross-validation by the leave-one-out (LOOCV) methods were applied in order to evaluate the regression models and baseline-correction methods.NMR
Performance of the proposed baseline correction algorithms was also tested on NMR signals. NMR signals are available from ref. 35.Result and discussion
Comparison with other algorithms using simulated results
The subtraction of linear and curved baselines has been done using the proposed airPLS algorithm, the fully automatic baseline-correction procedure of Carlos Cobas15 (short for FABC algorithm) and Asymmetric Least Squares baseline correction of P. H. C Eilers20,21 (short for ALS algorithm). The corrected results of the airPLS algorithm can be seen in Fig. 4. Both linear and curved baselines are removed successfully, which has proven the flexibility of the airPLS algorithm. One can also see that both the linear and curved baselines are fitted only in three iterations. It means that the airPLS algorithm converges swiftly. Because simulated data are constructed using three known Gaussian peaks, the expected heights of peaks are also known. Hence heights before and after correction are compared to the expected heights. The comparison results of the FABC algorithm, the ALS algorithm and the airPLS algorithm are shown in Table 2. The airPLS algorithm corrected the linear baseline accurately, especially for the small peaks. In the curved baseline, the airPLS algorithm corrected the baseline as well as the FABC algorithm and the ALS algorithm for the large peaks, but with a much better result for the small peak. One can infer from Table 2 that the airPLS algorithm corrected the baseline as well as the other algorithm for large peaks, but much better than the FABC and ALS algorithm for small peaks which were swamped by either linear or curved baselines.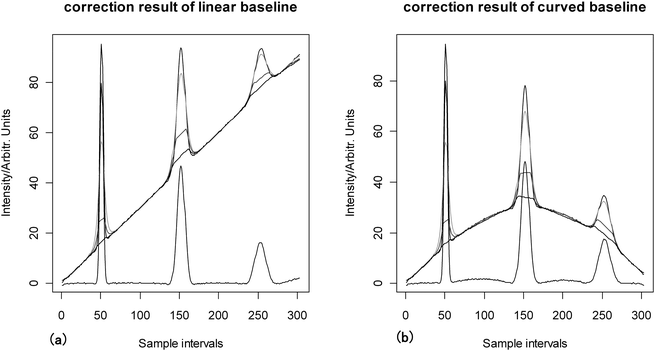 | ||
| Fig. 4 Correction results of simulated data with different baselines, the iteration steps are illustrated using gray colors. (a) Linear baseline, (b) curved baseline. | ||
| Baseline type | Peak ID | Peak Height | ||||
|---|---|---|---|---|---|---|
| Uncorrected | Expected | FABCa | ALSb | airPLSc | ||
| a Parameters for the FABC method: a = 10, lambda = 10. b Parameters for the ALS method: lambda = 10, p = 0.001, d = 2. c Parameters for the airPLS method: lambda = 10. | ||||||
| linear | Peak 1 | 94.45 | 79.78 | 79.71 | 77.83 | 79.97 |
| Peak 2 | 78.06 | 47.87 | 48.40 | 38.25 | 48.29 | |
| Peak 3 | 34.73 | 17.09 | 6.077 | 10.89 | 17.42 | |
| curved | Peak 1 | 95.10 | 79.78 | 79.59 | 77.83 | 79.55 |
| Peak 2 | 93.70 | 47.87 | 47.73 | 38.25 | 46.60 | |
| Peak 3 | 93.38 | 17.09 | 6.505 | 10.89 | 16.26 | |
Result of chromatograms
8 HPLC chromatograms of Red Peony Root were corrected using λ = 30. Fig. 5 is the corrected chromatograms. As there was a standard chromatogram, principle component analysis (PCA) was applied to the matrix consisting of original, corrected and standard chromatograms. Then the scores of the first and the second principle components were plotted in Fig. 6 to investigate the influences on clustering analysis of the proposed airPLS algorithm. In Fig. 6, circle means standard chromatograms; plus signs mean corrected chromatograms; and triangles mean original chromatograms. Since movement trends of points are indicated using arrows in Fig. 6, one can obviously observe that corrected chromatograms tend to approach the standard chromatogram after correction. It can demonstrate the validity of the airPLS algorithm. The corrected chromatograms were more compact in pattern space and closer to the standard chromatogram. The compactness and closeness in principle components pattern space would improve clustering and classification results to some extent. | ||
| Fig. 5 Correction results of chromatograms of Red Peony Root. | ||
 | ||
| Fig. 6 First two principal components of the PCA scores of original, corrected and standard chromatograms. Circle means standard; Plus signs mean corrected; and Triangles mean original. Movement trends are marked out with arrows. | ||
Classification of Raman spectra of medicine tablets
The proposed airPLS algorithm was applied to Raman spectra of PATs and GTS with highly fluorescent baselines. All the baselines of 48 spectra of tablets from different factories were removed successfully (see Fig. 7). PCA was used to investigate the classification result of the proposed airPLS algorithm. In the first case, PCA was performed on the matrix consisting of original spectra. The first two principal components were taken out and plotted in Fig. 8(a). One can see that PATs samples and GTs samples were mixed in the principal component spaces, which means that the classification result is not satisfied. Then PCA was also performed with the same spectra, but they were preprocessed by the airPLS algorithm to remove baselines. Fig. 8(b) is the scatter-plots of the two principal components. One can see that the classification result is obviously improved, which is attributed to the airPLS algorithm. In summary, the airPLS algorithm could correct the baseline effectively with reserving primary useful information, which is good for classification. | ||
| Fig. 7 Baseline-correction results of the Raman spectra of PATs and GTs. (a) And (c) are original spectra. (b) And (d) are corrected ones. | ||
 | ||
| Fig. 8 Plots of PCA scores. (a) First two principal components of the PCA score of the original spectra without any preprocessing. (b) First four principal components of the PCA score of the corrected spectra. The ijth scatter plot contains PCi plotted against PCj. | ||
Comparison of regression results of methanol solutions
Before, the PLS and LOOCV methods were used to evaluate the regression models and baseline-correction algorithms. The FABC algorithm, the ALS algorithm and the airPLS algorithm were applied to the 94 spectra to remove the baselines. Then three corrected spectra datasets were obtained using these three different baseline-correction algorithms. The PLS regression models were built with the three corrected spectra datasets to calculate the value of R2 and evaluate the fitting abilities of models. In order to estimate the predictive abilities of the three models, the LOOCV method was also used to calculate the Q2 and Root mean square error of cross validation (RMSECV). The R2, Q2 and RMSECV were listed in Table 3. The values of R2, Q2 and RMSECV of regression models pretreated by the airPLS algorithm were evidently better than those pretreated by FABC, ALS and uncorrected, especially when the principal number is small.| Correction algorithm | Parameters | Number of principal components | ||||
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| a Only 5 principal components were used, because we know that the methanol solutions were ternary mixtures. | ||||||
| Uncorrected | R2 | 0.9156 | 0.9932 | 0.9965 | 0.9975 | 0.9990 |
| Q2 | 0.9117 | 0.9928 | 0.9961 | 0.9973 | 0.9989 | |
| RMSECV | 0.1739 | 0.0261 | 0.0186 | 0.0156 | 0.0099 | |
| FABC | R2 | 0.9370 | 0.9680 | 0.9840 | 0.9902 | 0.9933 |
| Q2 | 0.9353 | 0.9658 | 0.9699 | 0.9803 | 0.9908 | |
| RMSECV | 0.0931 | 0.0554 | 0.0519 | 0.0426 | 0.0286 | |
| ALS | R2 | 0.9588 | 0.9951 | 0.9968 | 0.9984 | 0.9990 |
| Q2 | 0.9581 | 0.9946 | 0.9970 | 0.9982 | 0.9988 | |
| RMSECV | 0.0724 | 0.0225 | 0.0166 | 0.0128 | 0.0104 | |
| airPLS | R2 | 0.9705 | 0.9973 | 0.9975 | 0.9983 | 0.9991 |
| Q2 | 0.9702 | 0.9971 | 0.9973 | 0.9982 | 0.9989 | |
| RMSECV | 0.0668 | 0.0160 | 0.0156 | 0.0131 | 0.0098 | |
Result obtained from NMR signals
The performance of the proposed approach was also tested on the NMR signal described in the experimental section. This NMR signal is used to test the performance of the airPLS algorithm on high-throughput data, which has approximately 16500 variables. A satisfactory correction result could be obtained with λ = 500. One can see that 6 iterations were accomplished to fit the final baseline in Fig. 9. The execution was only 0.2340 s, which means that the airPLS algorithm is extremely fast. It is the magic of the sparse matrix. | ||
| Fig. 9 Baseline-correction results of NMR signal with 16384 variables. | ||
Tuning λ to obtain a better estimation of the baseline
The λ parameter should be tuned to obtain a better estimation of the real baseline. Since λ varies from 1 to 109, the common grid searching method will fail in this situation. Eilers20 recommended searching for the optimal λ on a grid that is approximately linear for logλ. If λ is too large, the fitted baseline will be too flat. If λ is too small, the fitted baseline will be too flexible to include the peak parts. Because there are significant differences when λ is too large or too small, one can optimize the parameter manually using a method like binary search algorithm. Start with λ = 1, and multiply λ by 10 when the fitted baseline is too flexible and includes some parts of the peaks. If λ is large enough and the fitted baseline is flatter than the real baseline, stop multiplying λ by 10 and search for the optimal λ in the region using binary search until satisfactory.We have implemented this airPLS algorithm in C++ and MFC to provide a better user interface for baseline-correction. One can tune the lambda parameter by dragging the slider easily.
Speed issue and expansibility
The 165000 variables NMR signal is used to test the speed of the proposed algorithm. The result showed that the airPLS algorithm is amazingly fast. It can finish six iterations in only 0.2340 s. The number of variables, total execution time, iteration times and execution time per iteration of simulated data, chromatograms, Raman spectra and NMR signal are listed in Table 4. One could infer from the table that the airPLS algorithm is extremely fast even for large datasets with sixteen thousand variables. The relationship between number of variables and execution time per iteration was investigated in detail. It was found that the execution time per iteration is exactly a linear relationship with the number of variables, which can be seen in Fig. 10. The exactly linear relationship between the number of variables and the execution time per iteration guarantees the performance of the airPLS algorithm in data with even more number of variables. This is mainly attributed to the use of a sparse matrix. One could also infer from Table 4 that the airPLS algorithm converges swiftly in only several iterations, which is mainly attributed to the exponential reweigh strategy. It could be concluded that the use of sparse matrix and exponential reweigh strategy enable the application of the airPLS algorithm in more high-throughput domain and two dimensional datasets (such as GC-MS and HPLC-DAD). | ||
| Fig. 10 Relation between number of variables and execution time per iteration. | ||
| Dataset | number of variables | total execution time(s) | iteration times | execution time per iteration(s) |
|---|---|---|---|---|
| a Different datasets were used to deduce the relationship between the execution time per iteration and the number of variables. | ||||
| Simulated data | 603 | 0.0160 | 4 | 0.0040 |
| Raman spectra | 1751 | 0.0320 | 5 | 0.0064 |
| Chromatograms | 4000 | 0.0460 | 5 | 0.0092 |
| NMR signal | 16384 | 0.1880 | 6 | 0.0313 |
Conclusion
The airPLS algorithm provides a simple but flexible, valid and fast algorithm for estimating baselines in analytical chemistry. There is one crucial but intuitional parameter λ to control the smoothness of the fitted baseline. It gives extremely fast and accurate baseline corrected signals for both simulated and real signals. The successful results of the simulated and real signals have proven that the proposed approach can be applied to chromatograms, Raman spectra and NMR signals. Now the airPLS algorithm is being tested for correcting MALDI-TOF and GC-MS datasets and the results will be published elsewhere soon.Acknowledgements
This work is financially supported by the National Nature Foundation Committee of P.R. China (Grants No. 20875104 and Grants No. 10771217) and the international cooperation project on traditional Chinese medicines of the ministry of science and technology of China (Grant No. 2007DFA40680). The studies meet the approval of the university's review board. We are grateful to all employees of this institute for their encouragement and support of this research. Also, the authors want to thank Peishan Xie of Chromap Co., Ltd Zhuhai, China for providing the chromatograms dataset; Fei Ye, Hua Zhou (B&W Tek, Inc.), Zhao-xia Liu, Qi-Ming Zhang, Li-xia Ding (National Institute For The Control Of Pharmaceutical and Biological Products) for providing the Raman dataset. Hai Wu and Hui-ying Lv of the College of Chemistry and Chemical Engineering, Research Center of Modernization of Chinese Medicines, Central South University for providing the Raman spectra of the methanol solutions for regression.References
- A. Jirasek, G. Schulze, M. M. L. Yu, W. Blades and R. F. B. Turner, Appl. Spectrosc., 2004, 58, 1488–1499 CrossRef CAS
.
- Y. Z. Liang, A. K. M. Leung and F. T. Chau, J. Chemom., 1999, 13, 511–524 CrossRef CAS
.
- X. G. Shao, W. S. Cai and Z. X. Pan, Chemom. Intell. Lab. Syst., 1999, 45, 249–256 CrossRef CAS
.
- X. G. Shao, A. K. M. Leung and F. T. Chau, Acc. Chem. Res., 2003, 36, 276–283 CrossRef CAS
.
- H. F. M. Boelens, R. J. Dijkstra, P. H. C. Eilers, F. Fitzpatrick and J. A. Westerhuis, J. Chromatogr., A, 2004, 1057, 21–30 CrossRef CAS
.
- W. Cheung, Y. Xu, C. L. P. Thomas and R. Goodacre, Analyst, 2009, 134, 557–563 RSC
.
- A. F. Ruckstuhl, M. P. Jacobson, R. W. Field and J. A. Dodd, J. Quant. Spectrosc. Radiat. Transfer, 2001, 68, 179–193 CrossRef CAS
.
- I. Schechter, Anal. Chem., 2002, 67, 2580–2585
.
- C. A. Lieber and A. Mahadevan-Jansen, Appl. Spectrosc., 2003, 57, 1363–1367 CrossRef CAS
.
- V. Mazet, C. Carteret, D. Brie, J. Idier and B. Humbert, Chemom. Intell. Lab. Syst., 2005, 76, 121–133 CrossRef CAS
.
- J. Zhao, H. Lui, D. I. McLean and H. Zeng, Appl. Spectrosc., 2007, 61, 1225–1232 CrossRef CAS
.
- M. Morh and V. Matou?ek, Appl. Spectrosc., 2008, 62, 91–106 CrossRef
.
- Z. M. Zhang, S. Chen, Y. Z. Liang, Z. X. Liu, Q. M. Zhang, L. X. Ding, F. Ye and H. Zhou, J. Raman Spectrosc., 2009 DOI:10.1002/jrs.2500
.
- S. Golotvin and A. Williams, J. Magn. Reson., 2000, 146, 122–125 CrossRef CAS
.
- J. Carlos Cobas, M. A. Bernstein, M. Mart-Pastor and P. G. Tahoces, J. Magn. Reson., 2006, 183, 145–151 CrossRef CAS
.
- D. Chang, C. D. Banack and S. L. Shah, J. Magn. Reson., 2007, 187, 288–292 CrossRef CAS
.
- D. E. Brown, J. Magn. Reson., Ser. A, 1995, 114, 268–270 CrossRef CAS
.
- A. M. David and J. H. M. Halliday, J. Chemom., 1997, 11, 1–11 CrossRef CAS
.
- M. N. Leger and A. G. Ryder, Appl. Spectrosc., 2006, 60, 182–193 CrossRef CAS
.
- P. H. C. Eilers and H. F. M. Boelens, 2005, http://www.science.uva.nl/%7Ehboelens/publications/draftpub/Eilers_2005.pdf.
- P. H. C. Eilers, Anal. Chem., 2004, 76, 404–411 CrossRef CAS
.
- Z. Pan, X. Shao, H. Zhong, W. Liu, H. Wang and M. Zhang, Chin. J. Anal. Chem., 1996, 24, 149–153 CAS
.
- C. R. Mittermayr, H. W. Tan and S. D. Brown, Appl. Spectrosc., 2001, 55, 827–833 CrossRef
.
- Y. G. Hu, T. Jiang, A. G. Shen, W. Li, X. P. Wang and J. M. Hu, Chemom. Intell. Lab. Syst., 2007, 85, 94–101 CrossRef CAS
.
- C. D. Brown, L. Vega-Montoto and P. D. Wentzell, Appl. Spectrosc., 2000, 54, 1055–1068 CAS
.
- P. H. C. Eilers, Anal. Chem., 2003, 75, 3631–3636 CrossRef CAS
.
- F. Gan, G. Ruan and J. Mo, Chemom. Intell. Lab. Syst., 2006, 82, 59–65 CrossRef CAS
.
- E. T. Whittaker, P. Edinburgh Math. Soc., 1922, 41, 63–75 Search PubMed
.
-
P. J. Green and B. W. Silverman, Nonparametric regression and generalized linear models: a roughness penalty approach, Chapman & Hall/CRC, London, 1994 Search PubMed
.
-
J. O. Ramsay and B. W. Silverman, Functional data analysis, Springer, New York, 1998 Search PubMed
.
- W. K. Newey and J. L. Powell, Econometrica, 1987, 819–847 CrossRef
.
- P. W. Holland and R. E. Welsch, Commun. Stat. Theory Methods, 1977, 6, 813–827 CrossRef
.
-
D. B. Rubin, Iteratively reweighted least squares, Wiley, New York, 1983 Search PubMed
.
- P. J. Green, J.R. Stat. Soc. Ser. B Stat. Methodol., 1984, 149–192 Search PubMed
.
- T. Wang, K. Shao, Q. Chu, Y. Ren, Y. Mu, L. Qu, J. He, C. Jin and B. Xia, BMC Bioinformatics, 2009, 10, 83 CrossRef
.
| This journal is © The Royal Society of Chemistry 2010 |
