Interfacial self-assembly of SiO2–PNIPAM core–shell particles with varied crosslinking density†
Maret
Ickler
ab,
Johannes
Menath
 ab,
Laura
Holstein
ab,
Marcel
Rey
ab,
Laura
Holstein
ab,
Marcel
Rey
 abc,
D. Martin A.
Buzza
abc,
D. Martin A.
Buzza
 d and
Nicolas
Vogel
d and
Nicolas
Vogel
 *ab
*ab
aInstitute of Particle Technology (LFG), Friedrich-Alexander-Universität Erlangen-Nürnberg (FAU), Cauerstrasse 4, 91058 Erlangen, Germany. E-mail: Nicolas.Vogel@fau.de
bInterdisciplinary Center for Functional Particle Systems (FPS), Friedrich-Alexander-Universität Erlangen-Nürnberg (FAU), Haberstrasse 9a, 91058 Erlangen, Germany
cSchool of Physics & Astronomy, The University of Edinburgh, Peter Guthrie Tait Road, Edinburgh, EH9 3FD, UK
dG W Gray Centre for Advanced Materials, Department of Physics & Mathematics, University of Hull, Hull HU6 7RX, UK
First published on 11th July 2022
Abstract
Spherical particles confined to liquid interfaces generally self-assemble into hexagonal patterns. It was theoretically predicted by Jagla two decades ago that such particles interacting via a soft repulsive potential are able to form complex, anisotropic assembly phases. Depending on the shape and range of the potential, the predicted minimum energy configurations include chains, rhomboid and square phases. We recently demonstrated that deformable core–shell particles consisting of a hard silica core and a soft poly(N-isopropylacrylamide) shell adsorbed at an air/water interface can form chain phases if the crosslinker is primarily incorporated around the silica core. Here, we systematically investigate the interfacial self-assembly behavior of such SiO2–PNIPAM core–shell particles as a function of crosslinker content and core size. We observe chain networks predominantly at low crosslinking densities and smaller core sizes, whereas higher crosslinking densities lead to the formation of rhomboid packing. We correlate these results with the interfacial morphologies of the different particle systems, where the ability to expand at the interface and form a thin corona at the periphery depends on the degree of crosslinking close to the core. We perform minimum energy calculations based on Jagla-type pair potentials with different shapes of the soft repulsive shoulder. We compare the theoretical phase diagram with experimental findings to infer to which extent the interfacial interactions of the experimental system may be captured by Jagla pair–wise interaction potentials.
Introduction
The adsorption and self-assembly of colloidal particles at liquid interfaces is of interest both for fundamental science and technological applications.1,2 Fundamental investigations of such systems have provided understanding of the adsorption process itself,3,4 the shape and morphology of the adsorbed particles, in particular for deformable systems,5–8 as well as the phase behavior9–11 and the formation of defects.12–14 From a technological point of view, the presence of particles at a liquid interface impacts, for example, the kinetic stability of emulsions,15,16 foams17,18 and liquid marbles.19,20 Furthermore, the interfacial assembly can be transferred onto solid substrates to obtain nanoscale surface patterns with high fidelity over macroscopic areas21,22 which are exploited in photonic23,24 or phononic25,26 applications, or serve as a template for the fabrication of more complex plasmonic nanostructure-27–29 or nanowire arrays.26,30–32Typically, monodispersed spherical colloidal particles confined at a liquid interface self-assemble into hexagonal close packed or non-close packed structures, depending on the balance of attractive capillary and van-der-Waals forces and repulsive electrostatic and dipole forces.21,33,34 Soft colloidal particles, however, can deform under the influence of surface tension. The shell spreads at the interface and the particles assume a characteristic core–corona morphology.5–7
The resultant interfacial phase behavior of such soft colloidal particles is therefore more complex and dominated by the structure and interactions between the expanded coronae. At low surface pressure, corresponding to a large available area per particle, soft particles typically assemble into hexagonal non-close packed arrangements, where the particles are in corona–corona contact but the cores spatially separated.5,35–42 Upon compression, causing a decrease in the available area per particle, soft particles either undergo a continuous,37–39,43,44 an isostructural35–39,41,45 or a heterostructural phase transition.9,46,47 The continuous transition describes the continuous decrease in lattice spacing upon compression while preserving the hexagonal lattice structure and was observed for small39 or hollow44 soft microgels with a low37,38 or ultralow crosslinking density.42 The isostructural phase transition describes the discontinuous transition from a non-close packed hexagonal phase, where the particles are in corona–corona contact, to a close packed hexagonal phase, where the particles are in core–core contact. This transition is typically observed for microgels,35,37–39 core–shell particles36,41,45 and core-interlayer-shell particles.40 The heterostructural phase transition describes a discontinuous transition into a phase of different symmetry, for example into a chain or a rhomboid phase. Such complex phases were predicted by Jagla in 1998 for particles interacting via a hard incompressible core and a repulsive soft shell.48,49 These phases can exist as minimum energy configurations even for isotropic particles as the system minimizes its energy by fully overlapping the repulsive shells of neighboring particles within a chain to prevent overlap of shells between different chains. Depending on the shape and spatial extend of the soft repulsive shoulder, even more complex phases, such as honey-comb structures and quasicrystals, were predicted.50–56
Even though those theoretical predictions date back two decades, experimental realizations of heterostructural phase transitions are rare. Previously, chain and square phases were observed for binary systems consisting of hard polystyrene cores mixed with soft amphiphilic components such as proteins,47 surfactants47 or microgels.46 Recently, we observed a heterostructural phase transition for single-component core–shell particles consisting of a silica core and a PNIPAM shell with N,N′-methylenebis(acrylamide) (BIS) crosslinker synthesized in a batch synthesis.57 The higher reactivity of BIS compared to the monomer NIPAM58 induces a preferential incorporation of the crosslinker around the silica core and leads to a formation of dangling chains towards the periphery of the core–shell particle. A common characteristic of the interfacial morphology of these different particles is the presence of a very thin, quasi two-dimensional corona surrounding the core, which seemingly is a necessary condition for the system to undergo heterostructural phase transitions.57 Simulations based on augmented potentials, which qualitatively reproduce all different phase transitions of soft particle systems reveal that heterostructural phase transitions also require a pair–wise interaction potential.57 For an experimental system, this criterion translates into a corona that has little57 or no crosslinks9 between the dangling chains and can therefore collapse anisotropically with one neighboring particle without destabilizing the corona of the same particle in contact with a different neighbor.57
In this manuscript, we build on our recent results and investigate the interfacial phase behavior of silica–PNIPAM core–shell particles synthesized via a batch synthesis with different core sizes as well as different crosslinking densities. We investigate the interfacial self-assembly at the air/water interface of a Langmuir trough using the simultaneous compression and deposition method,31 followed by an ex situ characterization using scanning electron microscopy (SEM) and atomic force microscopy (AFM). We find indications of heterostructural phase transitions into chain phases for small cores or low crosslinking densities, while particles with larger cores and higher crosslinking densities tend to transition into rhomboid phases or directly form aggregates with core–core contact. We compare these phase transitions to theoretical predictions of minimum energy configurations obtained for particles interacting via Jagla potentials in the context of Jagla phases and discuss similarities and differences of the experimental systems.
Results
Particle characterization
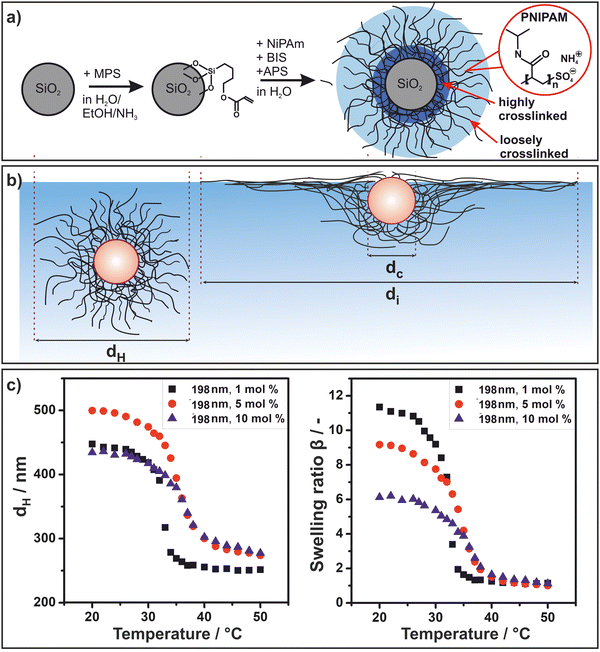
We started by synthesizing Stöber silica particles with three different diameters (dc = 198 nm, dc = 295 nm, dc = 448 nm). We then surface-functionalized these cores with 3-(trimethoxysilyl)propyl methacrylate (MPS) to covalently anchor the polymeric shell (Fig. 1(a)). Subsequently, PNIPAM microgel shells were grown onto the core via a radical polymerization in a batch process to achieve a high cross-linking gradient, whereby the crosslinker is primarily integrated around the particle core (Fig. 1(a)) as demonstrated in previous work by Stieger et al. using neutron scattering.59 For each core size, shells with 1 mol%, 5 mol% and 10 mol% crosslinker were synthesized. The morphology of the core–shell particles in bulk and adsorbed to the air/water interface is schematically illustrated in Fig. 1(b). We measured the hydrodynamic diameter dH of the core–shell particles as a function of temperature using dynamic light scattering (Fig. 1(c) left, Fig. S1, ESI†). In bulk, the core–shell particles undergo a volume phase transition due to the stimuli responsive nature of PNIPAM60,61 with a lower critical solution temperature known to be around 32 °C.60,61 Here, we observed a shift from 32 to 35 °C with increasing amount of crosslinker (Fig. 1(c) left). This can be rationalized by the more hydrophilic nature of BIS in comparison to NIPAM as BIS does not contain the hydrophobic isopropyl groups.62 We tentatively attribute the slightly larger diameter of the particles with higher crosslinker concentration in the collapsed state to an increase in total polymer mass of the polymer shell.The degree of swelling depends on the crosslinking density of the microgel shell63 and can be quantified by the swelling ratio. The temperature dependent swelling ratio β is defined as
| β = VS(T)/VS(50 °C) | (1) |
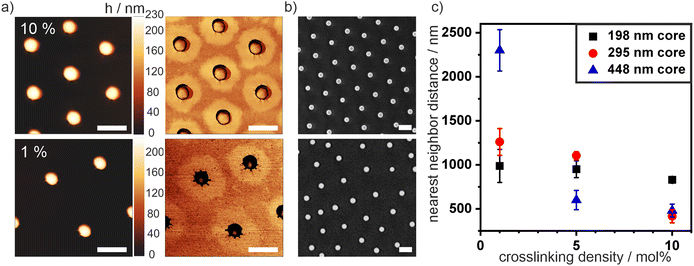
Next, we spread the synthesized core–shell particles at the air/water interface on a Langmuir trough and transferred the assembly onto a silicon wafer at a low surface pressure (5 mN m−1). We characterized the morphology ex situ using atomic force microscopy (AFM). Fig. 2(a) shows AFM height and phase images of deposited core–shell particles with a 198 nm core and shells containing 1 mol% and 10 mol% crosslinker (top and bottom, respectively). We observed the characteristic core–corona morphology, typical for PNIPAM microgels and core–shell particles.6,36 The polymer chains of the shell extend along the air/water interface to minimize its surface energy. Therefore, core–shell particles have a higher interfacial diameter di compared to their bulk diameter dH (Fig. 1(a)). In addition, for all particle systems, we observed a sharp transition from the silica core to the flat PNIPAM corona independent of the crosslinker concentration. This sharp transition indirectly reveals the accumulation of the crosslinking points near the particle core due to the batch synthesis, as dangling chains with few crosslinks can stretch out very efficiently and form an extended, very thin corona. In contrast, typical core–shell systems synthesized by a semi-batch method where the crosslinker is continuously injected throughout the synthesis exhibit a much thicker, three-dimensional polymer shell that extends towards the periphery.57
We used scanning electron microscopy (SEM) images to characterize the interfacial dimensions of the different particles (Fig. 2(b)). In the absence of compression, the particles formed a hexagonal non-close packed phase, where the cores are separated by the extended coronae. Therefore, we assigned the nearest neighbor distance that can be analyzed from the SEM images at low surface pressure (5 mN) to the interfacial diameter of the core–shell particles. We statistically evaluated these nearest neighbor distances as a function of crosslinking density from image analysis with a custom-written Matlab script8 (Fig. 2(c)). For all core sizes, a decrease in nearest neighbor distance with an increasing crosslinking density was observed. This systematic change indicates that a polymeric shell with fewer crosslinks can spread more efficiently at the interface, which can also be observed in the AFM phase images (Fig. 2(a)). This difference in shell agrees with previous studies on pure microgels, where the swelling efficiency and size is inversely proportional to the crosslinking density.37,38 Note that nearest neighbor distance of the samples with the largest core sizes and high crosslinker content is close to the core diameter. In these samples, the core–shell particles directly aggregated into core–core contact at the interface and did not form a hexagonal non-close packed phase.
We further noticed that the quality of the hexagonal arrangement (Fig. 2(b)) of our core–shell particles synthesized in the batch process was significantly lower than for comparable samples prepared in semi-batch processes.36,45 We calculated the hexagonal order parameter Ψ6 by statistical image analysis from SEM images to quantify the degree of order and thus assess the polydispersity of the samples from their self-assembly properties (Fig. S2, ESI†). A Ψ6 value of 1 refers to perfect hexagonal order. Fig. S2 (ESI†) reveals that the order increases with increasing crosslinking density. For particles with a silica core of dc = 198 nm, Ψ6 increased from 0.45 (1 mol%) to 0.74 (10 mol%). Similarly, for cores with dc = 295 nm, Ψ6 increased from 0.6 (1 mol%) to a high ordering of 0.92 (5 mol%). The higher polydispersity of the samples with low crosslinking density is further reflected by larger errors in interparticle distances of the interfacial colloidal monolayer, seen in Fig. 2(c) and Fig. S2d (ESI†). We tentatively attribute the low ordering for small particles with low crosslinker content to their inhomogeneous corona structure, which is affected by multiple factors. The free radical polymerization generally leads to a broad molecular weight distribution of individual polymer chains. In addition, a low crosslinker content presumably creates longer but also fewer dangling polymer chains forming the corona. Together, these factors collude to form less homogeneous coronae for small particles with low crosslinking densities (Fig. 2(a)). On the other hand, a higher crosslinker concentration leads to a larger number of smaller dangling chains, which may form more homogenous coronae (Fig. 2(b)). Similarly, a larger particle size also increases the number of chains able to participate in the formation of the corona and increases the homogeneity of the corona.
Compression-induced phase behavior
Next, we investigated the two-dimensional phase behavior of the core–shell particle at the liquid interface under compression using the simultaneous compression and deposition method.31 Hereby, the particles were spread at the air/water interface of a Langmuir–Blodgett trough and were continuously compressed while simultaneously being deposited onto a silicon wafer. The complete phase diagram, from low to high compression is thus encoded on the solid substrate and can be characterized by electron microscopy and image analysis ex situ. The surface pressure-area per particle isotherms for all particles can be seen in Fig. S3 (ESI†). The increasing area for lower crosslinking densities is in accordance with the data shown in Fig. 1(c) and 2(c).Fig. 3 shows the progression of different interfacial phases observed for the 198 nm–10 mol% core–shell particles upon compression by ex situ SEM images (Fig. 3(a)–(f)) and the corresponding nearest neighbor distributions (Fig. 3(g)). At low surface pressures, a hexagonal non-close packed phase with particles in corona–corona contact was observed (Fig. 3(a)). Upon compression, this hexagonal non-close packed phase is compressed without a change in structure (Fig. 3(b)), as revealed by the nearest neighbor distribution (Fig. 3(g), orange curve). With increasing compression, the onset of a phase transition into structures with core–core contact was observed and we found a coexistence of dimers, trimers, small chains and small, close packed clusters (Fig. 3(c)). This phase transition is also reflected in the nearest neighbor distribution, which showed a broad peak at larger interparticle distances (attributed to neighbors in corona–corona contact) and a second peak at small interparticle distances, indicative of particles in core–core contact (Fig. 3(g), green). Increasingly, the particles in core–core contact arranged in a network of chains when the surface pressure was increased upon further compression (Fig. 3(d)–(f)). The presence of two length scales, corresponding to core–core contact within the chains and corona–corona contact between two chains persisted in the nearest neighbor distribution (Fig. 3(g), dark blue, light blue, black). Finally, at maximal compression, the chain network became more condensed and partially exhibited hexagonal symmetries (Fig. 3(f)). A complete phase transition into a hexagonal close-packed phase was not observed, possibly due to jamming. A qualitatively similar phase behavior with the formation of chain networks upon compression was observed for 198 nm–1 mol% core–shell particles (Fig. S4, ESI†), 198 nm–5 mol% core–shell particles (Fig. S5, ESI†) and 295 nm–1 mol% core–shell particles (Fig. S6, ESI†).
Core–shell particles with a 295 nm core and 5 mol% crosslinker showed a qualitatively different phase behavior (Fig. 4). At low surface pressure, the particles formed a hexagonal non-close packed phase (Fig. 4(a) and (b)) and their nearest neighbor distance could be reduced by compression (Fig. 4(g). red, orange). Above 23 mN m−1, the particles started to form small clusters with closer contact (Fig. 4(c)), which, at first glance, appeared similar to the frequently observed isostructural phase transition into a hexagonal close packed phase.35–39,41,45 On closer inspection, however, it seems that that the clusters are distorted and not hexagonal. In addition, the nearest neighbor distribution reveals that the particles are more than 400 nm apart and therefore not in direct core–core contact (Fig. 4(g), green). Instead of growing isotropically into larger regions of close-packed particles, as expected for the typical isostructural phase transition,35–39,41,45 the clusters transitioned into more anisotropic structures, forming percolated networks of chains, often with a characteristic zig-zac structure (Fig. 4(d)). At higher pressures, these percolated networks transitioned into a well-defined rhomboid lattice, present over large areas (Fig. 4(e)). The rhomboid symmetry is evidenced in the nearest neighbor distribution (Fig. 4(g), light blue) with a characteristic splitting into two peaks. At maximal compression hexagonal close packed phases (Fig. 4(f)) in coexistence with rhomboid phases were observed. Noteworthily, the angles of the rhomboid tiles varied between 70° up to 85°. Therefore, the energy difference between the hexagonal close packed state and the rhomboid state may be close and the kinetic pathway may also affect the assembly. Other particles exhibiting at least partially rhomboid phases at high compression were 295 nm–1 mol% core–shell particles (Fig. S6, ESI†), 295 nm–10 mol% core–shell particles (Fig. S7, ESI†) and 448 nm–1 mol% core–shell particles (Fig. 5).
Particles with the largest core tended to form aggregates where the particles are directly in core–core contact at low surface pressure.64 This behavior indicates that the corona formed by the polymeric shell of these large particles is not sufficient to stabilize them against capillary attraction, which increases with increasing core size (Fig. S8 and S9, ESI†). Capillary forces acting on particles may cause aggregation directly at the air/water interface (floatation capillary forces), or during drying after transfer to solid substrate (immersion capillary forces). From our experiments, which rely on indirect imaging after transfer, it is not possible to distinguish between these two. The difficulty in stabilizing particles with large cores against aggregation is known in literature and found for different silica–core–shell particles.9,45 Noteworthily, we found a stable hexagonal non-close packed phase for 448 nm–1 mol% core–shell particles despite the large core size (Fig. 5(a)). We hypothesize that the low crosslinking density and the increasing ability of the free dangling chains to spread at the interface and form a very extended corona is important to counteract capillary attraction. This difference in behavior of the core–shell particles synthesized by the batch polymerization compared to continues monomer feeding (which does not allow stabilizing non-close packed phases with such large cores)45 highlights the important role of the crosslinker and its distribution within the core–shell particles. Upon compression, the 448 nm–1 mol% core–shell particles arranged in chain-like networks, which became increasingly denser (Fig. 5(b)–(e)). The nearest neighbor distance shows peak splitting characteristic for chain phase, with particle populations in close distance within the chains, and particles at larger distance in between chains. At largest pressure, the chains were compressed into an ill-defined close-packed structure with local hexagonal and rhomboid structure. (Fig. 5(f)). The corresponding nearest neighbor distribution is characterized by a pronouced peak of the particles in direct core–core contact and a shoulder attributed to particles in local rhomboid arrangement.
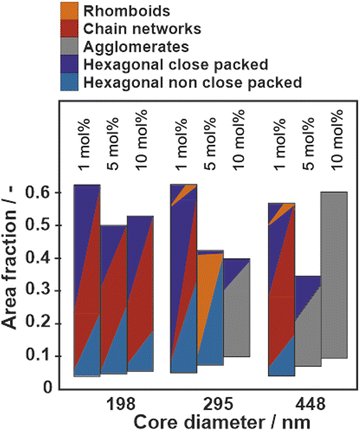
Fig. 6 summarizes the phase behavior of all particle systems as a function of core diameter and crosslinker content in the PNIPAM shell. The area fraction, used as y-axis is defined as the ratio of the area covered by cores to the total available area. A high area fraction corresponds to a low available area per particle and a high surface pressure. Note that the area fraction was determined from SEM images where the polymer shell was removed and the data therefore systematically underestimates the true area fraction of the core–shell particles. The images without a polymer shell are shown in Fig. S10–S12 (ESI†). The phases are classified based on the visual impression and the distribution of nearest neighbor distances as shown in Fig. 3–5 and Fig. S4–S9 (ESI†). We observe three general trends:
(1) Particles with large cores and high crosslinking density tend to aggregate directly at the interface (Fig. S8 and S9, ESI†), suggesting that attractive capillary forces are stronger than the steric repulsion of the polymeric corona. The notable exception are the particles with large core (dc = 448 nm) and lowest crosslinker content (1 mol%), which maintain a corona–corona contact upon spreading at the liquid interface (Fig. 5(a)).
(2) Particles with small core size and low crosslinking densities form chain networks at intermediate compressions, as identified in the binary distributions of nearest neighbor distributions (Fig. 3 and Fig. S3, S4, ESI†).
(3) Particles with intermediate core sizes and high crosslinking density form rhomboid phases at high compressions (Fig. S6 and S7, ESI†), which can at least partially be replaced by hexagonal close packed phases at maximum compression (Fig. 4 and Fig. S7, ESI†).
Discussion
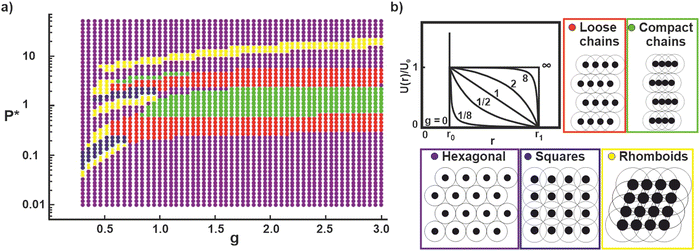
In the following, we discuss the experimentally observed phase transitions and compare them to theoretical minimum energy calculations using a simple Jagla hard–core soft–shell pair potential, assuming the interaction potentials are pair–wise additive and that each unit cell contains only one particle.45,49 The shape of the soft compressible shoulder is defined by the parameter g (Fig. 7(b)).49 The phase behavior as a function of g vs. normalized pressure P* = Pr02/U0 for a fixed shell to core diameter ratio r1/r0 of 3 is depicted in Fig. 7(a), where P is the surface pressure, r0 is the core diameter and U0 is the energy of two core–shell particles in core–core contact. From the experimental data, we determined the shell diameter r1 as the nearest neighbor distance of the core–shell particles in corona–corona contact before the onset of phase formation and r0 as the diameter of the particle core. For all the nine particle systems, the r1/r0 ratio was between 2.72 and 3.59, decreasing with increasing crosslinking density. The r1/r0 value of 3 in the calculations therefore generally approximates the experimental systems. Note that we are justified in using minimum energy calculations to determine the local structure of the different phases since the experimental system is effectively in the zero-temperature regime (U0 ≫ kBT) as demonstrated elsewhere.9,46 Since U0 ≫ kBT, the system is non-ergodic and not necessarily in the ground state; our minimum energy calculations therefore only allows us to predict the local structure of the system. A more accurate modelling of the system (including defects), would require particle-based simulations at finite temperature which take into account the kinetic history of the sample due to uniaxial compression.9Noteworthily, several non-intuitive structural motifs observed in the experiments are found in the theoretical evaluation of the minimum energy phases of particles interaction via Jagla potentials. For example, the calculations show the phase transitions from a hexagonal non-close packed phase to a chain phase (particularly the compact chains that are observed experimentally) for g-parameters ≥1. Similarly, rhomboid phases are found for convex potentials with g < 1. At high pressures, hexagonal phases have the lowest energy for all chosen g parameters. Despite this general coincidence, there are clear differences between the phase behavior as calculated from Jagla pair–wise interactions and the experimental observations. The calculations are able to resolve the phases in high detail and differentiate between loosely packed and dense chain structures. In contrast, the experimentally observed phases are more irregular and disordered. A distinction between loose and compact chains cannot be made and the difference between rhomboids and squares is blurred. We also do not experimentally resolve the frequent change between phases found in the calculations, but rather observe a coexistence of phases. The restriction of our theoretical model to one particle per unit cell precludes the appearance of more complex phases, such as small clusters or complex chains that are seen in the experiments. Some phases observed in the phase diagram restricted by the single-partilce unit cell may be proxies for more complex phases. As an example, the rhomboid phase observed at the highest pressure in Fig. 7(a) is probably a proxy for a complex chain phase that we previously observed for a theoretical model involving two particles per unit cell.9
In the following, we hypothesize on the connection between experimental phase behavior and the phase behavior theoretically predicted by Jagla phases, using a heuristic picture of the interfacial morphology of soft particle systems.
We first focus on the similarities between theory and experiments. We have previously argued that the interfacial morphology of core–shell particles can influence the interaction potential.9,46,47,57 In particular, for an ideally two-dimensional corona structure extending from a hard core, potential shapes approximating Jagla-type interactions can be hypothesized. When assuming that the polymer coronae generate a repulsive behavior that scales with their overlap upon compression, a long-range repulsive shoulder may arise. Based on these considerations, three key criteria to observe Jagla-like phases have been identified: (i) a hard core is required to generate the two characteristic length scales; (ii) the corona needs to be very flat and confined to the interface to limit the overlap volume upon compression;9 (iii) the degree of connectivity between polymer chains forming the corona needs to be minimized, so that the corona can locally collapse with certain neighbors (i.e. within a chain), but maintain a corona–corona contact with others (i.e. in-between chains).57 We now argue that these criteria are at least partially fulfilled in the present experimental system. The core–shell nature naturally provides the two length scales. The batch synthesis process is known to provide long, dangling chains with limited crosslinking at the periphery, as the crosslinker is predominantly integrated at early stages of the reaction, close to the core.59 In fact, the AFM images shown in Fig. 2 support the presence of a very thin, spread out corona and a clear separation from the core. Note that for typical semi-batch processes, the distinction between core and shell is much more blurred, presumably due to a more homogeneous distribution of crosslinking points.57 Therefore, the general formation of non-intuitive chain network and rhombic phases in the experimental system may be rationalized from an assumed Jagla-like interaction behavior.
Next, we focus on differences between theory and experiment, notably the poor resolution of the phases in experiment. While the different reactivity of monomer and crosslinker59 provides the required interfacial morphology in our batch synthesis (Fig. 2),57 it can be assumed that it also causes inhomogeneites in the corona structure. With little crosslinker available at later stages of the reaction, we expect that the outer part of the shell to consist mainly of linear PNIPAM polymer chains. However, due to the free radical polymerization process, these shells will have a comparably broad molecular weight distribution. Upon adsorption the air/water interface, we assume that the corona is predominantly formed by these linear dangling chains, since they are most flexible and can more readily adsorb and spread at the interface to reduce surface tension. Assuming a broad molecular weight distribution of these chains, the formed corona may thus be inhomogeneous in width, a picture that is supported by the AFM phase images (Fig. 2(a)), and indirectly evidenced by the low hexagonal order parameter for particle systems with low crosslinking density, as discussed above. These inhomogeneities in the corona structure may explain why the experimentally observed structures are less defined compared to the calculated ones.
We now discuss the differences in phase behavior of the different particle systems based on the hypotheses provided above. We start with the hypothesis that the repulsive potential of the core–shell particles can be ascribed to steric repulsions between overlapping shells and we assume that the overlap volume influences the shape of the repulsive interaction potential.57 We assume that purely long polymer chains attached to a core form an overlap that can be approximated by a linear ramp potential, evidenced by a close agreement between simulations based on Jagla-potentials with g = 1 and experiments using more defined model systems with uniform, non-crosslinked shells.9,46,55 In the present case, we note that the experimental systems with low crosslinker concentration form chain networks (Fig. 3 and 6), which coincide with regions in the theoretical phase diagram around g = 1 (Fig. 7).
Increasing crosslinker content leads to a denser polymer network around the core. We speculate that in this case, the repulsion generated from compression of two polymer coronae at the interfaces is non-linear. Initially, the less-crosslinked polymer chains may rearrange and cause less resistance, while the resistance will increase when the more-crosslinked parts of the corona are forced into overlap at higher surface pressure. This non-linear behavior would correspond to a convex potential shape, described by g < 1. Notably, the theoretical phase diagram predicts rhomboid packing for such lower g parameters (Fig. 7), coinciding with the experimental observation that rhomboid structures are observed for particles with high crosslinking densities (Fig. 4 and 6). We should, however, also point out that for higher crosslinking densities multibody interactions are likely to be of importance and should be taken into account in an accurate description.57
Finally, we emphasize the presence of attractive capillary interactions, which are neglected in the simplistic picture of interactions via Jagla potentials, but are key to understand the observed phase behavior of the core–shell particles. Attractive capillary forces are present in all our synthesized particle systems as none exhibits any liquid/gaseous phase at very low interface coverage. Instead, all samples directly form clusters with corona–corona contact even with excess interfacial area available (Fig. S13, ESI†), revealing the presence of attractive interparticle forces. As the particles are small and therefore gravity can be neglected, floatation capillary forces should be negligible in our systems,65–67 yet are frequently observed for core–shell particles with a soft shell, or even plain microgels.36,68,69 Capillary attraction can arise from contact line undulations due to inhomogeneities on the particle surface even when flotation forces due to gravity are negligible.70 Huang et al. found that nanometer-sized undulations of the contact line are the origin of the capillary forces between large microgels (dH = 700 nm) without a rigid core as well.69 These observations indicate that a rigid core enhances the strain in the shell and thereby the surface roughness. Our experimental results corroborate with this interpretation as attractive forces seemingly increase with larger core diameters and larger crosslinking density, evidenced by the pronounced tendency to aggregate into core–core contact at low area fractions (Fig. 6 and Fig. S8, S9, ESI†). A stable hexagonal non-close packed phase with the largest core sizes is only observed for the lowest crosslinker content (1 mol%), indicating that extended corona with little crosslinking and a high propensity to spread at the interface is important to counteract the attractive forces.
So far, we discussed the balance between repulsive or attractive interactions at low surface pressure and we will now discuss them at higher pressures. First, we note that the transitions into complex phases, most notably the rhombic phase only occurs at large area fractions. In this situation, the interface is already crowded and the polymeric coronae significantly overlap (see e.g.Fig. 3(e) and Fig. S6f, ESI†), especially when considering their spatial extend in the absence of compression (Fig. 2). Therefore, we hypothesize that in these situations, the repulsion induced by the compressed polymer chains dominates over capillary attractions. The dominance of repulsion at high area fractions may explain why such phase transitions are reproduced by the repulsive Jagla-potentials, which are clearly an oversimplified representation of the real interfacial interactions. However, it is noteworthy that theoretical investigations of Grishina et al., who take into account longer range capillary attractions in a triangular lattice model with similar particle dimensions also recover several of the observed phases, including clusters and particle chains, which may indicate that capillary attraction indeed influences the phase behavior for such complex phases.34,71,72 A full understanding of the phase behavior will necessitate a direct correlation between the molecular structure of the particles, its morphology at the interface and the changes upon compression, and the resultant interaction potential.
Conclusions
In this work, we study the influence of the crosslinking density and core size on the interfacial self-assembly behavior of SiO2–PNIPAM core–shell particles. We find a rich phase behavior that includes phase transitions into rhomboid and chain phases.Upon compression, we observe three typical phase behaviors: (1) core–shell particles with small cores and a low crosslinking density show a phase transition from a hexagonal non-close packed phase to chain networks. (2) Phase transitions into rhomboid phases are found for 5 and 10 mol% crosslinked particles and medium sized cores. (3) core–shell particles with large cores and higher crosslinking densities directly aggregate and do not form hexagonal non-close packed phases.
We corroborate the experimental results by minimum energy calculations assuming Jagla potentials as a simplistic representation of the repulsive interactions of the polymer coronae at the interface. From the comparison between similarities and differences of the theoretically predicted and experimentally observed phase behavior, we hypothesize on potential links between shell architecture and nature of the interfacial interaction potential. This discussion remains speculative in nature as the true interaction potentials between hard core–soft shell particles spread at liquid interfaces remain to be experimentally assessed. However, even in this heuristic approach, the comparison yields insights into the connection between internal architecture of hard core–soft shell particles, the structure of the formed corona upon interfacial adsorption, and the resultant phase behavior.
Experimental
Materials
Ammonium peroxodisulfate (APS, ≥98%), N,N′-methylenebis(acrylamide) (BIS, 99%), ethanol (EtOH, ≥99.8%) and 3-(trimethoxysilyl)propyl methacrylate (MPS, 98%) were purchased from Sigma Aldrich. Tetraethyl orthosilicate (TEOS, ≥99.8%) was obtained from VWR Chemicals and ammonium hydroxide solution (30–33% NH3 basis), isopropanol (≥99.8%) and denatured ethanol (EtOH, ≥99.8%) from ROTH. N-Isopropylacrylamide (NIPAM, 97%) from Sigma Aldrich was purified by recrystallization from hexane. Water was purified by using a Milli-Q system (18.2 MΩ cm, Elga™ PURELAB™ Flex). All other chemicals were used as received.Synthesis of the SiO2–PNIPAM core–shell particles
The silica cores were synthesized according to a modified Stöber-process.73 In a 250 mL round bottom flask, pure ethanol (137.5 g), Milli-Q water and NH3(aq.) (11.72 g) were stirred together and heated in an oil bath to 47 °C. We varied the amount of water from 18 to 80 mL to obtain different particle sizes. After an equilibration time of one hour, TEOS (20 g) was rapidly added to start the reaction. We let the reaction proceed for 24 h and then added according to a modified version of Tang et al. MPS (ca. 100 μL) with a syringe to functionalize the cores.45 After further 24 h, the solution was cooled down to room temperature. The functionalized silica particles were purified by centrifugation and redispersing three times in denatured ethanol and three times in Milli-Q water.The microgel shell was grown onto the silica cores via a batch surfactant-free precipitation polymerization according to a modified synthesis of Tang et al.45 In a 500 mL three-neck round bottom flask, NIPAM (0.1414 g/25 mmol L−1) and BIS (0 g/0 mol%, 0.0002 g/0.1 mol%, 0.0019 g/1 mol%, 0.0097 g/5 mol%, 0.0194 g/10 mol%, respectively) were dissolved in Milli-Q water (47 mL). The molar ratios of BIS are related to the total amount of NIPAM. The solution was heated to 80 °C, purged with nitrogen and equilibrated for 30 min. Meanwhile, core dispersion (ca. 1019 nm2/100 mL) was added dropwise with a syringe. After the equilibration time expired, a balloon filled with nitrogen was used to keep the nitrogen atmosphere and the gas inlet could be removed. Subsequently, APS (0.0114 g/2 mol%) was rapidly added to initiate the reaction. We let the reaction proceed for 4 h and after it cooled down, we purified the suspension by centrifugation in Milli-Q water between 6 and 15 times.
Characterization
Dynamic light scattering was performed with a Malvern Zetasizer Nano-ZS in disposable polystyrene cuvettes at a scattering angle of 173°. The hydrodynamic diameter of the particles was measured as a function of the temperature, ranging from 16 to 50 °C. For each temperature step, the measurements were performed four times after equilibration for 15 min.Langmuir trough compression and deposition
The core–shell particles were self-assembled at the air/water interface on a Teflon® Langmuir trough (KSVNIMA, area = 550 cm2, width = 7.5 cm) with Delrin® barriers and a platinum Wilhelmy plate. All components of the Langmuir trough were thoroughly rinsed with Milli-Q water and ethanol and then dried with an air jet. The trough was filled with Milli-Q water. Silicon wafers (Siltronix®) were cut to 8 × 1 cm2 and cleaned by ultra-sonication in ethanol and Milli-Q water. The wafer was fixed to a substrate holder on the Langmuir trough under a 45° angle. The substrate was lowered from the top to penetrate through the air/water interface into the reservoir.The core–shell particle suspensions were diluted to 0.1 wt%, mixed with 50% ethanol as spreading agent and added to the air/water interface using a 100 μL pipette. The interface was equilibrated for 20 minutes before starting the simultaneous compression and deposition.35,36 The barriers closed 8 mm min−1. Simultaneously, the dipper with the substrate was raised with a speed of 0.8 mm min−1.
AFM analysis
The information on the height and phase images of the deposited core–shell particles was extracted by AFM using a JPK NanoWizard instrument in AC mode using a NSC-36 cantilever B (resonance frequency 130 kHz, spring constant 2 N m−1). We scanned regions of 2 × 2 μm2 with a resolution of 512 × 512 pixels2. The images were post processed with Gwyddion, using flattening and median fits.Statistical image analysis
For each substrate SEM images were taken every 1 mm, using Inlens mode with a current of 2 kV and a resolution of 2048 × 1536 pixel2. For the statistical image analysis, SEM images were taken at each millimeter of the coated wafer with 3 kV after the PNIPAM shell was removed by oxygen plasma. This facilitates identification of individual particles and allows analysis of area fraction and interparticle distance.The SEM images were analysed using a custom-written Matlab software based on the thresholding method. The nearest neighbors of each particle were found by Voronoi tessellation. The nearest neighbor distribution was fitted with one or two Gauss fits. The Area fraction was determined by counting the numbers of black and white pixels and setting them in the relation white pixels/black pixels. The 2D hexagonal order parameter Ψ6 was calculated by using the formula:
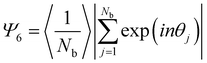 | (2) |
The r1/r0-ratio was determined from SEM image analysis when the phase transition started. At this point most of the particles are in shell–shell contact and some shells are already collapsed. The ratio was calculated by dividing the shell–shell distance through the core–core distance.
Author contributions
M. I. synthesized the core–shell particles. L. H., M. I., J. H. and M. R. characterized the interfacial self-assembly behavior of the particles. D. M. A. B. performed the minimum energy calculations. J. H., M. R. and N. V. designed the experiments and the study. All authors contributed to the writing of the manuscript.Funding sources
The research was supported by the Deutsche Forschungsgemeinschaft (DFG) under grant number VO 1824/6-2. M. R. acknowledges funding from the Swiss National Science Foundation Project-ID P2SKP2_194953 and temporary funding from EAM. N. V. also acknowledges support by the Interdisciplinary Center for Functional Particle Systems (FPS).Conflicts of interest
There are no conflicts to declare.References
- R. McGorty, J. Fung, D. Kaz and V. N. Manoharan, Colloidal self-assembly at an interface, Mater. Today, 2010, 13(6), 34–42, DOI:10.1016/S1369-7021(10)70107-3.
- B. P. Binks, Particles as surfactants—similarities and differences, Curr. Opin. Colloid Interface Sci., 2002, 7(1–2), 21–41, DOI:10.1016/S1359-0294(02)00008-0.
- P. Pieranski, Two-dimensional interfacial colloidal crystals, Phys. Rev. Lett., 1980, 45(7), 569–572, DOI:10.1103/PhysRevLett.45.569.
- D. M. Kaz, R. McGorty, M. Mani, M. P. Brenner and V. N. Manoharan, Physical ageing of the contact line on colloidal particles at liquid interfaces, Nat. Mater., 2011, 11(2), 138–142, DOI:10.1038/nmat3190.
- M. Rey, M. A. Fernandez-Rodriguez, M. Karg, L. Isa and N. Vogel, Poly-N-isopropylacrylamide nanogels and microgels at fluid interfaces, Acc. Chem. Res., 2020, 53(2), 414–424, DOI:10.1021/acs.accounts.9b00528.
- K. Geisel, L. Isa and W. Richtering, Unraveling the 3D localization and deformation of responsive microgels at oil/water interfaces: A step forward in understanding soft emulsion stabilizers, Langmuir, 2012, 28(45), 15770–15776, DOI:10.1021/la302974j.
- R. W. Style, L. Isa and E. R. Dufresne, Adsorption of soft particles at fluid interfaces, Soft Matter, 2015, 11(ii), 1–8, 10.1039/C5SM01743B.
- J. Harrer, M. Rey, S. Ciarella, H. Löwen, L. M. C. Janssen and N. Vogel, Stimuli-responsive behavior of PNiPAm microgels under interfacial confinement, Langmuir, 2019, 35(32), 10512–10521, DOI:10.1021/acs.langmuir.9b01208.
- J. Menath, J. Eatson, R. Brilmayer, A. Andrieu-Brunsen, D. M. A. Buzza and N. Vogel, Defined core–shell particles as the key to complex interfacial self-assembly, Proc. Natl. Acad. Sci. U. S. A., 2021, 118(52), 1–10, DOI:10.1073/pnas.2113394118.
- M. A. Fernandez-Rodriguez, M. N. Antonopoulou and L. Isa, Near-zero surface pressure assembly of rectangular lattices of microgels at fluid interfaces for colloidal lithography, Soft Matter, 2021, 17(2), 335–340, 10.1039/d0sm01823f.
- F. Grillo, M. A. Fernandez-Rodriguez, M. N. Antonopoulou, D. Gerber and L. Isa, Self-templating assembly of soft microparticles into complex tessellations, Nature, 2020, 582(7811), 219–224, DOI:10.1038/s41586-020-2341-6.
- A. R. Bausch, M. J. Bowick, A. Cacciuto, A. D. Dinsmore, M. F. Hsu, D. R. Nelson, M. G. Nikolaides, A. Travesset and D. A. Weitz, Grain boundary scars and spherical crystallography, Science, 2003, 299(5613), 1716–1718 CrossRef CAS PubMed.
- J. Harrer, S. Ciarella, M. Rey, H. Löwen, L. M. C. Janssen and N. Vogel, Collapse-induced phase transitions in binary interfacial microgel monolayers, Soft Matter, 2021, 17(17), 4504–4516, 10.1039/d1sm00318f.
- R. E. Guerra, C. P. Kelleher, A. D. Hollingsworth and P. M. Chaikin, Freezing on a sphere, Nature, 2018, 554(7692), 346–350, DOI:10.1038/nature25468.
- W. Richtering, Responsive emulsions stabilized by stimuli-sensitive microgels: Emulsions with special non-pickering properties, Langmuir, 2012, 28(50), 17218–17229, DOI:10.1021/la302331s.
- T. Liu, S. Seiffert, J. Thiele, A. R. Abate, D. A. Weitz and W. Richtering, Non-coalescence of oppositely charged droplets in PH-sensitive emulsions, Proc. Natl. Acad. Sci. U. S. A., 2012, 109(2), 384–389, DOI:10.1073/pnas.1019196109.
- B. P. Binks and T. S. Horozov, Aqueous foams stabilized solely by silica nanoparticles, Angew. Chem., Int. Ed., 2005, 44(24), 3722–3725, DOI:10.1002/anie.200462470.
- U. T. Gonzenbach, A. R. Studart, E. Tervoort and L. J. Gauckler, Ultrastable particle-stabilized foams, Angew. Chem., Int. Ed., 2006, 45(21), 3526–3530, DOI:10.1002/anie.200503676.
- P. Aussillous and D. Quéré, Liquid marbles, Nature, 2001, 411(6840), 924 CrossRef CAS PubMed.
- R. Murakami, H. Moriyama, T. Noguchi, M. Yamamoto and B. P. Binks, Effects of the density difference between water and oil on stabilization of powdered oil-in-water emulsions, Langmuir, 2014, 30(2), 496–500, DOI:10.1021/la4042056.
- N. Vogel, C. K. Weiss and K. Landfester, From soft to hard: The generation of functional and complex colloidal monolayers for nanolithography, Soft Matter, 2012, 8(15), 4044–4061, 10.1039/c1sm06650a.
- V. Lotito and T. Zambelli, Approaches to self-assembly of colloidal monolayers: A guide for nanotechnologists, Adv. Colloid Interface Sci., 2017, 246, 217–274, DOI:10.1016/j.cis.2017.04.003.
- M. Kolle, P. M. Salgard-Cunha, M. R. J. Scherer, F. Huang, P. Vukusic, S. Mahajan, J. J. Baumberg and U. Steiner, Mimicking the colourful wing scale structure of the papilio blumei butterfly, Nat. Nanotechnol., 2010, 5(7), 511–515 CrossRef CAS PubMed.
- C. Stelling, C. Bernhardt and M. Retsch, Subwavelength etched colloidal monolayers: A model system for tunable antireflective coatings, Macromol. Chem. Phys., 2015, 216(16), 1682–1688, DOI:10.1002/macp.201500167.
- N. Boechler, J. K. Eliason, A. Kumar, A. A. Maznev, K. A. Nelson and N. Fang, Interaction of a contact resonance of microspheres with surface acoustic waves, Phys. Rev. Lett., 2013, 111(3), 1–5, DOI:10.1103/PhysRevLett.111.036103.
- F. J. Wendisch, M. S. Saller, A. Eadie, A. Reyer, M. Musso, M. Rey, N. Vogel, O. Diwald and G. R. Bourret, Three-dimensional electrochemical axial lithography on Si micro- and nanowire arrays, Nano Lett., 2018, 18(11), 7343–7349, DOI:10.1021/acs.nanolett.8b03608.
- T. Honold, K. Volk, A. Rauh, J. P. S. Fitzgerald and M. Karg, Tunable plasmonic surfaces via colloid assembly, J. Mater. Chem. C, 2015, 3, 11449–11457, 10.1039/x0xx00000x.
- E. S. A. Goerlitzer, R. Mohammadi, S. Nechayev, K. Volk, M. Rey, P. Banzer, M. Karg and N. Vogel, Chiral surface lattice resonances, Adv. Mater., 2020, 2001330, DOI:10.1002/adma.202001330.
- A. Nemiroski, M. Gonidec, J. M. Fox, P. Jean-Remy, E. Turnage and G. M. Whitesides, Engineering shadows to fabricate optical metasurfaces, ACS Nano, 2014, 8(11), 11061–11070, DOI:10.1021/nn504214b.
- M. Rey, F. J. Wendisch, E. S. Aaron Goerlitzer, J. S. Julia Tang, R. S. Bader, G. R. Bourret and N. Vogel, Anisotropic silicon nanowire arrays fabricated by colloidal lithography, Nanoscale Adv., 2021, 3(12), 3634–3642, 10.1039/d1na00259g.
- M. Rey, R. Elnathan, R. Ditcovski, K. Geisel, M. Zanini, M. A. Fernandez-Rodriguez, V. V. Naik, A. Frutiger, W. Richtering, T. Ellenbogen, N. H. Voelcker and L. Isa, Fully tunable silicon nanowire arrays fabricated by soft nanoparticle templating, Nano Lett., 2016, 16(1), 157–163, DOI:10.1021/acs.nanolett.5b03414.
- F. J. Wendisch, M. Abazari, H. Mahdavi, M. Rey, N. Vogel, M. Musso, O. Diwald and G. R. Bourret, Morphology-graded silicon nanowire arrays via chemical etching: Engineering optical properties at the nanoscale and macroscale, ACS Appl. Mater. Interfaces, 2020, 12(11), 13140–13147, DOI:10.1021/acsami.9b21466.
- R. Aveyard, J. H. Clint, D. Nees and V. N. Paunov, Compression and structure of monolayers of charged latex particles at air/water and octane/water interfaces, Langmuir, 2000, 16(4), 1969–1979, DOI:10.1021/la990887g.
- A. Ciach and J. Pekalski, Exactly solvable model for self-assembly of hard core–soft shell particles at interfaces, Soft Matter, 2017, 13(14), 2603–2608, 10.1039/c7sm00191f.
- M. Rey, M. Á. Fernández-Rodríguez, M. Steinacher, L. Scheidegger, K. Geisel, W. Richtering, T. M. Squires and L. Isa, Isostructural solid–solid phase transition in monolayers of soft core–shell particles at fluid interfaces: Structure and mechanics, Soft Matter, 2016, 12(15), 3545–3557, 10.1039/C5SM03062E.
- A. Rauh, M. Rey, L. Barbera, M. Zanini, M. Karg and L. Isa, Compression of hard core–soft shell nanoparticles at liquid–liquid interfaces: Influence of the shell thickness, Soft Matter, 2017, 13(1), 158–169, 10.1039/C6SM01020B.
- M. Rey, X. Hou, J. S. J. Tang and N. Vogel, Interfacial arrangement and phase transitions of pNiPAm microgels with different crosslinking densities, Soft Matter, 2017, 13(46), 8717–8727, 10.1039/c7sm01558e.
- C. Picard, P. Garrigue, M.-C. Tatry, V. Lapeyre, S. Ravaine, V. Schmitt and V. Ravaine, Organization of microgels at the air–water interface under compression: Role of electrostatics and cross-linking density, Langmuir, 2017, 33(32), 7968–7981, DOI:10.1021/acs.langmuir.7b01538.
- L. Scheidegger, M. Á. Fernández-Rodríguez, K. Geisel, M. Zanini, R. Elnathan, W. Richtering and L. Isa, Compression and deposition of microgel monolayers from fluid interfaces: Particle size effects on interface microstructure and nanolithography, Phys. Chem. Chem. Phys., 2017, 19(13), 8671–8680, 10.1039/C6CP07896F.
- A. S. El-Tawargy, D. Stock, M. Gallei, W. A. Ramadan, M. A. Shams El-Din, G. Reiter and R. Reiter, Multiple structural transitions in langmuir monolayers of charged soft–shell nanoparticles, Langmuir, 2018, 34(13), 3909–3917, DOI:10.1021/acs.langmuir.7b03656.
- S. A. Vasudevan, A. Rauh, L. Barbera, M. Karg and L. Isa, Stable in bulk and aggregating at the interface: Comparing core–shell nanoparticles in suspension and at fluid interfaces, Langmuir, 2018, 34(3), 886–895, DOI:10.1021/acs.langmuir.7b02015.
- A. Scotti, S. Bochenek, M. Brugnoni, M. A. Fernandez-Rodriguez, M. F. Schulte, J. E. Houston, A. P. H. Gelissen, I. I. Potemkin, L. Isa and W. Richtering, Exploring the colloid-to-polymer transition for ultra-low crosslinked microgels from three to two dimensions, Nat. Commun., 2019, 10(1), 1418, DOI:10.1038/s41467-019-09227-5.
- S. Bochenek, A. Scotti, W. Ogieglo, M.-A. Fernandez-Rodriguez, M. F. Schulte, R. A. Gumerov, N. V. Bushuev, I. I. Potemkin, M. Wessling, L. Isa and W. Richtering, Effect of the 3D swelling of microgels on their 2D phase behavior at the liquid–liquid interface, Langmuir, 2019, 35(51), 16780–16792, DOI:10.1021/acs.langmuir.9b02498.
- J. Vialetto, F. Camerin, F. Grillo, S. N. Ramakrishna, L. Rovigatti, E. Zaccarelli and L. Isa, Effect of internal architecture on the assembly of soft particles at fluid interfaces, ACS Nano, 2021, 15(8), 13105–13117, DOI:10.1021/acsnano.1c02486.
- J. S. J. Tang, R. S. Bader, E. S. A. Goerlitzer, J. F. Wendisch, G. R. Bourret, M. Rey and N. Vogel, Surface patterning with SiO2@PNiPAm core–shell particles, ACS Omega, 2018, 3(9), 12089–12098, DOI:10.1021/acsomega.8b01985.
- M. Rey, A. D. Law, D. M. A. Buzza and N. Vogel, Anisotropic self-assembly from isotropic colloidal building blocks, J. Am. Chem. Soc., 2017, 139(48), 17464–17473, DOI:10.1021/jacs.7b08503.
- M. Rey, T. Yu, K. Bley, K. Landfester, D. M. A. Buzza and N. Vogel, Amphiphile-induced anisotropic colloidal self-assembly, Langmuir, 2018, b01382, DOI:10.1021/acs.langmuir.8b01382.
- E. A. Jagla, Minimum energy configurations of repelling particles in two dimensions, J. Chem. Phys., 1999, 110(1), 451–456, DOI:10.1063/1.478105.
- E. A. Jagla, Phase behavior of a system of particles with core collapse, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1998, 58(2), 11, DOI:10.1103/PhysRevE.58.1478.
- J. Fornleitner and G. Kahl, Pattern formation in two-dimensional square-shoulder systems, J. Phys.: Condens. Matter, 2010, 22(10), 104118, DOI:10.1088/0953-8984/22/10/104118.
- J. Fornleitner and G. Kahl, Lane formation vs. cluster formation in two-dimensional square-shoulder systems – A genetic algorithm approach, EPL, 2008, 82(1), 18001, DOI:10.1209/0295-5075/82/18001.
- Y. Du, H. Jiang and Z. Hou, Self-assembly of active core corona particles into highly ordered and self-healing structures, J. Chem. Phys., 2019, 151(15), 154904, DOI:10.1063/1.5121802.
- G. Malescio and G. Pellicane, Stripe Phases from Isotropic Repulsive Interactions, Nat. Mater., 2003, 2(2), 97–100, DOI:10.1038/nmat820.
- A. J. Archer, A. M. Rucklidge and E. Knobloch, Quasicrystalline order and a crystal-liquid state in a soft-core fluid, Phys. Rev. Lett., 2013, 111(16), 1–5, DOI:10.1103/PhysRevLett.111.165501.
- W. R. C. Somerville, A. D. Law, M. Rey, N. Vogel, A. J. Archer and D. M. A. Buzza, Pattern formation in two-dimensional hard–core/soft–shell systems with variable soft shell profiles, Soft Matter, 2020, 16(14), 3564–3573, 10.1039/d0sm00092b.
- T. Dotera, T. Oshiro and P. Ziherl, Mosaic two-lengthscale quasicrystals, Nature, 2014, 506(7487), 208–211, DOI:10.1038/nature12938.
- S. Ciarella, M. Rey, J. Harrer, N. Holstein, M. Ickler, H. Löwen, N. Vogel and L. M. C. Janssen, Soft particles at liquid interfaces: From molecular particle architecture to collective phase behavior, Langmuir, 2021, 37(17), 5364–5375, DOI:10.1021/acs.langmuir.1c00541.
- X. Wu, R. H. Pelton, A. E. Hamielec, D. R. Woods and W. McPhee, The kinetics of poly(N-Isopropylacrylamide) microgel latex formation, Colloid Polym. Sci., 1994, 272(4), 467–477, DOI:10.1007/BF00659460.
- M. Stieger, W. Richtering, J. S. Pedersen and P. Lindner, Small-angle neutron scattering study of structural changes in temperature sensitive microgel colloids, J. Chem. Phys., 2004, 120(13), 6197, DOI:10.1063/1.1665752.
- M. Kwok, Z. Li and T. Ngai, Controlling the synthesis and characterization of micrometer-sized PNIPAM microgels with tailored morphologies, Langmuir, 2013, 29, 9581–9591, DOI:10.1021/la402062t.
- R. A. Ramli and W. Laftah, Core–shell polymers: A review, RSC Adv., 2013, 3, 15543–15565, 10.1039/c3ra41296b.
- Y. Zhang, S. Furyk, D. E. Bergbreiter and P. S. Cremer, Specific ion effects on the water solubility of macromolecules: PNIPAM and the Hofmeister series, J. Am. Chem. Soc., 2005, 127(41), 14505–14510, DOI:10.1021/ja0546424.
- J. Zhang and R. Pelton, Poly(N-isopropylacrylamide) microgels at the air–water interface, Langmuir, 1999, 15(23), 8032–8036 CrossRef CAS.
- M. Litniewski and A. Ciach, Effect of aggregation on adsorption phenomena, J. Chem. Phys., 2019, 150(23), 234702, DOI:10.1063/1.5102157.
- N. Ballard, A. D. Law and S. A. F. Bon, Colloidal particles at fluid interfaces: Behaviour of isolated particles, Soft Matter, 2018, 15(6), 1186–1199, 10.1039/C8SM02048E.
- R. Di Leonardo, F. Saglimbeni and G. Ruocco, Very-long-range nature of capillary interactions in liquid films, Phys. Rev. Lett., 2008, 100(10), 1–4, DOI:10.1103/PhysRevLett.100.106103.
- M. P. Boneva, K. D. Danov, N. C. Christov and P. A. Kralchevsky, Attraction between particles at a liquid interface due to the interplay of gravity- and electric-field-induced interfacial deformations, Langmuir, 2009, 25(16), 9129–9139, DOI:10.1021/la9006873.
- S. Huang, K. Gawlitza, R. Von Klitzing, L. Gilson, J. Nowak, S. Odenbach, W. Steffen and G. K. G. K. Auernhammer, Microgels at the water/oil interface: In situ observation of structural aging and two-dimensional magnetic bead microrheology, Langmuir, 2016, 32(3), 712–722, DOI:10.1021/acs.langmuir.5b01438.
- S. Huang, K. Gawlitza, R. Von Klitzing, W. Steffen and G. K. Auernhammer, Structure and rheology of microgel monolayers at the water/oil interface, Macromolecules, 2017, 50(9), 3680–3689, DOI:10.1021/acs.macromol.6b02779.
- D. Stamou, C. Duschl and D. Johannsmann, Long-range attraction between colloidal spheres at the air–water interface: The consequence of an irregular meniscus, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 2000, 62(4B), 5263–5272, DOI:10.1103/PhysRevE.62.5263.
- V. S. Grishina, V. S. Vikhrenko and A. Ciach, Triangular lattice models for pattern formation by core–shell particles with different shell thicknesses, J. Phys.: Condens. Matter, 2020, 32(40), 405102, DOI:10.1088/1361-648X/ab9979.
- V. Grishina, V. Vikhrenko and A. Ciach, Structural and thermodynamic peculiarities of core–shell particles at fluid interfaces from triangular lattice models, Entropy, 2020, 22(11), 1–17, DOI:10.3390/e22111215.
- B. Viel, Strukturierte Kolloidpartikel Für Ultrahydrophobe, Schmutzabweisende Oberflächen, 2007 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2sm00644h |
| This journal is © The Royal Society of Chemistry 2022 |