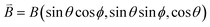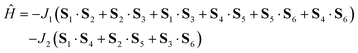Open Access Article
Open Access ArticleA trigonal prismatic Cu6-pyrazolato complex containing a μ6-F ligand†
Logesh
Mathivathanan
a,
Karrar
Al-Ameed‡
b,
Katerina
Lazarou
c,
Zdeněk
Trávníček
d,
Yiannis
Sanakis
c,
Radovan
Herchel
*d,
John E.
McGrady
*b and
Raphael G.
Raptis
*a
aDepartment of Chemistry and Biochemistry, Florida International University, 11200 SW 8th ST, Miami, FL, USA 33199. E-mail: rraptis@fiu.edu
bDepartment of Chemistry, South Parks Road, University of Oxford, OX1 3QR, UK. E-mail: john.mcgrady@chem.ox.ac.uk
cInstitute of Nanoscience and Nanotechnology, NCSR “Demokritos”, 15310 Ag. Paraskevi, Attiki, Greece
dRegional Centre of Advanced Technologies and Materials, Department of Inorganic Chemistry, Faculty of Science, Palacký University, 17. listopadu 12, CZ-77146 Olomouc, Czech Republic. E-mail: radovan.herchel@upol.cz
First published on 4th November 2015
Abstract
The encapsulation of a fluoride ion in a trigonal prismatic CuII6-pyrazolato cage results in a small expansion of the Cu6-host. The structural, electronic and magnetic features of the Cu6-complex, containing an endohedral fluoride in the rare μ6-F coordination mode, are compared with those of the parent complex with a vacant Cu6-cage.
Introduction
Structural changes in multinuclear complexes of open-shell metals are reflected in their intramolecular isotropic Heisenberg exchange parameters (J), whose sign and magnitude are related to the topology of the magnetically coupled cluster. Simple magnetostructural relationships exist for several dinuclear and trinuclear systems with a single (or one predominant) magnetic exchange path. Among such complexes, those of M2(μ-O/OR) and M3(μ3-O/OR), M = Cu and Fe, are the best studied.1–4 Even subtle structural changes, such as the M–O–M angle, are often clearly reflected in the magnitude of J values, determined by analysis of the solid state, variable temperature, magnetic susceptibility measurements.5 However, in larger clusters, simple magnetostructural relationships are often less easy to define, and a priori prediction of the magnetic properties remains a challenge.6 As part of our ongoing work exploring the chemistry of new molecular architectures based on trinuclear Cu(II)-pyrazolato triangles, we have reported the structures, electrochemistry and magnetochemistry of hexanuclear trigonal prismatic Cu6-pyrazolato complexes of the general formula [PPN][{Cu3(μ3-O)(μ-4-R-pz)3}2(3,5-Ph2-4-R′-pz)3)], (Cu6-cages, [PPN][1], R = R′ = H, [PPN] = bis(triphenylphospine)iminium cation).7 Magnetic susceptibility studies of [PPN][1] showed a spin-frustrated system with a stronger antiferromagnetic isotropic exchange within the triangular Cu3(μ3-O)-units and a weaker one between them.8 We have also shown that [PPN][1] and its analogues (R, R′ = Cl) undergo two reversible one-electron electrochemical oxidations to mixed-valent CuII/III species.Here we describe a related homovalent Cu(II)6–pyrazolate cluster, [{Cu3(μ3-OH)(μ-pz)3}2(μ-3,5-Ph2pz)3(μ6-F)], 2, now containing an encapsulated μ6-fluoride ion, isolated in the course of our efforts to prepare the aforementioned chemically oxidized variants of [PPN][1] with [Fc][PF6] as an oxidizing agent. Fluoride ions typically form complexes with the alkali and alkaline earth metals where the coordination numbers are generally high,9 but complexes with the coinage metals are less common.10 Whilst encapsulated halide ions have recent precedent, Cu–F bonds are in general uncommon; fluorides have often been used to stabilize higher oxidation states of Cu such as CuIII as in the paramagnetic K3CuF6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10a and CuII–F and CuIII–F bonds have also been proposed as intermediates in aryl fluorinating reagents.10b Fluoride coordination to trinuclear Cu-complexes also has some biological relevance as even concentrations of F− as low as 10−6 to 10−4 M can inhibit the electron transfer chemistry of laccase-like enzymes.11 The original serendipitous synthesis of 2 was subsequently reproduced systematically, and we report here its X-ray crystal structure and magnetic properties along with a comparison of its electronic structure to [PPN][1].
10a and CuII–F and CuIII–F bonds have also been proposed as intermediates in aryl fluorinating reagents.10b Fluoride coordination to trinuclear Cu-complexes also has some biological relevance as even concentrations of F− as low as 10−6 to 10−4 M can inhibit the electron transfer chemistry of laccase-like enzymes.11 The original serendipitous synthesis of 2 was subsequently reproduced systematically, and we report here its X-ray crystal structure and magnetic properties along with a comparison of its electronic structure to [PPN][1].
Results and discussion
Ferricinium hexafluorophosphate, [Fc][PF6], is a convenient one-electron oxidant, especially for sequential oxidations, and we have used it extensively in the course of studies of redox-active clusters. However, the inadvertent generation of F− from the hydrolysis of [PF6]− is a known phenomenon when humidity is not vigorously excluded, and hydrolysis products of [PF6]− in the presence of Ag+ have been reported in the literature.12 In fact, controlled decomposition of [BF4]− or [PF6]− has been used systematically to prepare transition metal fluoride complexes.13 A variant of [Fc][PF6] has been found to hydrolyze into F− and phosphate, forming a metal–organometallic framework (MOMF) that contains a Co12(μ3-F)-cage. Attempts to prepare the MOMF with deliberate addition of H3PO4 and HF were not successful.14 A similar fluoride abstraction under oxidizing conditions leads here to a new Cu6-pyrazolato complex containing novel (μ6-F). The nature of the μ6-ion was probed quantitatively by elemental analysis of the bulk product.Complex 2 was crystallized – by layering MeCN, hexane, or toluene over a CH2Cl2 solution – in the triclinic P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) space group with the whole molecule in the asymmetric unit (Fig. 1) and crystallographically disordered MeCN solvent molecules, which were removed by the SQUEEZE program of the PLATON suite. Selected bond lengths of [PPN][1], along with the corresponding distances of similar [Cu6(μ6-Cl)] and [Cu6(μ6-CF)]-complexes, are listed in Table 1.
space group with the whole molecule in the asymmetric unit (Fig. 1) and crystallographically disordered MeCN solvent molecules, which were removed by the SQUEEZE program of the PLATON suite. Selected bond lengths of [PPN][1], along with the corresponding distances of similar [Cu6(μ6-Cl)] and [Cu6(μ6-CF)]-complexes, are listed in Table 1.
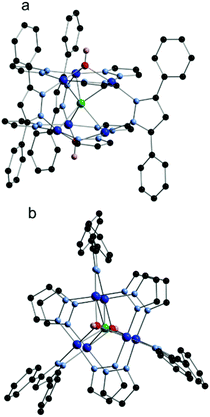 | ||
| Fig. 1 Molecular structure of 2. (a) Side view and (b) top view. Carbonic H atoms are not shown. Color coding: Cu, blue; O, red; N, light blue, C, black; H, pink; and F, green. | ||
| Cu6F, 2 | Cu6Cla | Cu6Fb | Cu6, PPN[1] | |
|---|---|---|---|---|
| a From ref. 15. b From ref. 17. | ||||
| Cu⋯Cu (inter-trimer) | 3.281(2), 3.335(2), 3.289(2) | 3.621, 3.675 | 3.056–3.382 | 2.975, 2.999, 3.028 |
| Cu⋯Cu (intra-trimer) | 3.234(2)–3.289(2) | 3.209, 3.233 | 2.832–3.112 | 3.206–3.279 |
| Cu⋯X | 2.383(5)–2.605(5) (X = F) | 2.603, 2.623 (X = Cl) | 2.338, 2.344, 2.420 (X = F) | N/A |
| Cu⋯(μ3-OR) | 2.048(3)–2.096(5) (R = H) | 2.083, 2.084 (R = Me) | 1.984, 1.991, 2.012, 2.013 (R = Me) | 1.883–1.894 |
The hexanuclear core of complex 2 is very similar to that of the anion [1]−, consisting of two triangular Cu3(μ-pz)3-units, clipped together by three μ-3,5-Ph2-pz bridges which hold the two Cu3-units in a trigonal prism. The trigonal prismatic arrangement of Cu3-triangles is uncommon in Cu–pyrazolate chemistry, and only three examples are available in the literature, reported by us7,8 and by others.15–17 The capping (μ3-OH) ligands of 2 are located 0.824 and 0.858 Å above the Cu3-planes, a somewhat larger deviation than found in typical Cu3(μ3-OH) complexes where the capping-OH is located only ca. 0.50 Å above the plane.18 Complex 2 contains an unsymmetrically encapsulated μ6-F ion with Cu–F distances in the range 2.383(5)–2.605(5) Å and the fluoride ligand located 1.610 and 1.693 Å from the two Cu3-planes, forming Cu–F–Cu angles of 81.3(1)°–83.7(1)°. In related [Cu3(μ3-X)2]-complexes (X = Cl and Br) the μ3-X ligands are again located farther from the Cu3-plane, forming similarly acute Cu–X–Cu angles (Cu3-plane⋯μ3-X: 1.769 Å and 1.927 Å for X = Cl and Br, respectively; Cu–X–Cu: ∼80°).18,19 The Cu⋯F distances are significantly longer than the sums of copper and fluorine ionic radii (1.98 Å) and covalent radii (2.09 Å), but shorter than the sum of their van der Waals radii (2.87 Å). No single radius can capture the size of a highly anisotropic ion like Cu2+: in this case the fluoride ligand is directed towards the doubly occupied dz2, so the van der Waals radius gives the most faithful estimate of the size of the cavity required to accommodate the fluoride ion. In the [Cu6(μ6-F)] complex reported by Cañon-Mancisidor et al., [Cu6(μ6-F)(μ-OH)(μ3-OCH3)2(μ-OCH3)2(3,5-Me2pz)6], has two pyrazolate and one methoxy “clips” between Cu3-units, making both the Cu⋯Cu and Cu–F bonds shorter than those of 2 (see Table 1). The structural parameters of 2 are also comparable to those previously reported for the corresponding [Cu6(μ6-Cl] complex in which the μ6-Cl is equidistant from both Cu3-planes at 1.829 Å. Similar Cu–Cl distances are also present in a related [Cu6(μ6-Cl)]-complex where the Cu3-triangles are connected only by the μ6-Cl ligand, as a result of which the Cu centres are much farther apart (4.21 Å).20 Comparison of the structure with that of PPN[1] shows that the endohedral F– brings about only minor structural changes to the Cu6-cage, although the trigonal prismatic cavity expands to accommodate the fluoride ion in 2. In PPN[1] the planarity of Cu3(μ3-O) triangles imposes a strained geometry on the four-coordinate Cu-centres with trans O–Cu–N angles of 156.6(2)°–168.6(2)°. In contrast, the pyramidal Cu3(μ3-OH) moieties in 2 allow a relaxed coordination sphere with trans HO–Cu–N angles approximating the ideal 180°.
Analysis of the magnetic data
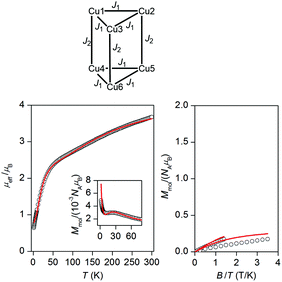
The temperature dependence of effective magnetic moment and the isothermal magnetization data for the reported compound 2 are depicted in Fig. 2. The effective magnetic moment is 3.67μB at room temperature, decreasing almost linearly to 2.36μB at 50 K and finally dropping sharply to 0.64μB at 1.9 K. The 50 K value of 2.36μB is much lower than the theoretical spin only value for six non-interacting Cu(II) ions with g = 2.0 (4.24μB), indicating the existence of strong antiferromagnetic exchange interactions. The observed behaviour of μeff/μB can be rationalized on a qualitative level by assuming dominant antiferromagnetic exchange within each μ3-OH–Cu3 triangle, which leads to SCu3 = 1/2 ground spin states. The two doublet states then couple weakly through pyrazolate ligands to generate a singlet and triplet: in the limit of weak coupling two independent S = 1/2 paramagnets yield a μeff of 2.45μB for g = 2.0, close to the experimental value at 50 K.A more quantitative analysis comes from considering the spin Hamiltonian shown in eqn (1), which is precisely analogous to that used in the analysis of [1]−.
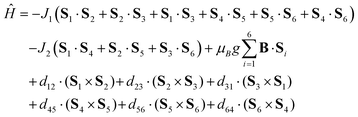 | (1) |
J 1 and J2 describe the isotropic exchange within μ3-OH–Cu3 triangles and between the two triangles (mediated by pyrazolate ligands), respectively. Antisymmetric exchange within each μ3-OH–Cu3 triangle was shown to be important in [1] and is expressed by dij vectors, (dx, dy, dz)ij.21 Application of Moriya symmetry rules22 for the triangle results in only one non-zero component: dij = (0, 0, dz)ij and it was assumed that (dz)ij are equal for all pairs. Furthermore, the averaged molar magnetization was calculated as an integral average (eqn (2)), because the measurement was performed on a powder sample (eqn (2))
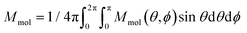 | (2) |
The temperature- and field-dependent magnetic data were fitted simultaneously to the Hamiltonian (1), resulted in best-fit values of J1 = −147 cm−1, J2 = −35 cm−1, |dz| = 30.2 cm−1 with an isotropic g-factor fixed to 2.1 (as used for [1]−). A small amount of monomeric paramagnetic impurity (PI) was introduced (mole fraction xPI = 2.7%), leading to a correction of the overall magnetization according to Msample = (1 − xPI)Mmol + 6·xPI·MPI, where MPI was calculated using the Brillouin function. The fitted J values are comparable to the constants reported by Kamiyama: (Cu6Cl, J1 = −133 cm−1, J2 = −34 cm−1) and Coronado (Cu6F J1(a) = −94 cm−1, J1(b) = −131 cm−1, J2(a) = −22 cm−1 and J2(b) = −4 cm−1 where J-values have been scaled according to definition in eqn (1). A comparison of the fitted parameters of 2 with those previously reported for [1]− (J1(av) = −675 cm−1, J2 = −26 cm−1, g = 1.95 and |dz| = 30.0 cm−1),8 suggests that intra-triangular coupling is significantly reduced in 2, while the inter-triangular coupling and the antisymmetric exchange parameters are very similar. Attempts to fit the magnetic data of 2 without the antisymmetric exchange, as done in Cu6Cl15 and Cu6F,17 resulted in J1 = −151 cm−1, J2 = −47 cm−1, xPI = 4.2% (Fig. S1, ESI†) and a rather larger deviation of the fit from the magnetic data, particularly at low temperature. On this basis, it seems that non-Heisenberg interactions may play a role in determining the magnetic behavior of 2.
EPR spectroscopy
The magnetic susceptibility measurements of 2 indicate antiferromagnetic interactions, which result in a diamagnetic ground state. At 4.2 K, the X-band EPR spectrum from a powdered sample of 2 gives rise to a weak signal, which is consistent with a monomeric Cu2+ (S = 1/2) species, most probably arising from impurities. At higher temperatures a new signal emerges at g ∼ 2.05 (Fig. 3), whose temperature dependence indicates that it arises from excited states with S ≠ 0. The spectra across the whole temperature range consist of a derivative-like Lorrentzian signal with a linewidth, ΔHpp, of ∼400 G. No notable temperature-dependent shift in the resonance field or in linewidth is observed. The line-shape of the spectrum does not allow to identify contributions of sub-spectra attributable to distinct spin manifolds. The derivative-like signal is isotropic, apparently inconsistent with the antisymmetric exchange that proved significant in the fitting of the magnetic data. We suggest that at a given temperature the observed spectrum represents a thermal distribution over several spin states, averaging out any anisotropic effect. Similar isotropic signals have been observed in copper containing clusters and they have been interpreted on the basis of fast transition between different spin manifolds.23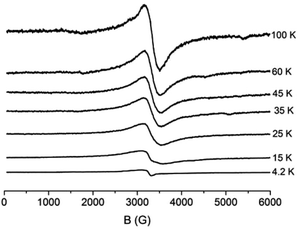 | ||
| Fig. 3 X-band EPR spectra from a powdered sample of 2. The spectra have been scaled as I × T. EPR conditions: microwave power, 1.5 mW, modulation amplitude, 15 Gpp, microwave frequency, 9.42 GHz. | ||
Computational analysis
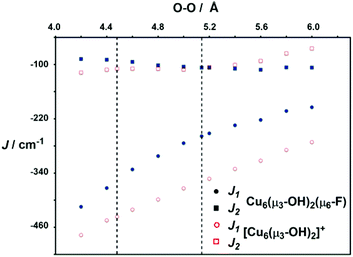
In order to explore the nature of the magnetic interactions in 2, we have performed a series of computations using broken-symmetry density functional theory, following the protocol developed in our previous paper on the μ3-O bridged Cu6 cluster, [{Cu3(μ3-O)(μ-4-R-pz)3}2(3,5-Ph2-4-R′-pz)3)]− ([1]−). All calculations were performed using the B3LYP functional in the ADF2013 software package (see Computational methods for further details). In order to extract the coupling constants, J, differences in energy between various configurations are mapped onto differences between the diagonal elements of a Heisenberg spin Hamiltonian of the formusing the pairwise protocol proposed by Ruiz et al. The resulting values of J1 and J2 are −130 cm−1 and −51 cm−1, respectively, entirely consistent with the values of −151 cm−1 and −47 cm−1 obtained from the best fits to the experimental data. In comparison, the μ3-O analogue [1]− studied previously has a very similar value of J2 but more strongly antiferromagnetic J1 (calculated: J1 = –390 cm−1J2 = –40 cm−1vs. measured J1 = ∼ −630 cm−1J2 = –44 cm−1, respectively.§ The reduction in the intra-triangle coupling, J1, is typical of a switch from a μ3-O architecture with approximately planar Cu3O units to a highly pyramidalised Cu3(μ3-OH). In contrast the inter-triangle coupling, J2, is largely unaffected by the change in μ3 bridging ligand. The presence of the μ6-F ligand is unlikely to provide effective exchange pathways for inter-triangle coupling as the Cu–F vectors are almost orthogonal to the magnetic orbitals (Cu dx2−y2 in a local coordinate system), and indeed removing the fluoride (without allowing any structural relaxation) in fact alters the magnitude of both J1 (−146 cm−1) and J2 (−71 cm−1). However, when the cluster is allowed to relax after removal of the fluoride ion, the separation between the OH oxygen atoms decreases to 4.48 Å from a value of 5.14 Å in 2 (dashed lines in Fig. 4): the steric pressure exerted by the fluoride effectively inflates the cluster, pushing the μ3-OH ligand out of the Cu3 plane.
In both 2 and the corresponding cation where the fluoride has been removed, the values of J1 are strongly dependent on the O–O separation: shorter distances allow the Cu3(μ3-OH) units to approach planarity more closely, and so maximise the overlap of the magnetic orbitals with the hydroxy bridge. The contraction of the O–O distance in the absence of fluoride causes a further indirect increase in J1 to −220 cm−1. Thus the presence of the fluoride clearly distorts the structure substantially, with the consequence that the magnetic exchange within the triangles is reduced.
Conclusions
In this paper we report the synthesis and characterisation of a trigonal prismatic Cu6 cluster containing an encapsulated μ6-F− ligand. The original observation of this cluster arose from serendipitous hydrolysis of a [PF6]− anion, but it was subsequently synthesised via a rational route. The pre-formed Cu6-cage acts as a host for the fluoride ion; fluoride is not a template for the organization of the Cu6-cage around it. Structural characterization and a detailed analysis of the magnetic properties suggest that the fluoride ion inflates the Cu6 cage, and the resultant greater pyramidalisation of the Cu3(μ3-OH) triangles causes a significant reduction in the intra-triangle coupling.Experimental section
Materials and methods
All reagents were purchased from commercial sources and used without further purification. Solvents were dried according to standard procedures. PPN[1] was prepared according to published procedure. Elemental analysis was performed at Galbraith Laboratories, Inc. 1H-NMR was recorded in CD2Cl2 in a Bruker Avance 400 spectrometer.X-ray crystallography
Single crystal X-ray crystallography data (Table 2) were obtained from a crystal mounted atop a glass fiber using a Bruker SMART APEX II diffractometer fitted with a graphite-monochromated Mo-Kα radiation at ambient temperature. Data were collected using the APEX 2 suite and corrected for Lorentz and polarization effects.24 The structure was refined using the SHELXTL-direct methods and refined by full-matrix least squares on F2.25 The disordered interstitial water electron densities were removed by employing the SQUEEZE procedure supplied with the PLATON suite.26 CCDC reference number 1429538.| 2 | |
|---|---|
| Formula | C63H53Cu6FN18O2 |
| M r | 1494.47 |
| Space group |
P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) |
| a (Å) | 13.344(6) |
| b (Å) | 16.175(8) |
| c (Å) | 16.597(8) |
| α (°) | 91.652(6) |
| β (°) | 105.727(6) |
| γ (°) | 93.025(6) |
| V (Å3) | 3440(3) |
| Z | 2 |
| μ (mm−1) | 1.878 |
| ρ calc (g cm−3) | 1.443 |
| N t | 37![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 037 037 |
| N | 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 483 483 |
| R 1/wR2 (I > 2σ(I)) | 0.0653/0.1654 |
| R 1/wR2 (all data) | 0.1337/0.1897 |
| GOF | 0.817 |
| max/min Δe (e Å−3) | 1.194/−0.708 |
Magnetic measurements
The temperature dependence of the magnetization at an applied field of B = 0.1 T and the field dependence of the magnetization up to B = 7 T at T = 2 and 5 K were acquired for a powder sample of 2 using MPMS XL7 SQUID magnetometer (Quantum Design). The experimental data were corrected for the underlying diamagnetism using empirical equation, χdia = −5M × 10−12 m3 mol−1 (SI units), where M is molar mass of the compound in g mol−1.27EPR spectroscopy
X-band EPR measurements were carried out on an upgraded Bruker ER-200D spectrometer equipped with an Oxford ESR 9000 cryostat, an Anritsu MF76A frequency counter, and a Bruker 035M NMR Gaussmeter with the perpendicular mode standard cavity 4102ST.Computational methods
Calculations reported in this paper were performed using the geometry of 2, and spin-unrestricted DFT as implemented in the ADF2013 package.28 The hybrid B3LYP exchange–correlation functional was used throughout,29–31 in conjunction with the polarized triple-zeta and double-zeta quality Slater-type basis functions on Cu and main-group atoms, respectively. All phenyl groups were replaced by hydrogens in the model structure, the geometry of which was optimised in the all-ferromagnetic S = 3 state. The exchange coupling constants, Jij, of the Heisenberg–Dirac–van Vleck (HDVV) spin Hamiltonian can be estimated using the broken-symmetry approach developed by Noodleman et al.32 This method establishes the one-to-one mapping between diagonal elements of the HDVV spin Hamiltonian matrix computed in products of single-centre spin functions and the diagonal elements of the exact non-relativistic Hamiltonian matrix computed in single-determinant configurations. The configurations used correspond to the highest total spin (|αααααα>, MS = 3) and so-called broken-symmetry (BS) states with different occupation of magnetic spin-orbitals. In this case there are 31 distinct broken-symmetry states that are permutations of |αααααβ〉 (MS = 2), |ααααββ〉 (MS = 1) and |αααβββ〉 (MS = 0). The remaining 32 spin functions (there are 26 = 64 in total) are simply the spin-inverted counterparts of those listed above. The energies of the broken-symmetry states were computed as single points at the optimised geometry of the ferromagnetic state. Due to the non-orthogonality of the computed HS and BS single determinants, the mapping between the diagonal elements holds only approximately.33,34 Exchange coupling constants computed in this way within the DFT framework are typically overestimated and Ruiz and co-workers have suggested that this is because the spin-projection implied in the mapping of broken-symmetry-state energies onto the diagonal elements of the isotropic exchange Hamiltonian accounts for non-dynamical electron correlation, which is already accounted for to some extent in the UDFT-BS solutions.35a,g For bimetallic systems, Ruiz and co-workers have proposed an alternative expression, where the energy of the BS state is mapped directly onto the energy of the lowest spin state (i.e. the eigenvalue of the Heisenberg Hamiltonian rather than the diagonal element).| EHS − EBS = −Jij(2SiSj + Si) |
This approach has been shown to give good agreement between the computed and experimental values of Jij, particularly when the B3LYP functional is used.35a–f,36 This equation has been applied to polynuclear systems within the pairwise interaction approach,6,35g,37 notably in our previous work on the [{Cu3(μ3-O)(μ-4-R-pz)3}2(3,5-Ph2-4-R′-pz)3)]+ cation.8 We therefore adopt the Ruiz protocol in this work, noting that the alternative mapping proposed by Noodleman results in Jij values that are larger by a factor of 2.
Acknowledgements
L. M. and R. G. R. acknowledge financial support for this work by the National Science Foundation, USA (CHE 1213683). K. A. acknowledges support from the HCED in Iraq. R.H. and Z.T. acknowledge the Ministry of Education, Youth and Sports of the Czech Republic (project no. LO1305).Notes and references
- C. Cañada-Vilalta, T. A. O'Brien, E. K. Brechin, M. Pink, E. R. Davidson and G. Christou, Inorg. Chem., 2004, 43, 5505–5521 CrossRef PubMed.
- S. M. Gorun, G. C. Papaefthymiou, R. B. Frankel and S. J. Lippard, J. Am. Chem. Soc., 1987, 109, 4244–4255 CrossRef CAS.
- S. M. Gorun and S. J. Lippard, J. Am. Chem. Soc., 1985, 107, 4568–4570 CrossRef CAS.
- A. Riisio, M. M. Hanninen and R. Sillanpaa, Eur. J. Inorg. Chem., 2012, 1048–1053 CrossRef.
- I. Bertini, C. Luchinat and G. Parigi, Solution NMR of paramagnetic molecules: applications to metallobiomolecules and models, Elsevier Science, 2001 Search PubMed.
- E. Ruiz, Struct. Bonding, 2004, 113, 71 CrossRef CAS.
- G. Mezei, M. Rivera-Carrillo and R. G. Raptis, Dalton Trans., 2007, 37–40 RSC.
- E. M. Zueva, M. M. Petrova, R. Herchel, Z. Travnicek, R. G. Raptis, L. Mathivathanan and J. E. McGrady, Dalton Trans., 2009, 5924–5932 RSC.
- (a) S. Wuttke, A. Lehmann, G. Scholz, M. Feist, A. Dimitrov, S. I. Troyanov and E. Kemnitz, Dalton Trans., 2009, 4729–4734 RSC; (b) C. Knapp, E. Lork, P. G. Watson and R. Mews, Inorg. Chem., 2002, 41, 2014–2025 CrossRef CAS PubMed; (c) F.-Q. Liu, A. Kuhn, R. Herbst-Irmer, D. Stalke and H. W. Roesky, Angew. Chem., Int. Ed., 1994, 33, 555–556 CrossRef.
- (a) T. V. Popova and N. V. Aksenova, Russ. J. Coord. Chem., 2003, 29, 743–765 CrossRef CAS; (b) Y. Ye, S. D. Schimler, P. S. Hanley and M. S. Sanford, J. Am. Chem. Soc., 2013, 135, 16292–16295 CrossRef CAS PubMed.
- (a) A. Naqui and S. D. Varfolomeev, FEBS Lett., 1980, 113, 157 CrossRef CAS; (b) K. P. Kepp, Inorg. Chem., 2015, 54, 476–483 CrossRef CAS PubMed.
- R. Fernandez-Galan, B. R. Manzano, A. Otero, M. Lanfranchi and M. A. Pellinghelli, Inorg. Chem., 1994, 33, 2309–2312 CrossRef CAS.
- (a) J. Vela, J. M. Smith, Y. Yu, N. A. Ketterer, C. J. Flaschenriem, R. J. Lachicotte and P. L. Holland, J. Am. Chem. Soc., 2005, 127, 7857–7870 CrossRef CAS PubMed; (b) D. L. Reger, R. P. Watson, J. R. Gardinier, M. D. Smith and P. J. Pellechia, Inorg. Chem., 2006, 45, 10088–10097 CrossRef CAS PubMed; (c) B. F. Straub, F. Rominger and P. Hofmann, Inorg. Chem., 2000, 39, 2113–2119 CrossRef CAS PubMed.
- S. A. Kumalah Robinson, M.-V. L. Mempin, A. J. Cairns and K. T. Holman, J. Am. Chem. Soc., 2011, 133, 1634–1637 CrossRef CAS PubMed.
- A. Kamiyama, T. Kajiwara and T. Ito, Chem. Lett., 2002, 17, 9–12 Search PubMed.
- H. Zhang, Y. Lu, Z.-m. Zhang and E.-b. Wang, Inorg. Chem. Commun., 2012, 17, 9–12 CrossRef CAS.
- W. Cañon-Mancisidor, C. J. Gomez-Garcia, G. M. Espallargas, A. Vega, E. Spodine, D. Venegas-Yazigi and E. Coronado, Chem. Sci., 2014, 5, 324–332 RSC.
- P. A. Angaridis, P. Baran, R. Boca, F. Cervantes-Lee, W. Haase, G. Mezei, R. G. Raptis and R. Werner, Inorg. Chem., 2002, 41, 2219–2228 CrossRef CAS PubMed.
- R. Boca, L. Dlhan, G. Mezei, T. Ortiz-Pérez, R. G. Raptis and J. Telser, Inorg. Chem., 2003, 42, 5801–5803 CrossRef CAS PubMed.
- E. V. Lider, E. V. Persypkina, A. I. Smolentsev, V. N. Elokhina, T. I. Yaroshenko, A. V. Virovets, V. N. Ikorskii and L. G. Lavrenova, Polyhedron, 2007, 26, 1612–1618 CrossRef CAS.
- R. Boča and R. Herchel, Coord. Chem. Rev., 2010, 254, 2973–3025 CrossRef.
- T. Moriya, Phys. Rev., 1960, 120, 91–98 CrossRef CAS.
- (a) L. Banci, A. Bencini and D. Gatteschi, Inorg. Chem., 1983, 22, 2681–2683 CrossRef CAS; (b) I. A. Koval, H. Akhideno, S. Tanase, C. Belle, C. Duboc, E. Saint-Aman, P. Gamez, D. M. Tooke, A. L. Spek, J.-L. Pierre and J. Reedijk, New J. Chem., 2007, 31, 512–518 RSC; (c) M. V. Fedin, S. L. Veber, I. A. Gromov, V. I. Ovcharenko, R. Z. Sagdeev and E. G. Bagryanskaya, J. Phys. Chem. A, 2007, 111, 4449–4455 CrossRef CAS PubMed; (d) M. V. Fedin, S. L. Veber, E. L. Bagryanskaya and V. I. Ovcharenko, Coord. Chem. Rev., 2015, 289–290, 341–356 CrossRef CAS and references therein.
- (a) Data collection: APEX2 suite, Bruker AXS Inc., Madison, WI, USA, 2010 Search PubMed; (b) Data reduction and refinement: SAINT, SHELXT and SHELXL in APEX3 suite, Bruker AXS Inc., Madison, WI, USA, 2015 Search PubMed.
- G. M. Sheldrick, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 2015, 71, 3–8 CrossRef PubMed.
- A. L. Spek, Acta Crystallogr., Sect. D: Biol. Crystallogr., 2009, 65, 148–155 CrossRef CAS PubMed.
- R. Boča, A Handbook of Magnetochemical Formulae, Elsevier, Amsterdam, 2012 Search PubMed.
- (a) G. te Velde, F. M. Bickelhaupt, S. J. A. van Gisbergen, C. Fonseca Guerra, E. J. Baerends, J. G. Snijders and T. Ziegler, J. Comput. Chem., 2001, 22, 931–967 CrossRef; (b) C. Fonseca Guerra, J. G. Snijders, G. te Velde and E. J. Baerends, Theor. Chem. Acc., 1998, 99, 391–403 CAS; (c) ADF2013, SCM, Theoretical Chemistry, Vrije Universiteit, Amsterdam, The Netherlands, http://www.scm.com.
- D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef.
- P. J. Stevens, J. F. Devlin, C. F. Chabalowski and M. J. Frisch, J. Phys. Chem., 1994, 98, 11623–11627 CrossRef.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789 CrossRef CAS.
- (a) L. Noodleman and J. G. Norman Jr., J. Chem. Phys., 1979, 70, 4903–4906 CrossRef CAS; (b) L. Noodleman, J. Chem. Phys., 1981, 74, 5737–5743 CrossRef CAS; (c) L. Noodleman and E. R. Davidson, Chem. Phys., 1986, 109, 131–143 CrossRef; (d) L. Noodleman and D. A. Case, Adv. Inorg. Chem., 1992, 38, 423–470 CrossRef CAS.
- A. Bencini and F. Totti, Int. J. Quantum Chem., 2005, 101, 819–825 CrossRef CAS.
- (a) R. Caballol, O. Castell, F. Illas, P. R. Moreira and J. P. Malrieu, J. Phys. Chem. A, 1997, 101, 7860–7866 CrossRef CAS; (b) T. Soda, Y. Kitagawa, T. Onishi, Y. Takano, Y. Shigeta, H. Nagao, Y. Yoshioka and K. Yamaguchi, Chem. Phys. Lett., 2000, 319, 223–230 CrossRef CAS; (c) E. Ruiz, A. Rodriguez-Fortea, J. Cano, S. Alvarez and P. Alemany, J. Comput. Chem., 2003, 24, 982–989 CrossRef CAS PubMed; (d) M. Shoji, K. Koizumi, Y. Kitagawa, T. Kawakami, S. Yamanaka, M. Okumura and K. Yamaguchi, Chem. Phys. Lett., 2006, 432, 343–347 CrossRef CAS; (e) E. M. Zueva, S. A. Borshch, M. M. Petrova, H. Chermette and An. M. Kuznetsov, Eur. J. Inorg. Chem., 2007, 4317–4325 CrossRef CAS.
- (a) E. Ruiz, J. Cano, S. Alvarez and P. Alemany, J. Comput. Chem., 1999, 20, 1391–1400 CrossRef CAS; (b) E. Ruiz, P. Alemany, S. Alvarez and J. Cano, J. Am. Chem. Soc., 1997, 119, 1297–1303 CrossRef CAS; (c) E. Ruiz, P. Alemany, S. Alvarez and J. Cano, Inorg. Chem., 1997, 36, 3683–3688 CrossRef CAS PubMed; (d) E. Ruiz, J. Cano, S. Alvarez and P. Alemany, J. Am. Chem. Soc., 1998, 120, 11122–11129 CrossRef CAS; (e) E. Ruiz, C. Graaf, P. Alemany and S. Alvarez, J. Phys. Chem. A, 2002, 106, 4938–4941 CrossRef CAS; (f) A. Rodriguez-Fortea, P. Alemany, S. Alvarez and E. Ruiz, Eur. J. Inorg. Chem., 2004, 143–153 CrossRef CAS; (g) E. Ruiz, A. Rodriguez-Fortea, J. Cano, S. Alvarez and P. Alemany, J. Comput. Chem., 2003, 24, 982–989 CrossRef CAS PubMed; (h) E. Ruiz, A. Rodriguez-Fortea, P. Alemany and S. Alvarez, Polyhedron, 2001, 20, 1323–1330 CrossRef CAS; (i) E. Ruiz, J. Cano, S. Alvarez, A. Caneschi and D. Gatteschi, J. Am. Chem. Soc., 2003, 125, 6791–6794 CrossRef CAS PubMed.
- E. Ruiz, S. Alvarez, J. Cano and V. Polo, J. Chem. Phys., 2005, 123, 164110–164117 CrossRef PubMed.
- J. Cano, R. Costa, S. Alvarez and E. Ruiz, J. Chem. Theory Comput., 2007, 3, 782–788 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available: Fit of the magnetic data of 2 without antisymmetric exchange and total energies and optimised cartesian coordinates for all computed spin states. CCDC 1429538. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c5dt03892h |
| ‡ Permanent address: Faculty of Science, University of Kufa, Najaf, Iraq. |
| § The value for J1 is somewhat smaller than that reported in our previous work on 1+,8 where Gaussian basis sets were used. |
| This journal is © The Royal Society of Chemistry 2015 |