 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Quantized friction across ionic liquid thin films†
Alexander M.
Smith
a,
Kevin R. J.
Lovelock
b,
Nitya Nand
Gosvami
c,
Tom
Welton
b and
Susan
Perkin
*a
aDepartment of Chemistry, Physical and Theoretical Chemistry Laboratory, University of Oxford, South Parks Road, Oxford OX1 3QZ, UK. E-mail: susan.perkin@chem.ox.ac.uk
bDepartment of Chemistry, Imperial College London, London SW7 2AZ, UK
cDepartment of Mechanical Engineering and Applied Mechanics, University of Pennsylvania, 220 S. 33rd St., Philadelphia, PA 19104, USA
First published on 7th August 2013
Abstract
Ionic liquids – salts in the liquid state under ambient conditions – are of great interest as precision lubricants. Ionic liquids form layered structures at surfaces, yet it is not clear how this nano-structure relates to their lubrication properties. We measured the friction force between atomically smooth solid surfaces across ionic liquid films of controlled thickness in terms of the number of ion layers. Multiple friction–load regimes emerge, each corresponding to a different number of ion layers in the film. In contrast to molecular liquids, the friction coefficients differ for each layer due to their varying composition.
The importance of friction, and its reduction by lubrication of the sliding surfaces, has been recognized since ancient times and yet some of the most fundamental questions in this area remain unresolved.1,2 The classical laws of friction and lubrication do not apply at the nano-scale, where molecular interactions and arrangements determine the surface forces.2–4 The current renaissance in the study of friction mechanisms is motivated by the need to understand and control shear motion and lubrication in microscopic devices and between nano-scale objects.5–9 Of particular significance in microscopic systems, or when the external load is relatively small, is the adhesion contribution to the measured friction force.9–12 The presence of a thin liquid film between two solid surfaces can dramatically modify the friction and adhesion forces between them, and a particularly interesting case arises when the liquid molecules are arranged in layers between the surfaces leading to multiple adhesion values corresponding to different numbers of ion layers in the film.13–15
Ionic liquids16 are a particularly attractive class of fluids for precision tribological applications due to their low melting point and wide liquid range, extremely low volatility, high thermal stability, lubrication and wear-protection characteristics, and electrical and thermal conductivity.17–19 The interfacial structure of ionic liquids at charged surfaces consists of alternating positive and negative ion layers extending several layers into the bulk.20,21 This alternating cation/anion structure is even more striking when the liquid is confined to a film between two surfaces: measurements of the surface interaction force as a function of surface separation reveal large oscillations, substantially stronger than van der Waals or mean-field electrostatic interactions, corresponding to sequential squeeze-out of layers from between the surfaces. In contrast to molecular liquids, ionic liquids squeeze out two layers at a time – one cation layer and one anion layer – in order to maintain electroneutrality in the film.15,21–25 Despite the burgeoning interest in ionic liquids and their intricate nano-structure, very little is currently known about their mechanism of lubrication.26,27 To address this, we performed measurements of friction across films of ionic liquid with key features distinct from earlier studies15,26–28 and allowing new quantitative analysis: friction is measured across ionic liquid films of precisely controlled thickness (number of ion layers), at both positive and negative applied loads, and the adhesion and real contact area are measured concurrently. Our high resolution measurements reveal the following notable features for the first time in ionic liquid: (i) discrete friction regimes for each integer number of ion layers in the film, leading to discrete multi-valued (‘quantized’) friction as a function of load; (ii) stick–slip friction observed below a critical velocity (different for each number of ion layers); and (iii) different friction coefficients measured for each film thickness. This latter point implies that the mechanism of friction across ionic liquids is qualitatively different to non-polar liquids, where the friction coefficient is independent of film thickness.14 Put together, these findings point at new ways to control friction in microscopic systems and to develop ionic liquid lubricants for specialized applications.
The ionic liquid, 1-butyl-1-methylpyrrolidinium bis[(trifluoromethane)sulfonyl]imide or [C4C1Pyrr][NTf2] (Fig. 1(a)), was confined between two mica sheets in a Surface Force Balance (SFB) (Fig. 1(b), and further details provided in ESI†). The mica sheets are each ∼1 cm2 area and ∼2 μm thickness, atomically smooth and step-free over the whole area, mounted in crossed-cylinder orientation with radius of curvature R ∼ 0.01 m. When immersed in ionic liquids, mica surfaces have a high negative charge due to dissociation of K+ ions from the lattice.15,29 The thickness of the liquid film between the sheets was measured with sub-molecular resolution using optical interference according to a method described in detail earlier.30 We measured the normal interaction force, FN, as a function of mica–mica surface separation, D, and the lateral force, FL, between them (as a function of D and FN) which arises when one surface is translated by a lateral displacement xS at velocity vS. The measured friction responses contained certain features which are defined here as follows (and indicated in Fig. 2): If the film supports a finite stress then during initial translation FL will increase up to a yield force, FS,y. If shearing then proceeds by smooth sliding, the lateral force required to maintain sliding is the kinetic friction force, FS,k. If shearing proceeds by stick–slip, FL ranges between a minimum of FS,k at the stick-point and a maximum of the static friction force, FS,st, at the slip-point. If FS,y > FS,k (or FS,y > FS,st in the case of stick–slip) then a stiction spike is observed, of height FS,y − FS,k.
![Normal and shear forces between mica sheets across films of [C4C1Pyrr][NTf2]. (a) The cation and anion structures for the ionic liquid [C4C1Pyrr][NTf2]. (b) Schematic showing the system of ionic liquid arranged in layers between negative mica surfaces. (c) FNvs. D showing the oscillatory force law due to sequential squeeze-out of pairs of ion layers, labeled with the number of ion layers at each distance and the corresponding values of Fadh/R; data reproduced with permission.24 (d) FS,kvs. FN measured for different numbers of ion layers, i, in the film. The lines are linear fits to the data according to eqn (1). Inset diagrams indicate the liquid structure for each regime, and the circled data points are those corresponding to the traces in (e). (e) Friction loops showing FLvs. lateral displacement, xS, showing three examples measured at similar FN and vS but different numbers of ion layers, demonstrating the discrete or quantized nature of the friction (i = 9, 7, and 5).](/image/article/2013/CP/c3cp52779d/c3cp52779d-f1.gif) | ||
| Fig. 1 Normal and shear forces between mica sheets across films of [C4C1Pyrr][NTf2]. (a) The cation and anion structures for the ionic liquid [C4C1Pyrr][NTf2]. (b) Schematic showing the system of ionic liquid arranged in layers between negative mica surfaces. (c) FNvs. D showing the oscillatory force law due to sequential squeeze-out of pairs of ion layers, labeled with the number of ion layers at each distance and the corresponding values of Fadh/R; data reproduced with permission.24 (d) FS,kvs. FN measured for different numbers of ion layers, i, in the film. The lines are linear fits to the data according to eqn (1). Inset diagrams indicate the liquid structure for each regime, and the circled data points are those corresponding to the traces in (e). (e) Friction loops showing FLvs. lateral displacement, xS, showing three examples measured at similar FN and vS but different numbers of ion layers, demonstrating the discrete or quantized nature of the friction (i = 9, 7, and 5). | ||
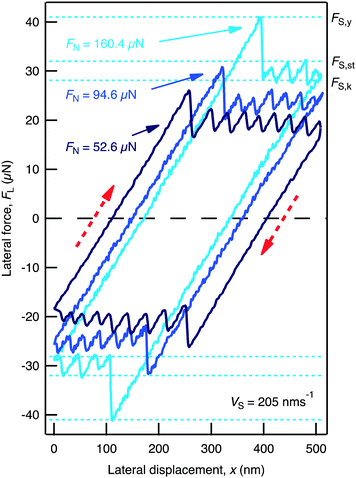 | ||
| Fig. 2 Friction loops, showing FL as a function of xS at a constant film thickness of i = 7 and for three different values of FN. The velocity is constant at vS = 205 nm s−1, and the back-and-forth displacement is in the directions indicated by (red) dashed arrows. Friction features FS,y, FS,k, and FS,st are defined for the FN = 160.4 μN trace. | ||
The profile of FN with D is an oscillatory function (Fig. 1(c)) due to the packing of the ions into layers and the sequential squeeze-out of pairs of ion layers, as expected for ionic liquids: in the case of [C4C1Pyrr][NTf2] between negatively charged surfaces the stable film structures contain odd-integer numbers of ion layers,24 which we label as i = 3, 5, 7, or 9, as shown schematically in the insets to Fig. 1(d). As a result of the oscillatory force-law between the surfaces across the liquid it is possible to vary FN – over a certain range including positive and negative values – while the number of ion layers, i, in the film remains constant. By performing this compression–de-compression at constant i, and at the same time applying lateral displacement to the top surface and detecting the resulting FL, we were able to measure FS,k as a function of FN for each number of ion layers between the surfaces. The result reveals quantized friction regimes (Fig. 1(d)). Thus there exists a friction–load relationship for each value of i, and the friction is multi-valued for each single value of load. This latter point is illustrated in Fig. 1(e) where closely similar values of FN give rise to different values of FS,y and FS,k depending on the number of ion layers.
Each of the quantized friction regimes follows an approximately linear FS,kvs. FN relationship with non-zero FS,k measured at zero (and negative) values of FN. The friction at zero applied load originates in the contribution from the adhesion force between the surfaces, Fadh, which is different for each i, as seen from the FN minima in Fig. 1c. FS,k can be expressed as a linear combination of load-dependent and adhesion-dependent contributions:10
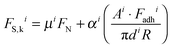 | (1) |
To obtain further insight into the molecular reorganization taking place during shear we recorded high resolution traces of FL as a function of lateral displacement of the top surface for a range of FN and vS. Fig. 2 and 3 show examples for i = 7; qualitatively similar results were observed for i = 9, 7, 5, and 3. Over the range of FN and vS studied the films exhibit a well defined yield point, with FS,y increasing in magnitude as FN increases, and stiction spikes at the onset of sliding (Fig. 2). At low vS, shearing of the film then progresses by way of a series of stick–slip cycles characterized by saw-tooth traces (Fig. 3(a)). At a critical vS (Fig. 3(b)) the stick–slip disappears and above this velocity the film shears with a smooth sliding motion (Fig. 3(c)). It was notable that FS,k is independent of vS, whilst FS,y is weakly dependent on vS. Once the direction of applied lateral motion is reversed, similar behavior is observed in the opposite direction.
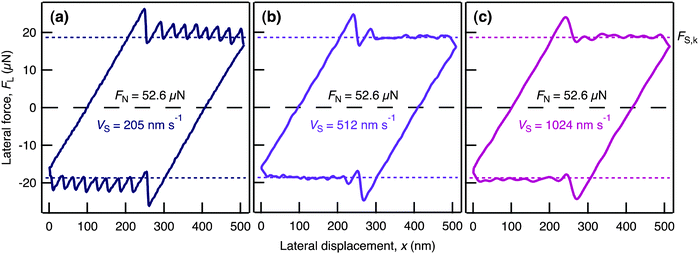 | ||
| Fig. 3 Friction loops for varying vS at constant FN. (a) vS = 205 nm s−1; (b) vS = 512 nm s−1; (c) vS = 1024 nm s−1; each measured at FN = 52.6 μN. FS,y > FS,k leading to a stiction spike in all cases, but only at slower vS are regular stick–slip cycles observed. At the critical velocity, here 512 nm s−1, one stick–slip cycle is followed by smooth sliding. At higher vS smooth sliding occurs after the initial spike. | ||
The clear yield points indicate solid-like behavior of the ionic liquid confined to films of i ≤ 9 ion layers. Subsequent stick–slip behavior observed at lower vS is most often attributed to a series of freeze-melt transitions.5,31 However in the case of ionic liquids a full-film melt is unlikely due to the high Coulombic energy barrier of ions swapping between layers, so the stick–slip is likely to involve either interlayer slips32 or intra-layer (two dimensional) melting. Furthermore, the particularly high values of FS,ki=3 compared to FS,ki>3 indicates that mid-film cation layers – the structural feature present in films of greater thickness but not in the i = 3 film – may shear-melt or slip at lower stress than the other layers and thus be responsible for the lower yield force of the thicker films.
The quantized friction presented here is a direct result of the multiple discrete values of the adhesion-controlled contribution to the total friction, and is expected to be general for liquids which form layered structures in thin films. Indeed, experiments in our laboratory with a range of other ionic liquids have revealed quantized regimes corresponding to the layer structure in every case. The result rationalizes previous reports of discontinuities in the friction across molecular liquids when the number of layers changes,10,14 here demonstrating multiple quantized friction regimes with varying friction coefficients and quantifying the effects of adhesion on the overall friction force. This result will be pivotal in explaining the boundary lubrication of rough surfaces where the liquid film is of varying thicknesses across the contact zone: the total friction is made up of differently weighted contributions from each film thickness despite uniform applied load. Thus the quantized friction regimes resolved here using atomically-smooth surfaces will provide a link between single-asperity and rough-contact friction.
Acknowledgements
This work was supported by The Leverhulme Trust (F/07 134/DK and F/07 134/DN), Taiho Kogyo Tribology Research Foundation, Weizmann UK, Infineum UK, The Office of Naval Research (N00014-10-1-0096) and the EPSRC (EP/J015202/1). Andrew Dolan is thanked for synthesis of the ionic liquid used in this work.Notes and references
- B. N. J. Persson, Sliding Friction, Springer-Verlag, 1998 Search PubMed.
- M. Urbakh, J. Klafter, D. Gourdon and J. Israelachvili, Nature, 2004, 430, 525–528 CrossRef CAS.
- B. Bhushan, J. Israelachvili and U. Landman, Nature, 1995, 374, 607–616 CrossRef CAS.
- Y. Mo, K. T. Turner and I. Szlufarska, Nature, 2009, 457, 1116–1119 CrossRef CAS.
- P. A. Thompson and M. O. Robbins, Science, 1990, 250, 792–794 CrossRef CAS.
- J. Y. Park, D. F. Ogletree, P. A. Thiel and M. Salmeron, Science, 2006, 313, 186 CrossRef CAS.
- A. Socoliuc, E. Gnecco, S. Maier, O. Pfeiffer, A. Baratoff, R. Bennewitz and E. Meyer, Science, 2006, 313, 207–210 CrossRef CAS.
- C. Lee, Q. Li, W. Kalb, X.-Z. Liu, H. Berger, R. W. Carpick and J. Hone, Science, 2010, 328, 76–80 CrossRef CAS.
- R. Guerra, U. Tartaglino, A. Vanossi and E. Tosatti, Nat. Mater., 2010, 9, 634–637 CrossRef CAS.
- J. Israelachvili, Y. L. Chen and H. Yoshizawa, J. Adhes. Sci. Technol., 1994, 8, 1231–1249 CrossRef CAS.
- Z. Deng, A. Smolyanitsky, Q. Li, X.-Q. Feng and R. J. Cannara, Nat. Mater., 2012, 11, 1032–1037 CAS.
- B. Luan and M. O. Robbins, Nature, 2005, 435, 929–932 CrossRef CAS.
- R. Horn and J. Israelachvili, J. Chem. Phys., 1981, 75, 1400–1411 CrossRef CAS.
- E. Kumacheva and J. Klein, J. Chem. Phys., 1998, 108, 7010–7022 CrossRef CAS.
- S. Perkin, T. Albrecht and J. Klein, Phys. Chem. Chem. Phys., 2010, 12, 1243–1247 RSC.
- J. P. Hallett and T. Welton, Chem. Rev., 2011, 111, 3508–3576 CrossRef CAS.
- M. Palacio and B. Bhushan, Tribol. Lett., 2010, 40, 247–268 CrossRef CAS.
- F. Zhou, Y. Liang and W. Liu, Chem. Soc. Rev., 2009, 38, 2590–2599 RSC.
- A. Somers, P. Howlett, D. MacFarlane and M. Forsyth, Lubricants, 2013, 1, 3–21 CrossRef.
- M. Mezger, H. Schröder, H. Reichert, S. Schramm, J. S. Okasinski, S. Schöder, V. Honkumaki, M. Deutsch, B. M. Ocko, J. Ralston, M. Rohwerder, M. Stratmann and H. Dosch, Science, 2008, 322, 424–428 CrossRef CAS.
- R. Atkin and G. G. Warr, J. Phys. Chem. C, 2007, 111, 5162–5168 CAS.
- K. Ueno, M. Kasuya, M. Watanabe, M. Mizukami and K. Kurihara, Phys. Chem. Chem. Phys., 2010, 12, 4066–4071 RSC.
- I. Bou-Malham and L. Bureau, Soft Matter, 2010, 6, 4062–4065 RSC.
- A. M. Smith, K. R. J. Lovelock, N. N. Gosvami, P. Licence, A. Dolan, T. Welton and S. Perkin, J. Phys. Chem. Lett., 2013, 4, 378–382 CrossRef CAS.
- S. Perkin, L. Crowhurst, H. Niedermeyer, T. Welton, N. N. Gosvami and A. M. Smith, Chem. Commun., 2011, 47, 6572–6574 RSC.
- J. Sweeney, F. Hausen, R. Hayes, G. B. Webber, F. Endres, M. W. Rutland, R. Bennewitz and R. Atkin, Phys. Rev. Lett., 2012, 109, 155502 CrossRef.
- O. Werzer, E. D. Cranston, G. G. Warr, R. Atkin and M. W. Rutland, Phys. Chem. Chem. Phys., 2012, 24, 5147–5152 RSC.
- A. Elbourne, J. Sweeney, G. B. Webber, E. J. Wanless, G. G. Warr, M. W. Rutland and R. Atkin, Chem. Commun., 2013, 49, 6797–6799 RSC.
- A. M. Smith, K. R. J. Lovelock and S. Perkin, Faraday Discuss. 10.1039/C3FD00075C.
- S. Perkin, L. Chai, N. Kampf, U. Raviv, W. Briscoe, I. Dunlop, S. Titmuss, M. Seo, E. Kumacheva and J. Klein, Langmuir, 2006, 22, 6142–6152 CrossRef CAS.
- M. Schoen, C. L. Rhykerd, D. J. Diestler and J. H. Cushman, Science, 1989, 245, 1223–1225 CAS.
- Y. Lei and Y. Leng, Phys. Rev. Lett., 2011, 107, 147801 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c3cp52779d |
| This journal is © the Owner Societies 2013 |
