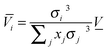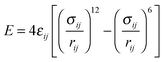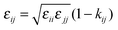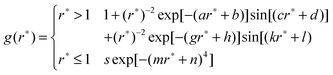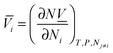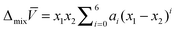Open Access Article
Open Access Article
Rapid determination of entropy and free energy of mixtures from molecular dynamics simulations with the two-phase thermodynamic model†
Received
15th June 2012
, Accepted 14th September 2012
First published on 17th September 2012
Abstract
The two-phase thermodynamic (2PT) model is generalized to determine the thermodynamic properties of mixtures. In this method, the vibrational density of states (DoS), obtained from the Fourier transform of the velocity autocorrelation function, and quantum statistics are combined to determine the entropy and free energy from the trajectory of a molecular dynamics simulation. In particular, the calculated DoS is decomposed into a solid-like and a gas-like component through the fluidicity parameter, allowing for treatments for the anharmonic effects in fluids. The 2PT method has been shown to provide reliable thermodynamic properties of pure substances over the whole phase diagram with only about a 20 ps MD trajectory. Here we show how the 2PT method can be used for mixtures with the same degree of accuracy and efficiency. We have examined the 2PT determined excess Gibbs free energies of Lennard-Jones (LJ) mixtures over a wide range of conditions (1 ≤ T* ≤ 3, 0.5 ≤ P* ≤ 2.5, 1 ≤ σBB/σAA ≤ 2, and 1 ≤ εBB/εAA ≤ 2), including the change of the off-diagonal LJ interactions. The 2PT determined values are in good agreement with those from Widom insertion or thermodynamic integration (TI). Our results suggest that the 2PT method can be a powerful method for understanding thermodynamic properties in more complicated multicomponent systems.
1. Introduction
Molecular dynamics (MD) simulations are a powerful technique for understanding the structural, energetic, dynamic, and equilibrium properties of a system at the molecular level. However, some physically significant properties, such as entropy and free energy, normally cannot be obtained from the same MD simulation. A separately designed simulation with specific algorithms or techniques is often necessary for such properties. For example, the Widom insertion,1 one of the most renowned methods for calculation of chemical potential, requires additional samplings using a ghost particle. Unfortunately, the efficiency of Widom's test particle method deteriorates quickly at high system densities because of the low fraction of successful insertions. While many more sophisticated methods are developed for high density systems, they are either not compatible with MD simulations (e.g., overlapping distribution method, umbrella sampling, etc.)2,3 or require specifically designed simulation paths (e.g. thermodynamic integration).4
Another class of methods5–10 for determination of entropy and free energy from MD simulations is based on the characterization of vibrations within a system. Assuming that the vibrations (i.e., normal modes or the density of states (DoS)) correspond to a series of independent harmonic oscillators, all thermodynamic properties of the system can be calculated based on the quantum statistics of harmonic vibrations. This approach provides excellent properties for solids (e.g., the Debye crystal)11 but becomes less accurate for liquids and gases, where the diffusive and low frequency modes are highly anharmonic. Despite these deficiencies, Karplus and Kushick6 showed that the entropy difference of a macromolecule in two conformations can be obtained from the covariance matrix of atom positions and the quasiharmonic approximations.
Recently, the effect of anharmonic modes on the thermodynamic properties was addressed in the two-phase thermodynamic (2PT) model.12 In this model, the DoS of a system, determined from the Fourier transform of the velocity autocorrelation function, is regarded as the supposition of a solid component, which contains all the harmonic modes, and a gas component, which considers all the anharmonic, diffusive modes. The essence of 2PT is to provide a fluidicity parameter for the gas/solid decomposition. Applying suitable statistical weighting functions to the gas and solid components, it has been shown that such a treatment of DoS can result in accurate absolute entropy and free energy of a variety of fluids (from Lennard-Jonesium,12 to water,13 carbon dioxide,14 and many common organic solvents)15 from a short (about 20 ps) MD trajectory. The efficiency and accuracy of this approach make it a promising tool for understanding thermodynamic driving forces in complicated systems, such as dendrimers,16–18 nanotubes,19,20 biomolecular systems,21–24etc.
Although the 2PT method has shown great success in a variety of problems, the fundamental theory was developed for pure fluids. Extension of the theory to mixtures25–27 has not been validated. The goal of the present study is to examine several possible approaches to determine the fluidicity parameter in mixtures. In pure fluids, this parameter is determined based on the temperature, molar volume, and the zero frequency intensity of the DoS. We find that for mixtures the molar volume should be replaced by the partial molar volume of each component. The excess Gibbs free energies thus obtained for Lennard-Jones mixtures are in good agreement with those from thermodynamic integration and Widom insertion. This work provides the theoretical basis for the use of 2PT in mixtures.
2. Method and theory
2.1 The vibrational density of state function
The vibrational density of state (DoS) function of component i is defined as the mass weighted sum of velocity spectral density from all atoms in the system,5| | 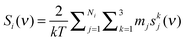 | (1) |
where mj is the mass of atom j. The velocity spectral density skj(ν) of atom j in the kth coordinate (k = x, y, and z in the Cartesian coordinate) is determined from the square of the Fourier transform of the velocities as| | 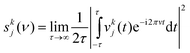 | (2) |
The DoS can also be calculated from the Fourier transform of the velocity autocorrelation function (VAC).5
2.2 Thermodynamic properties of mixtures from two-phase thermodynamic (2PT) model
The Two-Phase Thermodynamic (2PT) model12 of mixtures defines that the DoS of component i, skj(ν), with 3Ni degrees of freedom consists of a gas-like and a solid-like portion.| | | Si(ν) = Sgi(ν) + Ssi(ν) | (3) |
where the gas-like diffusive component sgi(ν) corresponds to 3Ngi = 3fiNi degrees of freedom with fi being the gas fraction of component i and the remainder, ssi(ν), describes a solid-like part (non-diffusive) of component i. Therefore, there are 3Ni − 3Ngi = 3Ni(1 − fi) solid-like degrees of freedom for component i. The thermodynamic properties Pi of the system are determined from the individual DoS components with proper weighting functions.12| | 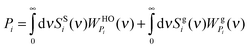 | (4) |
where 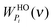 and
and 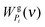 are the weighting functions of a harmonic oscillator and the corresponding gas part of component i, respectively.
are the weighting functions of a harmonic oscillator and the corresponding gas part of component i, respectively.
The decomposition of DoS is achieved by considering the gas-component as a hard sphere fluid, whose density of state is known
| | 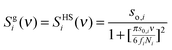 | (5) |
The solid component
Ssi(
ν) is then determined by subtracting
sgi(
ν) from the total density of state
Si(
ν). The DoS for the gas component is completely determined using two parameters:
s0,i and
fi. In order to include all the diffusive modes to the gas component,
s0,i is set to be a zero frequency DoS value for component
i,
Si(0). This guarantees that the solid component has no contribution to the diffusivity. The “fluidicity” factor
fi that determines the conceptual partition of each component between solid and gas parts can be calculated from the equation below (readers are referred to
ref. 12 for derivation details).
| | 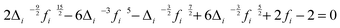 | (6) |
where Δ
i is some normalized diffusivity, whose value depends on the temperature, volume, the particle mass and
s0,i.
| | 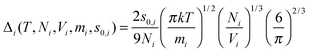 | (7) |
In the case of pure fluids,
Vi is the same as the system total volume
V. For a mixture, the system volume is shared by all components, and the partial molar volume (
![[V with combining macron]](https://www.rsc.org/images/entities/i_char_0056_0304.gif) i
i) should be used,
i.e.,
| | Vi = Ni![[V with combining macron]](https://www.rsc.org/images/entities/i_char_0056_0304.gif) i i | (8) |
To complete the 2PT model for mixtures, we need to specify the weighting functions. Conventionally, the solid-like portion is calculated from the quantum partition function, which gives the harmonic oscillator weighting functions for energy, entropy, and Helmholtz free energy as follows
5| | 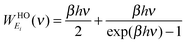 | (9a) |
| | 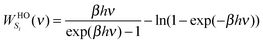 | (9b) |
| | 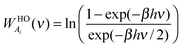 | (9c) |
where
β = 1/
kT. For the gas-component, the weighting functions are derived from the corresponding properties of hard sphere gas
12| | 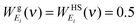 | (10a) |
| | 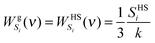 | (10b) |
| | 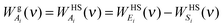 | (10c) |
Once the decomposition of the DoS is done, the partial molar thermodynamic properties of each component (without the ideal mixture contribution) can be obtained
| | 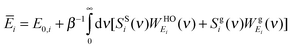 | (11a) |
| | 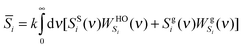 | (11b) |
| | 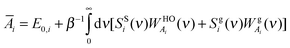 | (11c) |
where
E0,i is the reference energy and takes the form
| | | E0,i = EMDi − β−13Ni(1 − 0.5fi) | (12) |
and the properties of the mixture become
| | 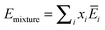 | (13a) |
| | 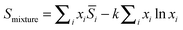 | (13b) |
| | 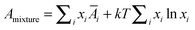 | (13c) |
The second terms (
xi ln
xi) on the right hand side of
eqn (13b) and
(13c) ensures the proper composition dependence for ideal mixtures.
2.3 The partial molar volume
The partial molar volume is needed (eqn (7)) for the determination of the fluidicity parameter in 2PT properties for a mixture. In this work we examine three estimation methods for the partial molar volume: (1) the Kirkwood–Buff theory, (2) the molecular size, and (3) the one-fluid approximation.
The Kirkwood–Buff (KB) theory28 provides a rigorous method to determine partial molar volume from the radial distribution function. According to the KB theory, the partial molar volume of component i is
| | 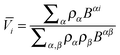 | (14) |
where
ρi =
Ni/
V is the number density;
Bαβ stands for the
cofactor of the element
Bαβ in the determinant |
B|. The elements of
matrix B is defined as
| | | Bαβ = ραρβGαβ + ραδαβ | (15) |
with
δαβ being the Kronecker delta function.
Gαβ is the Kirkwood–Buff integral (KBI) or the fluctuation integral
29| | 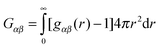 | (16) |
where
gαβ(
r) is the radial distribution function between components
α and
β. For a binary mixture,
eqn (14) simplifies to
| | 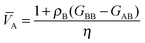 | (17a) |
| | 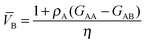 | (17b) |
where
| | | η = ρA + ρB + ρAρB(GAA + GBB − 2GAB) | (18) |
Although the KB theory provides a basis for the evaluation of partial molar volume for any mixture, the KBI is found to converge very slowly with separation distance
r.
30 As a result, a very long simulation trajectory and a very large simulation box may be necessary to obtain a reliable converged value of the KBI. To circumvent such problems, we also examined two additional means for a simpler estimation of the partial molar volume in
eqn (8). The first is to assume that all particles occupy the same volume regardless of its size (the one-fluid approximation),
11 in this case the partial molar volume is assumed to be the molar volume
| | ![[V with combining macron]](https://www.rsc.org/images/entities/i_char_0056_0304.gif) i = i = ![[V with combining low line]](https://www.rsc.org/images/entities/i_char_0056_0332.gif) = V/N = V/N | (19) |
It is expected that this approximation would fail when the size of the particles in the mixture is very dissimilar. A somewhat improved estimation for the partial molar volume is to assume its proportionality to the molecular size,
i.e.,
| | 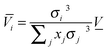 | (20) |
where
xi is the mole fraction of species
i in the mixture,
σi is the atom diameter. The advantage of these approximations (
eqn (19) and (20)) is that the partial molar volume is estimated without performing MD simulations.
3. Computational details
The molar excess entropy and Gibbs free energies of Lennard-Jones (LJ) binary mixtures are used to examine the accuracy of the two-phase (2PT) thermodynamic model. The interaction potential E between two LJ particles is expressed through the standard LJ-12-6 equation| | 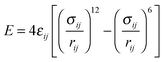 | (21) |
where rij is the separation distance between particles i and j, and σij and εij are two parameters characterizing the size and strength of interaction between LJ particles. The cross terms between two different species are described through the Lorentz–Berthelot combination rule,| | 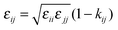 | (23) |
where kij is a binary interaction parameter for tuning unlike species interactions. Open software LAMMPS31 is used for all molecular dynamic simulations. Equimolar mixtures of binary LJ particles (with a total of 1000 particles) are equilibrated under constant temperature, pressure and the number of particles (NPT) for 800 ps with a timestep of 8 fs. Additional 160 ps was subsequently performed and the trajectory file was recorded every 32 fs for the 2PT analysis. The Nosé–Hoover thermostat and barostat time constants 0.1 ps and 1 ps, respectively, are used. The nonbond cutoff used is 20 (Å). All particles are assumed to have the same mass of 39.94 (g mol−1).
The partial molar volume is estimated based on three methods: the one-fluid approximation (eqn (19)), the molecular size (eqn (20)), and the KB theory (eqn (17)). The RDF needed in the KB theory is calculated from the final 160 ps trajectory of the MD simulation. However, as noted previously, the direct use of the simulated RDF in the KBI results in very slow convergence with distance r because of the long range fluctuation in the RDF.30 Although the fluctuations may be suppressed in NPT and NVT ensembles, our experience shows that the uncertainty caused by finite simulation length and finite system size also results in the slow convergence of the Kirkwood–Buff integration. To circumvent this problem, we fit the RDF to the following analytical expression,32 which captures the main features of the RDF of the mixture of Lennard-Jones particles.
| | 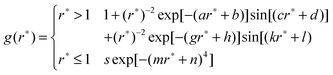 | (24) |
where
r* =
rij/
σij,
rij is the distance between particles
i and
j;
a, b, c, d, g, h , k, l, m, n, and
s are parameters adjusted to reproduce the RDF determined from the MD trajectory. This expression guarantees that the radial distribution function is smooth and converges to 1 at long distances. The partial molar volume is then obtained from
eqn (17) with
eqn (24) used for
g(
r) (the integration is done for
r = 20 Å). As a validation, we have checked the determined partial molar volume with that determined from the change of the system volume with composition (see Appendix for details). There is a good agreement in the partial molar volume from both approaches.
Once the partial molar volume is determined, the fluidicity parameter of the corresponding species is calculated from eqn (6), and the determination of 2PT thermodynamic properties is the same as that for pure fluids.12 The excess Gibbs free energy is calculated from the difference between the mixture Gibbs free energy (by summing up the component contributions) and that of the ideal mixing of pure fluids under the same temperature and pressure,
| |  | (25) |
In the present work, we focus on the comparison of the excess determined from 2PT and those from TI found in the literature or the Widom insertion method determined from open-source molecular simulation program
ms2.
33,34
4. Results and discussion
A total of 32 sets of simulations of equimolar LJ mixtures is carried out with varying interaction parameters and the simulation conditions (see Table 1 for summary). The size and energy parameters of component A are fixed (σAA = 3.405 Å, εAA = 0.238 kcal mol−1), and the parameters of component B vary from 1 ≤ σBB/σAA ≤ 2, and 1≤ εBB/εAA ≤2 in order to study the size and energy effects on the performance of 2PT. The cross term parameter kij is zero in all cases; however, for case 17 the value of kij is changed from −0.9 to 0.3 to study the effect of the off-diagonal LJ interactions. The simulation conditions range from 1 ≤ T* ≤ 3, 0.5 ≤ P* ≤ 2.5, covering the gas, liquid and supercritical regions. The 2PT excess Gibbs free energies are determined using three different estimates for the partial molar volume: (1) the one-fluid approximation (eqn (19)), (2) the molecular size (eqn (20)), and (3) the KB theory (eqn (14)).
Table 1 Simulation conditions and interactions parameters of equimolar mixtures
| id |
T*a |
T (K) |
P*a |
P (atm) |
σ
BB/σAAb |
ε
BB/εAAb |
|
Reduced temperature T* = kT/εAA and pressure P*=PσAA3/εAA.
σ
AA = 3.405 (Å) and εAA=0.238 (kcal mol−1)).
|
| 1 |
1 |
119.8 |
0.5 |
206.27 |
1.25 |
1 |
| 2 |
1 |
119.8 |
0.5 |
206.27 |
1.5 |
1 |
| 3 |
1 |
119.8 |
0.5 |
206.27 |
1.85 |
1 |
| 4 |
1 |
119.8 |
0.5 |
206.27 |
2 |
1 |
| 5 |
2 |
240.0 |
1.2 |
495.43 |
1.25 |
1 |
| 6 |
2 |
240.0 |
1.2 |
495.43 |
1.5 |
1 |
| 7 |
2 |
240.0 |
1.2 |
495.43 |
1.75 |
1 |
| 8 |
2 |
240.0 |
1.2 |
495.43 |
2 |
1 |
| 9 |
3 |
359.0 |
2.5 |
1033.305 |
1.5 |
1 |
| 10 |
3 |
359.0 |
2.5 |
1033.305 |
1.75 |
1 |
| 11 |
3 |
359.0 |
2.5 |
1033.305 |
2 |
1 |
| 12 |
3 |
359.0 |
2.5 |
1033.305 |
1 |
1 |
| 13 |
2 |
240.0 |
2.5 |
1033.305 |
1 |
1 |
| 14 |
2 |
240.0 |
2.5 |
1033.305 |
1 |
1.25 |
| 15 |
2 |
240.0 |
2.5 |
1033.305 |
1 |
1.5 |
| 16 |
2 |
240.0 |
2.5 |
1033.305 |
1 |
1.75 |
| 17 |
2 |
240.0 |
2.5 |
1033.305 |
1 |
2 |
| 18 |
2 |
240.0 |
2.5 |
1033.305 |
1.125 |
1 |
| 19 |
2 |
240.0 |
2.5 |
1033.305 |
1.125 |
1.25 |
| 20 |
2 |
240.0 |
2.5 |
1033.305 |
1.125 |
1.5 |
| 21 |
2 |
240.0 |
2.5 |
1033.305 |
1.125 |
1.75 |
| 22 |
2 |
240.0 |
2.5 |
1033.305 |
1.125 |
2 |
| 23 |
2 |
240.0 |
2.5 |
1033.305 |
1.5 |
1 |
| 24 |
2 |
240.0 |
2.5 |
1033.305 |
1.5 |
1.25 |
| 25 |
2 |
240.0 |
2.5 |
1033.305 |
1.5 |
1.5 |
| 26 |
2 |
240.0 |
2.5 |
1033.305 |
1.5 |
1.75 |
| 27 |
2 |
240.0 |
2.5 |
1033.305 |
1.5 |
2 |
| 28 |
2 |
240.0 |
1.2 |
495.43 |
1.5 |
1 |
| 29 |
2 |
240.0 |
1.2 |
495.43 |
1.5 |
1.25 |
| 30 |
2 |
240.0 |
1.2 |
495.43 |
1.5 |
1.5 |
| 31 |
2 |
240.0 |
1.2 |
495.43 |
1.5 |
1.75 |
| 32 |
2 |
240.0 |
1.2 |
495.43 |
1.5 |
2 |
4.1 The density of state distribution
Fig. 1 illustrates the DoS of a LJ binary mixture (id 4 in Table 1) and its decomposition into different contributions. Because the DoS is additive from contributions of atoms (eqn (1)), it can be easily separated into contributions from each component in the mixture. The 2PT can then be used to decompose the DoS of each species into a gas (indicated by Sg) and a solid (indicated by Ss) component. The higher value of the zero frequency intensity of component A (SA(0)) indicates that it is more diffusive than B because of its smaller size compared to B. The results here demonstrate that the 2PT method can nicely decompose the DoS to various components for further property calculations.
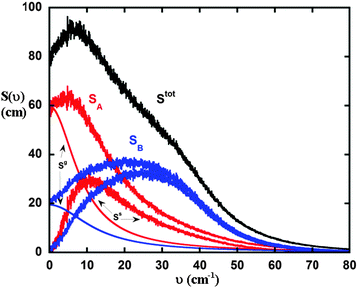 |
| | Fig. 1 Illustration of the density of state decomposition of an equimolar LJ mixture. Each component can be partitioned into gas (Sg) and solid (Ss) contributions. The total density of state of the system (Stot) is the superposition of each contribution. The state point of this plot corresponds to simulation 4 in Table 1. Red curves (or light grey curves in print) stands for properties of component A (SA), and blue curves (or grey curves in print) are corresponding properties of component B (SB). | |
4.2 Thermodynamic properties for mixtures from 2PT model
The 2PT determined excess Gibbs free energies are compared to those determined by thermodynamic integration35,36 (Fig. 2 and Table S1 in the ESI†). The 2PT properties are determined based on three estimates of the partial molar volume. The KB method provides the most accurate estimate to the partial molar volume (see Appendix for further details). The 2PT determined excess Gibbs free energies based on KB partial molar volume (Fig. 2c) are in good agreement with results from TI for mixtures with very different sizes and energetic interactions. Discernible discrepancies are observed when the sizes of the two species are most different (i.e., σBB/σAA = 2). The one-fluid approximation (Fig. 2a assuming molar volume to be the same as partial molar volume) results in more negative deviations as the size ratio (σBB/σAA) increases. On the other hand, estimating the partial molar volume with the particle size (Fig. 2b) leads to results that are in comparable accuracy to that from the KB method. In most cases, the molecular size method leads to more positive values in excess Gibbs free energy than those from the KB method. The results show that the description of partial molar volume is important for 2PT properties, especially for highly asymmetric mixtures. Furthermore, the use of molecular size may be an efficient approach for 2PT properties without much loss of its accuracy.
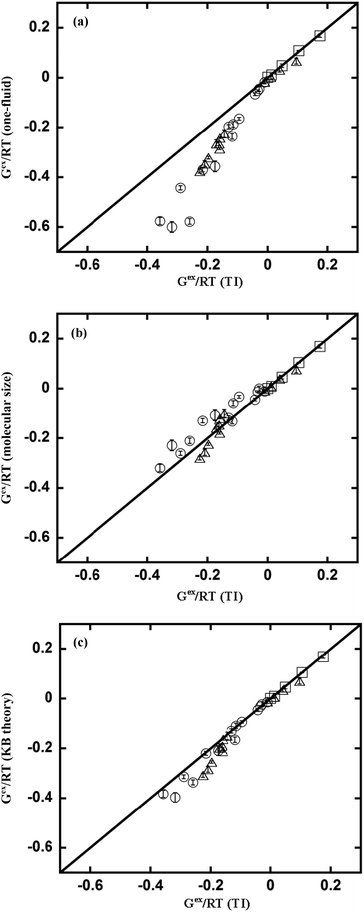 |
| | Fig. 2 Comparison of excess Gibbs free energy of equimolar LJ mixtures from 2PT with three different methods to that from thermodynamic integration (TI).35,36 (a) one-fluid. (b) molecular size. (c) Kirkwood–Buff theory (squares: particles are equal in size but with different interaction parameters; circles: particles are different in size but having the same interactions; triangles: both size and interaction parameters are different). | |
4.3 Energy-cross term effect of 2PT model
To examine whether the 2PT method can capture correct thermodynamic properties for specific cross interactions, we performed additional simulations using simulation parameters from simulation 17 (see Table 1) but with different values of kij (eqn (23)): −0.9, −0.7, −0.5, −0.1, 0.1, 0.3. (Note that phase separation is observed when the value of kij is greater than 0.5. Therefore, larger values of kij are not considered.) Fig. 3 shows the result of excess Gibbs free energy from the 2PT model with different kij. For comparison, the excess Gibbs free energies were determined based on the Widom insertion method using the open-source molecular simulation program ms2.33,34 It can be seen that the results from 2PT are in close agreement with those from Widom's method. The 2PT model can therefore correctly capture the change in thermodynamic properties in the mixture due to specific cross interactions.
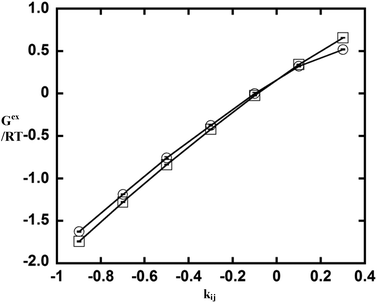 |
| | Fig. 3 The excess Gibbs free energy of equimolar mixtures from the 2PT model (circle) and from Widom's particle insertion method (square) for simulation 17 but using different cross interaction parameters kij. | |
4.4 Fluidicity parameter and partial molar volume in binary mixtures
The fluidicity and partial molar volume are two important quantities in the 2PT method for calculation of thermodynamic properties in a mixture. Their values from the three different methods discussed above are listed in Table S2 of the ESI.† In one-fluid approximation, the two components in the mixture share the same fluidicity and molar volume. For the molecular size and Kirkwood–Buff approaches, the partial molar volume of each component differs significantly when the ratio of particle diameters is away from unity. One-fluid approximation fails to consider the size effect as expected. As a consequence, the fluidicity from one-fluid approximation is very different from the other two methods. This deviation affects thermodynamic properties significantly, as given in the previous section.
4.5 Convergence of 2PT properties
One outstanding feature of the 2PT model is its need for very short sampling time. Fig. 4a and b show the 2PT entropy for each component and the mixture evaluated using different lengths of a MD trajectory. Fig. 4a corresponds to simulation 4 in Table 1. While the excess entropy of the mixture is converged in about 20 ps, it is noteworthy that the partial molar excess entropy of each component may take a longer time to converge. In simulation 4, component A is smaller than component B (σBB/σAA = 2), and the time needed for its entropy to converge is found to be longer. The fluidicity parameters of these two components are 0.56 (A) and 0.25 (B), respectively. The significantly larger value of component A indicates that it is in a state more similar to a gas. The longer time for convergence in this case is a result of the time needed for enough collisions to establish a converged DoS. Fig. 4b shows another simulation using a larger diameter for component A (σAA = 5.448 (Å)). In this case, the fluidicity parameters are 0.35 and 0.28 for components A and B, respectively. With both components having a smaller fraction of the gas-like component, the convergence of both the excess and the partial molar entropies is observed within 20 ps. Thus the convergence of 2PT properties in mixtures is quite similar to that found in pure fluids.12
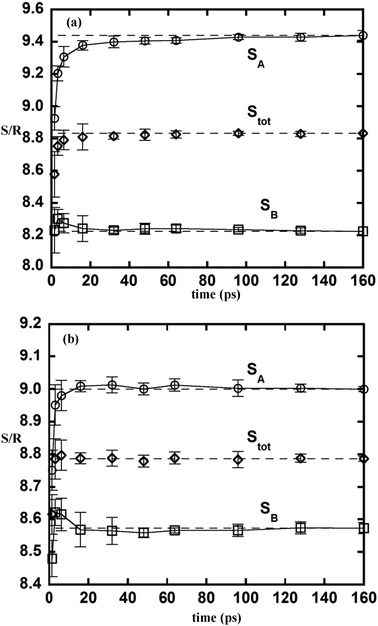 |
| | Fig. 4 The partial molar (circles and squares) and molar (diamonds) entropy of a binary equimolar LJ mixture determined using different lengths of a trajectory from simulation 4 in Table 1 (a) and another simulation with a change of the diameter of component A to σAA = 5.448 Å (b). | |
5. Conclusion
In the present work, we validated the use of the 2PT method for determination of thermodynamic properties in mixtures of Lennard-Jones particles. In this method the vibrational density of states of the system is decomposed into a solid-like component, which is treated as a series of harmonic oscillators, and a gas-like component, which is considered as a hard sphere gas. The 2PT theory provides a way to determine the fraction, fluidicity parameter, of the gas-like component. For mixtures, the partial molar volume of each component in the mixture is found to be important for the determination of the fluidicity parameter. We examined the accuracy of 2PT properties based on three different estimates of the partial molar volume. The KB theory provides the most accurate estimation of the partial molar volume, and hence most accurate 2PT excess Gibbs free energy; however, it is rather demanding on the accuracy/convergence in the long-range tail of the radial distribution function. The one-fluid approximation (assuming the partial molar volume to be the same as the molar volume) provides reasonable 2PT properties for mixtures consisting of particles with similar sizes; however, the accuracy deteriorates rapidly as the difference in the particle sizes increases. One-fluid approximation is only applicable when the LJ size parameter difference (σBB/σAA) is less than 10%, which agrees with previous observation.37 We found that by assuming the partial molar volume to be proportional to the volume of the constituent particles the 2PT method can also provide excess Gibbs free energy with satisfactory accuracy. We conclude that estimation of partial molar volume from the size of molecules is a simple yet accurate approach for evaluation of 2PT thermodynamic properties.
Appendix: Comparison of methods for estimation of partial molar volume
The partial molar volume is defined as the increment in the total system volume when a component is added to the mixture under constant temperature and pressure, i.e.,| | 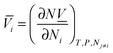 | (A1) |
One typical approach to determine the partial molar volume is to determine the molar volume of the mixture at different compositions. These data are used to fit a Redlich–Kister type of expansion (eqn (A2)) and the partial molar volume can then be obtained from eqn (A1) (see, for example, ref. 38 for details).| | 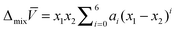 | (A2) |
To validate the partial molar volume obtained from the KB theory, we determined the values based on a set of simulations at compositions (xA = 0.0,0.1,…,1.0). The results are shown in Fig. A1. It can be seen that the partial molar volume from the KB theory (open circles) is in close agreement with that from eqn (A1). Also shown in Fig. A1 are the partial molar volumes estimated from the one-fluid approximation (eqn (19)) and the molecular size (eqn (20)) approximation. The one-fluid approximation (i.e., the total molar volume) leads to a composition independent partial molar volume that may deviate significantly from the exact values. The molecular size approximation leads to a somewhat improved estimation, with the tendency properly captured (e.g., the partial molar volume of component B being larger than that of component A). Largest deviation is observed for the large particle in the infinite dilution limit.
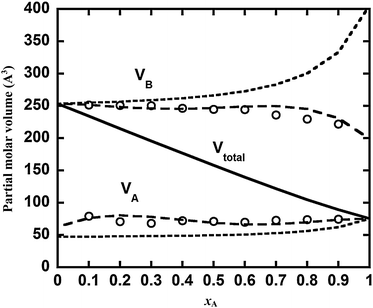 |
| | Fig. A1 The variation of partial molar volume with mixture composition for simulation 7 in Table 1. Solid line is the total volume; long dash lines are the partial molar volumes determined from the Redlich–Kister expansion (eqn (A2)); short dashed lines are those based on molecular size approximation (eqn (20)); circles are from Kirkwood–Buff theory (eqn (14)). | |
Acknowledgements
The authors like to acknowledge the funding support from the National Science Council of Taiwan under grants NSC 100-2221-E-002-175 and 98-2221-E-002-087-MY3. The computation resources from the National Center for High-Performance Computing of Taiwan and the Computing and Information Networking Center of the National Taiwan University are acknowledged.
Notes and references
- B. Widom, J. Chem. Phys., 1963, 39, 2808–2812 CrossRef CAS.
- C. H. Bennett, J. Comput. Phys., 1976, 22, 245–268 CrossRef.
- G. M. Torrie and J. P. Valleau, J. Comput. Phys., 1977, 23, 187–199 CrossRef.
- D. A. Kofke, Mol. Phys., 1993, 78, 1331–1336 CAS.
- P. H. Berens, D. H. J. Mackay, G. M. White and K. R. Wilson, J. Chem. Phys., 1983, 79, 2375–2389 Search PubMed.
- M. Karplus and J. N. Kushick, Macromolecules, 1981, 14, 325–332 CrossRef CAS.
- J. Schlitter, Chem. Phys. Lett., 1993, 215, 617–621 CrossRef.
- I. Andricioaei and M. Karplus, J. Chem. Phys., 2001, 115, 6289 CrossRef CAS.
- H. Schäfer, A. E. Mark and W. F. van Gunsteren, J. Chem. Phys., 2000, 113, 7809 CrossRef CAS.
- H. Schäfer, X. Daura, A. E. Mark and W. F. van Gunsteren, Proteins: Struct., Funct., Bioinf., 2001, 43, 45–56 CrossRef CAS.
-
D. A. McQuarrie, Statistical mechanics, University Science Books, 2000 Search PubMed.
- S.-T. Lin, M. Blanco and W. A. Goddard, J. Chem. Phys., 2003, 119, 11792 CrossRef CAS.
- S.-T. Lin, P. K. Maiti and W. A. Goddard, J. Phys. Chem. B, 2010, 114, 8191–8198 CrossRef CAS.
- S.-N. Huang, T. A. Pascal, W. A. Goddard, P. K. Maiti and S.-T. Lin, J. Chem. Theory Comput., 2011, 7, 1893–1901 CrossRef CAS.
- T. A. Pascal, S.-T. Lin and W. A. Goddard III, Phys. Chem. Chem. Phys., 2011, 13, 169 RSC.
- V. Vasumathi and P. K. Maiti, Macromolecules, 2010, 43, 8264–8274 CrossRef CAS.
- B. Nandy and P. K. Maiti, J. Phys. Chem. B, 2011, 115, 217–230 CrossRef CAS.
- S.-T. Lin, P. K. Maiti and W. A. Goddard, J. Phys. Chem. B, 2005, 109, 8663–8672 CrossRef CAS.
- H. Kumar, B. Mukherjee, S.-T. Lin, C. Dasgupta, A. K. Sood and P. K. Maiti, J. Chem. Phys., 2011, 134, 124105 Search PubMed.
- Y. Zhao, C.-C. Ma, L.-H. Wong, G. Chen, Z. Xu, Q. Zheng, Q. Jiang and A. T. Chwang, J. Comput. Theor. Nanosci., 2006, 3, 852–856 CrossRef CAS.
- T. A. Pascal, R. Abrol, R. Mittal, Y. Wang, N. V. Prasadarao and W. A. Goddard, J. Biol. Chem., 2010, 285, 37753–37761 CrossRef CAS.
- M. Santosh, S. Panigrahi, D. Bhattacharyya, A. K. Sood and P. K. Maiti, J. Chem. Phys., 2012, 136, 065106 Search PubMed.
- B. Jana, S. Pal and B. Bagchi, J. Phys. Chem. B, 2010, 114, 3633–3638 Search PubMed.
- A. Debnath, B. Mukherjee, K. G. Ayappa, P. K. Maiti and S.-T. Lin, J. Chem. Phys., 2010, 133, 174704 CrossRef.
- A. M. Teweldeberhan and S. A. Bonev, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 134120 Search PubMed.
- L. Spanu, D. Donadio, D. Hohl, E. Schwegler and G. Galli, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 6843–6846 Search PubMed.
- G. Zhang, Q. An and W. A. Goddard, J. Phys. Chem. C, 2011, 115, 2320–2331 Search PubMed.
- J. Kirkwood and F. Buff, J. Chem. Phys., 1951, 19, 774–777 CrossRef CAS.
- N. Patel, D. N. Dubins, R. Pomes and T. V. Chalikian, J. Phys. Chem. B, 2011, 115, 4856–4862 CrossRef CAS.
- A. V. Sangwai and H. S. Ashbaugh, Ind. Eng. Chem. Res., 2008, 47, 5169–5174 CrossRef CAS.
- P. Steve, J. Comput. Phys., 1995, 117, 1–19 CrossRef CAS.
- E. Matteoli and G. A. Mansoori, J. Chem. Phys., 1995, 103, 4672–4677 Search PubMed.
-
http://www.ms-2.de/
.
- S. Deublein, B. Eckl, J. Stoll, S. V. Lishchuk, G. Guevara-Carrion, C. W. Glass, T. Merker, M. Bernreuther, H. Hasse and J. Vrabec, Comput. Phys. Commun., 2011, 182, 2350–2367 Search PubMed.
- K. P. Shukla and J. M. Haile, Mol. Phys., 1987, 62, 617–636 Search PubMed.
- K. P. Shukla and J. M. Haile, Mol. Phys., 1988, 64, 1041–1059 Search PubMed.
- K. S. Shing and K. E. Gubbins, Mol. Phys., 1983, 49, 1121–1138 Search PubMed.
-
S. I. Sandler, Chemical, Biochemical, and Engineering Thermodynamics, 4th edn., 2006 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Tables containing the numerical values of data in Fig. 2, the fluidicity parameters, and partial molar volumes. See DOI: 10.1039/c2cp42011b |
|
| This journal is © the Owner Societies 2012 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article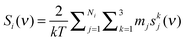
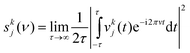
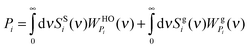
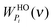 and
and 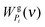 are the weighting functions of a harmonic oscillator and the corresponding gas part of component i, respectively.
are the weighting functions of a harmonic oscillator and the corresponding gas part of component i, respectively.
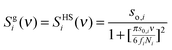
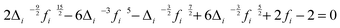
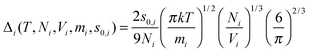
![[V with combining macron]](https://www.rsc.org/images/entities/i_char_0056_0304.gif) i) should be used, i.e.,
i) should be used, i.e.,![[V with combining macron]](https://www.rsc.org/images/entities/i_char_0056_0304.gif) i
i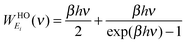
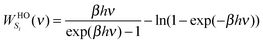
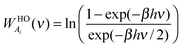
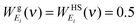
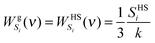
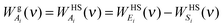
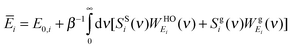
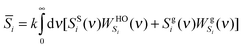
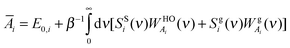
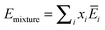
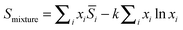
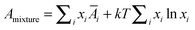
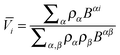
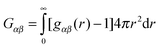
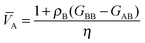
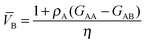
![[V with combining macron]](https://www.rsc.org/images/entities/i_char_0056_0304.gif) i =
i = ![[V with combining low line]](https://www.rsc.org/images/entities/i_char_0056_0332.gif) = V/N
= V/N