Coupled-cluster methods with perturbative inclusion of explicitly correlated terms: a preliminary investigation
Received
12th September 2007
, Accepted 19th October 2007
First published on 13th November 2007
Abstract
We propose to account for the large basis-set error of a conventional coupled-cluster energy and wave function by a simple perturbative correction. The perturbation expansion is constructed by Löwdin partitioning of the similarity-transformed Hamiltonian in a space that includes explicitly correlated basis functions. To test this idea, we investigate the second-order explicitly correlated correction to the coupled-cluster singles and doubles (CCSD) energy, denoted here as the CCSD(2)R12 method. The proposed perturbation expansion presents a systematic and easy-to-interpret picture of the “interference” between the basis-set and correlation hierarchies in the many-body electronic-structure theory. The leading-order term in the energy correction is the amplitude-independent R12 correction from the standard second-order Møller–Plesset R12 method. The cluster amplitudes appear in the higher-order terms and their effect is to decrease the basis-set correction, in accordance with the usual experience. In addition to the use of the standard R12 technology which simplifies all matrix elements to at most two-electron integrals, we propose several optional approximations to select only the most important terms in the energy correction. For a limited test set, the valence CCSD energies computed with the approximate method, termed 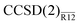 , are on average precise to (1.9, 1.4, 0.5 and 0.1%) when computed with Dunning’s aug-cc-pVXZ basis sets [X = (D, T, Q, 5)] accompanied by a single Slater-type correlation factor. This precision is a roughly an order of magnitude improvement over the standard CCSD method, whose respective average basis-set errors are (28.2, 10.6, 4.4 and 2.1%). Performance of the
, are on average precise to (1.9, 1.4, 0.5 and 0.1%) when computed with Dunning’s aug-cc-pVXZ basis sets [X = (D, T, Q, 5)] accompanied by a single Slater-type correlation factor. This precision is a roughly an order of magnitude improvement over the standard CCSD method, whose respective average basis-set errors are (28.2, 10.6, 4.4 and 2.1%). Performance of the 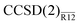 method is almost identical to that of the more complex iterative counterpart, CCSD(R12). The proposed approach to explicitly correlated coupled-cluster methods is technically appealing since no modification of the coupled-cluster equations is necessary and the standard Møller–Plesset R12 machinery can be reused.
method is almost identical to that of the more complex iterative counterpart, CCSD(R12). The proposed approach to explicitly correlated coupled-cluster methods is technically appealing since no modification of the coupled-cluster equations is necessary and the standard Møller–Plesset R12 machinery can be reused.
1. Introduction
A low-rank coupled-cluster (CC) ansatz1–4 has sufficient accuracy for confident quantitative description of molecular structure, properties and reactivity.5 Unfortunately, large one-electron basis sets are required to reach the quantitative threshold of precision. The problem is the determinantal n-electron basis, which differs qualitatively from the exact wave function at short interelectronic distances rij where the Coulomb repulsion dominates. Terms with explicit dependence on rij can model the Coulomb hole more directly and efficiently6 and, therefore, dramatically reduce the basis-set error of the correlation energy. The Achilles heel of the explicitly correlated methods is the appearance of nonfactorizable many-electron integrals. Although such integrals can be evaluated in closed form,7 the high computational cost of even three-electron integrals makes such methods non-competitive in the “chemical” accuracy regime with the basis-set extrapolation. The R12 (or F12†) methods8–10 are the most practical of modern explicitly correlated techniques because the many-electron integrals are ingeniously reduced to two-electron integrals only.
The R12 version of the second-order Møller–Plesset energy (MP2) method has been most studied because it is technically the simplest. Several types of three- and four-electron integrals appear in the MP2-R12 methods, but all can be reduced,9 although tediously, to at most two-electron integrals with controlled and negligible error.11 The MP2-R12 method becomes competitive with extrapolation schemes when combined with a Slater-type correlation factor, suggested by Ten-no,12 which is more appropriate for modeling the Coulomb hole than the linear term. A precision of 1–2% can typically be achieved on average for valence correlation contributions to electronic energies, reaction enthalpies, and atomization energies with only a triple-zeta orbital basis set accompanied by a single Slater-type geminal correlation factor.13–16 Use of several Gaussian-type correlation factors can result in a slightly higher precision.14
It is difficult to translate the high precision of the MP2-R12 method to predictive chemical applications because the MP2 method generally lacks the necessary accuracy. One possible solution is to use the MP2-R12 method to correct the basis-set incompleteness of the energy in the context of additive model chemistries, such as Gaussian-n (Gn) methods,17–19 Weizmann-n (Wn) methods,20,21 the “focal point” framework,22,23 or the correlation-consistent composite approach24 among many. Unfortunately, because of the “interference effects”25,26 between the correlation and basis-set hierarchies, the basis-set incompleteness at the MP2 level is usually larger than that of higher-order correlated methods.27,28 Such interference effects are accounted for in the complete basis-set (CBS) model chemistry of Petersson et al.29,30via an empirical formula, and in principle such an approach could lead to a model chemistry based on an MP2-R12 method. It is, however, desirable to exploit the high precision of the state-of-the-art R12 methodology by directly combining it with methods of comparable accuracy.
The rigorous R12 version of the coupled-cluster method using the modern R12 technology, marked by the use of a separate basis for the resolution-of-the-identity (RI) approximation, is technically very demanding compared to the MP2-R12 method. Numerous new three-, four-, and five-electron integrals appear in the CC-R12 amplitude equations and make implementation of such methods difficult. The CC-R12 methods through CCSD(T)-R12 have been explored by Noga et al.,31–35 but only using the “old” R12 technology. The old approach simplified the equations but required the use of a very large Hartree–Fock basis and therefore was aimed at benchmark-accuracy applications for rather small systems. Fliegl and co-workers introduced the “(R12)” approximation36–38 to the CC-R12 method, with the coupling between the standard and explicitly correlated amplitudes drastically simplified à laCCn methods.39 The amplitudes of the R12 terms in the CC(R12) method are optimized iteratively (or could be simply kept fixed, as in the rational generator variant40 of the MP2-R12 method, to satisfy the cusp conditions for the exact wave function). The authors found that the (R12) approach closely tracks the results of the rigorous one-basis CC-R12 method at a much lower computational cost. The overall performance of the recent extension of the CC(R12) method to nonlinear correlation factors has been very promising: correlation energies and reaction enthalpies computed with a triple-zeta basis are precise to better than 2%, on a par with the conventional quintuple-zeta result.41
Here we consider a new way to introduce the explicitly correlated terms into the coupled-cluster method. Instead of making approximations to the CC-R12 equations, as is done in the CC(R12) method, our approach introduces the explicitly correlated terms by perturbing the standard coupled-cluster wave function via Löwdin partitioning42 of the similarity-transformed Hamiltonian. This experiment is motivated by the argument for the R12 method itself, i.e. the standard low-rank determinantal expansion can effectively recover a significant portion (>80%) of the correlation energy and the rest can be handled with few explicitly correlated terms. The coupling between the standard and explicitly correlated amplitudes is weak in the MP2-R12 method, and, therefore, the same can be assumed in general. This coupling should be well described by a low-order perturbation theory and not require the infinite-order treatment of CC-R12 or CC(R12) methods.
Development of perturbation expansions for the eigenvalues and eigenvectors of the similarity-transformed coupled-cluster Hamiltonian by Löwdin partitioning is not a new idea. The formalism in its current form was suggested by Stanton and Gauss43 as a way to correct EOMIP-CCSD energies to account for higher-order excitations. A related approach was used earlier by Head-Gordon et al. to correct configuration-interaction single-excitation energies for the effect of double excitations,44 as well as later to develop the “(2)” corrections for coupled-cluster energies.45,46 Notably, Stanton used this route to “derive” the celebrated CCSD(T) method by treating triple excitations via a perturbation expansion defined with respect to the zeroth-order CCSD wave function.47 The asymmetric,48 or Λ,49 (T) correction naturally follows from such treatment. The general approach has since been used in many related disguises.50–56 The common theme is that, until now, the use of explicitly correlated basis functions has never been considered in such perturbative approaches.
Our main hypothesis is that the effect of the explicitly correlated terms on the coupled-cluster energy and wave function can be recovered accurately with only a low-order perturbation treatment. The immediate goal of this work is strictly to examine this hypothesis and lay the groundwork for a more thorough study. Thus this work will be limited to the coupled-cluster singles and doubles model corrected up to second-order for the explicitly correlated terms (corrections due to triple and higher conventional excitations will be incorporated in a future study). Furthermore, only the dominant terms will be included here to simplify the equations.
2. Methodology
The present approach begins with the similarity-transformed Hamiltonian of the standard CC method, ![[H with combining macron]](https://www.rsc.org/images/entities/i_char_0048_0304.gif) = e−
= e−![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) Ĥe
Ĥe![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) . In this work,
. In this work, ![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) will be limited to one- and two-electron excitations:
will be limited to one- and two-electron excitations:| | 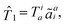 | (1) |
| | 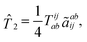 | (2) |
where we used the standard tensor notation.9,32,57 The T-amplitudes in eqn (1) and (2) are obtained from the standard CCSD method. Matrix representation of ![[H with combining macron]](https://www.rsc.org/images/entities/i_char_0048_0304.gif) will be constructed in a basis that spans a “reference” space P, comprised of Slater determinants up to the same rank as the excitation operator (vacuum 0, singles S, and doubles D), and an “external space”Q, including the explicitly correlated double substitutions Γ:
will be constructed in a basis that spans a “reference” space P, comprised of Slater determinants up to the same rank as the excitation operator (vacuum 0, singles S, and doubles D), and an “external space”Q, including the explicitly correlated double substitutions Γ:| | 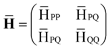 | (3) |
The explicitly correlated basis functions are defined as usual:| | 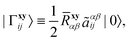 | (4) |
where the choice of orbitals x and y that “generate” the geminal space is flexible (such orbital pairs will be typeset in bold33). In this work x and y will be occupied orbitals (this is known as the kl-ansatz), but other choices have also been considered.58 To ensure strong orthogonality, the geminal integrals in eqn (5) are defined as in ref. 9.‡| | 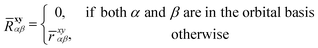 | (5) |
This ansatz ensures that space Γ, despite the non-unit metric SΓΓ, is orthogonal to D. The integral rrspq is over a correlation function f(r12), which can be any well-behaved function.
Note that the Hamiltonian in eqn (3) is not identical to the matrix that would be used in the EOM-CCSD-R12 method because in the latter the full excitation operator (including excitations into Γ block) would be used for the similarity transformation. Therefore the ![[H with combining macron]](https://www.rsc.org/images/entities/b_char_0048_0304.gif) PP block is the similarity-transformed Hamiltonian used in the EOM-CCSD method. Its left and right-hand ground-state eigenvectors,
PP block is the similarity-transformed Hamiltonian used in the EOM-CCSD method. Its left and right-hand ground-state eigenvectors,
| | 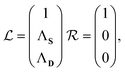 | (6) |
can be considered a good approximation to the left- and right-hand eigenvectors,
L and
R, of the full matrix in
eqn (3).
§
Löwdin partitioning42 of the Hamiltonian matrix expresses the exact eigenvalue E of the full matrix in terms of sub-blocks LP and RP of the exact eigenvectors:
| | 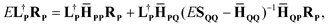 | (7) |
where
S is the overlap matrix. Rayleigh–Schrödinger perturbation theory can then be straightforwardly applied to this expression. We define the zeroth-order eigenvectors in terms of the EOM-CCSD eigenvectors as
| | 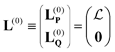 | (8) |
| | 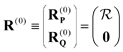 | (9) |
whereas the zeroth- and first-order Hamiltonians will be defined as follows:
| | 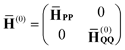 | (10) |
| | 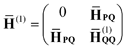 | (11) |
The zeroth-order energy is the ground-state CCSD energy:
| | 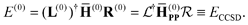 | (12) |
The first-order energy correction vanishes whereas the second-order energy is
| | 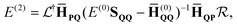 | (13) |
or, in terms of spaces
0,
S,
D, and
Γ,
| | 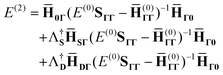 | (14) |
To evaluate
eqn (14) we must define
![[H with combining macron]](https://www.rsc.org/images/entities/b_char_0048_0304.gif) (0)ΓΓ
(0)ΓΓ. Before doing so, note that the explicitly correlated correction of the MP2-R12 theory can be derived using the same approach if the bare electronic Hamiltonian
Ĥ is used in place of
![[H with combining macron]](https://www.rsc.org/images/entities/i_char_0048_0304.gif)
and the “reference” space only includes the vacuum. Then the energy correction has the form of the first term on the right-hand side of
eqn (14):
| | 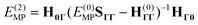 | (15) |
The standard MP2-R12 expression is obtained if the Fock operator is chosen as the zeroth-order Hamiltonian, or
Ĥ(0)MP =
E(0)MP +
![[F with combining circumflex]](https://www.rsc.org/images/entities/i_char_0046_0302.gif) N
N in the normal-ordered form. To maximize the resemblance to the MP2-R12 method, we will choose the zeroth-order Hamiltonian as
| | 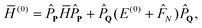 | (16) |
with normal-ordered Fock operator
![[F with combining circumflex]](https://www.rsc.org/images/entities/i_char_0046_0302.gif) N
N. In this formulation the
E(0)SΓΓ−
![[H with combining macron]](https://www.rsc.org/images/entities/b_char_0048_0304.gif) (0)ΓΓ
(0)ΓΓ matrix of
eqn (14) is independent of
T-amplitudes and identical to the
E(0)SΓΓ−
H(0)ΓΓ matrix of
eqn (15). Its evaluation has been discussed elsewhere
9,10,15,59,60.
Eqn (14) and (16) correspond to the method that we term CCSD(2)R12, by analogy with the established convention.52 All remaining matrices in eqn (14) include up to three-electron integrals and have truncating partial wave expansions (it was not the case for the matrix elements of the exchange operator in the H(0)ΓΓ matrix8,9). They can be evaluated straightforwardly using the standard approximation of the R12 method (full details will be given elsewhere). To judge the performance of the proposed method, here we are only interested in computing the dominant contributions to each matrix. Thus we propose several approximations, which, while not mandatory, will simplify the equations drastically:
1. Each term can be classified according to the standard CC perturbation theory defined with respect to the Hartree–Fock reference, in which the one-electron Hamiltonian elements are zeroth-order, T2-amplitudes have a leading first-order contribution, etc. For example, ![[H with combining macron]](https://www.rsc.org/images/entities/b_char_0048_0304.gif) 0Γ matrix elements,
0Γ matrix elements,
| | 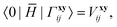 | (17) |
are purely first-order. The
![[H with combining macron]](https://www.rsc.org/images/entities/b_char_0048_0304.gif) Γ0 matrix
Γ0 matrix is more complicated: in addition to the same first-order term identical to
![[H with combining macron]](https://www.rsc.org/images/entities/b_char_0048_0304.gif) †0Γ
†0Γ, it contains second and higher-order terms:
| | 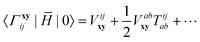 | (18) |
In this work we will include up to third-order contributions to the energy and up to second-order terms in the matrix elements.
2. Most many-electron integrals that appear in matrices ![[H with combining macron]](https://www.rsc.org/images/entities/b_char_0048_0304.gif) Γ0,
Γ0, ![[H with combining macron]](https://www.rsc.org/images/entities/b_char_0048_0304.gif) 0Γ,
0Γ, ![[H with combining macron]](https://www.rsc.org/images/entities/b_char_0048_0304.gif) SΓ and
SΓ and ![[H with combining macron]](https://www.rsc.org/images/entities/b_char_0048_0304.gif) DΓ vanish if the Hartree–Fock basis is used to resolve the identity (such an approach was used in the original R12 method). In this work we will keep only the integrals that do not vanish under such an approximation: namely, the V intermediate of the R12 theory.
DΓ vanish if the Hartree–Fock basis is used to resolve the identity (such an approach was used in the original R12 method). In this work we will keep only the integrals that do not vanish under such an approximation: namely, the V intermediate of the R12 theory.
3. Although the left-hand eigenvector is not necessary to compute the reference energy, it is needed to evaluate the energy correction. To avoid having to solve Λ-equations, we can simply replace them with the corresponding T-amplitudes (they have the same leading-order term). The motivation for such replacement can be found in the argument for the standard (T) correction to the CCSD energy.
4. Extended (EBC) and generalized Brillouin conditions (GBC)9,11 will be assumed in this work. While the effect of the generalized Brillouin condition is always small,11 its extended counterpart usually affects the MP2-R12 energies appreciably, especially if only a double-zeta basis is used. If EBC is not assumed, the coupling term between the doubles and geminals functions appears in the zeroth-order operator.¶10,59 In the current method the coupling between doubles and geminals blocks only appears in the first-order (see eqn (10) and (11)). For consistent comparison with the MP2-R12 results, we will postpone this issue until later and simply assume EBC here.
The CCSD(2)R12 method using these approximations will be termed 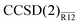 . Its energy correction is extremely simple:
. Its energy correction is extremely simple:
| | 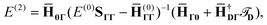 | (19) |
where
![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) D
D is a vector of
T2 amplitudes. Furthermore, the elements of matrices
H0Γ,
HΓ0 and
HDΓ become, respectively,
| | 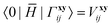 | (20) |
| | 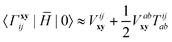 | (21) |
| | 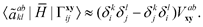 | (22) |
The final energy correction
E(2) is a sum of pair contributions
| | 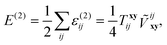 | (23) |
computed from the “dressed” interaction matrix,
| | 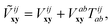 | (24) |
and the geminal amplitudes
Txyij determined from the linear system,
| | 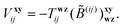 | (25) |
The zeroth-order
matrix in
eqn (25) is expressed in terms of the standard
B and
X intermediates of the MP2-R12 method
9,59 as:
| | 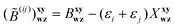 | (26) |
A diagrammatic representation for the
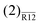
correction is shown in
Fig. 1.
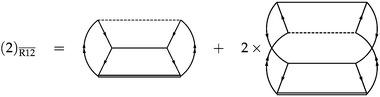 |
| | Fig. 1 A diagrammatic illustration of the  correction. The T amplitudes, the two-electron component of the Hamiltonian and the correlation factor are denoted as single lines, dashed lines and double lines respectively. correction. The T amplitudes, the two-electron component of the Hamiltonian and the correlation factor are denoted as single lines, dashed lines and double lines respectively. | |
It is immediately clear that the pair energy correction in eqn (23) becomes identical to its MP2-R12 counterpart if the dressed interaction Ṽ is replaced with the standard interaction V. Since the second term on the r.h.s. of eqn (24) has the second-order leading contribution according to the standard Hartree–Fock-based CCPT, it should be small compared to the first. The MP2 basis-set incompleteness error (BSIE) is, therefore, the leading-order contribution to the CCSD BSIE, whereas the dependence on T-amplitudes only appears in the next order. This next-order term can be understood as the source of interference effects, identified by Petersson and Nyden25,26 as responsible for lower BSIE of infinite-order theories, like CI and CC, compared to the MP2 counterpart. We must note that Petersson and Nyden also exploited a perturbation expansion of a correlated wave function to develop an empirical correction for the interference effect. It is striking that the current non-empirical picture of the interference effect is not only reminiscent of these pioneering efforts, but was also obtained from a similar mathematical approach.
The computational implementation of the proposed method is very straightforward. Converged coupled-cluster amplitudes from a coupled-cluster code and the standard MP2-R12 intermediates V, B, and X are all that is needed to evaluate the energy correction. The expressions for the intermediate B in standard approximations B or C involve two-electron integrals with 2 indices from the complementary auxiliary basis set (CABS) space; however, such terms may be ignored15,62 (this was not done in this work). The computation of the intermediates formally scales with the sixth power of the size of the system, i.e. the same as the cost of the CCSD procedure. Although the cost of solving the linear system in eqn (25) scales with the eighth power of the system size, the prefactor is so small that this step has a negligible cost (the scaling of this step can be reduced to the sixth power if the linear system is solved iteratively). The extra cost of the explicitly correlated correction can be decreased by the use of density-fitting techniques63 and/or their combination with the resolution-of-the-identity method.64
3. Computational details
Geometries for H2O and F2 were fixed at their experimental equilibrium values: rOH = 95.72 pm,65αHOH = 104.52°,65rFF = 141.193 pm.66
Hartree–Fock orbitals were expanded in standard correlation-consistent basis sets of Dunning and co-workers.67,68 The RI basis sets consisted of the primitive 19s14p8d6f4g3h2i and 9s6p4d3f2g sets of spherical harmonic Gaussians for Ne/O/F and H respectively.59
The Slater-type correlation factor exp(−1.5r12) was represented as a least-squares fit to 6 Gaussian-type geminals (the optimal exponents and coefficients are (303.393, 54.8852, 14.6991, 4.50631, 1.36066, 0.36439) and (0.0510844, 0.081916, 0.129811, 0.205298, 0.299458, 0.207455) respectively). All integrals necessary for the explicitly correlated calculations were evaluated using the recurrence relations of Valeev and Schaefer69 and Weber and Daul70 as implemented by an integrals code generator LIBINT.71 The complementary auxiliary basis set (CABS) method in its CABS+ variant72 was used to reduce the many-electron integrals. The geminal–geminal block of the zeroth-order Hamiltonian was treated using standard approximation C of Kedžuch et al.60 Since approximation C does not assume either extended or generalized Brillouin conditions, it is slightly inconsistent to assume such conditions elsewhere (in matrices HΓ0, and HDΓ). However, the effect of these conditions on the zeroth-order Hamiltonian matrix is negligible: we recomputed Ne correlation energies with the linear correlation factor using standard approximation B, in which EBC and GBC were avoided, and the energy changed by less than 0.05 mEh.
All computations were performed with the developers’ versions of MPQC73 and PSI374 programs. The massively-parallel implementation of the MP2-R12 method in MPQC75 is used to compute intermediates V, B, and X in a fully integral-direct fashion. These intermediates are then combined with the converged CCSD amplitudes obtained from PSI3. Both programs were made to adhere to the recently-developed Common Components Architecture standard for the molecular integrals76 to enable data exchange between the programs. Snapshots of the MPQC and PSI3 source codes can be obtained from the respective code repositories using tags libint2-branch-ccsd-pt2r12 and 3499.
4. Results
Table 1 lists MP2 and CCSD valence correlation energies for the neon atom computed with a “partial wave”-style basis set accompanied by a linear correlation factor. Convergence of the standard and explicitly correlated energies is expected to follow the established (at least for the MP2 case27) ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) [(Lmax + 1)−3] and
[(Lmax + 1)−3] and ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) [(Lmax + 1)−7] asymptotics. The basis-set incompleteness errors plotted in Fig. 2 indeed follow these trends. With every basis set, precision of the
[(Lmax + 1)−7] asymptotics. The basis-set incompleteness errors plotted in Fig. 2 indeed follow these trends. With every basis set, precision of the 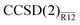 energy is close to that of the MP2-R12 energy. The explicitly correlated energies computed with the largest basis set are at most 0.1 mEh removed from their CBS estimates. We conclude that the approximations introduced in this work do not seem to affect the convergence in the asymptotic regime. However, a more complete study is still warranted.
energy is close to that of the MP2-R12 energy. The explicitly correlated energies computed with the largest basis set are at most 0.1 mEh removed from their CBS estimates. We conclude that the approximations introduced in this work do not seem to affect the convergence in the asymptotic regime. However, a more complete study is still warranted.
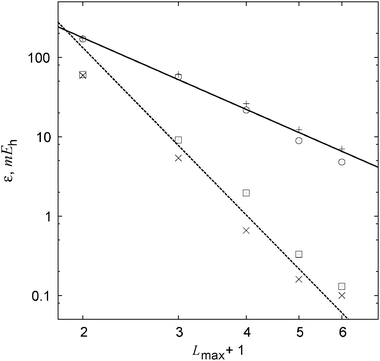 |
| | Fig. 2 Convergence of the basis-set error in standard and explicitly correlated valence correlation energies for the Ne atom (see Table 1). A (L + 1)−3 fit to the average error of the standard MP2 (+) and CCSD (⊙) energies is shown with the solid line. The dashed line shows a (L + 1)−7 fit to the average error of the MP2-R12 (×) and 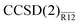 (⊡) energies. (⊡) energies. | |
Table 1 Valence MP2 and CCSD correlation energies for the neon atom, in mEh. The explicitly correlated values were obtained with the r12 correlation factor
| |
MP2 |
MP2-R12 |
CCSD
|

|
| Basis seta |
E
|
% |
δ
b
|
E
|
% |
E
|
% |
δ
c
|
E
|
% |
Subsets of the 20s14p11d9f7g5h3i basis set from ref. 59.
E(MP2-R12) −E(MP2).
 .
MP2-R12 20s14p11d9f7g5h3i energy from ref. 59.
The CCSD-R12 19s14p8d6f4g3h energy from ref. 78 including the residual basis-set error correction estimated as the difference between the MP2-R12 20s14p11d9f7g5h3i energy from ref. 59 and the MP2-R12 19s14p8d6f4g3h energy from ref. 78. .
MP2-R12 20s14p11d9f7g5h3i energy from ref. 59.
The CCSD-R12 19s14p8d6f4g3h energy from ref. 78 including the residual basis-set error correction estimated as the difference between the MP2-R12 20s14p11d9f7g5h3i energy from ref. 59 and the MP2-R12 19s14p8d6f4g3h energy from ref. 78.
|
|
sp
|
−146.38 |
45.7 |
−114.57 |
−260.92 |
81.5 |
−145.25 |
46.0 |
−109.75 |
−254.97 |
80.8 |
|
spd
|
−259.24 |
81.0 |
−55.56 |
−314.81 |
98.3 |
−258.97 |
82.0 |
−47.67 |
−306.61 |
97.1 |
|
spdf
|
−294.08 |
91.8 |
−25.50 |
−319.54 |
99.8 |
−294.03 |
93.1 |
−19.74 |
−313.74 |
99.4 |
|
spdfg
|
−307.93 |
96.2 |
−12.11 |
−320.04 |
100.0 |
−306.78 |
97.2 |
−8.59 |
−315.37 |
99.9 |
|
spdfgh
|
−313.19 |
97.8 |
−6.92 |
−320.11 |
100.0 |
−310.90 |
98.5 |
−4.68 |
−315.59 |
100.0 |
| Complete |
−320.2d |
100 |
0 |
−320.2d |
100 |
−315.7e |
100 |
0 |
−315.7e |
100 |
It is clear that the T-dependent contribution to the basis-set incompleteness is non-negligible even with the largest basis set. Whereas the explicitly correlated corrections at the MP2 and coupled-cluster levels differ by less than 5 mEh with the smallest basis set, they still differ by more than 2 mEh when computed with the largest basis set. The assumption of additivity, often employed to approximate the CBS limit of a coupled-cluster method by combining the CBS limit at the MP2 level and a small basis CC energy,22,77 does not seem to work well for absolute electronic energies.28 For example, if it were applied to estimate the CCSD CBS limit from the MP2-R12/spdfgh energy (precise to 0.1 mEh) and the CCSD/spdfgh energy, the predicted energy would be −317.81 mEh, certainly more than 2 mEh below the actual CCSD CBS limit. The interference effects,25,26 which are responsible for this discrepancy, seem to be quantitatively described by the 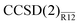 method.
method.
Use of more practical correlation-consistent basis sets calls for short-range nonlinear correlation factors, such as a Slater-type geminal. The results for Ne, presented in Table 2, are essentially similar to those from Table 1. Errors smaller than 2% are achieved with all basis sets with both MP2-R12 and 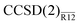 methods (the double-zeta energies are, in all likelihood, artificially precise because of the fortuitous effect of assuming the extended Brillouin condition). With the largest, sextuple-zeta basis set, the MP2-R12 and
methods (the double-zeta energies are, in all likelihood, artificially precise because of the fortuitous effect of assuming the extended Brillouin condition). With the largest, sextuple-zeta basis set, the MP2-R12 and 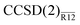 energies are within a few tenths of a millihartree of the CBS-limit estimates. As with the r12 results in Table 1, the T-dependent contribution to the BSIE is also unequivocally important here.
energies are within a few tenths of a millihartree of the CBS-limit estimates. As with the r12 results in Table 1, the T-dependent contribution to the BSIE is also unequivocally important here.
Table 2 Valence MP2 and CCSD correlation energies for the neon atom, in mEh. The explicitly correlated values were obtained with the exp(−1.5r12) correlation factor
| |
MP2 |
MP2-R12 |
CCSD
|

|
| Basis set |
E
|
% |
δ
a
|
E
|
% |
E
|
% |
δ
b
|
E
|
% |
E(MP2-R12) −E(MP2).
 .
MP2-R12 20s14p11d9f7g5h3i energy from ref. 59.
The CCSD-R12 19s14p8d6f4g3h energy from ref. 78 including the residual basis-set error correction estimated as the difference between the MP2-R12 20s14p11d9f7g5h3i energy from ref. 59 and the MP2-R12 19s14p8d6f4g3h energy from ref. 78. .
MP2-R12 20s14p11d9f7g5h3i energy from ref. 59.
The CCSD-R12 19s14p8d6f4g3h energy from ref. 78 including the residual basis-set error correction estimated as the difference between the MP2-R12 20s14p11d9f7g5h3i energy from ref. 59 and the MP2-R12 19s14p8d6f4g3h energy from ref. 78.
|
| aug-cc-pVDZ |
−206.87 |
64.6 |
−112.44 |
−319.31 |
99.7 |
−210.15 |
66.6 |
−100.78 |
−310.93 |
98.5 |
| aug-cc-pVTZ |
−272.52 |
85.1 |
−43.71 |
−316.22 |
98.8 |
−274.09 |
86.8 |
−35.83 |
−309.93 |
98.2 |
| aug-cc-pVQZ |
−297.24 |
92.8 |
−20.51 |
−317.75 |
99.2 |
−297.76 |
94.3 |
−15.47 |
−313.23 |
99.2 |
| aug-cc-pV5Z |
−307.97 |
96.2 |
−11.37 |
−319.34 |
99.7 |
−306.79 |
97.2 |
−8.14 |
−314.94 |
99.8 |
| aug-cc-pV6Z |
−312.87 |
97.7 |
−6.98 |
−319.85 |
99.9 |
−310.61 |
98.4 |
−4.81 |
−315.41 |
99.9 |
| Complete |
−320.2c |
100 |
0 |
−320.2c |
100 |
−315.7d |
100 |
0 |
−315.7d |
100 |
Molecular MP2 and CCSD valence correlation energies, presented in Tables 3 and 4, fully support the above analysis. For the molecules we are also able to compare the 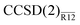 energies to those obtained with the CCSD(F12) method of Klopper et al.41 Although the latter values were evaluated at geometries different from ours, the apparent differences in the CBS limits are small. We found that the
energies to those obtained with the CCSD(F12) method of Klopper et al.41 Although the latter values were evaluated at geometries different from ours, the apparent differences in the CBS limits are small. We found that the 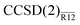 and CCSD(F12) methods perform almost identically to each other unless the aug-cc-pVDZ basis is used. The likely issue with the latter is, again, the assumption of EBC in our method. Assuming EBC has little effect on the explicitly correlated energies for larger basis sets, the two methods can be compared directly. Even disregarding the geometrical differences, the
and CCSD(F12) methods perform almost identically to each other unless the aug-cc-pVDZ basis is used. The likely issue with the latter is, again, the assumption of EBC in our method. Assuming EBC has little effect on the explicitly correlated energies for larger basis sets, the two methods can be compared directly. Even disregarding the geometrical differences, the 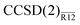 and CCSD(F12) energies differ by less than 0.6 mEh for H2O and less than 1.6 mEh for F2. If we subtract the difference in the CBS limit, the two methods agree to within 0.2 and 0.5 mEh respectively. Although the CCSD(F12) method couples the standard and explicitly correlated amplitudes iteratively, it appears that this coupling is very weak and can be confidently treated using our perturbative approach.
and CCSD(F12) energies differ by less than 0.6 mEh for H2O and less than 1.6 mEh for F2. If we subtract the difference in the CBS limit, the two methods agree to within 0.2 and 0.5 mEh respectively. Although the CCSD(F12) method couples the standard and explicitly correlated amplitudes iteratively, it appears that this coupling is very weak and can be confidently treated using our perturbative approach.
Table 3 Valence MP2 and CCSD correlation energies for the water molecule, in mEh. The MP2-R12 and 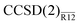 values were obtained with the exp(−1.5r12) correlation factor
values were obtained with the exp(−1.5r12) correlation factor
| |
MP2 |
MP2-R12 |
CCSD
|

|
CCSD(F12)a |
| Basis set |
E
|
% |
E
|
% |
E
|
% |
E
|
% |
E
|
% |
|
See ref. 41. These values were computed with the exp(−1.3r12) correlation factor at the optimized MP2(fc)/aug-cc-pVTZ geometry.
Estimate from ref. 78.
Obtained from the CCSD/aug-cc-pVXZ data (X = Q, 5) of ref. 41 using a Schwenke extrapolation scheme.79
|
| aug-cc-pVDZ |
−219.34 |
73.0 |
−297.34 |
99.0 |
−227.11 |
76.2 |
−290.72 |
97.6 |
−284.79 |
95.4 |
| aug-cc-pVTZ |
−268.35 |
89.3 |
−298.72 |
99.4 |
−273.05 |
91.7 |
−294.75 |
98.9 |
−295.02 |
98.9 |
| aug-cc-pVQZ |
−285.91 |
95.2 |
−299.59 |
99.7 |
−288.21 |
96.7 |
−296.93 |
99.7 |
−297.49 |
99.7 |
| aug-cc-pV5Z |
−292.90 |
97.5 |
−300.18 |
99.9 |
−293.65 |
98.6 |
−297.65 |
99.9 |
−298.10 |
99.9 |
| Complete |
−300.4b |
100 |
−300.4b |
100 |
−297.9b |
100 |
−297.9b |
100 |
−298.4c |
100 |
Table 4 Valence MP2 and CCSD correlation energies for the fluorine molecule, in mEh. The MP2-R12 and 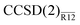 values were obtained with the exp(−1.5r12) correlation factor
values were obtained with the exp(−1.5r12) correlation factor
| |
MP2 |
MP2-R12 |
CCSD
|

|
CCSD(F12)a |
| Basis set |
E
|
% |
E
|
% |
E
|
% |
E
|
% |
E
|
% |
|
See ref. 41. These values were computed with the exp(−1.3r12) correlation factor at the optimized MP2(fc)/aug-cc-pVTZ geometry.
Estimate from ref. 78.
Obtained from the CCSD/aug-cc-pVXZ data (X = Q, 5) of ref. 41 using a Schwenke extrapolation scheme.79
|
| aug-cc-pVDZ |
−428.06 |
70.0 |
−608.52 |
99.5 |
−435.45 |
72.5 |
−591.02 |
98.3 |
−568.58 |
94.8 |
| aug-cc-pVTZ |
−536.12 |
87.7 |
−606.56 |
99.2 |
−538.96 |
89.7 |
−593.59 |
98.8 |
−592.01 |
98.7 |
| aug-cc-pVQZ |
−575.84 |
94.2 |
−608.58 |
99.5 |
−575.16 |
95.7 |
−598.20 |
99.5 |
−597.57 |
99.6 |
| aug-cc-pV5Z |
−592.78 |
97.0 |
−610.79 |
99.9 |
−588.57 |
97.9 |
−600.50 |
99.9 |
−599.43 |
99.9 |
| Complete |
−611.4b |
100 |
−611.4b |
100 |
−601.0b |
100 |
−601.0b |
100 |
−599.9c |
100 |
5. Conclusions and perspective
Here we outlined a simple perturbative approach to coupled-cluster R12 methods and explored the second-order explicitly correlated correction to the coupled-cluster singles and doubles energy, dubbed CCSD(2)R12. Although the formalism does not require use of any approximations other than the resolution of the identity for the many-electron integrals, we introduced a simplified method, 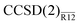 , with several additional approximations that maximally truncated the working equations without apparent negative impact. In the future we will test these approximations in more detail as well as explore various partitioning of the similarity-transformed Hamiltonian.
, with several additional approximations that maximally truncated the working equations without apparent negative impact. In the future we will test these approximations in more detail as well as explore various partitioning of the similarity-transformed Hamiltonian.
The proposed perturbation expansion is a systematic, easy-to-interpret view of the “interference” between the basis-set and correlation hierarchies in the many-body electronic-structure theory. The leading-order term in the second-order energy expression in the 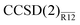 method is simply the R12 correction of the MP2-R12 method and does not depend on the coupled-cluster amplitudes (hence it is the same for any CC method). The next-order term includes coupled-cluster amplitudes linearly and makes the correction dependent on the particular coupled-cluster method used. This term is responsible for the interference effects25,26 and its effect is to lower the magnitude of the correction compared to the MP2-R12 method, in accordance with the usual experience.
method is simply the R12 correction of the MP2-R12 method and does not depend on the coupled-cluster amplitudes (hence it is the same for any CC method). The next-order term includes coupled-cluster amplitudes linearly and makes the correction dependent on the particular coupled-cluster method used. This term is responsible for the interference effects25,26 and its effect is to lower the magnitude of the correction compared to the MP2-R12 method, in accordance with the usual experience.
Performance of the 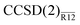 method is (unexpectedly) good. It is remarkable that, despite several approximations, a simple non-iterative correction can be used to compute the CCSD energy of a Ne atom precise to a few tenths of a millihartree, i.e. much better than 0.1%. With a single Slater-type geminal as a correlation factor, the CCSD valence correlation energy can be computed to better than 2% precision with only a triple-zeta basis set. We also found that the
method is (unexpectedly) good. It is remarkable that, despite several approximations, a simple non-iterative correction can be used to compute the CCSD energy of a Ne atom precise to a few tenths of a millihartree, i.e. much better than 0.1%. With a single Slater-type geminal as a correlation factor, the CCSD valence correlation energy can be computed to better than 2% precision with only a triple-zeta basis set. We also found that the 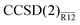 method performed almost identically to the more expensive, iterative CCSD(F12) method of Klopper et al.36–38,41
method performed almost identically to the more expensive, iterative CCSD(F12) method of Klopper et al.36–38,41
Another virtue of the 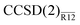 is its technical simplicity: no modification of a standard coupled-cluster program is required and an MP2-R12 energy program has to be changed very little. The computational cost of the second-order energy correction is virtually identical to that of the MP2-R12 energy, the dominant contribution of which scales with the sixth power of the size of the system. Therefore, the presented method can be applied to systems of the same size as the underlying coupled-cluster method. The idea of the presented approach is very general and should be widely applicable, for example, to accurate computation of excited-state energies and properties, or in combination with multireference coupled-cluster methods.
is its technical simplicity: no modification of a standard coupled-cluster program is required and an MP2-R12 energy program has to be changed very little. The computational cost of the second-order energy correction is virtually identical to that of the MP2-R12 energy, the dominant contribution of which scales with the sixth power of the size of the system. Therefore, the presented method can be applied to systems of the same size as the underlying coupled-cluster method. The idea of the presented approach is very general and should be widely applicable, for example, to accurate computation of excited-state energies and properties, or in combination with multireference coupled-cluster methods.
Acknowledgements
I would like to thank Daniel Crawford for helpful discussions and recognize his long-time development of the coupled-cluster codes in PSI3. Acknowledgement is made to the Donors of the American Chemical Society Petroleum Research Fund for partial support of this research via grant 46811-G6.
References
- J. Čížek, J. Chem. Phys., 1966, 45, 4256 CrossRef CAS.
- R. J. Bartlett and J. F. Stanton, Rev. Comput. Chem., 1995, 5, 65 Search PubMed.
- J. Paldus and X. Li, Adv. Chem. Phys., 1999, 110, 1–175 CAS.
- T. D. Crawford and H. F. Schaefer, Rev. Comput. Chem., 2000, 14, 33–136 Search PubMed.
-
T. Helgaker, P. Jørgensen and J. Olsen, Modern Electronic Structure Theory, Wiley, Chichester, 1st edn, 2000 Search PubMed.
- T. L. Gilbert, Rev. Mod. Phys., 1963, 35, 491 CrossRef CAS.
- P. M. Kozlowski and L. Adamowicz, J. Chem. Phys., 1991, 95, 6681–6698 CrossRef CAS.
- W. Kutzelnigg, Theor. Chim. Acta, 1985, 68, 445 CAS.
- W. Kutzelnigg and W. Klopper, J. Chem. Phys., 1991, 94, 1985 CrossRef CAS.
- W. Klopper, F. R. Manby, S. Ten-no and E. F. Valeev, Int. Rev. Phys. Chem., 2006, 25, 427 CrossRef CAS.
- A. J. May, E. Valeev, R. Polly and F. R. Manby, Phys. Chem. Chem. Phys., 2005, 7, 2710–2713 RSC.
- S. Ten-no, Chem. Phys. Lett., 2004, 398, 56–61 CrossRef CAS.
- D. P. Tew and W. Klopper, J. Chem. Phys., 2005, 123, 074101 CrossRef.
- E. F. Valeev, J. Chem. Phys., 2006, 125, 244106 CrossRef.
- H. J. Werner, T. B. Adler and F. R. Manby, J. Chem. Phys., 2007, 126(16), 164102 CrossRef.
- S. Ten-no, J. Chem. Phys., 2007, 126(1), 014108 CrossRef.
- J. A. Pople, M. Head-Gordon, D. J. Fox, K. Raghavachari and L. A. Curtiss, J. Chem. Phys., 1989, 90(10), 5622–5629 CrossRef CAS.
- L. A. Curtiss, K. Raghavachari, G. W. Trucks and J. A. Pople, J. Chem. Phys., 1991, 94(11), 7221–7230 CrossRef CAS.
- L. A. Curtiss and K. Raghavachari, Theor. Chem. Acc., 2002, 108(2), 61–70 CrossRef CAS.
- J. M. L. Martin and G. de Oliveira, J. Chem. Phys., 1999, 111, 1843–1856 CrossRef CAS.
- A. D. Boese, M. Oren, O. Atasoylu, J. M. L. Martin, M. Kallay and J. Gauss, J. Chem. Phys., 2004, 120(9), 4129–4141 CrossRef CAS.
-
W. D. Allen, A. L. L. East and A. G. Császár, in Structures and Conformations of Non-Rigid Molecules, ed. J. Laane, M. Dakkouri, B. van der Vecken and H. Oberhammer, Kluwer, Dordrecht, 1993 Search PubMed.
- A. G. Császár and W. D. Allen, J. Chem. Phys., 1996, 104, 2746 CrossRef CAS.
- N. J. DeYonker, T. R. Cundari and A. K. Wilson, J. Chem. Phys., 2006, 124(11), 114104 CrossRef.
- M. R. Nyden and G. A. Petersson, J. Chem. Phys., 1981, 75(4), 1843–1862 CrossRef CAS.
- G. A. Petersson and M. R. Nyden, J. Chem. Phys., 1981, 75(7), 3423–3425 CrossRef CAS.
- W. Kutzelnigg and J. D. Morgan, J. Chem. Phys., 1992, 96, 4484 CrossRef CAS.
- T. H. Dunning and K. A. Peterson, J. Chem. Phys., 2000, 113(18), 7799–7808 CrossRef CAS.
- G. A. Petersson, A. Bennett, T. G. Tensfeldt, M. A. Allaham, W. A. Shirley and J. Mantzaris, J. Chem. Phys., 1988, 89(4), 2193–2218 CrossRef CAS.
- J. W. Ochterski, G. A. Petersson and J. A. Montgomery, J. Chem. Phys., 1996, 104(7), 2598–2619 CrossRef CAS.
- J. Noga, W. Kutzelnigg and W. Klopper, Chem. Phys. Lett., 1992, 199(5), 497–504 CrossRef CAS.
- J. Noga and W. Kutzelnigg, J. Chem. Phys., 1994, 101, 7738 CrossRef CAS.
-
J. Noga, W. Klopper and W. Kutzelnigg, in Recent Advances in Coupled-Cluster Methods, ed. R. J. Bartlett, World Scientific, Singapore, 1997, p. 1 Search PubMed.
- J. Noga, W. Kutzelnigg, W. Klopper, J. Noga and P. Valiron, Chem. Phys. Lett., 2000, 324(1–3), 166–174 CrossRef CAS.
- J. Noga, P. Valiron and W. Klopper, J. Chem. Phys., 2001, 115(5), 2022–2032 CrossRef CAS.
- H. Fliegl, W. Klopper and C. Hättig, J. Chem. Phys., 2005, 122(8), 084107 CrossRef.
- H. Fliegl, C. Hättig and W. Klopper, Int. J. Quantum Chem., 2006, 106(11), 2306–2317 CrossRef CAS.
- H. Fliegl, C. Hättig and W. Klopper, J. Chem. Phys., 2006, 124(4), 084107.
- O. Christiansen, H. Koch and P. Jørgensen, Chem. Phys. Lett., 1995, 243(5–6), 408–418.
- S. Ten-no, J. Chem. Phys., 2004, 121, 117–129 CrossRef CAS.
- D. P. Tew, W. Klopper, C. Neiss and C. Hättig, Phys. Chem. Chem. Phys., 2007, 9(16), 1921–1930 RSC.
- P.-O. Löwdin, J. Math. Phys., 1962, 3(5), 969 CrossRef.
- J. F. Stanton and J. Gauss, Theor. Chim. Acta, 1996, 93(5), 303–313 CrossRef CAS.
- M. Head-Gordon, R. J. Rico, M. Oumi and T. J. Lee, Chem. Phys. Lett., 1994, 219(1–2), 21–29 CrossRef CAS.
- S. R. Gwaltney and M. Head-Gordon, Chem. Phys. Lett., 2000, 323(1–2), 21–28 CrossRef CAS.
- S. R. Gwaltney and M. Head-Gordon, J. Chem. Phys., 2001, 115(5), 2014–2021 CrossRef CAS.
- J. F. Stanton, Chem. Phys. Lett., 1997, 281(1–3), 130–134 CrossRef CAS.
- T. D. Crawford and J. F. Stanton, Int. J. Quantum Chem., 1998, 70(4–5), 601–611 CrossRef CAS.
- S. A. Kucharski and R. J. Bartlett, J. Chem. Phys., 1998, 108(13), 5243–5254 CrossRef CAS.
- Y. J. Bomble, J. F. Stanton, M. Kállay, J. Gauss, T. D. Crawford and J. F. Stanton, J. Chem. Phys., 1998, 70(4–5), 601–611.
- S. Hirata, M. Nooijen, I. Grabowski and R. J. Bartlett, J. Chem. Phys., 2001, 114(9), 3919–3928 CrossRef CAS.
- S. Hirata, P. D. Fan, A. A. Auer, M. Nooijen and P. Piecuch, J. Chem. Phys., 2004, 121(24), 12197–12207 CrossRef CAS.
- P. R. Surján, A. Szabados and Z. Szekeres, Int. J. Quantum Chem., 2002, 90(4–5), 1309–1320 CrossRef CAS.
- K. Kowalski and P. Piecuch, J. Chem. Phys., 2000, 113(1), 18–35 CrossRef CAS.
- P. Piecuch and M. Włoch, J. Chem. Phys., 2005, 123(22), 224105 CrossRef.
- M. Kállay and J. Gauss, J. Chem. Phys., 2005, 123(21), 214105 CrossRef.
- W. Kutzelnigg, J. Chem. Phys., 1982, 77, 3081 CrossRef CAS.
- P. Dahle, T. Helgaker, D. Jonsson and P. R. Taylor, Phys. Chem. Chem. Phys., 2007, 9(24), 3112–3126 RSC.
- W. Klopper and C. C. M. Samson, J. Chem. Phys., 2002, 116, 6397 CrossRef CAS.
- S. Kedžuch, M. Milko and J. Noga, Int. J. Quantum Chem., 2005, 105, 929–936 CrossRef CAS.
- W. Klopper and J. Almlöf, J. Chem. Phys., 1993, 99, 5167 CrossRef CAS.
- W. Klopper, J. Chem. Phys., 2004, 120(23), 10890–10895 CrossRef CAS.
- F. R. Manby, J. Chem. Phys., 2003, 119, 4607–4613 CrossRef CAS.
- S. Ten-no and F. R. Manby, J. Chem. Phys., 2003, 119, 5358–5363 CrossRef CAS.
- A. Hoy, I. Mills and G. Strey, Mol. Phys., 1972, 24, 1265 CAS.
-
K. P. Huber and G. Herzberg, Molecular Spectra and Molecular Structure. IV. Constants of Diatomic Molecules, Van Nostrand Reinhold, New York, 1979 Search PubMed.
- T. H. Dunning, J. Chem. Phys., 1989, 90, 1007 CrossRef CAS.
- R. A. Kendall, T. H. Dunning and R. J. Harrison, J. Chem. Phys., 1992, 96, 6796 CrossRef CAS.
- E. F. Valeev and H. F. Schaefer, J. Chem. Phys., 2000, 113, 3990 CrossRef CAS.
- V. Weber and C. Daul, Comput. Phys. Commun., 2004, 158, 1–11 CrossRef CAS.
- E. F. Valeev, LIBINT: machine-generated library for efficient evaluation of molecular integrals over Gaussians, http://www.chem.vt.edu/chem-dept/valeev/, 2007.
- E. F. Valeev, Chem. Phys. Lett., 2004, 395(4–6), 190–195 CrossRef CAS.
- C. L. Janssen, I. B. Nielsen, M. L. Leininger, E. F. Valeev and E. T. Seidl, The Massively Parallel Quantum Chemistry Program (MPQC): Version 2.4 (alpha), Sandia National Laboratories, Livermore, CA USA, 2006.
- T. D. Crawford, C. D. Sherrill, E. F. Valeev, J. T. Fermann, R. A. King, M. L. Leininger, S. T. Brown, C. L. Janssen, E. T. Seidl, J. P. Kenny and W. D. Allen, J. Comput. Chem., 2007, 28(9), 1610–1616 CrossRef CAS.
- E. F. Valeev and C. L. Janssen, J. Chem. Phys., 2004, 121(3), 1214–1227 CrossRef CAS.
- J. P. Kenny, C. L. Janssen, E. F. Valeev and T. L. Windus, J. Comput. Chem., 2007 DOI:10.1002/jcc.20815.
- N. J. DeYonker, T. R. Cundari and A. K. Wilson, J. Chem. Phys., 2006, 124(11), 114104 CrossRef.
- W. Klopper, Mol. Phys., 2001, 99, 481 CrossRef CAS.
- D. W. Schwenke, J. Chem. Phys., 2005, 122(1), 014107 CrossRef.
Footnotes |
| † The R12 methods that use nonlinear correlation factors are often called F12 in the literature to distinguish them from the methods with the linear r12 factor. The F12 method is formally identical to the R12 method, and, furthermore, the F12 notation does not uniquely identify the method because the correlation factor must be fully specified. Hence, we use the name “R12” here, except when referring to previously published data. |
| ‡ Werner et al. recently referred to this choice as Ansatz.15 |
| § Λ amplitudes are the standard lambda-amplitudes of the ground-state coupled-cluster theory,2 also known as the Lagrange multipliers in the variational formulation of the coupled-cluster method.5 |
| ¶ Such coupling is zero if the less-efficient Ansatz 159,61 is used. |
|
| This journal is © the Owner Societies 2008 |
Click here to see how this site uses Cookies. View our privacy policy here. 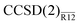 , are on average precise to (1.9, 1.4, 0.5 and 0.1%) when computed with Dunning’s aug-cc-pVXZ basis sets [X = (D, T, Q, 5)] accompanied by a single Slater-type correlation factor. This precision is a roughly an order of magnitude improvement over the standard CCSD method, whose respective average basis-set errors are (28.2, 10.6, 4.4 and 2.1%). Performance of the
, are on average precise to (1.9, 1.4, 0.5 and 0.1%) when computed with Dunning’s aug-cc-pVXZ basis sets [X = (D, T, Q, 5)] accompanied by a single Slater-type correlation factor. This precision is a roughly an order of magnitude improvement over the standard CCSD method, whose respective average basis-set errors are (28.2, 10.6, 4.4 and 2.1%). Performance of the 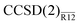 method is almost identical to that of the more complex iterative counterpart, CCSD(R12). The proposed approach to explicitly correlated coupled-cluster methods is technically appealing since no modification of the coupled-cluster equations is necessary and the standard Møller–Plesset R12 machinery can be reused.
method is almost identical to that of the more complex iterative counterpart, CCSD(R12). The proposed approach to explicitly correlated coupled-cluster methods is technically appealing since no modification of the coupled-cluster equations is necessary and the standard Møller–Plesset R12 machinery can be reused.![[H with combining macron]](https://www.rsc.org/images/entities/i_char_0048_0304.gif) = e−
= e−![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) Ĥe
Ĥe![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) . In this work,
. In this work, ![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) will be limited to one- and two-electron excitations:
will be limited to one- and two-electron excitations: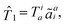
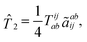
![[H with combining macron]](https://www.rsc.org/images/entities/i_char_0048_0304.gif) will be constructed in a basis that spans a “reference” space P, comprised of Slater determinants up to the same rank as the excitation operator (vacuum 0, singles S, and doubles D), and an “external space”Q, including the explicitly correlated double substitutions Γ:
will be constructed in a basis that spans a “reference” space P, comprised of Slater determinants up to the same rank as the excitation operator (vacuum 0, singles S, and doubles D), and an “external space”Q, including the explicitly correlated double substitutions Γ: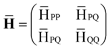
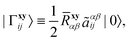
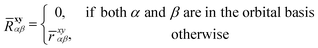
![[H with combining macron]](https://www.rsc.org/images/entities/b_char_0048_0304.gif) PP block is the similarity-transformed Hamiltonian used in the EOM-CCSD method. Its left and right-hand ground-state eigenvectors,
PP block is the similarity-transformed Hamiltonian used in the EOM-CCSD method. Its left and right-hand ground-state eigenvectors, 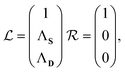
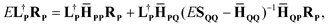
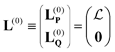
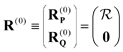
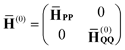
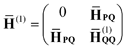
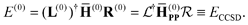
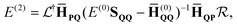
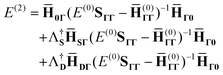
![[H with combining macron]](https://www.rsc.org/images/entities/b_char_0048_0304.gif) (0)ΓΓ. Before doing so, note that the explicitly correlated correction of the MP2-R12 theory can be derived using the same approach if the bare electronic Hamiltonian Ĥ is used in place of
(0)ΓΓ. Before doing so, note that the explicitly correlated correction of the MP2-R12 theory can be derived using the same approach if the bare electronic Hamiltonian Ĥ is used in place of ![[H with combining macron]](https://www.rsc.org/images/entities/i_char_0048_0304.gif) and the “reference” space only includes the vacuum. Then the energy correction has the form of the first term on the right-hand side of eqn (14):
and the “reference” space only includes the vacuum. Then the energy correction has the form of the first term on the right-hand side of eqn (14):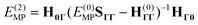
![[F with combining circumflex]](https://www.rsc.org/images/entities/i_char_0046_0302.gif) N in the normal-ordered form. To maximize the resemblance to the MP2-R12 method, we will choose the zeroth-order Hamiltonian as
N in the normal-ordered form. To maximize the resemblance to the MP2-R12 method, we will choose the zeroth-order Hamiltonian as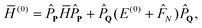
![[F with combining circumflex]](https://www.rsc.org/images/entities/i_char_0046_0302.gif) N. In this formulation the E(0)SΓΓ−
N. In this formulation the E(0)SΓΓ−![[H with combining macron]](https://www.rsc.org/images/entities/b_char_0048_0304.gif) (0)ΓΓ matrix of eqn (14) is independent of T-amplitudes and identical to the E(0)SΓΓ−H(0)ΓΓ matrix of eqn (15). Its evaluation has been discussed elsewhere9,10,15,59,60.
(0)ΓΓ matrix of eqn (14) is independent of T-amplitudes and identical to the E(0)SΓΓ−H(0)ΓΓ matrix of eqn (15). Its evaluation has been discussed elsewhere9,10,15,59,60.
![[H with combining macron]](https://www.rsc.org/images/entities/b_char_0048_0304.gif) 0Γ matrix elements,
0Γ matrix elements,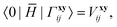
![[H with combining macron]](https://www.rsc.org/images/entities/b_char_0048_0304.gif) Γ0 matrix is more complicated: in addition to the same first-order term identical to
Γ0 matrix is more complicated: in addition to the same first-order term identical to ![[H with combining macron]](https://www.rsc.org/images/entities/b_char_0048_0304.gif) †0Γ, it contains second and higher-order terms:
†0Γ, it contains second and higher-order terms: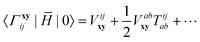
![[H with combining macron]](https://www.rsc.org/images/entities/b_char_0048_0304.gif) Γ0,
Γ0, ![[H with combining macron]](https://www.rsc.org/images/entities/b_char_0048_0304.gif) 0Γ,
0Γ, ![[H with combining macron]](https://www.rsc.org/images/entities/b_char_0048_0304.gif) SΓ and
SΓ and ![[H with combining macron]](https://www.rsc.org/images/entities/b_char_0048_0304.gif) DΓ vanish if the Hartree–Fock basis is used to resolve the identity (such an approach was used in the original R12 method). In this work we will keep only the integrals that do not vanish under such an approximation: namely, the V intermediate of the R12 theory.
DΓ vanish if the Hartree–Fock basis is used to resolve the identity (such an approach was used in the original R12 method). In this work we will keep only the integrals that do not vanish under such an approximation: namely, the V intermediate of the R12 theory.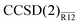 . Its energy correction is extremely simple:
. Its energy correction is extremely simple: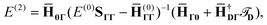
![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) D is a vector of T2 amplitudes. Furthermore, the elements of matrices H0Γ, HΓ0 and HDΓ become, respectively,
D is a vector of T2 amplitudes. Furthermore, the elements of matrices H0Γ, HΓ0 and HDΓ become, respectively,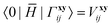
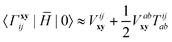
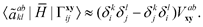
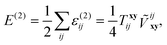
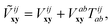
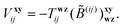
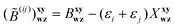
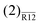 correction is shown in Fig. 1.
correction is shown in Fig. 1.

 correction. The T amplitudes, the two-electron component of the Hamiltonian and the correlation factor are denoted as single lines, dashed lines and double lines respectively.
correction. The T amplitudes, the two-electron component of the Hamiltonian and the correlation factor are denoted as single lines, dashed lines and double lines respectively.![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) [(Lmax + 1)−3] and
[(Lmax + 1)−3] and ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) [(Lmax + 1)−7] asymptotics. The basis-set incompleteness errors plotted in Fig. 2 indeed follow these trends. With every basis set, precision of the
[(Lmax + 1)−7] asymptotics. The basis-set incompleteness errors plotted in Fig. 2 indeed follow these trends. With every basis set, precision of the 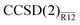 energy is close to that of the MP2-R12 energy. The explicitly correlated energies computed with the largest basis set are at most 0.1 mEh removed from their CBS estimates. We conclude that the approximations introduced in this work do not seem to affect the convergence in the asymptotic regime. However, a more complete study is still warranted.
energy is close to that of the MP2-R12 energy. The explicitly correlated energies computed with the largest basis set are at most 0.1 mEh removed from their CBS estimates. We conclude that the approximations introduced in this work do not seem to affect the convergence in the asymptotic regime. However, a more complete study is still warranted.

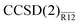 (⊡) energies.
(⊡) energies. .
d MP2-R12 20s14p11d9f7g5h3i energy from ref. 59.
e The CCSD-R12 19s14p8d6f4g3h energy from ref. 78 including the residual basis-set error correction estimated as the difference between the MP2-R12 20s14p11d9f7g5h3i energy from ref. 59 and the MP2-R12 19s14p8d6f4g3h energy from ref. 78.
.
d MP2-R12 20s14p11d9f7g5h3i energy from ref. 59.
e The CCSD-R12 19s14p8d6f4g3h energy from ref. 78 including the residual basis-set error correction estimated as the difference between the MP2-R12 20s14p11d9f7g5h3i energy from ref. 59 and the MP2-R12 19s14p8d6f4g3h energy from ref. 78.
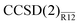 method.
method.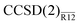 methods (the double-zeta energies are, in all likelihood, artificially precise because of the fortuitous effect of assuming the extended Brillouin condition). With the largest, sextuple-zeta basis set, the MP2-R12 and
methods (the double-zeta energies are, in all likelihood, artificially precise because of the fortuitous effect of assuming the extended Brillouin condition). With the largest, sextuple-zeta basis set, the MP2-R12 and 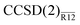 energies are within a few tenths of a millihartree of the CBS-limit estimates. As with the r12 results in Table 1, the T-dependent contribution to the BSIE is also unequivocally important here.
energies are within a few tenths of a millihartree of the CBS-limit estimates. As with the r12 results in Table 1, the T-dependent contribution to the BSIE is also unequivocally important here. .
c MP2-R12 20s14p11d9f7g5h3i energy from ref. 59.
d The CCSD-R12 19s14p8d6f4g3h energy from ref. 78 including the residual basis-set error correction estimated as the difference between the MP2-R12 20s14p11d9f7g5h3i energy from ref. 59 and the MP2-R12 19s14p8d6f4g3h energy from ref. 78.
.
c MP2-R12 20s14p11d9f7g5h3i energy from ref. 59.
d The CCSD-R12 19s14p8d6f4g3h energy from ref. 78 including the residual basis-set error correction estimated as the difference between the MP2-R12 20s14p11d9f7g5h3i energy from ref. 59 and the MP2-R12 19s14p8d6f4g3h energy from ref. 78.
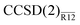 energies to those obtained with the CCSD(F12) method of Klopper et al.41 Although the latter values were evaluated at geometries different from ours, the apparent differences in the CBS limits are small. We found that the
energies to those obtained with the CCSD(F12) method of Klopper et al.41 Although the latter values were evaluated at geometries different from ours, the apparent differences in the CBS limits are small. We found that the 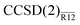 and CCSD(F12) methods perform almost identically to each other unless the aug-cc-pVDZ basis is used. The likely issue with the latter is, again, the assumption of EBC in our method. Assuming EBC has little effect on the explicitly correlated energies for larger basis sets, the two methods can be compared directly. Even disregarding the geometrical differences, the
and CCSD(F12) methods perform almost identically to each other unless the aug-cc-pVDZ basis is used. The likely issue with the latter is, again, the assumption of EBC in our method. Assuming EBC has little effect on the explicitly correlated energies for larger basis sets, the two methods can be compared directly. Even disregarding the geometrical differences, the 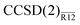 and CCSD(F12) energies differ by less than 0.6 mEh for H2O and less than 1.6 mEh for F2. If we subtract the difference in the CBS limit, the two methods agree to within 0.2 and 0.5 mEh respectively. Although the CCSD(F12) method couples the standard and explicitly correlated amplitudes iteratively, it appears that this coupling is very weak and can be confidently treated using our perturbative approach.
and CCSD(F12) energies differ by less than 0.6 mEh for H2O and less than 1.6 mEh for F2. If we subtract the difference in the CBS limit, the two methods agree to within 0.2 and 0.5 mEh respectively. Although the CCSD(F12) method couples the standard and explicitly correlated amplitudes iteratively, it appears that this coupling is very weak and can be confidently treated using our perturbative approach.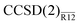 values were obtained with the exp(−1.5r12) correlation factor
values were obtained with the exp(−1.5r12) correlation factor
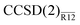 values were obtained with the exp(−1.5r12) correlation factor
values were obtained with the exp(−1.5r12) correlation factor
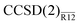 , with several additional approximations that maximally truncated the working equations without apparent negative impact. In the future we will test these approximations in more detail as well as explore various partitioning of the similarity-transformed Hamiltonian.
, with several additional approximations that maximally truncated the working equations without apparent negative impact. In the future we will test these approximations in more detail as well as explore various partitioning of the similarity-transformed Hamiltonian.
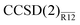 method is simply the R12 correction of the MP2-R12 method and does not depend on the coupled-cluster amplitudes (hence it is the same for any CC method). The next-order term includes coupled-cluster amplitudes linearly and makes the correction dependent on the particular coupled-cluster method used. This term is responsible for the interference effects25,26 and its effect is to lower the magnitude of the correction compared to the MP2-R12 method, in accordance with the usual experience.
method is simply the R12 correction of the MP2-R12 method and does not depend on the coupled-cluster amplitudes (hence it is the same for any CC method). The next-order term includes coupled-cluster amplitudes linearly and makes the correction dependent on the particular coupled-cluster method used. This term is responsible for the interference effects25,26 and its effect is to lower the magnitude of the correction compared to the MP2-R12 method, in accordance with the usual experience.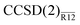 method is (unexpectedly) good. It is remarkable that, despite several approximations, a simple non-iterative correction can be used to compute the CCSD energy of a Ne atom precise to a few tenths of a millihartree, i.e. much better than 0.1%. With a single Slater-type geminal as a correlation factor, the CCSD valence correlation energy can be computed to better than 2% precision with only a triple-zeta basis set. We also found that the
method is (unexpectedly) good. It is remarkable that, despite several approximations, a simple non-iterative correction can be used to compute the CCSD energy of a Ne atom precise to a few tenths of a millihartree, i.e. much better than 0.1%. With a single Slater-type geminal as a correlation factor, the CCSD valence correlation energy can be computed to better than 2% precision with only a triple-zeta basis set. We also found that the 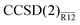 method performed almost identically to the more expensive, iterative CCSD(F12) method of Klopper et al.36–38,41
method performed almost identically to the more expensive, iterative CCSD(F12) method of Klopper et al.36–38,41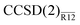 is its technical simplicity: no modification of a standard coupled-cluster program is required and an MP2-R12 energy program has to be changed very little. The computational cost of the second-order energy correction is virtually identical to that of the MP2-R12 energy, the dominant contribution of which scales with the sixth power of the size of the system. Therefore, the presented method can be applied to systems of the same size as the underlying coupled-cluster method. The idea of the presented approach is very general and should be widely applicable, for example, to accurate computation of excited-state energies and properties, or in combination with multireference coupled-cluster methods.
is its technical simplicity: no modification of a standard coupled-cluster program is required and an MP2-R12 energy program has to be changed very little. The computational cost of the second-order energy correction is virtually identical to that of the MP2-R12 energy, the dominant contribution of which scales with the sixth power of the size of the system. Therefore, the presented method can be applied to systems of the same size as the underlying coupled-cluster method. The idea of the presented approach is very general and should be widely applicable, for example, to accurate computation of excited-state energies and properties, or in combination with multireference coupled-cluster methods.



