Themed collection Real-space numerical grid methods in quantum chemistry

Real-space numerical grid methods in quantum chemistry
This themed issue reports on recent progress in the fast developing field of real-space numerical grid methods in quantum chemistry.
Phys. Chem. Chem. Phys., 2015,17, 31357-31359
https://doi.org/10.1039/C5CP90198G
Magnetic properties with multiwavelets and DFT: the complete basis set limit achieved
Multiwavelets are emerging as an attractive alternative to traditional basis sets such as Gaussian-type orbitals and plane waves.
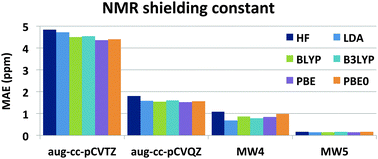
Phys. Chem. Chem. Phys., 2016,18, 21145-21161
https://doi.org/10.1039/C6CP01294A
Multipole-preserving quadratures for the discretization of functions in real-space electronic structure calculations
Discretizing an analytic function on a uniform real-space grid is often done via a straightforward collocation method.
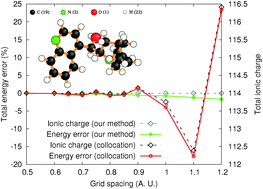
Phys. Chem. Chem. Phys., 2015,17, 31582-31591
https://doi.org/10.1039/C5CP01236H
Wavelet formulation of the polarizable continuum model. II. Use of piecewise bilinear boundary elements
The sparsity pattern obtained in the wavelet Galerkin boundary element representation of the PCM boundary integral operators. By employing a wavelet basis on a smooth solvent-excluded molecular surface the method is able to guarantee solutions with high accuracy at a linear cost in memory and computational time.
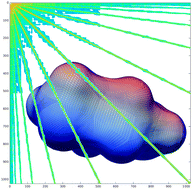
Phys. Chem. Chem. Phys., 2015,17, 31566-31581
https://doi.org/10.1039/C5CP03410H
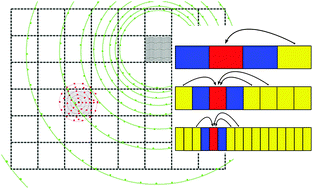
An auxilliary grid method for the calculation of electrostatic terms in density functional theory on a real-space grid
The calculation of electrostatic integrals is performed using domain decomposition and auxiliary non-uniform grids for density functional theory real-space implementation.
Phys. Chem. Chem. Phys., 2015,17, 31550-31557
https://doi.org/10.1039/C5CP01090J
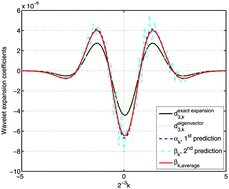
An economic prediction of the finer resolution level wavelet coefficients in electronic structure calculations
A highly economic prediction method for fine resolution wavelet coefficients of wave functions and energy expectation values is presented.
Phys. Chem. Chem. Phys., 2015,17, 31558-31565
https://doi.org/10.1039/C5CP01214G
High order forces and nonlocal operators in a Kohn–Sham Hamiltonian
Real space pseudopotentials have a number of advantages in solving for the electronic structure of materials.
Phys. Chem. Chem. Phys., 2015,17, 31542-31549
https://doi.org/10.1039/C5CP02561C
Singular analysis and coupled cluster theory
The primary motivation for systematic bases in first principles electronic structure simulations is to derive physical and chemical properties of molecules and solids with predetermined accuracy. This requires, however, a detailed asymptotic analysis of singularities.

Phys. Chem. Chem. Phys., 2015,17, 31530-31541
https://doi.org/10.1039/C5CP01183C
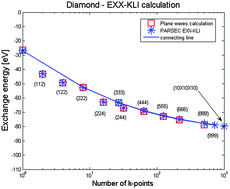
Fock-exchange for periodic structures in the real-space formalism and the KLI approximation
The calculation of Fock-exchange interaction is an important task in the computation of molecule and solid properties.
Phys. Chem. Chem. Phys., 2015,17, 31510-31515
https://doi.org/10.1039/C5CP01093D
Tensor numerical methods in quantum chemistry: from Hartree–Fock to excitation energies
We resume the recent successes of the grid-based tensor numerical methods and discuss their prospects in real-space electronic structure calculations.
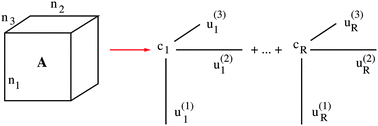
Phys. Chem. Chem. Phys., 2015,17, 31491-31509
https://doi.org/10.1039/C5CP01215E
Orbital free DFT versus single density equation: a perspective through quantum domain behavior of a classically chaotic system
Regular to chaotic transition takes place in a driven van der Pol oscillator in both classical and quantum domains.
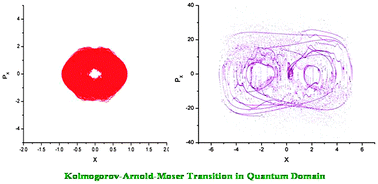
Phys. Chem. Chem. Phys., 2015,17, 31516-31529
https://doi.org/10.1039/C5CP00995B
The grid-based fast multipole method – a massively parallel numerical scheme for calculating two-electron interaction energies
A grid-based fast multipole method has been developed for calculating two-electron interaction energies for non-overlapping charge densities.
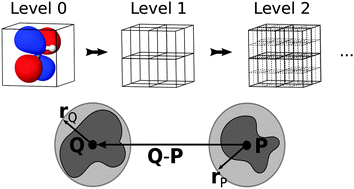
Phys. Chem. Chem. Phys., 2015,17, 31480-31490
https://doi.org/10.1039/C5CP01173F
A real-space stochastic density matrix approach for density functional electronic structure
A novel stochastic approach aimed at solving for the ground-state one-particle density matrix in density functional theory is developed.
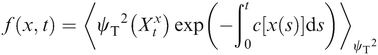
Phys. Chem. Chem. Phys., 2015,17, 31472-31479
https://doi.org/10.1039/C5CP01222H
Optimizing a parametrized Thomas–Fermi–Dirac–Weizsäcker density functional for atoms
A systematic study of the parameter space of a kinetic functional is used as a route to understand the transferability problems and improve the kinetic density functionals.

Phys. Chem. Chem. Phys., 2015,17, 31463-31471
https://doi.org/10.1039/C5CP01211B
Accurate and efficient linear scaling DFT calculations with universal applicability
Density functional theory calculations are computationally extremely expensive for systems containing many atoms due to their intrinsic cubic scaling.
Phys. Chem. Chem. Phys., 2015,17, 31360-31370
https://doi.org/10.1039/C5CP00437C
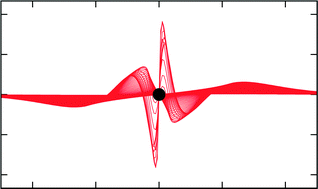
Numerically accurate linear response-properties in the configuration-interaction singles (CIS) approximation
The spatial extent of the singlet 21B3u excitation of the ethylene molecule. The depicted box is 50 bohr wide.
Phys. Chem. Chem. Phys., 2015,17, 31453-31462
https://doi.org/10.1039/C5CP00345H
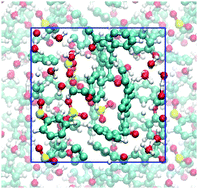
An adaptive finite-element method for large-scale ab initio molecular dynamics simulations
A snapshot of ab initio molecular dynamics simulations for a polymer electrolyte membrane at low hydration.
Phys. Chem. Chem. Phys., 2015,17, 31444-31452
https://doi.org/10.1039/C5CP00320B
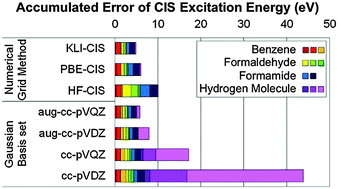
Configuration interaction singles based on the real-space numerical grid method: Kohn–Sham versus Hartree–Fock orbitals
We developed a program code of CIS based on a numerical grid method and showed that Kohn–Sham orbitals from the Krieger–Li–Iafrate (KLI) approximation provide better reference configurations for CIS than the standard Hartree–Fock and Kohn–Sham orbitals.
Phys. Chem. Chem. Phys., 2015,17, 31434-31443
https://doi.org/10.1039/C5CP00352K
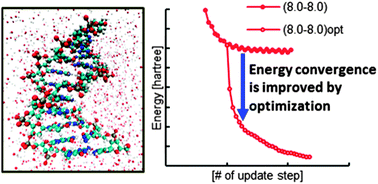
Optimized multi-site local orbitals in the large-scale DFT program CONQUEST
Newly introduced numerical optimization of multi-site support functions in the linear-scaling DFT code CONQUEST improves the accuracy and stability of the support functions with small cutoffs.
Phys. Chem. Chem. Phys., 2015,17, 31427-31433
https://doi.org/10.1039/C5CP00934K
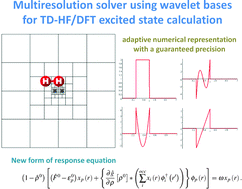
Multiresolution quantum chemistry in multiwavelet bases: excited states from time-dependent Hartree–Fock and density functional theory via linear response
A fully numerical method for the time-dependent Hartree–Fock and density functional theory (TD-HF/DFT) with the Tamm–Dancoff (TD) approximation is presented in a multiresolution analysis (MRA) approach.
Phys. Chem. Chem. Phys., 2015,17, 31405-31416
https://doi.org/10.1039/C4CP05821F
Confined helium on Lagrange meshes
The Lagrange-mesh method has the simplicity of a calculation on a mesh and can have the accuracy of a variational method.
Phys. Chem. Chem. Phys., 2015,17, 31417-31426
https://doi.org/10.1039/C5CP00110B
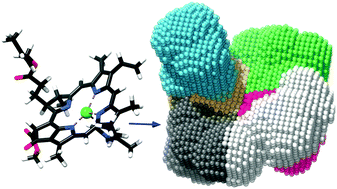
Real-space grids and the Octopus code as tools for the development of new simulation approaches for electronic systems
We explore how strategies to simulate various phenomena of electronic systems have been implemented in the Octopus code, using the versatility and performance of real-space grids.
Phys. Chem. Chem. Phys., 2015,17, 31371-31396
https://doi.org/10.1039/C5CP00351B
Edge reconstruction in armchair phosphorene nanoribbons revealed by discontinuous Galerkin density functional theory
We use DGDFT based AIMD calculations to reveal that a 2 × 1 edge reconstruction appears in ACPNRs at room temperature.
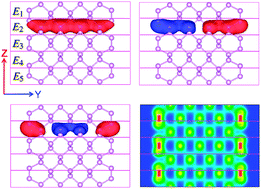
Phys. Chem. Chem. Phys., 2015,17, 31397-31404
https://doi.org/10.1039/C5CP00333D
About this collection
In recent years, real-space numerical methods have attracted attention as they are mathematically robust, very accurate and well suited for modern, massively parallel computing resources. However such methods are still not a mainstream activity in quantum chemistry: on the one hand their current computational overhead and memory footprint need improvement; on the other hand the scientific community lacks widely available software with standard features such as computation of molecular structures, solvent effects and electric and magnetic properties to a high order. These challenges can be overcome only by gathering scientific expertise from numerical mathematics, computer science, quantum physics, quantum chemistry, and material science.
The aim of this themed issue is to gather research contributions from leading scientists in the field and draw attention to this challenging yet very promising field. The guest editors for this themed issue are Luca Frediani (The Arctic University of Norway) and Dage Sundholm (University of Helsinki).