Acoustic resonance in periodically sheared glass: damping due to plastic events

Abstract

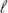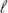Using molecular dynamics simulation, we study acoustic resonance in a low-temperature model glass by applying a small periodic shear at a boundary wall. Shear wave resonance occurs as the frequency ω approaches ω = πc_⊥/L (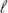 = 1, 2…). Here, c_⊥ is the transverse sound speed and L is the cell width. At resonance, large-amplitude sound waves appear after many cycles even if the applied strain γ₀ is very small. They then induce plastic events, which are heterogeneous on the mesoscopic scale and intermittent on timescales longer than the oscillation period t_p = 2π/ω. We visualize them together with the extended elastic strains around them. These plastic events serve to damp sounds. We obtain the nonlinear damping Q⁻¹ = tan δ due to the plastic events near the first resonance at ω ≅ ω₁, which is linear in γ₀ and independent of ω. After many resonant cycles, we observe an increase in the shear modulus (measured after switching-off the oscillation). We also observe catastrophic plastic events after a very long time (∼10³t_p), which induce system-size elastic strains and cause a transition from resonant to off-resonant states. At resonance, stroboscopic diffusion becomes detectable.