A cluster size distribution theory to study the thermodynamics and phase behavior of multi-bonding single site solutes in patchy colloidal mixtures

Abstract

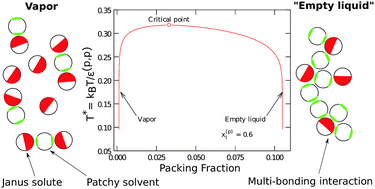
We study binary mixtures of multi-bonding single site solute particles in a solvent comprising patchy colloid particles. The particles in the mixture interact by very short-ranged attraction and hard-sphere repulsion. The attractive patch on the solute can bond with multiple solvent particles, whereas the patch on the solvent is restricted to bond only once. From a quasi-chemical analysis of association, in the hard-sphere reference we develop an accurate multi-body correlation information for the distribution of solvent particles over the patch region of the solute. We use this information within Wertheim's multi-density formalism to develop a cluster size distribution theory that is capable of capturing the physics of multi-body association for any geometry of association sites on the solute. We use this general framework to study a mixture containing Janus solutes and one- or two-patch solvent particles over a range of concentration of the solute and association strengths. We find that a mixture of two-patch solvent (with both patches of the same kind) and multi-bonding solutes with different patch geometries can have a vapor–liquid equilibrium, although the pure components themselves cannot phase separate. The liquid state occurs at very low densities, forming a so-called empty liquid. For the relative association strengths studied in this work, we observe that the vapor–liquid coexistence curve broadens as the concentration of the patchy solvent particles in the liquid phase is increased. The pressure-composition phase equilibrium curves show negative azeotropes for these mixtures. We also observe that, for these mixtures, as the size of the patch on the solute particles is decreased, the critical temperature and the critical packing fraction decreases.