Diffusive escape through a narrow opening: new insights into a classic problem

Abstract

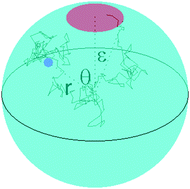
We study the mean first exit time (T_ε) of a particle diffusing in a circular or a spherical micro-domain with an impenetrable confining boundary containing a small escape window (EW) of an angular size ε. Focusing on the effects of an energy/entropy barrier at the EW, and of the long-range interactions (LRIs) with the boundary on the diffusive search for the EW, we develop a self-consistent approximation to derive for T_ε a general expression, akin to the celebrated Collins–Kimball relation in chemical kinetics and accounting for both rate-controlling factors in an explicit way. Our analysis reveals that the barrier-induced contribution to T_ε is the dominant one in the limit ε → 0, implying that the narrow escape problem is not “diffusion-limited” but rather “barrier-limited”. We present the small-ε expansion for T_ε, in which the coefficients in front of the leading terms are expressed via some integrals and derivatives of the LRI potential. Considering a triangular-well potential as an example, we show that T_ε is non-monotonic with respect to the extent of the attractive LRI, being minimal for the ones having an intermediate extent, neither too concentrated on the boundary nor penetrating too deeply into the bulk. Our analytical predictions are in good agreement with the numerical simulations.