Surface tension regularizes the crack singularity of adhesion
Abstract
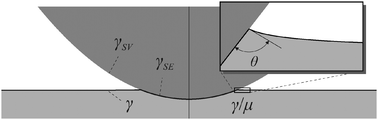
The elastic and adhesive properties of a solid surface can be quantified by indenting it with a rigid sphere. Indentation tests are classically described by the JKR-law when the solid is very stiff, while recent work highlights the importance of surface tension for exceedingly soft materials. Here we show that surface tension plays a crucial role even in stiff solids: Young's wetting angle emerges as a boundary condition and this regularizes the crack-like singularity at the edge of adhesive contacts. We find that the edge region exhibits a universal, self-similar structure that emerges from the balance of surface tension and elasticity. The similarity theory is solved analytically and provides a complete description of adhesive contacts, by which we reconcile global adhesion laws and local contact mechanics.

 Please wait while we load your content...
Please wait while we load your content...