The magnetocaloric effect with critical behavior of a periodic Anderson-like organic polymer

Abstract

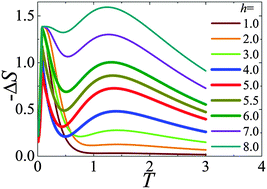
We study the magnetocaloric effect and the critical behavior of a periodic Anderson-like organic polymer using Green's function theory, in which the localized f orbitals hybridize with the conduction orbitals at even sites. The field-induced metal–insulator transitions with the magnetic Grüneisen parameter showing |Γ_h| ∼ T⁻¹ power-law critical behaviour are revealed, which provides a new thermodynamic means for probing quantum phase transitions. It is found that the competition of up-spin and down-spin hole excitations is responsible for the double peak structure of magnetic entropy change (−ΔS) for the dominant Kondo coupling case, implying a double magnetic cooling process via demagnetization, which follows a power law dependence of the magnetic field h: −ΔS ∼ hⁿ. The local exponent n tends to 1 and 2 below and above T_C, while has a minimum of 0.648 at T_C, which is in accordance with the experimental observation of perovskite manganites Pr_0.55Sr_0.45MnO₃ and Nd_0.55Sr_0.45MnO₃ (J. Y. Fan et al., Appl. Phys. Lett., 2011, 98, 072508; Europhys. Lett., 2015, 112, 17005) corresponding to the conventional ferromagnets within the mean field theory −ΔS ∼ h^2/3. At T_C, the −ΔS ∼ h curves with a convex curvature superpose each other for small V values, which are separated by the large V case, distinguishing the RKKY interaction and Kondo coupling explicitly. Furthermore, the critical scaling law n(T_C) = 1 + (β − 1)/(β + γ) = 1 + 1/δ(1 − 1/β) is related to the critical exponents (β, γ, and δ) extracted from the Arrott–Noakes equation of state and the Kouvel–Fisher method, which fulfill the Widom scaling relation δ = 1 + γβ⁻¹, indicating the self-consistency and reliability of the obtained results. In addition, based on the scaling hypothesis through checking the scaling analysis of magnetization, the M–T–h curves collapse into two independent universal branches below and above T_C.