Dynamics of suspensions of hydrodynamically structured particles: analytic theory and applications to experiments

Abstract

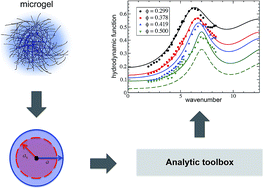
We present an easy-to-use analytic toolbox for the calculation of short-time transport properties of concentrated suspensions of spherical colloidal particles with internal hydrodynamic structure, and direct interactions described by a hard-core or soft Hertz pair potential. The considered dynamic properties include self-diffusion and sedimentation coefficients, the wavenumber-dependent diffusion function determined in dynamic scattering experiments, and the high-frequency shear viscosity. The toolbox is based on the hydrodynamic radius model (HRM) wherein the internal particle structure is mapped on a hydrodynamic radius parameter for unchanged direct interactions, and on an existing simulation data base for solvent-permeable and spherical annulus particles. Useful scaling relations for the diffusion function and self-diffusion coefficient, known to be valid for hard-core interaction, are shown to apply also for soft pair potentials. We further discuss extensions of the toolbox to long-time transport properties including the low-shear zero-frequency viscosity and the long-time self-diffusion coefficient. The versatility of the toolbox is demonstrated by the analysis of a previous light scattering study of suspensions of non-ionic PNiPAM microgels [Eckert et al., J. Chem. Phys., 2008, 129, 124902] in which a detailed theoretical analysis of the dynamic data was left as an open task. By the comparison with Hertz potential based calculations, we show that the experimental data are consistently and accurately described using the Verlet–Weis corrected Percus–Yevick structure factor as input, and for a solvent penetration length equal to three percent of the excluded volume radius. This small amount of solvent permeability of the microgel particles has a significant dynamic effect at larger concentrations.