Connecting local active forces to macroscopic stress in elastic media

Abstract

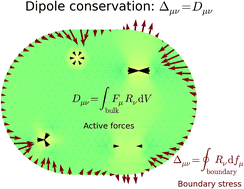
In contrast with ordinary materials, living matter drives its own motion by generating active, out-of-equilibrium internal stresses. These stresses typically originate from localized active elements embedded in an elastic medium, such as molecular motors inside the cell or contractile cells in a tissue. While many large-scale phenomenological theories of such active media have been developed, a systematic understanding of the emergence of stress from the local force-generating elements is lacking. In this paper, we present a rigorous theoretical framework to study this relationship. We show that the medium's macroscopic active stress tensor is equal to the active elements' force dipole tensor per unit volume in both continuum and discrete linear homogeneous media of arbitrary geometries. This relationship is conserved on average in the presence of disorder, but can be violated in nonlinear elastic media. Such effects can lead to either a reinforcement or an attenuation of the active stresses, giving us a glimpse of the ways in which nature might harness microscopic forces to create active materials.