Exactly solvable approximating models for Rabi Hamiltonian dynamics

Abstract

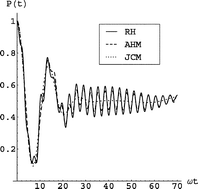
The interaction between an atom and a one mode external driving field is an ubiquitous problem in many branches of physics and is often modeled using the Rabi Hamiltonian. In this paper we present a series of analytically solvable Hamiltonians that approximate the Rabi Hamiltonian and compare our results to the Jaynes–Cummings model which neglects the so-called counter-rotating term in the Rabi Hamiltonian. Through a unitary transformation that diagonalizes the Jaynes–Cummings model, we transform the counter-rotating term into separate terms representing several different physical processes. By keeping only certain terms, we can achieve an excellent approximation to the exact dynamics within specified parameter ranges.