Do hydrodynamic interactions affect the swim pressure?
Abstract
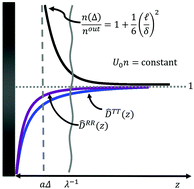
We study the motion of a spherical active Brownian particle (ABP) of size a, moving with a fixed speed U0, and reorienting on a time scale τR in the presence of a confining boundary. Because momentum is conserved in the embedding fluid, we show that the average force per unit area on the boundary equals the bulk mechanical pressure P∞ = p∞f + Π∞, where p∞f is the fluid pressure and Π∞ is the particle pressure; this is true for active and passive particles alike regardless of how the particles interact with the boundary. As an example, we investigate how hydrodynamic interactions (HI) change the particle-phase pressure at the wall, and find that Πwall = n∞(kBT + ζ(Δ)U0 (Δ)/6), where ζ is the (Stokes) drag on the swimmer,
(Δ)/6), where ζ is the (Stokes) drag on the swimmer,  = U0τR is the run length, and Δ is the minimum gap size between the particle and the wall; as Δ → ∞ this is the familiar swim pressure [Takatori et al., Phys. Rev. Lett., 2014, 113, 1–5].
= U0τR is the run length, and Δ is the minimum gap size between the particle and the wall; as Δ → ∞ this is the familiar swim pressure [Takatori et al., Phys. Rev. Lett., 2014, 113, 1–5].


 Please wait while we load your content...
Please wait while we load your content...