Effects of surface roughness on the self-diffusion dynamics of a single polymer
Abstract
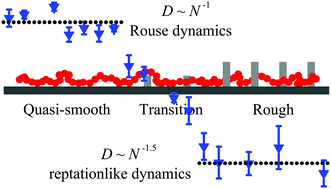
We employ molecular dynamics simulations to simulate the diffusion dynamics of a single polymer adsorbed on surfaces with different roughnesses, which are characterized by the separation distance between obstacles and the height of obstacles. Our simulations demonstrate that for strong adsorption and when the confinement of obstacles is strong enough for all chains, the scaling exponent α of the diffusion coefficient on the chain length exhibits three cases with increase of the height of obstacles: a Rouse plateau with α ≈ −1 (the lateral motion of the polymer chains is free), a reptationlike plateau with α ≈ −1.5 (the polymer chains can hardly stride over the obstacles in the perpendicular direction) and a transition from the Rouse plateau to the reptationlike plateau with −1.5 < α < −1 (the obstacles hinder the lateral motion of the polymer chains). However, with increase of the separation distance between obstacles, the confinement from the obstacles exhibits a decrease (more lateral motions of the polymer chains are allowed), which results in a higher plateau (no longer separate reptationlike dynamics). Our results clarify the effects of surface roughness on the diffusion mechanism of polymer chains strongly adsorbed on solid surfaces in dilute solutions and the resulting transition mechanism from the Rouse scaling to the reptationlike scaling, which is significant for the understanding of the physical nature and the development of the corresponding applications.


 Please wait while we load your content...
Please wait while we load your content...