Dynamics of networks in a viscoelastic and active environment

Abstract

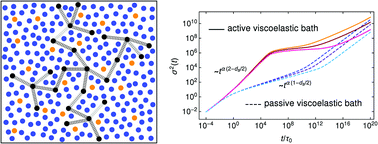
We investigate the dynamics of fractals and other networks in a viscoelastic and active environment. The viscoelastic dynamics is modeled based on the generalized Langevin equation, where the activity is introduced to it by means of the exponentially correlated noise. The intramolecular interactions are taken into account by the bead–spring picture. The microscopic connectivity (studied in the form of Vicsek fractals, of dual Sierpiński gaskets, of NT_D trees, and of a family of deterministic small-world networks) reveals itself in the multiscale monomeric dynamics, which shows vastly different behaviors in the active and passive baths. In particular, the dynamics under active forces leads to a swelling that is characterized through power laws which are not present in the passive case. In all cases, the dynamics reflects the broad scaling behavior of the density of states and not necessarily the maximal relaxation time of the structures in a passive bath, as it is exemplified on the NT_D trees.