Universal behaviour of the glass and the jamming transitions in finite dimensions for hard spheres
Abstract
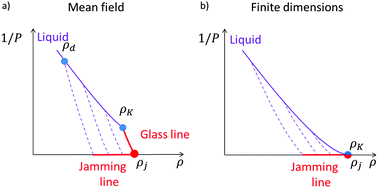
We investigate the glass and the jamming transitions of hard spheres in finite dimensions d, through a revised cell theory, that combines the free volume and the Random First Order Theory (RFOT). Recent results show that in infinite dimension the ideal glass transition and jamming transitions are distinct, while based on our theory we argue that they indeed coincide for finite d. As a consequence, jamming results into a percolation transition described by RFOT, with a static length diverging with exponent ν = 2/d, which we verify through finite size scaling, and standard critical exponents α = 0, β = 0 and γ = 2 independent on d.


 Please wait while we load your content...
Please wait while we load your content...